Mit der Monte-Carlo-Methode Handelsstrategien optimieren

Inhalt

• Allgemeine Theorie
• Wahrscheinlichkeitsmodell des EAs
• Anwenden der Theorie
• Stabilität des Gewinns auf zufällige Veränderungen
• Die Stabilität des Profits im Vergleich zum Drawdown
• Stabilität der Gewinnverteilung gegenüber Preisschwankungen
• Schlussfolgerung
• Angehängte Dateien
  

Allgemeine Theorie

Die Idee jenseits der Monte-Carlo-Methode kann analog beschrieben werden - es ist eine wissenschaftliche Erkenntnismethode. Andere Beispiele sind die optisch-mechanische Analogie von Hamilton oder ähnliche Parallelen in der Biologie.

Wenn wir zwei Objekte haben, die durch die gleiche Theorie beschrieben werden können, dann ist das Wissen aus dem Studium des einen auf das andere übertragbar. Diese Methode ist sehr nützlich, wenn das ein Objekt viel einfacher zu studieren ist als das andere. Das leichter zugängliche Objekt wird als Modell eines anderen betrachtet. Die Methode selbst heißt Modellierung. Je nach Kontext ist es ein Modell eines der beiden Objekte oder es ist eine gemeinsame Theorie.

Manchmal missverstehen Forscher die Ergebnisse der Modellierung. Wenn wir einige explizite Beispiele betrachten, wie das Strömungsverhalten einer verkleinerten Kopie eines Flugzeugs in einem Windkanal, scheint alles offensichtlich. Wenn Objekte jedoch nicht verwandt sind und auf den ersten Blick nicht gleich aussehen, scheinen die Schlussfolgerungen manchmal eine Art Trick zu sein oder dienen als Grundlage für unvernünftige, aber weitreichende Verallgemeinerungen. Die gängige Theorie für Objekte beschreibt nur grob einige ihrer Aspekte. Je geringer die geforderte Genauigkeit der Objektbeschreibung, desto breiter ist die Menge der Objekte, die sich an eine Theorie halten. Beispielsweise ist die optisch-mechanische Analogie von Hamilton nur dann exakt erfüllt, wenn die Länge einer Lichtwelle gegen Null tendiert. In Wirklichkeit ist diese Analogie nur für eine kleine, aber immer endliche Länge annähernd gerechtfertigt. Da jedes theoretische Modell einfach genug sein sollte, um als Grundlage für Berechnungen und Schlussfolgerungen zu dienen, wird es immer zu stark vereinfacht.

Lassen Sie uns nun das Konzept der Monte-Carlo-Methode klären. Dies ist ein Ansatz zur Modellierung von Objekten, deren Theorie einen probabilistischen (stochastischen) Charakter hat. Das Modell ist ein Computerprogramm mit einem nach dieser Theorie konstruierten Algorithmus. Es verwendet Pseudozufallszahlengeneratoren, um die notwendigen Zufallsvariablen (Zufallsprozesse) mit den gewünschten Verteilungen zu simulieren.

Es lohnt sich zu betonen (obwohl es für uns hier keine Rolle spielt), dass die Natur eines untersuchten Objekts sowohl probabilistisch als auch deterministisch sein kann. Das Vorhandensein einer Theorie mit probabilistischem Charakter ist für uns hier von Bedeutung. Zum Beispiel wird die Monte-Carlo-Methode verwendet, um gewöhnliche Integrale näherungsweise zu berechnen. Dies ist möglich, da ein solches Integral als mathematische Erwartung einer Zufallsvariablen angesehen werden kann.

Das erste Beispiel für die Anwendung der Monte-Carlo-Methode wird normalerweise als Lösung des Problems der Buffonschen Nadel betrachtet, bei dem die Zahl pi durch zufälliges Werfen einer Nadel auf einen Tisch bestimmt wird. Der Name der Methode erschien viel später, in der Mitte des XX Jahrhunderts. Schließlich sind Glücksspiele - zum Beispiel ein Roulette - Zufallszahlengeneratoren. Ein bewusster Verweis auf Glücksspiele weist zudem auf die Ursprünge der Wahrscheinlichkeitstheorie hin, die mit Berechnungen zum Würfeln und Kartenspielen begann.

Der Algorithmus des Modellierungsprogramms ist einfach, was einer der Gründe für die Verbreitung der Methode ist. Der Algorithmus enthält mehrere zufällig generierte Varianten (Stichproben) eines untersuchten Objektzustands mit der der Theorie entsprechenden Verteilung. Für jedes dieser Merkmale wird eine erforderliche Menge von Merkmalen berechnet. Als Ergebnis erhalten wir eine große Stichprobe. Während wir nur einen Reihe von Merkmalen für das untersuchte Objekt haben, erlaubt uns die Monte-Carlo-Methode, sie in großer Zahl zu erhalten und ihre Verteilungsfunktionen zu konstruieren, was uns mehr Daten liefert.

Die oben beschriebene Struktur des allgemeinen Monte-Carlo-Modells erscheint einfach. Es entstehen jedoch mehrere und manchmal recht komplexe Varianten, wenn man versucht, sie zu implementieren. Selbst wenn wir unsere Anwendung auf die Finanzierung beschränken, können wir immer noch sehen, wie umfangreich sie ist, zum Beispiel in diesem Buch. Wir werden die Monte-Carlo-Methode anzuwenden, um die Stabilität eines Expert Advisors zu untersuchen. Um dies zu erreichen, brauchen wir ein probabilistisches Modell, das dessen Arbeitsweise beschreibt.

Wahrscheinlichkeitsmodell des EAs

Bevor wir den echten Handel mit einem EA starten, testen und optimieren wir ihn in der Regel in der Kurshistorie. Aber warum glauben wir, dass die Handelsergebnisse der Vergangenheit ihre Ergebnisse in der Zukunft beeinflussen? Natürlich erwarten wir nicht, dass alle Transaktionen in der Zukunft die gleiche Reihenfolge wie in der Vergangenheit bilden. Obwohl wir immer noch eine Vermutung über ihre "Ähnlichkeit" haben. Lassen Sie uns diese intuitive Vorstellung von "Ähnlichkeit" mit Hilfe der Wahrscheinlichkeitstheorie formalisieren. In Übereinstimmung mit dieser Formalisierung glauben wir, dass das Ergebnis jedes Handels eine bestimmte Realisierung einer Zufallsvariablen ist. Die "Ähnlichkeit" der Positionen wird in diesem Fall durch die Nähe der entsprechenden Verteilungsfunktionen bestimmt. In einer solchen Formalisierung helfen vergangene Positionen, die Art der Verteilung für zukünftige Positionen zu klären und ihre möglichen Ergebnisse zu bewerten.

Probabilistische Formalisierung erlaubt es uns, verschiedene Theorien zu konstruieren. Betrachten wir die einfachste und am häufigsten verwendete. In dieser Theorie wird ein Ergebnis jeder Position eindeutig durch einen relativen Gewinn k=C1/C0 definiert, wobei C0 und C1 Kapitalvolumen vor und nach der Position sind. Weiterhin wird der relative Handelsgewinn einfach als Gewinn bezeichnet, während die Differenz C1-C0 ein absoluter Handelsgewinn ist. Angenommen, die Gewinne aller Positionen (sowohl in der Vergangenheit als auch in der Zukunft) sind unabhängig voneinander und bestehen aus gleichmäßig verteilten Zufallswerten. Ihre Verteilung wird durch die F(x) Verteilungsfunktion bestimmt. Daher ist es unsere Aufgabe, die Art dieser Funktion anhand der Werte der vergangenen profitablen Positionen zu definieren. Dies ist das Standardproblem der mathematischen Statistik - Wiederherstellung der Verteilungsfunktion durch Stichproben. Jede ihrer Lösungen liefert immer nur eine ungefähre Antwort. Werfen wir einen Blick auf einige dieser Methoden werfen.

1. Empirische Verteilungsfunktion wird als Näherung verwendet.

2. Wir nehmen eine einfache diskrete Verteilung, bei der ein Handelsgewinn einen der beiden Werte annimmt. Dies ist entweder ein durchschnittlicher Verlust mit einer Verlustwahrscheinlichkeit oder ein durchschnittlicher Gewinn mit einer Gewinnwahrscheinlichkeit.

3. Wir konstruieren keine diskrete, sondern eine kontinuierliche (mit einer Dichte) Näherung für die Verteilungsfunktion. Um dies zu erreichen, verwenden wir Methoden wie Kerndichteschätzung.
   

Weiter werden wir die erste Option verwenden - sie ist die einfachste und universellste. Händler sind nicht sehr daran interessiert, die Funktion selbst zu kennen. Es ist jedoch wichtig zu wissen, welche Beträge auf einen möglichen Gewinn aus der EA-Operation, ein Risikoniveau der Verwendung oder die Nachhaltigkeit der Gewinne hindeuten. Diese Werte können mit Kenntnis der Verteilungsfunktion ermittelt werden.

Geben wir in unserem Fall den Algorithmus für das Modell an. Was uns interessiert, ist ein mögliches Ergebnis zukünftiger EA-Operationen. Sie wird durch die Reihenfolge der Positionen eindeutig definiert. Jede Position wird durch den Gewinnwert bestimmt. Die Gewinne erfolgt nach der oben beschriebenen empirischen Verteilung. Wir sollten eine große Anzahl solcher Sequenzen generieren und die notwendigen Merkmale für jede dieser Sequenzen berechnen. Die Generierung jeder solchen Sequenz ist einfach. Definieren wir die Reihenfolge der vergangenen Handelsgewinne mit k1, k2, ...., kn. Indem wir die Reihe mit dem Umfang N erzeugen, wählen wir zufällig (mit der gleichen Wahrscheinlichkeit von 1/n) eine von ki (Stichprobe mit Rückgabewert) N Mal. Es wird üblicherweise angenommen, dass N=n, da sich bei großen N die Annäherungsgenauigkeit von F(x) durch empirische Verteilung verschlechtert. Diese Version der Monte-Carlo-Methode wird manchmal als Bootstrapping bezeichnet.

Erklären wir alles von oben durch die Grafik. Sie zeigt mehrere Kapitalkurven. Jede wird durch eine eigens erzeugte Reihenfolge der Positionen bestimmt. Der Übersichtlichkeit halber sind die Kurven in verschiedenen Farben dargestellt. Tatsächlich ist ihre Zahl aber viel größer - es sind mehrere zehntausend. Für jeden von ihnen berechnen wir die notwendigen Parameter und treffen statistische Schlussfolgerungen auf der Grundlage ihrer Gesamtheit. Die wichtigste dieser Eigenschaften ist natürlich der Endgewinn.

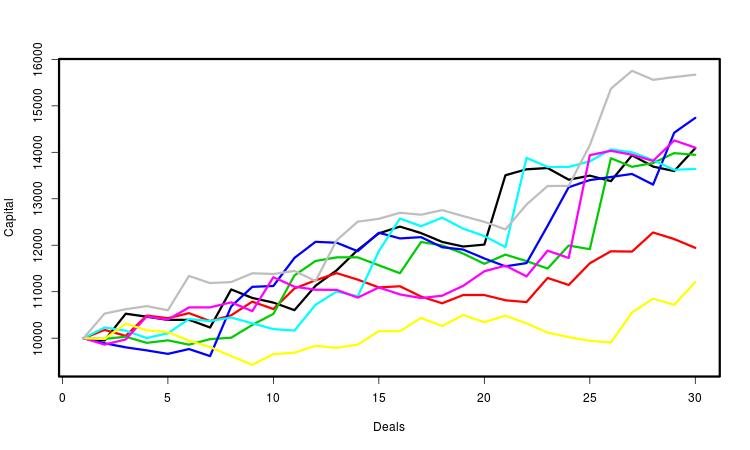
Andere Ansätze zur probabilistischen Formalisierung und weiteren EA-Operationsmodellierung sind ebenfalls möglich. Zum Beispiel können wir anstelle von Handelsfolgen Preisfolgen simulieren und die Gesamtgewinne untersuchen, die ein EA mit ihnen erzielt hat. Das Prinzip der Generierung von Preisreihen kann je nach Aufgabenstellung gewählt werden. Diese Methode benötigt jedoch viel mehr Rechenleistung. Darüber hinaus bietet MetaTrader derzeit keine regulären Möglichkeiten, das auf beliebige EAs anzuwenden.

Anwenden der Theorie

Wir müssen spezifische Optimierungskriterien konstruieren. Jedes von ihnen entspricht einem bestimmten Ziel. Das wichtigste ist der Endgewinn, der durch die komplette Reihe der Positionen erzielt wird. Die Optimierung des Gewinns ist im Tester eingebaut. Da wir am Gewinn in der Zukunft interessiert sind, sollten wir irgendwie den möglichen Grad seiner Abweichung vom Gewinn in der Gegenwart bewerten. Je kleiner die Abweichung, desto stabiler der Gewinn des Systems. Betrachten wir drei Ansätze.

1. Nachdem wir eine große Stichprobe möglicher Gewinnwerte durch die Monte-Carlo-Methode erhalten haben, können wir ihre Verteilung und die damit verbundenen Mengen untersuchen. Der Durchschnittswert dieses Gewinns ist sehr wichtig. Die Varianz ist auch wichtig - je kleiner sie ist, desto stabiler arbeitet der EA und desto geringer ist die Unsicherheit über seine zukünftigen Ergebnisse. Unser Kriterium ist das Verhältnis von durchschnittlichem Gewinn zur durchschnittlicher Verteilung. Es ist ähnlich wie das Sharpe-Ratio.
2. Ein weiteres wichtiges Merkmal ist der Drawdown durch eine Reihe von Positionen. Ein zu großer Drawdown kann zum Verlust der Einlage führen, selbst wenn der eigentlich EA profitabel wäre. Aus diesem Grund ist der Drawdown in der Regel zu beschränken. Es ist wichtig zu wissen, wie er sich auf den möglichen Gewinn auswirkt. Das Kriterium wird einfach als durchschnittlicher Gewinn definiert, jedoch unter der Bedingung, dass die Beendigung des Handels modelliert wird, wenn die zulässige Höhe der Inanspruchnahme überschritten wird.

3. Wir werden ein Kriterium erstellen, das die Stabilität des Gewinns im Hinblick auf die Beständigkeit der Handelsgewinnverteilung misst. Aus Sicht der Wahrscheinlichkeitstheorie bedeutet dies Stationarität der Handelsgewinne, was im Prinzip bei nichtstationären Preissteigerungen möglich ist. Dazu verwenden wir eine ähnliche Idee wie bei Vorwärts-Tests. Lassen Sie uns die erste Stichprobe der Positionen in die ersten und letzten Teilstichproben unterteilen. Um ihre Homogenität zu überprüfen, können wir einen statistischen Test durchführen. Basierend auf diesem Test erstellen wir ein Optimierungskriterium.
   

Um unsere Theorie zu demonstrieren, verwenden wir den EA "Moving Average.mq5", der mit dem Terminal des MetaTrader 5 mitkommt. Wir müssen den Code etwas ändern. Wir fügen am Anfang des EA einen Programmzeile hinzu, um unsere Header-Datei einzubinden:

#include <mcarlo.mqh>

Der folgende Code muss hinzugefügt werden, um die Optimierungsparameter am Testende des EAs zu erhalten und zu verwenden.

double OnTester()
  {
   return optpr();         // optimization parameter
  }

Grundlegende Berechnungen werden mit Funktionen durchgeführt, die sich in der Datei "mcarlo.mqh" befinden. Wir kopieren sie in den Ordner "MQL5/Include/". Die wichtigste Funktion in dieser Datei ist optpr(). Wenn die notwendigen Bedingungen erfüllt sind, berechnet sie die durch den Parameter noptpr angegebene Optimierungskriteriumsvariante, andernfalls gibt sie Null zurück.

double optpr()
  {
   if(noptpr<1||noptpr>NOPTPRMAX) return 0.0;
   double k[];
   if(!setks(k)) return 0.0;
   if(ArraySize(k)<NDEALSMIN) return 0.0;
   MathSrand(GetTickCount());
   switch(noptpr)
     {
      case 1: return mean_sd(k);
      case 2: return med_intq(k);
      case 3: return rmnd_abs(k);
      case 4: return rmnd_rel(k);
      case 5: return frw_wmw(k);
      case 6: return frw_wmw_prf(k);
     }
   return 0.0;
  }

Die Funktion setks() berechnet den Array mit den Gewinnen der Positionen auf Basis der Handelshistorie.

bool setks(double &k[])
  {
   if(!HistorySelect(0,TimeCurrent())) return false;
   uint nhd=HistoryDealsTotal();
   int nk=0;
   ulong hdticket;
   double capital=TesterStatistics(STAT_INITIAL_DEPOSIT);
   long hdtype;
   double hdcommission,hdswap,hdprofit,hdprofit_full;
   for(uint n=0;n<nhd;++n)
     {
      hdticket=HistoryDealGetTicket(n);
      if(hdticket==0) continue;

      if(!HistoryDealGetInteger(hdticket,DEAL_TYPE,hdtype)) return false;
      if(hdtype!=DEAL_TYPE_BUY && hdtype!=DEAL_TYPE_SELL) continue;

      hdcommission=HistoryDealGetDouble(hdticket,DEAL_COMMISSION);
      hdswap=HistoryDealGetDouble(hdticket,DEAL_SWAP);
      hdprofit=HistoryDealGetDouble(hdticket,DEAL_PROFIT);
      if(hdcommission==0.0 && hdswap==0.0 && hdprofit==0.0) continue;

      ++nk;
      ArrayResize(k,nk,NADD);
      hdprofit_full=hdcommission+hdswap+hdprofit;
      k[nk-1]=1.0+hdprofit_full/capital;
      capital+=hdprofit_full;
     }
   return true;
  }

Die Funktion sample() erzeugt eine zufällige Reihenfolge b[] aus der originalen Reihe a[].

void sample(double &a[],double &b[])
  {
   int ner;
   double dnc;
   int na=ArraySize(a);
   for(int i=0; i<na;++i)
     {
      dnc=MathRandomUniform(0,na,ner);
      if(!MathIsValidNumber(dnc)) {Print("MathIsValidNumber(dnc) error ",ner); ExpertRemove();}
      int nc=(int)dnc;
      if(nc==na) nc=na-1;
      b[i]=a[nc];
     }
  }

Als nächstes werden wir jede der drei oben genannten Arten von Optimierungskriterien im Detail betrachten. In allen Fällen erfolgt die Optimierung im gleichen Zeitintervall - Frühjahr/Sommer 2017 mit EURUSD. Der Zeitrahmen beträgt immer 1 Stunde, und der Testmodus ist OHLC auf einem Minutenchart. Es wird immer der genetische Algorithmus nach dem benutzerdefinierten Optimierungskriterium verwendet. Da es unsere Aufgabe ist, die Theorie zu demonstrieren, anstatt den EA auf den realen Handel vorzubereiten, erscheint ein solcher vereinfachender Ansatz natürlich.

Stabilität des Gewinns auf zufällige Veränderungen

Angenommen, wir haben eine Stichprobe der erzielten Endgewinne. Wir können es mit statistischen Methoden untersuchen. Das folgende Bild zeigt ein Histogramm mit einem ausgewählten Median, der mit einer gestrichelten Linie markiert ist.

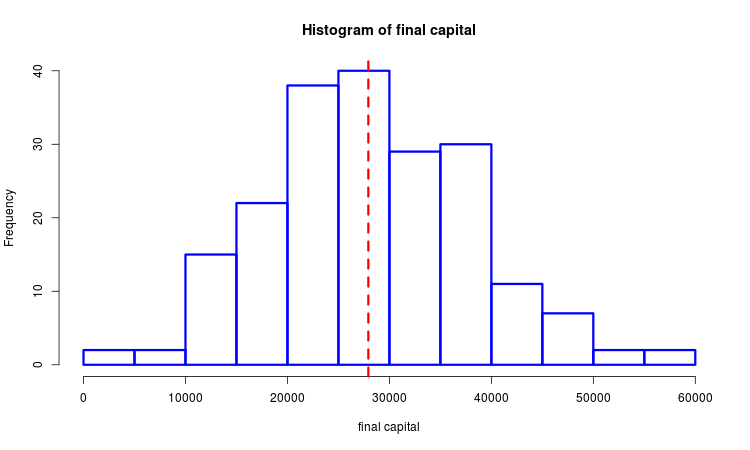
Wir konstruieren zwei ähnliche Versionen des Optimierungskriteriums. Sie werden in den Funktionen mean_sd() und med_intq() berechnet. Der gemeinsame Teil dieser Optionen ist, dass sie das Verhältnis von Mittelwert zu Streumaß darstellen. Der Unterschied besteht darin, wie der Mittelwert und das Streumaß ermittelt werden. Im ersten Fall sind dies der arithmetische Mittelwert und die Standardabweichung, im zweiten Fall - selektiv Median und Interquartilsabstand. Je höher der Gewinn und je geringer die Streuung, desto höher die Werte beider. Es gibt eine offensichtliche Ähnlichkeit mit dem Sharpe-Ratio, obwohl wir hier den Gewinn der gesamten Serie von Positionen und nicht einer einzelnen Position meinen. Die zweite Variante des Kriteriums ist widerstandsfähiger gegen Spikes als die erste.

double mean_sd(double &k[])
  {
   double km[],cn[NSAMPLES];
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      cn[n]=1.0;
      for(int i=0; i<nk;++i) cn[n]*=km[i];
      cn[n]-=1.0;
     }
   return MathMean(cn)/MathStandardDeviation(cn);
  }

double med_intq(double &k[])
  {
   double km[],cn[NSAMPLES];
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      cn[n]=1.0;
      for(int i=0; i<nk;++i) cn[n]*=km[i];
      cn[n]-=1.0;
     }
   ArraySort(cn);
   return cn[(int)(0.5*NSAMPLES)]/(cn[(int)(0.75*NSAMPLES)]-cn[(int)(0.25*NSAMPLES)]);
  }

Nachfolgend sind zwei Paare von Testergebnissen des EAs, optimiert nach diesem Kriterium. Auf dem ersten Paar gibt es ein Optimierungsergebnis für die erste Variante und zum Vergleich das Ergebnis mit dem maximalen Gewinn. Offensichtlich ist die erste vorzuziehen, da sie eine glattere Kapitalkurve ergibt. Der Endgewinn kann auf Wunsch durch Erhöhung des Handelsvolumens erhöht werden.

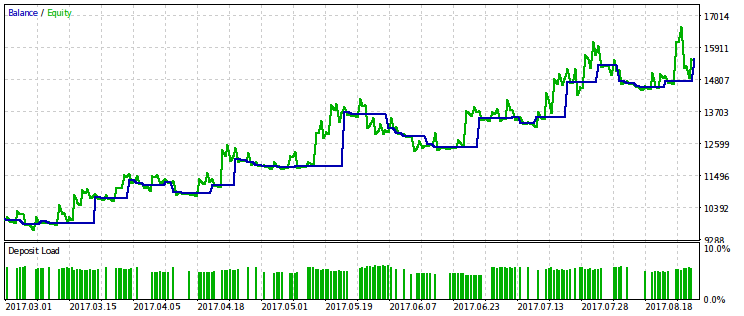
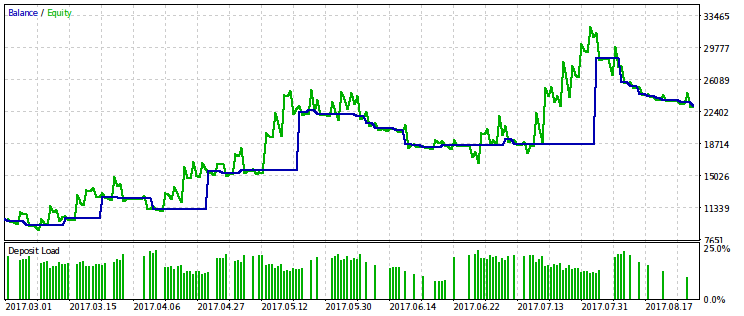
Für die zweite Variante des Optimierungskriteriums wird das gleiche Ergebnispaar zur Verfügung gestellt. Es ist möglich, daraus die gleichen Schlüsse zu ziehen.

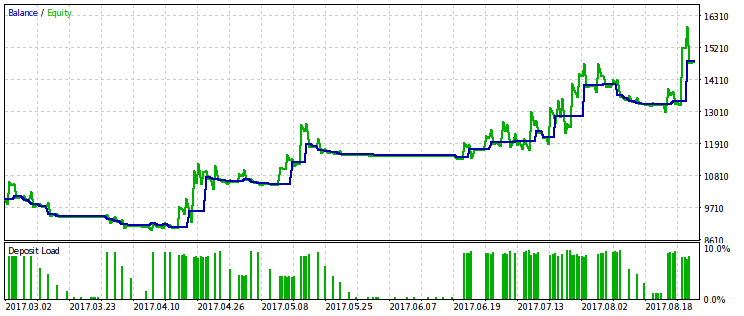
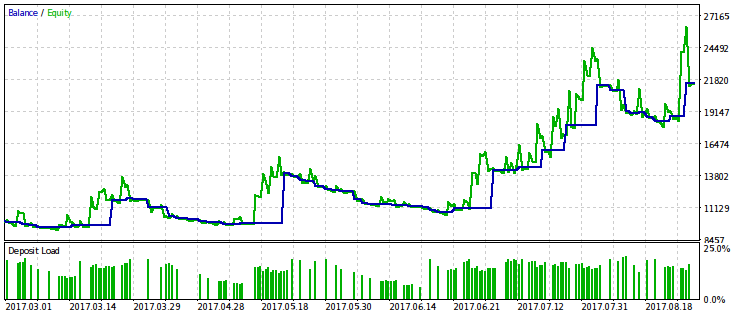
Die Stabilität des Profits im Vergleich zum Drawdown

Wir überwachen das Ausmaß des Drawdowns in jeder generierten Handelsfolge. Wenn das nach dem ersten Teil der Handelsserie verbleibende Kapital einen geringeren Anteil aufweist, als durch den Parameter rmndmin festgelegt, werden die restlichen Geschäfte verworfen. Das folgende Bild zeigt, dass sich das Kapital nicht mehr verändert und der letzte Abschnitt der Kapitallinie horizontal wird, wenn der Drawdowns ein gewisses Maß überschritten hat.

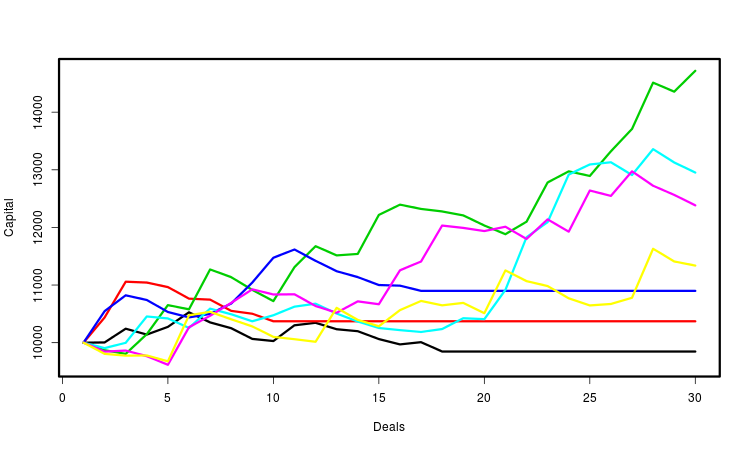
Kapitalkurven bei Beschränkung des relativen Drawdowns - für absolute und relative Drawdowns. Bei einem absoluten Drawdowns wird der Anteil des Kapitals auf seinem Anfangswert bezogen, bei einem relativen Drawdown auf den Maximalwert. Die Funktionen, die diese Parametervarianten berechnen, heißen rmnd_abs() und rmnd_rel() entsprechend. In beiden Fällen ist der Wert des Kriteriums der Durchschnitt der erzielten Gewinne.

double rmnd_abs(double &k[])
  {
   if (rmndmin<=0.0||rmndmin>=1.0) return 0.0;
   double km[],cn[NSAMPLES];
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      cn[n]=1.0;
      for(int i=0; i<nk;++i)
        {
         cn[n]*=km[i];
         if(cn[n]<rmndmin) break;
        }
      cn[n]-=1.0;
     }
   return MathMean(cn);
  }

double rmnd_rel(double &k[])
  {
   if (rmndmin<=0.0||rmndmin>=1.0) return 0.0;
   double km[],cn[NSAMPLES],x;
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      x=cn[n]=1.0;
      for(int i=0; i<nk;++i)
        {
         cn[n]*=km[i];
         if(cn[n]>x) x=cn[n];
         else if(cn[n]/x<rmndmin) break;
        }
      cn[n]-=1.0;
     }
   return MathMean(cn);
  }

Wir können die Optimierung entweder mit dem geeigneten festen Parameter rmndmin durchführen oder nach seinem optimalen Wert suchen.

Berechnen wir die Ergebnisse nur für das mit dem relativen Drawdown verbundene Kriterium, da seine Begrenzung einen stärkeren Effekt hat. Wir werden die Optimierung mit mehreren Varianten des Festwertes rmndmin durchführen: 0.95, 0.75 und 0.2.

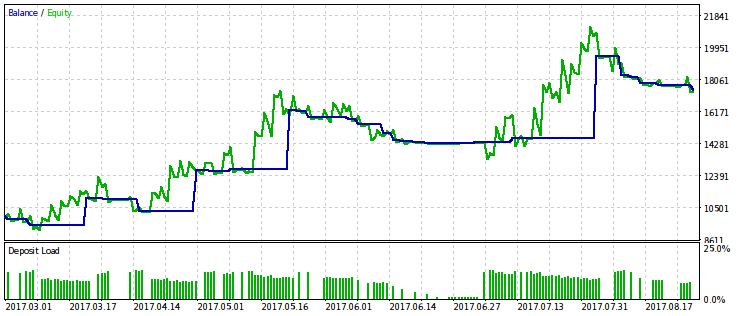
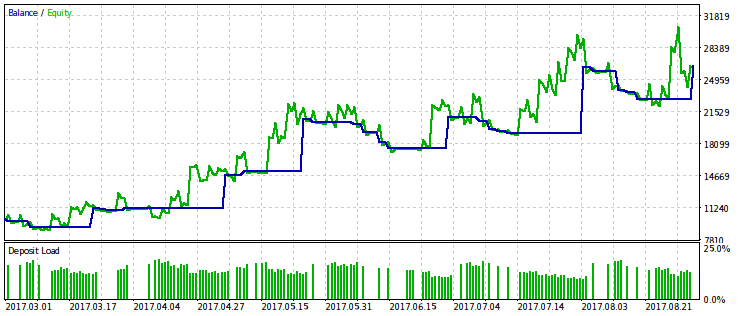
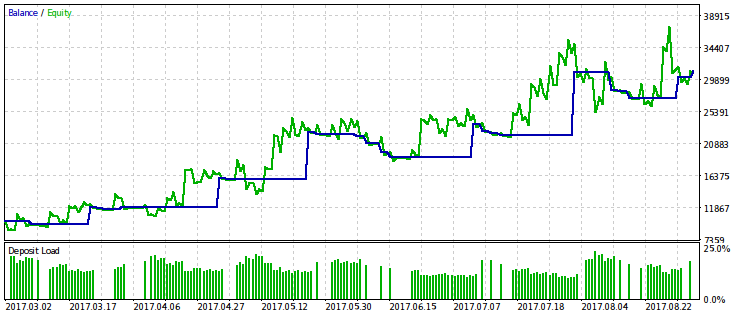
Je niedriger der Wert rmndmin, desto weniger spürbar ist der Drawdown, während die Ergebnisse der Optimierung denen mit der üblichen Gewinnmaximierung immer ähnlicher werden. Dies kann als Folge des Gesetzes der großen Zahlen - des Wahrscheinlichkeitsprinzips - betrachtet werden. Auf den Bildern ist dieser Effekt nicht sofort spürbar, da sie eine andere Skalierung durch die vertikale Achse haben (durch die Anpassung der Skalierung aller Bilder). Außerdem ist der zunehmende Drawdown durch abnehmenden Wert von rmndmin nicht sofort ersichtlich.

Wir optimieren nun auch mit dem Parameter rmndmin, und werden die Optimierung nach dem gleichen Kriterium fortsetzen.

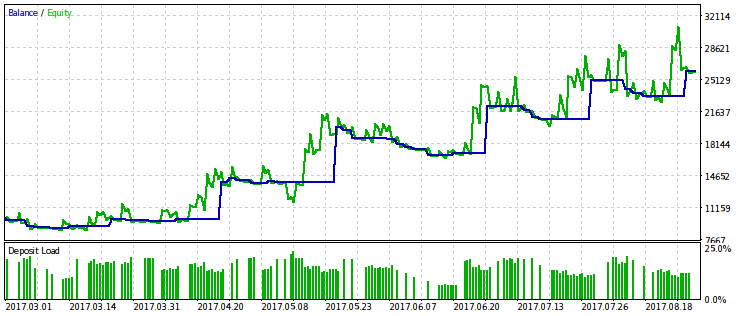
Nehmen wir den Optimalwert rmndmin=0.55. Mit diesem Wert kann ein Drawdown das Konto um fast die Hälfte reduzieren, was inakzeptabel ist. Daher ist er im realen Handel kaum verwendbar. Allerdings gibt es hier noch einen weiteren Vorteil. Wir sehen, dass das "Warten" auf einen noch größeren Drawdown höchstwahrscheinlich keinen Sinn macht. Dies entspricht der zweiten Hälfte der Handelsregel: "Gewinne laufen lassen - Verluste begrenzen".

Stabilität der Gewinnverteilung gegenüber Preisschwankungen

Das Preisverhalten kann sich ändern. Gleichzeitig möchten wir, dass die Ergebnisse des EA stabil sind. Aus der Sicht unseres EA-Wahrscheinlichkeitsmodells bedeutet dies, dass wir auch bei nicht-stationären Preissteigerungen eine Stationarität der Handelsgewinne benötigen.

Unser Optimierungskriterium vergleicht den Anfang der Handelssequenz mit dem Ende. Je näher sie sind, desto größer ist ihr Wert. Die Nähe wird anhand des Wilcoxon-Mann-Whitney-Test bestimmt. Erklären wir, wie er funktioniert. Angenommen, wir haben zwei Beispiele von Positionen. Das Kriterium bestimmt, wie stark eine der Proben relativ zu einer anderen verschoben ist. Je kleiner die Verschiebung, desto höher der Wert des Tests. Lassen Sie uns das mit Bildern erklären. Jede Stichprobe wird durch das entsprechende Histogramm dargestellt. Der größte Wert des Kriteriums befindet sich auf dem mittleren Bild.

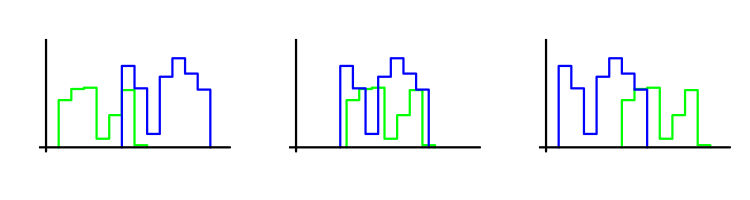
In diesem Fall wird die Monte-Carlo-Methode nicht verwendet. Der große Wert des WMW-Tests rechtfertigt jedoch seine Anwendung, da er die Annahme bestätigt, dass die Art der Verteilung der Handelsgewinne erhalten bleibt.

Die Datei umfasst eine weitere Variante des Kriteriums - das Produkt aus WMW-Test und Gewinn

double frw_wmw(double &k[])
  {
   if (fwdsh<=0.0||fwdsh>=1.0) return 0.0;
   int nk=ArraySize(k), nkf=(int)(fwdsh*nk), nkp=nk-nkf;
   if(nkf<NDEALSMIN||nkp<NDEALSMIN) return 0.0;
   double u=0.0;
   for (int i=0; i<nkp; ++i)
     for (int j=0; j<nkf; ++j)
       if(k[i]>k[nkp+j]) ++u;
   return 1.0-MathAbs(1.0-2.0*u/(nkf*nkp));
  }

double frw_wmw_prf(double &k[])
  {
   int nk=ArraySize(k);
   double prf=1.0;
   for(int n=0; n<nk; ++n) prf*=k[n];
   prf-=1.0;
   if(prf>0.0) prf*=frw_wmw(k);
   return prf;
  }

Die direkte Anwendung des WMW-Tests ist problematisch, da es eine verlustbringende Option mit der optimalen verwechseln kann. Es wäre besser, den EA über den Gewinn zu optimieren und Optionen mit einem kleinen Wert dieses Parameters zu verwerfen, aber es ist noch unklar, wie dies zu tun ist. Wir können eine Reihe der besten Optionen aus der Sicht des WMW-Tests auswählen und dann unter ihnen diejenige, die einen maximalen Gewinn bringt.

Wir werden Beispiele für zwei der zehn besten Durchläufe geben. Der eine ist profitabel, der andere verlustreich.

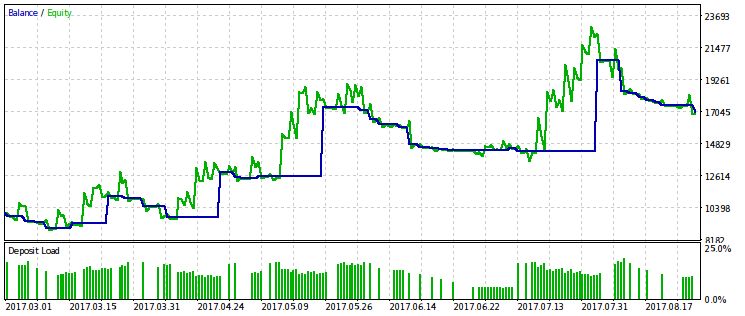
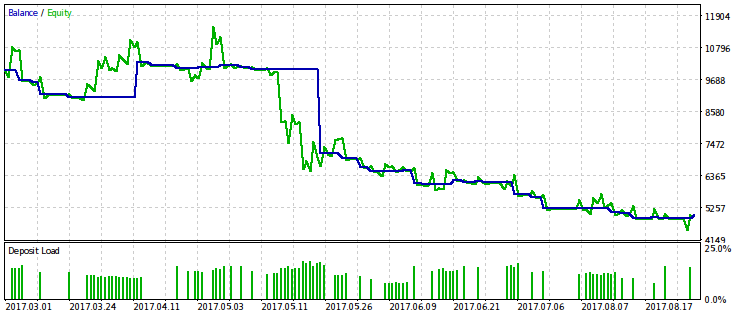
Es scheint, dass der WMW-Test nützlicher wäre, wenn zwei verschiedene EAs im gleichen Zeitintervall oder ein EA in verschiedenen Zeitintervallen verglichen würden. Aber es ist noch nicht klar, wie man einen solchen Vergleich standardisieren macht.

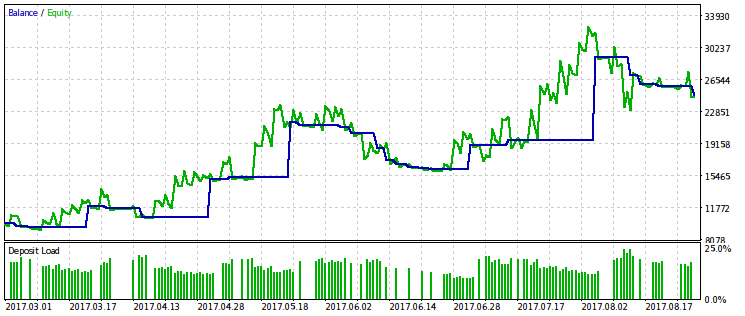
Wir werden auch ein Beispiel für die Optimierung nach einem Kriterium geben, das dem Produkt des WMW-Tests nach Gewinn entspricht. Anscheinend ist es einer einfachen Optimierung durch Profit sehr ähnlich, was bedeutet, dass der Einsatz übertrieben ist.

Schlussfolgerung

In diesem Artikel haben wir einige Aspekte des angesprochenen Themas kurz erläutert. Wir beschließen sie mit ein paar kurzen Bemerkungen.

• Die im Artikel konstruierten Optimierungskriterien können helfen, intuitive Ideen über die effizienteste Abfolge von Gewerken zu formalisieren. Dies ist nützlich, wenn Sie aus einer Vielzahl von Optionen wählen.
  
• Es gibt bekannte Risikomaße, wie VaR (Value at Risk) oder das Risiko des Ruins. Wenn sie direkt als Optimierungskriterium verwendet werden, ist das Ergebnis schlecht. Handelsvolumen und Anzahl der Geschäfte werden unterbewertet. Daher ist ein Kompromisskriterium erforderlich, das von den beiden Variablen - Risiko und Gewinn - abhängt. Die Frage ist, welche Version dieses Kriteriums wir wählen sollten, da die Funktionen der beiden Variablen unendlich sind. Das Kriterium kann z.B. auf der Ebene einer Handelsstrategie "Aggressivität" gewählt werden, die sehr unterschiedlich ist.
  
• Verschiedene Varianten von Optimierungskriterien zur Messung der Stabilität können für verschiedene Klassen von EAs sinnvoll sein. Beispielsweise unterscheiden sich trendfolgende EAs von denen, die in einem Kanal handeln, während Systeme mit einem festen Take Profit sich von denen unterscheiden, die Positionen durch einen Trailing Stop schließen. Gewinnverteilungen solcher EAs werden ebenfalls verschiedenen Klassen angehören. Abhängig davon ist das eine oder andere Kriterium besser geeignet.
• Einige Kriterien sind nützlich, um zwei verschiedene EAs zu vergleichen, anstatt das Verhalten desselben EAs in einem festen Zeitintervall bei verschiedenen Parametersätzen zu vergleichen. Mit Hilfe solcher Kriterien ist es möglich, die Arbeit eines einzelnen EA in unterschiedlichen Zeitintervallen zu vergleichen.
  
• Das Monte-Carlo-Modell wäre vollständiger, wenn es möglich wäre, nicht nur die bestehende Preishistorie, sondern auch deren zufällig veränderte Kopien als Eingabe an den EA weiterzugeben. Dieses würde uns erlauben, die Stabilität von EAs gänzlich zu studieren, obwohl an den Kosten der Erhöhung der Menge von Berechnungen.
  

Angehängte Dateien

#	Name	Typ	Beschreibung
1	Moving Average_mcarlo.mq5	Skript	Modifizierter Moving Average.mq5 der Standardauslieferung
2	mcarlo.mqh	Header Datei	Hauptdatei mit den Funktionen für alle benötigten Berechnungen