蒙特卡洛方法在交易策略优化中的应用
5 064
38
目录
理论概述
上面的想法即蒙特卡洛方法可以用类比的方法来描述 — 一种科学知识方法，其他类比法的例子有哈密顿(Hamilton)的视神经机械类比于生物学中的类似器官。
如果我们有两个对象可以使用相同的理论来描述，则从研究它们其中一种所获得的知识可以用于另外一种，这种方法在一个对象比另一个更容易作研究的情况下非常有用。更容易访问的对象可以当作另一个对象的模型，这种方法本身被称为建模。根据上下文，所谓模型是指两个对象都通用的其中一个对象或者一种理论。
有的时候，研究者会错误理解建模的结果。当我们探讨一些明显的例子时，例如在一个风洞内摧毁一个飞机的简单复制品时，一切看起来很明显。但是，当对象不相关并且第一眼看来并不像的时候，结论有的时候看起来会有些奇怪，或者从基础上看都很不合理。对象的通用类理论一般只能描述它们中的某些方面，所要求的对象描述精确度越低，可以应用某个理论的对象集合就越宽。例如，只有当光波的长度趋于零时，哈密顿的光学机械类比才是完全满足的。在现实中，这种类比近似于一个小但总是有限的长度。由于任何理论模型应该足够简单，作为计算和结论的基础，所以总是过于简化。
现在让我们清晰了解一下蒙特卡洛方法的概念，这是以一种对于理论上有概率（随机）性质的对象建模的方法。该模型是在按照这一理论构建了一个算法的计算机程序，它使用的伪随机数发生器模拟所必需的随机变量（随机过程）所需的分布。
值得强调的是（尽管我们这里并不重要），研究对象的性质可以是概率的和确定性的。一个具有概率性质的理论的存在对我们来说是重要的，例如，蒙特卡洛方法用于近似计算普通积分，这是可能的，因为任何这样的积分都可以看作是随机变量的数学期望。
使用蒙特卡洛方法的第一个例子通常是布丰投针问题的解决方案，其中 Pi 数是由在表格上随机投针来决定的，方法的名称在很久之后才出现，是在某某世纪的中叶。毕竟，赌博游戏——例如轮盘赌——是随机数发生器。此外，对赌博的深思熟虑暗示了概率理论的起源，它从玩骰子和纸牌的计算开始。
建模程序算法简单，这是该方法流行的原因之一。该算法具有多个随机生成的变体（样本）的研究对象状态与理论对应的分布，为它们中的每个都计算所需的特征集合，这样，我们就有了很多的样本。虽然我们对所研究的对象只有一组特征，但是蒙特卡洛方法允许我们大量地获得它们，并构造它们的分布函数，这给了我们更多的数据。
上面描述的通用蒙特卡洛建模结构似乎很简单，然而，当尝试实现时，它会产生多个甚至有时相当复杂的变化。即使我们把我们的应用限制在金融方面，我们仍然可以看到它有多广泛, 例如在 这本书中。我们将会尝试把蒙特卡洛方法应用在 EA 交易的稳定性研究上，为此，我们需要一个概率模型来描述它们的工作。
概率性 EA 模型
在开始使用 EA 交易开始实际交易之前，我们通常会在报价历史上测试和优化它。但是为什么我们会相信，过去的交易结果会影响到未来的交易结果呢?当然，我们并不期望未来的所有交易都会形成与过去相同的顺序，尽管我们还是有假定它们会有“相似性”。让我们用概率论对这种“相似性”的直觉概念进行形式化。根据这种形式化，我们认为每个交易的结果都是某种随机变量的某种实现。在这种情况下，交易的“相似性”是通过对应的分布函数的接近来确定的。在这种形式化中，过去的交易有助于澄清未来的分配类型，并评估其可能的结果。
概率形式化使我们能够构建各种理论，让我们考虑最简单和最常用的一个。在这个理论中，由于各行业明确定义的相对利润在这个理论中，由于每个交易明确定义的相对利润k=C1/C0, 其中 C0和 C1 是交易前后的资产量。此外，相对交易利润将简单被称为利润，而 C1-C0 的差是绝对交易利润。假设所有交易的利润（无论是过去还是将来）都是相互独立的，包括均匀分布的随机值。它们的分布由 F(x) 分布函数决定，这样，我们的任务就是通过使用过去获利交易的数值来定义这个函数的类型，这是数理统计的标准问题——通过样本恢复分布函数，它的任何解决方案总是提供近似答案，让我们看看其中一些方法。
-
经验分布函数用作近似值，
-
我们使用一个简单的离散分布，其中以交易利润作为两个值中的一个。这是一个亏损概率的平均亏损，或者是一个获利概率的平均利润。
- 我们构造一个不是离散的，而是连续的（具有密度）近似的分布函数。为此，我们使用例如核密度估计这样的方法。
此外，我们将使用第一个选项-它是最简单和通用的。交易者对于了解函数本身并不是很感兴趣，然而，重要的是要知道什么金额表示可能的利润，从EA操作，其使用的风险水平或利润的可持续性。这些值可以通过了解分布函数来获得。
让我们在我们的例子中指定建模算法，我们的兴趣对象就是 EA 运行在未来的可能结果。它使用交易序列来定义是很明确的，每个交易都设置利润值，利润是根据上面描述的经验分布来分布的，我们应当生成大量这样的序列来计算它们每个可能的特性。生成这样的序列很简单，让我们定义，在历史中交易利润的序列为 k1, k2, ..., kn，通过使用长度 N 来生成序列, 我们将会随机(使用相等的概率 1/n) 选择 ki (有返回的样本) N 次。通常假定 N=n, 因为 N 较大时, F(x) 经验分布的近似精确度会下降。这个版本的蒙特卡洛方法有时被称为 bootstrap 方法，
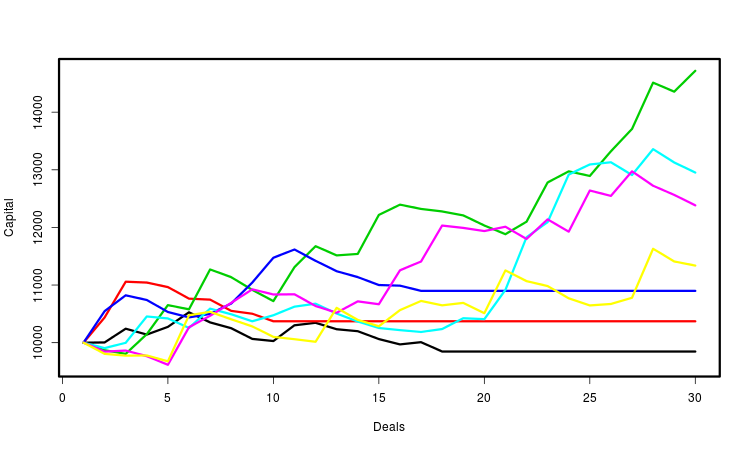
让我们通过图片来解释上面的内容，它显示了几条资金曲线，它们中的每个都是根据生成的交易序列决定的。为了更方便，我使用不同的颜色对曲线做了标记，实际上，它们的数量要大得多 — 有好几万。对于它们中的每一个，我们都计算所需的参数并根据其整体性做出统计结论，很明显，这些特性中最重要的就是最终的利润。
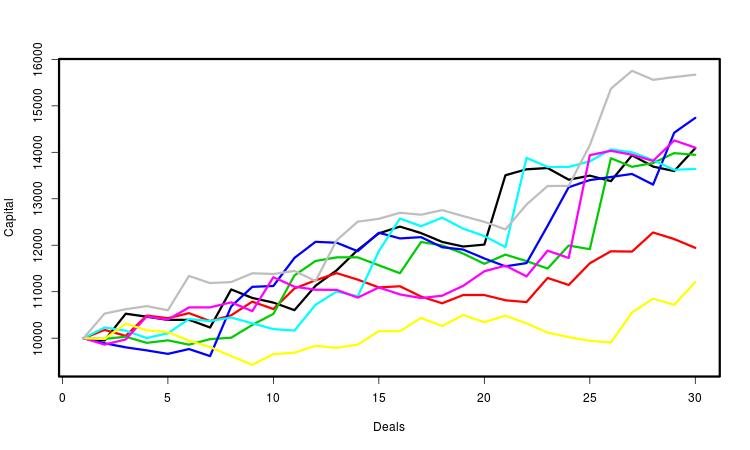
其他形式的概率形式化和进一步的EA操作建模也是可能的，例如，不是通过交易序列，我们可以模拟价格序列和研究EA所获得的总利润。可以根据要解决的任务来选择生成价格系列的原理，然而，这种方法需要更多的计算资源。此外，MetaTrader 目前还没有提供使用随机EA的常规方法。
应用理论
我们的任务是构建特定的优化标准，它们中的每个都对应某个目标，主要的一个是一系列交易所获得的最终利润。根据利润优化已经在测试器中内建了，由于我们对未来的利润感兴趣，所以我们应该以某种方式来评估其目前偏离利润的可能程度。偏差越小，系统的利润越稳定。让我们探讨三种方法。
- 通过蒙特卡洛方法获得了一个可能的利润值的大样本，我们可以研究它的分布和与之相关的数量。这个利润的平均值非常重要，方差也很重要——它越小，EA的工作就越稳定，其未来结果的不确定性也就越小。我们的标准将等于平均利润与平均分散的比率，这与夏普比率类似。
- 另一个重要的特点是一系列交易中利润的回撤，回撤太大可能会导致存款的亏损，哪怕 EA 是获利的。为此，回撤通常会被约束。了解它会怎样影响到可能的利润很有用，该标准简单地定义为平均利润，但是条件是当超过允许的回撤水平时，交易终止。
-
我们将建立一个衡量利润的稳定性的持久性的贸易利润分配。从概率论的角度，这意味着交易利润在原则上，价格变化不稳定的时候的 稳定性。为此，我们将会使用类似于前瞻测试的想法。让我们把最初的交易样本分为最初和最终子样本，为了验证它们的同质性，我们可以应用统计学检验。基于这个测试，我们将创建一个优化准则。
#include <mcarlo.mqh> 加上代码用于在 EA 的最后获得和使用我们的优化参数:
double OnTester() { return optpr(); // 优化参数 }
基本计算都是在位于 "mcarlo.mqh" 头文件的函数中进行的，我们把它放在 "MQL5/Include/" 文件夹下。这个文件中的主函数是 optpr()，满足必要条件时，它计算由noptpr参数指定的优化标准，否则它就返回零。
double optpr() { if(noptpr<1||noptpr>NOPTPRMAX) return 0.0; double k[]; if(!setks(k)) return 0.0; if(ArraySize(k)<NDEALSMIN) return 0.0; MathSrand(GetTickCount()); switch(noptpr) { case 1: return mean_sd(k); case 2: return med_intq(k); case 3: return rmnd_abs(k); case 4: return rmnd_rel(k); case 5: return frw_wmw(k); case 6: return frw_wmw_prf(k); } return 0.0; }
setks() 函数根据交易历史计算出交易利润的数组。
bool setks(double &k[]) { if(!HistorySelect(0,TimeCurrent())) return false; uint nhd=HistoryDealsTotal(); int nk=0; ulong hdticket; double capital=TesterStatistics(STAT_INITIAL_DEPOSIT); long hdtype; double hdcommission,hdswap,hdprofit,hdprofit_full; for(uint n=0;n<nhd;++n) { hdticket=HistoryDealGetTicket(n); if(hdticket==0) continue; if(!HistoryDealGetInteger(hdticket,DEAL_TYPE,hdtype)) return false; if(hdtype!=DEAL_TYPE_BUY && hdtype!=DEAL_TYPE_SELL) continue; hdcommission=HistoryDealGetDouble(hdticket,DEAL_COMMISSION); hdswap=HistoryDealGetDouble(hdticket,DEAL_SWAP); hdprofit=HistoryDealGetDouble(hdticket,DEAL_PROFIT); if(hdcommission==0.0 && hdswap==0.0 && hdprofit==0.0) continue; ++nk; ArrayResize(k,nk,NADD); hdprofit_full=hdcommission+hdswap+hdprofit; k[nk-1]=1.0+hdprofit_full/capital; capital+=hdprofit_full; } return true; }
sample() 函数从最初的a[]序列生成随机的 b[] 序列。
void sample(double &a[],double &b[]) { int ner; double dnc; int na=ArraySize(a); for(int i=0; i<na;++i) { dnc=MathRandomUniform(0,na,ner); if(!MathIsValidNumber(dnc)) {Print("MathIsValidNumber(dnc) error ",ner); ExpertRemove();} int nc=(int)dnc; if(nc==na) nc=na-1; b[i]=a[nc]; } }
下面，我们将详细探讨上面所述的三种优化标准中的每一个，在每个例子中，我们都针对相同的时间段 - EURUSD 在2017年春/夏, 来进行优化。时段将总是1小时，而测试模式是1分钟图表的 OHLC。全都使用自定义优化中的遗传算法，因为我们的任务是证明理论而不是准备实际交易的EA，这种简单化的方法似乎是很自然的。
利润鲁棒性对随机散射
假设我们有一个产生最终利润的样本，我们可以借助数理统计的方法进行研究。面的图像显示了一个带有虚线标记的选择中值的直方图。
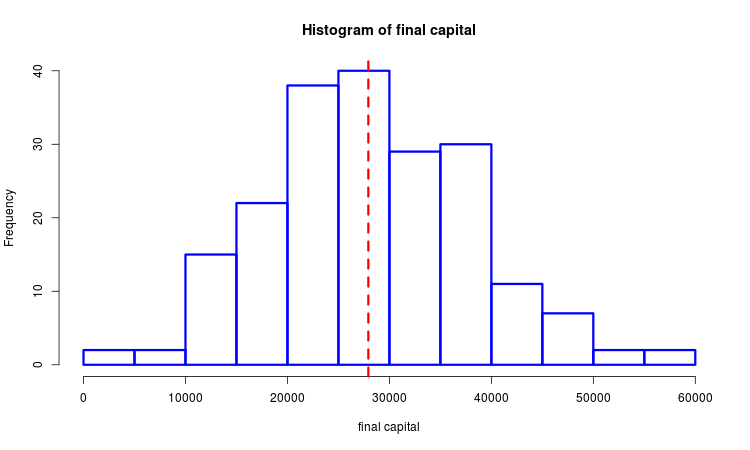
我们构建了两个类似版本的优化标准，它们分别在mean_sd() 和 med_intq() 函数中计算，这些选项的共同部分是它们代表平均值与散射度量的比值。区别在于如何确定平均值和散射量。在第一种情况下，这是算术平均值和标准差，而在第二选项中 - 选择中位数和四分数范围。利润越高，分散性越小，两者的价值越高。与夏普比率有明显的相似之处，虽然我们这里指的是整个系列交易中的利润，而不是单一交易。标准的第二个变体与第一个相比更能抵抗尖峰。
double mean_sd(double &k[]) { double km[],cn[NSAMPLES]; int nk=ArraySize(k); ArrayResize(km,nk); for(int n=0; n<NSAMPLES;++n) { sample(k,km); cn[n]=1.0; for(int i=0; i<nk;++i) cn[n]*=km[i]; cn[n]-=1.0; } return MathMean(cn)/MathStandardDeviation(cn); } double med_intq(double &k[]) { double km[],cn[NSAMPLES]; int nk=ArraySize(k); ArrayResize(km,nk); for(int n=0; n<NSAMPLES;++n) { sample(k,km); cn[n]=1.0; for(int i=0; i<nk;++i) cn[n]*=km[i]; cn[n]-=1.0; } ArraySort(cn); return cn[(int)(0.5*NSAMPLES)]/(cn[(int)(0.75*NSAMPLES)]-cn[(int)(0.25*NSAMPLES)]); }
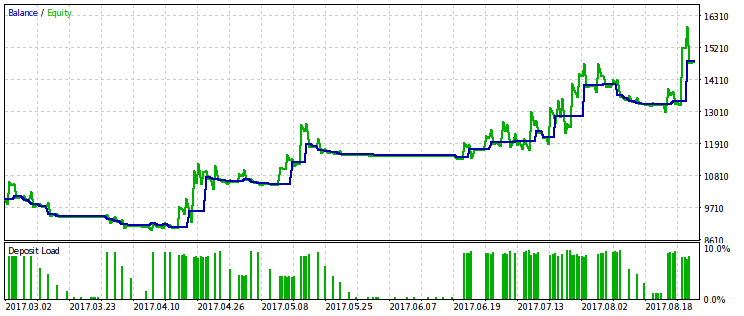
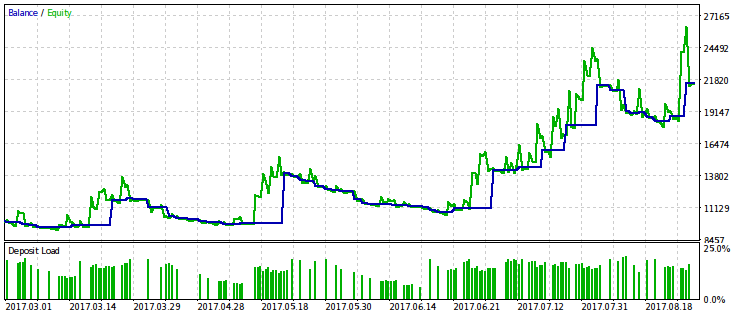
下面是由该准则优化的EA的两对测试结果。在第一对中，对于第一变型有一个优化结果，为了比较结果与最大利润。显然，第一个是比较好的，因为它提供了更平滑的资金曲线。最后的利润，如果需要，可以通过增加交易量来增加。
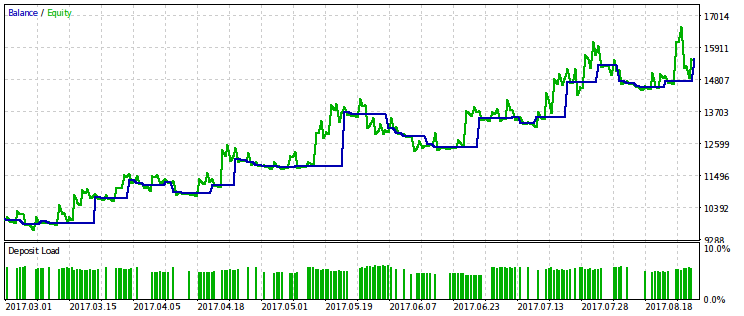
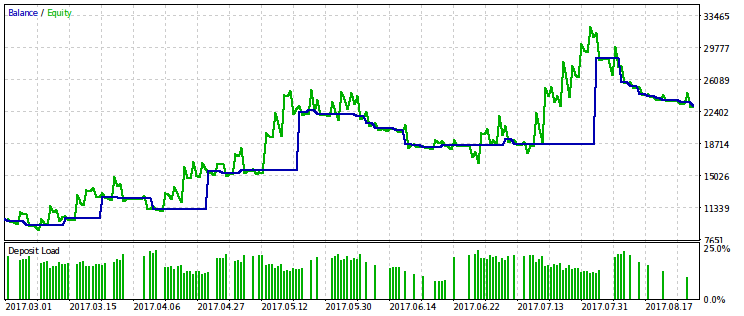
为优化准则的第二变型提供相同的结果对，可能会从中得出相同的结论。
利润鲁棒性对回撤
我们会监控所生成交易序列中每个交易的回撤量，如果剩余资金在进行一部分交易之后，占据的比例小于 rmndmin 参数的设置，剩余的交易就会被关闭。下面的图片显示出，如果相对回撤水平被超过，资金就会停止变化，而最后部分的资金曲线就成了一条水平线。
我们有两个计算选项标准 — 绝对和相对回撤。如果是绝对回撤，资金比例是按照它的初始值来计算的，而对于相对回撤，计算是根据最大值来计算。计算这些参数变化的函数分别被称为 rmnd_abs() 和 rmnd_rel()。在这两种情况下，标准的值都是所生成利润的平均值。
double rmnd_abs(double &k[]) { if (rmndmin<=0.0||rmndmin>=1.0) return 0.0; double km[],cn[NSAMPLES]; int nk=ArraySize(k); ArrayResize(km,nk); for(int n=0; n<NSAMPLES;++n) { sample(k,km); cn[n]=1.0; for(int i=0; i<nk;++i) { cn[n]*=km[i]; if(cn[n]<rmndmin) break; } cn[n]-=1.0; } return MathMean(cn); } double rmnd_rel(double &k[]) { if (rmndmin<=0.0||rmndmin>=1.0) return 0.0; double km[],cn[NSAMPLES],x; int nk=ArraySize(k); ArrayResize(km,nk); for(int n=0; n<NSAMPLES;++n) { sample(k,km); x=cn[n]=1.0; for(int i=0; i<nk;++i) { cn[n]*=km[i]; if(cn[n]>x) x=cn[n]; else if(cn[n]/x<rmndmin) break; } cn[n]-=1.0; } return MathMean(cn); }
我们可以或者使用合适的 rmndmin 固定参数，也可以寻找最佳值来进行优化，
让我们只为与相对回撤相关的标准提供结果，因为它的限制给出了更明显的效果。我们将使用几种变化的 rmndmin 确定值来进行优化: 0.95, 0.75 和 0.2.
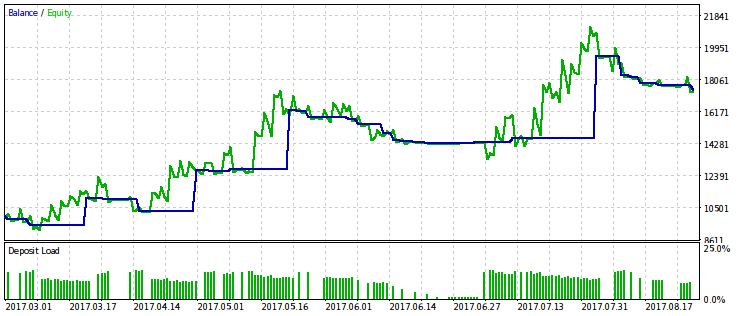
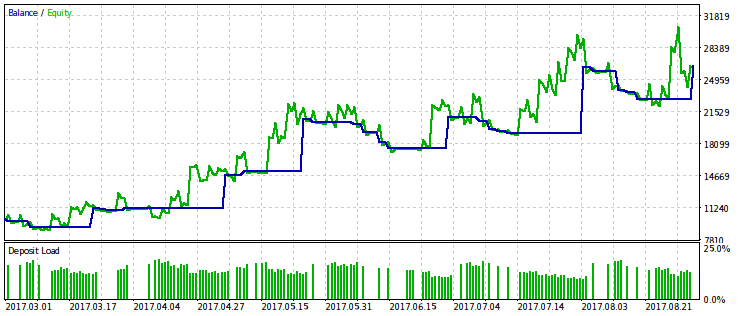
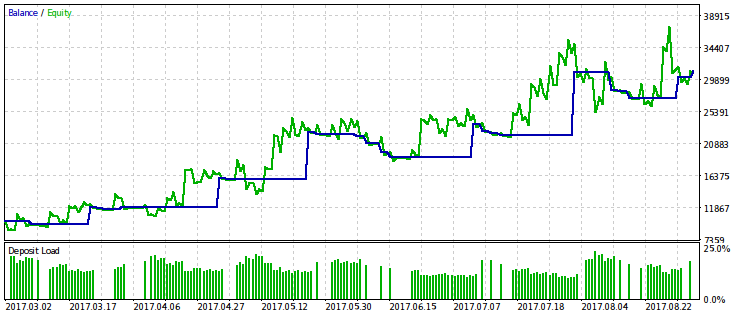
rmndmin 的值越小，回撤就越不明显，而优化的结果和通常的利润最大化就越接近，这可以被认为是大数定律的结果——概率论原理。在图像上，这种效果并不是立即被注意到的，因为它们通过垂直轴具有不同的尺度（由于所有图像到相同维度的调整）。另外，因为减小 rmndmin 值而增加的回撤没有立即出现。
现在，让我们把 rmndmin 参数加到优化的参数中，而我们将继续以相同标准进行优化。
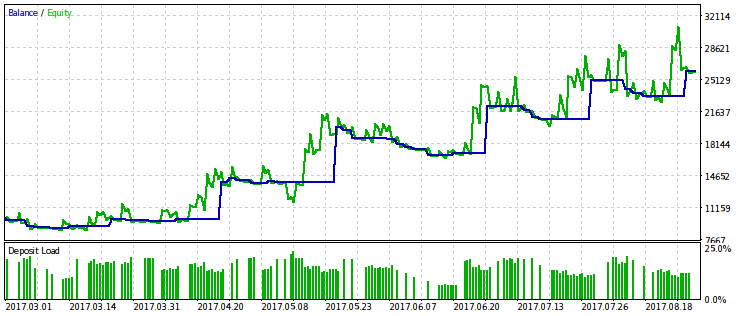
我们得到的最佳值是 rmndmin=0.55，使用这样的值，回撤可能达到账户余额的几乎一半，而这是不能接受的，所以，它在实际交易中很难使用，但是，这里有另一点好处。我们可以看到，在有很大回撤时 "扛单"，很可能是没有用的。这对应着交易守则的另一半: "斩断亏损，让您的利润奔跑".
利润分布的鲁棒性对价格不稳定性
价格行为可能会改变. 同时，我们会希望 EA 工作的结果要稳定，从我们 EA 获利性模型的角度，这意味着我们需要在价格变化不稳定的时候还要交易获利。
我们的优化标准会比较交易序列的初始部分和结束部分，它们越接近，这个值就越大。近似度是根据 Wilcoxon-Mann-Whitney 标准确定的，让我解释一下它的含义。假定我们有两个交易样本，这个标准确定了其中一个样本和另一个比会相差多少，偏移越少，标准值就越高。让我们用图片来解释它，每个样本都由对应的柱形图来表示，标准的最大值可以在中间的图片中找到。
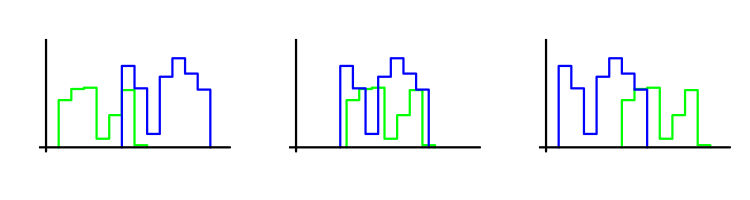
在这种情况下，蒙特卡洛方法本身没有用，但是，WMW 标准值大可以评价它的实用性，因为它确认了交易利润分布类型的假定。
我们的文件还有另一个标准 — WMW 标准和利润的乘积.
double frw_wmw(double &k[]) { if (fwdsh<=0.0||fwdsh>=1.0) return 0.0; int nk=ArraySize(k), nkf=(int)(fwdsh*nk), nkp=nk-nkf; if(nkf<NDEALSMIN||nkp<NDEALSMIN) return 0.0; double u=0.0; for (int i=0; i<nkp; ++i) for (int j=0; j<nkf; ++j) if(k[i]>k[nkp+j]) ++u; return 1.0-MathAbs(1.0-2.0*u/(nkf*nkp)); } double frw_wmw_prf(double &k[]) { int nk=ArraySize(k); double prf=1.0; for(int n=0; n<nk; ++n) prf*=k[n]; prf-=1.0; if(prf>0.0) prf*=frw_wmw(k); return prf; }
直接使用 WMW 标准是有问题的，因为它可能会把产生亏损的选项作为最优，如果能根据利润来优化 EA ，并弃掉这个参数值较小的选项可能会更好，但是还不清楚怎样做。我们可以选择一些从 WMW 标准的最佳选项，然后选择其中利润最大的一个。
我们将提供例子，给出10个通过中最好的两个，其中一个是获利，而另一个是导致亏损。
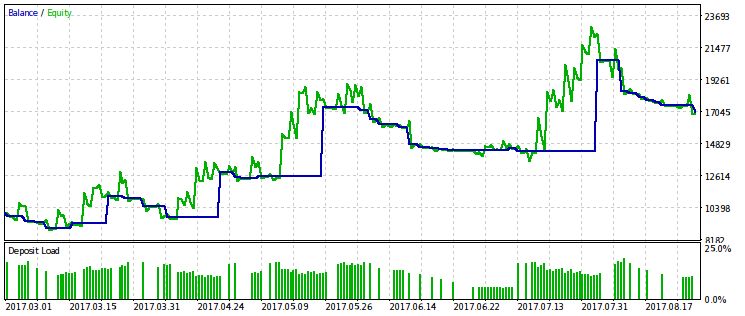
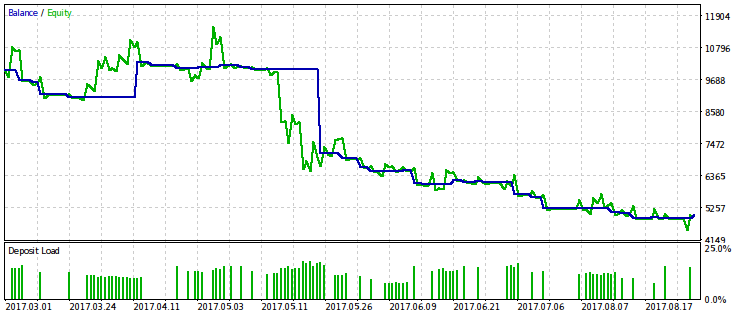
看起来，WMW 标准在比较两个不同 EA 交易在相同的时间段或者一个 EA 在不同时间段中的工作会更有用，但是还不清楚怎样进行正确的比较，
我们将会提供实例，根据 WMW 标准与利润的乘积来进行优化。显然，这和简单根据利润来进行优化很类似，而这意味着这样使用有些多余了。
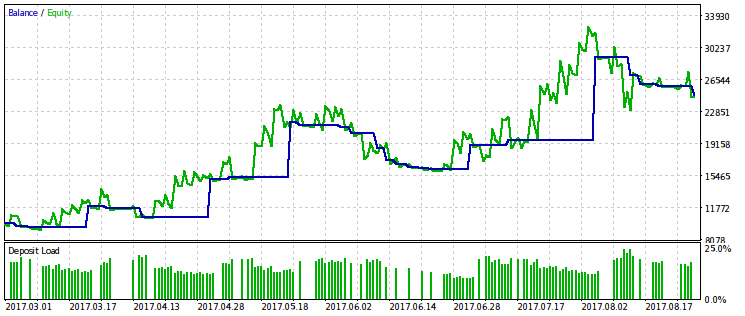
结论
在这篇文章中，我们简要地谈到了一些标记的主题，让我们简短地总结一下。
- 在文章中构建的优化标准可以帮助形式化关于最有效的交易顺序的直觉想法，当从大量选项中选择时，这是有用的。
- 有我们已知的风险衡量方法, 例如VaR (Value At Risk, 风险值) 或者破产概率。如果您在优化标准中直接使用它们，结果将会很糟。交易量和交易的数量将会被低估。因此，需要一个折衷的标准，这取决于两个变量-风险和利润。问题是，我们应该选择哪个标准的版本，因为这两个变量的函数是无限的。例如，可以根据交易策略“激进性”的水平来选择该标准，其差别很大。
- 不同的优化标准的测量稳定性可以是有用的不同的EA种类，例如，跟随趋势的EA将不同于在一个范围内交易的EA，而具有固定获利利润的系统将不同于使用跟踪止损来关闭交易的系统。这样 EA 的利润分布也将属于不同的种类，根据这一点，一个或另一个标准将会更加合理。
- 有些标准对于比较不同的 EA 交易比比较在固定时间段内行为相同而参数集不同的相同 EA 更加有用，而在这样标准的帮助下，就可能比较单一的 EA 交易在不同时间段的工作。
- 蒙特卡洛建模将更加完整，如果有可能通过不仅现有的价格历史，而且它的随机改变的副本到EA的输入。这将允许我们更深入地研究EA的稳定性，尽管以增加计算量为代价。
附件中的文件
| # | 名称 | 类型 | 描述 |
|---|---|---|---|
| 1 | Moving Average_mcarlo.mq5 | 脚本 | 修改过的标准移动平均 mq5 EA |
| 2 | mcarlo.mqh | 头文件 | 进行所有所需计算的函数的主文件 |
本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/4347
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
改进面板：增加透明化、改变背景色以及继承于 CAppDialog/CWndClient
深度神经网络 (第六部分)。 神经网络分类器的融合: 引导聚合
您好。我在 EA 中添加了 Ontester () 方法，在回溯测试中，Ontester 结果中出现了一个数值（4.3222）。我该如何解释这个值以提高 EA 性能？
在优化输入参数时，它被用作 "自定义最大值 "标准。
好主意，但它只适用 于固定头寸。
它只是一个粗略的策略评估工具，基于拉尔夫-文斯理论的假设（第 1 章）。