Aplicando el método de Monte Carlo para optimizar estrategias comerciales

Índice

• Teoría general
• Modelo probabilista del Asesor Experto
• Aplicando la teoría
• Estabilidad del beneficio hacia la dispersión al azar
• Estabilidad del beneficio hacia el drawdown
• Estabilidad de la distribución del beneficio de transacciones hacia la no-estacionariedad de los precios
• Conclusión
• Archivos adjuntos
  

Teoría general

La esencia delmétodo de Monte Carlo puede ser descrita como ejemplo del uso de la analogía, es decir, uno de los métodos del conocimiento científico. Otros ejemplos de la analogía es analogía óptico mecánica de Hamilton o los órganos análogos en la biología.

Si tenemos dos objetos que pueden ser descritos con la misma teoría, entonces, los conocimiento obtenidos al estudiar uno de ellos, se aplicarán al otro. Este método es muy útil cuando resulta que estudiar un objeto es mucho más fácil que el otro. En este caso, el objeto más fácil para estudiar se considera un modelo del otro, mientras que el propio método se llama modelación. A veces, al modelo (o modelo teórico) lo llaman no a uno de los objetos, sino a la teoría común para ellos; pero normalmente, está claro del contexto de quá se trata exactamente.

A veces, los investigadores interpretan los resultados de la modelación de forma incorrecta. Cuando se trata de los ejemplos evidentes (por ejemplo, el soplado de una copia reducida del avión en el tubo aerodinámico), todo parece claro. Pero cuando los objetos no están vinculados y no parecen uno a otro a primera vista, las conclusiones a veces hacen el efecto de un trucaje astuto, o bien sirven de la base para las conclusiones y generalizaciones infundadas, pero de vastas proyecciones. En realidad, la cosa es que la teoría común para los objetos siempre describe sólo aproximadamente algunos de sus aspectos. Cuanto menos será la precisión necesaria de la descripción de los objetos por la teoría, más amplio sea el conjunto de los objetos que va a someterse a ella. Por ejemplo, la analogía óptico mecánica de Hamilton se ejecuta con exactitud solamente dentro del rango, cuando la longitud de la onda de luz tiende a cero. En realidad, sólo para una longitud pequeña, pero siempre final, ella se ejecuta aproximadamente. Puesto que cualquier modelo teórico tiene que ser bastante simple para servir de base para los cálculos y conclusiones, ella siempre será aproximada.

Ahora, vamos a detallar el concepto del método de Monte Carlo. Es un enfoque en la modelación de objetos cuya teoría tiene una naturaleza probabilista (estocástica). En este caso, de modelo nos sirve un programa de ordenador, cuyo algoritmo concuerda con esta teoría. Este programa utiliza los generadores de números aleatorios con el fin de imitar los valores aleatorios necesarios (procesos aleatorios) con distribuciones necesarias.

Cabe mencionar (aunque para nuestra exposición siguiente no es tan importante) que la naturaleza del objeto analizado puede ser tanto estocástica, como determinista. Lo importante es que haya una teoría que tiene un carácter probabilista. Por ejemplo, el método de Monte Carlo se usa para un cálculo aproximado de las integrales comúnes. Eso es posible ya que cualquier integral puede ser considerado como el valor esperado de una cierta variable aleatoria.

El primer ejemplo del uso del método de Monte Carlo suele considerarse la resolución del problema de Buffon, donde el número Pi se determina a través del lanzamiento aleatorio de la aguja sobre la mesa. El nombre del método apareció mucho más tarde, a mediados del siglo XX. Es que todos los juegos de azar (por ejemplo, la ruleta) son generadores de los números aleatorios. Aparte de eso, la referencia concienzuda a los juegos de azar apunta a los fuentes de la teoría de probabilidades, que empieza con los cálculos relacionados con el juego de los dados o naipes.

El algoritmo del programa para la modelación es simple, y esa es una de las razones de la popularidad del método. Dentro del programa, se genera un conjunto de diferentes variantes (sampl) del estado del objeto a estudiar, de una manera aleatoria, con la distribución correspondiente a la teoría. Para cada uno de los samples se calcula el conjunto necesario de las características. Como resultado, tenemos una muestra grande. Mientras que para el objeto a estudiar tenemos sólo un conjunto de características, el método de Monte Carlo nos da la posibilidad de obtenerlas en gran cantidad y construir las funciones de su distribución, lo que nos proporciona mucha más información.

La esquema de la modelación de Monte Carlo descrita arriba parece simple. Pero al realizarla en la práctica, surgen muchas, a veces bastante complejas variaciones. Incluso si nos limitamos a su aplicación en el campo de las finanzas, se pude cerciorarse de su gran amplitud (por ejemplo, en este libro). Nosotros intentaremos aplicar el método de Monte Carlo para estudiar la estabilidad de los Asesores Expertos (EAs). Para eso, necesitamos un modelo probabilista que describe su trabajo.

Modelo probabilista del Asesor Experto

Antes de empezar a tradear en la cuenta real usando el EA, habitualmente lo probamos y optimizamos en el historial de las cotizaciones. Surge una pregunta razonable, ¿por qué nosotros suponemos que los resultados del trading en el pasado los determinan en el futuro? Desde luego, no esperamos que todas las transacciones en el futuro forman absolutamente la misma secuencia que en el pasado. Pero, evidentemente, tenemos la suposición sobre su cierto «parecido». Formalizamos esta representación intuitiva sobre el «parecido» usando la teoría de probabilidades. Conforme a esta formalización, suponemos que el resultado de cada transacción es una determinada realización de un cierto valor aleatorio. El «parecido» de las transacciones en este caso, se determina a través de la semejanza de las funciones de distribución que les corresponden. En esta formalización, las transacciones realizadas en el pasado ayudan a precisar el tipo de la distribución para las futuras transacciones y juzgar sobre sus posibles resultados.

En el marco de la formalización probabilista se puede construir diferentes teorías. Vamos a considerar la más simple y la que se usa con más frecuencia. En ella, el resultado de cada transacción se determina unívocamente por el beneficio relativo k=C1/C0, siendo C0 y C1 el volumen del capital antes y después de la transacción. A continuación, el beneficio relativo de la transacción se denominará el beneficio; y la diferencia C1-C0, el beneficio absoluto de la transacción. Supongamos que los beneficios de todas las transacciones (tanto en el pasado, como en el futuro) son conjuntamente los valores independientes y distribuidos uniformemente. Su distribución se determina por la función de la distribución F(x). De esta manera, nos enfrentamos a la tarea de definir el tipo de esta función usando los valores de los beneficios de las transacciones desde el pasado. Es un problema estándar de la estadística matemática, es decir, la recuperación de la función de la distribución por la muestra. Cualquier método de su resolución siempre da una respuesta aproximada. Aquí tenemos algunos de estos métodos.

1. Como aproximación, se utiliza la función de distribución empírica.

2. Se toma una distribución discreta simple con la que el beneficio de la transacción adquiere uno de dos valores. Se trata del beneficio medio con la probabilidad de la pérdida, o bien de un beneficio medio con la probabilidad del beneficio.

3. En vez de la aproximación discreta, se construye la aproximación continua (tiene la densidad) para la función de distribución. Para eso, se utilizan los métodos parecidos a la estimación de la densidad del Kernel.
   

En adelante, vamos a usar la primera variante, ya que es la más simple y universal. Al trader no le interesa mucho conocer la propia función. Es importante saber qué valores indican en un posible beneficio gracias al trabajo del EA, en el riesgo de su uso y en la estabilidad del beneficio. Se puede obtener estos valores sabiendo la función de la distribución.
Concretizamos el algoritmo de la modelación en nuestro caso. El objeto que nos interesa es un posible resultado del trabajo del EA en el futuro. Se establece unívocamente por la secuencia de transacciones. Cada transacción se establece por el valor del beneficio. Los beneficios están distribuidos de acuerdo con la descripción empírica descrita antes. Tenemos que generar un gran número de estas secuencias y calcular las características necesarias para cada una de ellas. La generación de cada de estas secuencias es simple. Definimos la secuencia de beneficios de las transacciones obtenidos en el historial a través de k1, k2, ..., kn. Generando las secuencias con longitud N, vamos a seleccionar uno de ki (muestra con devolución) N veces de modo aleatorio (con la probabilidad igual a 1/n). Habitualmente, es N=n, puesto que con N grandes la precisión de la aproximación F(x) con distribución empírica disminuye. A veces, esta versión del método de Monte Carlo se llama el método de bootstrap.

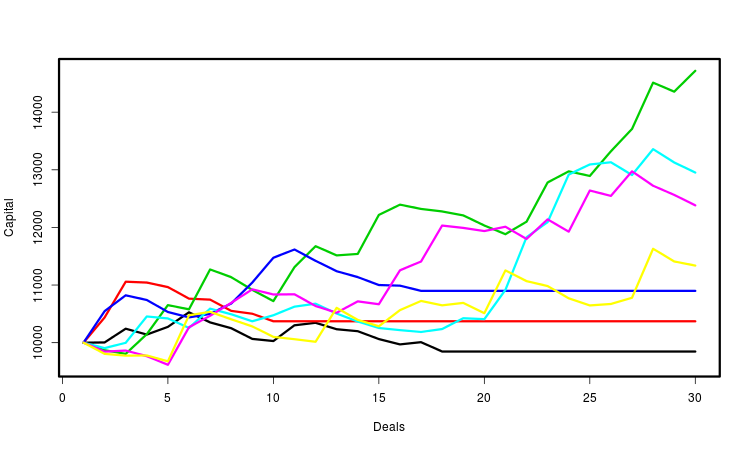
Vamos a ilustrar lo arriba mencionado con la imagen. Se muestran varias curvas del capital, cada una de las cuales se determina por la secuencia generada de transacciones. Para la conveniencia de la percepción, las he marcado con varios colores. En realidad, su cantidad es mucho más grande (varias decenas de miles). Para cada una de ellas, calculamos las características necesarias y hacemos conclusiones estadísticas a base de su conjunto. Es obvio que la característica más importante es el beneficio final.

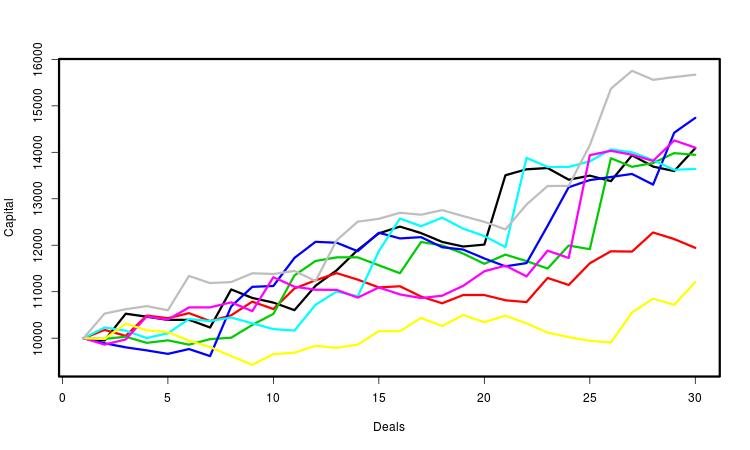
Existen otros enfoques en la formalización probabilista y la siguiente modelación del trabajo del EA. Por ejemplo, se puede modelar las secuencias de los precios en vez de las secuencias de las transacciones, y estudiar las secuencias de los beneficios que el EA ha obtenido de ellas. Dependiendo de los problemas a resolver, se puede seleccionar el principio de la generación de las series de precios. Pero este método requerirá una cantidad mucho más grande de los recursos computacionales. Además, actualmente en MetaTrader no hay métodos regulares de usarlo para un EA aleatorio.

Aplicando la teoría

Nuestra tarea consiste en construir determinados criterios de optimización. Cada uno de ellos corresponde a un objetivo determinado. El objetivo principal es el beneficio final obtenido como resultado de la serie completa de transacciones. Su optimización está incorporada en el Probador de Estrategias. Pero puesto que nos interesa el beneficio en el futuro, tenemos que estimar un posible grado de su desviación del beneficio actual. Cuanto menos sea esta desviación, más estable será el beneficio del sistema. Vamos a analizar tres enfoques.

1. Al obtener una muestra grande de posibles valores del beneficio a través del método de Monte Carlo, podemos estudiar su distribución y las variables relacionadas con ella. El valor medio de este beneficio es muy importante. La dispersión también importa. Cuanto menos sea, más estable será el trabajo del EA y menor será la incertidumbre en sus futuros resultados. Nuestro criterio será igual a la relación del beneficio medio y su dispersión media. Parece al Ratio de Sharpe.
2. Otra característica importante es la reducción (drawdown) del beneficio en una serie de transacciones. Una reducción muy grande puede llevar a la pérdida del depósito, incluso si el EA es rentable. Por esa razón, normalmente la reducción se limita. Es útil de saber cómo eso influye en posible beneficio. El criterio está determinado como beneficio medio, pero con la condición de que se modela la detención del trading cuando se supera el nivel permitido de la reducción.

3. Vamos a construir el criterio que mide la estabilidad del beneficio respecto a la constancia de la distribución de beneficios de las transacciones. Desde el punto de vista de la teoría de probabilidades, eso significa la estacionariedad de los beneficios de transacciones, la que, en principio, es posible también en los casos de la no-estacionariedad de los incrementos del precio. Para eso, usaremos la idea parecida a la simulación en tiempo real (Forward Testing). Dividimos la muestra original de transacciones en la submuestra inicial y final. Para verificar su homogeneidad, podemos aplicar alguna prueba estadística. Precisamente a base de esta prueba, crearemos el criterio para la optimización.
   

Para demostrar nuestra teoría, usaremos el EA «Moving Average.mq5» que entra en la entrega de MetaTrader 5. Vamos a modificar un poco su código. Insertamos la línea del código para incluir nuestro archivo de cabecera al principio:

#include <mcarlo.mqh>

Al final del EA insertamos el código de obtención y uso de nuestro parámetro optimizado:

double OnTester()
  {
   return optpr();         // optimization parameter
  }

Los cálculos principales se realizan en las funciones que se encuentran en el archivo de cabecera «mcarlo.mqh». Lo colocamos en la carpeta «MQL5/Include/». La función principal en este archivo es optpr(). Si se cumplen las condiciones necesarias, ella calcula la variante del criterio optimizado establecida por el parámetro noptpr, de lo contrario, devuelve cero.

double optpr()
  {
   if(noptpr<1||noptpr>NOPTPRMAX) return 0.0;
   double k[];
   if(!setks(k)) return 0.0;
   if(ArraySize(k)<NDEALSMIN) return 0.0;
   MathSrand(GetTickCount());
   switch(noptpr)
     {
      case 1: return mean_sd(k);
      case 2: return med_intq(k);
      case 3: return rmnd_abs(k);
      case 4: return rmnd_rel(k);
      case 5: return frw_wmw(k);
      case 6: return frw_wmw_prf(k);
     }
   return 0.0;
  }

La función setks() calcula el array de beneficios de las transacciones basándose en el historial del trading.

bool setks(double &k[])
  {
   if(!HistorySelect(0,TimeCurrent())) return false;
   uint nhd=HistoryDealsTotal();
   int nk=0;
   ulong hdticket;
   double capital=TesterStatistics(STAT_INITIAL_DEPOSIT);
   long hdtype;
   double hdcommission,hdswap,hdprofit,hdprofit_full;
   for(uint n=0;n<nhd;++n)
     {
      hdticket=HistoryDealGetTicket(n);
      if(hdticket==0) continue;

      if(!HistoryDealGetInteger(hdticket,DEAL_TYPE,hdtype)) return false;
      if(hdtype!=DEAL_TYPE_BUY && hdtype!=DEAL_TYPE_SELL) continue;

      hdcommission=HistoryDealGetDouble(hdticket,DEAL_COMMISSION);
      hdswap=HistoryDealGetDouble(hdticket,DEAL_SWAP);
      hdprofit=HistoryDealGetDouble(hdticket,DEAL_PROFIT);
      if(hdcommission==0.0 && hdswap==0.0 && hdprofit==0.0) continue;

      ++nk;
      ArrayResize(k,nk,NADD);
      hdprofit_full=hdcommission+hdswap+hdprofit;
      k[nk-1]=1.0+hdprofit_full/capital;
      capital+=hdprofit_full;
     }
   return true;
  }

La función sample() genera una secuencia aleatoria b[] desde la secuencia original a[].

void sample(double &a[],double &b[])
  {
   int ner;
   double dnc;
   int na=ArraySize(a);
   for(int i=0; i<na;++i)
     {
      dnc=MathRandomUniform(0,na,ner);
      if(!MathIsValidNumber(dnc)) {Print("MathIsValidNumber(dnc) error ",ner); ExpertRemove();}
      int nc=(int)dnc;
      if(nc==na) nc=na-1;
      b[i]=a[nc];
     }
  }

A continuación, analizaremos en detalle cada uno de los tipos de optimización de los criterios arriba mencionados. En todos los casos, vamos a optimizar en el mismo intervalo temporal: primavera/verano de 2017 para EURUSD. El timeframe será H1, y el modo de simulación será OHLC del gráfico de un minuto. Siempre usaremos el algoritmo genético usando el criterio personalizado de la optimización. Puesto que nuestra tarea consiste en demostrar la teoría, y no preparar el EA para el trading real, este enfoque simplificado parece bastante lógico.

Estabilidad del beneficio hacia la dispersión al azar

Supongamos que tenemos una muestra de los beneficios generados finalmente. Podemos usar los métodos de la estadística matemática para estudiarla. En la imagen de abajo, vemos el histograma con la línea punteada que muestra la mediana seleccionada.

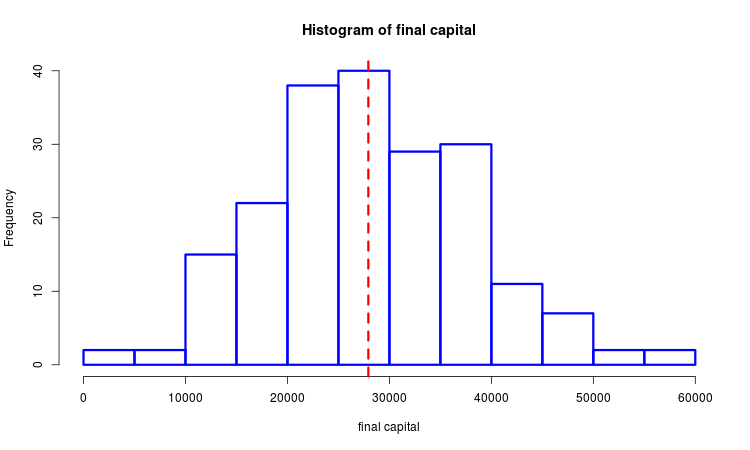
Vamos a construir des variantes semejantes del criterio de optimización. Se calculan en las funciones mean_sd() y med_intq(). Lo común en estas variantes es que ellas representan la relación entre la media y la medida de dispersión. La diferencia consiste en la manera de cómo la media y la medida de dispersión están determinadas. En el primer caso, se trata de la media aritmética y la desviación media cuadrática, en el segundo, es la mediana y el rango intercuartil selectivos. Cuanto más grande sea el beneficio y más pequeño sea su dispersión, ambos serán más grandes. Hay un parecido evidente con el Ratio de Sharpe, lo único que aquí se trata del beneficio en la serie completa de transacciones, y no en una transacción. La segunda variante del criterio es más estable hacia los spikes, en comparación con la primera.

double mean_sd(double &k[])
  {
   double km[],cn[NSAMPLES];
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      cn[n]=1.0;
      for(int i=0; i<nk;++i) cn[n]*=km[i];
      cn[n]-=1.0;
     }
   return MathMean(cn)/MathStandardDeviation(cn);
  }

double med_intq(double &k[])
  {
   double km[],cn[NSAMPLES];
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      cn[n]=1.0;
      for(int i=0; i<nk;++i) cn[n]*=km[i];
      cn[n]-=1.0;
     }
   ArraySort(cn);
   return cn[(int)(0.5*NSAMPLES)]/(cn[(int)(0.75*NSAMPLES)]-cn[(int)(0.25*NSAMPLES)]);
  }

Abajo podemos observar dos parejas de resultados de la simulación de los EAs optimizados según este criterio. En la primera pareja tenemos el resultado según la primera variante, y para la comparación, el resultado con el beneficio máximo. Es evidente que la primera de ellas es más preferible, ya que nos da una curva del capital más suavizada. Si quiere, puede aumentar el beneficio final, aumentando el volumen de transacciones.

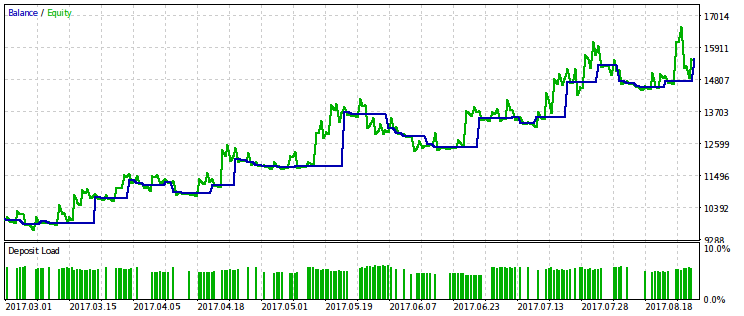
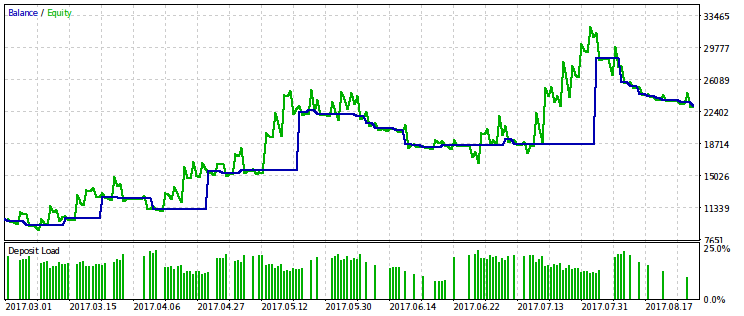
La misma pareja de resultados se muestra para la segunda variante del criterio de optimzación. Nos permite hacer las mismas conclusiones.

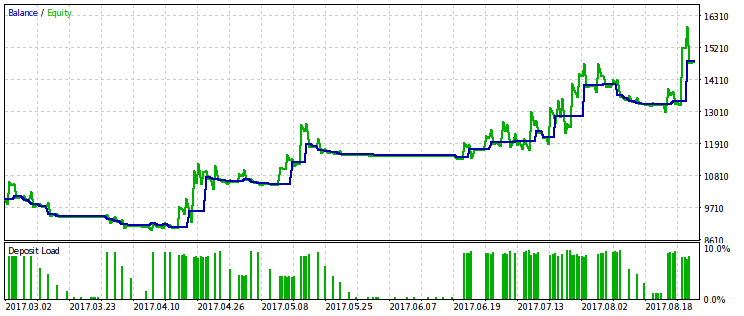
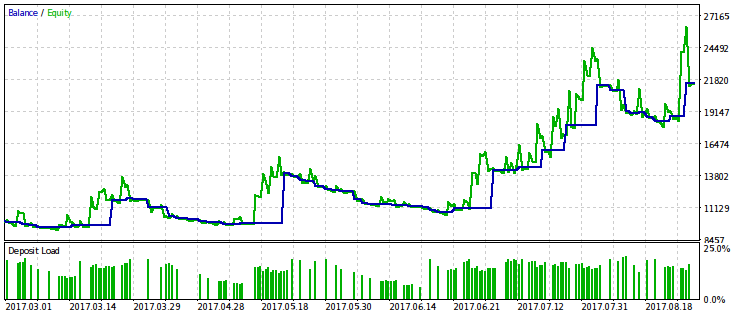
Estabilidad del beneficio respecto a la reducción

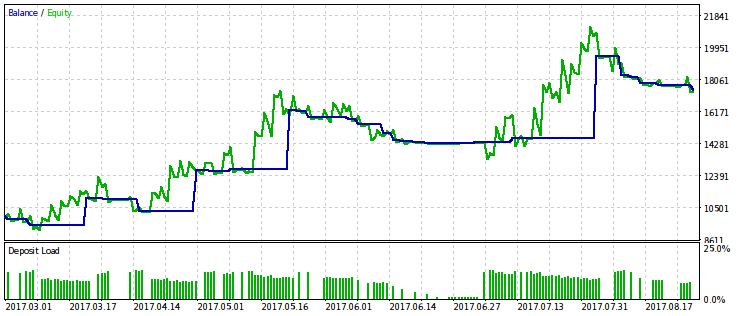
En cada secuencia generada de transacciones, monitoreamos el tamaño de la reducción. Si el resto del capital tras la parte inicial de la serie de transacciones compone la parte menor que se establece por el parámetro rmndmin, las transacciones restantes se omiten. En la imagen de abajo podemos observar que si el nivel de la reducción relativa se supera, el capital deja de cambiar, y la sección final de la línea del capital se hace horizontal.

Tenemos dos opciones del calculo del criterio: para la reducción absoluta y para la relativa. En caso de la reducción absoluta, la parte del capital se calcula a partir de su valor inicial; y en caso de la relativa, a partir del valor máximo. Las funciones que calculan estas variantes de los parámetros se denominan respectivamente: rmnd_abs() t rmnd_rel(). En ambos casos, el valor del criterio es la media de los beneficios generados.

double rmnd_abs(double &k[])
  {
   if (rmndmin<=0.0||rmndmin>=1.0) return 0.0;
   double km[],cn[NSAMPLES];
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      cn[n]=1.0;
      for(int i=0; i<nk;++i)
        {
         cn[n]*=km[i];
         if(cn[n]<rmndmin) break;
        }
      cn[n]-=1.0;
     }
   return MathMean(cn);
  }

double rmnd_rel(double &k[])
  {
   if (rmndmin<=0.0||rmndmin>=1.0) return 0.0;
   double km[],cn[NSAMPLES],x;
   int nk=ArraySize(k);
   ArrayResize(km,nk);
   for(int n=0; n<NSAMPLES;++n)
     {
      sample(k,km);
      x=cn[n]=1.0;
      for(int i=0; i<nk;++i)
        {
         cn[n]*=km[i];
         if(cn[n]>x) x=cn[n];
         else if(cn[n]/x<rmndmin) break;
        }
      cn[n]-=1.0;
     }
   return MathMean(cn);
  }

Podemos realizar la optimización bien usando el parámetro fijo conveniente rmndmin, bien buscando su valor óptimo.

Mostraremos los resultados sólo para el criterio relacionado con la reducción relativa, ya que su limitación muestra un efecto más expresivo. Realizamos la optimización con varias variantes del valor fijo rmndmin: 0.95, 0.75 y 0.2.

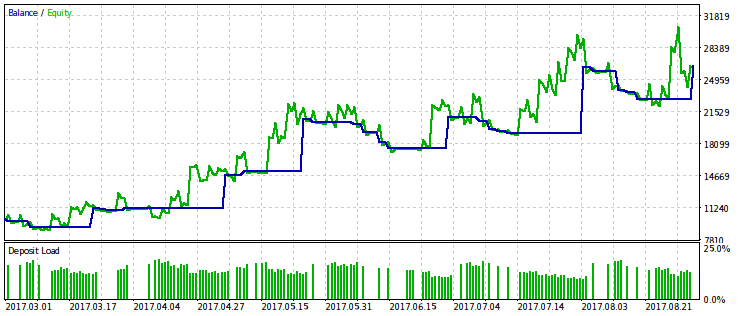
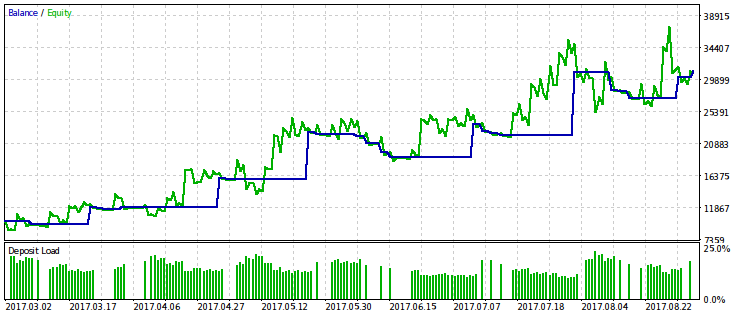
Cuanto menos sea el valor rmndmin, menos efecto tendrá la limitación para la reducción, y los resultados de la optimización serán más parecidos a los que se obtienen durante la maximización común del beneficio. Eso puede ser considerado como consecuencia de la ley de números grandes: principio de la teoría de probabilidades. En las imágenes este efecto no se salta a los ojos a la primera, porque tienen la escala diferente por el eje vertical (debido al ajuste de todas las imágenes a los tamaños iguales) y el crecimiento del drawdown con la disminución de rmndmin tampoco es tan evidente a la primera vista.

Ahora incluiremos el parámetro rmndmin en los que optimizamos y continuaremos la optimización según el mismo criterio.

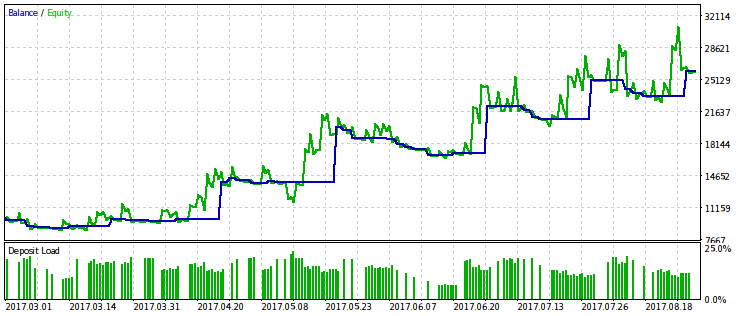
Obtenemos el valor óptimo rmndmin=0.55. Con este valor, podemos tener una reducción de la mitad de la cuenta, lo que parece poco aceptable. Por eso, es dudoso que merece la pena usarlo en el trading real. La utilidad aquí consiste en otra cosa: se ve que el «sobreaguante» de las reducciones aún más grandes seguramente no tiene ningún sentido. Eso corresponde a la segunda parte del dicho: «Permite crecer al beneficio, recorta las pérdidas».

Estabilidad de la distribución del beneficio de transacciones hacia la no-estacionariedad de los precios

El comportamiento de los precios puede cambiar. Además, sería de desear que los resultados del Trabajo del EA sean estables. Desde el punto de vista de nuestro modelo probabilista del EA, eso significa que necesitamos la estacionariedad de los beneficios de transacciones, incluso en los casos de la no-estacionariedad de los incrementos del precio.

Nuestro criterio de optimización compara la parte inicial de la secuencia de las transacciones con la parte final, y cuanto más próximas estén, su valor será más alto. La proximidad se determina a base del criterio de Mann-Whitney-Wilcoxon. Explicaremos su esencia. Que tengamos dos muestras de las transacciones. El criterio determina a qué grado una está desplazada respecto a la otra. Cuanto menos sea el desplazamiento, mayor será el valor del criterio. Vamos a explicarlo usando la imagen: ahí cada muestra se representa por un histograma correspondiente. El valor más grande del criterio se observa en la imagen del centro.

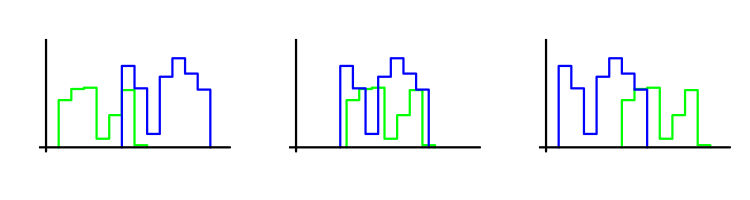
En este caso, el método de Monte Carlo no se utiliza por sí mismo. No obstante, el valor grande del criterio WMW sirve del argumento para su aplicación, ya que confirma la suposición de que el tipo de la distribución de los beneficios de transacciones no se altera.

En nuestro archivo hay otra versión del criterio: producto del criterio WMW por el beneficio.

double frw_wmw(double &k[])
  {
   if (fwdsh<=0.0||fwdsh>=1.0) return 0.0;
   int nk=ArraySize(k), nkf=(int)(fwdsh*nk), nkp=nk-nkf;
   if(nkf<NDEALSMIN||nkp<NDEALSMIN) return 0.0;
   double u=0.0;
   for (int i=0; i<nkp; ++i)
     for (int j=0; j<nkf; ++j)
       if(k[i]>k[nkp+j]) ++u;
   return 1.0-MathAbs(1.0-2.0*u/(nkf*nkp));
  }

double frw_wmw_prf(double &k[])
  {
   int nk=ArraySize(k);
   double prf=1.0;
   for(int n=0; n<nk; ++n) prf*=k[n];
   prf-=1.0;
   if(prf>0.0) prf*=frw_wmw(k);
   return prf;
  }

El uso directo del criterio WMW es problemático, porque puede tomar una variante de pérdidas por la óptima. Sería mejor optimizar el EA por el beneficio y rechazar las variantes con valores pequeños de este parámetro, pero por ahora no está claro como hacer eso. Se puede seleccionar alguna cantidad de variantes que son mejores desde el punto de vista del criterio WMW, y luego, de ellas elegir aquél que proporciona el beneficio máximo.

Mostraremos los ejemplos de dos mejores repasos de diez. Uno será rentable, el otro, de pérdidas.

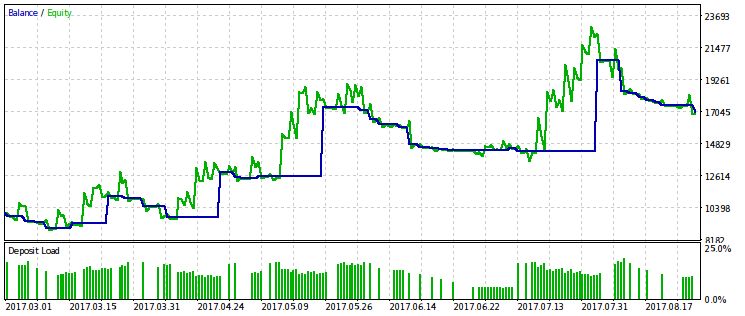
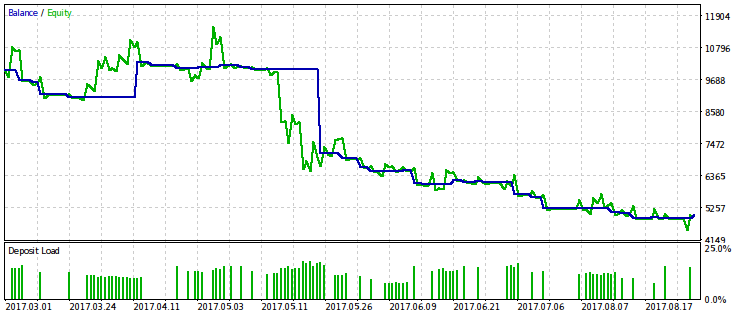
Se tiene la impresión que el criterio WMW sería más útil al comparar dos EAs diferentes en el mismo intervalo temporal, o el mismo EA en intervalos diferentes. Pero por ahora, no está de todo claro cómo hacer que esta comparación sea constante.

Además, mostraremos el ejemplo de la optimización según el criterio que es igual al resultado del criterio WMW por el beneficio. Por las señas, parece mucho a una optimización simple por el beneficio, y eso significa que su aplicación será sobrante.

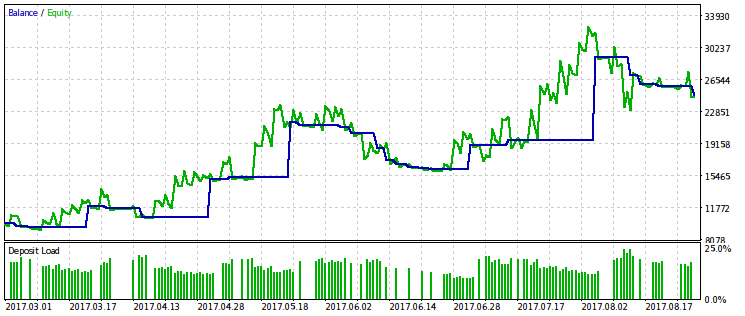
Conclusión

En este artículo, apenas hemos aludido a algunos aspectos del tema planteado. Vamos a concluirlo con algunos comentarios.

• Los criterios de la optimización construidos en este artículo pueden ser útiles al formalizar las representaciones intuitivas sobre cuál de las secuencias de transacciones es mejor. Eso es útil para hacer la selección de una cantidad grande de variantes.
  
• Hay medidas conocidas para el riesgo, como VaR (Value At Risk), o la probabilidad de la quiebra. Si se usan directamente como criterio para la optimización, el resultado será regular. Los volúmenes del trading y el número de transacciones estarán reducidos. Por eso, necesitamos un criterio de compromiso,, que depende de dos variables: tanto del riesgo, como del beneficio. El problema es el siguiente, ¿cuál variante de este criterio se debe eligir? ya que hay una cantidad enorme de las funciones a partir de dos variables. La elección del criterio, por ejemplo, puede determinarse por el nivel de la «agresividad» de la estrategia comercial, que puede variar muchísimo.
  
• Diferentes variantes de los criterios de la optimización que miden la estabilidad pueden ser útiles para diferentes clases de los EAs. Por ejemplo, los EAs de tendencia van a diferenciarse de los que tradean en el rango, mientras que los sistemas con el Take Profit fijo van a diferenciarse de los que cierran las transacciones por el Trailing Stop. Las distribuciones de los beneficios de estos EAs también van a pertenecer a clases diferentes, y dependiendo de eso uno u otro criterio será más conveniente.
• Algunos criterios son útiles no tanto para comparar el comportamiento del mismo EA en un intervalo de tiempo fijo con diferentes conjuntos de parámetros, sino para comparar dos EAs diferentes. Usando estos criterios, se puede comparar también el trabajo de un EA en diferentes intervalos de tiempo.
  
• La modelación por el método de Monte Carlo sería más completa si tuviéramos la posibilidad de poner en la entrada del EA no sólo el historial de precios disponible, sino también sus copias alteradas de forma aleatoria. Eso permitiría estudiar la estabilidad de los EAs más a fondo, aunque a costa del aumento del volumen de los cálculos.
  

Archivos adjuntos

№	nombre	tipo	descripción
1	Moving Average_mcarlo.mq5	Script	Moving Average.mq5 estándar modificado
2	mcarlo.mqh	Archivo de cabecera	Archivo principal con las funciones que realizan todos los cálculos necesarios