Индикатор CAPM модели на рынке Forex

Историческое развитие модели CAPM

Появление модели оценки капитальных активов стало результатом революционных изменений в понимании взаимосвязи между риском и доходностью на финансовых рынках. В начале 1960-х годов финансовая наука переживала период интенсивного развития, когда исследователи стремились создать математически строгие модели для объяснения ценообразования активов.

Предпосылки для создания CAPM были заложены в работах Гарри Марковица, который в 1952 году представил современную портфельную теорию. Марковиц продемонстрировал, как инвесторы могут оптимизировать соотношение риска и доходности путем диверсификации портфеля. Его концепция эффективной границы стала фундаментом для дальнейших теоретических разработок в области финансов.

Уильям Шарп, работая над развитием идей Марковица, столкнулся с практической проблемой вычислительной сложности оптимизации портфелей. В то время компьютерные мощности были ограничены, и расчет ковариационной матрицы для большого количества активов представлял серьезную техническую проблему. Это побудило Шарпа к поиску упрощенной модели, которая сохранила бы теоретическую строгость, но была бы более практичной в применении.

В 1964 году Шарп опубликовал свою знаменитую статью "Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk", где впервые была представлена модель CAPM. Независимо от Шарпа, схожие идеи развивали Джон Линтнер и Ян Моссин, что подтверждало фундаментальность открытых закономерностей. За свой вклад в развитие финансовой теории Шарп был удостоен Нобелевской премии по экономике в 1990 году.

Модель быстро получила признание в академических кругах и стала основой для множества практических приложений в управлении инвестициями. К 1970-м годам CAPM уже широко использовалась инвестиционными фондами и корпорациями для оценки стоимости капитала и принятия инвестиционных решений.

Математическое устройство классической модели CAPM

Классическая модель CAPM основывается на ряде ключевых допущений, которые определяют ее математическую структуру и практическую применимость. Центральная формула модели выражает ожидаемую доходность актива через систему взаимосвязанных параметров:

E(Ri) = Rf + βi × (E(Rm) - Rf)

где E(Ri) представляет ожидаемую доходность актива i, Rf обозначает безрисковую ставку доходности, βi является коэффициентом бета для актива i, а E(Rm) — ожидаемая доходность рыночного портфеля.

Коэффициент бета играет центральную роль в модели и определяется как отношение ковариации доходности актива с доходностью рынка к дисперсии рыночной доходности:

βi = Cov(Ri, Rm) / Var(Rm)

Этот показатель измеряет чувствительность доходности конкретного актива к изменениям общей рыночной доходности. Активы с бетой больше единицы демонстрируют большую волатильность по сравнению с рынком, в то время как активы с бетой меньше единицы являются менее волатильными.

Модель предполагает существование линейной зависимости между систематическим риском (измеряемым через бету) и ожидаемой доходностью. Эта зависимость графически представляется в виде линии рынка ценных бумаг (Security Market Line), которая показывает равновесные соотношения между риском и доходностью для всех активов в экономике.

Фундаментальные допущения CAPM включают совершенную конкуренцию на рынках, отсутствие транзакционных издержек, одинаковые ожидания всех инвесторов относительно будущих доходностей, возможность неограниченного кредитования и заимствования по безрисковой ставке, а также нормальное распределение доходностей активов.

Модель также предполагает, что все инвесторы являются рациональными максимизаторами полезности, которые принимают решения исключительно на основе ожидаемой доходности и риска портфеля. Кроме того, предполагается, что инвесторы имеют одинаковый инвестиционный горизонт и одинаковую информацию о рынке.

Несистематический риск в рамках CAPM полностью элиминируется через диверсификацию портфеля, поэтому инвесторы получают компенсацию только за принятие систематического риска. Это означает, что в равновесии все эффективные портфели должны находиться на одной прямой линии в координатах "риск-доходность".

Теоретические основы адаптации CAPM для валютного рынка

Классическая формула CAPM выражает ожидаемую доходность актива через безрисковую ставку и премию за систематический риск. В контексте валютных пар эта концепция приобретает особое значение, поскольку каждая валютная пара представляет собой относительную стоимость двух национальных экономик со всеми присущими им макроэкономическими рисками.

В нашей реализации для платформы MetaTrader 5 мы модифицировали классический подход, заменив коэффициент бета на динамическую премию за риск, основанную на исторической волатильности валютной пары. Это решение обусловлено спецификой валютного рынка, где систематический риск проявляется через изменчивость курсовых колебаний, а не через корреляцию с рыночным портфелем.

//--- input parameters
input int      InpPeriod = 20;              // Период для расчета
input double   InpRiskFreeRate = 0.05;      // Безрисковая ставка (годовая)
input double   InpRiskPremium = 0.02;       // Премия за риск валютной пары
input bool     InpShowInfo = true;          // Показывать информационную панель

//--- indicator buffers
double ExpectedReturnBuffer[];
double RiskPremiumBuffer[];

Ключевой особенностью реализации является использование робастного подхода к вычислению дисперсии доходностей. Мы применяем несмещенную оценку дисперсии и корректно обрабатываем случаи недостаточности данных, что критически важно для поддержания стабильности расчетов в условиях рыночных разрывов или низкой ликвидности.

Аннуализация волатильности производится с использованием стандартного коэффициента квадратного корня из 252, что соответствует количеству торговых дней в году. Этот подход позволяет привести показатели волатильности к сопоставимому масштабу с безрисковыми ставками, которые традиционно котируются в годовом исчислении.

//--- аннуализируем показатели (252 торговых дня)
double annual_volatility = volatility * MathSqrt(252.0);
double annual_return = mean_return * 252.0;

//--- рассчитываем премию за риск на основе волатильности
double dynamic_risk_premium = InpRiskPremium * (annual_volatility / 0.15);

Экономическая интерпретация результатов индикатора

Наиболее интересным аспектом разработанного индикатора является его поведение в различных рыночных условиях. Эмпирические наблюдения показывают, что ожидаемая доходность и премия за риск демонстрируют выраженную тенденцию к росту именно в периоды рыночных экстремумов. Это явление имеет глубокие экономические корни и отражает фундаментальные принципы ценообразования на финансовых рынках.

Во время формирования локальных пиков волатильность валютной пары естественным образом возрастает, поскольку участники рынка пересматривают свои ожидания относительно будущих движений курса. Увеличение неопределенности приводит к росту премии за риск, которую инвесторы требуют за владение данным активом. Аналогичная ситуация наблюдается и во время формирования рыночных впадин, когда панические настроения и массовая фиксация убытков создают избыточную будущую доходность.

void ShowInfoPanel(int current_bar)
{
    string info = "";
    info += "=== CAPM Forex Model ===\n";
    info += StringFormat("Risk Premium: %.2f%%\n", RiskPremiumBuffer[current_bar] * 100);
    info += StringFormat("Expected Return: %.2f%%\n", ExpectedReturnBuffer[current_bar] * 100);
    
    if(current_volatility > 0.20)
        info += "Status: HIGH RISK\n";
    else if(current_volatility > 0.10)
        info += "Status: MEDIUM RISK\n";
    else
        info += "Status: LOW RISK\n";
}

Это поведение индикатора согласуется с классической теорией эффективных рынков, согласно которой, более высокий риск должен компенсироваться более высокой ожидаемой доходностью. В контексте валютного трейдинга это означает, что периоды повышенной волатильности потенциально предоставляют более благоприятные возможности для получения прибыли, но требуют соответственно более осторожного подхода к управлению рисками.

Техническая реализация и вычислительные аспекты

Архитектура индикатора построена на использовании двух основных буферов данных, каждый из которых выполняет специфическую аналитическую функцию. ExpectedReturnBuffer содержит значения ожидаемой доходности, рассчитанные на основе модифицированной формулы CAPM, в то время как RiskPremiumBuffer отражает динамику премии за риск в зависимости от изменений волатильности.

//--- plot Expected Return
#property indicator_label1  "Expected Return"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  2

//--- plot Risk Premium
#property indicator_label2  "Risk Premium"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrRed
#property indicator_style2  STYLE_DASH
#property indicator_width2  1

Функция CalculateCurrentVolatility представляет собой оптимизированную реализацию алгоритма расчета текущей волатильности с использованием встроенных функций MetaTrader 5 для работы с историческими данными. Применение функции CopyClose обеспечивает эффективный доступ к ценовым данным без необходимости итерации по всему массиву котировок.

double CalculateCurrentVolatility(int current_bar)
{
    if(current_bar < InpPeriod) 
        return 0.0;
    
    double returns_sum = 0.0;
    double returns_sq_sum = 0.0;
    int valid_count = 0;
    
    // Получаем данные цен закрытия для расчета
    double prices[];
    int copied = CopyClose(Symbol(), PERIOD_CURRENT, current_bar - InpPeriod, InpPeriod + 1, prices);
    
    if(copied <= InpPeriod)
        return 0.0;
    
    // Рассчитываем доходности
    for(int j = 1; j < ArraySize(prices); j++)
    {
        if(prices[j-1] > 0)
        {
            double daily_return = (prices[j] - prices[j-1]) / prices[j-1];
            returns_sum += daily_return;
            returns_sq_sum += daily_return * daily_return;
            valid_count++;
        }
    }
    
    if(valid_count < 2) 
        return 0.0;
    
    double mean_return = returns_sum / valid_count;
    double variance = (returns_sq_sum / valid_count) - (mean_return * mean_return);
    double volatility = MathSqrt(MathMax(variance, 0.0));
    
    return volatility * MathSqrt(252.0); // аннуализированная волатильность
}

Практическая значимость индикатора в торговых системах

Разработанный CAPM-индикатор демонстрирует высокую практическую ценность, именно благодаря своей способности количественно оценивать изменения в соотношении риска и доходности в динамике рынка. Когда валютная пара приближается к критическим уровням поддержки или сопротивления, индикатор фиксирует возрастание волатильности и, соответственно, увеличивает оценку ожидаемой доходности.

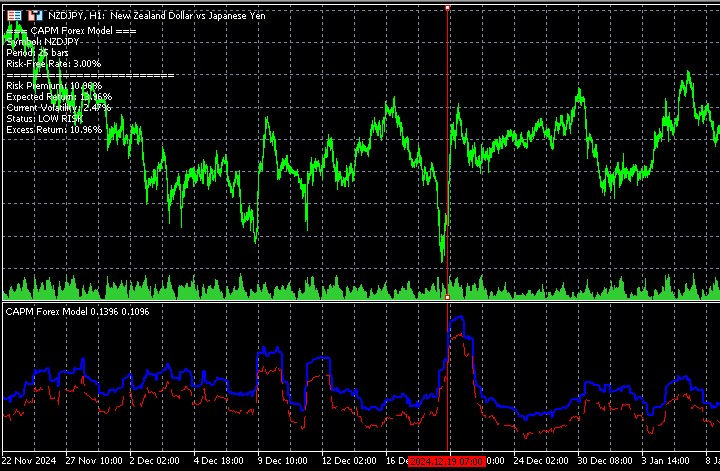
Эта особенность делает индикатор особенно полезным для трейдеров, применяющих контртрендовые стратегии. Рост показателей риска и доходности на экстремумах может служить сигналом для поиска точек входа против текущего тренда, поскольку повышенная волатильность часто предшествует разворотным движениям.

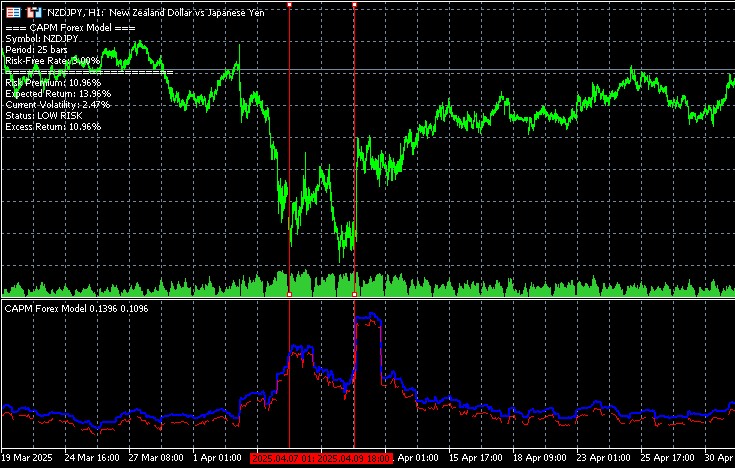
Для трендовых стратегий индикатор предоставляет информацию о том, насколько текущее движение цены соответствует справедливой оценке риска. Если фактическое движение существенно превышает ожидаемую доходность, рассчитанную индикатором, это может указывать на формирование спекулятивного пузыря или избыточной реакции рынка на новости.

Минусы модели и направления развития

Несмотря на практическую полезность, адаптированная CAPM-модель для валютного рынка имеет ряд концептуальных ограничений, которые необходимо учитывать при интерпретации результатов. Основное допущение о нормальном распределении доходностей не всегда соответствует реальным характеристикам валютных рынков, особенно в периоды макроэкономических шоков или политических кризисов.

Модель также не учитывает эффекты автокорреляции в рядах доходностей, которые могут быть значимыми для высокочастотных данных. Кроме того, использование фиксированной безрисковой ставки может не отражать реальную динамику процентных ставок центральных банков, особенно в периоды активной монетарной политики.

Перспективным направлением развития индикатора является интеграция с макроэкономическими данными для динамической корректировки безрисковой ставки в соответствии с текущими решениями центральных банков. Также представляет интерес внедрение адаптивных алгоритмов для автоматической настройки параметров модели в зависимости от режима волатильности конкретной валютной пары.

Включение элементов машинного обучения может позволить индикатору адаптироваться к изменяющимся рыночным условиям и повысить точность прогнозирования ожидаемой доходности. Такой подход особенно актуален в контексте современных алгоритмических торговых систем, где скорость адаптации к новым рыночным режимам является критическим фактором успеха.

Разработанный CAPM-индикатор представляет собой успешную попытку применения классической финансовой теории к специфике валютного трейдинга. Его способность количественно оценивать динамику соотношения риска и доходности делает его ценным инструментом для принятия обоснованных торговых решений в условиях постоянно изменяющейся рыночной конъюнктуры.

Заключение

Проведённое исследование показало, что адаптация модели CAPM к валютному рынку может быть эффективно реализована в виде индикатора для MetaTrader 5. Разработанный инструмент динамически оценивает ожидаемую доходность валютных пар на основе волатильности и успешно выявляет периоды повышенного риска и потенциала.

Индикатор демонстрирует, что классические модели, при корректной технической реализации, остаются актуальными в современной торговле и способны улучшить качество торговых решений.