Neuinterpretation klassischer Strategien in MQL5 (Teil III): Prognose des FTSE 100

Künstliche Intelligenz (KI) bietet potenziell unendlich viele Anwendungsmöglichkeiten für die Strategie des modernen Anlegers. Bedauerlicherweise hat kein einzelner Anleger genügend Zeit, um jede Strategie sorgfältig zu analysieren, bevor er sich entscheidet, welcher er sein Kapital anvertraut. In dieser Artikelserie werden wir Ihnen helfen, die riesige Landschaft möglicher KI-basierter Strategien zu durchforsten, um eine Strategie zu finden, die zu Ihrem Anlegerprofil passt.

Überblick über die Handelsstrategie

Die Londoner Börse (LSE) ist eine der ältesten Börsen in der entwickelten Welt. Sie wurde 1801 gegründet und ist die wichtigste Börse des Vereinigten Königreichs. Sie wird neben der New Yorker und der Tokioter Börse als eine der großen Drei angesehen. Die Londoner Börse ist die größte Börse Europas, und laut ihrer offiziellen Website beläuft sich die aktuelle Marktkapitalisierung aller an der Börse notierten Unternehmen auf etwa 4,4 Billionen britische Pfund.

Der Financial Times Stock Exchange (FTSE) 100 ist ein von der LSE abgeleiteter Index, der die 100 größten an der LSE notierten Unternehmen abbildet. Diese Unternehmen werden gemeinhin als Blue-Chip-Aktien bezeichnet und gelten angesichts des guten Rufs, den sich die Unternehmen im Laufe der Zeit erworben haben, und ihrer nachgewiesenen Erfolgsbilanz als relativ sichere Anlagen. Wir können unser Wissen darüber, wie der FTSE 100 Index berechnet wird, nutzen, um eine neue Handelsstrategie zu entwickeln, die den zukünftigen Schlusskurs des FTSE 100 vorhersagt, indem sie den aktuellen Schlusskurs des Index sowie die Performance von 10 großen, im Index enthaltenen Aktien berücksichtigt.

Überblick über die Methodik

Wir haben unseren KI-gesteuerten Expert Advisor vollständig in MQL5 entwickelt. Das gibt uns Flexibilität, denn unser Modell kann für verschiedene Zeiträume verwendet werden, ohne dass es ständig angepasst werden muss. Außerdem können wir die Modellparameter dynamisch anpassen, z. B. wie weit in die Zukunft das Modell prognostizieren soll. Unser Modell verwendete insgesamt 12 Eingaben, um den zukünftigen Schlusskurs des FTSE 100 in 20 Schritten in die Zukunft zu prognostizieren.

Wir haben eine Z-Standardisierung durchgeführt, um jede unserer Modelleingaben anhand der Spaltenmittelwerte und der Standardabweichung zu normalisieren und zu skalieren. Unser Ziel war der künftige Schlusskurs des FTSE100-Index in 20 Schritten in die Zukunft, und wir erstellten ein multiples lineares Regressionsmodell zur Prognose des künftigen Schlusskurses des Index.

Nicht alle Modelle des maschinellen Lernens sind gleich gut, was besonders bei Aufgaben im Zusammenhang mit Prognosen deutlich wird. Betrachten wir die Entscheidungsbäume: Baumalgorithmen arbeiten im Allgemeinen mit einer Aufteilung der Daten in Gruppen, und wenn das Modell eine Vorhersage treffen soll, gibt es einfach den Gruppenmittelwert derjenigen Gruppe zurück, die am besten zu den aktuellen Eingabedaten passt. Daher führen baumbasierte Algorithmen keine Extrapolation durch, d. h. sie verfügen nicht über die Fähigkeit, in die Zukunft zu blicken und eine Vorhersage zu treffen. Wenn also ein baumbasiertes Modell fünf ähnliche Eingaben von fünf verschiedenen Zeitpunkten erhält, könnte es für alle fünf den gleichen Schlusskurs vorhersagen, wenn sie ähnlich genug sind, während unser lineares Regressionsmodell in der Lage ist, zu extrapolieren und uns eine Vorhersage über den zukünftigen Schlusskurs eines Wertpapiers zu geben.

Ursprünglicher Entwurf als Skript

Wir werden unsere Idee zunächst als einfaches Skript in MQL5 aufbauen, damit wir uns ein Bild davon machen können, wie die Teile unseres Systems zusammenarbeiten. Wir beginnen mit der Definition unserer globalen Variablen.

//+------------------------------------------------------------------+
//|                                                        UK100.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+

//1) ADM.LSE  - Admiral
//2) AAL.LSE  - Anglo American
//3) ANTO.LSE - Antofagasta
//4) AHT.LSE  - Ashtead
//5) AZN.LSE  - AstraZeneca
//6) ABF.LSE  - Associated British Foods
//7) AV.LSE   - Aviva
//8) BARC.LSE - Barclays
//9) BP.LSE   - BP
//10) BKG.LSE - Berkeley Group 
//11) UK100   - FTSE 100 Index

//+-------------------------------------------------------------------+
//| Global variables                                                  |
//+-------------------------------------------------------------------+
int fetch = 2000;
int look_ahead = 20;
double mean_values[11],std_values[11];
string list_of_companies[11] = {"ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"};
vector intercept = vector::Ones(fetch);
matrix target = matrix::Zeros(1,fetch);
matrix coefficients;
matrix input_matrix = matrix::Zeros(12,fetch);

Die erste Aufgabe, die wir erledigen werden, ist das Abrufen und Normalisieren der Eingabedaten. Wir speichern die Eingabedaten in einer Matrix und die Zieldaten in einer eigenen Matrix

void OnStart()
  {
//--- Fetch the target
target.CopyRates("UK100",PERIOD_CURRENT,COPY_RATES_CLOSE,1,fetch);

//--- Fill in the input matrix
for(int i = 0; i < 11; i++)
   {
      //--- Add the symbol to market watch
      SymbolSelect(list_of_companies[i],true);
      //--- Fetch historical data
      vector temp = vector::Zeros(fetch);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,1+look_ahead,fetch);
      //--- Store the mean value and standard deviation, also scale the data
      mean_values[i] = temp.Mean();
      std_values[i] = temp.Std();
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i);
   }
//--- Add the intercept
input_matrix.Row(intercept,11);

//--- Show the input data
Print("Input data:");
Print(input_matrix);

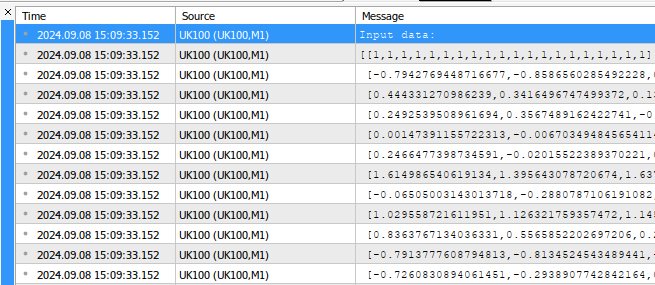
Abb. 1: Ein Beispiel für die von unserem Skript erzeugte Ausgabe

Nachdem wir unsere Eingabedaten abgerufen haben, können wir nun mit der Berechnung unserer Modellparameter fortfahren. Glücklicherweise können die Koeffizienten eines multiplen linearen Regressionsmodells mit einer geschlossenen Formel berechnet werden. Nachstehend finden Sie ein Beispiel für die Modellkoeffizienten.

//--- Calculating coefficient values
coefficients = target.MatMul(input_matrix.PInv());

//--- Display the coefficient values
Print("UK100 Coefficients:");
Print(coefficients.Transpose());

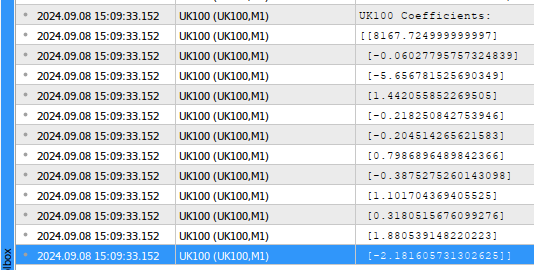
Abb. 2: Unsere Modellparameter

Lassen Sie uns die Ergebnisse gemeinsam interpretieren: Der erste Koeffizientenwert stellt den Durchschnittswert des Ziels dar, wenn alle Modelleingaben 0 sind. Dies ist die mathematische Definition des Bias-Parameters. In unserer Handelsanwendung macht dies jedoch intuitiv wenig Sinn. Technisch gesehen, wenn alle Aktien des FTSE 100 mit 0 Britischen Pfund bewertet würden, dann würde der durchschnittliche zukünftige Wert des FTSE 100 ebenfalls 0 Britische Pfund betragen. Der zweite Koeffiziententerm stellt die marginale Veränderung des zukünftigen Wertes des FTSE 100 dar, wenn man davon ausgeht, dass alle anderen Aktien zu demselben Preis schließen. Wenn also die Admiral-Aktien um eine Einheit steigen, ist zu beobachten, dass der künftige Schlusskurs des Index leicht zu fallen scheint.

Die Vorhersage unseres Modells ist so einfach wie die Multiplikation des aktuellen Kurses jeder Aktie mit dem berechneten Koeffizientenwert und die Summierung all dieser Produkte. Nachdem wir nun eine Vorstellung davon haben, wie wir unser Modell aufbauen können, sind wir bereit, mit dem Aufbau unseres Expert Advisors zu beginnen.

Implementierung unseres Expert Advisors

Wir beginnen mit der Definition von Eingaben, die der Nutzer ändern kann, um das Verhalten des Programms zu verändern.

//+------------------------------------------------------------------+
//|                                                  FTSE 100 AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| User inputs                                                      |
//+------------------------------------------------------------------+
input int look_ahead = 20;       // How far into the future should we forecast?
input int rsi_period = 20;       // The period of our RSI
input int profit_target = 20;     // After how much profit should we close our positions?
input bool ai_auto_close = true; // Should the AI automatically close positions?

Dann werden wir die Handelsbibliothek importieren, die uns bei der Verwaltung unserer Positionen hilft.

//+------------------------------------------------------------------+
//| Libraries we need                                                |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

Nun werden wir einige globale Variablen definieren, die wir in unserem Expert Advisor benötigen.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
double position_profit = 0;
int fetch = 20;
matrix coefficients;
matrix input_matrix = matrix::Zeros(12,fetch);
double mean_values[11],std_values[11],rsi_buffer[1];
string list_of_companies[11] = {"ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"};
ulong open_ticket;

Wir werden nun eine Funktion definieren, die unsere Trainingsdaten abruft. Erinnern Sie sich daran, dass wir die Trainingsdaten abrufen und dann unsere Daten normalisieren und standardisieren wollen, bevor wir sie der Eingabematrix hinzufügen.

//+------------------------------------------------------------------+
//| This function will fetch our training data                       |
//+------------------------------------------------------------------+
void fetch_training_data(void)
  {
//--- Fetch the target
   target.CopyRates("UK100",PERIOD_CURRENT,COPY_RATES_CLOSE,1,fetch);

//--- Add the intercept
   input_matrix.Row(intercept,0);

//--- Fill in the input matrix
   for(int i = 0; i < 11; i++)
     {
      //--- Add the symbol to market watch
      SymbolSelect(list_of_companies[i],true);
      //--- Fetch historical data
      vector temp = vector::Zeros(fetch);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,1+look_ahead,fetch);
      //--- Store the mean value and standard deviation, also scale the data
      mean_values[i] = temp.Mean();
      std_values[i] = temp.Std();
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i+1);
     }
  }

Nachdem wir unsere Trainingsdaten abgerufen haben, sollten wir auch eine Funktion zur Anpassung unserer Modellkoeffizienten definieren.

//+---------------------------------------------------------------------+
//| This function will fit our multiple linear regression model         |
//+---------------------------------------------------------------------+
void model_fit(void)
  {
//--- Calculating coefficient values
   coefficients = target.MatMul(input_matrix.PInv());
  }

Nachdem wir unser Modell trainiert und angepasst haben, können wir endlich Vorhersagen von unserem Modell erhalten. Zunächst werden wir aktuelle Marktdaten aus unserem Modell abrufen und normalisieren, um damit zu beginnen. Nach dem Abrufen der Daten wenden wir die lineare Regressionsformel an, um eine Prognose aus unserem Modell zu erhalten. Schließlich speichern wir die Vorhersage des Modells als binäres Flag, damit wir mögliche Umkehrungen im Auge behalten können.

//+---------------------------------------------------------------------+
//| This function will fetch a prediction from our model                |
//+---------------------------------------------------------------------+
void model_predict(void)
  {
//--- Add the intercept
   intercept = vector::Ones(1);
   input_matrix.Row(intercept,0);

//--- Fill in the input matrix
   for(int i = 0; i < 11; i++)
     {
      //--- Fetch historical data
      vector temp = vector::Zeros(1);
      temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,0,1);
      //--- Normalize and scale the data
      temp = ((temp - mean_values[i]) / std_values[i]);
      //--- Add the data to the matrix
      input_matrix.Row(temp,i+1);
     }

//--- Calculate the model forecast
   forecast = (
                 (1 * coefficients[0,0]) +
                 (input_matrix[0,1] * coefficients[0,1]) +
                 (input_matrix[0,2] * coefficients[0,2]) +
                 (input_matrix[0,3] * coefficients[0,3]) +
                 (input_matrix[0,4] * coefficients[0,4]) +
                 (input_matrix[0,5] * coefficients[0,5]) +
                 (input_matrix[0,6] * coefficients[0,6]) +
                 (input_matrix[0,7] * coefficients[0,7]) +
                 (input_matrix[0,8] * coefficients[0,8]) +
                 (input_matrix[0,9] * coefficients[0,9]) +
                 (input_matrix[0,10] * coefficients[0,10]) +
                 (input_matrix[0,11] * coefficients[0,11])
              );
//--- Store the model's state
//--- Whenever the system and model state aren't the same, we may have a potential reversal
   if(forecast > iClose("UK100",PERIOD_CURRENT,0))
     {
      model_state = 1;
     }

   else
      if(forecast < iClose("UK100",PERIOD_CURRENT,0))
        {
         model_state = -1;
        }
  }
//+------------------------------------------------------------------+

Außerdem benötigen wir eine Funktion, die für das Abrufen der aktuellen Marktdaten von unserem Terminal zuständig ist.

//+------------------------------------------------------------------+
//| Update our market data                                           |
//+------------------------------------------------------------------+
void update_market_data(void)
  {
//--- Update the bid and ask prices
   bid = SymbolInfoDouble("UK100",SYMBOL_BID);
   ask = SymbolInfoDouble("UK100",SYMBOL_ASK);
//--- Update the RSI readings
   CopyBuffer(rsi_handler,0,1,1,rsi_buffer);
  }

Wir wollen nun Funktionen erstellen, die die Marktstimmung analysieren, um zu sehen, ob sie mit unserem Modell übereinstimmt. Wenn unser Modell einen Kauf vorschlägt, prüfen wir zunächst die Preisveränderung auf dem wöchentlichen Zeitrahmen über einen Konjunkturzyklus hinweg. Wenn die Preise gestiegen sind, prüfen wir auch, ob unser RSI-Indikator auf eine bullische Marktstimmung hindeutet. Wenn dies der Fall ist, werden wir unsere Kaufposition einrichten. Andernfalls werden wir nichts tun und keine Position eröffnen.

//+------------------------------------------------------------------+
//| Check if we have an opportunity to sell                          |
//+------------------------------------------------------------------+
void check_sell(void)
  {
   if(iClose("UK100",PERIOD_W1,0) < iClose("UK100",PERIOD_W1,12))
     {
      if(rsi_buffer[0] < 50)
        {
         Trade.Sell(0.3,"UK100",bid,0,0,"FTSE 100 AI");
         //--- Remeber the ticket
         open_ticket = PositionGetTicket(0);
         //--- Whenever the system and model state aren't the same, we may have a potential reversal
         system_state = -1;
        }
     }
  }

//+------------------------------------------------------------------+
//| Check if we have an opportunity to buy                           |
//+------------------------------------------------------------------+
void check_buy(void)
  {
   if(iClose("UK100",PERIOD_W1,0) > iClose("UK100",PERIOD_W1,12))
     {
      if(rsi_buffer[0] > 50)
        {
         Trade.Buy(0.3,"UK100",ask,0,0,"FTSE 100 AI");
         //--- Remeber the ticket
         open_ticket = PositionGetTicket(0);
         //--- Whenever the system and model state aren't the same, we may have a potential reversal
         system_state = 1;
        }
     }
  }

Wenn unsere Anwendung initialisiert wird, bereiten wir zunächst unseren RSI-Indikator vor.  Von dort aus werden wir unseren RSI-Indikator validieren. Wenn dieser Test bestanden wird, fahren wir mit der Erstellung unseres multiplen, linearen Regressionsmodells fort. Wir beginnen mit dem Abrufen der Trainingsdaten und berechnen dann unsere Modellkoeffizienten. Schließlich werden wir die Eingaben des Nutzers validieren, um sicherzustellen, dass der Nutzer eine Maßnahme zur Kontrolle der Risikostufen definiert hat.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Prepare the technical indicator
   rsi_handler = iRSI(Symbol(),PERIOD_CURRENT,rsi_period,PRICE_CLOSE);

//--- Validate the indicator handler
   if(rsi_handler == INVALID_HANDLE)
     {
      //--- We failed to load the indicator
      Comment("Failed to load the RSI indicator");
      return(INIT_FAILED);
     }

//--- This function will fetch our training data and scaling factors
   fetch_training_data();

//--- This function will fit our multiple linear regression model
   model_fit();

//--- Ensure the user's inputs are valid
   if((ai_auto_close == false && profit_target == 0))
     {
      Comment("Either set AI auto close true, or define a profit target!")
      return(INIT_FAILED);
     }

//--- Everything went well
   return(INIT_SUCCEEDED);
  }

Immer wenn unser Expert Advisor nicht in Gebrauch ist, geben wir die nicht mehr benötigten Ressourcen frei. Insbesondere werden wir den RSI-Indikator und den Expert Advisor aus dem Hauptchart entfernen.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we are no longer using
   IndicatorRelease(rsi_handler);
   ExpertRemove();
  }

Wenn wir aktualisierte Kurse erhalten, wählen wir zunächst das FTSE 100-Symbol aus, bevor wir aktualisierte Marktdaten und technische Indikatorwerte abrufen. Von dort aus können wir eine neue Vorhersage von unserem Modell erhalten und Maßnahmen ergreifen. Wenn unser System keine offenen Positionen hat, prüfen wir, ob die aktuelle Marktstimmung mit den Vorhersagen unseres Modells übereinstimmt, bevor wir eine Position eröffnen. Wenn wir bereits offene Positionen haben, testen wir auf eine potenzielle Umkehr. Diese lassen sich leicht erkennen, wenn der Zustand unseres Modells und der des Systems nicht übereinstimmen.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Since we are dealing with a lot of different symbols, be sure to select the UK1OO (FTSE100)
//--- Select the symbol
   SymbolSelect("UK100",true);

//--- Update market data
   update_market_data();

//--- Fetch a prediction from our AI model
   model_predict();

//--- Give the user feedback
   Comment("Model forecast: ",forecast,"\nPosition Profit: ",position_profit);



//--- Look for a position
   if(PositionsTotal() == 0)
     {
      //--- We have no open positions
      open_ticket = 0;

      //--- Check if our model's prediction is validated
      if(model_state == 1)
        {
         check_buy();
        }

      else
         if(model_state == -1)
           {
            check_sell();
           }
     }

//--- Do we have a position allready?
   if(PositionsTotal() > 0)
     {

      //--- Should we close our positon manually?
      if(PositionSelectByTicket(open_ticket))
        {
         if((profit_target > 0) && (ai_auto_close == false))
           {
            //--- Update the position profit
            position_profit = PositionGetDouble(POSITION_PROFIT);
            if(profit_target < position_profit)
              {
               Trade.PositionClose("UK100");
              }
           }
        }

      //--- Should we close our positon using a hybrid approach?
      if(PositionSelectByTicket(open_ticket))
        {
         if((profit_target > 0) && (ai_auto_close == true))
           {
            //--- Update the position profit
            position_profit = PositionGetDouble(POSITION_PROFIT);
            //--- Check if we have passed our profit target or if we are expecting a reversal
            if((profit_target < position_profit) || (model_state != system_state))
              {
               Trade.PositionClose("UK100");
              }
           }
        }


      //--- Are we closing our system just using AI?
      else
         if((system_state != model_state) &&
            (ai_auto_close == true) &&
            (profit_target == 0))
           {
            Trade.PositionClose("UK100");
           }
     }
  }
//+------------------------------------------------------------------+

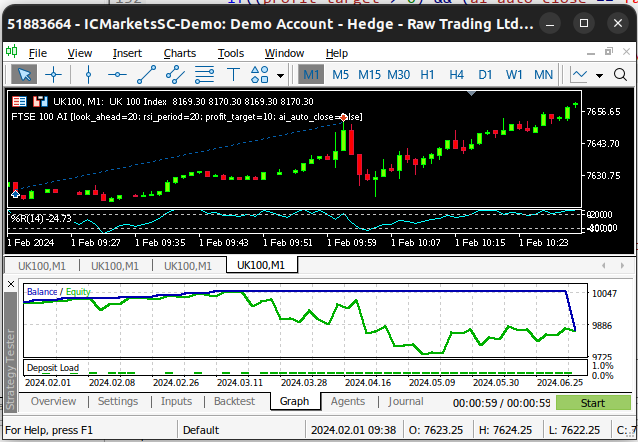
Abb. 3: Backtesting unseres Expert Advisors

Optimierung unseres Expert Advisors

Bis jetzt scheint unsere Handelsanwendung instabil zu sein. Wir können versuchen, die Stabilität unserer Handelsanwendung zu verbessern, indem wir Ideen verwenden, die von dem amerikanischen Ökonomen Harry Markowitz festgelegt wurden. Markowitz ist es zu verdanken, dass er die Grundlagen der modernen Portfoliotheorie (MPT), wie wir sie heute kennen, konzipiert hat. Im Wesentlichen erkannte er, dass die Performance eines einzelnen Vermögenswerts im Vergleich zur Performance des gesamten Portfolios eines Anlegers vernachlässigbar ist.

Abb. 4: Ein Bild des Nobelpreisträgers Harry Markowitz

Versuchen wir, einige der Ideen von Markowitz anzuwenden, um die Leistung unserer Handelsanwendung hoffentlich zu stabilisieren. Wir beginnen damit, die benötigten Bibliotheken zu importieren.

#Import the libraries we need
import pandas            as pd
import numpy             as np
import seaborn           as sns
import MetaTrader5       as mt5
import matplotlib.pyplot as plt
from   scipy.optimize    import  minimize

Wir müssen eine Liste der Aktien erstellen, die wir in Betracht ziehen.

#Create the list of stocks
stocks = ["ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"]

Initialisieren des Terminals.

#Initialize the terminal
if(!mt5.initialize()):
    print('Failed to load the MT5 Terminal')

„True“

Nun müssen wir einen Datenrahmen erstellen, um die Erträge der einzelnen Symbole zu speichern.

#Create a dataframe to store our returns
amount  = 10000
returns = pd.DataFrame(columns=stocks,index=np.arange(0,amount))

Wir holen uns die benötigten Daten von unserem MetaTrader 5 Terminal.

#Fetch the data
for stock in stocks:
     temp = pd.DataFrame(mt5.copy_rates_from_pos(stock,mt5.TIMEFRAME_M1,0,amount))
     returns[[stock]] = temp[['close']]

Für diese Aufgabe werden wir die Renditen der einzelnen Aktien anstelle des normalen Schlusskurses verwenden.

#Store the data as returns
returns = returns.pct_change()
returns.dropna(inplace=True)

Standardmäßig müssen wir jeden Eintrag mit 100 multiplizieren, um die tatsächlichen prozentualen Erträge zu erhalten.

#Let's look at our dataframe
returns = returns * (10.0 ** 2)

Schauen wir uns nun die Daten an, die uns vorliegen.

returns

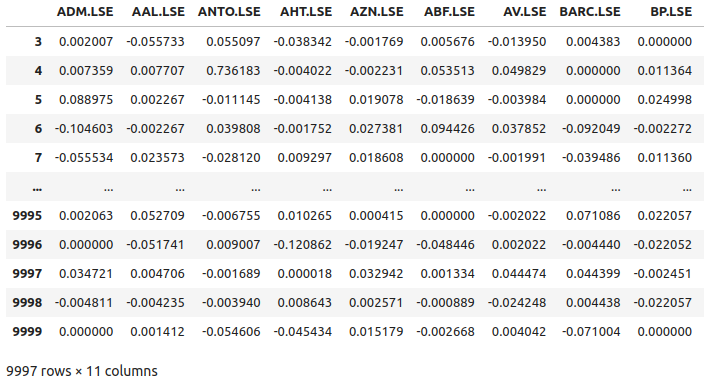
Abb. 5: Einige der Renditen der Aktien aus unserem Korb von FTSE100-Aktien

Lassen Sie uns nun die Marktrenditen der einzelnen Aktien aufzeichnen. Es ist deutlich zu erkennen, dass bestimmte Aktien wie Ashtead Group (AHT.LSE) ein kräftigen, starken Ausschlag haben, der von der durchschnittlichen Performance des Portfolios der 11 von uns untersuchten Aktien abweicht. Im Wesentlichen hilft uns der Algorithmus von Markowitz dabei, empirisch weniger Aktien mit hoher Varianz und mehr Aktien mit geringerer Varianz auszuwählen. Der Ansatz von Markowitz ist analytisch und befreit uns von jeglichem Rätselraten.

#Let's visualize our market returns
returns.plot()

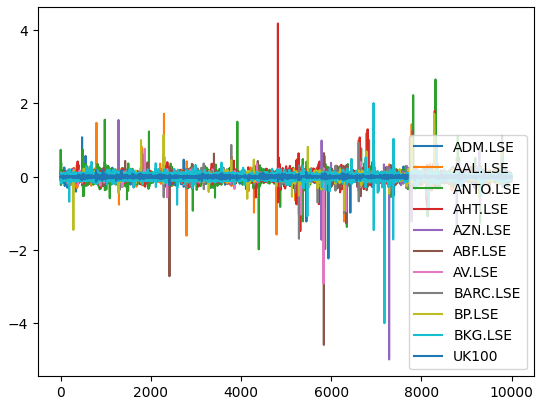
Abb. 6: Die Marktrenditen unseres Korbs von FTSE 100-Aktien

Beobachten wir, ob es in unseren Daten aussagekräftige Korrelationsniveaus gibt. Leider gab es keine signifikanten Korrelationswerte, die wir interessant fanden.

#Let's analyze the correlation coefficients
fig, ax = plt.subplots(figsize=(8,8)) 
sns.heatmap(returns.corr(),annot=True,linewidths=.5, ax=ax)

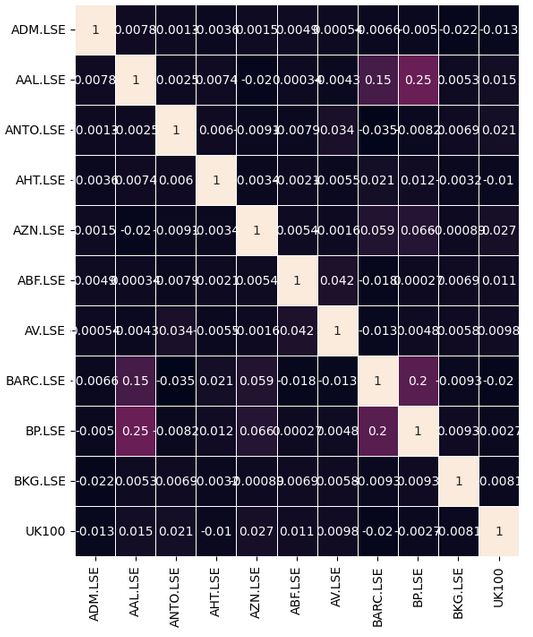
Abb. 7: Unsere Korrelations-Heatmap des FTSE 100

Einige Beziehungen sind nicht leicht zu finden und erfordern einige Vorverarbeitungsschritte, um aufgedeckt zu werden. Anstatt einfach nur nach einer direkten Korrelation zwischen dem Aktienkorb zu suchen, können wir auch nach einer Korrelation zwischen den aktuellen Werten der einzelnen Aktien und dem zukünftigen Wert des UK100-Symbols suchen. Dies ist eine klassische Technik, die als Lead-Lag-Korrelation (Korrelation zwischen Vor- und Nachlauf) bekannt ist.

Wir beginnen damit, unseren Aktienkorb um 20 Plätze nach hinten zu verschieben und das Symbol UK100 um 20 Plätze nach vorne zu schieben.

# Let's also analyze for lead-lag correlation
look_ahead  = 20
lead_lag    = pd.DataFrame(columns=stocks,index=np.arange(0,returns.shape[0] - look_ahead))
for stock in stocks:
    if stock == 'UK100':
        lead_lag[[stock]] = returns[[stock]].shift(-20)
    else:
        lead_lag[[stock]] = returns[[stock]].shift(20)

# Returns
lead_lag.dropna(inplace=True)

Wir wollen sehen, ob sich die Korrelationsmatrix verändert hat. Leider haben wir durch dieses Verfahren keine Verbesserungen erzielt.

#Let's see if there are any stocks that are correlated with the future UK100 returns
fig, ax = plt.subplots(figsize=(8,8)) 
sns.heatmap(lead_lag.corr(),annot=True,linewidths=.5, ax=ax)

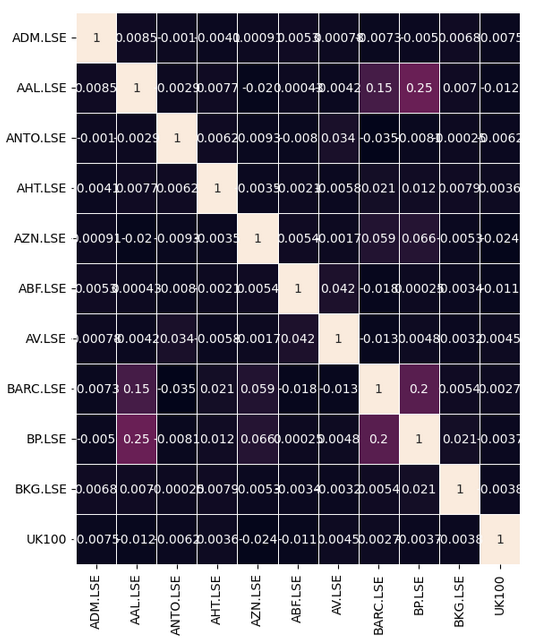
Abb. 8: Unsere Heatmap der Lead-Lag-Korrelation

Wir wollen nun versuchen, die Varianz unseres gesamten Portfolios zu minimieren. Wir werden unser Portfolio so gestalten, dass wir verschiedene Aktien kaufen und verkaufen können, um das Risiko unseres Portfolios zu minimieren. Um unser Ziel zu erreichen, werden wir die Optimierungsbibliothek von SciPy nutzen. Wir haben 11 verschiedene Gewichte, die optimiert werden müssen, wobei jedes Gewicht die Kapitalallokation darstellt, die für die jeweilige Aktie vorgenommen werden muss. Der Koeffizient jeder Gewichtung symbolisiert, ob wir eine bestimmte Aktie kaufen (positiver Koeffizient) oder verkaufen (negativer Koeffizient) sollten. Genauer gesagt, wollen wir sicher sein, dass alle unsere Koeffizienten zwischen -1 und 1 einschließlich liegen, oder in Intervallschreibweise [-1,1].

Darüber hinaus möchten wir unser gesamtes Kapital einsetzen, und nicht mehr. Daher müssen wir unser Optimierungsverfahren an bestimmte Bedingungen knüpfen. Wir müssen insbesondere sicherstellen, dass die Summe aller Gewichte im Portfolio gleich 1 ist. Das bedeutet, dass wir das gesamte Kapital, das wir haben, investiert. Es sei daran erinnert, dass einige unserer Koeffizienten negativ sein werden, was es schwierig machen kann, dass die Summe aller unserer Koeffizienten gleich 1 ist. Daher müssen wir diese Bedingung dahingehend ändern, dass nur die absoluten Werte der einzelnen Gewichte berücksichtigt werden. Mit anderen Worten: Wenn wir unsere 11 Gewichte in einem Vektor speichern, wollen wir sicherstellen, dass die L1-Norm gleich 1 ist.

Zunächst initialisieren wir unsere Gewichte mit Zufallswerten und berechnen die Kovarianz der Ergebnismatrix.

#Let's attempt to minimize the variance of the portfolio
weights = np.array([0,0,0,0,0,0,-1,1,1,0,0])
covariance = returns.cov()

Verfolgen wir nun die anfänglichen Varianzen.

#Store the initial portfolio variance
initial_portfolio_variance = np.dot(weights.T,np.dot(covariance,weights))
initial_portfolio_variance

0.011959689589562724

Bei der Optimierung suchen wir nach den optimalen Eingaben für eine Funktion, die zu der niedrigsten Ausgabe der Funktion führen. Diese Funktion wird als Kostenfunktion bezeichnet. Unsere Kostenfunktion ist die Varianz des Portfolios unter den aktuellen Gewichten. Zum Glück lässt sich dies mit Befehlen der linearen Algebra leicht berechnen.

#Cost function
def cost_function(x):
    return(np.dot(x.T,np.dot(covariance,x)))

Wir werden nun unsere Beschränkungen definieren, die festlegen, dass unsere Portfoliogewichte gleich 1 sein sollten.

#Constraints
def l1_norm(x):
    return(np.sum(np.abs(x))) - 1

constraints = {'type': 'eq', 'fun':l1_norm}

SciPy erwartet von uns, dass wir ihm bei der Optimierung eine erste Schätzung liefern.

#Initial guess
initial_guess = weights

Erinnern Sie sich, dass wir wollen, dass unsere Gewichte alle zwischen -1 und 1 liegen, wir übergeben diese Anweisungen an SciPy mit einem Tupel von Grenzen.

#Add bounds
bounds =   [(-1,1)] * 11

Wir werden nun die Varianz unseres Portfolios mit Hilfe des Algorithmus der Sequentiellen Kleinsten Quadrate Programmierung (SLSQP) minimieren. Der SLSQP-Algorithmus wurde ursprünglich in den 1980er Jahren von dem bekannten deutschen Ingenieur Dieter Kraft entwickelt.  Die ursprüngliche Routine wurde in FORTRAN implementiert. Die wissenschaftliche Originalarbeit von Kraft, in der der Algorithmus beschrieben wird, finden Sie hier. SLSQP ist ein Quasi-Newton-Algorithmus, d.h. er schätzt die zweite Ableitung (Hesse-Matrix) der Zielfunktion, um die Optima der Zielfunktion zu finden.

#Minimize the portfolio variance
result = minimize(cost_function,initial_guess,method="SLSQP",constraints=constraints,bounds=bounds)

Wir haben dieses Optimierungsverfahren erfolgreich durchgeführt und wollen uns nun die Ergebnisse ansehen.

result

 message: Optimization terminated successfully
 success: „True“
  status: 0
     fun: 0.0004706570068070814
       x: [ 5.845e-02 -1.057e-01  8.800e-03  2.894e-02 -1.461e-01
            3.433e-02 -2.625e-01  6.867e-02  1.653e-01  3.450e-02
            8.675e-02]
     nit: 12
     jac: [ 3.820e-04 -9.886e-04  3.242e-05  4.724e-04 -1.544e-03
            4.151e-04 -1.351e-03  5.850e-04  8.880e-04  4.457e-04
            4.392e-05]
    nfev: 154
    njev: 12

Lassen Sie uns die optimalen Gewichte speichern, die von unserem SciPy für uns gefunden hat.

#Store the optimal weights
optimal_weights = result.x

Überprüfen wir nun, ob die L1-Norm-Bedingung nicht verletzt wurde. Beachten Sie, dass sich unsere Gewichte aufgrund der begrenzten Speicherpräzision von Computern nicht genau zu 1 addieren werden.

#Validating the weights add up to one
np.sum(np.abs(optimal_weights))

0.9999999998893961

Speichern der neuen Varianz des Portfolios.

#Store the new portfolio variance
otpimal_variance = cost_function(optimal_weights)

Wir erstellen einen Datenrahmen, mit dem wir unsere Leistung vergleichen können

#Portfolio variance
portfolio_var = pd.DataFrame(columns=['Old Var','New Var'],index=[0])

und speichern unsere Varianz-Werte in dem Datenrahmen.

portfolio_var.iloc[0,0] = initial_portfolio_variance * (10.0 ** 7)
portfolio_var.iloc[0,1] = otpimal_variance * (10.0 ** 7)

Stellen wir die Varianz unseres Portfolios dar. Wie wir sehen können, ist sie deutlich gesunken.

portfolio_var.plot.bar()

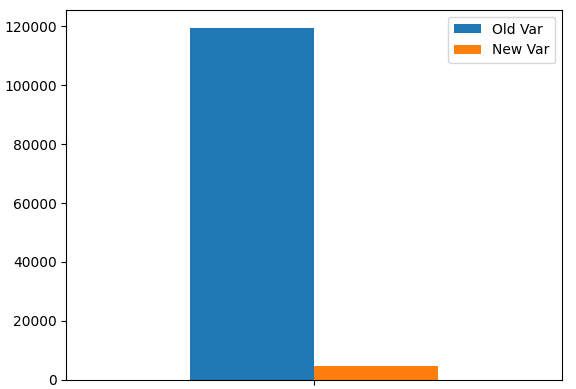
Abb. 9: Unsere neue Portfolio-Varianz

Ermitteln wir nun die Anzahl der Positionen, die wir auf jedem Markt entsprechend unserer optimalen Gewichtung eröffnen sollten. Unsere Daten deuten darauf hin, dass wir immer dann, wenn wir eine Kaufposition im UK100-Symbol eröffnen, keine Positionen mit Admiral Group (ADM.LSE) eröffnen sollten und 2 entsprechende Verkaufspositionen in Anglo-American (AAL.LSE) eröffnen sollten.

int_weights = (optimal_weights / optimal_weights[-1]) // 1
int_weights

array([ 0., -2.,  0.,  0., -2.,  0., -4.,  0.,  1.,  0.,  1.])

Aktualisierung unseres Expertenberaters

Jetzt können wir uns der Aktualisierung unseres Handelsalgorithmus zuwenden, um von unserem neuen Verständnis des FTSE 100-Marktes zu profitieren. Laden wir zunächst die optimalen Gewichte, die wir mit SciPy berechnet haben.

int    optimization_weights[11] = {0,-2,0,0,-2,0,-4,0,1,0,1};

Wir brauchen auch eine Einstellung, um unser Optimierungsverfahren auszulösen, wir werden eine Verlustgrenze festlegen. Wenn der Verlust unseres offenen Handels größer als unser Verlustlimit ist, eröffnen wir Handelsgeschäfte in anderen FTSE100-Märkten, um unser Risiko zu minimieren.

input double  loss_limit = 20;        // After how much loss should we optimize our portfolio?

Definieren wir nun die Funktion, die für den Aufruf des Verfahrens zur Minimierung unseres Portfoliorisikos verantwortlich sein wird. Vergessen wir nicht, dass wir diese Routine nur durchführen, wenn das Konto sein Verlustlimit überschritten hat oder die Gefahr besteht, dass es seine Eigenkapitalschwelle überschreitet.

      //--- Should we optimize our portfolio variance using the optimal weights we have calculated
      if((loss_limit > 0))
        {
         //--- Update the position profit
         position_profit = AccountInfoDouble(ACCOUNT_EQUITY) - AccountInfoDouble(ACCOUNT_BALANCE);
         //--- Check if we have passed our profit target or if we are expecting a reversal
         if(((loss_limit * -1) < position_profit))
           {
            minimize_variance();
           }
        }
        

Diese Funktion führt die eigentliche Portfolio-Optimierung durch. Die Funktion durchläuft unsere Aktienliste und prüft dann die Anzahl und Art der zu eröffnenden Positionen.

//+------------------------------------------------------------------+
//| This function will minimize the variance of our portfolio        |
//+------------------------------------------------------------------+
void minimize_variance(void)
  {
   risk_minimized = true;

   if(!risk_minimized)
     {
      for(int i = 0; i < 11; i++)
        {
         string current_symbol = list_of_companies[i];

         //--- Add that stock to the portfolio to minimize our variance, buy
         if(optimization_weights[i] > 0)
           {
            for(int i = 0; i < optimization_weights[i]; i++)
              {
               Trade.Buy(0.3,current_symbol,ask,0,0,"FTSE Optimization");
              }
           }
         //--- Add that stock to the portfolio to minimize our variance, sell
         else
            if(optimization_weights[i] < 0)
              {
               for(int i = 0; i < optimization_weights[i]; i--)
                 {
                  Trade.Sell(0.3,current_symbol,bid,0,0,"FTSE Optimization");
                 }
              }
        }
     }
  }

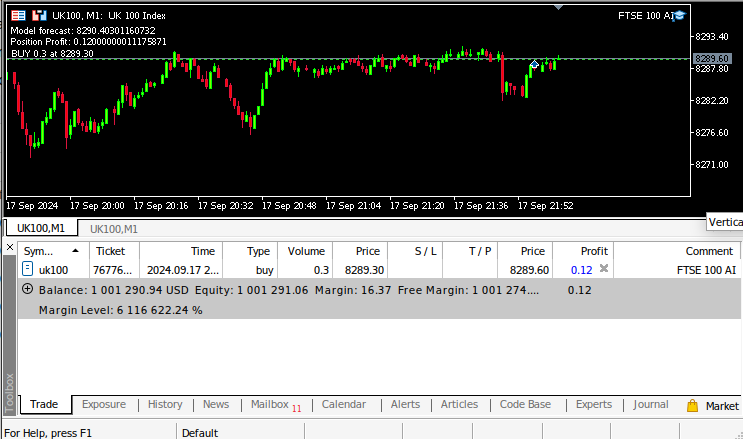
Abb. 10: Vorwärtsprüfung unseres Algorithmus

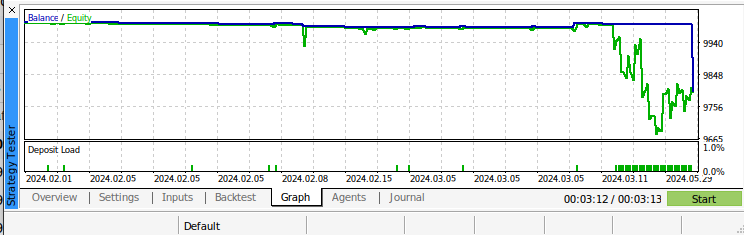
Abb. 11: Backtesting unseres Algorithmus

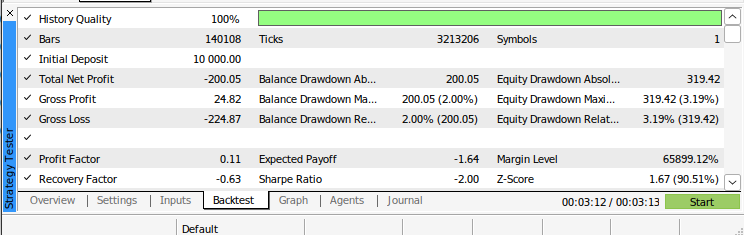
Abb. 12: Die Ergebnisse des Backtests unseres Algorithmus

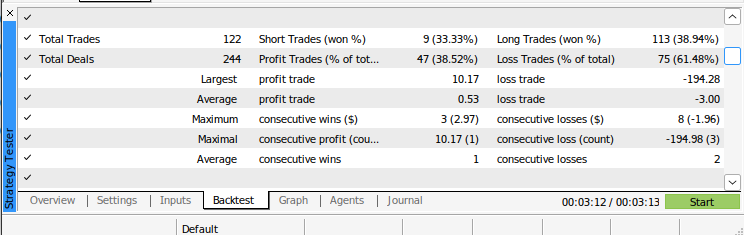
Abb. 13: Weitere Ergebnisse aus dem Backtesting unseres Algorithmus

Schlussfolgerung

In diesem Artikel haben wir gezeigt, wie Sie ein Ensemble aus technischer Analyse und KI problemlos mit Python und MQL5 aufbauen können. Unsere Anwendung ist in der Lage, sich dynamisch an alle im MetaTrader 5 Terminal verfügbaren Zeitrahmen anzupassen. Wir haben die wichtigsten Grundprinzipien der modernen Portfolio-Optimierung unter Verwendung moderner Optimierungsalgorithmen erläutert. Wir haben gezeigt, wie die menschliche Voreingenommenheit bei der Portfolioauswahl minimiert werden kann. Außerdem haben wir gezeigt, wie man Marktdaten nutzen kann, um optimale Entscheidungen zu treffen. Unser Algorithmus ist noch verbesserungsfähig. In zukünftigen Artikeln werden wir zum Beispiel zeigen, wie man 2 Kriterien gleichzeitig optimieren kann, z.B. das Risikoniveau unter Berücksichtigung der risikofreien Rendite.

Die meisten der heute vorgestellten Grundsätze bleiben jedoch auch bei differenzierteren Optimierungsverfahren gleich, wir müssen lediglich unsere Kostenfunktionen und Nebenbedingungen anpassen und den für unsere Bedürfnisse geeigneten Optimierungsalgorithmus ermitteln.