重构MQL5中的经典策略（第三部分）：富时100指数预测
50
0
人工智能（AI）在现代投资者的策略中有着潜在的无限应用场景。遗憾的是，没有任何一位投资者会有足够的时间去仔细分析每一个策略，然后再决定将他们的资金托付给哪一个策略。在本系列文章中，我们将带领您穿越广阔的基于AI的策略领域，以帮助您找到一个适合您投资喜好的策略。
交易策略概览
伦敦证券交易所（LSE）是发达世界中最古老的证券交易所之一。它成立于1801年，是英国的主要证券交易所。它被认为是除纽约证券交易所和东京证券交易所之外的“三大”交易所之一。伦敦证券交易所是欧洲最大的证券交易所，根据其官方网站，目前在该交易所上市的所有公司的总市值约为4.4万亿英镑。
金融时报证券交易所（FTSE）100指数是从伦敦证券交易所衍生出来的一个指数，它跟踪在伦敦证券交易所上市的100家最大公司。这些公司通常被称为蓝筹股，鉴于这些公司随着时间的推移所获得的声誉以及它们经过验证的业绩记录，它们被视为相对安全的投资。我们可以利用对富时100指数计算方式的理解，并且通过考虑指数的当前收盘价以及指数中上市的10只大盘股的表现，可能会创造出一个新的交易策略，来预测富时100指数的未来收盘价。
方法论概述
我们完全用MQL5构建了AI驱动的EA。这给了我们灵活性，因为我们的模型可以在不同的时间框架上使用，而无需不断调整。此外，我们可以动态调整模型参数，例如模型应该预测多远的未来。我们的模型总共使用了12个输入来预测富时100指数20步后的未来收盘价。
我们进行了Z标准化，使用每列的均值和标准差值来规范化和缩放模型的每一个输入。我们的目标是富时100指数20步后的未来收盘价，因此我们创建了一个多元线性回归模型来预测该指数的未来收盘价。
并非所有的机器学习模型都是平等创建的，这在预测任务中尤为明显。让我们考虑决策树，树算法通常通过将数据划分为组，然后每当模型需要进行预测时，它只需返回与当前输入数据最匹配的组的均值。因此，基于树的算法不执行外推（预测），换句话说，它们没有前瞻性和进行未来预测的能力。那么，如果一个基于树的模型接收到5个来自不同时刻的相似输入，且这些输入足够相似，那么它可以为所有5个预测相同的收盘价，而我们的线性回归模型能够进行外推，并且可以为我们提供关于证券未来收盘价的预测。
脚本的初始设计
我们最初会将理念构建为MQL5中的一个简单脚本，以便可以明白系统的各个部分是如何协同工作的。我们将从定义全局变量开始。//+------------------------------------------------------------------+ //| UK100.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ //1) ADM.LSE - Admiral //2) AAL.LSE - Anglo American //3) ANTO.LSE - Antofagasta //4) AHT.LSE - Ashtead //5) AZN.LSE - AstraZeneca //6) ABF.LSE - Associated British Foods //7) AV.LSE - Aviva //8) BARC.LSE - Barclays //9) BP.LSE - BP //10) BKG.LSE - Berkeley Group //11) UK100 - FTSE 100 Index //+-------------------------------------------------------------------+ //| Global variables | //+-------------------------------------------------------------------+ int fetch = 2000; int look_ahead = 20; double mean_values[11],std_values[11]; string list_of_companies[11] = {"ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"}; vector intercept = vector::Ones(fetch); matrix target = matrix::Zeros(1,fetch); matrix coefficients; matrix input_matrix = matrix::Zeros(12,fetch);
我们将要完成的第一项任务是获取和规范化输入数据。我们将把输入数据存储在一个矩阵中，而目标数据将保存在它自己的矩阵中。
void OnStart() { //--- Fetch the target target.CopyRates("UK100",PERIOD_CURRENT,COPY_RATES_CLOSE,1,fetch); //--- Fill in the input matrix for(int i = 0; i < 11; i++) { //--- Add the symbol to market watch SymbolSelect(list_of_companies[i],true); //--- Fetch historical data vector temp = vector::Zeros(fetch); temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,1+look_ahead,fetch); //--- Store the mean value and standard deviation, also scale the data mean_values[i] = temp.Mean(); std_values[i] = temp.Std(); temp = ((temp - mean_values[i]) / std_values[i]); //--- Add the data to the matrix input_matrix.Row(temp,i); } //--- Add the intercept input_matrix.Row(intercept,11); //--- Show the input data Print("Input data:"); Print(input_matrix);
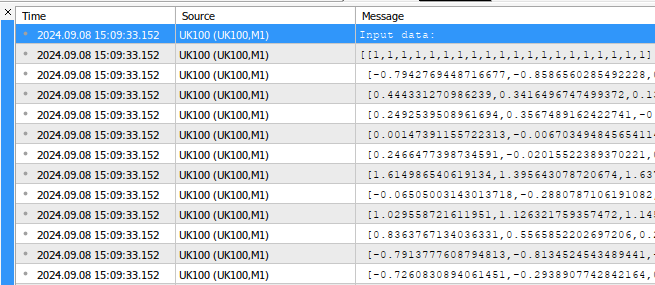
图1：我们脚本生成的输出示例
在获取我们的输入数据之后，我们现在可以继续计算模型参数。幸运的是，多元线性回归模型的系数可以通过一个封闭形式的公式来计算。以下我们可以看到一个模型系数的实例。
//--- Calculating coefficient values coefficients = target.MatMul(input_matrix.PInv()); //--- Display the coefficient values Print("UK100 Coefficients:"); Print(coefficients.Transpose());
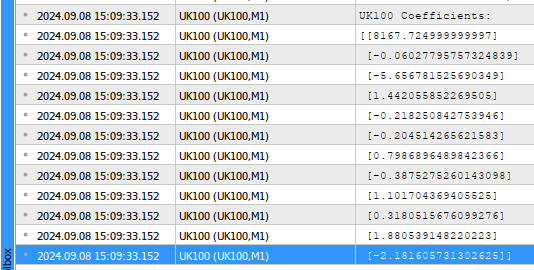
图2：我们的模型参数
让我们一起解读这些结果，第一个系数值表示当所有模型输入都为0时目标变量的平均值。这就是偏差参数的数学定义。然而，在我们的交易应用中，这几乎没有直观意义。从技术上讲，如果富时100指数中的所有股票价值都为0英镑，那么富时100指数的平均未来价值也将是0英镑。第二个系数项表示在假设其他所有股票收盘价相同的情况下，富时100指数未来价值的边际变化。因此，每当阿迪尔股票增加一个单位，我们观察到指数的未来收盘价似乎略有下降。
从我们的模型中获得一个预测值，就像将每只股票的当前价格乘以其计算出的系数值，然后将所有这些乘积相加一样简单。现在我们已经了解到如何构建我们的模型，那么我们就可以开始构建EA了。
实现我们的EA
我们将从定义用户可以更改的输入开始，从而调整程序的行为。
//+------------------------------------------------------------------+ //| FTSE 100 AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| User inputs | //+------------------------------------------------------------------+ input int look_ahead = 20; // How far into the future should we forecast? input int rsi_period = 20; // The period of our RSI input int profit_target = 20; // After how much profit should we close our positions? input bool ai_auto_close = true; // Should the AI automatically close positions?
然后我们将导入交易库，以帮助我们管理仓位。
//+------------------------------------------------------------------+ //| Libraries we need | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
现在，我们将定义一些全局变量，这些变量将在我们整个EA中使用。
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ double position_profit = 0; int fetch = 20; matrix coefficients; matrix input_matrix = matrix::Zeros(12,fetch); double mean_values[11],std_values[11],rsi_buffer[1]; string list_of_companies[11] = {"ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"}; ulong open_ticket;
我们现在将定义一个用于获取我们训练数据的函数。回想一下，我们的目标是获取训练数据，然后在将其添加到输入矩阵之前，对数据进行规范化和标准化。
//+------------------------------------------------------------------+ //| This function will fetch our training data | //+------------------------------------------------------------------+ void fetch_training_data(void) { //--- Fetch the target target.CopyRates("UK100",PERIOD_CURRENT,COPY_RATES_CLOSE,1,fetch); //--- Add the intercept input_matrix.Row(intercept,0); //--- Fill in the input matrix for(int i = 0; i < 11; i++) { //--- Add the symbol to market watch SymbolSelect(list_of_companies[i],true); //--- Fetch historical data vector temp = vector::Zeros(fetch); temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,1+look_ahead,fetch); //--- Store the mean value and standard deviation, also scale the data mean_values[i] = temp.Mean(); std_values[i] = temp.Std(); temp = ((temp - mean_values[i]) / std_values[i]); //--- Add the data to the matrix input_matrix.Row(temp,i+1); } }
在获取到训练数据之后，我们也应该定义一个用于拟合我们模型系数的函数。
//+---------------------------------------------------------------------+ //| This function will fit our multiple linear regression model | //+---------------------------------------------------------------------+ void model_fit(void) { //--- Calculating coefficient values coefficients = target.MatMul(input_matrix.PInv()); }
一旦我们训练并拟合好我们的模型，就可以从模型中获取预测了。我们首先会获取并规范化来自模型的当前市场数据，以便开始。在获取数据之后，我们应用线性回归公式来从模型中获得一个预测。最后，我们将模型的预测作为一个二进制标识存储起来，以帮助我们跟踪潜在的反转。
//+---------------------------------------------------------------------+ //| This function will fetch a prediction from our model | //+---------------------------------------------------------------------+ void model_predict(void) { //--- Add the intercept intercept = vector::Ones(1); input_matrix.Row(intercept,0); //--- Fill in the input matrix for(int i = 0; i < 11; i++) { //--- Fetch historical data vector temp = vector::Zeros(1); temp.CopyRates(list_of_companies[i],PERIOD_CURRENT,COPY_RATES_CLOSE,0,1); //--- Normalize and scale the data temp = ((temp - mean_values[i]) / std_values[i]); //--- Add the data to the matrix input_matrix.Row(temp,i+1); } //--- Calculate the model forecast forecast = ( (1 * coefficients[0,0]) + (input_matrix[0,1] * coefficients[0,1]) + (input_matrix[0,2] * coefficients[0,2]) + (input_matrix[0,3] * coefficients[0,3]) + (input_matrix[0,4] * coefficients[0,4]) + (input_matrix[0,5] * coefficients[0,5]) + (input_matrix[0,6] * coefficients[0,6]) + (input_matrix[0,7] * coefficients[0,7]) + (input_matrix[0,8] * coefficients[0,8]) + (input_matrix[0,9] * coefficients[0,9]) + (input_matrix[0,10] * coefficients[0,10]) + (input_matrix[0,11] * coefficients[0,11]) ); //--- Store the model's state //--- Whenever the system and model state aren't the same, we may have a potential reversal if(forecast > iClose("UK100",PERIOD_CURRENT,0)) { model_state = 1; } else if(forecast < iClose("UK100",PERIOD_CURRENT,0)) { model_state = -1; } } //+------------------------------------------------------------------+
我们还需要一个负责从终端获取当前市场数据的函数。
//+------------------------------------------------------------------+ //| Update our market data | //+------------------------------------------------------------------+ void update_market_data(void) { //--- Update the bid and ask prices bid = SymbolInfoDouble("UK100",SYMBOL_BID); ask = SymbolInfoDouble("UK100",SYMBOL_ASK); //--- Update the RSI readings CopyBuffer(rsi_handler,0,1,1,rsi_buffer); }
现在让我们创建一些函数，用于分析市场情绪，看看是否与我们的模型一致。每当我们的模型建议买入时，我们首先会检查在1个商业周期内周时间框架上的价格变化，如果价格水平有所上涨，那么我们还会检查相对强弱指数（RSI）指标是否表明看涨的市场情绪。如果符合该情况，那么我们将设置买入仓位。否则，我们将退出而不设置任何仓位。
//+------------------------------------------------------------------+ //| Check if we have an opportunity to sell | //+------------------------------------------------------------------+ void check_sell(void) { if(iClose("UK100",PERIOD_W1,0) < iClose("UK100",PERIOD_W1,12)) { if(rsi_buffer[0] < 50) { Trade.Sell(0.3,"UK100",bid,0,0,"FTSE 100 AI"); //--- Remeber the ticket open_ticket = PositionGetTicket(0); //--- Whenever the system and model state aren't the same, we may have a potential reversal system_state = -1; } } } //+------------------------------------------------------------------+ //| Check if we have an opportunity to buy | //+------------------------------------------------------------------+ void check_buy(void) { if(iClose("UK100",PERIOD_W1,0) > iClose("UK100",PERIOD_W1,12)) { if(rsi_buffer[0] > 50) { Trade.Buy(0.3,"UK100",ask,0,0,"FTSE 100 AI"); //--- Remeber the ticket open_ticket = PositionGetTicket(0); //--- Whenever the system and model state aren't the same, we may have a potential reversal system_state = 1; } } }
当应用程序正在初始化时，我们首先将准备RSI指标。之后，我们将验证RSI指标。如果通过了这个测试，我们将继续创建多元线性回归模型。我们首先获取训练数据，然后计算模型系数。最后，我们将验证用户的输入，以确保用户已经定义了控制风险水平的措施。
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Prepare the technical indicator rsi_handler = iRSI(Symbol(),PERIOD_CURRENT,rsi_period,PRICE_CLOSE); //--- Validate the indicator handler if(rsi_handler == INVALID_HANDLE) { //--- We failed to load the indicator Comment("Failed to load the RSI indicator"); return(INIT_FAILED); } //--- This function will fetch our training data and scaling factors fetch_training_data(); //--- This function will fit our multiple linear regression model model_fit(); //--- Ensure the user's inputs are valid if((ai_auto_close == false && profit_target == 0)) { Comment("Either set AI auto close true, or define a profit target!") return(INIT_FAILED); } //--- Everything went well return(INIT_SUCCEEDED); }
每当不需要EA时，我们将释放不再使用的资源。特别是，我们将移除RSI指标和主图上的EA。
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Free up the resources we are no longer using IndicatorRelease(rsi_handler); ExpertRemove(); }
最后，每当收到更新的价格时，我们将首先选择富时100指数的交易品种，然后获取更新的市场数据和技术指标值。之后，我们可以从模型中获得一个新的预测并采取行动。如果系统没有持仓，我们将检查当前的市场情绪是否与模型的预测一致，然后再开仓。如果已经有持仓，我们将测试潜在的反转，这些反转可以通过模型状态和系统状态不一致的情况轻松地识别出来。
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Since we are dealing with a lot of different symbols, be sure to select the UK1OO (FTSE100) //--- Select the symbol SymbolSelect("UK100",true); //--- Update market data update_market_data(); //--- Fetch a prediction from our AI model model_predict(); //--- Give the user feedback Comment("Model forecast: ",forecast,"\nPosition Profit: ",position_profit); //--- Look for a position if(PositionsTotal() == 0) { //--- We have no open positions open_ticket = 0; //--- Check if our model's prediction is validated if(model_state == 1) { check_buy(); } else if(model_state == -1) { check_sell(); } } //--- Do we have a position allready? if(PositionsTotal() > 0) { //--- Should we close our positon manually? if(PositionSelectByTicket(open_ticket)) { if((profit_target > 0) && (ai_auto_close == false)) { //--- Update the position profit position_profit = PositionGetDouble(POSITION_PROFIT); if(profit_target < position_profit) { Trade.PositionClose("UK100"); } } } //--- Should we close our positon using a hybrid approach? if(PositionSelectByTicket(open_ticket)) { if((profit_target > 0) && (ai_auto_close == true)) { //--- Update the position profit position_profit = PositionGetDouble(POSITION_PROFIT); //--- Check if we have passed our profit target or if we are expecting a reversal if((profit_target < position_profit) || (model_state != system_state)) { Trade.PositionClose("UK100"); } } } //--- Are we closing our system just using AI? else if((system_state != model_state) && (ai_auto_close == true) && (profit_target == 0)) { Trade.PositionClose("UK100"); } } } //+------------------------------------------------------------------+
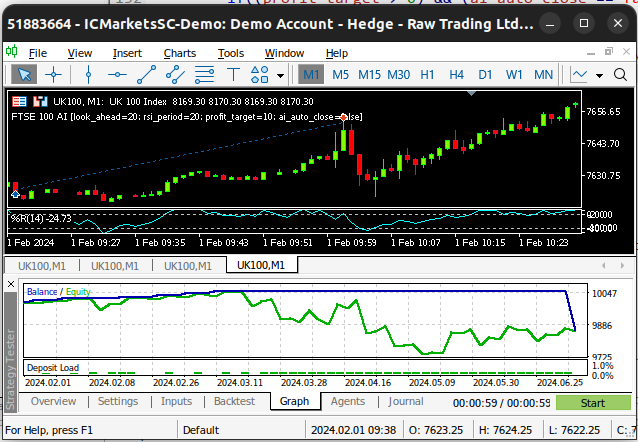
图3：回测我们的EA
优化我们的EA
到目前为止，我们的交易应用似乎不太稳定，我们可以尝试使用美国经济学家哈里·马科维茨提出的一些观点来提高交易应用的稳定性。马科维茨被认为是现代投资组合理论（MPT）的奠基人。从本质上讲，他意识到任何单一资产的表现与投资者整个投资组合的表现相比是微不足道的。
图4：诺贝尔奖得主哈里·马科维茨的照片
让我们尝试应用一些马科维茨的观点，希望能稳定交易应用的表现。我们将首先导入所需的库。
#Import the libraries we need import pandas as pd import numpy as np import seaborn as sns import MetaTrader5 as mt5 import matplotlib.pyplot as plt from scipy.optimize import minimize
我们需要创建一个将考虑持有的股票清单。
#Create the list of stocks stocks = ["ADM.LSE","AAL.LSE","ANTO.LSE","AHT.LSE","AZN.LSE","ABF.LSE","AV.LSE","BARC.LSE","BP.LSE","BKG.LSE","UK100"]
初始化终端。
#Initialize the terminal
if(!mt5.initialize()):
print('Failed to load the MT5 Terminal') 现在，我们需要创建一个数据帧来存储每个交易品种的返回值。
#Create a dataframe to store our returns amount = 10000 returns = pd.DataFrame(columns=stocks,index=np.arange(0,amount))
从MetaTrader 5终端获取我们需要的数据。
#Fetch the data for stock in stocks: temp = pd.DataFrame(mt5.copy_rates_from_pos(stock,mt5.TIMEFRAME_M1,0,amount)) returns[[stock]] = temp[['close']]
对于该项任务，我们将使用每只股票的收益率，而不是通常的收盘价。
#Store the data as returns returns = returns.pct_change() returns.dropna(inplace=True)
默认情况下，我们必须将每个条目乘以100，以获得实际的百分比收益率。
#Let's look at our dataframe returns = returns * (10.0 ** 2)
现在让我们看一下现有的数据。
收益率
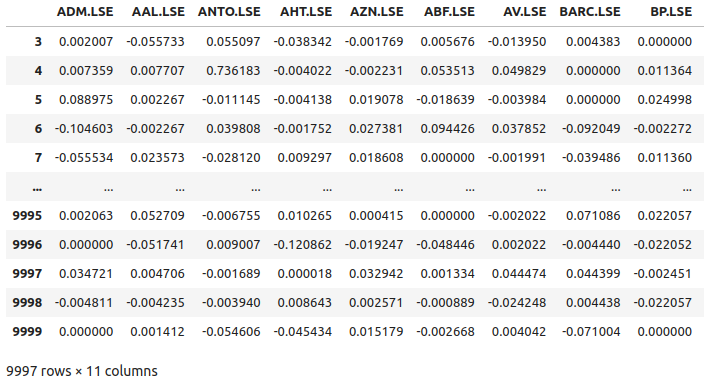
图5：我们富时100指数股票池中部分股票的收益率
现在让我们绘制目前持有的每只股票的市场收益率。我们可以清楚地看到，某些股票，比如Ashtead Group（AHT.LSE），有明显且有力的尾部，偏离了我们所拥有的11只股票投资组合的平均表现。从本质上讲，马科维茨的算法将帮助我们在实战中较少地选择那些具有高方差的股票，而更多地选择方差较小的股票。马科维茨的方法是具有分析性的，消除了我们在这一过程中任何猜测的成分。
#Let's visualize our market returns returns.plot()
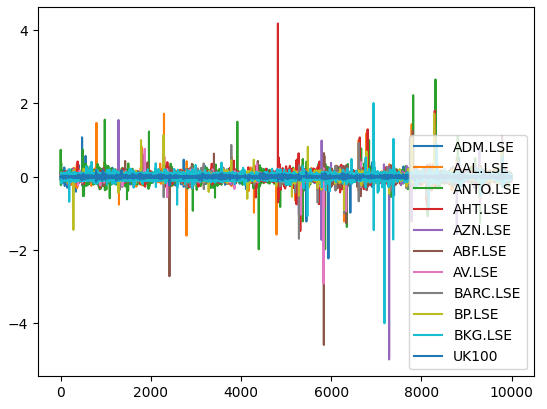
图6：我们富时100指数股票池的市场收益率
让我们观察一下数据中是否存在任何有意义的相关性水平。遗憾的是，我们没有发现任何有意义且显著的相关性水平。
#Let's analyze the correlation coefficients fig, ax = plt.subplots(figsize=(8,8)) sns.heatmap(returns.corr(),annot=True,linewidths=.5, ax=ax)
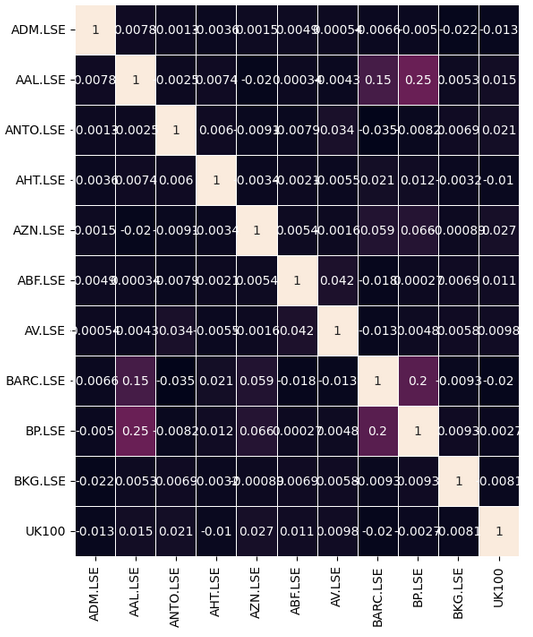
图7：富时100指数的相关性热力图
有些关系不容易被发现，需要进行一些预处理步骤才能揭示。除了直接寻找股票池之间的相关性外，我们还可以寻找每只股票的当前值与英国100指数未来值之间的相关性。这是一种被称为领先-滞后相关性的经典技术。
我们将首先把我们的股票池向后推20个位置，同时把英国100指数向前推20个位置。
# Let's also analyze for lead-lag correlation look_ahead = 20 lead_lag = pd.DataFrame(columns=stocks,index=np.arange(0,returns.shape[0] - look_ahead)) for stock in stocks: if stock == 'UK100': lead_lag[[stock]] = returns[[stock]].shift(-20) else: lead_lag[[stock]] = returns[[stock]].shift(20) # Returns lead_lag.dropna(inplace=True)
让我们看一下相关性矩阵是否有所变化。遗憾的是，这一调整并没有给我们带来任何收获。
#Let's see if there are any stocks that are correlated with the future UK100 returns fig, ax = plt.subplots(figsize=(8,8)) sns.heatmap(lead_lag.corr(),annot=True,linewidths=.5, ax=ax)
图8：我们的领先-滞后相关性热力图
现在让我们尝试最小化整个投资组合的方差。我们将以一种允许买卖不同股票的方式来构建投资组合，以最小化投资组合的风险。为了实现目标，我们将利用SciPy的优化库。我们将有11个不同的权重需要优化，每个权重代表必须分配给每只相应股票的资本。每个权重的系数将代表我们是否应该买入（正系数）或卖出（负系数）每只特定的股票。更具体地说，我们希望确保所有的系数都位于-1和1之间，包括-1和1，或者用区间表示法表示为[-1,1]。
除此之外，我们希望使用所有的资本，不多也不少。因此，我们必须为我们的优化过程设置约束。具体来说，我们必须强制投资组合中所有权重的总和等于1。这意味着我们已经分配了所有的资本。回想一下，我们的一些系数将是负数，这可能会使所有系数的总和等于1变得具有挑战性。因此，我们必须修改这个约束，只考虑每个权重的绝对值。换句话说，如果我们把11个权重存储在一个向量中，我们希望确保L1范数等于1。
开始之前，我们将首先用随机值初始化权重，并计算收益率矩阵的协方差。
#Let's attempt to minimize the variance of the portfolio weights = np.array([0,0,0,0,0,0,-1,1,1,0,0]) covariance = returns.cov()
现在让我们记录初始的方差水平。
#Store the initial portfolio variance
initial_portfolio_variance = np.dot(weights.T,np.dot(covariance,weights))
initial_portfolio_variance 在进行优化时，我们寻找一个函数的最优输入，这样会使得该函数产生最低的输出。这个函数被称为成本函数。我们的成本函数将是当前权重下投资组合的方差。幸运的是，使用线性代数命令可以很容易地计算这个值。
#Cost function def cost_function(x): return(np.dot(x.T,np.dot(covariance,x)))
我们现在将定义约束条件，规定投资组合权重应等于1。
#Constraints
def l1_norm(x):
return(np.sum(np.abs(x))) - 1
constraints = {'type': 'eq', 'fun':l1_norm} 在执行优化时，SciPy希望我们提供一个初始的估计值。
#Initial guess
initial_guess = weights 回想一下，我们希望权重都介于-1和1之间，我们通过一个界限的元组将这些指令传递给SciPy。
#Add bounds bounds = [(-1,1)] * 11
我们现在将使用序贯最小二乘法规划（SLSQP）算法来最小化投资组合的方差。SLSQP算法最初是由杰出的德国工程师迪特尔·克拉夫特（ Dieter Kraft）在20世纪80年代开发的。原始的例程是用FORTRAN语言实现的。克拉夫特关于该算法的原始科学论文可以在该链接（这里）找到。SLSQP是一种拟牛顿算法，这意味着它通过估计目标函数的二阶导数（海森矩阵）来寻找目标函数的最优值。
#Minimize the portfolio variance result = minimize(cost_function,initial_guess,method="SLSQP",constraints=constraints,bounds=bounds)
我们已经成功地执行了这个优化过程，让我们来看一下结果。
结果
成功状态：True
状态：0
fun: 0.0004706570068070814
x: [ 5.845e-02 -1.057e-01 8.800e-03 2.894e-02 -1.461e-01
3.433e-02 -2.625e-01 6.867e-02 1.653e-01 3.450e-02
8.675e-02]
nit: 12
jac: [ 3.820e-04 -9.886e-04 3.242e-05 4.724e-04 -1.544e-03
4.151e-04 -1.351e-03 5.850e-04 8.880e-04 4.457e-04
4.392e-05]
nfev: 154
njev: 12
让我们将SciPy求解器作为找到的最优权重存储起来。
#Store the optimal weights
optimal_weights = result.x 让我们验证一下没有违反L1范数约束。请注意，由于计算机有限的浮点精度，我们的权重不会精确地加起来等于1。
#Validating the weights add up to one
np.sum(np.abs(optimal_weights)) 存储新的投资组合方差。
#Store the new portfolio variance otpimal_variance = cost_function(optimal_weights)
创建一个数据帧，以便能够比较我们的表现。
#Portfolio variance portfolio_var = pd.DataFrame(columns=['Old Var','New Var'],index=[0])
在数据帧中保存我们的方差水平。
portfolio_var.iloc[0,0] = initial_portfolio_variance * (10.0 ** 7) portfolio_var.iloc[0,1] = otpimal_variance * (10.0 ** 7)
绘制投资组合方差。正如我们所见，方差水平显著下降。
portfolio_var.plot.bar()
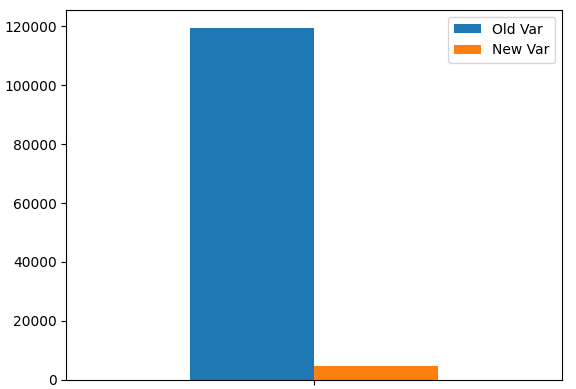
图9：我们的新投资组合方差
现在让我们根据最优权重获得在每个市场应该开仓的数量。根据数据显示，每当我们开启1个英国100指数的多头仓位时，不应在阿迪尔集团（ADM.LSE）开设任何仓位，却应在英美资源集团（AAL.LSE）开设2个等量的空头仓位。
int_weights = (optimal_weights / optimal_weights[-1]) // 1 int_weights
更新我们的EA
现在我们可以将注意力转向更新交易算法，以便应用我们对富时100市场的新理解。让我们首先加载使用SciPy计算出的最优权重。
int optimization_weights[11] = {0,-2,0,0,-2,0,-4,0,1,0,1};
我们还需要一个设置来触发优化程序，我们将设置一个亏损限制。每当我们的未平仓交易的亏损超过亏损限制时，我们将在其他富时100市场开设交易，以试图降低风险水平。
input double loss_limit = 20; // After how much loss should we optimize our portfolio?
现在让我们定义一个负责调用最小化投资组合风险水平程序的函数。回想一下，我们只有在账户突破其亏损限制或有超过其权益阈值的风险时，才会执行这个程序。
//--- Should we optimize our portfolio variance using the optimal weights we have calculated if((loss_limit > 0)) { //--- Update the position profit position_profit = AccountInfoDouble(ACCOUNT_EQUITY) - AccountInfoDouble(ACCOUNT_BALANCE); //--- Check if we have passed our profit target or if we are expecting a reversal if(((loss_limit * -1) < position_profit)) { minimize_variance(); } }
该函数将实际执行投资组合的优化，其将会遍历我们的股票列表，然后检查应该开设的仓位数量和类型。
//+------------------------------------------------------------------+ //| This function will minimize the variance of our portfolio | //+------------------------------------------------------------------+ void minimize_variance(void) { risk_minimized = true; if(!risk_minimized) { for(int i = 0; i < 11; i++) { string current_symbol = list_of_companies[i]; //--- Add that stock to the portfolio to minimize our variance, buy if(optimization_weights[i] > 0) { for(int i = 0; i < optimization_weights[i]; i++) { Trade.Buy(0.3,current_symbol,ask,0,0,"FTSE Optimization"); } } //--- Add that stock to the portfolio to minimize our variance, sell else if(optimization_weights[i] < 0) { for(int i = 0; i < optimization_weights[i]; i--) { Trade.Sell(0.3,current_symbol,bid,0,0,"FTSE Optimization"); } } } } }
图10：对我们的算法进行前瞻性测试
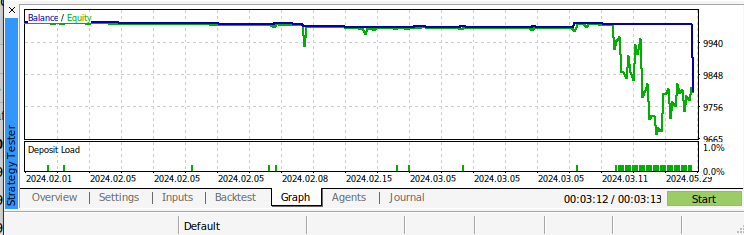
图11：回测我们的算法
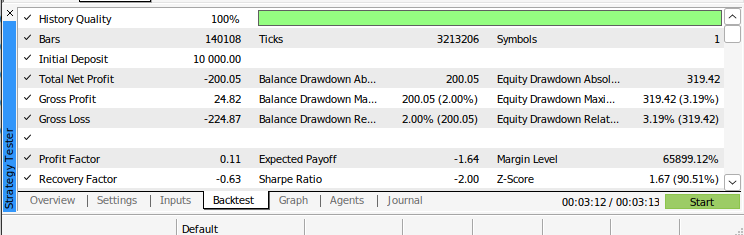
图12：回测我们算法的结果
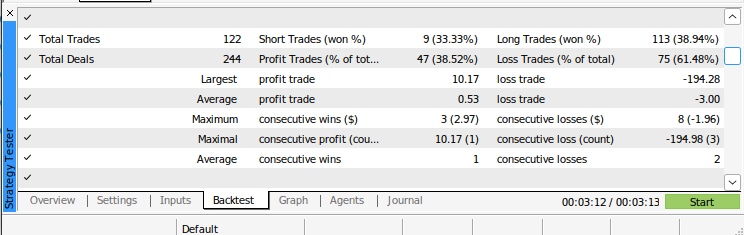
图13：回测我们算法的附加结果
结论
在本文中，我们展示了如何使用Python和MQL5无缝地构建技术分析和AI的集成，并且应用程序能够动态调整自身以适应MetaTrader 5终端中所有可用的时间框架。我们概述了使用现代优化算法进行现代投资组合优化的基本原则。我们展示了如何在投资组合选择过程中最小化人为的偏见。此外，我们还展示了如何使用市场数据来做出最优决策。当前的算法仍有改进的空间，例如在未来的文章中，我们将展示如何同时优化两个标准，比如在考虑无风险回报率的同时优化风险水平。然而，我们今天概述的大多数原则即使在进行更精细的优化程序时仍将保持不变，只需要调整成本函数、约束条件，并确定适合我们需求的适当优化算法。
本文由MetaQuotes Ltd译自英文
原文地址： https://www.mql5.com/en/articles/15818
交易中的神经网络：统一轨迹生成模型（UniTraj）
基于MQL5的订单剥头皮交易系统
使用MQL5和Python构建自优化的EA（第四部分）：模型堆叠
