
トレンドとは何か、相場の構造はトレンドかレンジかで決まるのか?
イントロダクション
メリアムウェブスター(Merriam-Webster)の定義の一つによると、トレンドとは、統計的に検出可能な変化の経時的一般的な動きであり、また、そのような変化を反映した統計的な曲線です。 数学では、トレンドは線形、対数、多項式などの様々な方程式を使って記述することができます。 実際のトレンドタイプは、統計的手法による関数モデルの選択や、初期時系列の平滑化などに基づいて設定されます。
経済学では、トレンドとは経済指標の全体的な方向性のことを指します。 通常、価格の動きやインジケータ値の方向性を示唆するテクニカル分析の枠組みの中で考えられています。 チャールズ・ダウによると、上昇トレンド(強気のトレンド)は、チャート上の各トレーリングの天井が前のものよりも高くなっていることが特徴ですが、下降トレンド(弱気のトレンド)は、各底が前のものよりも低くなるべきであることを意味します(ダウ理論を参照してください)。 チャートが横ばいになった場合は、横ばいの動きを意味します。 強気トレンドの場合は、トレンドラインが2つ以上の価格の底を結んでいます(チャートの下には、目視でサポートして押し上げるようにラインが配置されています)。 弱気トレンドの場合、トレンドラインは2つ以上の価格の天井を結んでいます(レジスタンスしているようにチャートの上にポジションしており、目視で押し下げるようにしています)。 トレンドラインは支持線(上昇トレンドの場合)とレジスタンス(下降トレンドの場合)として機能します。
しかし、気になるのは用語ではなく、その用語から利益を得る方法です。 上記の用語を見ても、どのように数学的に形式化できるかはわかりません。 よく知られている定義はすべて、むしろ曖昧に聞こえ、複数の方法で解釈することができます。 代わりとしては、科学は正確さを好みます。 定義は、その方法を使用する人が、その方法を以前に使用した別の人の結果を再現できるように、明確で、理解しやすく、解釈が1つしかないものでなければなりません。
勝ちトレード戦略の基本
トレンドやレンジの概念に進むためには、まず基本的なこと、つまり資金を稼ぐためには何をしなければならないのかを理解する必要があります。 任意のトレード戦略は、0以上の期待ペイオフがある必要があります。 数学に詳しい人はそれ以上の説明は必要ありませんが、でも説明します。 シンプルに言えば、期待ペイオフ(利益の数学的な期待値)が平均的な利益です。 当然、平均利益は0を超えるはずです。 0になると利益が出ない。 0以下になったら損切りです。
予想ペイオフは、利益が出る確率、平均的な利益、平均的な損失から構成されています。 この方程式はシンプルで、利益確率に平均的な利益を掛け合わせたものです。 得られた結果から、平均損失に損失確率を乗じた値を差し引く。
m=(P(tp)*tp)-(P(sl)*sl),
ただし
- m -期待されるペイオフ。
- P(tp) - 儲かる取引確率。
- P(sl) -負けた取引の確率。
- tp- 平均的に勝ちトレード。
- sl- 平均的な負けのトレード。
勝ちトレードの確率が50%で、勝ちトレードの平均サイズが負けトレードのサイズと同じであれば、期待値は0、つまり何も稼げないということを意味します。 例えば、勝った取引と負けた取引の平均サイズが10ドルだとすると、m=(50*10)-(50*10)=0となります。 正規分布のランダム変数の期待ペイオフは0です(数学的事実です)。 前回の記事価格系列離散化とランダム成分と「ノイズ」では、実物相場のインクリメントの分布が正規分布に似ていて、ランダムウォークに怪しくも似ていると考えました。
利益を出すためには、勝つ確率を上げるか、勝つ確率を上げて平均サイズを大きくして、負けた時の平均サイズを小さくするか、どちらかにした方が良いと思います。 勝ちトレードの確率を60%まで上げ、平均的な勝ちトレードは平均的な負けたトレード=10ドルに等しいとします。 そして、100件の取引を完了したら、M=(60*10)-(40*10)=200ドルを稼ぐことになります。 勝ちトレード確率が変わらないのであれば、安定した利益を得ることができます。 同様に、平均的な利益が出るトレードサイズを大きくして、平均的な負けトレードサイズを小さくして、確率を50%にしておけば、安定した利益も得られます。
ここで、多くのトレーダー、特に新規参入者は、しばしば認知バイアスを経験し始めます。 彼らは考える: 「"わかった、負けたトレードの平均サイズよりも利益のあるトレードの平均サイズを2倍にして、ポジションを開けばいい。移動平均のクロスで"」(ここでは、エントリーアルゴリズムは重要ではありません)。 無意識のうちに結果を達成したいと思っています:m=(50*20)-(50*10)=$500ですが、実際には期待されるペイオフm=(33,3*20)-(66,6*10)=0、または、おそらくスプレッドと手数料による損失しか得られません。 スプレッドや手数料はここでは重要ではないので、この記事では考えないことにします。 他のトレーダーの中には、反対のトラップに陥ることがあります:観察によると、利益のあるトレードは、この場合にはより頻繁にトリガーされるべきであるとして、損失よりも2回少ない利益を上げることを決定することができます。 その結果、そのようなシステムの本当の期待ペイオフはm=(66,6*10)-(33,3*20)=0であることが判明し、手数料やスプレッドによる損失を被ることになります。 こうすることで、SLを大幅に増やし、利益を減らして90~99%以上の確率で利益をもたらすことができますが、その利益はすべて最終的に損失で相殺されてしまいます。 これは、損失を得ることは時間的に大幅に遅れるだけかもしれませんが、0 のままなので、期待されるペイオフを変更しないすべてのマーチンゲール システムも含まれています。
これは実際には儲かるパターンが見当たらないために起こります。 その代わり、トレーダーはランダムウォークに基づいてトレードを行います。 ランダムウォークの期待ペイオフは0です。 予想ペイオフが0の場合、利益が出る確率は50%のままです。 変わるのは比率だけです(「50%均衡」と呼ぶことにします)。 なので、サイズを小さくしながら勝ちトレードの確率を上げるか、サイズを大きくしながら勝ちトレードの確率を下げるかのどちらかになります。 どうにかしてこの「50%均衡」を打破し、期待ペイオフゼロを超える必要があります。 負けず嫌いのシステムを開発することは、同じように困難であることは注目に値します。 トレーダーは、手数料や有限の預り金によって損失を被ることになります。
ロウソク足からブロックまで
ポイントで起こっている価格の変化をトレードしており(可能な限りの最小の価格変化)、利益は価格が何ポイントを通過したかに依存するため、ローソク足/足の形で価格を表現する標準的な方法は、大きく歪め、プロセスを理解することを困難にするので、距離を置く必要があります。 ポイントでの値動きのみを考慮した表示方法に移りましょう。 今回は、価格が一定のポイント数で動いた後にブロックを構築するインジケータを使ってみたいと思います。 下記にインジケータを添付します。 ただし、その他のメソッドを自由に使えます。 図1は、ブロックがどのように構築されているかを示します。 ブロックの大きさは、1点から無限大まで、1点単位で任意の大きさにできます。 ブロックサイズが10ポイントの場合は、価格が10ポイント上下に移動した後、任意のブロックが形成された時点で終了となります。 このブロックは、上下10ポイントのインクリメントで閉じることができます。 ブロックの特徴は、始値、高値、安値、終値がローソク足と機能的に似ていることです。 1ブロックは1ステップと考えてください。 これは後で重要になります。
図1
トレンドの概念に移るには、何かしらのサンプルが必要です。 ランダムウォークでは、トレーリングの各ステップは前のステップに依存せず、プロセスは記憶を持たず、次のステップが方向を変える確率は50%です。 しかし、ランダムウォークはトレンドやレンジを基準にしているのでしょうか? 図2.のランダム・ウォーク・チャートを見てみましょう。
図2
欲を言えば、図2にトレンドとレンジな部分がありますが、実際にはH1ローソク足でサンプリングしたランダムウォークチャートです。 ここでは、次の各ステップが上下に移動する確率は50%であり、前のステップの方向には依存しません。 トレンドの概念を展開する際には、先ほど書いたように、この場合の期待ペイオフは0なので、ランダムウォークを基準にします。 これは、各次のステップがここで方向を変えたり維持したりする確率が50%であるという事実から導かれます。 平均損失は、ポジションが開いたままのステップ数に関係なく、常に平均利益と同じになります。 方向を推測する確率も50%となっています。 したがって、ランダムウォークチャートは、トレンドに基づくものでも、レンジに基づくものでもないと仮定します。 これはランダムです。
この価格シリーズがトレンドに基づいているか、レンジに基づいているかを決定しながら、価格シリーズを比較することができるサンプルがあります。
リファレンスモデルの開発
図2は、H1ロウソク足によってサンプリングされたランダムウォークチャートを示す図です。 このような表現は、あまりにも直感的ではなく、プロセスの知覚を歪めてしまう。 図3のソースコードを見てみましょう。 以下にシリーズをCSV形式で添付しました。 ターミナルでダウンロードできます。
図3
図3は、1点のステップを有するランダムウォークチャートと、同チャートを1点の大きさのブロック状にしたものです。 ブロックのおかげでステップが見やすくなりました。 他のすべての点で、チャートは同じです。 ランダムウォークは価格系列のトレンド性を定義するための基準であると仮定していますので、実際の価格系列と基準とを比較するために、ランダムウォークの増分確率密度分布チャートを構築してみましょう。 この問題は、ガウス関数を用いて解析的に解くことができます。 しかし、解決策はビジュアルではありません。 数学に詳しい人でも、得られたすべての分布形式の意味を十分に理解していないかもしれません。 基準となる確率密度を構築するために、組み合わせルールを使って表を作ってみます。 その断片を図4に示します。 以下にエクセルの全表を添付します。
図4
この表では、ランダムウォークがどのくらい垂直に進むかを40段階で評価することができます。 qs比(表の式の中の)は、表を作成するサンプル数を設定することができます。 この例では、10万サンプルのテーブルが構築されています。 垂直方向のステップ数」の列は、関数が垂直方向に進むステップ数を特徴とし、「イベントの確率 %」の列は、垂直方向のステップの頻度を表示します。 例えば、プロセスは合計で40段階のステップを作り、40段階のアップダウンが可能なので、10万個のサンプル(測定値)を用意します。 平均すると、10万回のうち0.00000009回は垂直方向に40回移動します。 38ステップは0.0000036回、36ステップは10万分の1の0.00007回。 このように、「事象の確率 %」の欄に値の配列を設定することで、図5に表示されているインクリメント確率密度分布チャートを構築することができます。
図5
このテーブルによれば、各トレーリングのステップの方向転換確率と継続確率が50%に等しい処理について、40ステップでの基準増分確率密度分布を求めることができます。 すべてが正しいことを確認するために、ランダムウォークの確率密度分布を測定し、基準値と比較することができます。 この測定は、図2と図3に断片が表示されているランダムウォークについて行われます。 40ステップ、10万サンプル(測定値)の中で、その関数が垂直方向に何段になったかを測定してみたいと思います。 その結果を図6に示します。 Х軸は-40...0...40の垂直ステップの振幅を示し、Y軸は垂直ステップ数ごとのイベント数を指定します。
図6
10万サンプル40ステップごとの基準分布(表に従って算出)は赤色で表示され、白色のヒストグラムは生成されたランダムウォークの10万サンプルの実測値を示します。 見ての通り、参照分布とヒストグラムはほぼ同じです。 偏差は取るに足らないものです。 使用するサンプル数が多ければ多いほど、実際の測定値は基準値とより正確に対応することができます。 これで、系列分布が参照分布とどの程度異なるかを定義できるようになりました。 インクリメントの確率分布を考えると、現在のところ、解析された系列が可能な限り正確にランダムウォークと一致すると仮定することができます。 なぜそのようなことが必要なのかは、後ほど説明します。
実際の相場でのインクリメントディストリビューション
測定を行うために、実際のGBPUSDのチャートを使って、ブロックサイズ0.00022のブロックチャートに変換してみましょう。 上記の例と同様に、10万サンプルを用いて40ステップで価格がどのくらい上下に動いたかを計算し、図7のリファレンスと比較します。
図7
先ほどと同様に、基準分布は赤で、実測分布は白で示されています。 あとは、以前に紹介したシンプル化(ガウス関数の代わりにコンビナトリアル)が必要になってきます。 GBPUSDのインクリメントの分布がゼロに対して対称的であることがわかります。 ゼロに対する対称性は、上昇トレンドや下降トレンドへの明確な傾斜がないことを示します。 つまり、各アップブロックがダウンブロックに追従する確率は、各ダウンブロックがアップブロックに追従する確率と等しい。 つまり、目に見えて上値や下値の動きに傾くことはありません。
GBPUSDの分布図が参考値よりも低く、広くなっているのは、もっと面白いですね。 40歩以内では、価格はランダムウォークに必要なよりもはるかに少ない頻度でゼロを通過し、多くの場合、はるかに多くのブロックを垂直に通過することを示します。 各次のステップが方向転換する確率が50%未満であることを意味します。 チャートを見ると、アップブロックの後に別のアップブロックが続く確率は50%を超えており、ダウンブロックの後に別のダウンブロックが続く確率も50%を超えていることがわかります。
これをどうやって役に立てるのでしょうか? 利益を評価することができる期待ペイオフ方程式を思い出してみましょう。 利益を得るという全体の問題は、「正しい」インプットの確率が50%以上であれば、平均損失が平均利益に等しいことを条件に、利益を得たままにしておくということです。 利益を出すためには「50%均衡」をブレイクする必要があります。 現在のところ、反転確率の評価はしていません。 チャートを使って計算することもできますが、このチャート上の継続確率が55%、反転確率が45%で、平均利益が平均損失と一致して10ステップ(ステップサイズ0.00022*10=0.0022)とすると、期待ペイオフm=(55*0.0022)-(45*0.0022)=0.121-0.099=0.022となります。 代わりに、100件のトレードを完了した後、0.022の利益が残ることになります。 GBPUSDで0.1ロットをトレードした場合、220ドルの利益を意味します。
トレンド継続確率が50%を超えていることを知って、トレンド継続戦略、つまり上昇ブロックの後の買いを利用することができます。 つまり、トレンド継続確率が50%を超えたら、トレンドフォロー戦略を使って利益を得るということです。 逆に、反転の確率が50%以上(アップブロックの後にダウンブロックが続くことが多い)と分かっている場合は、アップブロックがクローズするたびに売りポジションをオープンし、レンジ(逆張り)戦略で利益を得ることになります。
トレンド/レンジの定義
トレンド/レンジの定義は、直接特定の相場で利益を上げるために使用する戦略に依存します。 この場合、トレンド継続確率が50%であり、ランダムウォークがトレンドに基づくものでもレンジに基づくものでもないとすれば
トレンドの動きがあった場合、トレンド継続の確率がトレンド反転の確率を上回る。 価格が10ポイント動いた場合は、50%を超える確率でさらに10ポイント動くことになります。
横ばいの動きの場合、トレンド反転の確率がトレンド継続確率を上回る。 価格が10ポイント動いた場合は、50%を超える確率で反転してさらに10ポイント逆方向に動きます。
価格が(上で説明したように)10ポイントずつのブロックとして表示されている場合、トレンドの動きは、トレーリングの上昇ブロックが閉じられた後に買いを開き、トレーリングの下落ブロックが閉じられた後に売りを開くことを示唆します。 逆に言えば、レンジな動きは、上昇ブロックごとに売り、下降ブロックごとに買いを入れた後に開くことを示唆します。
つまり、相場がトレンドに乗っていれば、その方向にトレードすればいいのです。 相場が横ばいの場合は、逆張りトレード。 相場がトレンドでもなく、レンジでもない場合は、エントリーしないでください。
ここでは、ランダムウォークで稼ぐことができないと言っているのではありません。 個別に徹底して勉強するための話題です。
主張の確認
一見論理的な発言も、時には偽であることが判明することもあります。 そこで、簡単なモデルを使って結論を確認してみましょう。 そのためには、反転確率80%(図8)と20%(図9)の2つのプロセスを作成します。
図8
図9
図8は、測定された確率密度分布が基準値よりもかなり狭いことを示します。 この処理がゼロに戻ることが多くなります。 図9を見ると、測定された確率密度分布が基準値よりもはるかに広いことがわかります。 この処理がゼロに戻る回数はかなり少なくなります。 したがって、先に実行された操作が正しいと結論づけられるのは、ロジック通りです。 反転の確率が50%未満の場合、分布が基準値よりも広いことがわかり、このロジックを使って、ある商品のトレンド性の度合いを分析することができます。 ここでは、トレンドを継続させるプロセスのトレンドを定量的に反映した「トレンド性」という概念を紹介します。
ツールのトレンド度の推定
基準値を持つことで、1つの商品の異なる時間枠と異なる商品の異なる時間枠のトレンド性の度合いを絶対値で推定することができます。 しかし、その前に絶対値を比較する方法を開発する必要があります。 2つの方法を提案します。
- 密度偏差。 振幅の範囲を選択し、参照用にこの範囲に入ったイベントの数を数えます。 次に、測定値に対しても同じことを行います。 基準値を測定値で割って絶対単位を求めます。 値が1を超える場合、系列はトレンド性であり、1未満であれば、系列はレンジです。 例えば、全振幅範囲が-40...0...40です。 100%の値が-40...40に落ちた値を数えても意味がないので、別の値にしてみましょう。 確率論によると、「正規分布からの値の約68%は、平均から1σ標準偏差以下の距離にポジションしており、値の約95%は2標準偏差以内にポジションしており、99,7%は3標準偏差以下に位置している」とのことです。 つまり、特定の範囲内でどれだけの事象が発生するかを定義し、正規分布と比較することが標準であると考えられています。 しかし、タスクでは標準偏差を測る必要がないので測りませんでした。 なので、絶対数を使うことにします。 以下の方法が好ましいです。
- リファレンスでは、気になるサンプルの割合を設定します。 例えば、80%のサンプルに興味があります。 つまり、80%のサンプルが該当する範囲を定義する必要があるということです。 我々の例では、10万個のサンプルを特徴としており、80%が8万個のサンプルとなります。 この8万サンプルの振幅範囲を計算してみましょう。 84.6%のサンプルが-8...8の範囲にあり、73.18%のサンプルが-6...6の範囲にあります。 84.6%は80%に近いので、-8...8 -の範囲に入るサンプル数を定義すると、84,614サンプルになります。
- ここで、80%の反転確率を持つ系列に作られた分布上で、-8~8の範囲に入る標著書の数を定義してみましょう。 この場合は、10万サンプルの範囲を特徴とします。 84,614/100,000=0.8416. したがって、図8のチャートのトレンド度は0.8416となります。
- 図9のチャートのトレンド度を確認します。 -8...8の範囲は52,034サンプルを特徴としているので、20%の反転確率84,614/52,325=1.617の系列トレンド度が得られます。
- 平均振幅 中心極限定理から、ランダムウォークの平均垂直振幅はステップ数の0.5の乗に比例すると結論づけることができます。 前回、図4に部分的に表示されている参照分布を構築するためのテーブルを作成しました。 他のものとは別に、参照ランダムウォークによって渡された垂直方向の平均ステップ数を計算する「垂直方向の平均ブロック」セルを特徴とします。 この数値は、0...40垂直ステップをサンプル数(ここでは10万)で割った範囲の「振幅周波数」の欄の和として求められました。 表では5.0148の値になっています。 つまり、平均的な推移では-5.0148...5.0148の垂直方向のステップを平均40ステップ分通過することになります。 これは段数の0.437乗に比例します。 0.5乗からの逸脱は、40歩しか歩かないという事実に起因しており、酔っぱらいの船乗りの定理では、ランダムウォークは歩数の0.5乗におおよそ比例するべきであるとされています。 この表を用いて、与えられたステップ数の正確な値が得られました。
- 図2及び図3に表示されている反転確率50%の処理で通過した垂直ステップ数の平均値を測定すると、5.0363です。 50%の反転確率で系列のトレンド度を定義してみましょう。 これを行うには、基準値を測定値で割る 5.0148/5.0363=0.9957 とします。 ご覧のように、トレンド度はほぼ1で、系列が可能な限りランダムウォークに近いことを示唆しており、論理は正しいです。
- 80%の反転確率を持つプロセスのトレンド度を計算します。 これを行うには、その平均振幅を測定します。 これは1.6495に等しい。 次に、測定値を基準値1.6495/5.0148=0.3289で割る。 値が1よりもはるかに低いのは、分析されたシリーズの価格レートのトレンド性が低いことを意味します。
- 反転確率が20%のプロセスのトレンド度を計算します。 これを行うには、その平均振幅を測定します。 これは9.95に等しい。 次に、測定値を基準値9.95/5.0148=1.98で割る。 この値は1の2倍近い値であり、分析されたシリーズの値率のトレンド性が高いことを示唆します。
このようなツールがあれば、1つの測定器の異なるスケール(時間枠)でのトレンド度を直接比較し、その統計パラメータを視覚的に評価することができます。 例として、20%と80%の反転確率を持つ同じ2つのプロセスを用いて、それぞれの統計パラメータを異なるスケールで視覚的に評価してみましょう。 前回は、ブロックサイズが1点に等しいものを使用しました。 トレーリングの各ブロックのサイズに1.1の比率を乗算して、より大きなサイズのブロックを作成します。 したがって、ブロックサイズが 1; 1.1; 1.21; 1.33 ..... のスケールが得られます。 6.12. 図10は、反転確率80%のプロセスについて、スケールが大きくなるにつれてトレンド性が変化する様子を示します。 図11は、反転確率が20%の場合の処理についても同様です。
図10
図11
図10及び図11において、最小の目盛(1点)は左にポジションし、最大の目盛はX軸上で右に位置します。 Y軸は、「平均振幅」度を用いて計算された測定器のトレンド度を特徴とします。 80%反転確率過程が最初はレンジである図10では、ヒストグラムの1列目の価格率のトレンド性は低いが、スケールが大きくなるにつれてトレンド性は1(基準ランダムウォーク値)になるトレンドがあります。 最小スケールでの反転確率が高いそれにも関わらず、プロセスが「メモリ」を失ってランダムウォークになってしまうのは、より大きなスケールでも同じではないことを示唆します。 図11は、同様の図です。 最初は2.053という高いトレンド度を持つプロセスであれば、縮小され、より大きなスケールでランダムウォークの基準値にトレンドがあります。
図10と図11は、プロセスが最小のスケールでのみ「メモリ」を持ち、スケールが大きくなるにつれてランダムウォークのようになっていくことを示します。 この結論を裏付けるのが、シリーズ化されたことです。 2つのプロセスを生成する際には、前のステップ方向のみを考慮しました。 残りのステップは考慮に入れられていなかったため、「メモリ」効果はスケールの増加に伴ってすぐに消滅します。
トレンド度のステップ数依存性の構築
現実の相場は、合成的に生成されたシリーズとは異なります。 パターンを検出するには、より多くの分析ツールが必要です。 したがって、一定のステップ数でトレンド度を分析するだけでなく、通過ステップ数の増加に伴って相場のトレンド度がどのように変化するかを評価することも有用です。 参照テーブルは異なるステップ数用に作成できるので、ステップ数が増えたときのツールの挙動だけでなく、ステップ数が増えたときのツールの挙動も同時に見ることができます。 図12は、ブロックサイズが0.00314の10,000サンプルについて、10から100までのステップ数についてのGBPUSDのトレンド度のダイナミクスを示します。 左端のヒストグラム列は10段分、右端のヒストグラム列は100段分構築されています。 ヒストグラムの各列では、ステップ数を2ずつ増やしていきます。
図12
図12によれば、現在のスケールでは、GBPUSDのトレンド性は1を超えており、分析を行うステップ数に応じて1.133〜1.166の範囲で変動します。 図13は、スケールが大きくなるにつれてトレンド度がどのように変化するかを示します。 チャートは10,000サンプル40ステップずつ、ステップサイズは0.00021から0.00495までの範囲で作成されています。 左端のヒストグラム列はブロックサイズ0.00021に対して構築されていますが、以降のヒストグラム列はそれぞれ前のヒストグラム列の1.1倍を超えています。
図13
図13 は、スケールが大きくなるにつれてトレンド度が下がる様子を示します。 小スケールのものでは1.425に等しいが、すでに1に傾いており、最大のものでは1.062に等しい。 スケールが大きくなるにつれて、GBPUSDの挙動は20%の確率で合成系列の挙動に似ています。
このようなアプローチにより、トレード商品のトレンド度の変化速度を動的に評価することができます。 下のアニメーションは、AMD株の増分確率密度分布の基準分布に対するダイナミクスを示します。 M1タイムフレームのロウソク足をベースにします。 アニメーションは40ステップ、1000サンプルに構築されています。 ブロックサイズは、現在の平均ボラティリティに応じて動的に変化します。
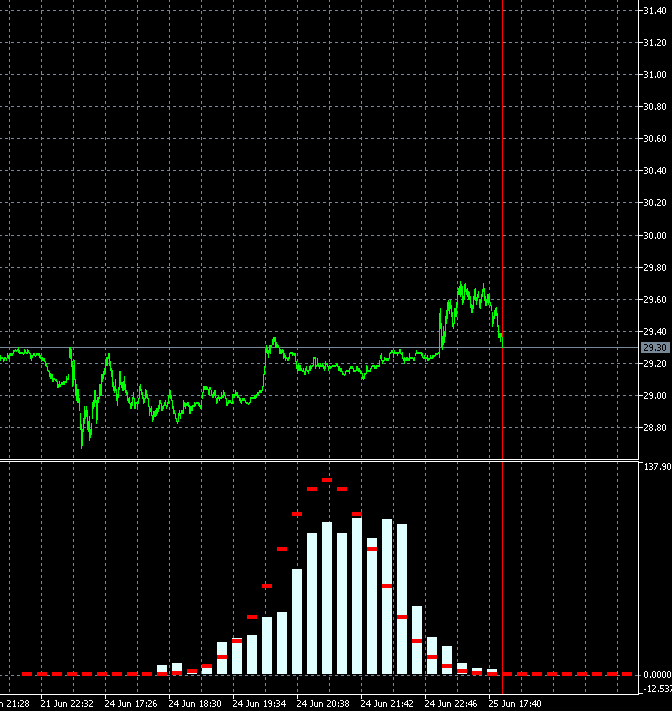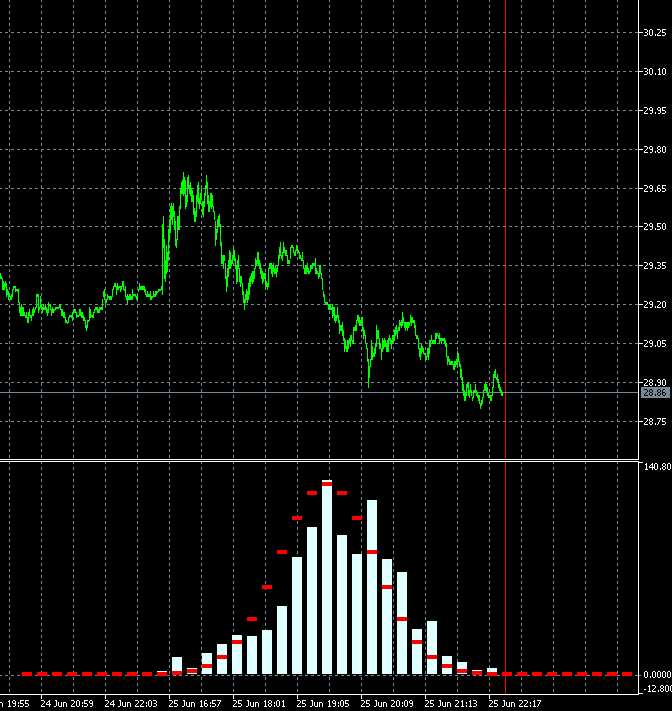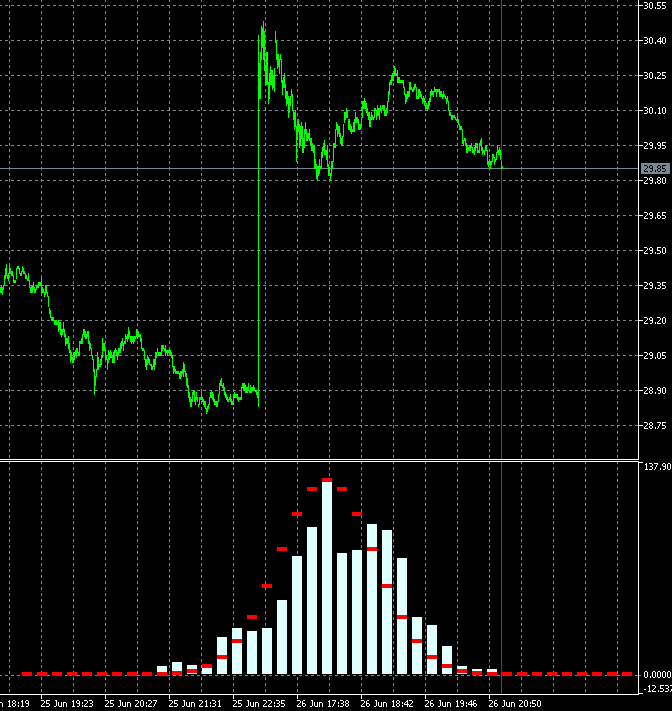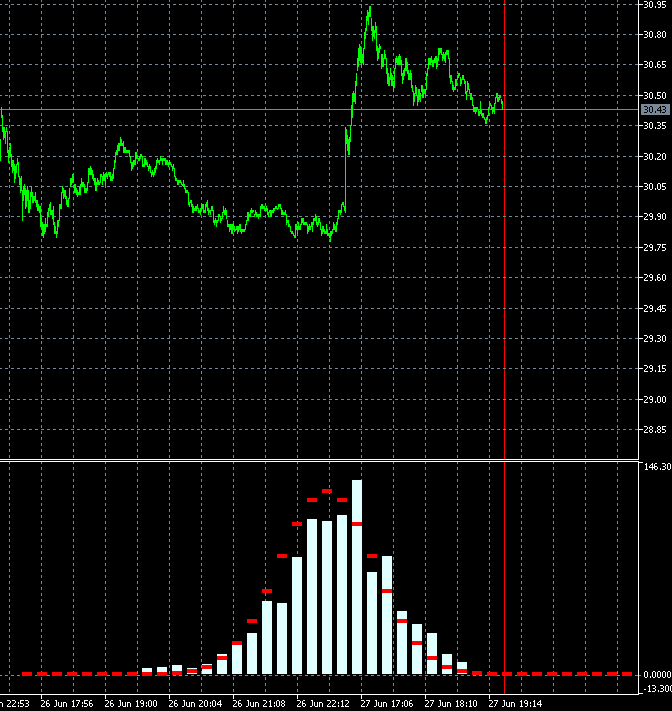
GBPUSDと違って、AMD株のインクリメント確率密度の分布はゼロに対称ではありません。 上昇トレンド成分が明確に存在します。 つまり、上昇ステップが続いた場合は、下降ステップが続いた場合に比べて、トレンド継続確率が若干高くなっています。 このようなツールの買いトレードを開く方が合理的であることを意味します。 この場合、ランダムポイントでインプットしながらでも利益を出し続けることが可能です。
相場構造は、トレンドに基づくものなのか、それともレンジなのか。
以上のことを考えると、相場はトレンドが優勢なのか、レンジなのか、もランダムベースなのか、という疑問が出てくるかもしれません。 この質問に答えることで、どの戦略や分析を適用するかを明確にすることができます。 ここまでに30以上の通貨ペア、ロシアと米国の両方の50以上の銘柄を分析してきました。 相場、クリプトカレンシー、コモディティ相場のほかにも。 商品相場には、金属、エネルギー、食品が含まれていました。 研究の結果、こう結論づけられます。
- 先進国通貨ペアの多くは、スケールやトレード量が大きくなるにつれて減少していく弱気なトレンドがあります。 例えば、EURUSDはGBPUSDよりもトレンド性が低いです。 FXにおける確率分布密度は正規分布に近いです。
- 株式相場は通貨よりもトレンド性がありますが、スケールが大きくなるとトレンド性は低下します。 先進企業の資産よりも積極的に開発している資産の方がトレンドになっています。 企業が開発に傾いていて、その可能性が低いほど、その企業の株はトレンドに左右されない。 完全に「面白くない」アセットは、レンジな動きを表すると言えます。 商品の流動性が高いほど、トレンド性の度合いは低くなります。 スケールの文脈でトレンド性の分布を分析することで、資本の流れの構造を理解することができます。 ある株が小さいスケールではトレンド、大きいスケールではレンジになっているとします。 これは会社が発展していないことを示しており、短期的にしか資金が投資されていないことを示します。 言い換えれば、分配形態は、ある商品が投資性のものか、純粋に投機性のものかを示します。 このように、チャートは、間接的ではあるが、企業の信用格付けを評価することができます。
- 商品相場には、現在の原材料需要や生産水準に応じて、トレンド商品とレンジ商品があります。 生産量が変わらない間に需要が増えれば、トレンドになります。 同様に、需要が減少しても、プロダクトレベルが変わらなければ、トレンド性の度合いも大きくなる。 商品需給が均衡に近い場合、その動きはよりレンジになる。
- 仮想通貨は、関心が高まって回転率が上がっている段階で、よりトレンドになっています。 公益性が薄れるとレンジになる。 その結果、ヒストリー全体の価格は、ランダムウォーク的な傾向があります。 しかし、新しい波が始まるとすぐに、再びトレンドになります。
ここではより広い結論を出すことができますが、それは別の記事のトピックです。
下記はトレードツールの特徴を説明したチャートです。
- BTCUSDは、暗号通貨に関する興奮が収まると横ばいになります。 興味深いことに、ビットコインの確率密度分布は、視覚的にはビットコインが上昇トレンドにあるように見えるという事実それにも関わらず、ゼロに対して対称的です。
- AMDとAAPL株は一貫して小幅なディップで推移します。 確率密度分布は、上昇方向にゼロに対して相対的に右にシフトします。 また、銘柄が着実に上昇トレンドにあることは目に見えて明らかです。
- 原油はスケールが大きくなっても全体的にトレンドになっています。
- EURUSDでは、大きなスケールでトレンド性がほとんどなくなりました。 一部のスケールではレンジになります。 一般的には、ランダムウォークの確率密度分布に他よりも多くのトレンドがあります。
- ロシア相場のリーダーは、小スケールでは安定したトレンド、大規模ではほとんどトレンドがないという似たようなところがあります。
なぜ小さいスケールの方がトレンドで、大きいスケールの方がレンジなのか? 次回は、そのような行動の理由について解説してみたいと思います。 現在の研究を元にアルゴリズムを開発して、利益が出るかどうかを見てみたいと思います。
結論
トレンドとレンジの概念を明確に、そして完全に定義することができました。 また、異なる尺度での単一の尺度と同様に、異なる尺度のトレンド性の度合いを比較することが可能です。 このような分析を行うことで、金融商品の特徴や特徴を評価し、各金融商品の個別の挙動を考慮したトレードアルゴリズムを構築することができます。
統計的特性とその経時変化を知ることで、トレードアルゴリズムを開発する際の最適化パラメータを取り除くことができます。 その代わりに、測定を行い、トレードされる商品の統計的特性に応じてトレードアルゴリズムのパラメータを意図的に変更することができます。
下記は、20%、50%、80%の確率反転チャートのヒストリーファイルです。 また、参照分布を構築するためのExcelファイルと、分析に使用するインジケータの構成要素があります。
このインジケータのアルゴリズムはMaxim Romanovによって開発され、インジケータのコードはKonstantin Gruzdevによって作成されました。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/8184
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 ニューラルネットワークが簡単に(第2回): ネットワークのトレーニングとテスト
ニューラルネットワークが簡単に(第2回): ネットワークのトレーニングとテスト
 価格系列の離散化、ランダム成分とノイズ
価格系列の離散化、ランダム成分とノイズ
 カスタムシンボル。実用的な基礎
カスタムシンボル。実用的な基礎
 外部アプリケーションで暗号を使用する
外部アプリケーションで暗号を使用する
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
入手方法
今のところ、このインジケーターは配布していません。もしかしたら将来、別のインジケーターを作って、それを共有できるかもしれません。
ヒストグラムのバーは、たった1本のバーを変更しただけで、不審なほど大きくジャンプします:1000本のバーのうち1本のバーを最後から削除し、1本のバーを最初に追加する必要があります。つまり、ヒストグラムのすべてのバーが一度に1/500の割合で変化し、実質的には1~2本のバーが変化するはずです。

スピードが速いので滑らかさに気づかないのかもしれないと思ったが...
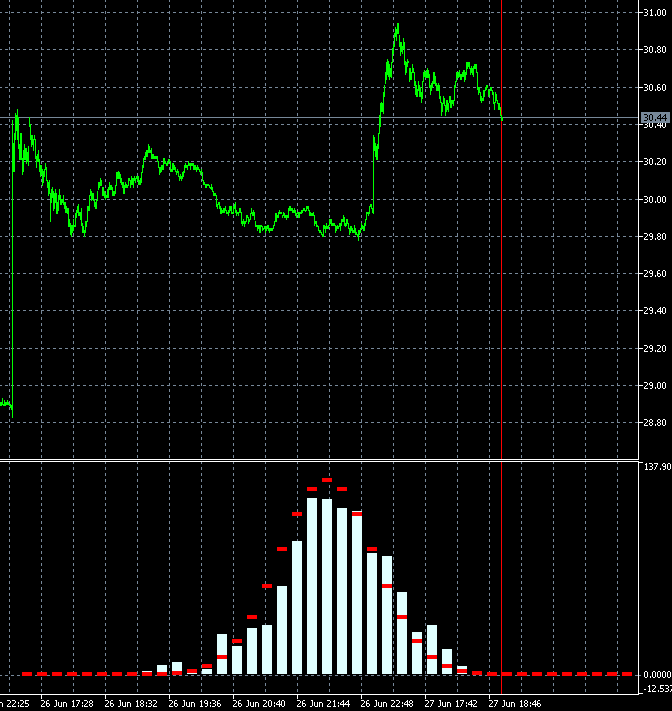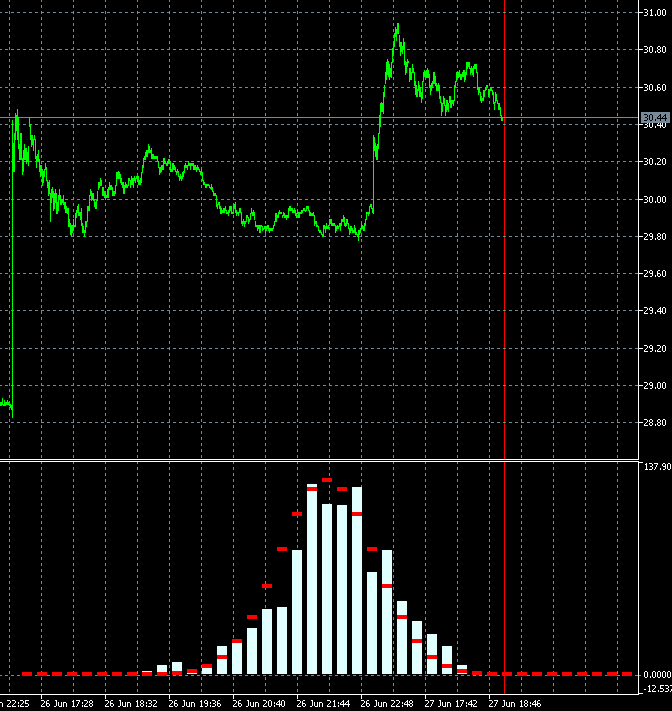
340と341の2つのフレームを隣のバーでコピーし、スピードを遅くしてみた:
すべての小節で一度に強い変化が見られます。多分、計算のどこかに間違いがあるのでは?1000本中2本でこんなに変わるわけがない。
計算が変わったのは2本ではなく1000本すべてで、1000本分のウィンドウ(1週間分、1ヶ月分...)が1本分ではなく過去にシフトしているようだ。
ヒストグラムのバーが1本だけ変化するとき、不審なほど大きくジャンプする:おそらく1000本のうち1本が最後から削除され、1本が最初に追加されるはずである。つまり、すべてのヒストグラム・バーについて、一度に1/500の割合で変化するはずであり、実質的には1本か2本のバーが変化するはずである。
340と341の2フレームをコピーして、隣り合うバーをより遅くした:
すべての小節で一度に強い変化が見られます。多分、計算のどこかに間違いがあるのでは?1000本中2本でこんなに変わるわけがない。
計算が変わったのは2本ではなく1000本すべてで、1000本分のウィンドウ(1週間分、1ヶ月分...)が1本分ではなく過去にシフトしているようだ。
そう、不審に思われるかもしれない)しかし、ブロックの構築には特殊性がある。ブロックは未来ではなく、最後の日付から過去に構築されます。したがって、ローソク足が来ると、ブロックを構築する価格がシフトし、ブロック自体が異なっていることが判明した。10ポイントでもずれると積み木の構成が変わり、その結果、分布の形も変わる。
なぜこのようにしたのか。理由は2つある。
1.ブロックを構築する方法は最初の価格に非常に敏感であり、異なる価格から構築した場合に分布がどのように変化するかを見たかった。この方法によって、分布が時間とともにどのように変化するか、また、分布が最初の価格からどのように変化するかを力学的に見ることができた。
2.私は大型ロボット用のブロック・インディケータを作りましたが、そこでは、履歴のためにパラメータを最適化するのを避けるためにこのアプローチを使いました。ブロックの構成は初期状態から大きく変化するため、1日前/後方にシフトすることで、履歴に対するパラメーターの最適化がすべてなくなります。こうすることで、履歴への大まかなフィッティングを避け、検出されたパターンがどれだけ安定しているかを評価することができる。パラメータを最適化することなく、どのような取引商品でも動作するロボットを作ることが重要でした。
そう、不審に思われるかもしれない)しかし、ブロックの構造には特殊性がある。積み木は未来ではなく、前回の日付から過去に作られる。したがって、ローソク足が来ると、ブロックを構築する価格がシフトし、ブロック自体が異なることが判明した。たとえ10ピップスのシフトは、ブロックの構成、ひいては分布の形状を変更することができます。
なぜこのようにしたのか。2つの理由があります
1.ブロック構築法自体が初値に非常に敏感であり、異なる価格から構築した場合に分布がどのように変化するかを見たかった。この方法によって、分布が時間とともにどのように変化するか、また初値の変化によって分布がどのように変化するかを力学的に見ることができた。
2.私は大型ロボット用のブロック・インジケータを作りましたが、そこではまさにこのアプローチを使って、履歴に対するパラメータの最適化を避けました。ブロックの構成は初期条件から大きく変化するため、1日前/後ろにずらすだけで、履歴に対するパラメーターの最適化をすべて行うことができます。こうすることで、履歴への大まかなフィッティングを避け、検出されたパターンがどれだけ安定しているかを評価することができる。パラメータを最適化することなく、どのような取引商品でも動作するロボットを作ることが重要でした。
このようなジャンプの理由は理解できましたが、私はまだ好きではありません。このヒストグラムインジケーターはどこかに掲載されていますか?画像ではなく、ライブで見るのは興味深いです。
MA計算のアルゴリズムについて考えてみた。このようなジャンプの理由は理解できましたが、私はまだ好きではありません。このヒストグラムインジケーターはどこかに掲載されていますか?画像ではなく、ライブで見るのは興味深いです。
いいえ、準備のできたインジケータは掲載していません。