MetaTrader 5 / 統計と分析
English Русский 中文 Español Deutsch Português 한국어 Français Italiano Türkçe
指数平滑法を用いた時系列予測

指数平滑法を用いた時系列予測

MetaTrader 5 — 統計と分析 | 28 10月 2015, 18:01
3 795 0
Victor
Victor

はじめに

時系列の過去のデーターの分析のみに基づいた様々な有名な予測方法、テクニカル分析にて使用される規則を用いる方法が数多く存在しています。これらメソッドは、ある一定の時間に認識された連続的な特性が制限を超える推定スキームです。

同時に、将来の連続的な特性は、過去・現在と同様です。予測期間内のこのようなダイナミクスにおけるシーケンスの特性の変動率の研究を必要とする、より複雑な外挿スキームは、あまり頻繁に予測に使用されていません。

外挿に基づいたよく知られている予測メソッドは、 自己回帰型移動平均モデル (ARIMA)を使用したものだと思います。これらのメソッドの任意は主に統合ARIMAモデルを開発し、提案したBoxとJenkinsによるものです。BoxとJenkinsによって紹介されたモデル以外にもその他のモデルや予測メソッドはもちろんあります。

この記事は、簡潔によりシンプルなメソッド - BoxとJenkinsの出現前にHoltとBrownによって提唱された指数平滑モデルについて紹介します。

よりシンプルで明確な数学的ツールであるにも関わらず、指数平滑法モデルを使用する予測は、時折ARIMAモデルを用いて取得される結果と匹敵する結果に繋がります。指数平滑法モデルがARIMAモデルの特別なケースであることは驚きではありません。言い換えれば、この記事の指数平滑法は、ARIMAモデルと一致する同等のものを持っているということです。これらの同等のモデルは、この記事では紹介されず、それについての情報のみ言及されています。

すべての場合における予測は、個別のアプローチを必要とし、多数の手順を要することは知られています。

例えば:

  1. 欠如した値や異常値に関する時系列分析これらの値の調整
  2. トレンドと型の特定シーケンスの周期の決定
  3. シーケンスの定常性チェック
  4. シーケンス前処理の分析（対数や差異の取得etc）
  5. モデル選択
  6. モデルパラメーターの決定選択したモデルに基づく予測
  7. モデル予測の正確な評価
  8. 選択モデルのエラー分析
  9. 選択モデルの妥当性の決定や、必要であれば、モデルの置換や先行する項目の返還

これは、効果的な予測に必要なアクションの全リストではありません。

モデルパラメーターの決定や予測結果の取得は、一般的な予測プロセスの一部でしかありません。しかし、一つの記事に予測に関連する問題全範囲をカバーすることは不可能に思えます。

この記事は、指数平滑法モデルのみを取り扱い、テストシーケンスとして前処理なしの通過見積もりを使用します。付随する問題は記事では避けられませんが、モデルのレビューにおいて必要な分だけ触れられます。


1. 定常性

外挿の概念は、研究下のプロセスの将来の開発が過去と現在と同様になるということを指します。言い換えれば、プロセスの定常性があることを言います。定常のプロセスは、予測の観点からとても魅力的ですが、開発中において常に変化にさらされており、不幸にもそれらは存在しません。

実際のプロセスは予測が難しく、差異がありますが、特性がゆっくり変化するプロセスは、定常のプロセスに帰属することができます。この場合の「ゆっくり」とは、限られた監視期間における変化が、無視できるほど重要ではないことを指します。

監視期間が短ければ、プロセスの定常性に関する異なる判断を行う可能性が高まります。他方で、もし短期間の予測を計画している差異に、プロセスの状態に興味があれば、サンプルのサイズの減少は、そのような予測での正確性の向上につながります。

もしそのプロセスが、変化しうるのであれば、監視期間にて決定されたシーケンスパラメーターは、制限の外で異なります。従って、予測期間が長ければ、予測エラーにおけるシーケンスの特性の差異効果が強くなります。このため、短期間予測に限る必要があります：予測期間における縮小は、変化のあるシーケンスの特性が大きな予測エラーにつながらないようにします。

さらに、シーケンスパラメーターの差異は、パラメーターがそのインターバルにおいて一定のものではないので、監視期間による推定時に取得された値が平均化されることにつながります。取得されたパラメーター値は、この期間の最後のインスタンスには関連しませんが、特定の平均値は繁栄します。不幸にも、完全にこの不快な現象を除去することはできませんが、もしモデルパラメーターの推定における監視期間の長さが縮小されれば、その現象を少なくすることができます。

同時に、その期間がもし極端にそれが縮小されれば、シーケンスパラメーターの推定の正確性が減少します。シーケンスの特性の差異に関連するエラーの効果と、監視期間の極端な減少によるエラーの拡大との間の妥協点を探す必要があります。

ARIMAモデルのようなプロセスの定常性への想定に基づいているため、これらすべてが指数平均モデルによる予測に当てはまります。しかし、単純化のため、すべてのシーケンスのパラメーターは、監視期間内に変換するが、これらの変化は無視できるレベルのもだと想定します。

従って、この記事は指数平均法モデルに基づいて、変化の遅いシーケンスの短期間の予測に関連する問題を紹介します。「短期間予測」は、この場合、１年未満の予測ではなく、二つかそれ以上のインターバルでの予測を指します。


2. テストシーケンス

この記事を書く上で、以前保存したM!、M5、M30におけるEURRUR、EURUSD、USDJPY、XAUUSDが使用されました。保存されたそれぞれのファイルは、1100の「オープン」値を持ちます。「最も古い」値は、ファイルの初めに位置しており、「最新」のものは最後の部分にあります。ファイルに保存された最後の値は、ファイルがされた時間と一致します。テストシーケンスを保持するファイルは、HitoryToCSV.mq5スクリプトを使用して作成されました。それらが作成される際に使用したスクリプトやデータファイルは、この記事の最後にあるFiles.zipにあります。

すでに言及した通り、保存された見積もりは、注意を喚起したい明確な問題にもかかわらず前処理なしで使用されています。例えば、12から13バーを含む日中のEURRUR_H1や金曜日のXAUUSDはその他の日よりも一つバーが少ないです。これらの例は、見積もりが不規則なサンプリング期間により作成されていることを示します：これは、単一の数量化期間を提示する正確な時間のシーケンスを扱うために設計されたアルゴリズムにおいては受け入れがたいものです。

たとえ、欠如した見積もり値が外挿により置き換えられても、週末の見積もり値の欠如に関する問題は開かれたままです。週末に全世界で起こるイベントは平日のイベントと同様の影響を世界経済に与えます。革命や、注意を引きつけるスキャンダル、政府の変化などの大きなイベントはいつでも起こります。もしそのようなイベントが土曜日に発生すれば、世界のマーケットには、平日に発生するよりも影響がすくないでしょう。

これらのイベントは見積もり額のギャップにつながるので、週末に監視されるのです。一見、世界はFOREXが動作しないときでも、彼らのルールで進んで行くと思います。ただ、テクニカル分析の意図された週末に一致する見積もり値が再生産されるのか否か、どのような利益を提供するかについてはまだ不明確です。

明らかに、これらの問題は、この記事の範囲を超えていますが、少なくとも周期的なコンポーネントの発見においては、ギャップのないシーケンスは分析に適しているようです。

さらなる分析におけるデータの予備的な準備の重要性は、評価しすぎることはありません。我々の場合、それは主要な独立した問題であり、いかにターミナル内に現れるかは、テクニカル分析には適していません。上記のギャップに関する問題の他に、その他たくさんの問題があります。

例えば、見積もりを作成する際に、一定の期間が「オープン」・「クローズ」の値に割り当てられます。これらの値は、選択したタイムフレームのチャートの固定の一時の代わりに、ティック形成時間と一致しています。一方、ティックは非常にまれであると知られています。

その他の例は、完全なサンプリング原則への無視において見られます。1分間のサンプリング率は、上記の原則を満足させると保証できないためです。（言うまでもなくより大きい期間においてもです）さらに、見積もり額に上書きされる値段差の存在を心に留める必要があります。

しかしながら、この記事の扱う範囲外においておき、主題へと戻りましょう。


3. 指数平滑法

まずは、最もシンプルなモデルを見てみましょう。

,

where:

  • X(t) – (simulated) process under study,
  • L(t) – variable process level,
  • r(t)– zero mean random variable.

ご覧の通り、このモデルは、二つのコンポーネントの合計からなります；特に L(t)プロセスレベルに関心を持ち、これを抜き出していきます。

ランダムシーケンスの平均化は、減少された分散化を生み出します。つまり、中間からの減少した逸脱範囲につながります。そのため、もしそのシンプルなモデルにてよって記述されたプロセスが平均化（平滑化）にさらされていれば、ランダムなコンポーネントr(t)を完全に取り除くことができませんが、少なくともある程度弱めることはでき、ターゲットレベルL(t)を選び抜くことはできると想定できます。

このために、シンプルな指数平滑法（SES）を使用します。

このよく知られた公式は、平滑化の度合いは、0から1のアルファ係数によって設定されます。もしアルファが０であれば、入力シーケンスXの新しい値は、平滑化の結果になんの影響も与えません。 will have no effect whatsoever on the smoothing result. どの時点においても平滑化の結果は一定した値となります。

結果として、このような極端なケースにおいても、ランダムなコンポーネントは、抑圧されますが、プロセスレベルは、水平に平滑化されます。もしアルファ係数が１であれば、入力シーケンスは、平滑化に全く影響されません。そのレベルL(t)は、この場合変形されず、ランダムコンポーネントは抑圧もされません。

アルファ値を選択する際に、葛藤する要求を満たす必要があります。一方で、アルファ値は、ランダムコンポーネントr(t)を抑圧するためには０に近くなります。他方で、L(t)コンポーネントを変化させないために統一のものに近いアルファ値を設定することが望ましいです。最適なアルファ値を取得するために、そのような値が最適化される上での基準を特定する必要があります。

そのような基準を決定するにあたって、この記事は、シーケンスの平滑化ではなく、予測を取り扱うことを忘れないでください。

シンプルな指数平滑法モデルに関して、複数のステップにおいての予測として特定の時間に取得された値を考察することが習慣となっています。

t時刻における mステップ先の予測

t時刻でのシーケンス値の予測は以前のステップにて作成された１ステップ先の予測になります。

この場合、アルファ係数値の最適化基準として、１ステップ先予測エラーを使用することができます。

したがって、サンプル全体のこれらエラーの合計の最小化により、特定のシーケンスにおいて最適なアルファ値を決定することができます。最適なアルファ値は、エラーの合計がある地点のものです。

図１は、テストシーケンスUSDJPY M1のアルファ係数値に対する一ステップ先の予測エラーの二乗の合計の図を示しています。

図1. シンプル指数平滑法

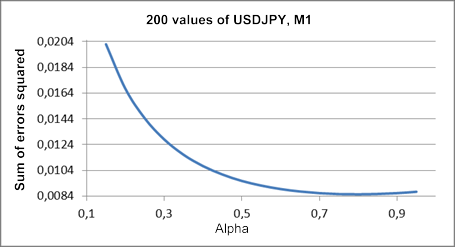
図1. シンプル指数平滑法

結果としてのプロットにおける最小値は、認識することができず、0.8のアルファ値に近いところに位置しています。しかし、そのような図は必ずしもシンプル指数へい買う法に関する場合ではありません。この記事で使用されるテストシーケンスにおける最適なアルファ値を取得する際、しばしば統一のものに当てはまるプロットを取得します。

そのような高い平滑化係数値は、このシンプルなモデルが、我々のテストシーケンスの記述に適さないことを提示しています。プロセスレベルL(t)は、急速に変化するか、プロセスにトレンドがあるかのどちらかです。

別のコンポーネントを追加して少しモデルを複雑なものにしてみましょう。

,

where:

  • X(t) - 調査中のプロセス：
  • L(t) - 変異するプロセスレベル；
  • T(t) - 線形トレンド；
  • r(t) - ０のランダム変数

線形回帰係数は、シーケンスの二重平滑化によって決定されます。

係数のために、この方法で取得されたa1とa2、t時のmステップ先予測は以下に等しくなります。

同じアルファ係数はが最初と繰り返しの平滑化のために上記の公式が使用されています。このモデルは、線形成長の１パラメーター追加モデルと呼ばれます。

シンプル萌えると線形成長モデルの違いを紹介します。

長い間、そのプロセスは、一定のコンポーネントを示します。すなわち、直接の水平線としてチャートに現れますが、いくつかの地点で線形のトレンドが始まります。上記のモデルを使用して行われたこのプロセスの予測は、図２にて示されています。

図２モデル比較

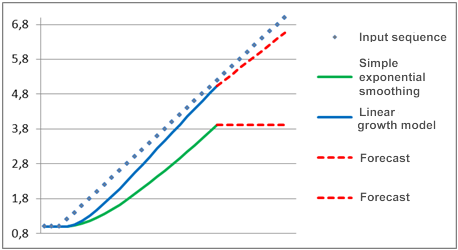
図２モデル比較

ご覧の通り、シンプルな指数平滑方モデルは明らかに戦場に変化する入力シーケンスの後ろにあり、このモデルを使用した予測は、少し遅れて動きます。線形成長モデルが使用された際には異なったパターンを見ることができます。そのトレンドが出現した際、このモデルは、まるで線形に変化するシーケンスや予測に追いつくことが変化する入力値の方向により近いかのようだ。

もし例の平滑化係数が高ければ、線形成長モデルは、特定の期間の間に入力シグナルに「達する」ことができ、その予測は入力シーケンスと一致します。

線形成長モデルは、線形トレンド出現時に良い結果を提供するにも関わらず、トレンドに「追いつく」ためには少しの時間がいることがわかります。従って、もしトレンドの方向が頻繁に変わる場合、そのモデルと入力シーケンスにはギャップが生じます。加えて、もしトレンドが非線形に成長するが、二乗則で進んだ場合、線形成長モデルは、それに「たどり着く」ことはできません。しかし、これらの欠点に関わらず、このモデルは線形トレンド出現時は、そのシンプルな指数平滑モデルよりも有益です。

すでに述べた通り、線形成長のワンパラメーターモデルを使用しました。テストシーケンスUSDJPY M1におけるアルファパラメーターの最適な値を見つけるために、アルファ係数値に対するワンステップ先予測エラーの二乗の合計を描画しましょう。

図１と同じシーケンスの一部に基づいて作成されたこの描画は、図３にて表示されています。

図３. 線形成長モデル

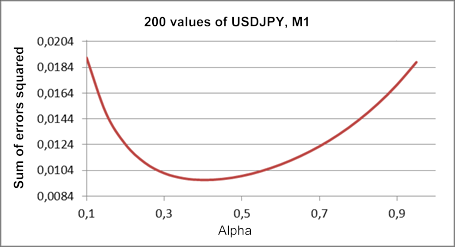
図３. 線形成長モデル

図１の結果と比較すると、アルファ係数の最適地は、この場合、およそ0.4まで下がりました。理論上、その値は異なりますが、最初と二番目の平滑化は、このモデルでは同じ係数を持っています。二つの異なる平滑係数の線形成長モデルはさらに検証されます。

両方の指数平滑モデルは、MetaTrader 5にて類似体を持っており、インジケーターの形で存在していまっす。これらは、よく知られるEMAやDEMAであり、予測のためではなく、シーケンスの値の平滑化を目的として設計されています。

DEMAインジケーターを使用すると、a1係数に一致する値は、１ステップ予測値の代わりに表示されます。a2係数（線形成長モデルの上記の公式を見てください）は、この場合、計算や使用はされません。さらに、平滑化係数は、同等のn期間において計算されます。


例えば、0.8に等しいアルファが2に等しいnに一致します。


4. 初期値

すでに述べた通り、平滑係数値は、指数平滑化の適用により取得されます。しかし、これでは十分ではありません。指数平滑化では、現在の値は以前のものを基準として計算されるので、そのような値が０の時に存在しない状況があります。言い換えれば、線形成長モデルにおいてはSかS1や S2の初期値は、０の時に計算されます。

初期値の取得における問題は必ずしも解決が簡単ではありません。もし（MetaTrader4の見積もりを使用する場合のように）とても長い履歴を持っている場合、指数平滑カーブは、初期値が間違って決定されていれば、その初期値を正し、現在のポイントにより安定する時間を持ちます。これは、平滑係数値に依存し、10から200の期間を要します。。

この場合、初期値をおおよそで推定し、ターゲット時刻よりも200-300ほどの期間手前で指数平滑化プロセスを始めれば十分です。サンプルが100の値のみを持っている際はより難しくなります。

初期値の選択に関して、様々な推奨があります。たとえば、シンプル指数平滑化においての初期値は、シーケンス内の最初の要素と同等になるか、3から4の初期要素として計算されます。線形成長モデルの初期値S1、S2は、予測カーブの初期レベルは、シーケンスの最初の要素に等しくなるという想定のもとに決定され、線形トレンドの傾斜は０になります。

初期値の選択に関してより多くの推奨が見つかりますが、それらすべては、平滑化アルゴリズムの初期段階でエラーの欠如を保証することができません。安定した状態を維持するために多くの期間が必要である際には、低い値の平滑係数の使用により注意を引きます。

従って、初期値の選択に関連する問題の影響を最小化するために、最小の予測エラーへつながる値の検索に関するメソッドを使用します。それは、全シーケンス内で少ない増加で変化する初期値における予測エラーの計算に関する問題です。

最も適切なものは、すべての可能な初期値の組み合わせの範囲のエラーを計算したのちに選択されます。しかし、このメソッドは多くの計算を必要としとても骨の折れるものであり、直接の形では使用されません。

その問題は、最適化か、最小のマルチ変数の関数値における検索と関係します。そのような問題は、必要な計算の範囲を縮小させるために開発された様々なアルゴリズムを用いて解決されます。予測での初期値や平滑化パラメーターの最適化における問題に後ほど戻ってきます。


5. 予測正確性評価

予測の手順や初期値、パラメーターの選択は、予測の正確性の問題を生み出します。正確性の評価は、二つの異なるモデルを比較する、もしくは、取得された予測の一貫性を判断する際には重要です。予測正確性評価における推定方法は数多くありますが、それらの計算は各ステップごとの予測エラーの知識を要します。

すでに述べたように、ワンステップ先予測のエラーは以下に等しくなります。

where:

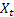  • – t時の入力シーケンスの値
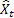  • – t時の一つ手間のステップでの予測

最も基本的な予測正確性評価は、平均平方誤差（MSE）です。


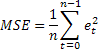
nがシーケンスの要素数であるところ

大きい値のシングルエラーへの極端な感受性は、時折MSEの欠点であると指摘されます。エラー値はMSE計算時に二乗されるという事実に由来します。代案として、平均絶対誤差を使用することが望ましいです。

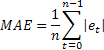
二乗誤差は、絶対誤差の値により取り替えられます。MAEにより得られた推定はより安定していると考えられています。

両方の推定は、異なるモデルパラメーターや異なるモデルを使用した同じシーケンスの正確性の評価においてはかなり適切ですが、異なるシーケンスで取得された予測結果の比較においては使用できません。

さらに、これらの推定値は、予測結果の質を示しません。例えば、その他の値の取得された値や、0.03のMAEが良いか、悪いかはいうことはできません。

異なるシーケンスの予測の正確性を比較するために、関連したRelMSEとRelMAEを使用できます：


取得された予測正確性の評価は、予測テストメソッドを持ちいて得られたそれぞれの評価によって分けられます。テストメソッドとして、いわゆるプロセスの将来の値が現在の値に等しいことを示すネィテイブメソッドを使用することが適しています。


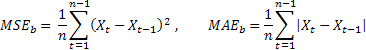
もし予測結果がネィティブメソッドを用いて取得されたエラー値と等しい場合、関連する推定値は１に等しくなります。もし関連推定値が１以下であれば、平均では、予測エラー値はネィテイブメソッドよりも小さくなることを意味します。言い換えれば、予測結果の正確性は、ネィティブメソッドの正確性に勝ります。また逆も然りで、もし関連する推定値が１以上であれば、予測結果の正確性は、ネィティブメソッドの正確性に劣ります。

これらの推定値は、２かそれ以上のステップ先における予測正確性評価に適しています。計算におけるワンステップ先予測エラーは、適切なステップ数において予測エラー値と取り替えられる必要があります。

例として、以下のテーブルは、ワンパラメーターの線形成長モデルでReIMAEを使用して推定されたワンステップ先の予測エラーを持っています。エラーはそれぞれのテストシーケンスの最後200の値を使用して計算されました。


alpha = 0,3
alpha = 0,4
alpha = 0,5
EURRUR M1
1.14
 1.10
 1.09
EURRUR M30
1.14
 1.11
 1.14
EURUSD M1
1.17
 1.11
 1.10
EURUSD M30
1.17
 1.11
 1.11
USDJPY M1
1.10
 1.08
 1.10
USDJPY M30
1.17
 1.13
 1.13
XAUUSD M1
1.20
 1.11
 1.10
XAUUSD M30
1.11
 1.12
 1.13


図表１ReIMAEを用いて推定されたワンステップ先の予測エラー

RelMAEは、異なるシーケンスを予測する際に選択したメソッドの効果を比較することができるようにします。図表１が示すように、私たちの予測はネィティブメソッドをこれ以上こえることはないほどの正確性がありました。全てのReIMAE値が１以上でした。


6. 補助モデル

この記事の序盤にあったモデルで、プロセスのレベルの合計や線形トレンド、ランダム変数からなるモデルがありました。上記のコンポーネントに加えて、周期的なコンポーネントを含める別のモデルを追加し、この記事にて見られるモデルのリストを拡大していきます。

合計としての全てのコンポーネントから構成される指数平滑化モデルは、補助モデルと呼ばれています。これらのモデルとは異なり、一つか、それ以上のコンポーネントが一つの製品として構成される増殖性のモデルがあります。補助モデルのグループを見てみましょう。

ワンステップ先予測エラーは、繰り返しこの記事で述べられています。このエラーは、指数平滑法に基づく予測に関連するアプリケーションでは全て計算されています。予測エラーの値を知り、紹介されている指数平滑化モデルの公式が多少異なった形で示されます。

使用する予定であるそのモデルの表現形式は、以前取得された値に追加される表現におけるエラーを保持しています。そのような表現は、補助的エラーモデルと呼ばれます。指数平滑化モデルは、増殖的なエラー形式にて表現され、それはこの記事では使用されません。

補助的指数平滑化モデルを見てみましょう。

シンプル指数平滑法：

等価モデル – ARIMA(0,1,1):

補助的線形成長モデル：

以前紹介されたワンパラメーター線形成長モデルと比較して、二つの異なる平滑化パラメーターはこちらで使用されます。

等価モデル – ARIMA(0,2,2):

ダンピング付き線形成長モデル

そのようなダンピングの意味は、トレンドの傾斜がタンピング係数値に応じて、毎予測ステップごとに減退するということです。この効果は、図４にて紹介されています。

図４

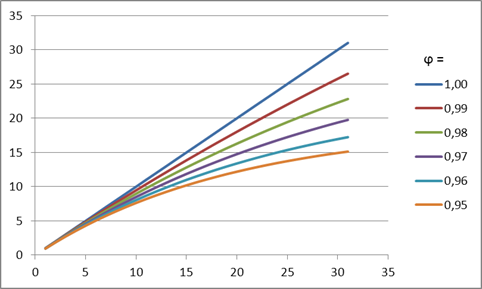
図4. ダンピング係数効果

図にてご覧の通り、予測を行う場合、ダンピング係数の減退する値がトレンドの強さを失わせ、線形成長がより阻害されます。

等価モデルj - ARIMA(1,1,2):

これら３つのモデルとして周期性のコンポーネントを追加することで、追加の三つのモデルを得ることができます。

補助的周期性のシンプルモデル

補助的周期性の線形成長モデル

補助的周期性とダンピングの線形成長モデル

周期性のモデルに等しいARIMAモデルもありますが、実用的な重要性はほとんどないので、ここでは記されていません。

公式にて使用された表記が以下になります：

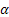  • – [0:1]シーケンスレベルの平滑化パラメーター;
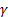  • – トレンドの平滑化パラメーター [0:1];
  • – 周期インデックスにおける平滑化パラメーター [0:1];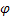
  • – ダンピングパラメーター [0:1];
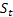  • – t時に計算されたシーケンスのレベル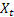が監視されています。
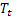  • – t時に計算された平滑化された補助的トレンド
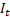  • – t時に計算された平滑化周期インデックス
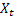  • – t時のシーケンス値
  • m – 予測がなされる前のステップ数
  • p – 周期における期間数
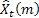  • – t時になされるmステップ先の予測
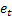  • – t時のワンステップ先予測エラー.

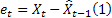最後のモデルにおける公式が全てで６つの異なる形が含んでいることは見て取れます。

ダンピングや補助的周期性のある線形成長モデルにおける公式にて、

,

周期性は予測においては無視されます。さらに、線形成長が行われるところでは、ダンピングのある線形成長を得ることができます。

シンプル指数平滑モデルは以下に一致します。.

周期性を持つモデルを使用する際、周期性の存在や周期の期間は、周期インデックス値の初期化のためにデータを使用するため可能なメソッドを用いて決定される必要があります。

予測が短期間で行われるケースにて使用されるテストシーケンスの安定した周期性を発見できません。従って、この記事では、関連する例は紹介せず、周期性に関連する特性については深く述べません。

モデルにおける予想インターバルの決定のため、文献[3]で見られる分析的派生物を使用します。nサイズのサンプルにて計算されたワンステップ先の予測エラーの二乗の合計は、そのようなエラーの推定誤差として使用されます。

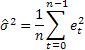
そして、以下の表現はモデルの２ステップ以上先の予測における誤差の決定においては正しいものです。

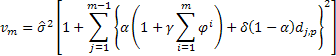
もしk mojulo pが０であれば、 同じく０です。

全てのステップにおける予測の推定誤差を計算すれば、95%の予想インターバルの制限を発見できます。

そのような予測インターバルを予測確信インターバルと名付けることには納得できます。

MQL5にて記述されているクラスの指数平滑化モデルにて提供されている表現を実装していきます。


7. AdditiveESクラスの実装

そのクラスの実装は、ダンピングや補助的周期を持つ線形成長モデルにおける表現の使用を要します。

以前述べられた通り、その他のモデルは、適切なパラメーターの選択から由来します。

//-----------------------------------------------------------------------------------
//                                                                     AdditiveES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>

//-----------------------------------------------------------------------------------
// Forecasting. 指数平滑化補助モデル
// References:
// 1. Everette S. Gardner Jr. 指数平滑化：最高水準 – Part II.
//    June 3, 2005.
// 2. Rob J Hyndman. 指数平滑化のための状態スペースモデルに基づく予測
//   29 August 2002.
// 3. Rob J Hyndman et al. 指数平滑化のための予想インターバル - 
//    状態スペースモデルの二つの新しいクラスを使用する。30 January 2003.
//-----------------------------------------------------------------------------------
class AdditiveES:public CObject
  {
protected:
  double Alpha;    // Smoothed parameter for the level of the series
  double Gamma;    // Smoothed parameter for the trend
  double Phi;      // Autoregressive or damping parameter
  double Delta;    // Smoothed parameter for seasonal indices
  int    nSes;     // Number of periods in the seasonal cycle
  double S;        // Smoothed level of the series, computed after last Y is observed
  double T;        // Smoothed additive trend
  double Ises[];   // Smoothed seasonal indices
  int    p_Ises;   // Pointer for Ises[] shift register
  double F;        // Forecast for 1 period ahead from origin t

public:
         AdditiveES();
  double Init(double s,double t,double alpha=1,double gamma=0,
              double phi=1,double delta=0,int nses=1);
  double GetS()                 { return(S); }
  double GetT()                 { return(T); }
  double GetF()                 { return(F); }
  double GetIs(int m);
  void   IniIs(int m,double is);  // Initialization of smoothed seasonal indices
  double NewY(double y);          // Next calculating step
  double Fcast(int m);            // m-step ahead forecast
  double VarCoefficient(int m);   // Coefficient for calculating prediction intervals

  };
//-----------------------------------------------------------------------------------
// Constructor
//-----------------------------------------------------------------------------------
void AdditiveES::AdditiveES()
  {
  Alpha=0.5; Gamma=0; Delta=0; Phi=1; nSes=1;
  ArrayResize(Ises,nSes);
  ArrayInitialize(Ises,0);
  p_Ises=0; S=0; T=0;
  }
//-----------------------------------------------------------------------------------
// Initialization
//-----------------------------------------------------------------------------------
double AdditiveES::Init(double s,double t,double alpha=1,double gamma=0,
                       double phi=1,double delta=0,int nses=1)
  {
  S=s; T=t;
  Alpha=alpha; if(Alpha<0)Alpha=0; if(Alpha>1)Alpha=1;
  Gamma=gamma; if(Gamma<0)Gamma=0; if(Gamma>1)Gamma=1;
  Phi=phi; if(Phi<0)Phi=0; if(Phi>1)Phi=1;
  Delta=delta; if(Delta<0)Delta=0; if(Delta>1)Delta=1;
  nSes=nses; if(nSes<1)nSes=1;
  ArrayResize(Ises,nSes);
  ArrayInitialize(Ises,0);
  p_Ises=0;
  F=S+Phi*T;
  return(F);
  }
//-----------------------------------------------------------------------------------
// Calculations for the new Y
//-----------------------------------------------------------------------------------
double AdditiveES::NewY(double y)
  {
  double e;
  
  e=y-F;
  S=S+Phi*T+Alpha*e;
  T=Phi*T+Alpha*Gamma*e;
  Ises[p_Ises]=Ises[p_Ises]+Delta*(1-Alpha)*e;
  p_Ises++; if(p_Ises>=nSes)p_Ises=0;
  F=S+Phi*T+GetIs(0);
  return(F);
  }
//-----------------------------------------------------------------------------------
// Return smoothed seasonal index
//-----------------------------------------------------------------------------------
double AdditiveES::GetIs(int m)
  {
  if(m<0)m=0;
  int i=(int)MathMod(m+p_Ises,nSes);
  return(Ises[i]);
  }
//-----------------------------------------------------------------------------------
// Initialization of smoothed seasonal indices
//-----------------------------------------------------------------------------------
void AdditiveES::IniIs(int m,double is)
  {
  if(m<0)m=0;
  if(m<nSes)
    {
    int i=(int)MathMod(m+p_Ises,nSes);
    Ises[i]=is;
    }
  }
//-----------------------------------------------------------------------------------
// m-step-ahead forecast
//-----------------------------------------------------------------------------------
double AdditiveES::Fcast(int m)
  {
  int i,h;
  double v,v1;

  if(m<1)h=1; else h=m;  
  v1=1; v=0;
  for(i=0;i<h;i++){v1=v1*Phi; v+=v1;}
  return(S+v*T+GetIs(h));
  }
//-----------------------------------------------------------------------------------
// Coefficient for calculating prediction intervals
//-----------------------------------------------------------------------------------
double AdditiveES::VarCoefficient(int m)
  {
  int i,h;
  double v,v1,a,sum,k;
  
  if(m<1)h=1; else h=m;
  if(h==1)return(1);
  v=0; v1=1; sum=0;
  for(i=1;i<h;i++)
    {
    v1=v1*Phi; v+=v1;
    if((int)MathMod(i,nSes)==0)k=1; else k=0;
    a=Alpha*(1+v*Gamma)+k*Delta*(1-Alpha);
    sum+=a*a;
    }
  return(1+sum);
  }
//-----------------------------------------------------------------------------------

AdditiveESクラスのメソッドを簡単に見ていきましょう。

Initメソッド

入力パラメーター：

  • double s - 平滑化レベルの初期値を設定する：
  • double t - 平滑化のトレンドの初期値を設定する
  • double alpha=1 - シーケンスレベルにおける平滑化パラメーターを設定する；
  • double gamma=0 - トレンドの平滑化パラメーターを設定する；
  • double phi=1 - ダンピングパラメーターの設定を行う；
  • double delta=0 - 周期的インデックスの平滑化パラメーターを設定する；
  • int nses=1 - 周期においての期間数を設定する。

戻り値:

  • 初期値に基づきワンステップ先予測を返します。

Initメソッドは最初に呼ばれます。これは、平滑化パラメーターや初期値の設定に必要です。Initメソッドは任意の値で周期的なインデックスの初期化を提供しません；このメソッドを呼び出す際に、周期的インデックスはーにセットされます。

Inilsメソッド

入力パラメーター：

  • Int m - 周期的インデックス数
  • double is -周期インデックス数mの値をセットします。

戻り値:

  • None

IniIs(...)メソッドは周期的インデックスの初期値が０以外である必要がある際に呼ばれます。周期的インデックスは、Initメソッドが呼ばれたのちに初期化されます。

NewYメソッド

入力パラメーター：

  • double 入力シーケンスの新しい値

戻り値:

  • シーケンスの新しい値に基づきワンステップ先の予測を返します。

このメソッドは、ワンステップ先の予測を入力シーケンスの新しい値が入力されるたびに、計算するように設計されています。Initによりクラスの初期化のあと呼ばれる必要があります。

Fcast メソッド

入力パラメーター：

  • int m –1、2、3の期間の水平性の予測

戻り値:

  • mステップ先の予測値を返します。

このメソッドは、平滑化プロセスの状態には影響を与えず、予測の値のみ計算します。NewYがよばれたのちに、よばれます。

VarCoefficientメソッド

入力パラメーター：

  • int m –1、2、3の期間の水平性の予測

戻り値:

  • 予測の誤差を計算する係数値を返します。

この係数値は、ワンステップ先の予測に比べてmステップ先の予測の誤差がどれほど上昇しているかを示します。

GetS、GetT、GetF、GetIs methods

これらのメソッドは、クラスの保護された変数へのアクセスを提供します。GetS、GetTやGetFは、平滑化レベル、トレンド、ワンステップ先予測の値をそれぞれ返します。GetIsメソッドは、周期的インデックスへのアクセスを提供し、インデックス数mのインデックス化をインデックスの引数として必要とします。

最も複雑なモデルは AdditiveESクラスに基づくダンピングや補助的周期の線形成長モデル です。これは、とても合理的な質問を喚起します - 残りのより単純なモデルは必要なのでしょうか？

より複雑なモデルは明確な利点を持っているにも関わらず、必ずしも必要とは限りません。少数のパラメーターを持つよりシンプルなモデルは多くの場合、予測エラーの少ない誤差、より安定した実行に至ります。この事実は、簡単なものから複雑なものまでの全てのモデルの同時並列処理に基づく予測アルゴリズムの作成に使用されます。

そのシーケンスが処理されれば、最も低いエラーを示した予測モデルが選択されます。この目的のために開発された基準がたくさんあり、例えばAkaike’s Information Criterion (AIC)です。最も安定した予測を作成するモデルの選択に帰結します。

AdditiveESクラスの使用の紹介をするため、シンプルなインジケーターが作成され、全ての平滑化パラメーターは手動で設定されます。

AdditiveES_Test.mq5インジケーターのソースコードは、以下のように設定されます。

//-----------------------------------------------------------------------------------
//                                                                AdditiveES_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"      // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "PInterval+"    // Prediction interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCadetBlue
#property indicator_style3  STYLE_SOLID
#property indicator_width3  1
#property indicator_label4  "PInterval-"    // Prediction interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCadetBlue
#property indicator_style4  STYLE_SOLID
#property indicator_width4  1

double HIST[];
double FORE[];
double PINT1[];
double PINT2[];

input double Alpha=0.2;     // Smoothed parameter for the level
input double Gamma=0.2;     // Smoothed parameter for the trend
input double Phi=0.8;       // Damping parameter
input double Delta=0;       // Smoothed parameter for seasonal indices
input int    nSes=1;        // Number of periods in the seasonal cycle
input int    nHist=250;     // History bars, nHist>=100
input int    nTest=150;     // Test interval, 50<=nTest<nHist
input int    nFore=12;      // Forecasting horizon, nFore>=2

#include "AdditiveES.mqh"
AdditiveES fc;

int    NHist;               // history bars
int    NFore;               // forecasting horizon
int    NTest;               // test interval
double ALPH;                // alpha
double GAMM;                // gamma
double PHI;                 // phi
double DELT;                // delta
int    nSES;                // Number of periods in the seasonal cycle
//-----------------------------------------------------------------------------------
// Custom indicator initialization function
//-----------------------------------------------------------------------------------
int OnInit()
  {
  NHist=nHist; if(NHist<100)NHist=100;
  NFore=nFore; if(NFore<2)NFore=2;
  NTest=nTest; if(NTest>NHist)NTest=NHist; if(NTest<50)NTest=50;
  ALPH=Alpha; if(ALPH<0)ALPH=0; if(ALPH>1)ALPH=1;
  GAMM=Gamma; if(GAMM<0)GAMM=0; if(GAMM>1)GAMM=1;
  PHI=Phi; if(PHI<0)PHI=0; if(PHI>1)PHI=1;
  DELT=Delta; if(DELT<0)DELT=0; if(DELT>1)DELT=1;
  nSES=nSes; if(nSES<1)nSES=1;

  MqlRates rates[];
  CopyRates(NULL,0,0,NHist,rates);           // Load missing data
  
  SetIndexBuffer(0,HIST,INDICATOR_DATA);
  PlotIndexSetString(0,PLOT_LABEL,"History");
  SetIndexBuffer(1,FORE,INDICATOR_DATA);
  PlotIndexSetString(1,PLOT_LABEL,"Forecast");
  PlotIndexSetInteger(1,PLOT_SHIFT,NFore);
  SetIndexBuffer(2,PINT1,INDICATOR_DATA);
  PlotIndexSetString(2,PLOT_LABEL,"Conf+");
  PlotIndexSetInteger(2,PLOT_SHIFT,NFore);
  SetIndexBuffer(3,PINT2,INDICATOR_DATA);
  PlotIndexSetString(3,PLOT_LABEL,"Conf-");
  PlotIndexSetInteger(3,PLOT_SHIFT,NFore);
  
  IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
  return(0);
  }
//-----------------------------------------------------------------------------------
// Custom indicator iteration function
//-----------------------------------------------------------------------------------
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
  int i,j,init,start;
  double v1,v2;
  
  if(rates_total<NHist){Print("Error: Not enough bars for calculation!"); return(0);}
  if(prev_calculated>rates_total||prev_calculated<=0||(rates_total-prev_calculated)>1)
    {init=1; start=rates_total-NHist;}
  else
    {init=0; start=prev_calculated;}
  if(start==rates_total)return(rates_total);    // New tick but not new bar
//-----------------------
  if(init==1)                                   // Initialization
    {
    i=start;
    v2=(open[i+2]-open[i])/2;
    v1=(open[i]+open[i+1]+open[i+2])/3.0-v2;
    fc.Init(v1,v2,ALPH,GAMM,PHI,DELT,nSES);
    ArrayInitialize(HIST,EMPTY_VALUE);
    }
  PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFore);
  PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFore);
  PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFore);

  for(i=start;i<rates_total;i++)                // History
    {
    HIST[i]=fc.NewY(open[i]);
    }
  v1=0;
  for(i=0;i<NTest;i++)                          // Variance
    {
    j=rates_total-NTest+i;
    v2=close[j]-HIST[j-1];
    v1+=v2*v2;
    }
  v1/=NTest;                                    // v1=var
  j=1;
  for(i=rates_total-NFore;i<rates_total;i++)
    {
    v2=1.96*MathSqrt(v1*fc.VarCoefficient(j));  // Prediction intervals
    FORE[i]=fc.Fcast(j++);                    // Forecasting
    PINT1[i]=FORE[i]+v2;
    PINT2[i]=FORE[i]-v2;
    }
  
  return(rates_total);
  }
//-----------------------------------------------------------------------------------

インジケーターの呼び出しや、繰り返しの初期化は、指数平滑化初期値を設定します。

このインジケーターにおいて周期的インデックスの初期設定はなく、初期値は、常に０に等しいです。そのような初期化後において、予測結果への周期性の影響は徐々に０からある安定した値に、新しい値の導入とともに増加します。

安定した処理状態に達するための周期数は、周期的インデックスにおける平滑化係数値に依存しています。その値が小さければ、より長い時間を要します。

初期設定でのAdditiveES_Test.mq5インジケーターの処理結果は、図５に示されています。

図５

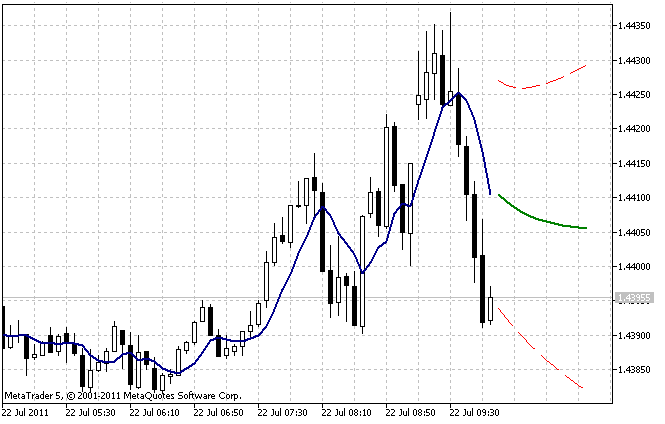
図5. AdditiveES_Test.mq5インジケーター

予測とは別に、そのインジケーターは、シーケンスの過去の値におけるワンステップ先予測に一致する追加の線と、95%の予測信頼区間の制限を表示します。

信頼区間は、ステイされたワンステップ先のエラーの誤差に基づきます。選択した初期値の間違いの効果を減らすために、推定された誤差は、nHistの全ての長さにて計算されるのではなく、入力パラメーターnTestにて数が明記される最後のバーに関するのみになります。

この記事の最後のFiles.zipアーカイブは、AdditiveES.mqhとAdditiveES_Test.mq5ファイルを含みます。そのインジケーターをコンパイルするために、AdditiveES.mqhファイルがAdditiveES_Test.mq5と同じディレクトリに位置している必要があります。

初期値の選択の問題は、ある程度AdditiveES_Test.mq5インジケーター作成時に解決されましたが、平滑化パラメーターの最適な値の選択の問題はまだ解決されていません。


8. 最適なパラメーターの値の選択

シンプルな指数平滑モデルは、シングル平滑化パラメーターを持ち、その最適な値は、列挙型メソッドを用いて見つけられます。予測エラー値を全てのシーケンスを通して計算した後、そのパラメーターの値は、小さい増加にて変更され、全ての計算が再度行われます。この手順は、全ての可能なパラメーターの値が列挙さえるまで繰り返されます。現在は、最小のエラー値になるパラメーターの値を選択しさえすれば良いです。

0.05の増加における0.1から0.9の範囲での平滑係数の最適な値を見つけるためには、予測エラー値の計算が数回行われる必要があります。ご覧の通り、計算に必要な数はそこまで大きくありません。しかし、ダンピングの線形成長モデルは、３つの平滑化パラメーターの最適化を要し、この場合、4913回の計算を、全ての組み合わせを指定の範囲内で行うためにする必要があります。

全ての可能なパラメーター値の列挙のための実行回数は、急速にパラメーター数の上昇に伴い増加し、列挙範囲の拡大により減少します。平滑化パラメーターに加えて、モデルの初期値の最適化を行う必要があれば、シンプルな列挙型メソッドを用いて行うには難しいです。

いくつかの変数を持つ関数の最小値を発見することに関連する問題は、よく研究されており、この種類のアルゴリズムが数多くあります。関数の最小値を発見するための様々なメソッドの詳細や比較は、文献[7]にて見ることができます。これら全てのメソッドは、主に客観的な関数の呼び出し数の削減を意図されています。つまり、最小値を発見するプロセスにおける計算幾科学的な努力の削減です。

異なるソースは、いわゆるquasi-Newton最適化メソッドを参照しています。これは、大抵高い効率性に関連していますが、よりシンプルなメソッドの実装は予測の最適化におけるアプローチを示す上で重要なはずです。Powellのメソッドを選択してみましょう。Powellのメソッドは、目的関数の派生物の計算を必要とせず、検索メソッドに属します。

このメソッドは、その他のメソッドと同じく、様々な方法でプログラムにより実装されます。その検索は、ある目的関数の値や引数の値が取得された際に完成します。加えて、認可可能な関数パラメーターの変化の範囲における制限を与える可能性をある実装が含んでいます。

今回は、Powellのメソッドを用いて最小値を発見するアルゴリズムがPowellsMethod.classにて実装されています。そのアルゴリズムは、目的関数の値の正確さが得られれば、このメソッドの実装において、文献[8]にて見つけられるアルゴリズムがプロトタイプとして使用されました。

以下がPowellsMethodクラスのソースコードです。

//-----------------------------------------------------------------------------------
//                                                                  PowellsMethod.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>

#define GOLD   1.618034
#define CGOLD  0.3819660
#define GLIMIT 100.0
#define SHFT(a,b,c,d) (a)=(b);(b)=(c);(c)=(d);
#define SIGN(a,b) ((b) >= 0.0 ? fabs(a) : -fabs(a))
#define FMAX(a,b) (a>b?a:b)
//-----------------------------------------------------------------------------------
// Minimization of Functions.
// Unconstrained Powell’s Method.
// References:
// 1. Numerical Recipes in C. The Art of Scientific Computing.
//-----------------------------------------------------------------------------------
class PowellsMethod:public CObject
  {
protected:
  double P[],Xi[];
  double Pcom[],Xicom[],Xt[];
  double Pt[],Ptt[],Xit[];
  int    N;
  double Fret;
  int    Iter;
  int    ItMaxPowell;
  double FtolPowell;
  int    ItMaxBrent;
  double FtolBrent;
  int    MaxIterFlag;
public:
  void   PowellsMethod(void);
  void   SetItMaxPowell(int n)           { ItMaxPowell=n; }
  void   SetFtolPowell(double er)        { FtolPowell=er; }
  void   SetItMaxBrent(int n)            { ItMaxBrent=n;  }
  void   SetFtolBrent(double er)         { FtolBrent=er;  }
  int    Optimize(double &p[],int n=0);
  double GetFret(void)                   { return(Fret);  }
  int    GetIter(void)                   { return(Iter);  }
private:
  void   powell(void);
  void   linmin(void);
  void   mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc);
  double brent(double ax,double bx,double cx,double &xmin);
  double f1dim(double x);
  virtual double func(const double &p[]) { return(0); }
  };
//-----------------------------------------------------------------------------------
// Constructor
//-----------------------------------------------------------------------------------
void PowellsMethod::PowellsMethod(void)
  {
  ItMaxPowell= 200;
  FtolPowell = 1e-6;
  ItMaxBrent = 200;
  FtolBrent  = 1e-4;
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::powell(void)
  {
  int i,j,m,n,ibig;
  double del,fp,fptt,t;
  
  n=N; Fret=func(P);
  for(j=0;j<n;j++)Pt[j]=P[j];
  for(Iter=1;;Iter++)
    {
    fp=Fret; ibig=0; del=0.0;
    for(i=0;i<n;i++)
      {
      for(j=0;j<n;j++)Xit[j]=Xi[j+n*i];
      fptt=Fret;
      linmin();
      if(fabs(fptt-Fret)>del){del=fabs(fptt-Fret); ibig=i;}
      }
    if(2.0*fabs(fp-Fret)<=FtolPowell*(fabs(fp)+fabs(Fret)+1e-25))return;
    if(Iter>=ItMaxPowell)
      {
      Print("powell exceeding maximum iterations!");
      MaxIterFlag=1; return;
      }
    for(j=0;j<n;j++){Ptt[j]=2.0*P[j]-Pt[j]; Xit[j]=P[j]-Pt[j]; Pt[j]=P[j];}
    fptt=func(Ptt);
    if(fptt<fp)
      {
      t=2.0*(fp-2.0*(Fret)+fptt)*(fp-Fret-del)*(fp-Fret-del)-del*(fp-fptt)*(fp-fptt);
      if(t<0.0)
        {
        linmin();
        for(j=0;j<n;j++){m=j+n*(n-1); Xi[j+n*ibig]=Xi[m]; Xi[m]=Xit[j];}
        }
      }
    }
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::linmin(void)
  {
  int j,n;
  double xx,xmin,fx,fb,fa,bx,ax;

  n=N;
  for(j=0;j<n;j++){Pcom[j]=P[j]; Xicom[j]=Xit[j];}
  ax=0.0; xx=1.0;
  mnbrak(ax,xx,bx,fa,fx,fb);
  Fret=brent(ax,xx,bx,xmin);
  for(j=0;j<n;j++){Xit[j]*=xmin; P[j]+=Xit[j];}
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::mnbrak(double &ax,double &bx,double &cx,
                                 double &fa,double &fb,double &fc)
  {
  double ulim,u,r,q,fu,dum;

  fa=f1dim(ax); fb=f1dim(bx);
  if(fb>fa)
    {
    SHFT(dum,ax,bx,dum)
    SHFT(dum,fb,fa,dum)
    }
  cx=bx+GOLD*(bx-ax); fc=f1dim(cx);
  while(fb>fc)
    {
    r=(bx-ax)*(fb-fc); q=(bx-cx)*(fb-fa);
    u=bx-((bx-cx)*q-(bx-ax)*r)/(2.0*SIGN(FMAX(fabs(q-r),1e-20),q-r));
    ulim=bx+GLIMIT*(cx-bx);
    if((bx-u)*(u-cx)>0.0)
      {
      fu=f1dim(u);
      if(fu<fc){ax=bx; bx=u; fa=fb; fb=fu; return;}
      else if(fu>fb){cx=u; fc=fu; return;}
      u=cx+GOLD*(cx-bx); fu=f1dim(u);
      }
    else if((cx-u)*(u-ulim)>0.0)
      {
      fu=f1dim(u);
      if(fu<fc)
        {
        SHFT(bx,cx,u,cx+GOLD*(cx-bx))
        SHFT(fb,fc,fu,f1dim(u))
        }
      }
    else if((u-ulim)*(ulim-cx)>=0.0){u=ulim; fu=f1dim(u);}
      else {u=cx+GOLD*(cx-bx); fu=f1dim(u);}
    SHFT(ax,bx,cx,u)
    SHFT(fa,fb,fc,fu)
    }
  }
//-----------------------------------------------------------------------------------
double PowellsMethod::brent(double ax,double bx,double cx,double &xmin)
  {
  int    iter;
  double a,b,d,e,etemp,fu,fv,fw,fx,p,q,r,tol1,tol2,u,v,w,x,xm;

  a=(ax<cx?ax:cx); b=(ax>cx?ax:cx);
  d=0.0; e=0.0; x=w=v=bx; fw=fv=fx=f1dim(x);
  for(iter=1;iter<=ItMaxBrent;iter++)
    {
    xm=0.5*(a+b); tol2=2.0*(tol1=FtolBrent*fabs(x)+2e-19);
    if(fabs(x-xm)<=(tol2-0.5*(b-a))){xmin=x; return(fx);}
    if(fabs(e)>tol1)
      {
      r=(x-w)*(fx-fv); q=(x-v)*(fx-fw);
      p=(x-v)*q-(x-w)*r; q=2.0*(q-r);
      if(q>0.0)p=-p; q=fabs(q);
      etemp=e; e=d;
      if(fabs(p)>=fabs(0.5*q*etemp)||p<=q*(a-x)||p>=q*(b-x))
        d=CGOLD*(e=(x>=xm?a-x:b-x));
      else {d=p/q; u=x+d; if(u-a<tol2||b-u<tol2)d=SIGN(tol1,xm-x);}
      }
    else d=CGOLD*(e=(x>=xm?a-x:b-x));
    u=(fabs(d)>=tol1?x+d:x+SIGN(tol1,d));
    fu=f1dim(u);
    if(fu<=fx)
      {
      if(u>=x)a=x; else b=x;
      SHFT(v,w,x,u)
      SHFT(fv,fw,fx,fu)
      }
    else
      {
      if(u<x)a=u; else b=u;
      if(fu<=fw||w==x){v=w; w=u; fv=fw; fw=fu;}
      else if(fu<=fv||v==x||v==w){v=u; fv=fu;}
      }
    }
  Print("Too many iterations in brent");
  MaxIterFlag=1; xmin=x;
  return(fx);
  }
//-----------------------------------------------------------------------------------
double PowellsMethod::f1dim(double x)
  {
  int j;
  double f;
  
  for(j=0;j<N;j++) Xt[j]=Pcom[j]+x*Xicom[j];
  f=func(Xt);
  return(f);
  }
//-----------------------------------------------------------------------------------
int PowellsMethod::Optimize(double &p[],int n=0)
  {
  int i,j,k,ret;
  
  k=ArraySize(p);
  if(n==0)N=k;
  else N=n;
  if(N<1||N>k)return(0);
  ArrayResize(P,N); ArrayResize(Xi,N*N);
  ArrayResize(Pcom,N); ArrayResize(Xicom,N);
  ArrayResize(Xt,N); ArrayResize(Pt,N);
  ArrayResize(Ptt,N); ArrayResize(Xit,N);
  for(i=0;i<N;i++)for(j=0;j<N;j++)Xi[i+N*j]=(i==j?1.0:0.0);
  for(i=0;i<N;i++)P[i]=p[i];
  MaxIterFlag=0;
  powell();
  for(i=0;i<N;i++)p[i]=P[i];
  if(MaxIterFlag==1)ret=-1;
  else ret=Iter;
  return(ret);
  }
//-----------------------------------------------------------------------------------

Optimizeメソッドは、そのクラスの主要なメソッドです。

Optimizeメソッド

入力パラメーター:

  • double &p[] - パラメーターの初期値を含んでいる配列であり、これらのパラメーターの取得された最適な値は配列のアウトプットにあります。
  • int n=0 - p[]配列における引数の数Where n=0, パラメーター数は、配列p[]に等しいと考えられています。

戻り値:

  • もし最大の数に達した場合、そのアルゴリズムの処理に必要な反復回数、もしくはその−１が返されます。

最適なパラメーターの値を検索している際、目的関数の最小値への近似が発生します。Optimizeメソッドは、その関数の最小値に達する上で必要な反復回数を返します。その目的関数は、全ての繰り返しにおいて数回呼び出されます。つまり、目的関数の呼び出し回数がOpimizeメソッドによって返される反復数よりもかなり大きいです。


そのクラスの他のメソッド：

SetItMaxPowellメソッド

入力パラメーター：

  • Int n - Powellのメソッドにおいての最大の反復数です。そのデフォルトの値は200です。

戻り値:

  • None.

最大の反復回数を設定します；この数に達すると、その検索は目的関数の最小値が見つかったか否かに関係なく、その検索は終了されます。そして、関連するメッセージがログに追加されます。

SetFtolPowellメソッド

入力パラメーター：

  • double er - 正確性目的関数の最小値からのこの逸脱値が達成されると、Powellのメソッドは検索を終了します。デフォルトの値は1e-6です。

戻り値:

  • None.

SetItMaxBrentメソッド

入力パラメーター：

  • Int n - 補助のBrentメソッドにおける最大の反復回数そのデフォルトの値は200です。

戻り値:

  • None.

最大の反復回数を設定します。もしそれが達成されると、補助のBrentメソッドは、検索を終了し、ログにメッセージを投げます。

SetFtolBrentメソッド

入力パラメーター：

  • double er – 正確性この値は、補助のBrentメソッドにおける最小値の検索の正確性を定義します。デフォルトの値は1e-4.

戻り値:

  • None.

GetFret メソッド

入力パラメーター：

  • None.

戻り値:

  • 取得された目的関数の最小値を返します。

GetIterメソッド

入力パラメーター：

  • None.

戻り値:

  • そのアルゴリズムの実行において必要な反復数を返します。

仮想関数 func(const double &p[])

入力パラメーター：

  • const double &p[] – 最適化されたパラメーターの配列のアドレスその配列のサイズは、関数パラメーターの数に一致します。

戻り値:

  • それに渡されたパラメーターに一致する関数の値を返します。

仮想関数 func()は、あらゆる場合において、PowellsMethodクラスから派生したクラスにて再定義されます。func()関数は、目的関数であり、その引数は、その関数によって返された最小の値と一致し、その検索アルゴリズムを適用時に見つけられます。

このPowellのメソッドの実装は、Brentの放物線補間これらのメソッドの反復の正確な最大の回数は、SetItMaxPowell、SetFtolPowell、SetItMaxBrent、SetFtolBrentを呼ぶことで、設定されます。

そのアルゴリズムのデフォルトの特性は、この方法にて変化できます。これは、ある目的関数に設定されたデフォルトの正確性が高すぎる際に役に立ちます。また、そのアルゴリズムはその検索プロセスにおいて多すぎるほどの反復を要します。必要な正確性の値における変化は、目的関数の異なるカテゴリーに関してその検索を最適化することができます。

Powellメソッドを使用するそのアルゴリズムの複雑さにもかかわらず、使用するのはかなり簡単です。

例を見てみましょう。ある関数があると想定してください。

パラメーターの値を見つける必要があり、また その関数が最小の値をどの地点で取得するのかについて発見する必要があります。

この問題への解決策を示すスクリプトを記述しましょう。

//-----------------------------------------------------------------------------------
//                                                                        PM_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
class PM_Test:public PowellsMethod
  {
public:
  void   PM_Test(void) {}
private:
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
double PM_Test::func(const double &p[])
  {
  double f,r1,r2;
  
  r1=p[0]-0.5;
  r2=p[1]-6.0;
  f=r1*r1*4.0+r2*r2;
  return(f);
  }
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  int it;
  double p[2];

  p[0]=8; p[1]=9;                                 // Initial point
  PM_Test *pm = new PM_Test;
  it=pm.Optimize(p);
  Print("Iter= ",it,"        Fret= ",pm.GetFret());
  Print("p[0]= ",p[0],"    p[1]= ",p[1]);
  delete pm;
  }
//-----------------------------------------------------------------------------------

このスクリプトを記述する際、まず、func()関数をPM_TESTクラスのメンバーとして作成します。このクラスは、p[0]とp[1]のパラメーターの値を使用し、テストの関数の値を計算します。OnStart()関数内に、初期値が必要なパラメーターに割り当てられます。その検索は、これらの値から始まります。

さらに、PM_TESTクラスのコピーが作成され、そのp[0]、p[1]の必要な値の検索は、Optimizeメソッドを呼び出し開始されます；親クラスPowellsMethodクラスのメソッドが再定義されたfunc関数を呼び出します。その検索が終了すれば、反復の数、最小地点の関数の値や取得されたパラメーターの値p[0]=0.5とp[1]=6がログに追加されます。

PowellsMethod.mqhとテストのPM_Test.mq5は、記事の最後にあるFiles.zipアーカイブに保存されています。PM_Test.mq5をコンパイルするために、PowellsMethod.mqhと同じディレクトリに保存されている必要があります。


9. モデルパラメーター値の最適化

この記事の以前の章が、関数の最小値を検索するためのメソッドの実装について扱っており、使用方法について簡単な例を紹介しています。それでは、指数平滑モデルの最適化に関連する問題に進みます。

まず初めに、冒頭で紹介したAdditiveESクラス周期的なコンポーネントに関連する要素を全て除去し、単純化します。というのも、周期性を考慮するそのモデルは、この記事においてはもう考察されないためです。これにより、そのクラスのソースコードは、理解しやすくなり、計算の数を削減することができます。さらに、予測や、予測信頼区間の計算を、線形成長モデルのパラメーターの最適化へのアプローチの簡単な紹介のために全て除去します。

//-----------------------------------------------------------------------------------
//                                                                     OptimizeES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
// Class OptimizeES
//-----------------------------------------------------------------------------------
class OptimizeES:public PowellsMethod
  {
protected:
  double Dat[];            // Input data
  int    Dlen;             // Data lenght
  double Par[5];           // Parameters
  int    NCalc;            // Number of last elements for calculation
public:
  void   OptimizeES(void) {}
  int    Calc(string fname);
private:
  int    readCSV(string fnam,double &dat[]);
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
// Calc
//-----------------------------------------------------------------------------------
int OptimizeES::Calc(string fname)
  {
  int i,it;
  double relmae,naiv,s,t,alp,gam,phi,e,ae,pt;
  
  if(readCSV(fname,Dat)<0){Print("Error."); return(-1);}
  Dlen=ArraySize(Dat);
  NCalc=200;                               // number of last elements for calculation
  if(NCalc<0||NCalc>Dlen-1){Print("Error."); return(-1);}
  Par[0]=Dat[Dlen-NCalc];                  // initial S
  Par[1]=0;                                // initial T
  Par[2]=0.5;                              // initial Alpha
  Par[3]=0.5;                              // initial Gamma
  Par[4]=0.5;                              // initial Phi
  it=Optimize(Par);                        // Powell's optimization
  s=Par[0]; t=Par[1]; alp=Par[2]; gam=Par[3]; phi=Par[4];
  relmae=0; naiv=0;
  for(i=Dlen-NCalc;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t);
    relmae+=MathAbs(e); naiv+=MathAbs(Dat[i]-Dat[i-1]);
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  relmae/=naiv;
  PrintFormat("%s:    N=%i,  RelMAE=%.3f",fname,NCalc,relmae);
  PrintFormat("Iter= %i,  Fmin= %e",it,GetFret());
  PrintFormat("p[0]= %.5f,  p[1]= %.5f,  p[2]= %.2f,  p[3]= %.2f,  p[4]= %.2f",
                                             Par[0],Par[1],Par[2],Par[3],Par[4]);
  return(0);
  }
//-----------------------------------------------------------------------------------
// readCSV
//-----------------------------------------------------------------------------------
int OptimizeES::readCSV(string fnam,double &dat[])
  {
  int n,asize,fhand;
    
  fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
  if(fhand==INVALID_HANDLE)
    {
    Print("FileOpen Error!");
    return(-1);
    }
  asize=512;
  ArrayResize(dat,asize);
  n=0;
  while(FileIsEnding(fhand)!=true)
    {
    dat[n++]=FileReadNumber(fhand);
    if(n+128>asize)
      {
      asize+=128;
      ArrayResize(dat,asize);
      }
    }
  FileClose(fhand);
  ArrayResize(dat,n-1);
  return(0);

  }
//------------------------------------------------------------------------------------
// func
//------------------------------------------------------------------------------------
double OptimizeES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}                 // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}                 // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}                 // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}                 // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }                 // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}                 // Phi     < 0.05
  sse=0; 
  for(i=Dlen-NCalc;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(NCalc*MathLog(k1*k2*k3*sse));
  }
//------------------------------------------------------------------------------------

OptimizeESクラスは、PowellsMethodクラスから派生し、仮想関数func()の再定義を含んでいます。以前述べた通り、最適化の中で最小化される計算された値を持つパラメーターがこの関数の入力に渡されます。

そのメソッドに応じて、func()関数は、ワンステップ先の予測エラーの二乗の合計における対数を計算します。そのシーケンスのNCalcの値に関したループにてそのエラー値が計算されます。
そのモデルの安定性を保持するために、パラメーターの変化の範囲に制限を設ける必要があります。AlphaやGammaパラメーターにおける範囲は、0.05から0.95までになり、Phiパラメーターは0.05から1.0の範囲になります。しかし、今回は最適化のために、目的関数の引数において制限の使用を意味しない、制限されない最小値を発見するメソッドを使用します。

制限付きのマルチ変数の関数の最小値の発見における問題を制限のない最小値の発見の問題に変換し、検索アルゴリズムを変更せず、パラメーターに課された制限を考察できるようにします。この目的のために、いわゆるペナルティ関数が使用されます。このメソッドは一次元の場合において紹介することができます。

一つの引数を持ち、（領域は2.0から3.0）検索プロセスにて、いかなる値を関数のパラメーターに割り当てるアルゴリズムを持つ関数があると想定してください。この場合、以下のように行います：もし検索アルゴリズムは、最大値、3.5を超える引数を渡された場合、その関数は、3.0に等しい引数において計算され、 取得される結果は、例えば、k=1+(3.5-3)*200などの最大値を超えるものに比例する係数によって掛けられます。

もし以下の最小の値になる引数に関する処理を実行する場合、その目的関数は、引数の変化の範囲外で上昇することが保証されています。目的関数の結果の値でのそのような上昇は検索アルゴリズムの検索が、その関数に渡された引数は制限されていることを認識させないようにし、その関数の最小値は、引数の設定された制限内になります。そのようなアプローチは、いくつかの変数の関数に適用されています。

OptimizeESクラスの主なメソッドは、Calcメソッドです。このメソッドを呼び出すと、ファイルからのデータの読み込みや、モデルの最適なパラメータ値の検索、取得されたパラメーター値においてReIMAEを使用し、予測正確性の推定を行います。ファイルから読み込まれるシーケンスの処理済みの値の数は、この場合、NCalcに設定されます。

OptimizeESクラスを使用するOptimization_Test.mq5スクリプトの例は以下になります。

//-----------------------------------------------------------------------------------
//                                                              Optimization_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "OptimizeES.mqh"

OptimizeES es;
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  es.Calc("Dataset\\USDJPY_M1_1100.TXT");
  }
//-----------------------------------------------------------------------------------

このスクリプトの実行に沿うと、以下のような結果を取得できます。

図6. Optimization_Test.mq5スクリプト実行結果 

図6. Optimization_Test.mq5スクリプト実行結果

最適なパラメーターの値や、モデルの初期値を見つけることができますが、シンプルなツールを使用し、最適化できないパラメーターがまだあります。それは、最適化にて使用されるシーケンスの値数です。大きいシーケンスの最適化において、平均して、シーケンスよりも大きい最小のエラーを保証するパラメーター値を取得します。

しかし、シーケンスの性質は、このインターバル内にて変化すれば、取得された値は、これ以上は最適ではないです。一方、シーケンスが、劇的に縮小すれば、そのような短期間で得られた最適なパラメーターは、長い期間においては最適ではないかもしれません。

OptimizeES.mqhとOptimization_Test.mq5はこの記事の最後のFiles.zipアーカイブにあります。コンパイル時に、 OptimizeES.mqhとPowellsMethod.mqhがコンパイル済みのOptimization_Test.mq5と同じディレクトリに格納されます。その例の中では、USDJPY_M1_110.TXTファイルは、テストシーケンスを含んでおり、\MQL5\Files\Dataset\のディレクトリに保存されています。

図２は、ReIMAEを使用し取得された予測正確性の推定を示しています。この記事の冒頭にて紹介された、これらのシーケンスの値、100、200、400の値を使用し、８つのテストシーケンについて予測が行われます。


 N=100
 N=200
 N=400
EURRUR M1
0.980
 1.000
 0.968
EURRUR M30
0.959
 0.992
 0.981
EURUSD M1
0.995
 0.981
 0.981
EURUSD M30
1.023
 0.985
 0.999
USDJPY M1
1.004
 0.976
 0.989
USDJPY M30
0.993
 0.987
 0.988
XAUUSD M1
0.976
 0.993
 0.970
XAUUSD M30
0.973
 0.985
 0.999


Table 2. ReIMAEを使用して推定される予測エラー

ご覧の通り、予測エラーの推定は、ほぼ単一ですが、多くの場合、特定のシーケンスに関する予測は、ネィティブメソッドよりも正確です。


10. IndicatorES.mq5インジケーター

AdditiveES.mqhに基づくAdditiveES_Test.mq5インジケータークラスは、以前述べられています。このインジケーター全ての平滑化パラメーターは手動で設定されます。

そのモデルのパラメーターを最適化するメソッドについて考察したのち、最適なパラメーター値や初期値が自動で決定されるような類似するインジケーターを作成でき、処理されたサンプルの期間が手動でセットされます。周期性に関連する全ての計算を除去します。

インジケーターを作成するために使用されるCIndiсatorESクラスのソースコードは以下のように設定されます。

//-----------------------------------------------------------------------------------
//                                                                   CIndicatorES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
// Class CIndicatorES
//-----------------------------------------------------------------------------------
class CIndicatorES:public PowellsMethod
  {
protected:
  double Dat[];                                              // Input data
  int    Dlen;                                               // Data lenght
  double Par[5];                                             // Parameters
public:
  void   CIndicatorES(void)       { }
  void   CalcPar(double &dat[]);
  double GetPar(int n)            { if(n>=0||n<5)return(Par[n]); else return(0); }
private:
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
// CalcPar
//-----------------------------------------------------------------------------------
void CIndicatorES::CalcPar(double &dat[])
  {

  Dlen=ArraySize(dat);
  ArrayResize(Dat,Dlen);
  ArrayCopy(Dat,dat);
 
  Par[0]=Dat[0];                                             // initial S
  Par[1]=0;                                                  // initial T
  Par[2]=0.5;                                                // initial Alpha
  Par[3]=0.5;                                                // initial Gamma
  Par[4]=0.5;                                                // initial Phi
  Optimize(Par);                                             // Powell's optimization
  }
//------------------------------------------------------------------------------------
// func
//------------------------------------------------------------------------------------
double CIndicatorES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}           // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}           // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}           // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}           // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }           // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}           // Phi     < 0.05
  sse=0; 
  for(i=0;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(Dlen*MathLog(k1*k2*k3*sse));
  }
//------------------------------------------------------------------------------------

このクラスはCalcPar、GetParメソッドを持っています；CalcParは、そのモデルの最適なパラメーター値の計算のために設計され、GetPerは、それらの値を取得するためのものです。さらに、CIndicatorESクラスは、仮想メソッドfunc()の再定義から構成されています。

IndicatorES.mq5インジケーターのソースコード：

//-----------------------------------------------------------------------------------
//                                                                    IndicatorES.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"                 // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "ConfUp"                   // Confidence interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCrimson
#property indicator_style3  STYLE_DOT
#property indicator_width3  1
#property indicator_label4  "ConfDn"                   // Confidence interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCrimson
#property indicator_style4  STYLE_DOT
#property indicator_width4  1

input int nHist=80; // History bars, nHist>=24

#include  "CIndicatorES.mqh"
#define   NFORE 12

double    Hist[],Fore[],Conf1[],Conf2[];
double    Data[];
int       NDat;

CIndicatorES   Es;
//-----------------------------------------------------------------------------------
// Custom indicator initialization function
//-----------------------------------------------------------------------------------
int OnInit()
  {
  NDat=nHist; if(NDat<24)NDat=24;
  MqlRates rates[];
  CopyRates(NULL,0,0,NDat,rates);                   // Load missing data
  ArrayResize(Data,NDat);
    
  SetIndexBuffer(0,Hist,INDICATOR_DATA);
  PlotIndexSetString(0,PLOT_LABEL,"History");
  SetIndexBuffer(1,Fore,INDICATOR_DATA);
  PlotIndexSetString(1,PLOT_LABEL,"Forecast");
  PlotIndexSetInteger(1,PLOT_SHIFT,NFORE);
  SetIndexBuffer(2,Conf1,INDICATOR_DATA);            // Confidence interval
  PlotIndexSetString(2,PLOT_LABEL,"ConfUp");
  PlotIndexSetInteger(2,PLOT_SHIFT,NFORE);
  SetIndexBuffer(3,Conf2,INDICATOR_DATA);            // Confidence interval
  PlotIndexSetString(3,PLOT_LABEL,"ConfDN");
  PlotIndexSetInteger(3,PLOT_SHIFT,NFORE);
  IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
  return(0);
  }
//-----------------------------------------------------------------------------------
// Custom indicator iteration function
//-----------------------------------------------------------------------------------
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int  &spread[])
  {
  int i,start;
  double s,t,alp,gam,phi,e,f,a,a1,a2,a3,var,ci;
  
  if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);}
  if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar
  start=rates_total-NDat;
//-----------------------
  PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat);
  PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE);
  PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE);
  PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE);
  
  for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data
  Es.CalcPar(Data);                                    // Optimization of parameters
  s=Es.GetPar(0); t=Es.GetPar(1); alp=Es.GetPar(2); gam=Es.GetPar(3); phi=Es.GetPar(4);
  f=(s+phi*t); var=0;
  for(i=0;i<NDat;i++)                                // History
    {
    e=Data[i]-f; var+=e*e;
    a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
    f=(s+phi*t); Hist[start+i]=f;
    }
  var/=(NDat-1); a1=1; a2=0; a3=1;
  for(i=rates_total-NFORE;i<rates_total;i++)
    {
    a1=a1*phi; a2+=a1;
    Fore[i]=s+a2*t;                                 // Forecast
    ci=1.96*MathSqrt(var*a3);                        // Confidence intervals
    a=alp*(1+a2*gam); a3+=a*a;
    Conf1[i]=Fore[i]+ci;
    Conf2[i]=Fore[i]-ci;
    }
  return(rates_total);
  }
//-----------------------------------------------------------------------------------

全ての新しいバーにて、そのインジケーターは、そのモデルのパラメーターの最適な値を見つけ、NHistバーの数において計算を行い、予測を立て、予測信頼区間を定義します。

そのインジケーターの唯一のパラメーターは、処理されるシーケンスの長さであり、その最小値は24バーに制限されています。このインジケーターの全ての計算は、open[]の値に基づいて行われます。予測の水平軸は、12バーです。IndicatorES.mq5インジケーターのコードやCIndicatorES.mqhファイルは、この記事の最後のFiles.zipにあります。

 図７IndicatorES.mq5インジケーターの実行結果

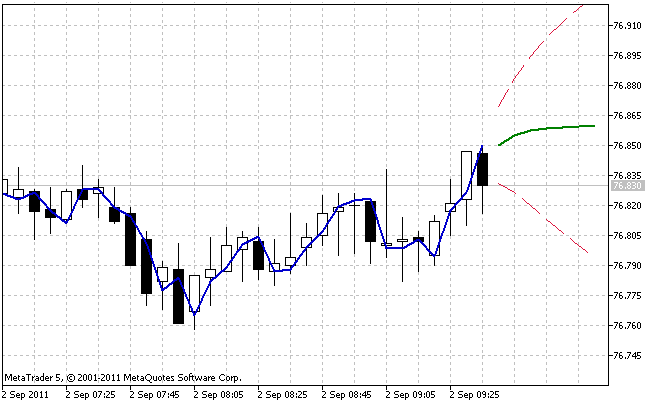
図７IndicatorES.mq5インジケーターの処理結果

IndicatorES.mq5インジケーターの処理結果の例が図７に示されています。. そのインジケーターの処理において、95%の予測信頼区間は、そのモデルの取得された最適なパラメーター値に一致する値を取得します。平滑化パラメーターの値が大きければ、予測水平軸の上昇に伴う信頼区間の拡大が速くなります。

その向上により、IndicatorES.mq5インジケーターは、予測の通貨見積もりのために使用されるだけでなく、様々なインジケーターや処理されたデータの予測値に使用されます。


結論

この記事の主な目的は、読者に予測にて使用される補助的な指数平滑モデルについて親しみを持ってもらうことにありました。その実用的な使用方法を紹介する中で、いくつかの付随する問題がありました。この記事で提供された資料は、予測に関連する問題や、解決法の大きい範囲に対するイントロダクションでしかないと考えられています。

提供されているクラスや関数、スクリプト、インジケーターは、この記事が記述される中で作成され、この記事の資料への例として主に作成されたという事実に注意を払ってもらいたいと思います。したがって、安定性やエラーにおけるテストは実行されていません。さらに、この記事のインジケーターは、そのメソッドの実装の紹介でしかありません。

この記事にて紹介されたIndicatorES.mq5インジケーターの予測正確性は、検討中の見積もりの特性において十分であるモデルの修正を使用することで向上されます。そのインジケーターは、その他のモデルにより増大されます。しかし、これらの問題は、この記事の範囲外にあたります。

結論として、指数平滑モデルはより複雑なモデルを適用して得られる予測と同じ正確性を保つ予測を行います。また、最も複雑なモデルが必ずしもベストではないということを証明します。


リファレンス

  1. Everette S. Gardner Jr. 指数平滑方：最先端技術 パートⅡ. 2005年6月3日
  2. Rob J Hyndman. 指数平滑法における状態スペースモデルに基づく予測2002年8月29日
  3. Rob J Hyndman et al. 状態スペースモデルの二つの新規クラスを使用した指数平滑方における予測区間2003年1月30日
  4. Rob J Hyndman、Muhammad Akram. 非線形指数平滑モデルは不安定である2006年1月17日
  5. Rob J Hyndman、Anne B Koehler. 予測正確性の基準への探求2005年11月2日
  6. Yu. P. Lukashin. 短期間の時系列予測におけるメソッド；教科書- М.: Finansy i Statistika, 2003.-416 pp.
  7. D. Himmelblau. 非線形プログラミングの適用М.: Mir, 1975.
  8. C. The Art of Scientific Computingにおける数値的レシピ第２版Cambridge University Press.

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/318

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
高度適応インディケータ理論および MQL5への実装 高度適応インディケータ理論および MQL5への実装
本稿は高度適応インディケータとその MQL5への実装について述べます。適応型サイバーサイクル、適応型重心、適応型RVIです。すべてのインディケータはJohn F. Ehlersの原著 "Cybernetic Analysis for Stocks and Futures" で紹介されていました。
インディケータの統計パラメータ分析 インディケータの統計パラメータ分析
テクニカル分析は基本クオートを「より明確に」示し、トレーダーがマーケット価格動向を分析し推定することのできるインディケータを幅広く採り入れます。インディケータを使用することに意味はなく、言うまでもなく最初のクオート変換と取得した結果の信頼性に関する問題を解決できないかぎり、インディケータを特定のトレーディングシステムに適用することにも意味がありません。本稿ではそのような結論について確たる理由があることを示していきます。
サルでも解るMQL5 ウィザード サルでも解るMQL5 ウィザード
2011年初頭、 MQL5 ウィザードの第一版を発売しました。この新しいアプリケーションはトレーディングロボットを自動で作成する便利なツールを提供します。MetaTrader 5 ユーザーはだれでも、MQL5でプログラミングする方法を知らなくても独自のExpert Advisor を作成することができるのです。
トレーディングシステム作成のための判別分析の利用 トレーディングシステム作成のための判別分析の利用
トレーディングシステムを開発するとき、たいていインディケータとそのシグナルの最良の組合せを選ぶのに問題が起こります。判別分析はそのような組合せを見つける方法の一つです。本稿では、マーケットデータ収集のための EA 開発例を提供し、f Statistica ソフトウェアにおいてFOREXマーケットに対する予測モデル構築のための判別分析の使用を解説します。