Previsione di serie temporali mediante livellamento esponenziale

Introduzione

Attualmente esiste un gran numero di diversi metodi di previsione ben noti che si basano solo sull'analisi dei valori passati di una sequenza temporale, ovvero metodi che utilizzano principi normalmente utilizzati nell'analisi tecnica. Lo strumento principale di questi metodi è lo schema di estrapolazione in cui le proprietà di sequenza identificate ad un certo intervallo di tempo vanno oltre i suoi limiti.

Allo stesso tempo, si presume che le proprietà della sequenza in futuro saranno le stesse del passato e del presente. Uno schema di estrapolazione più complesso, che implica uno studio della dinamica dei cambiamenti nelle caratteristiche della sequenza tenendo conto di tale dinamica all'interno dell'intervallo di previsione, è utilizzato meno frequentemente nella previsione.

I metodi di previsione più noti basati sull'estrapolazione sono forse quelli che utilizzano il modello di media mobile integrato autoregressivo (ARIMA). La popolarità di questi metodi è dovuta principalmente ai lavori di Box e Jenkins, i quali hanno proposto e sviluppato un modello ARIMA integrato. Esistono ovviamente altri modelli e metodi di previsione oltre ai modelli introdotti da Box e Jenkins.

Questo articolo tratterà brevemente i modelli più semplici, ovvero i modelli di livellamento esponenziale proposti da Holt e Brown ben prima della comparsa dei lavori di Box e Jenkins.

Nonostante gli strumenti matematici più semplici e chiari, la previsione che utilizza modelli di livellamento esponenziale porta spesso a risultati confrontabili con i risultati ottenuti utilizzando il modello ARIMA. Ciò non sorprende poiché i modelli di livellamento esponenziale sono un caso speciale del modello ARIMA. In altre parole, ogni modello di livellamento esponenziale studiato in questo articolo ha un corrispondente modello ARIMA equivalente. Questi modelli equivalenti non saranno considerati nell'articolo e sono menzionati solo a scopo informativo.

È noto che la previsione, in ogni caso particolare, richiede un approccio individuale e che, normalmente, comporta una serie di procedure.

Per esempio:

1. Analisi della sequenza temporale per valori mancanti e valori anomali. Adeguamento di questi valori.
2. Identificazione del trend e della sua tipologia. Determinazione della periodicità della sequenza.
3. Verifica della stazionarietà della sequenza.
4. Analisi di pre-elaborazione della sequenza (prendendo i logaritmi, differenziando, ecc.).
5. Selezione del modello.
6. Determinazione dei parametri del modello. Previsioni basate sul modello selezionato.
7. Valutazione dell'accuratezza della previsione del modello.
8. Analisi degli errori del modello selezionato.
9. Determinazione dell'adeguatezza del modello prescelto e, se necessario, sostituzione del modello e ritorno alle voci precedenti.

Questo non è certamente l'elenco completo delle azioni necessarie per una previsione efficace.

Va sottolineato che la determinazione dei parametri del modello e l'ottenimento dei risultati di previsione sono solo una piccola parte del processo di previsione generale. Ma sembra impossibile coprire in un modo o nell'altro l'intera gamma di problemi relativi alle previsioni in un articolo.

Questo articolo tratterà quindi solo i modelli di livellamento esponenziale e utilizzerà le quotazioni di valuta non pre-elaborate come sequenze di test. I problemi di accompagnamento non possono certo essere evitati del tutto nell'articolo, ma saranno affrontati solo nella misura in cui sono necessari per la revisione dei modelli.

1. Stazionarietà

La nozione di estrapolazione propriamente detta implica che lo sviluppo futuro del processo in esame sarà lo stesso del passato e del presente. In altre parole, riguarda la stazionarietà del processo. I processi stazionari sono molto attraenti dal punto di vista previsionale, ma purtroppo non esistono in natura in quanto ogni processo reale è soggetto a modifiche nel corso del suo sviluppo.

I processi reali possono avere aspettative, varianze e distribuzione notevolmente diverse nel corso del tempo, ma i processi le cui caratteristiche cambiano molto lentamente possono essere probabilmente attribuiti a processi stazionari. "Molto lentamente" in questo caso significa che i cambiamenti nelle caratteristiche del processo all'interno dell'intervallo di osservazione finito sembrano essere così insignificanti che tali cambiamenti possono essere trascurati.

È chiaro che più breve è l'intervallo di osservazione disponibile (campione corto), maggiore è la probabilità di prendere una decisione sbagliata riguardo alla stazionarietà del processo nel suo insieme. D'altra parte, se siamo più interessati allo stato del processo in un secondo momento, pianificando di fare una previsione a breve termine, la riduzione della dimensione del campione può in alcuni casi portare ad un aumento dell'accuratezza di tale previsione.

Se il processo è soggetto a modifiche, i parametri di sequenza determinati all'interno dell'intervallo di osservazione saranno diversi, al di fuori dei suoi limiti. Pertanto, più lungo è l'intervallo di previsione, più forte è l'effetto della variabilità delle caratteristiche della sequenza sull'errore di previsione. Per questo motivo dobbiamo limitarci ad una previsione a breve termine; una significativa riduzione dell'intervallo di previsione consente di aspettarsi che le caratteristiche della sequenza che cambiano lentamente non si traducano in errori di previsione considerevoli.

Inoltre, la variabilità dei parametri di sequenza porta al fatto che il valore ottenuto durante la stima dall'intervallo di osservazione viene mediato, poiché i parametri non sono rimasti costanti all'interno dell'intervallo. I valori dei parametri ottenuti non saranno quindi relativi all'ultimo istante di tale intervallo, ma ne rifletteranno una certa media. Sfortunatamente, è impossibile eliminare completamente questo spiacevole fenomeno, ma può essere ridotto se la lunghezza dell'intervallo di osservazione coinvolto nella stima dei parametri del modello (intervallo di studio) viene ridotta, per quanto possibile.

Allo stesso tempo, l'intervallo di studio non può essere abbreviato indefinitamente perché, se estremamente ridotto, diminuirà sicuramente l'accuratezza della stima dei parametri di sequenza. Si dovrebbe cercare un compromesso tra l'effetto degli errori associati alla variabilità delle caratteristiche della sequenza e l'aumento degli errori dovuto all'estrema riduzione dell'intervallo di studio.

Quanto detto sopra si applica pienamente alle previsioni che utilizzano modelli di livellamento esponenziale poiché si basano sull'assunzione di stazionarietà dei processi, come i modelli ARIMA. Tuttavia, per semplicità, di seguito assumeremo convenzionalmente che i parametri di tutte le sequenze in esame varino all'interno dell'intervallo di osservazione, ma in modo così lento da poter essere trascurati.

Pertanto, l'articolo affronterà questioni relative alla previsione a breve termine di sequenze con caratteristiche che cambiano lentamente sulla base di modelli di livellamento esponenziale. La "previsione a breve termine" dovrebbe, in questo caso, significare previsione per uno, due o più intervalli di tempo in anticipo, invece di previsione per un periodo inferiore a un anno come è solitamente inteso in economia.

2. Sequenze di prova

Durante la stesura di questo articolo, sono state utilizzate le quotazioni EURRUR, EURUSD, USDJPY e XAUUSD precedentemente salvate per M1, M5, M30 e H1. Ciascuno dei file salvati contiene 1100 valori "aperti". Il valore "più vecchio" si trova all'inizio del file e quello più "recente" alla fine. L'ultimo valore salvato nel file corrisponde all'ora in cui il file è stato creato. I file contenenti sequenze di test sono stati creati utilizzando lo script HistoryToCSV.mq5. I file di dati e lo script con cui sono stati creati si trovano alla fine dell'articolo nell'archivio Files.zip.

Come già accennato, le quotazioni salvate vengono utilizzate in questo articolo senza essere pre-elaborate, nonostante gli ovvi problemi su cui vorrei attirare la tua attenzione. Ad esempio, le quotazioni EURRUR_H1 contengono da 12 a 13 barre durante il giorno, le quotazioni XAUUSD il venerdì contengono una barra in meno rispetto agli altri giorni. Questi esempi dimostrano che le quotazioni sono prodotte con un intervallo di campionamento irregolare; questo è del tutto inaccettabile per algoritmi progettati per lavorare con sequenze temporali corrette e che suggeriscono di avere un intervallo di quantizzazione uniforme.

Anche se i valori delle quotazioni mancanti vengono riprodotti tramite estrapolazione, il problema relativo alla mancanza di quotazioni nei fine settimana rimane aperto. Possiamo supporre che gli eventi che si verificano nel mondo nei fine settimana abbiano lo stesso impatto sull'economia mondiale degli eventi nei giorni feriali. Rivoluzioni, atti di natura, scandali di alto profilo, cambiamenti di governo e altri eventi più o meno grandi di questo tipo possono verificarsi in qualsiasi momento. Se un evento del genere si svolgesse di sabato, difficilmente avrebbe un'influenza minore sui mercati mondiali rispetto a se si verificasse in un giorno feriale.

Sono forse questi eventi che portano a lacune nelle quotazioni osservate così frequentemente alla fine della settimana lavorativa. Apparentemente, il mondo continua ad andare avanti secondo le proprie regole anche quando il FOREX non funziona. Non è ancora chiaro se i valori nelle quotazioni corrispondenti ai fine settimana destinati ad un'analisi tecnica debbano essere riprodotti e quale beneficio potrebbe dare.

Ovviamente, questi problemi esulano dallo scopo di questo articolo, ma, a prima vista, una sequenza senza interruzioni sembra essere più appropriata per l'analisi, almeno in termini di rilevamento di componenti cicliche (stagionali).

L'importanza della preparazione preliminare dei dati per ulteriori analisi difficilmente può essere sopravvalutata; nel nostro caso si tratta di un grosso problema indipendente in quanto le quotazioni, così come appaiono nel Terminale, generalmente non sono molto adatte per un'analisi tecnica. Oltre ai problemi relativi al divario di cui sopra, ci sono molti altri problemi.

Quando si formano le quotazioni, ad esempio, a un punto temporale fisso vengono assegnati valori di "aperto" e "chiuso" che non gli appartengono; questi valori corrispondono al tempo di formazione del tick anziché a un momento fisso di un grafico temporale selezionato, mentre è comunemente noto che i tick sono a volte molto rari.

Un altro esempio può essere dato dal completo disprezzo del teorema di campionamento, poiché nessuno può garantire che la frequenza di campionamento anche all'interno di un intervallo di un minuto soddisfi il teorema di cui sopra (per non parlare di altri intervalli più grandi). Inoltre, va tenuta in conto la presenza di uno spread variabile che in alcuni casi può sovrapporsi ai valori di quotazione.

Lasciamo tuttavia queste questioni fuori dall'ambito di questo articolo e torniamo all'argomento principale.

3. Livellamento esponenziale

Diamo prima un'occhiata al modello più semplice

,

dove:

• X(t) – processo (simulato) in fase di studio,
  
• L(t) – livello di processo variabile,
  
• r(t) – variabile casuale media nulla.

Come si vede, questo modello comprende la somma di due componenti; siamo particolarmente interessati al livello di processo L(t) e cercheremo di individuarlo.

È noto che la media di una sequenza casuale può comportare una diminuzione della varianza, ovvero un intervallo ridotto della sua deviazione dalla media. Possiamo quindi supporre che, se il processo descritto dal nostro semplice modello è esposto alla media (livellamento), potremmo non essere in grado di eliminare completamente una componente casuale r(t) ma possiamo almeno indebolirla considerevolmente individuando così il livello obiettivo L(t).

A tal fine, utilizzeremo un semplice livellamento esponenziale (SES).

In questa ben nota formula, il grado di livellamento è definito dal coefficiente alfa che può essere impostato da 0 a 1. Se alfa è impostato su zero, i nuovi valori in ingresso della sequenza di input X non avranno alcun effetto sul risultato di livellamento. Il risultato di livellamento per qualsiasi punto temporale sarà un valore costante.

Di conseguenza, in casi estremi come questo, la componente casuale fastidiosa verrà completamente soppressa, ma il livello di processo in esame verrà livellato su una linea retta orizzontale. Se il coefficiente alfa è impostato su uno, la sequenza di input non sarà affatto influenzata dal livellamento. Il livello in esame L(t) non sarà in questo caso distorto e nemmeno la componente casuale sarà soppressa.

È intuitivamente chiaro che, quando si seleziona il valore alfa, si devono soddisfare contemporaneamente i requisiti in conflitto. Da un lato, il valore alfa deve essere vicino allo zero per sopprimere efficacemente la componente casuale r(t). Dall'altro, è consigliabile impostare il valore alfa vicino all'unità per non distorcere la componente L(t) che ci interessa tanto. Per ottenere il valore alfa ottimale, occorre individuare un criterio in base al quale tale valore può essere ottimizzato.

Dopo aver determinato tale criterio, si ricordi che questo articolo si occupa di previsione e non solo di livellamento delle sequenze.

In questo caso, per quanto riguarda il modello di livellamento esponenziale semplice è consuetudine considerare il valore ottenuto in un dato momento come una previsione per un numero qualsiasi di passi avanti.

dove è la previsione m-step-ahead al momento t.

Quindi, la previsione del valore della sequenza al momento t sarà una previsione un passo avanti fatta al passo precedente

In questo caso si può utilizzare un errore di previsione di un passo avanti come criterio per l'ottimizzazione del valore del coefficiente alfa

Quindi, minimizzando la somma dei quadrati di questi errori sull'intero campione, possiamo determinare il valore ottimale del coefficiente alfa per una data sequenza. Il miglior valore alfa sarà ovviamente quello in cui la somma dei quadrati degli errori sarebbe minima.

La Figura 1 mostra un grafico della somma dei quadrati degli errori di previsione di un passo avanti rispetto al valore del coefficiente alfa per un frammento della sequenza di test USDJPY M1.

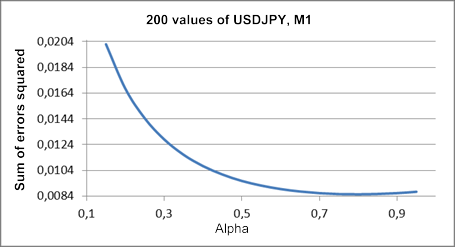
Figura 1. Livellamento esponenziale semplice

Il minimo sul grafico risultante è appena distinguibile e si trova vicino al valore alfa di circa 0,8. Ma una tale immagine non è sempre il caso per quanto riguarda il semplice livellamento esponenziale. Quando si cerca di ottenere il valore alfa ottimale per i frammenti di sequenza di test utilizzati nell'articolo, il più delle volte otterremo un grafico che cade continuamente all'unità.

Valori così elevati del coefficiente di livellamento suggeriscono che questo semplice modello non è del tutto adeguato per la descrizione delle nostre sequenze di test (quotazioni). O il livello di processo L(t) cambia troppo velocemente o c'è una tendenza presente nel processo.

Complichiamo un po' il nostro modello aggiungendo un altro componente

,

dove:

• X(t) - processo (simulato) in studio;
  
• L(t) - livello di processo variabile;
  
• T(t) - andamento lineare;
  
• r(t) - variabile casuale media nulla.

È noto che i coefficienti di regressione lineare possono essere determinati mediante doppio livellamento di una sequenza:

Per i coefficienti a1 e a2 così ottenuti, la previsione m-step-ahead all'istante t sarà uguale a

Va notato che lo stesso coefficiente alfa viene utilizzato nelle formule precedenti per il primo livellamento ripetuto. Questo modello è chiamato modello additivo a un parametro di crescita lineare.

Dimostriamo la differenza tra il modello semplice e il modello di crescita lineare.

Supponiamo che per lungo tempo il processo in esame abbia rappresentato una componente costante, cioè che apparisse sul grafico come una linea retta orizzontale, ma che ad un certo punto iniziasse ad emergere un trend lineare. Una previsione per questo processo effettuata utilizzando i modelli sopra menzionati è mostrata nella Figura 2.

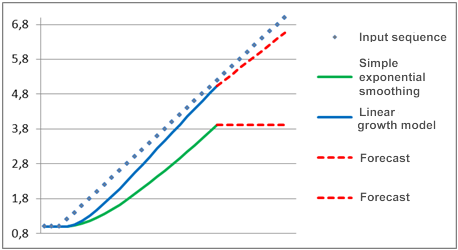
Figura 2. Confronto dei modelli

Come si può vedere, il semplice modello di livellamento esponenziale è sensibilmente dietro la sequenza di input che varia linearmente e la previsione fatta utilizzando questo modello si sta allontanando ancora di più. Possiamo vedere un modello molto diverso quando viene utilizzato il modello di crescita lineare. Quando emerge la tendenza, questo modello è come se cercasse di elaborare la sequenza che varia linearmente e la sua previsione è più vicina alla direzione dei valori di input variabili.

Se il coefficiente di livellamento nell'esempio dato fosse più alto, il modello di crescita lineare sarebbe in grado di "raggiungere" il segnale di ingresso nel tempo dato e la sua previsione coinciderebbe quasi con la sequenza di ingresso.

Nonostante il modello di crescita lineare nello stato stazionario dia buoni risultati in presenza di un trend lineare, è facile vedere che ci vuole un certo tempo per "recuperare" il trend. Pertanto, ci sarà sempre un divario tra il modello e la sequenza di input se la direzione di un trend cambia frequentemente. Inoltre, se il trend cresce in modo non lineare, ma segue invece la legge del quadrato, il modello di crescita lineare non sarà in grado di "raggiungerlo". Ma nonostante questi inconvenienti, questo modello è più vantaggioso del semplice modello di livellamento esponenziale in presenza di un trend lineare.

Come già accennato, abbiamo utilizzato un modello a un parametro di crescita lineare. Per trovare il valore ottimale del parametro alfa per un frammento della sequenza di test USDJPY M1, costruiamo un grafico della somma dei quadrati degli errori di previsione di un passo avanti rispetto al valore del coefficiente alfa.

Questo grafico, costruito sulla base dello stesso frammento di sequenza di quello in Figura 1, è mostrato in Figura 3.

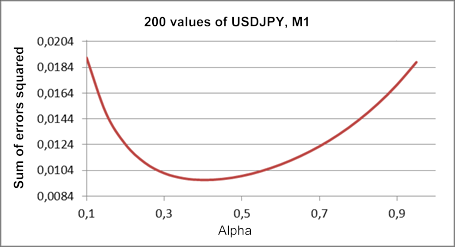
Figura 3. Modello di crescita lineare

Rispetto al risultato della Figura 1, il valore ottimale del coefficiente alfa è in questo caso sceso a circa 0,4. Il primo e il secondo livellamento hanno gli stessi coefficienti in questo modello, anche se teoricamente i loro valori possono essere diversi. Il modello di crescita lineare con due diversi coefficienti di livellamento sarà rivisto ulteriormente.

Entrambi i modelli di livellamento esponenziale che abbiamo considerato hanno i loro analoghi su MetaTrader 5, dove esistono sotto forma di indicatori. Questi sono i ben noti, EMA e DEMA, i quali non sono progettati per la previsione, ma per il livellamento dei valori di sequenza.

Va notato che quando si utilizza l'indicatore DEMA, viene visualizzato un valore corrispondente al coefficiente a1 invece del valore di previsione a un passo. Il coefficiente a2 (vedi le formule precedenti per il modello di crescita lineare) in questo caso non viene calcolato né utilizzato. Inoltre, il coefficiente di livellamento è calcolato in termini di periodo equivalente n

Ad esempio, alfa uguale a 0,8 corrisponderà a n essendo approssimativamente uguale a 2 e se alfa è 0,4, n è uguale a 4.

4. Valori iniziali

Come già accennato, un valore del coefficiente di livellamento deve essere ottenuto in un modo o nell'altro applicando il livellamento esponenziale. Ma questo sembra essere insufficiente. Poiché nel livellamento esponenziale il valore corrente viene calcolato sulla base di quello precedente, esiste una situazione in cui tale valore non esiste ancora all'istante zero. In altre parole, il valore iniziale di S o S1 e S2 nel modello di crescita lineare deve essere in qualche modo calcolato all'istante zero.

Il problema di ottenere i valori iniziali non è sempre di facile soluzione. Se (come nel caso dell'utilizzo delle quotazioni su MetaTrader 5) abbiamo a disposizione una storia molto lunga, la curva di livellamento esponenziale, avendo i valori iniziali non determinati in modo accurato, avrà il tempo di stabilizzarsi di un punto corrente dopo aver corretto il nostro errore iniziale. Ciò richiederà da 10 a 200 (e talvolta anche di più) periodi a seconda del valore del coefficiente di livellamento.

In questo caso sarebbe sufficiente stimare approssimativamente i valori iniziali e avviare il processo di livellamento esponenziale 200-300 periodi prima del periodo di tempo target. Diventa più difficile, tuttavia, quando il campione disponibile contiene solo, ad esempio, 100 valori.

Ci sono varie raccomandazioni in letteratura riguardo alla scelta dei valori iniziali. Ad esempio, il valore iniziale nel livellamento esponenziale semplice può essere equiparato al primo elemento in una sequenza o calcolato come la media di tre o quattro elementi iniziali in una sequenza al fine di livellare valori anomali casuali. I valori iniziali S1 e S2 nel modello di crescita lineare possono essere determinati sulla base dell'ipotesi che il livello iniziale della curva di previsione sia uguale al primo elemento di una sequenza e la pendenza dell'andamento lineare sia zero.

Si possono trovare ancora più raccomandazioni in diverse fonti per quanto riguarda la scelta dei valori iniziali, ma nessuna di esse può garantire l'assenza di errori evidenti nelle fasi iniziali dell'algoritmo di livellamento. È particolarmente evidente con l'uso di coefficienti di livellamento di basso valore quando è richiesto un numero elevato di periodi per raggiungere uno stato stazionario.

Pertanto, al fine di minimizzare l'impatto dei problemi associati alla scelta dei valori iniziali (soprattutto per brevi sequenze), a volte utilizziamo un metodo che prevede una ricerca di tali valori che risulterà nel minimo errore di previsione. Si tratta di calcolare un errore di previsione per i valori iniziali che variano a piccoli incrementi sull'intera sequenza.

La variante più appropriata può essere selezionata dopo aver calcolato l'errore all'interno dell'intervallo di tutte le possibili combinazioni di valori iniziali. Questo metodo è tuttavia molto laborioso, richiede molti calcoli e non viene quasi mai utilizzato nella sua forma diretta.

Il problema descritto ha a che fare con l'ottimizzazione o la ricerca di un valore minimo di funzione multivariabile. Tali problemi possono essere risolti utilizzando vari algoritmi sviluppati per ridurre notevolmente la portata dei calcoli richiesti. Torneremo un po' più avanti sui problemi di ottimizzazione dei parametri di livellamento e dei valori iniziali nelle previsioni.

5. Valutazione dell'accuratezza delle previsioni

La procedura di previsione e la selezione dei valori o dei parametri iniziali del modello pongono il problema della stima dell'accuratezza della previsione. La valutazione dell'accuratezza è importante anche quando si confrontano due modelli diversi o si determina la coerenza della previsione ottenuta. Esiste un gran numero di stime ben note per la valutazione dell'accuratezza della previsione, ma il calcolo di ognuna di esse richiede la conoscenza dell'errore di previsione in ogni fase.

Come già accennato, un errore di previsione di un passo avanti al tempo t è uguale a

dove:

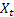• – inserire il valore della sequenza all'istante t;
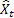• – previsione al momento t fatta al passo precedente.

Probabilmente la stima dell'accuratezza della previsione più comune è l'errore quadratico medio (MSE):

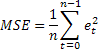
dove n è il numero di elementi in una sequenza.

L'estrema sensibilità a singoli errori occasionali di grande valore è talvolta indicata come uno svantaggio di MSE. Deriva dal fatto che il valore dell'errore nel calcolo di MSE è al quadrato. In alternativa, si consiglia di utilizzare in questo caso l'errore medio assoluto (MAE).

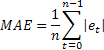
L'errore al quadrato qui è sostituito dal valore assoluto dell'errore. Si presume che le stime ottenute utilizzando MAE siano più stabili.

Entrambe le stime sono del tutto appropriate, ad esempio, per la valutazione dell'accuratezza della previsione della sequenza stessa, utilizzando diversi parametri del modello o modelli diversi. Invece, sembrano essere di scarsa utilità per il confronto dei risultati della previsione ricevuti in sequenze diverse.

Inoltre, i valori di queste stime non suggeriscono espressamente la qualità del risultato previsionale. Ad esempio, non possiamo dire se il MAE ottenuto di 0,03 o qualsiasi altro valore è buono o cattivo.

Per poter confrontare l'accuratezza delle previsioni di diverse sequenze, possiamo utilizzare le stime relative RelMSE e RelMAE:

Le stime ottenute dell'accuratezza della previsione sono qui divise per le rispettive stime ottenute utilizzando il metodo di prova della previsione. Come metodo di prova, è opportuno utilizzare il cosiddetto metodo ingenuo suggerendo che il valore futuro del processo sarà uguale al valore attuale.

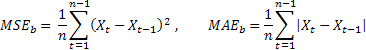
Se la media degli errori di previsione è uguale al valore degli errori ottenuti con il metodo ingenuo, il relativo valore di stima sarà pari a uno. Se il relativo valore di stima è inferiore a uno, significa che, in media, il valore di errore di previsione è inferiore rispetto al metodo ingenuo. In altre parole, l'accuratezza dei risultati delle previsioni è superiore all'accuratezza del metodo ingenuo. E viceversa, se il valore di stima relativo è maggiore di uno, l'accuratezza dei risultati della previsione è, in media, più scarsa rispetto al metodo di previsione ingenuo.

Queste stime sono adatte anche per la valutazione dell'accuratezza della previsione per due o più fasi successive. È sufficiente sostituire un errore di previsione di un passaggio nei calcoli con il valore degli errori di previsione per il numero appropriato di passaggi successivi.

Ad esempio, la tabella seguente contiene errori di previsione anticipati stimati utilizzando RelMAE in un modello a un parametro di crescita lineare. Gli errori sono stati calcolati utilizzando gli ultimi 200 valori di ciascuna sequenza di test.

alpha = 0,3 alpha = 0,4 alpha = 0,5 EURRUR M1 1,14 1,10 1,09 EURRUR M30 1,14 1.11 1,14 EURUSD M1 1,17 1,11 1,10 EURUSD M30 1,17 1,11 1,11 USDJPY M1 1,10 1,08 1,10 USDJPY M30 1,17 1,13 1,13 XAUUSD M1 1,20 1,11 1,10 XAUUSD M30 1,11 1,12 1,13

Tabella 1. Errori di previsione un passo avanti stimati utilizzando RelMAE

La stima RelMAE consente di confrontare l'efficacia di un metodo selezionato nella previsione di sequenze diverse. Come suggeriscono i risultati nella tabella 1, la nostra previsione non è mai stata più accurata del metodo ingenuo: tutti i valori RelMAE sono più di uno.

6. Modelli additivi

Prima, nell'articolo, si è incontrato un modello che comprendeva la somma del livello di processo, della tendenza lineare e di una variabile casuale. Espanderemo l'elenco dei modelli recensiti in questo articolo aggiungendo un altro modello che, oltre ai componenti di cui sopra, include un componente ciclico e stagionale.

I modelli di livellamento esponenziale che comprendono tutti i componenti come somma sono chiamati modelli additivi. Oltre a questi modelli ci sono modelli moltiplicativi in cui uno, tanti o tutti i componenti sono compresi come prodotto. Procediamo alla revisione del gruppo di modelli additivi.

L'errore di previsione di un passo avanti è stato ripetutamente menzionato in precedenza nell'articolo. Questo errore deve essere calcolato in quasi tutte le applicazioni relative alle previsioni basate sul livellamento esponenziale. Conoscendo il valore dell'errore di previsione, le formule per i modelli di livellamento esponenziale introdotti sopra possono essere presentate in una forma leggermente diversa (forma di correzione degli errori).

La forma della rappresentazione del modello che utilizzeremo nel nostro caso contiene un errore nelle sue espressioni che viene parzialmente o completamente sommato ai valori ottenuti in precedenza. Tale rappresentazione è chiamata modello di errore additivo. I modelli di livellamento esponenziale possono essere espressi anche in una forma di errore moltiplicativo che tuttavia non verrà utilizzata in questo articolo.

Diamo un'occhiata ai modelli di livellamento esponenziale additivo.

Livellamento esponenziale semplice:

Modello equivalente – ARIMA(0,1,1):

Modello di crescita lineare additivo:

In contrasto con il modello di crescita lineare a un parametro introdotto in precedenza, qui vengono utilizzati due diversi parametri di livellamento.

Modello equivalente – ARIMA(0,2,2):

Modello di crescita lineare con smorzamento:

Il significato di tale smorzamento è che la pendenza dell'andamento diminuirà ad ogni successivo passo di previsione a seconda del valore del coefficiente di smorzamento. Questo effetto è dimostrato nella Figura 4.

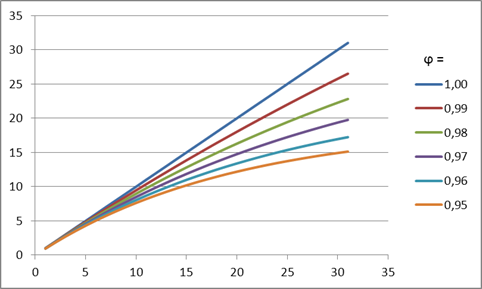
Figura 4. Effetto del coefficiente di smorzamento

Come si può vedere in figura, quando si fa una previsione, un valore decrescente del coefficiente di smorzamento farà sì che il trend perda forza più velocemente, quindi la crescita lineare sarà sempre più smorzata.

Modello equivalente - ARIMA(1,1,2):

Aggiungendo una componente stagionale come somma a ciascuno di questi tre modelli otterremo altri tre modelli.

Modello semplice con stagionalità additiva:

Modello di crescita lineare con stagionalità additiva:

Modello di crescita lineare con smorzamento e stagionalità additiva:

Esistono anche modelli ARIMA equivalenti ai modelli con stagionalità, ma qui verranno tralasciati in quanto difficilmente avranno alcuna importanza pratica.

Le notazioni utilizzate nelle formule fornite sono le seguenti:

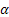• – parametro di livellamento per il livello della sequenza, [0:1];
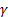• – parametro di livellamento del trend, [0:1];
• – parametro di livellamento per indici stagionali, [0:1];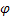
• – parametro di smorzamento, [0:1];
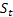• – livello livellato della sequenza calcolato al momento t dopo che 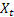è stato osservato;
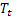• – andamento additivo livellato calcolato all'istante t;
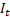• – indice stagionale livellato calcolato all'istante t;
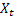• – valore della sequenza all'istante t;
• m – numero di passi avanti per i quali viene fatta la previsione;
• p – numero di periodi del ciclo stagionale;
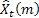• – previsione m-step-ahead fatta al momento t;
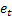• – errore di previsione un passo avanti al momento t, .

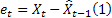È facile vedere che le formule per l'ultimo modello fornito includono tutte e sei le varianti in esame.

Se nelle formule per il modello di crescita lineare con smorzamento e stagionalità additiva prendiamo

,

la stagionalità sarà trascurata nelle previsioni. Inoltre, dove verrà prodotto un modello di crescita lineare e dove , otterremo un modello di crescita lineare con smorzamento.

Il modello di livellamento esponenziale semplice corrisponderà a .

Quando si utilizzano i modelli che coinvolgono la stagionalità, la presenza di ciclicità e periodo del ciclo dovrebbe essere prima determinata utilizzando qualsiasi metodo disponibile al fine di utilizzare ulteriormente questi dati per l'inizializzazione dei valori degli indici stagionali.

Non siamo riusciti a rilevare una notevole ciclicità stabile nei frammenti di sequenze di test utilizzati nel nostro caso, dove la previsione è fatta su brevi intervalli di tempo. Pertanto, in questo articolo non forniremo esempi rilevanti e approfondiremo le caratteristiche associate alla stagionalità.

Per determinare gli intervalli di previsione delle probabilità rispetto ai modelli in esame, utilizzeremo derivazioni analitiche presenti in letteratura [3]. La media della somma dei quadrati degli errori di previsione con un passo avanti calcolata sull'intero campione di dimensione n sarà utilizzata come varianza stimata di tali errori.

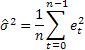
Quindi la seguente espressione sarà vera per la determinazione della varianza stimata in una previsione per 2 e per più passi avanti per i modelli in esame:

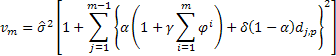
dove è uguale a uno se j modulo p è zero, altrimenti è zero.

Calcolata la varianza stimata della previsione per ogni passo m, possiamo trovare i limiti dell'intervallo di previsione del 95%:

Accetteremo di denominare tale intervallo di previsione come l'intervallo di confidenza della previsione.

Implementiamo le espressioni fornite per i modelli di livellamento esponenziale in una classe scritta in MQL5.

7. Implementazione della classe AdditiveES

L'implementazione della classe ha previsto l'utilizzo delle espressioni per il modello di crescita lineare con smorzamento e stagionalità additiva.

Come accennato in precedenza, altri modelli possono essere derivati da un'opportuna selezione di parametri.

//-----------------------------------------------------------------------------------
//                                                                     AdditiveES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>

//-----------------------------------------------------------------------------------
// Forecasting. Exponential smoothing. Additive models.
// References:
// 1. Everette S. Gardner Jr. Exponential smoothing: The state of the art – Part II.
//    June 3, 2005.
// 2. Rob J Hyndman. Forecasting based on state space models for exponential
//    smoothing. 29 August 2002.
// 3. Rob J Hyndman et al. Prediction intervals for exponential smoothing
//    using two new classes of state space models. 30 January 2003.
//-----------------------------------------------------------------------------------
class AdditiveES:public CObject
  {
protected:
  double Alpha;    // Smoothed parameter for the level of the series
  double Gamma;    // Smoothed parameter for the trend
  double Phi;      // Autoregressive or damping parameter
  double Delta;    // Smoothed parameter for seasonal indices
  int    nSes;     // Number of periods in the seasonal cycle
  double S;        // Smoothed level of the series, computed after last Y is observed
  double T;        // Smoothed additive trend
  double Ises[];   // Smoothed seasonal indices
  int    p_Ises;   // Pointer for Ises[] shift register
  double F;        // Forecast for 1 period ahead from origin t

public:
         AdditiveES();
  double Init(double s,double t,double alpha=1,double gamma=0,
              double phi=1,double delta=0,int nses=1);
  double GetS()                 { return(S); }
  double GetT()                 { return(T); }
  double GetF()                 { return(F); }
  double GetIs(int m);
  void   IniIs(int m,double is);  // Initialization of smoothed seasonal indices
  double NewY(double y);          // Next calculating step
  double Fcast(int m);            // m-step ahead forecast
  double VarCoefficient(int m);   // Coefficient for calculating prediction intervals

  };
//-----------------------------------------------------------------------------------
// Constructor
//-----------------------------------------------------------------------------------
void AdditiveES::AdditiveES()
  {
  Alpha=0.5; Gamma=0; Delta=0; Phi=1; nSes=1;
  ArrayResize(Ises,nSes);
  ArrayInitialize(Ises,0);
  p_Ises=0; S=0; T=0;
  }
//-----------------------------------------------------------------------------------
// Initialization
//-----------------------------------------------------------------------------------
double AdditiveES::Init(double s,double t,double alpha=1,double gamma=0,
                       double phi=1,double delta=0,int nses=1)
  {
  S=s; T=t;
  Alpha=alpha; if(Alpha<0)Alpha=0; if(Alpha>1)Alpha=1;
  Gamma=gamma; if(Gamma<0)Gamma=0; if(Gamma>1)Gamma=1;
  Phi=phi; if(Phi<0)Phi=0; if(Phi>1)Phi=1;
  Delta=delta; if(Delta<0)Delta=0; if(Delta>1)Delta=1;
  nSes=nses; if(nSes<1)nSes=1;
  ArrayResize(Ises,nSes);
  ArrayInitialize(Ises,0);
  p_Ises=0;
  F=S+Phi*T;
  return(F);
  }
//-----------------------------------------------------------------------------------
// Calculations for the new Y
//-----------------------------------------------------------------------------------
double AdditiveES::NewY(double y)
  {
  double e;
  
  e=y-F;
  S=S+Phi*T+Alpha*e;
  T=Phi*T+Alpha*Gamma*e;
  Ises[p_Ises]=Ises[p_Ises]+Delta*(1-Alpha)*e;
  p_Ises++; if(p_Ises>=nSes)p_Ises=0;
  F=S+Phi*T+GetIs(0);
  return(F);
  }
//-----------------------------------------------------------------------------------
// Return smoothed seasonal index
//-----------------------------------------------------------------------------------
double AdditiveES::GetIs(int m)
  {
  if(m<0)m=0;
  int i=(int)MathMod(m+p_Ises,nSes);
  return(Ises[i]);
  }
//-----------------------------------------------------------------------------------
// Initialization of smoothed seasonal indices
//-----------------------------------------------------------------------------------
void AdditiveES::IniIs(int m,double is)
  {
  if(m<0)m=0;
  if(m<nSes)
    {
    int i=(int)MathMod(m+p_Ises,nSes);
    Ises[i]=is;
    }
  }
//-----------------------------------------------------------------------------------
// m-step-ahead forecast
//-----------------------------------------------------------------------------------
double AdditiveES::Fcast(int m)
  {
  int i,h;
  double v,v1;

  if(m<1)h=1; else h=m;  
  v1=1; v=0;
  for(i=0;i<h;i++){v1=v1*Phi; v+=v1;}
  return(S+v*T+GetIs(h));
  }
//-----------------------------------------------------------------------------------
// Coefficient for calculating prediction intervals
//-----------------------------------------------------------------------------------
double AdditiveES::VarCoefficient(int m)
  {
  int i,h;
  double v,v1,a,sum,k;
  
  if(m<1)h=1; else h=m;
  if(h==1)return(1);
  v=0; v1=1; sum=0;
  for(i=1;i<h;i++)
    {
    v1=v1*Phi; v+=v1;
    if((int)MathMod(i,nSes)==0)k=1; else k=0;
    a=Alpha*(1+v*Gamma)+k*Delta*(1-Alpha);
    sum+=a*a;
    }
  return(1+sum);
  }
//-----------------------------------------------------------------------------------

Esaminiamo brevemente i metodi della classe AdditiveES.

Metodo di inizializzazione

Parametri di Input

• double s - imposta il valore iniziale del livello livellato；
• double t - imposta il valore iniziale del trend livellato；
• double alfa=1 - imposta il parametro di livellamento per il livello della sequenza；
• double gamma=0 - imposta il parametro di livellamento per il trend；
• double phi=1 - imposta il parametro di smorzamento；
• double delta=0 - imposta il parametro di livellamento per gli indici stagionali；
• int nses=1 - imposta il numero di periodi nel ciclo stagionale.

Valore restituito

• Restituisce una previsione anticipata calcolata sulla base dei valori iniziali impostati.

In primo luogo deve essere chiamato il metodo Init. Ciò è necessario per l'impostazione dei parametri di livellamento e dei valori iniziali. Si precisa che il metodo Init non prevede l'inizializzazione di indici stagionali a valori arbitrari; quando si chiama questo metodo, gli indici stagionali saranno sempre impostati a zero.

Metodo IniIs

Parametri di Input

• Int m - numero indice stagionale;
• double is - imposta il valore del numero indice stagionale m.

Valore restituito

• Nessuno

Il metodo IniIs(...) viene chiamato quando i valori iniziali degli indici stagionali devono essere diversi da zero. Gli indici stagionali devono essere inizializzati subito dopo aver chiamato il metodo Init(...).

Metodo NewY

Parametri di Input

• double y – nuovo valore della sequenza di input

Valore restituito

• Restituisce una previsione anticipata calcolata sulla base del nuovo valore della sequenza

Questo metodo è progettato per calcolare una previsione anticipata ogni volta che viene immesso un nuovo valore della sequenza di input. Dovrebbe essere chiamato solo dopo l'inizializzazione della classe da parte dei metodi Init e, ove necessario, IniIs.

Metodo Fcast

Parametri di Input

• int m – orizzonte di previsione di 1,2,3,… periodo;

Valore restituito

• Restituisce il valore di previsione m-step-ahead.

Questo metodo calcola solo il valore di previsione, senza influenzare lo stato del processo di livellamento. Di solito viene chiamato dopo aver chiamato il metodo NewY.

Metodo VarCoefficient

Parametri di Input

• int m – orizzonte di previsione di 1,2,3,… periodo;

Valore restituito

• Restituisce il valore del coefficiente per il calcolo della varianza della previsione.

Questo valore del coefficiente mostra l'aumento della varianza di una previsione con un passo avanti rispetto alla varianza della previsione con un passo avanti.

Metodi GetS, GetT, GetF, GetIs

Questi metodi forniscono l'accesso alle variabili protette della classe. GetS, GetT e GetF restituiscono rispettivamente i valori del livello livellato, della tendenza livellata e di una previsione con un passo avanti. GetIs fornisce l'accesso agli indici stagionali e richiede l'indicazione del numero di indice m come argomento di input.

Il modello più complesso tra quelli che abbiamo esaminato è il modello di crescita lineare con smorzamento e stagionalità additiva, in base al quale viene creata la classe AdditiveES. Ciò solleva una domanda molto ragionevole: quali tra i modelli restanti e più semplici sarebbero necessari?

Nonostante il fatto che i modelli più complessi dovrebbero apparentemente avere un chiaro vantaggio rispetto a quelli più semplici, in realtà non è sempre così. I modelli più semplici, i quali hanno meno parametri nella stragrande maggioranza dei casi, risulteranno in una minore varianza degli errori di previsione, ovvero il loro funzionamento sarà più stabile. Questo fatto viene impiegato nella creazione di algoritmi di previsione basati sul funzionamento parallelo simultaneo di tutti i modelli disponibili, dai più semplici ai più complessi.

Una volta che la sequenza è stata completamente elaborata, viene selezionato un modello di previsione che ha dimostrato l'errore più basso, dato il numero dei suoi parametri (cioè la sua complessità). C'è un certo numero di criteri sviluppati a questo scopo, ad esempio il Test di verifica delle informazioni di Akaike (AIC). Risulterà nella selezione di un modello che deve produrre la previsione più stabile.

Per dimostrare l'utilizzo della classe AdditiveES è stato creato un semplice indicatore i cui parametri di livellamento sono impostati manualmente.

Di seguito è riportato il codice sorgente dell'indicatore AdditiveES_Test.mq5.

//-----------------------------------------------------------------------------------
//                                                                AdditiveES_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"      // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "PInterval+"    // Prediction interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCadetBlue
#property indicator_style3  STYLE_SOLID
#property indicator_width3  1
#property indicator_label4  "PInterval-"    // Prediction interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCadetBlue
#property indicator_style4  STYLE_SOLID
#property indicator_width4  1

double HIST[];
double FORE[];
double PINT1[];
double PINT2[];

input double Alpha=0.2;     // Smoothed parameter for the level
input double Gamma=0.2;     // Smoothed parameter for the trend
input double Phi=0.8;       // Damping parameter
input double Delta=0;       // Smoothed parameter for seasonal indices
input int    nSes=1;        // Number of periods in the seasonal cycle
input int    nHist=250;     // History bars, nHist>=100
input int    nTest=150;     // Test interval, 50<=nTest<nHist
input int    nFore=12;      // Forecasting horizon, nFore>=2

#include "AdditiveES.mqh"
AdditiveES fc;

int    NHist;               // history bars
int    NFore;               // forecasting horizon
int    NTest;               // test interval
double ALPH;                // alpha
double GAMM;                // gamma
double PHI;                 // phi
double DELT;                // delta
int    nSES;                // Number of periods in the seasonal cycle
//-----------------------------------------------------------------------------------
// Custom indicator initialization function
//-----------------------------------------------------------------------------------
int OnInit()
  {
  NHist=nHist; if(NHist<100)NHist=100;
  NFore=nFore; if(NFore<2)NFore=2;
  NTest=nTest; if(NTest>NHist)NTest=NHist; if(NTest<50)NTest=50;
  ALPH=Alpha; if(ALPH<0)ALPH=0; if(ALPH>1)ALPH=1;
  GAMM=Gamma; if(GAMM<0)GAMM=0; if(GAMM>1)GAMM=1;
  PHI=Phi; if(PHI<0)PHI=0; if(PHI>1)PHI=1;
  DELT=Delta; if(DELT<0)DELT=0; if(DELT>1)DELT=1;
  nSES=nSes; if(nSES<1)nSES=1;

  MqlRates rates[];
  CopyRates(NULL,0,0,NHist,rates);           // Load missing data
  
  SetIndexBuffer(0,HIST,INDICATOR_DATA);
  PlotIndexSetString(0,PLOT_LABEL,"History");
  SetIndexBuffer(1,FORE,INDICATOR_DATA);
  PlotIndexSetString(1,PLOT_LABEL,"Forecast");
  PlotIndexSetInteger(1,PLOT_SHIFT,NFore);
  SetIndexBuffer(2,PINT1,INDICATOR_DATA);
  PlotIndexSetString(2,PLOT_LABEL,"Conf+");
  PlotIndexSetInteger(2,PLOT_SHIFT,NFore);
  SetIndexBuffer(3,PINT2,INDICATOR_DATA);
  PlotIndexSetString(3,PLOT_LABEL,"Conf-");
  PlotIndexSetInteger(3,PLOT_SHIFT,NFore);
  
  IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
  return(0);
  }
//-----------------------------------------------------------------------------------
// Custom indicator iteration function
//-----------------------------------------------------------------------------------
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
  int i,j,init,start;
  double v1,v2;
  
  if(rates_total<NHist){Print("Error: Not enough bars for calculation!"); return(0);}
  if(prev_calculated>rates_total||prev_calculated<=0||(rates_total-prev_calculated)>1)
    {init=1; start=rates_total-NHist;}
  else
    {init=0; start=prev_calculated;}
  if(start==rates_total)return(rates_total);    // New tick but not new bar
//-----------------------
  if(init==1)                                   // Initialization
    {
    i=start;
    v2=(open[i+2]-open[i])/2;
    v1=(open[i]+open[i+1]+open[i+2])/3.0-v2;
    fc.Init(v1,v2,ALPH,GAMM,PHI,DELT,nSES);
    ArrayInitialize(HIST,EMPTY_VALUE);
    }
  PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFore);
  PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFore);
  PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFore);

  for(i=start;i<rates_total;i++)                // History
    {
    HIST[i]=fc.NewY(open[i]);
    }
  v1=0;
  for(i=0;i<NTest;i++)                          // Variance
    {
    j=rates_total-NTest+i;
    v2=close[j]-HIST[j-1];
    v1+=v2*v2;
    }
  v1/=NTest;                                    // v1=var
  j=1;
  for(i=rates_total-NFore;i<rates_total;i++)
    {
    v2=1.96*MathSqrt(v1*fc.VarCoefficient(j));  // Prediction intervals
    FORE[i]=fc.Fcast(j++);                    // Forecasting
    PINT1[i]=FORE[i]+v2;
    PINT2[i]=FORE[i]-v2;
    }
  
  return(rates_total);
  }
//-----------------------------------------------------------------------------------

Una chiamata o un'inizializzazione ripetuta dell'indicatore imposta i valori iniziali di livellamento esponenziale

Non ci sono impostazioni iniziali per gli indici stagionali in questo indicatore, i loro valori iniziali sono quindi sempre uguali a zero. A seguito di tale inizializzazione, l'influenza della stagionalità sul risultato previsionale aumenterà progressivamente da zero ad un certo valore stazionario, con l'introduzione di nuovi valori in ingresso.

Il numero di cicli necessari per raggiungere una condizione di funzionamento a regime dipende dal valore del coefficiente di livellamento per indici stagionali: minore è il valore del coefficiente di livellamento, maggiore sarà il tempo necessario.

Il risultato dell'operazione dell'indicatore AdditiveES_Test.mq5 con le impostazioni predefinite è mostrato nella Figura 5.

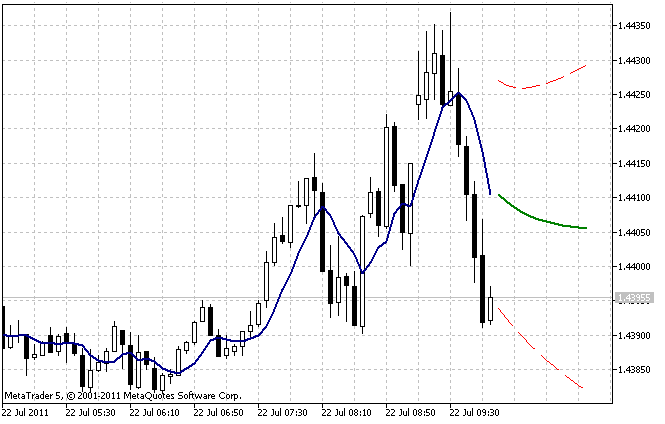
Figura 5. L'indicatore AdditiveES_Test.mq5

Oltre alla previsione, l'indicatore visualizza una riga aggiuntiva corrispondente alla previsione a un passo per i valori passati della sequenza e i limiti dell'intervallo di confidenza della previsione al 95%.

L'intervallo di confidenza si basa sulla varianza stimata dell'errore di un passo avanti. Per ridurre l'effetto di imprecisione dei valori iniziali selezionati, la varianza stimata non viene calcolata sull'intera lunghezza nHist, ma solo rispetto alle ultime barre il cui numero è specificato nel parametro di input nTest.

L'archivio Files.zip alla fine dell'articolo include i file AdditiveES.mqh e AdditiveES_Test.mq5. Quando si compila l'indicatore, è necessario che il file include AdditiveES.mqh si trovi nella stessa directory di AdditiveES_Test.mq5.

Mentre il problema della selezione dei valori iniziali è stato in parte risolto durante la creazione dell'indicatore AdditiveES_Test.mq5, il problema della selezione dei valori ottimali dei parametri di livellamento è rimasto aperto.

8. Selezione dei valori ottimali dei parametri

Il modello di livellamento esponenziale semplice ha un unico parametro di livellamento e il suo valore ottimale può essere trovato utilizzando il metodo di enumerazione semplice. Dopo aver calcolato i valori di errore di previsione sull'intera sequenza, il valore del parametro viene modificato con un piccolo incremento e viene eseguito nuovamente un calcolo completo. Questa procedura viene ripetuta fino a quando non sono stati enumerati tutti i possibili valori dei parametri. Ora dobbiamo solo selezionare il valore del parametro che ha generato il valore di errore più piccolo.

Per trovare un valore ottimale del coefficiente di livellamento nell'intervallo da 0,1 a 0,9 con incrementi di 0,05, sarà necessario eseguire diciassette volte il calcolo completo del valore dell'errore di previsione. Come si può vedere, il numero di calcoli richiesti non è così grande. Ma il modello di crescita lineare con smorzamento prevede l'ottimizzazione di tre parametri di livellamento e, in questo caso, saranno necessarie 4913 esecuzioni di calcolo per enumerare tutte le loro combinazioni nello stesso intervallo con gli stessi incrementi di 0,05.

Il numero di esecuzioni complete necessarie per l'enumerazione di tutti i possibili valori dei parametri aumenta rapidamente con l'aumento del numero di parametri, con la diminuzione dell'incremento e l'espansione dell'intervallo di enumerazione. Qualora fosse inoltre necessario ottimizzare i valori iniziali dei modelli oltre ai parametri di livellamento, sarà abbastanza difficile farlo utilizzando il semplice metodo di enumerazione.

I problemi associati alla ricerca del minimo di una funzione di più variabili sono ben studiati e ci sono molti algoritmi di questo tipo. La descrizione e il confronto di vari metodi per trovare il minimo di una funzione possono essere trovati nella letteratura [7]. Tutti questi metodi hanno principalmente lo scopo di ridurre il numero di chiamate della funzione obiettivo, ovvero ridurre gli sforzi computazionali nel processo di ricerca del minimo.

Diverse fonti contengono spesso un riferimento ai cosiddetti metodi di ottimizzazione Quasi-Newton. Molto probabilmente questo ha a che fare con la loro elevata efficienza, ma anche l'implementazione di un metodo più semplice dovrebbe essere sufficiente per dimostrare un approccio all'ottimizzazione delle previsioni. Optiamo per il metodo di Powell. Il metodo di Powell non richiede il calcolo delle derivate della funzione obiettivo e appartiene ai metodi di ricerca.

Questo metodo, come qualsiasi altro metodo, può essere implementato a livello di codice in vari modi. La ricerca deve essere completata quando viene raggiunta una certa accuratezza del valore della funzione obiettivo o del valore dell'argomento. Inoltre, una certa implementazione può includere la possibilità di utilizzare limitazioni sull'intervallo consentito di modifiche dei parametri di funzione.

Nel nostro caso, l'algoritmo per trovare un minimo non vincolato utilizzando il metodo di Powell è implementato in PowellsMethod.class. L'algoritmo interrompe la ricerca una volta raggiunta una data accuratezza del valore della funzione obiettivo. Nell'implementazione di questo metodo è stato utilizzato come prototipo un algoritmo trovato nella letteratura [8].

Di seguito è riportato il codice sorgente della classe PowellsMethod.

//-----------------------------------------------------------------------------------
//                                                                  PowellsMethod.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include <Object.mqh>

#define GOLD   1.618034
#define CGOLD  0.3819660
#define GLIMIT 100.0
#define SHFT(a,b,c,d) (a)=(b);(b)=(c);(c)=(d);
#define SIGN(a,b) ((b) >= 0.0 ? fabs(a) : -fabs(a))
#define FMAX(a,b) (a>b?a:b)
//-----------------------------------------------------------------------------------
// Minimization of Functions.
// Unconstrained Powell’s Method.
// References:
// 1. Numerical Recipes in C. The Art of Scientific Computing.
//-----------------------------------------------------------------------------------
class PowellsMethod:public CObject
  {
protected:
  double P[],Xi[];
  double Pcom[],Xicom[],Xt[];
  double Pt[],Ptt[],Xit[];
  int    N;
  double Fret;
  int    Iter;
  int    ItMaxPowell;
  double FtolPowell;
  int    ItMaxBrent;
  double FtolBrent;
  int    MaxIterFlag;
public:
  void   PowellsMethod(void);
  void   SetItMaxPowell(int n)           { ItMaxPowell=n; }
  void   SetFtolPowell(double er)        { FtolPowell=er; }
  void   SetItMaxBrent(int n)            { ItMaxBrent=n;  }
  void   SetFtolBrent(double er)         { FtolBrent=er;  }
  int    Optimize(double &p[],int n=0);
  double GetFret(void)                   { return(Fret);  }
  int    GetIter(void)                   { return(Iter);  }
private:
  void   powell(void);
  void   linmin(void);
  void   mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc);
  double brent(double ax,double bx,double cx,double &xmin);
  double f1dim(double x);
  virtual double func(const double &p[]) { return(0); }
  };
//-----------------------------------------------------------------------------------
// Constructor
//-----------------------------------------------------------------------------------
void PowellsMethod::PowellsMethod(void)
  {
  ItMaxPowell= 200;
  FtolPowell = 1e-6;
  ItMaxBrent = 200;
  FtolBrent  = 1e-4;
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::powell(void)
  {
  int i,j,m,n,ibig;
  double del,fp,fptt,t;
  
  n=N; Fret=func(P);
  for(j=0;j<n;j++)Pt[j]=P[j];
  for(Iter=1;;Iter++)
    {
    fp=Fret; ibig=0; del=0.0;
    for(i=0;i<n;i++)
      {
      for(j=0;j<n;j++)Xit[j]=Xi[j+n*i];
      fptt=Fret;
      linmin();
      if(fabs(fptt-Fret)>del){del=fabs(fptt-Fret); ibig=i;}
      }
    if(2.0*fabs(fp-Fret)<=FtolPowell*(fabs(fp)+fabs(Fret)+1e-25))return;
    if(Iter>=ItMaxPowell)
      {
      Print("powell exceeding maximum iterations!");
      MaxIterFlag=1; return;
      }
    for(j=0;j<n;j++){Ptt[j]=2.0*P[j]-Pt[j]; Xit[j]=P[j]-Pt[j]; Pt[j]=P[j];}
    fptt=func(Ptt);
    if(fptt<fp)
      {
      t=2.0*(fp-2.0*(Fret)+fptt)*(fp-Fret-del)*(fp-Fret-del)-del*(fp-fptt)*(fp-fptt);
      if(t<0.0)
        {
        linmin();
        for(j=0;j<n;j++){m=j+n*(n-1); Xi[j+n*ibig]=Xi[m]; Xi[m]=Xit[j];}
        }
      }
    }
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::linmin(void)
  {
  int j,n;
  double xx,xmin,fx,fb,fa,bx,ax;

  n=N;
  for(j=0;j<n;j++){Pcom[j]=P[j]; Xicom[j]=Xit[j];}
  ax=0.0; xx=1.0;
  mnbrak(ax,xx,bx,fa,fx,fb);
  Fret=brent(ax,xx,bx,xmin);
  for(j=0;j<n;j++){Xit[j]*=xmin; P[j]+=Xit[j];}
  }
//-----------------------------------------------------------------------------------
void PowellsMethod::mnbrak(double &ax,double &bx,double &cx,
                                 double &fa,double &fb,double &fc)
  {
  double ulim,u,r,q,fu,dum;

  fa=f1dim(ax); fb=f1dim(bx);
  if(fb>fa)
    {
    SHFT(dum,ax,bx,dum)
    SHFT(dum,fb,fa,dum)
    }
  cx=bx+GOLD*(bx-ax); fc=f1dim(cx);
  while(fb>fc)
    {
    r=(bx-ax)*(fb-fc); q=(bx-cx)*(fb-fa);
    u=bx-((bx-cx)*q-(bx-ax)*r)/(2.0*SIGN(FMAX(fabs(q-r),1e-20),q-r));
    ulim=bx+GLIMIT*(cx-bx);
    if((bx-u)*(u-cx)>0.0)
      {
      fu=f1dim(u);
      if(fu<fc){ax=bx; bx=u; fa=fb; fb=fu; return;}
      else if(fu>fb){cx=u; fc=fu; return;}
      u=cx+GOLD*(cx-bx); fu=f1dim(u);
      }
    else if((cx-u)*(u-ulim)>0.0)
      {
      fu=f1dim(u);
      if(fu<fc)
        {
        SHFT(bx,cx,u,cx+GOLD*(cx-bx))
        SHFT(fb,fc,fu,f1dim(u))
        }
      }
    else if((u-ulim)*(ulim-cx)>=0.0){u=ulim; fu=f1dim(u);}
      else {u=cx+GOLD*(cx-bx); fu=f1dim(u);}
    SHFT(ax,bx,cx,u)
    SHFT(fa,fb,fc,fu)
    }
  }
//-----------------------------------------------------------------------------------
double PowellsMethod::brent(double ax,double bx,double cx,double &xmin)
  {
  int    iter;
  double a,b,d,e,etemp,fu,fv,fw,fx,p,q,r,tol1,tol2,u,v,w,x,xm;

  a=(ax<cx?ax:cx); b=(ax>cx?ax:cx);
  d=0.0; e=0.0; x=w=v=bx; fw=fv=fx=f1dim(x);
  for(iter=1;iter<=ItMaxBrent;iter++)
    {
    xm=0.5*(a+b); tol2=2.0*(tol1=FtolBrent*fabs(x)+2e-19);
    if(fabs(x-xm)<=(tol2-0.5*(b-a))){xmin=x; return(fx);}
    if(fabs(e)>tol1)
      {
      r=(x-w)*(fx-fv); q=(x-v)*(fx-fw);
      p=(x-v)*q-(x-w)*r; q=2.0*(q-r);
      if(q>0.0)p=-p; q=fabs(q);
      etemp=e; e=d;
      if(fabs(p)>=fabs(0.5*q*etemp)||p<=q*(a-x)||p>=q*(b-x))
        d=CGOLD*(e=(x>=xm?a-x:b-x));
      else {d=p/q; u=x+d; if(u-a<tol2||b-u<tol2)d=SIGN(tol1,xm-x);}
      }
    else d=CGOLD*(e=(x>=xm?a-x:b-x));
    u=(fabs(d)>=tol1?x+d:x+SIGN(tol1,d));
    fu=f1dim(u);
    if(fu<=fx)
      {
      if(u>=x)a=x; else b=x;
      SHFT(v,w,x,u)
      SHFT(fv,fw,fx,fu)
      }
    else
      {
      if(u<x)a=u; else b=u;
      if(fu<=fw||w==x){v=w; w=u; fv=fw; fw=fu;}
      else if(fu<=fv||v==x||v==w){v=u; fv=fu;}
      }
    }
  Print("Too many iterations in brent");
  MaxIterFlag=1; xmin=x;
  return(fx);
  }
//-----------------------------------------------------------------------------------
double PowellsMethod::f1dim(double x)
  {
  int j;
  double f;
  
  for(j=0;j<N;j++) Xt[j]=Pcom[j]+x*Xicom[j];
  f=func(Xt);
  return(f);
  }
//-----------------------------------------------------------------------------------
int PowellsMethod::Optimize(double &p[],int n=0)
  {
  int i,j,k,ret;
  
  k=ArraySize(p);
  if(n==0)N=k;
  else N=n;
  if(N<1||N>k)return(0);
  ArrayResize(P,N); ArrayResize(Xi,N*N);
  ArrayResize(Pcom,N); ArrayResize(Xicom,N);
  ArrayResize(Xt,N); ArrayResize(Pt,N);
  ArrayResize(Ptt,N); ArrayResize(Xit,N);
  for(i=0;i<N;i++)for(j=0;j<N;j++)Xi[i+N*j]=(i==j?1.0:0.0);
  for(i=0;i<N;i++)P[i]=p[i];
  MaxIterFlag=0;
  powell();
  for(i=0;i<N;i++)p[i]=P[i];
  if(MaxIterFlag==1)ret=-1;
  else ret=Iter;
  return(ret);
  }
//-----------------------------------------------------------------------------------

Il metodo di ottimizzazione è il metodo principale della classe.

Metodo di ottimizzazione

Parametri di Input:

• double &p[] - array che in ingresso contiene i valori iniziali dei parametri di cui si dovranno trovare i valori ottimali; i valori ottimali ottenuti di questi parametri sono all'uscita dell'array.
• int n=0 - numero di argomenti nell'array p[]. Dove n=0, il numero di parametri è considerato uguale alla dimensione dell'array p[].

Valore restituito

• Restituisce il numero di iterazioni necessarie per il funzionamento dell'algoritmo, o -1 se è stato raggiunto il numero massimo consentito.

Quando si cercano i valori dei parametri ottimali, si verifica un'approssimazione iterativa al minimo della funzione obiettivo. Il metodo di ottimizzazione restituisce il numero di iterazioni necessarie per raggiungere il minimo della funzione con una determinata precisione. La funzione obiettivo viene chiamata più volte ad ogni iterazione, ovvero il numero di chiamate della funzione obiettivo può essere significativamente (dieci e anche cento volte) maggiore del numero di iterazioni restituito dal metodo di ottimizzazione.

Altri metodi della classe.

Metodo SetItMaxPowell

Parametri di Input:

• Int n - numero massimo consentito di iterazioni nel metodo di Powell. Il valore predefinito è 200.

Valore restituito

• Nessuno.

Imposta il numero massimo consentito di iterazioni; una volta raggiunto questo numero, la ricerca sarà terminata indipendentemente dal fatto che sia stato trovato il minimo della funzione obiettivo con una data accuratezza. E un messaggio pertinente verrà aggiunto al registro.

Metodo SetFtolPowell

Parametri di Input:

• doppio er - precisione. Se questo valore di deviazione dal valore minimo della funzione obiettivo viene raggiunto, il metodo di Powell interrompe la ricerca. Il valore predefinito è 1e-6.

Valore restituito

• Nessuno.

Metodo SetItMaxBrent

Parametri di Input:

• Int n - numero massimo consentito di iterazioni per un metodo di Brent ausiliario. Il valore predefinito è 200.

Valore restituito

• Nessuno.

Imposta il numero massimo consentito di iterazioni. Una volta raggiunto, il metodo dell'ausiliare Brent interromperà la ricerca e verrà aggiunto un messaggio relativo al registro.

Metodo SetFtolBrent

Parametri di Input:

• doppio er – precisione. Questo valore definisce l'accuratezza nella ricerca del minimo per il metodo di Brent ausiliario. Il valore predefinito è 1e-4.

Valore restituito

• Nessuno.

Metodo GetFret

Parametri di Input:

• Nessuno.

Valore restituito

• Restituisce il valore minimo della funzione obiettivo ottenuta.

Metodo GetIter

Parametri di Input:

• Nessuno.

Valore restituito

• Restituisce il numero di iterazioni necessarie per il funzionamento dell'algoritmo.

Funzione virtuale func(const double &p[])

Parametri di Input:

• const double &p[] – indirizzo dell'array contenente i parametri ottimizzati. La dimensione dell'array corrisponde al numero di parametri della funzione.

Valore restituito

• Restituisce il valore della funzione corrispondente ai parametri che gli sono passati.

La funzione virtuale func() deve essere ridefinita in ogni caso particolare in una classe derivata dalla classe PowellsMethod. La funzione func() è la funzione obiettivo i cui argomenti corrispondenti al valore minimo restituito dalla funzione verranno trovati quando si applica l'algoritmo di ricerca.

Questa implementazione del metodo di Powell utilizza il metodo di interpolazione parabolica univariata di Brent per determinare la direzione di ricerca rispetto a ciascun parametro. La precisione e il numero massimo consentito di iterazioni per questi metodi possono essere impostati separatamente chiamando SetItMaxPowell, SetFtolPowell, SetItMaxBrent e SetFtolBrent.

Quindi le caratteristiche predefinite dell'algoritmo possono essere modificate in questo modo. Questo può sembrare utile quando la precisione predefinita impostata su una determinata funzione obiettivo risulta essere troppo alta e l'algoritmo richiede troppe iterazioni nel processo di ricerca. La variazione del valore della precisione richiesta può ottimizzare la ricerca rispetto a diverse categorie di funzioni obiettivo.

Nonostante l'apparente complessità dell'algoritmo che utilizza il metodo di Powell, è abbastanza semplice da usare.

Rivediamo un esempio. Supponiamo di avere una funzione

e dobbiamo trovare i valori dei parametri e per i quali la funzione avrà il valore più piccolo.

Scriviamo uno script che dimostri una soluzione a questo problema.

//-----------------------------------------------------------------------------------
//                                                                        PM_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
class PM_Test:public PowellsMethod
  {
public:
  void   PM_Test(void) {}
private:
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
double PM_Test::func(const double &p[])
  {
  double f,r1,r2;
  
  r1=p[0]-0.5;
  r2=p[1]-6.0;
  f=r1*r1*4.0+r2*r2;
  return(f);
  }
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  int it;
  double p[2];

  p[0]=8; p[1]=9;                                 // Initial point
  PM_Test *pm = new PM_Test;
  it=pm.Optimize(p);
  Print("Iter= ",it,"        Fret= ",pm.GetFret());
  Print("p[0]= ",p[0],"    p[1]= ",p[1]);
  delete pm;
  }
//-----------------------------------------------------------------------------------

Quando scriviamo questo script, creiamo prima la funzione func() come membro della classe PM_Test, la quale calcola il valore della data funzione di test usando i valori passati dei parametri p[0] e p[1]. Quindi, nel corpo della funzione OnStart(), i valori iniziali vengono assegnati ai parametri richiesti. La ricerca partirà da questi valori.

Inoltre, viene creata una copia della classe PM_Test e la ricerca dei valori richiesti di p[0] e p[1] inizia chiamando il metodo di ottimizzazione; i metodi della classe genitore PowellsMethod chiameranno la funzione ridefinita func(). Al termine della ricerca, verranno aggiunti al log il numero di iterazioni, il valore della funzione al punto minimo e i valori dei parametri ottenuti p[0]=0.5 e p[1]=6.

PowellsMethod.mqh e un test case PM_Test.mq5 si trovano alla fine dell'articolo nell'archivio Files.zip. Per compilare PM_Test.mq5, dovrebbe trovarsi nella stessa directory di PowellsMethod.mqh.

9. Ottimizzazione dei valori dei parametri del modello

La sezione precedente dell'articolo si è occupata dell'implementazione del metodo per trovare il minimo di funzione e ha fornito un semplice esempio del suo utilizzo. Passiamo ora alle questioni relative all'ottimizzazione dei parametri del modello di livellamento esponenziale.

Per cominciare, semplifichiamo al massimo la classe AdditiveES introdotta in precedenza escludendo da essa tutti gli elementi associati alla componente stagionale, poiché i modelli che tengono conto della stagionalità non verranno comunque ulteriormente considerati in questo articolo. Ciò consentirà di rendere il codice sorgente della classe molto più facile da comprendere e di ridurre il numero di calcoli. Inoltre, escluderemo anche tutti i calcoli relativi alla previsione e il calcolo degli intervalli di confidenza previsti per una facile dimostrazione di un approccio all'ottimizzazione dei parametri del modello di crescita lineare con lo smorzamento in esame.

//-----------------------------------------------------------------------------------
//                                                                     OptimizeES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
// Class OptimizeES
//-----------------------------------------------------------------------------------
class OptimizeES:public PowellsMethod
  {
protected:
  double Dat[];            // Input data
  int    Dlen;             // Data lenght
  double Par[5];           // Parameters
  int    NCalc;            // Number of last elements for calculation
public:
  void   OptimizeES(void) {}
  int    Calc(string fname);
private:
  int    readCSV(string fnam,double &dat[]);
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
// Calc
//-----------------------------------------------------------------------------------
int OptimizeES::Calc(string fname)
  {
  int i,it;
  double relmae,naiv,s,t,alp,gam,phi,e,ae,pt;
  
  if(readCSV(fname,Dat)<0){Print("Error."); return(-1);}
  Dlen=ArraySize(Dat);
  NCalc=200;                               // number of last elements for calculation
  if(NCalc<0||NCalc>Dlen-1){Print("Error."); return(-1);}
  Par[0]=Dat[Dlen-NCalc];                  // initial S
  Par[1]=0;                                // initial T
  Par[2]=0.5;                              // initial Alpha
  Par[3]=0.5;                              // initial Gamma
  Par[4]=0.5;                              // initial Phi
  it=Optimize(Par);                        // Powell's optimization
  s=Par[0]; t=Par[1]; alp=Par[2]; gam=Par[3]; phi=Par[4];
  relmae=0; naiv=0;
  for(i=Dlen-NCalc;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t);
    relmae+=MathAbs(e); naiv+=MathAbs(Dat[i]-Dat[i-1]);
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  relmae/=naiv;
  PrintFormat("%s:    N=%i,  RelMAE=%.3f",fname,NCalc,relmae);
  PrintFormat("Iter= %i,  Fmin= %e",it,GetFret());
  PrintFormat("p[0]= %.5f,  p[1]= %.5f,  p[2]= %.2f,  p[3]= %.2f,  p[4]= %.2f",
                                             Par[0],Par[1],Par[2],Par[3],Par[4]);
  return(0);
  }
//-----------------------------------------------------------------------------------
// readCSV
//-----------------------------------------------------------------------------------
int OptimizeES::readCSV(string fnam,double &dat[])
  {
  int n,asize,fhand;
    
  fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
  if(fhand==INVALID_HANDLE)
    {
    Print("FileOpen Error!");
    return(-1);
    }
  asize=512;
  ArrayResize(dat,asize);
  n=0;
  while(FileIsEnding(fhand)!=true)
    {
    dat[n++]=FileReadNumber(fhand);
    if(n+128>asize)
      {
      asize+=128;
      ArrayResize(dat,asize);
      }
    }
  FileClose(fhand);
  ArrayResize(dat,n-1);
  return(0);

  }
//------------------------------------------------------------------------------------
// func
//------------------------------------------------------------------------------------
double OptimizeES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}                 // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}                 // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}                 // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}                 // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }                 // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}                 // Phi     < 0.05
  sse=0; 
  for(i=Dlen-NCalc;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(NCalc*MathLog(k1*k2*k3*sse));
  }
//------------------------------------------------------------------------------------

La classe OptimizeES deriva dalla classe PowellsMethod e include la ridefinizione della funzione virtuale func(). Come accennato in precedenza, i parametri il cui valore calcolato sarà ridotto al minimo nel corso dell'ottimizzazione verranno passati all'ingresso di questa funzione.

In accordo con il metodo della massima verosimiglianza, la funzione func() calcola il logaritmo della somma dei quadrati degli errori di previsione di un passo avanti. Gli errori vengono calcolati in un ciclo rispetto ai valori recenti di NCalc della sequenza.

Per preservare la stabilità del modello, dovremmo imporre limitazioni alla gamma di cambiamenti nei suoi parametri. Questo intervallo per i parametri Alpha e Gamma sarà compreso tra 0,05 e 0,95 e per il parametro Phi tra 0,05 e 1,0. Ma per l'ottimizzazione nel nostro caso, usiamo un metodo per trovare un minimo non vincolato che non implica l'uso di limitazioni sugli argomenti della funzione obiettivo.

Cercheremo di trasformare il problema del trovare il minimo della funzione multivariabile con limitazioni in un problema sul trovare un minimo non vincolato, per poter prendere in considerazione tutte le limitazioni imposte ai parametri senza modificare l'algoritmo di ricerca. A tal fine verrà utilizzato il cosiddetto metodo della funzione di penalità. Questo metodo può essere facilmente dimostrato per un caso unidimensionale.

Supponiamo di avere una funzione di un singolo argomento (il cui dominio va da 2.0 a 3.0) e un algoritmo che nel processo di ricerca può assegnare qualsiasi valore a questo parametro di funzione. In questo caso si può fare come segue: se l'algoritmo di ricerca ha passato un argomento che supera il valore massimo ammissibile, ad esempio 3,5, la funzione può essere calcolata per l'argomento pari a 3,0 e il risultato ottenuto viene ulteriormente moltiplicato per un coefficiente proporzionale al di sopra del valore massimo, ad esempio k=1+(3,5-3)*200.

Se operazioni simili vengono eseguite rispetto ai valori dell'argomento che si sono rivelati inferiori al valore minimo consentito, è garantito che la funzione obiettivo risultante aumenterà al di fuori dell'intervallo consentito di modifiche nel suo argomento. Tale aumento artificiale del valore risultante della funzione obiettivo consente di mantenere l'algoritmo di ricerca all'oscuro del fatto che l'argomento passato alla funzione era in qualche modo limitato e garantire che il minimo della funzione risultante rientri nei limiti impostati discussione. Tale approccio è facilmente applicabile a una funzione di più variabili.

Il metodo principale della classe OptimizeES è il metodo Calc. Una chiamata di questo metodo è responsabile della lettura dei dati da un file, della ricerca dei valori dei parametri ottimali di un modello e della stima dell'accuratezza della previsione utilizzando RelMAE per i valori dei parametri ottenuti. Il numero di valori elaborati della sequenza letta da un file è in questo caso impostato nella variabile NCalc.

Di seguito è riportato l'esempio dello script Optimization_Test.mq5 che utilizza la classe OptimizeES.

//-----------------------------------------------------------------------------------
//                                                              Optimization_Test.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "OptimizeES.mqh"

OptimizeES es;
//-----------------------------------------------------------------------------------
// Script program start function
//-----------------------------------------------------------------------------------
void OnStart()
  {
  es.Calc("Dataset\\USDJPY_M1_1100.TXT");
  }
//-----------------------------------------------------------------------------------

Dopo l'esecuzione di questo script, il risultato ottenuto sarà come mostrato di seguito.

 

Figura 6. Risultato dello script Optimization_Test.mq5

Sebbene ora possiamo trovare valori di parametro ottimali e valori iniziali del modello, esiste ancora un parametro che non può essere ottimizzato utilizzando strumenti semplici: il numero di valori di sequenza utilizzati nell'ottimizzazione. Nell'ottimizzazione rispetto a una sequenza di grande lunghezza, otterremo i valori dei parametri ottimali che, mediamente, assicurano un errore minimo su tutta la lunghezza della sequenza.

Tuttavia, se la natura della sequenza varia all'interno di questo intervallo, i valori ottenuti per alcuni dei suoi frammenti non saranno più ottimali. D'altra parte, se la lunghezza della sequenza viene drasticamente ridotta, non vi è alcuna garanzia che i parametri ottimali ottenuti per un intervallo così breve saranno ottimali per un intervallo di tempo più lungo.

OptimizeES.mqh e Optimization_Test.mq5 si trovano alla fine dell'articolo nell'archivio Files.zip. Durante la compilazione è necessario che OptimizeES.mqh e PowellsMethod.mqh si trovino nella stessa directory di Optimization_Test.mq5 compilato. Nell'esempio fornito, viene utilizzato il file USDJPY_M1_1100.TXT che contiene la sequenza di test e che dovrebbe trovarsi nella directory \MQL5\Files\Dataset\.

La tabella 2 mostra le stime dell'accuratezza della previsione ottenute utilizzando RelMAE mediante questo script. La previsione è stata effettuata in relazione a otto sequenze di test, menzionate in precedenza nell'articolo, utilizzando gli ultimi 100, 200 e 400 valori di ciascuna di queste sequenze.

N=100 N=200 N=400 EURRUR M1 0,980 1,000 0,968 EURRUR M30 0,959 0,992 0,981 EURUSD M1 0,995 0,981 0,981 EURUSD M30 1,023 0,985 0,999 USDJPY M1 1,004 0,976 0,989 USDJPY M30 0,993 0,987 0,988 XAUUSD M1 0,976 0,993 0,970 XAUUSD M30 0,973 0,985 0,999

Tabella 2. Errori di previsione stimati utilizzando RelMAE

Come si può vedere, le stime dell'errore di previsione sono vicine all'unità ma, nella maggior parte dei casi, la previsione per le sequenze date in questo modello è più accurata rispetto al metodo ingenuo.

10. L’Indicatore IndicatorES.mq5

L'indicatore AdditiveES_Test.mq5 basato sulla classe AdditiveES.mqh è stato menzionato in precedenza durante la revisione della classe. Tutti i parametri di livellamento in questo indicatore sono stati impostati manualmente.

Ora, dopo aver considerato il metodo che consente di ottimizzare i parametri del modello, possiamo creare un indicatore simile in cui i valori dei parametri ottimali e i valori iniziali saranno determinati automaticamente e sarà necessario impostare manualmente solo la lunghezza del campione processato. Detto questo, escluderemo tutti i calcoli relativi alla stagionalità.

Il codice sorgente della classe CIndiсatorES utilizzato nella creazione dell'indicatore è riportato di seguito.

//-----------------------------------------------------------------------------------
//                                                                   CIndicatorES.mqh
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//-----------------------------------------------------------------------------------
// Class CIndicatorES
//-----------------------------------------------------------------------------------
class CIndicatorES:public PowellsMethod
  {
protected:
  double Dat[];                                              // Input data
  int    Dlen;                                               // Data lenght
  double Par[5];                                             // Parameters
public:
  void   CIndicatorES(void)       { }
  void   CalcPar(double &dat[]);
  double GetPar(int n)            { if(n>=0||n<5)return(Par[n]); else return(0); }
private:
  virtual double func(const double &p[]);
  };
//-----------------------------------------------------------------------------------
// CalcPar
//-----------------------------------------------------------------------------------
void CIndicatorES::CalcPar(double &dat[])
  {

  Dlen=ArraySize(dat);
  ArrayResize(Dat,Dlen);
  ArrayCopy(Dat,dat);
 
  Par[0]=Dat[0];                                             // initial S
  Par[1]=0;                                                  // initial T
  Par[2]=0.5;                                                // initial Alpha
  Par[3]=0.5;                                                // initial Gamma
  Par[4]=0.5;                                                // initial Phi
  Optimize(Par);                                             // Powell's optimization
  }
//------------------------------------------------------------------------------------
// func
//------------------------------------------------------------------------------------
double CIndicatorES::func(const double &p[])
  {
  int i;
  double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt;
  
  s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1;
  if     (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;}           // Alpha   > 0.95
  else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;}           // Alpha   < 0.05
  if     (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;}           // Gamma   > 0.95
  else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;}           // Gamma   < 0.05
  if     (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; }           // Phi     > 1.0
  else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;}           // Phi     < 0.05
  sse=0; 
  for(i=0;i<Dlen;i++)
    {
    e=Dat[i]-(s+phi*t); sse+=e*e;
    ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae;
    }
  return(Dlen*MathLog(k1*k2*k3*sse));
  }
//------------------------------------------------------------------------------------

Questa classe contiene i metodi CalcPar e GetPar; il primo è progettato per il calcolo dei valori dei parametri ottimali del modello, il secondo è destinato all'accesso a tali valori. Inoltre, la classe CIndicatorES comprende la ridefinizione della funzione virtuale func().

Il codice sorgente dell'indicatore IndicatorES.mq5:

//-----------------------------------------------------------------------------------
//                                                                    IndicatorES.mq5
//                                                                      2011, victorg
//                                                                https://www.mql5.com
//-----------------------------------------------------------------------------------
#property copyright "2011, victorg"
#property link      "https://www.mql5.com"

#property indicator_chart_window
#property indicator_buffers 4
#property indicator_plots   4

#property indicator_label1  "History"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrDodgerBlue
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
#property indicator_label2  "Forecast"                 // Forecast
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrDarkOrange
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
#property indicator_label3  "ConfUp"                   // Confidence interval
#property indicator_type3   DRAW_LINE
#property indicator_color3  clrCrimson
#property indicator_style3  STYLE_DOT
#property indicator_width3  1
#property indicator_label4  "ConfDn"                   // Confidence interval
#property indicator_type4   DRAW_LINE
#property indicator_color4  clrCrimson
#property indicator_style4  STYLE_DOT
#property indicator_width4  1

input int nHist=80; // History bars, nHist>=24

#include  "CIndicatorES.mqh"
#define   NFORE 12

double    Hist[],Fore[],Conf1[],Conf2[];
double    Data[];
int       NDat;

CIndicatorES   Es;
//-----------------------------------------------------------------------------------
// Custom indicator initialization function
//-----------------------------------------------------------------------------------
int OnInit()
  {
  NDat=nHist; if(NDat<24)NDat=24;
  MqlRates rates[];
  CopyRates(NULL,0,0,NDat,rates);                   // Load missing data
  ArrayResize(Data,NDat);
    
  SetIndexBuffer(0,Hist,INDICATOR_DATA);
  PlotIndexSetString(0,PLOT_LABEL,"History");
  SetIndexBuffer(1,Fore,INDICATOR_DATA);
  PlotIndexSetString(1,PLOT_LABEL,"Forecast");
  PlotIndexSetInteger(1,PLOT_SHIFT,NFORE);
  SetIndexBuffer(2,Conf1,INDICATOR_DATA);            // Confidence interval
  PlotIndexSetString(2,PLOT_LABEL,"ConfUp");
  PlotIndexSetInteger(2,PLOT_SHIFT,NFORE);
  SetIndexBuffer(3,Conf2,INDICATOR_DATA);            // Confidence interval
  PlotIndexSetString(3,PLOT_LABEL,"ConfDN");
  PlotIndexSetInteger(3,PLOT_SHIFT,NFORE);
  IndicatorSetInteger(INDICATOR_DIGITS,_Digits);
  return(0);
  }
//-----------------------------------------------------------------------------------
// Custom indicator iteration function
//-----------------------------------------------------------------------------------
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int  &spread[])
  {
  int i,start;
  double s,t,alp,gam,phi,e,f,a,a1,a2,a3,var,ci;
  
  if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);}
  if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar
  start=rates_total-NDat;
//-----------------------
  PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat);
  PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE);
  PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE);
  PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE);
  
  for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data
  Es.CalcPar(Data);                                    // Optimization of parameters
  s=Es.GetPar(0); t=Es.GetPar(1); alp=Es.GetPar(2); gam=Es.GetPar(3); phi=Es.GetPar(4);
  f=(s+phi*t); var=0;
  for(i=0;i<NDat;i++)                                // History
    {
    e=Data[i]-f; var+=e*e;
    a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1;
    f=(s+phi*t); Hist[start+i]=f;
    }
  var/=(NDat-1); a1=1; a2=0; a3=1;
  for(i=rates_total-NFORE;i<rates_total;i++)
    {
    a1=a1*phi; a2+=a1;
    Fore[i]=s+a2*t;                                 // Forecast
    ci=1.96*MathSqrt(var*a3);                        // Confidence intervals
    a=alp*(1+a2*gam); a3+=a*a;
    Conf1[i]=Fore[i]+ci;
    Conf2[i]=Fore[i]-ci;
    }
  return(rates_total);
  }
//-----------------------------------------------------------------------------------

Con ogni nuova barra, l'indicatore trova i valori ottimali dei parametri del modello, effettua calcoli nel modello per un dato numero di barre NHist, costruisce una previsione e definisce i limiti di confidenza della previsione.

L'unico parametro dell'indicatore è la lunghezza della sequenza elaborata, il cui valore minimo è limitato a 24 barre. Tutti i calcoli nell'indicatore sono effettuati sulla base dei valori open[]. L'orizzonte di previsione è di 12 barre. Il codice dell'indicatore IndicatorES.mq5 e il file CIndicatorES.mqh si trovano alla fine dell'articolo nell'archivio Files.zip.

 

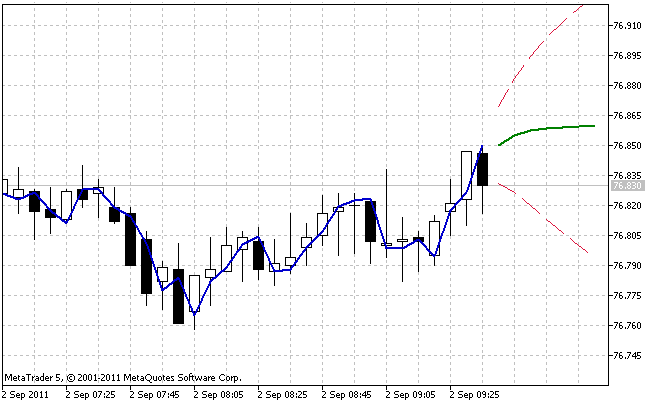
Figura 7. Risultato dell'operazione dell'indicatore IndicatorES.mq5

Un esempio del risultato dell'operazione dell'indicatore IndicatorES.mq5 è mostrato nella Figura 7. Nel corso del funzionamento dell'indicatore, l'intervallo di confidenza previsto al 95% assumerà valori corrispondenti ai valori dei parametri ottimali ottenuti dal modello. Più grandi sono i valori del parametro di livellamento, più veloce è l'aumento dell'intervallo di confidenza sull'orizzonte di previsione crescente.

Con un semplice miglioramento, l'indicatore IndicatorES.mq5 può essere utilizzato non solo per prevedere le quotazioni di valuta, ma anche per prevedere i valori di vari indicatori o dati pre-elaborati.

Conclusione

L'obiettivo principale dell'articolo era quello di permettere al lettore di familiarizzare con i modelli di livellamento esponenziale additivo utilizzati nelle previsioni. Pur dimostrandone l'utilizzo pratico, sono state affrontate anche alcune problematiche di accompagnamento. Tuttavia, i materiali forniti nell'articolo possono essere considerati semplicemente un'introduzione alla vasta gamma di problemi e soluzioni associati alla previsione.

Vorrei attirare la vostra attenzione sul fatto che le classi, le funzioni, gli script e gli indicatori forniti sono stati creati nel processo di scrittura dell'articolo e sono principalmente progettati per servire come esempi per i materiali dell'articolo. Pertanto non sono stati eseguiti test seri per la stabilità e gli errori. Inoltre, gli indicatori previsti dall'articolo devono essere considerati solo una dimostrazione dell'attuazione dei metodi coinvolti.

L'accuratezza previsionale dell'indicatore IndicatorES.mq5 introdotto nell'articolo può molto probabilmente essere leggermente migliorata utilizzando le modifiche del modello applicato che sarebbero più adeguate in termini di peculiarità delle quotazioni in esame. L'indicatore può essere amplificato anche da altri modelli. Ma questi problemi esulano dallo scopo di questo articolo.

In conclusione, va notato che i modelli di livellamento esponenziale possono in certi casi produrre previsioni della stessa accuratezza delle previsioni ottenute applicando modelli più complessi, dimostrando così ancora una volta che anche il modello più complesso non è sempre il migliore.

Fonti

1. Everette S. Gardner Jr. Exponential Smoothing: The State of the Art – Part II. June 3, 2005.
2. Rob J Hyndman. Forecasting Based on State Space Models for Exponential Smoothing. 29 August 2002.
3. Rob J Hyndman et al. Prediction Intervals for Exponential Smoothing Using Two New Classes of State Space Models. 30 January 2003.
4. Rob J Hyndman and Muhammad Akram. Some Nonlinear Exponential Smoothing Models Are Unstable. 17 January 2006.
5. Rob J Hyndman and Anne B Koehler. Another Look at Measures of Forecast Accuracy. 2 November 2005.
6. Yu. P. Lukashin. Adaptive Methods for Short-Term Forecasting of Time Series: Textbook. - М.: Finansy i Statistika, 2003.-416 pp.
7. D. Himmelblau. Applied Nonlinear Programming. М.: Mir, 1975.
8. Numerical Recipes in C. The Art of Scientific Computing. Second Edition. Cambridge University Press.