지수 평활을 이용한 시계열 예측
137
0
들어가며
현재 시계열의 과거 값 분석, 즉 일반적으로 기술 분석에 사용되는 원칙을 채택하는 방법에 기초한 잘 알려진 다양한 예측 방법이 다수 존재합니다. 이러한 방법의 주요 도구는 특정 시간 랙에서 식별된 시퀀스 특성이 한계를 벗어나는 외삽법 스케마입니다.
동시에 미래의 시퀀스 특성은 과거와 현재와 동일할 것으로 가정합니다. 예측 구간 내의 시퀀스 특성 변화 연구를 포함하는 더욱 복잡한 외삽법 스케마는 상대적으로 적게 선택됩니다.
외삽법에 기반한 것 중 가장 잘 알려진 예측 방법은 자기회귀누적이동평균 (autoregressive integrated moving average model, ARIMA)을 이용한 것일 수도 있습니다. ARIMA 방법의 인기는 통합 ARIMA 모델을 제안하고 개발한 Box와 Jenkins의 업적 덕분입니다. 물론 Box와 Jenkins가 도입한 모델 외에도 다른 모델이나 예측 방법은 있습니다.
이 문서는 단순 모델들만 다루기보다는 살짝 더 깊이 들어가 Box나 Jenkins의 저작이 등장하기 전에 Holt와 Brown에 의해 제안된 지수평활법을 간략히 다루어 볼 것입니다.
상대적으로 간단하고 깔끔한 수학적 도구를 사용하는 지수평활 모형이지만, 이 모델을 통한 예측은 ARIMA 모형을 사용하여 얻은 결과에 비슷한 수준의 결과를 낳는 경우가 잦습니다. 지수평활 모델들은 ARIMA 모델의 특별 케이스이니 딱히 놀랄만한 일은 아닙니다. 즉, 이 문서에서 다루게 될 각각의 지수평활 모형에는 대응되는 ARIMA 모형이 있습니다. 대응되는 모형은 이 문서에서 다루진 않을 것이며, 언급만 하고 넘어가게 될 것입니다.
어떠한 경우에도 예측은 각각에 맞춰진 접근법을 필요로 하며, 여러 절차를 수반한단 것은 널리 알려진 사실입니다..
예시:
- 손실값과 아웃라이어 판단을 위한 시계열 시퀀스 분석 이들 값에 대한 분석
- 트렌드와 타입의 식별 시퀀스 주기성의 판별
- 시퀀스 정상성의 확인
- 시퀀스 사전가공 분석 (로그 분석, 차별화, 등).
- 모델 선택
- 모델 패러미터 결정 선택한 모델을 기반으로 예측하기
- 모델 예측 정확성 분석
- 선택한 모델의 오류 분석
- 선택한 모델의 적정성을 결정하고 필요한 경우 모델의 교체 및 이전 항목으로 돌아갑니다.
효과적인 예측은 이것이 전부가 아닙니다.
모형 패러미터 결정과 예측 결과의 획득은 일반적인 예측 과정의 일부에 불과하다는 점을 강조하고 싶습니다. 하지만 문서 하나에서 예측과 관련된 모든 문제를 이런저런 방법으로 다루는 것은 불가능합니다.
따라서 이 문서에서는 지수평활 모형만 다룰 것이며, 사전에 처리되지 않은 통화 시세를 테스트 시퀀스로 사용할 것입니다. 그 과정에서 발생하는 이슈를 모두 무시할 수는 없으니, 모델 검토에 필요한 경우에만 언급될 것입니다.
1. 정상성
외삽적 적절성의 개념은 연구 대상의 미래가 과거와 현재와 동일할 것이라는 것을 암시합니다. 달리 말하면, 과정의 정상성을 논하게 됩니다. 정상 과정은 예측 관점에서 매우 매력적이지만, 실제 프로세스는 개발 과정에서 변경될 수 있기 때문에 현실에서는 존재하지 않습니다.
실제 공정은 시간이 지남에 따라 기대, 분산 및 분포가 현저하게 다를 수 있지만 특성이 매우 느리게 변화하는 프로세스는 고정 프로세스에 기인할 수 있습니다. 이 경우 "매우 느리게"는 것은 유한한 관측 간격 내의 공정 특성 변화가 매우 미미하여 그러한 변화가 무시될 수 있다는 것을 의미합니다.
사용 가능한 관측 구간(짧은 표본)이 짧을수록 공정 전체의 정상성에 대해 잘못된 결정을 내릴 확률이 높아집니다. 반면에, 우리가 단기예측을 위해 추후 계획하는 공정의 상태에 더 관심이 있다면, 표본크기의 감소가 경우에 따라서는 그러한 예측의 정확성을 높일 수 있습니다.
공정이 변경될 경우 관측치 구간 내에서 결정된 시퀀스 패라미터가 한계를 벗어나게 됩니다. 따라서 예측 구간이 길수록 시퀀스 특성의 변동성이 예측 오차에 미치는 영향이 강해집니다. 이러한 사실로 인해 단기 예측에서 그쳐야만 합니다. 예측 구간이 유의하게 감소하면 서서히 변화하는 결과 특성이 커다란 예측 오류를 초래하지 않을 것으로 예상할 수 있습니다.
또한 시퀀스 모수의 변동성으로 인해 모수가 구간 내에서 일정하게 유지되지 않았기 때문에 관측 구간으로 추정할 때 얻은 값이 평균화됩니다. 따라서 수집된 패러미터 값은 이 간격의 마지막 순간과 관련이 없지만 특정 평균을 반영합니다. 안타깝게도 이 불쾌한 현상을 완전히 제거하는 것은 불가능하지만 모형 모수 추정과 관련된 관측 구간(연구 구간)의 길이가 가능한 범위까지 줄어들면 줄어들 수 있습니다.
동시에 연구 간격은 무한정 단축될 수 없습니다. 극도로 감소하면 시퀀스 모수 추정의 정확도가 저하되기 때문입니다. 시퀀스 특성의 변동성과 관련된 오차의 효과와 연구 간격의 극단적인 감소로 인한 오차의 증가 사이의 절충점을 찾아야 합니다.
위의 모든 내용은 ARIMA 모형과 같이 정상 과정을 가정하기 때문에 지수 평활 모형을 사용한 예측에 완전히 적용됩니다. 그럼에도 불구하고, 단순하게 만들기 위해 이하에서 다룰 모든 시퀀스의 패러미터가 관찰 간격 내에 다양하지만 너무 느린 방식으로 이러한 변화를 무시할 수 있다고 가정하고 넘어갈 것입니다.
따라서 이 자료에서는 지수 평활 모형을 기반으로 특성이 서서히 변화하는 시퀀스의 단기 예측과 관련된 문제를 다룹니다. 이 경우 "단기예측"은 일반적으로 경제학에서 이해하는 바와 같이 1년 미만의 기간에 대한 예측이 아니라 1년 또는 2년 이상의 시간 간격에 대한 예측을 의미해야 한다.
2. 테스트 시퀀스
이 문서를 작성하면서, M1, M5, M30 그리고 H1 기간에 대한 EURRUR, EURUSD, USDJPY 및 XAUUSD의 시세가 사용되었습니다.. 각 세이브 파일은 1100 개의 "오픈" 값을 가지고 있습니다. 가장 "오래된" 값이 파일의 위쪽에 놓이고 가장 "최신" 값은 파일의 끝에 있습니다. 그 파일에 마지막으로 값이 추가된 시간이 파일이 생성된 시간입니다. 테스트 시퀀스를 포함한 파일들은 HistoryToCSV.mq5 스크립트를 통해 만들어졌습니다. 작성된 데이터 파일 및 스크립트는 Files.zip 아카이브의 문서 끝에 있습니다.
비록 저는 독자분들의 관심을 끌고 싶지만 앞에서 이미 언급했듯이, 저장된 시세는 사전가공 되지 않은 채 이 글에서 사용됩니다. 예를 들어 당일 EURRUR_H1 견적에는 12~13개의 막대가 포함되며 금요일 XAUUSD 견적에는 다른 요일에 비해 한 막대가 적게 포함됩니다. 이러한 예는 따옴표가 불규칙한 표본 추출 간격으로 생성된다는 것을 보여 줍니다. 이는 균일한 양자화 구간을 갖는 것을 제안하는 정확한 시간 시퀀스로 작업하도록 설계된 알고리즘에서는 일어나지 않는 일입니다.
누락된 시세 값을 외삽법을 사용하여 재현하더라도 주말 시세 부족에 관련한 대한 문제는 해결되지 않습니다. 이때문에 우리는 주말에 세계에서 일어나는 사건들이 평일이나 마찬가지로 세계 경제에 영향을 미친다고 가정하고 가게 됩니다. 혁명, 자연 행위, 세간의 이목을 끄는 스캔들, 정부 변화 등 이런 종류의 큰 사건들이 언제든지 일어날 수 있습니다. 토요일 이런 행사가 열린다면 평일에 일어났을 때보다 세계 시장에 미치는 영향력이 클 것 입니다.
주중 근무시간 동안 꽤나 자주 관찰되는 시세의 차이를 유발하는 것은 아마도 이러한 사건들일 것입니다. 아시다시피 외환시장(FOREX)가 문을 닫고 있어도 세상은 자기들만의 법칙에 의해 굴러갑니다. 기술 분석용으로 만들어내는 주말 시세의 값을 재현해야 하는지 여부와 그 값이 어떤 효과를 줄 수 있는지는 여전히 불확실합니다.
이러한 주제는 이 문서에서 다룰 범위를 벗어나지만, 적어도 주기적(계절적) 구성요소를 확인하는 측면에서, 얼핏 보기에는 공백이 없는 시퀀스가 분석에 더 적합한 것으로 볼 수도 있습니다.
추가 분석을 위한 데이터의 예비 준비는 몹시 중요합니다. 우리의 경우 시세가 터미널에 나타나는 방식은 일반적으로 기술 분석에 적합하지 않기 때문에 큰 문제입니다. 그러한 갭 관련 문제 외에도 많은 문제가 산재합니다.
예를 들어 시세를 작성할 때 고정 시점 값이 "오픈" 및 "클로즈" 값으로 지정됩니다. 이 값들은 선택한 타임프레임 차트의 선택한 시간이 아니라 틱 형성 시간에 호응하게되는데, 이런 케이스 자체는 상당히 드문 편입니다.
표본 추출 정리를 완전히 무시하는 다른 예를 볼 수 있습니다. 1분 간격 이내에서도 표본 추출 속도가 위의 정리를 만족한다고 보장할 수 없기 때문입니다(다른 간격은 말할 것도 없고 더 큰 간격). 또한, 일부 경우에는 인용구 값에 중첩될 수 있는 변수 스프레드의 존재에 유의해야 합니다.
그러나 이러한 문제는 이 문서가 다룰 주제에서 벗어나니 주요 주제로 돌아가도록 하겠습니다.
3. 지수 평활
우선 가장 간단한 모델을 살펴 봅시다.
,
각 지표 해설
- X(t) – (시뮬레이션) 연구중인 프로세스
- L(t) – 변수 프로세스 레벨,
- r(t)– 0 평균 랜덤 변수 .
여기에서 볼 수 있 듯, 이 모델은 두 성분의 합을 포함합니다. 프로세스 레벨 L(t)를 처리하려고 시도해볼 것입니다.
랜덤 시퀀스의 평균화는 분산 감소, 즉 평균으로부터의 편차의 범위를 줄일 수 있습니다. 따라서 단순 모형에 의해 설명된 프로세스가 평균화(평활화)에 노출되면 랜덤 성분 r(t)를 완전히 제거하지 못할 수 있다고 가정할 수 있지만, 최소한 상당히 약화시켜 목표 수준 L(t).를 선택할 수 있습니다.
이를 위해 단순 지수 평활(simple exponential smoothing, SES)을 사용합니다.
이 잘 알려진 공식에서 평활도는 0부터 1까지 설정할 수 있는 알파 계수로 정의됩니다. 알파를 0으로 설정하면 입력 시퀀스 X의 새 값은 평활 결과에 전혀 영향을 미치지 않습니다. 임의의 시점에 대한 평활 결과는 상수 값이 됩니다.
따라서 이와 같은 극단적인 경우 불필요한 랜덤 성분은 완전히 억제되지만 고려 중인 프로세스 레벨은 수평한 선 수준으로 평활됩니다. 알파 계수가 1로 설정된 경우 입력 시퀀스는 평활화의 영향을 전혀 받지 않습니다. 현재 연구 대상이 되는 레벨 L(t) 이 왜곡되지 않으며 랜덤 구성 요소도 억제되지 않습니다.
알파값을 선택할 때 상충되는 요구사항을 동시에 만족시켜야 한다는 것이 명확합니다. 한편, 랜덤 성분 r(t)를 효과적으로 억제하기 위해 알파 값은 0에 가까워야 합니다. 반면 주의를 기울여서 관측중인 L(t)성분이 왜곡되지 않도록 알파 값을 통일성에 가깝게 설정하는 것이 좋습니다. 최적의 알파값을 얻기 위해서는 그러한 값을 최적화할 수 있는 기준을 파악해야 합니다.
이러한 기준을 결정할 때 이 문서에서는 시퀀스의 평활화뿐만 아니라 예측에 대해서도 다룹니다.
이 경우 단순 지수 평활 모형과 관련하여 주어진 시간에 얻은 값을 
앞의 단계 수에 대한 예측값으로 고려하는 것이 일반적입니다.
은 t 시간 시점에서 m 단계 다음 예측
따라서 t 시간의 결과값 예측은 이전 단계에서 이루어진 한 단계 앞선 예측이 될 것입니다.
이 경우 알파 계수 값의 최적화를 위한 기준으로 1단계 선행 예측 오류를 사용할 수 있습니다.
따라서 전체 표본에 대한 이러한 오차의 제곱합을 최소화하여 주어진 순서에 대한 알파 계수의 최적 값을 결정할 수 있습니다. 물론 가장 좋은 알파 값은 오차의 제곱합이 최소가 되는 값입니다.
그림 1은 시험 시퀀스 USDJPY M1의 파편에 대한 1단계 선행 예측 오차의 제곱합 대 알파 계수 값의 그림을 보여줍니다.
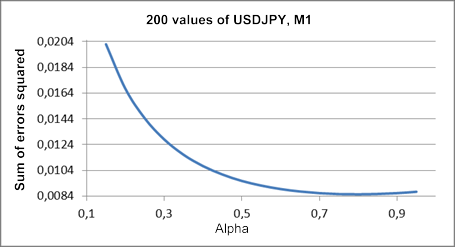
1번 그림. 단순 지수 평활
결과 그림의 최소값은 거의 식별되지 않으며 약 0.8의 알파 값에 가깝습니다. 그러나 이러한 그림은 단순 지수 평활과 관련하여 항상 그렇지는 않습니다. 이 문서에 사용된 테스트 시퀀스에 대한 최적의 알파 값을 얻으려고 시도할 때에, 통일성을 갖추지 못한 그림을 얻을 때가 제대로 된 그림을 얻을 때보다 많습니다.
높은 값의 평활화 계수는 단순 모델이 테스트 시퀀스(시세)를 설명하는 데 적합하지 않음을 나타냅니다. 이는 프로세스 레벨 L(t) 의 변화가 너무 빠르거나 프로세스 내에 트렌드가 존재하는 경우 둘 중 하나입니다.
한가지 구성 요소를 추가하여 모델을 조금 더 복잡하게 해봅시다.
,
각 지표 해설
- X(t) - (시뮬레이션) 현재 확인중 프로세스;
- L(t) - 프로세스 레벨 변수;
- T(t) - 선형 트렌드;
- r(t) - 0 평균 랜덤 변수
선형 회귀 계수는 시퀀스의 이중 평활을 통해 확인할 수 있습니다.
이러한 방법으로 얻은 계수 a1과 a2의 경우 t의 m단계 선행 예측은 다음과 같습니다.
위의 공식에서는 첫 번째 및 반복 평활에 대해 동일한 알파 계수가 사용됩니다. 이 모형을 선형 성장의 추가적인 단일 패러미터 모델이라고 합니다.
단순 모델과 선형 성장 모델의 차이를 보여드리겠습니다.
오랜 시간 동안 연구 대상 프로세스가 상수 성분을 나타냈다고 가정합니다. 즉, 선형 추세가 차트에 직선 수평선으로 나타나다가 어느 시점부터 선형트렌드가 나타나기 시작한 것입니다. 위에서 언급한 모델을 사용하여 이루어진 이 프로세스에 대한 예측은 그림 2에 나와 있습니다.
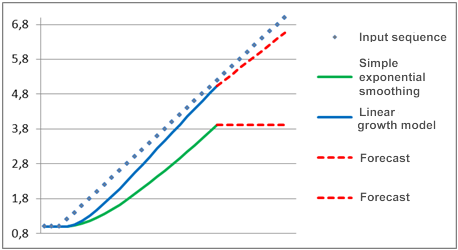
2번 그림. 모델 비교
보다시피 단순 지수 평활 모델은 선형적으로 변화하는 입력 시퀀스 뒤에 있는 것이 눈에 띄며 이 모델을 사용하여 얻은 예측 값은 실제하고 상당히 차이가 있습니다. 선형 성장 모델을 사용하면 매우 다른 패턴을 볼 수 있습니다. 트렌드가 나타나면 이 모델은 마치 선형적으로 변화하는 시퀀스를 추론해내려 것처럼 보이며 예측은 입력값의 변화 방향과 가깝습니다.
주어진 예제에서 평활 계수가 더 높으면 선형 성장 모형이 지정된 시간 동안 입력 신호에 "도달"할 수 있으며 예측은 입력 순서와 거의 일치합니다.
Despite the fact that the linear growth model in the steady state gives good results in the presence of a linear trend, it is easy to see that it takes a certain time for it to "catch up" with the trend. 따라서 추세 방향이 자주 바뀌면 모델과 입력 시퀀스 사이에 항상 간격이 있게 됩니다. 또한 추세가 비선형적으로 증가하지만 대신 제곱법을 따르면 선형 성장 모델이 이에 "도달"할 수 없습니다. 그러나 이러한 단점에도 불구하고 이 모델은 선형 추세가 있는 경우 단순 지수 평활 모델보다 더 유용합니다.
앞에서 말했듯이 우리가 사용한 것은 단일 패러미터 선형 성장 모델입니다. 테스트 시퀀스 USDJPY M1의 부분에 대한 알파 패러미터의 최적 값을 찾기 위해 1단계 선행 예측 오차 대 알파 계수 값의 제곱합에 대한 그래프를 작성합니다.
그림 1과 동일한 시퀀스 조각을 기초로 작성된 이 플롯은 그림 3에 표시됩니다.
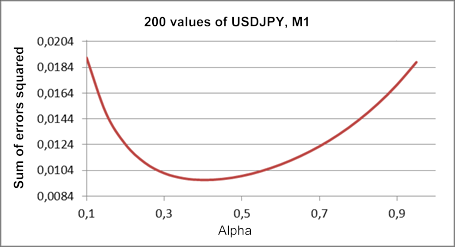
3번 그림. 선형 성장 모델
그림 1의 결과와 비교했을 때, 이 경우 알파 계수의 최적값은 약 0.4로 감소했습니다. 이론적으로 값이 다를 수 있지만 이 모델에서는 첫 번째와 두 번째 평활의 계수가 동일합니다. 서로 다른 두 평활 계수를 갖는 선형 성장 모형이 추가로 검토됩니다.
우리가 살펴본 지수 평활 모델들과 같은 것이 MetaTrader 5에 인디케이터의 형태로 존재합니다. 잘 알려진 EMA와 DEMA가 바로 그것들인데, 시퀀스 값의 평활화용으로 설계되어있습니다.
DEMA 지표를 사용할 경우, 1단계 예측 값 대신 a1 계수에 해당하는 값이 표시됩니다. 이 경우 a2 계수(위 선형 성장 모형에 대한 공식 참조)가 계산되거나 사용되지 않습니다. 또한 평활 계수는 동등한 기간 n으로 계산됩니다.
예를 들어 0.8인 알파는 n이 약 2이고, 알파가 0.4인 경우 n은 4입니다.
4. 초기 값
앞서 언급한 바와 같이, 지수 평활을 적용할 때 평활 계수 값은 한 가지 또는 다른 방법으로 구해야 합니다. 그러나 이것만으로는 부족해보입니다. 지수 평활에서는 현재 값이 이전 값을 기준으로 계산되므로 시간 0에 해당 값이 아직 존재하지 않는 상황이 발생합니다. 다시 말해 선형 성장 모델의 S나 S1혹은 S2의 초기 값이 시간이 0일 때 어떻게든 계산될 것이라는 의미입니다.
초기 값을 얻어오는 것은이 언제나 쉬운 것은 아닙니다. 만약 MetaTrader 5에서 따옴표를 사용하는 경우처럼 매우 긴 히스토리를 사용할 수 있는 경우, 초기 값이 부정확하게 결정되면 지수 평활 곡선은 초기 오차를 수정하여 현재 점에 의해 안정화되는 시간을 가지게 됩니다. 이를 위해서는 평활화 계수 값에 따라 약 10-200(때로는 그 이상)의 기간이 필요합니다.
이 경우 초기 값을 대략적으로 추정하여 목표 기간 200-300 기간 전에 지수 평활 프로세스를 시작하는 것으로 충분합니다. 만약 샘플에 오직 100 값밖에 없다면 점점 어려워집니다.
초기 값을 고르는 방법에는 여러 추천이 있습니다. 예를 들어, 단순 지수 평활의 초기 값은 시퀀스의 첫 번째 원소와 동일하거나 랜덤 특이치를 평활화하는 보기를 사용하여 시퀀스의 3~4개 초기 원소의 평균으로 계산할 수 있습니다. 선형 성장 모델의 초기값 S1 그리고 S2예측 곡선의 초기 수준은 시퀀스의 첫 번째 요소와 동일해야 하며 선형 경향의 기울기는 0이어야 한다는 가정에 기반을 두고 결정될 수 있습니다.
초기 값의 선택과 관련하여 여러 소스에서 많은 추천을 찾을 수 있지만 평활 알고리즘의 초기 단계에서 눈에 띄는 오차가 없을 것이라고 보장할 수 있는 방법은 전무합니다. 특히 안정적인 상태를 얻기 위해 많은 기간이 필요한 경우 낮은 값 평활 계수를 사용할 때 두드러집니다.
따라서 초기 값의 선택과 관련된 문제의 영향을 최소화하기 위해(특히 짧은 시퀀스의 경우), 최소 예측 오차를 발생시키는 그러한 값의 검색을 포함하는 방법을 사용하기도 합니다. 전체 시퀀스에 걸쳐 작은 단위로 변화하는 초기 값에 대한 예측 오차를 계산하는 문제입니다.
가능한 초기값의 모든 조합 범위 내에서 오차를 계산한 후 가장 적절한 변형을 선택할 수 있습니다. 그러나 이 방법은 많은 계산이 필요하며 직접적인 형태로는 거의 사용되지 않습니다.
설명된 문제는 최적화 또는 최소 다변수 함수 값 검색과 관련이 있습니다. 이러한 문제는 필요한 계산 범위를 상당히 줄이기 위해 개발된 다양한 알고리즘을 사용하여 해결할 수 있습니다. 평활화 패러미터의 최적화 문제와 예측의 초기 값에 대해서는 잠시 후에 다시 설명하겠습니다.
5. 예측 정확성 평가
예측 절차와 모델 초기 값 또는 패러미터를 선택하면 예측 정확도를 추정하는 데에 문제가 발생합니다. 정확도의 평가는 두 가지 다른 모델을 비교하거나 얻은 예측의 일관성을 결정할 때도 중요합니다. 예측 정확도 평가에는 잘 알려진 추정치가 많지만, 이 추정치 중 하나를 계산하려면 모든 단계에서 예측 오차를 알아야 합니다.
이미 언급한 바와 같이 t의 1단계 선행 예측 오류는 다음과 같습니다.
각 지표 해설
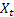– t 시간에서의 입력 시퀀스 값;
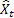– 이전 스텝에서 시행한 t 시점의 예측.
가장 일반적인 예측 정확도 추정법은 평균 제곱 오차(mean squared error, MSE)일 것입니다.
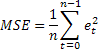
n은 시퀀스 내의 요소의 수.
때때로 큰 값의 단일 오류에 극도로 민감하다는 것은 MSE의 단점으로 지적되기도 합니다. MSE를 계산할 때 오차값이 제곱된 것에서 유래합니다. 대안으로, 이 경우에는 평균 절대 오차(mean absolute error, MAE)를 사용하는 것이 좋습니다.
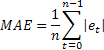
여기서 오차 제곱은 오차의 절대값으로 대체됩니다. MAE를 사용하여 얻은 추정치가 더 안정적이라고 가정합니다.
두 추정치는 예를 들어 서로 다른 모델 패러미터 또는 서로 다른 모델을 사용하여 동일한 시퀀스의 예측 정확성을 평가하는 데 매우 적절하지만, 서로 다른 시퀀스에서 받은 예측 결과의 비교에는 거의 유용하지 않은 것으로 보입니다.
이 예측의 값들은 예측 결과의 퀄리티가 어떤지에 대해서 아무 것도 알려주지 않습니다.. 예를 들어, 0.03이나 다른 MAE 값을 얻었을 때 이 값이 좋은지 나쁜지 알 수가 없다는 것입니다.
여러 시퀀스의 예측 정확성을 평가하기 위하여 우리는 상대 예측 RelMSE 및 RelMAE:를 사용할 수 있습니다.
구한 예측 정확도 추정치를 예측의 검정 방법을 사용하여 구한 각각의 추정치로 나눕니다. 테스트 방법으로는 프로세스의 미래가치가 현재가치와 같을 것이라는 이른바 순진한 방법을 사용하는 것이 좋습니다.
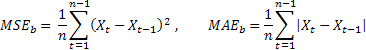
만약 예측오차의 평균이 순진한 방법을 사용하여 얻은 오류의 값과 같다면 상대적인 추정값은 1이 될 것입니다. 상대 추정값이 1보다 작다면 평균적으로 예측오차값이 순진한 방법보다 작다는 것을 의미합니다. 즉, 예측 결과의 정확도가 순진한 방법의 정확성보다 우선합니다. 그리고 그 반대로 상대적 추정치가 둘 이상인 경우, 예측 결과의 정확도는 평균적으로 순진한 예측 방법보다 낮습니다.
또한 이러한 추정치는 두 단계 이상의 예측 정확성을 평가하는 데에도 적합합니다. 계산의 한 단계 예측 오류는 앞으로 적절한 단계 수에 대한 예측 오류 값으로 대체하면 됩니다.
예를 들어, 아래 표에는 선형 성장의 단일 패러미터 모델에서 RelMAE를 사용하여 추정된 한 단계 앞선 예측 오차가 포함되어 있습니다. 오차는 각 테스트 시퀀스의 마지막 200개 값을 사용하여 계산되었습니다.
|
테이블 1. RelMAE를 이용하여 이루어진 1단계 선행 예측 오류 측정
RelMAE 추정치를 사용하면 각기 다른 시퀀스를 예측할 때 선택한 방법의 효과를 비교할 수 있습니다. 테이블 1의 결과에서 알 수 있듯이, 우리의 예측은 순진한 방법보다 정확하지 않았습니다. 모든 RelMAE 값은 1 이상입니다.
6. 가산 모델
이 문서 앞쪽에서 프로세스 레벨, 선형 트렌드 및 랜덤 변수의 합으로 구성된 모델을 보여드렸습니다. 이 문서에서 검토한 모델 목록을 위의 구성 요소 외에 사이클적이거나 시즌적인 구성 요소를 포함하는 다른 모델을 추가하여 확장할 것입니다.
모든 가치 성분을 합으로 구성하는 지수 평활 모델을 가산 모델이라고 합니다. 이러한 모델 외에도 하나, 더 많은 또는 모든 구성요소가 하나의 제품으로 구성된 복합 모델이 있습니다. 가산 모델 그룹에 대한 검토를 진행하겠습니다.
1단계 이전에서 예측하는 것의 오류는 이 문서에서 반복적으로 언급드렸습니다. 이 오차는 지수 평활을 기반으로 하는 예측 어플리케이션이라면 무조건 계산해야만 합니다. 예측 오차의 값을 알고 있으면 위에서 소개한 지수 평활 모델에 대한 공식은 다소 다른 형식(오차 수정 형식)으로 표시될 수 있습니다.
우리가 사례에서 사용할 모델 표현의 형태에는 이전에 얻은 값에 부분적으로 또는 완전히 추가된 표현식에 오류가 포함되어 있습니다. 이런 표현을 가산 오류 모델이라고 합니다. 지수 평활 모델은 곱셈 오차 형태로도 표현될 수 있지만 이 문서에서는 사용하지 않을 것입니다.
가산 지수 평활 모델을 살펴보겠습니다.
단순 지수 평활:
대응 모델 – ARIMA(0,1,1):
가산 선형 성장 모델:
앞서 소개된 단일 패러미터 선형 성장 모델과는 달리 여기서는 두 가지 평활화 패러미터가 사용됩니다.
대응 모델 – ARIMA(0,2,2): 
감쇠가 적용된 선형 성장 모델
이러한 감쇠의 의미는 감쇠 계수의 값에 따라 이후의 예측 단계마다 트렌드 기울기가 후퇴한다는 것입니다. 이 효과는 4번 그림에 나타나 있습니다.
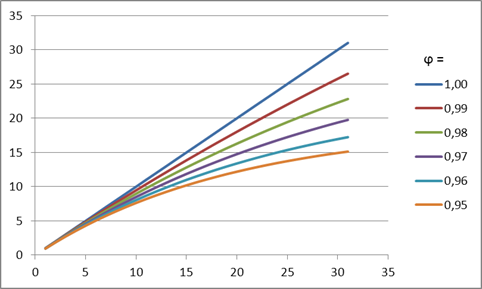
4번 그림. 감쇠 계수 효과
그림에서 볼 수 있듯이, 예측을 할 때, 감쇠 계수의 값이 감소하면 추세가 더 빨리 강해지므로 선형 성장은 점점 더 위축될 것입니다.
대응 모델 - ARIMA(1,1,2): 
이 세 가지 모델에 시즌성 성분을 합산하여 세 가지 모델을 더 받게 됩니다.
시즌성을 가산한 단순 모델:
시즌성을 가산한 선형 성장 모델:
시즌성을 가산하고 감쇠를 적용한 선형 성장 모델:
시즌성이 있는 모델에 대응되는 ARIMA 모델도 있지만 실질적으로 의미가 없으니 지금은 그냥 생략하고 넘어가겠습니다.
공식에 사용된 표현들은 이하와 같습니다:
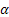– 시퀀스 레벨에 대한 평활 패러미터, [0:1];
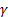– 트렌드에 대한 평활 패러미터 [0:1];
– 시즌성 인덱스에 대한 평활 패러미터, [0:1];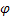
– 감쇠 패러미터, [0:1];
– 
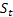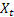가 관측된 뒤 t 시간 지난 때 계산된 시퀀스의 평활 레벨;
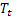– t 시간에 계산된 평활 가산 트렌드;
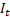– t 시간에 계산된 평활 시즌성 인덱스;
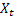– t 시간의 시퀀스 값;- m – 예측이 이루어진 단계와 현 단계의 차;
- p – 시즌성 사이클 내의 기간 수;
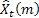– t 시간과 그로부터 m 단계 앞에서 이루어진 예상;
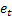– t 시간에 이루어진 1 단계 앞 예상 오류, 
.
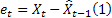제공된 마지막 모델의 공식에 고려 중인 6가지 변형이 모두 포함되어 있음을 쉽게 알 수 있습니다.
감쇠 및 가산된 시즌성이 포함된 선형 성장 모델의 공식에서 다음 식을 사용합니다.
,
이 시즌성은 예측에서는 무시될 것입니다. 추가적으로 
일 때, 선형 성장 모델이 생산되며 
일 때, 감쇠가 적용된 선형 성장 모델을 얻게됩니다.
단순 지수 평활 모델은 
에 대응할 것입니다.
시즌성을 포함하는 모델을 채택할 때 시즌 지수 값의 초기화에 이 데이터를 추가로 사용하기 위해 먼저 사용 가능한 방법을 사용하여 사이클 내의 기간을 결정해야 합니다.
짧은 시간 간격에 걸쳐 예측이 이루어지는 이 경우에 사용되는 테스트 시퀀스의 일부분에서 안정적인 사이클을 감지하지 못했습니다. 따라서 이 글에서는 시즌성과 관련된 특성을 설명하거나 관련 사례를 제시하지 않을 것입니다.
검토 중인 모델에 대한 확률 예측 구간을 결정하기 위해 참조자료 [3]에서 발견된 해석적 파생 모델을 사용할 것입니다. 전체 표본 크기 n에 대해 계산된 1단계 선행 예측 오차의 제곱합 평균이 이러한 오차의 추정 분산으로 사용됩니다.
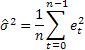
그러면 고려 중인 모델의 2 혹은 그 이상 단계 선행 예측에 대한 예측의 추정 분산을 결정할 때 다음 식이 참이 될 것입니다.
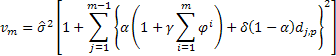
는 만약 j 나누기 p의 나머지가 0이라면 1, 아니라면
0입니다.
모든 단계 m에 대한 예측의 추정된 분산을 계산하면 95% 예측 구간의 한계를 확인할 수 있습니다.
이러한 예측 구간을 예측 신뢰도 구간으로 명명하였습니다.
지수 평활 모델에 대해 제공된 식을 MQL5로 작성된 클래스에서 구현하겠습니다.
7. AdditiveES 클래스 구현
클래스의 구현에는 선형 성장 모델에 대한 표현식과 감쇠 및 가산 시즌성의 사용이 포함되었습니다.
앞에서 언급한 바와 같이, 다른 모델들은 적절한 패러미터 선택에 의해 도출될 수 있습니다.
//----------------------------------------------------------------------------------- // AdditiveES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //----------------------------------------------------------------------------------- // Forecasting. Exponential smoothing. Additive models. // References: // 1. Everette S. Gardner Jr. Exponential smoothing: The state of the art – Part II. // June 3, 2005. // 2. Rob J Hyndman. Forecasting based on state space models for exponential // smoothing. 29 August 2002. // 3. Rob J Hyndman et al. Prediction intervals for exponential smoothing // using two new classes of state space models. 30 January 2003. //----------------------------------------------------------------------------------- class AdditiveES:public CObject { protected: double Alpha; // Smoothed parameter for the level of the series double Gamma; // Smoothed parameter for the trend double Phi; // Autoregressive or damping parameter double Delta; // Smoothed parameter for seasonal indices int nSes; // Number of periods in the seasonal cycle double S; // Smoothed level of the series, computed after last Y is observed double T; // Smoothed additive trend double Ises[]; // Smoothed seasonal indices int p_Ises; // Pointer for Ises[] shift register double F; // Forecast for 1 period ahead from origin t public: AdditiveES(); double Init(double s,double t,double alpha=1,double gamma=0, double phi=1,double delta=0,int nses=1); double GetS() { return(S); } double GetT() { return(T); } double GetF() { return(F); } double GetIs(int m); void IniIs(int m,double is); // Initialization of smoothed seasonal indices double NewY(double y); // Next calculating step double Fcast(int m); // m-step ahead forecast double VarCoefficient(int m); // Coefficient for calculating prediction intervals }; //----------------------------------------------------------------------------------- // Constructor //----------------------------------------------------------------------------------- void AdditiveES::AdditiveES() { Alpha=0.5; Gamma=0; Delta=0; Phi=1; nSes=1; ArrayResize(Ises,nSes); ArrayInitialize(Ises,0); p_Ises=0; S=0; T=0; } //----------------------------------------------------------------------------------- // Initialization //----------------------------------------------------------------------------------- double AdditiveES::Init(double s,double t,double alpha=1,double gamma=0, double phi=1,double delta=0,int nses=1) { S=s; T=t; Alpha=alpha; if(Alpha<0)Alpha=0; if(Alpha>1)Alpha=1; Gamma=gamma; if(Gamma<0)Gamma=0; if(Gamma>1)Gamma=1; Phi=phi; if(Phi<0)Phi=0; if(Phi>1)Phi=1; Delta=delta; if(Delta<0)Delta=0; if(Delta>1)Delta=1; nSes=nses; if(nSes<1)nSes=1; ArrayResize(Ises,nSes); ArrayInitialize(Ises,0); p_Ises=0; F=S+Phi*T; return(F); } //----------------------------------------------------------------------------------- // Calculations for the new Y //----------------------------------------------------------------------------------- double AdditiveES::NewY(double y) { double e; e=y-F; S=S+Phi*T+Alpha*e; T=Phi*T+Alpha*Gamma*e; Ises[p_Ises]=Ises[p_Ises]+Delta*(1-Alpha)*e; p_Ises++; if(p_Ises>=nSes)p_Ises=0; F=S+Phi*T+GetIs(0); return(F); } //----------------------------------------------------------------------------------- // Return smoothed seasonal index //----------------------------------------------------------------------------------- double AdditiveES::GetIs(int m) { if(m<0)m=0; int i=(int)MathMod(m+p_Ises,nSes); return(Ises[i]); } //----------------------------------------------------------------------------------- // Initialization of smoothed seasonal indices //----------------------------------------------------------------------------------- void AdditiveES::IniIs(int m,double is) { if(m<0)m=0; if(m<nSes) { int i=(int)MathMod(m+p_Ises,nSes); Ises[i]=is; } } //----------------------------------------------------------------------------------- // m-step-ahead forecast //----------------------------------------------------------------------------------- double AdditiveES::Fcast(int m) { int i,h; double v,v1; if(m<1)h=1; else h=m; v1=1; v=0; for(i=0;i<h;i++){v1=v1*Phi; v+=v1;} return(S+v*T+GetIs(h)); } //----------------------------------------------------------------------------------- // Coefficient for calculating prediction intervals //----------------------------------------------------------------------------------- double AdditiveES::VarCoefficient(int m) { int i,h; double v,v1,a,sum,k; if(m<1)h=1; else h=m; if(h==1)return(1); v=0; v1=1; sum=0; for(i=1;i<h;i++) { v1=v1*Phi; v+=v1; if((int)MathMod(i,nSes)==0)k=1; else k=0; a=Alpha*(1+v*Gamma)+k*Delta*(1-Alpha); sum+=a*a; } return(1+sum); } //-----------------------------------------------------------------------------------
AdditiveES 클래스의 메소드들에 대하여 간략하게 리뷰해봅시다.
Init 메소드
입력 패러미터
- double s - 평활 레벨의 초기 값 세팅；
- double t - 평활 트렌드의 초기 값 세팅；
- double alpha=1 - 시퀀스 레벨 평활 패러미터 세팅；
- double gamma=0 - sets the smoothing parameter for the trend；
- double phi=1 - 감쇠 패러미터 세팅；
- double delta=0 - 시즌성 인덱스 평활 패러미터 세팅；
- int nses=1 - 시즌성 사이클 내 기간의 숫자를 설정.
반환값:
- 설정된 초기값들을 기반으로 1단계 선행 예측 반환
Init 메소드가 제일 먼저 호출됩니다. 이는 평활 패러미터 및 기타 초기 값들을 세팅하는데에 필수적입니다. Init 메소드는 시즌성 인덱스를 임의 값으로 초기화하지 않습니다. 이 메소드을 호출할 때 시즌성 인덱스는 항상 0으로 설정됩니다.
IniIs 메소드
입력 패러미터
- Int m - 시즌성 인덱스 번호;
- double is - 시즌성 인덱스 번호 m의 값을 설정.
반환값:
- None
IniIs(...) 메소드는 시즌성 인덱스의 초기 값이 0이 아닌 다른 값이어야할 때 호출됩니다. 시즌성 인덱스는 Init(...) 메소드를 호출한 직후에 호출되어야합니다.
NewY 메소드
입력 패러미터
- double y – 입력 시퀀스의 새 값
반환값:
- 시퀀스의 새 값을 기반으로 계산된 1단계 선행 예측 반환
이 메소드는 입력 시퀀스의 새 값을 입력할 때마다 한 단계 앞서 예측값을 계산하기 위해 고안되었습니다 이 메소드는 Init 혹은 필요한 경우에 한해 IniIs 메소드에 의한 클래스 초기화 후에 호출되어야합니다.
Fcast 메소드
입력 패러미터
- int m – 예측 평선 1,2,3,… 기간;
반환값:
- m단계 선행 예측 값.
이 메소드는 평활 프로세스의 상태에 영향을 주지 않은 채 예측 값을 계산합니다. 이 메소드는 흔히 NewY 메소드 뒤에 호출됩니다.
VarCoefficient 메소드
입력 패러미터
- int m – 예측 평선 1,2,3,… 기간;
반환값:
- 이 메소드는 예측 분산 계산용 계수 값을 반환합니다.
이 계수 값은 m단계 선행 예측의 분산이 1단계 선행 예측의 분산과 비교하여 증가하는 것을 나타냅니다.
GetS, GetT, GetF, GetIs 메소드들
이 메소드들은 클래스 내 보호된 변수에의 액세스를 제공합니다. GetS, GetT 및 GetF는 평활된 레벨, 평활된 트렌드, 그리고 1단계 선행 예측 값을 각각 반환합니다. GetIs 메소드는 시즌성 인덱스에 접속할 수 있게 해주며, 인덱스 번호 m가 입력 패러미터로 사용되어야합니다.
우리가 여태까지 검토해본 것 중에서 가장 복잡한 모델은 AdditiveES 클래스가 생성된 기반인 가산된 시즌성과 감쇠가 적용된 선형 성장 모델입니다. 따라서 매우 합리적인 질문이 제시됩니다. 즉, 나머지 모델 중 더 단순한 모델이 필요한 것은 무엇일까요?
더 복잡한 모델이 더 단순한 모델보다 분명한 이점을 가져야 한다는 사실에도 불구하고, 꼭 언제나 그런 것은 아닙니다. 패러미터가 적은 단순한 모델은 대부분의 경우 예측 오차의 변동이 적어지기에 더 안정적으로 운영되기 때문입니다. 이 사실은 가장 단순한 모델에서 가장 복잡한 모델에 이르기까지 사용 가능한 모든 모델의 동시 병렬 연산에 기초한 예측 알고리즘을 만드는 데 사용됩니다.
시퀀스가 완전히 처리되면 패러미터의 수(예를 들면, 복잡도)에서 가장 낮은 오차를 나타내는 예측 모델이 선택됩니다. 이 목적으로 만들어진 기준이 여러개 있습니다. 예를 하나 들면 Akaike’s Information Criterion (AIC)이 있습니다. 가장 안정적인 예측을 할 것으로 예상되는 모델이 선택될 것입니다.
AdditiveES 클래스의 시연을 위해서 모든 평활 패러미터들은 수동으로 세팅된 후 간단한 인디케이터를 생성했습니다.
AdditiveES_Test.mq5 인디케이터의 소스 코드는 아래에 첨부되어 있습니다.
//----------------------------------------------------------------------------------- // AdditiveES_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" // Forecast #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "PInterval+" // Prediction interval #property indicator_type3 DRAW_LINE #property indicator_color3 clrCadetBlue #property indicator_style3 STYLE_SOLID #property indicator_width3 1 #property indicator_label4 "PInterval-" // Prediction interval #property indicator_type4 DRAW_LINE #property indicator_color4 clrCadetBlue #property indicator_style4 STYLE_SOLID #property indicator_width4 1 double HIST[]; double FORE[]; double PINT1[]; double PINT2[]; input double Alpha=0.2; // Smoothed parameter for the level input double Gamma=0.2; // Smoothed parameter for the trend input double Phi=0.8; // Damping parameter input double Delta=0; // Smoothed parameter for seasonal indices input int nSes=1; // Number of periods in the seasonal cycle input int nHist=250; // History bars, nHist>=100 input int nTest=150; // Test interval, 50<=nTest<nHist input int nFore=12; // Forecasting horizon, nFore>=2 #include "AdditiveES.mqh" AdditiveES fc; int NHist; // history bars int NFore; // forecasting horizon int NTest; // test interval double ALPH; // alpha double GAMM; // gamma double PHI; // phi double DELT; // delta int nSES; // Number of periods in the seasonal cycle //----------------------------------------------------------------------------------- // Custom indicator initialization function //----------------------------------------------------------------------------------- int OnInit() { NHist=nHist; if(NHist<100)NHist=100; NFore=nFore; if(NFore<2)NFore=2; NTest=nTest; if(NTest>NHist)NTest=NHist; if(NTest<50)NTest=50; ALPH=Alpha; if(ALPH<0)ALPH=0; if(ALPH>1)ALPH=1; GAMM=Gamma; if(GAMM<0)GAMM=0; if(GAMM>1)GAMM=1; PHI=Phi; if(PHI<0)PHI=0; if(PHI>1)PHI=1; DELT=Delta; if(DELT<0)DELT=0; if(DELT>1)DELT=1; nSES=nSes; if(nSES<1)nSES=1; MqlRates rates[]; CopyRates(NULL,0,0,NHist,rates); // Load missing data SetIndexBuffer(0,HIST,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,FORE,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFore); SetIndexBuffer(2,PINT1,INDICATOR_DATA); PlotIndexSetString(2,PLOT_LABEL,"Conf+"); PlotIndexSetInteger(2,PLOT_SHIFT,NFore); SetIndexBuffer(3,PINT2,INDICATOR_DATA); PlotIndexSetString(3,PLOT_LABEL,"Conf-"); PlotIndexSetInteger(3,PLOT_SHIFT,NFore); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } //----------------------------------------------------------------------------------- // Custom indicator iteration function //----------------------------------------------------------------------------------- int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,j,init,start; double v1,v2; if(rates_total<NHist){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated>rates_total||prev_calculated<=0||(rates_total-prev_calculated)>1) {init=1; start=rates_total-NHist;} else {init=0; start=prev_calculated;} if(start==rates_total)return(rates_total); // New tick but not new bar //----------------------- if(init==1) // Initialization { i=start; v2=(open[i+2]-open[i])/2; v1=(open[i]+open[i+1]+open[i+2])/3.0-v2; fc.Init(v1,v2,ALPH,GAMM,PHI,DELT,nSES); ArrayInitialize(HIST,EMPTY_VALUE); } PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFore); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFore); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFore); for(i=start;i<rates_total;i++) // History { HIST[i]=fc.NewY(open[i]); } v1=0; for(i=0;i<NTest;i++) // Variance { j=rates_total-NTest+i; v2=close[j]-HIST[j-1]; v1+=v2*v2; } v1/=NTest; // v1=var j=1; for(i=rates_total-NFore;i<rates_total;i++) { v2=1.96*MathSqrt(v1*fc.VarCoefficient(j)); // Prediction intervals FORE[i]=fc.Fcast(j++); // Forecasting PINT1[i]=FORE[i]+v2; PINT2[i]=FORE[i]-v2; } return(rates_total); } //-----------------------------------------------------------------------------------
인디케이터 호출 또는 반복 초기화가 지수 평활 초기 값을 설정합니다.
이 지표에는 시즌성 인덱스에 대한 초기 설정이 없으므로 초기 값은 항상 0입니다. 이러한 초기화에 따라 시즌성이 예측 결과에 미치는 영향은 새로운 값 도입과 함께 0에서 특정 안정 값으로 점진적으로 상승할 것입니다.
정상 상태 작동 조건에 도달하는 데 필요한 사이클 수는 시즌성 인덱스에 대한 평활 계수 값에 따라 달라집니다. 평활 계수 값이 작을수록 더 많은 시간이 소요됩니다.
AdditiveES_Test.mq5 인디케이터에 기본 세팅을 넣고 구동시킨 결과를 5번 그림에서 볼 수 있습니다.
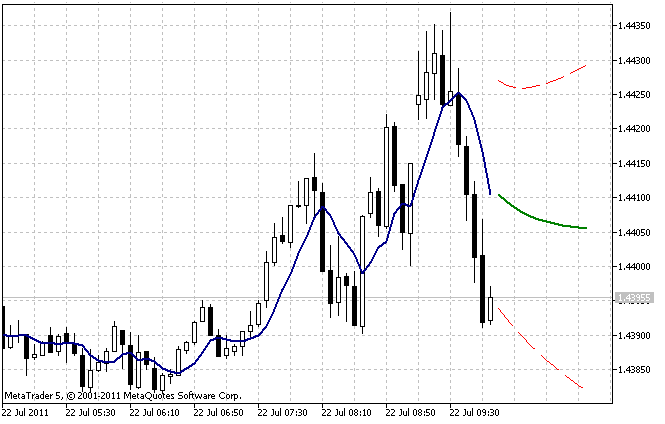
5번 그림. AdditiveES_Test.mq5 인디케이터
예측과는 별도로 인디케이터는 시퀀스의 과거 값과 95% 예측 신뢰도 구간의 한계에 대한 1단계 선행 예측에 해당하는 추가 선을 표시합니다.
그 신뢰도 구간은 1단계 선행 에러의 예측 분산에 기반을 두고 있습니다. 선택한 초기 값들의 부정확성 효과를 줄이기 위해 예측된 분산은 전체 길이 nHist에 대해 계산되지 않고 입력 패러미터 nTest에 지정된 마지막 바 들에 대해서만 계산됩니다.
이 문서 끝에 있는 Files.zip 아카이브에 AdditiveES.mqh 그리고 AdditiveES_Test.mq5 파일들이 들어있습니다.. 인디케이터를 컴파일할 때 include AdditiveES.mqh 파일은 AdditiveES_Test.mq5와 동일한 디렉토리에 있어야 합니다.
Additive ES_Test.mq5 인디케이터를 생성할 때의 초기 값 선택 문제가 어느 정도 해결되었지만 평활화 패러미터의 최적 값 선택 문제는 해결되지 않은 상태로 남아 있습니다.
8. 최적 패러미터 값 선택
단순 지수 평활 모델에는 단일 평활 패러미터가 있으며 단순 열거 방법을 사용하여 최적 값을 찾을 수 있습니다. 전체 시퀀스에 대한 예측 오차 값을 계산한 후 패러미터 값이 살짝 상승하고, 그 후 전체 계산이 다시 수행됩니다. 이 절차는 가능한 모든 패러미터 값이 열거될 때까지 반복됩니다. 그런 다음 가장 작은 오류 값을 초래한 패러미터 값만 선택하면 됩니다.
0.05 증분에서 0.1~0.9 범위의 평활화 계수의 최적 값을 찾으려면 예측 오차 값의 전체 계산을 17번 수행해야 합니다. 보시다시피 필요한 계산의 수가 그리 많지 않습니다. 그러나 감쇠를 사용한 선형 성장 모델에는 세 개의 평활화 패러미터의 최적화가 필요하며, 이 경우 동일한 범위에 있는 모든 패러미터의 조합을 동일한 0.05 단위로 열거하려면 총 4913번의 계산이 필요합니다.
가능한 모든 패러미터 값을 열거하는 데 필요한 전체 실행 수는 패러미터 수의 증가, 열거 범위의 증가 및 확장에 따라 빠르게 증가합니다. 평활화 패러미터 외에 모형의 초기 값을 최적화할 필요가 있는 경우에는 단순 열거 방법을 사용하는 것이 매우 어렵습니다.
여러 변수의 최소 함수를 찾는 것과 관련된 문제를 연구하는 이들이 많기에, 이러한 종류의 알고리즘이 상당히 많습니다. 어떠한 함수의 최소값을 찾는 다양한 방법에 대한 설명과 비교는 참조 [7]에서 확인할 수 있습니다. 이러한 모든 방법은 주로 목적 함수의 호출 수를 줄이는 것, 즉 최소를 찾는 과정에서 컴퓨팅 노력을 줄이는 것을 목표로 합니다.
서로 다른 방법인데도 흔히 콰시-뉴튼 최적화법이라는 것을 인용하는 경우가 있습니다. 대부분 효율성이 높지만, 더 간단한 방법으로도 최적화에 대한 접근방식을 충분히 입증할 수 있습니다.. 파월법(Powell's method)를 이용해봅시다. 파월법은 목표 함수의 미적 계산을 필요로 하지 않으며 탐색 메소드에 속합니다.
이 메소드는 다른 메소드들처럼 다양한 방법으로 구현될 수 있습니다. 목표 함수 값 또는 인수 값의 특정 정확도에 도달하면 검색을 완료해야 합니다. 게다가, 특정 구현에는 기능 패러미터 변경의 허용 범위에 대한 제한을 사용할 수 있는 가능성이 포함될 수 있습니다.
우리의 경우 파월법을 사용하여 제약없는 최소값을 찾는 알고리즘이 PowellsMethod.class에서 구현되어있습니다. 파월법은 목표 함수 값이 특정 정확도에 도달하면 정지합니다. 이 메소드의 구현에는 참조 [8]에 있는 알고리즘을 프로토타입으로 사용했습니다.
이하가 PowellsMethod 클래스의 소스 코드입니다.
//----------------------------------------------------------------------------------- // PowellsMethod.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #define GOLD 1.618034 #define CGOLD 0.3819660 #define GLIMIT 100.0 #define SHFT(a,b,c,d) (a)=(b);(b)=(c);(c)=(d); #define SIGN(a,b) ((b) >= 0.0 ? fabs(a) : -fabs(a)) #define FMAX(a,b) (a>b?a:b) //----------------------------------------------------------------------------------- // Minimization of Functions. // Unconstrained Powell’s Method. // References: // 1. Numerical Recipes in C. The Art of Scientific Computing. //----------------------------------------------------------------------------------- class PowellsMethod:public CObject { protected: double P[],Xi[]; double Pcom[],Xicom[],Xt[]; double Pt[],Ptt[],Xit[]; int N; double Fret; int Iter; int ItMaxPowell; double FtolPowell; int ItMaxBrent; double FtolBrent; int MaxIterFlag; public: void PowellsMethod(void); void SetItMaxPowell(int n) { ItMaxPowell=n; } void SetFtolPowell(double er) { FtolPowell=er; } void SetItMaxBrent(int n) { ItMaxBrent=n; } void SetFtolBrent(double er) { FtolBrent=er; } int Optimize(double &p[],int n=0); double GetFret(void) { return(Fret); } int GetIter(void) { return(Iter); } private: void powell(void); void linmin(void); void mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc); double brent(double ax,double bx,double cx,double &xmin); double f1dim(double x); virtual double func(const double &p[]) { return(0); } }; //----------------------------------------------------------------------------------- // Constructor //----------------------------------------------------------------------------------- void PowellsMethod::PowellsMethod(void) { ItMaxPowell= 200; FtolPowell = 1e-6; ItMaxBrent = 200; FtolBrent = 1e-4; } //----------------------------------------------------------------------------------- void PowellsMethod::powell(void) { int i,j,m,n,ibig; double del,fp,fptt,t; n=N; Fret=func(P); for(j=0;j<n;j++)Pt[j]=P[j]; for(Iter=1;;Iter++) { fp=Fret; ibig=0; del=0.0; for(i=0;i<n;i++) { for(j=0;j<n;j++)Xit[j]=Xi[j+n*i]; fptt=Fret; linmin(); if(fabs(fptt-Fret)>del){del=fabs(fptt-Fret); ibig=i;} } if(2.0*fabs(fp-Fret)<=FtolPowell*(fabs(fp)+fabs(Fret)+1e-25))return; if(Iter>=ItMaxPowell) { Print("powell exceeding maximum iterations!"); MaxIterFlag=1; return; } for(j=0;j<n;j++){Ptt[j]=2.0*P[j]-Pt[j]; Xit[j]=P[j]-Pt[j]; Pt[j]=P[j];} fptt=func(Ptt); if(fptt<fp) { t=2.0*(fp-2.0*(Fret)+fptt)*(fp-Fret-del)*(fp-Fret-del)-del*(fp-fptt)*(fp-fptt); if(t<0.0) { linmin(); for(j=0;j<n;j++){m=j+n*(n-1); Xi[j+n*ibig]=Xi[m]; Xi[m]=Xit[j];} } } } } //----------------------------------------------------------------------------------- void PowellsMethod::linmin(void) { int j,n; double xx,xmin,fx,fb,fa,bx,ax; n=N; for(j=0;j<n;j++){Pcom[j]=P[j]; Xicom[j]=Xit[j];} ax=0.0; xx=1.0; mnbrak(ax,xx,bx,fa,fx,fb); Fret=brent(ax,xx,bx,xmin); for(j=0;j<n;j++){Xit[j]*=xmin; P[j]+=Xit[j];} } //----------------------------------------------------------------------------------- void PowellsMethod::mnbrak(double &ax,double &bx,double &cx, double &fa,double &fb,double &fc) { double ulim,u,r,q,fu,dum; fa=f1dim(ax); fb=f1dim(bx); if(fb>fa) { SHFT(dum,ax,bx,dum) SHFT(dum,fb,fa,dum) } cx=bx+GOLD*(bx-ax); fc=f1dim(cx); while(fb>fc) { r=(bx-ax)*(fb-fc); q=(bx-cx)*(fb-fa); u=bx-((bx-cx)*q-(bx-ax)*r)/(2.0*SIGN(FMAX(fabs(q-r),1e-20),q-r)); ulim=bx+GLIMIT*(cx-bx); if((bx-u)*(u-cx)>0.0) { fu=f1dim(u); if(fu<fc){ax=bx; bx=u; fa=fb; fb=fu; return;} else if(fu>fb){cx=u; fc=fu; return;} u=cx+GOLD*(cx-bx); fu=f1dim(u); } else if((cx-u)*(u-ulim)>0.0) { fu=f1dim(u); if(fu<fc) { SHFT(bx,cx,u,cx+GOLD*(cx-bx)) SHFT(fb,fc,fu,f1dim(u)) } } else if((u-ulim)*(ulim-cx)>=0.0){u=ulim; fu=f1dim(u);} else {u=cx+GOLD*(cx-bx); fu=f1dim(u);} SHFT(ax,bx,cx,u) SHFT(fa,fb,fc,fu) } } //----------------------------------------------------------------------------------- double PowellsMethod::brent(double ax,double bx,double cx,double &xmin) { int iter; double a,b,d,e,etemp,fu,fv,fw,fx,p,q,r,tol1,tol2,u,v,w,x,xm; a=(ax<cx?ax:cx); b=(ax>cx?ax:cx); d=0.0; e=0.0; x=w=v=bx; fw=fv=fx=f1dim(x); for(iter=1;iter<=ItMaxBrent;iter++) { xm=0.5*(a+b); tol2=2.0*(tol1=FtolBrent*fabs(x)+2e-19); if(fabs(x-xm)<=(tol2-0.5*(b-a))){xmin=x; return(fx);} if(fabs(e)>tol1) { r=(x-w)*(fx-fv); q=(x-v)*(fx-fw); p=(x-v)*q-(x-w)*r; q=2.0*(q-r); if(q>0.0)p=-p; q=fabs(q); etemp=e; e=d; if(fabs(p)>=fabs(0.5*q*etemp)||p<=q*(a-x)||p>=q*(b-x)) d=CGOLD*(e=(x>=xm?a-x:b-x)); else {d=p/q; u=x+d; if(u-a<tol2||b-u<tol2)d=SIGN(tol1,xm-x);} } else d=CGOLD*(e=(x>=xm?a-x:b-x)); u=(fabs(d)>=tol1?x+d:x+SIGN(tol1,d)); fu=f1dim(u); if(fu<=fx) { if(u>=x)a=x; else b=x; SHFT(v,w,x,u) SHFT(fv,fw,fx,fu) } else { if(u<x)a=u; else b=u; if(fu<=fw||w==x){v=w; w=u; fv=fw; fw=fu;} else if(fu<=fv||v==x||v==w){v=u; fv=fu;} } } Print("Too many iterations in brent"); MaxIterFlag=1; xmin=x; return(fx); } //----------------------------------------------------------------------------------- double PowellsMethod::f1dim(double x) { int j; double f; for(j=0;j<N;j++) Xt[j]=Pcom[j]+x*Xicom[j]; f=func(Xt); return(f); } //----------------------------------------------------------------------------------- int PowellsMethod::Optimize(double &p[],int n=0) { int i,j,k,ret; k=ArraySize(p); if(n==0)N=k; else N=n; if(N<1||N>k)return(0); ArrayResize(P,N); ArrayResize(Xi,N*N); ArrayResize(Pcom,N); ArrayResize(Xicom,N); ArrayResize(Xt,N); ArrayResize(Pt,N); ArrayResize(Ptt,N); ArrayResize(Xit,N); for(i=0;i<N;i++)for(j=0;j<N;j++)Xi[i+N*j]=(i==j?1.0:0.0); for(i=0;i<N;i++)P[i]=p[i]; MaxIterFlag=0; powell(); for(i=0;i<N;i++)p[i]=P[i]; if(MaxIterFlag==1)ret=-1; else ret=Iter; return(ret); } //-----------------------------------------------------------------------------------
Optimize 메소드가 그 클래스의 주요 메소드입니다.
Optimize 메소드
입력 패러미터
- double &p[] - 최적화 값을 찾아야 하는 패러미터들의 초기 값을 담은 어레이. 얻어진 최적화 값이 어레이의 반환값입니다.
- int n=0 - p[] 어레이 내의 인수 수. n=0 일 때, 패러미터의 수는 p[] 어레이의 사이즈와 같은 것으로 간주됩니다.
반환값:
- 알고리즘을 수행하는데에 필요한 시행횟수를 반환, 혹은 만약 최대 시행가능 횟수에 도달했다면 -1을 반환.
최적 모수 값을 검색할 때 목표 함수의 최소값에 대한 반복 근사치가 발생합니다. Optimize 메소드는 지정된 정확도로 함수 최소값에 도달하는 데 필요한 반복 횟수를 반환합니다. 목표 함수는 반복할 때마다 여러 번 호출됩니다. 즉, 목표 함수의 호출 수는 Optimize 메소드에 의해 반환되는 반복 횟수보다 유의하게(10배, 심지어 100배) 클 수 있습니다.
본 클래스의 기타 메소드 들
SetItMaxPowell 메소드
입력 패러미터
- Int n - 파월법에서의 최대 허용 시행 횟수. 기본값은 200입니다.
반환값:
- None.
허용되는 최대 반복 횟수를 설정합니다. 이 수에 도달하면 지정된 정확도의 목표 함수의 최소값이 발견되었는지 여부에 관계없이 검색이 종료됩니다. 그리고 관련된 메세지가 로그에 추가됩니다.
SetFtolPowell 메소드
입력 패러미터
- double er - 정확도. 목표 함수의 최소값에서 이 편차 값에 도달하면 파월법은 검색을 중지합니다. 초기 값은 1e-6.
반환값:
- None.
SetItMaxBrent 메소드
입력 패러미터
- Int n - 보조 브렌트법의 최대 허용 시행 횟수. 기본값은 200입니다.
반환값:
- None.
최대 허용 시행 횟수를 설정합니다. 일단 도달하면 보조 브렌트법이 검색을 중지하고 로그에 관련 메시지가 추가됩니다.
SetFtolBrent 메소드
입력 패러미터
- double er – 정확도. 이 값은 보조 브렌트법에 대한 최소값 검색의 정확도를 정의합니다. 기본값은 1e-4.
반환값:
- None.
GetFret 메소드
입력 패러미터
- None.
반환값:
- 이는 목표 함수가 확보한 최소 값을 반환합니다.
GetIter 메소드
입력 패러미터
- None.
반환값:
- 알고리즘 작업에 필요한 반복 횟수를 반환합니다.
가상 함수 func(const double &p[])
입력 패러미터
- const double &p[] – 최적화된 패러미터를 담고있는 어레이의 주소 어레이의 사이즈는 함수 패러미터의 수에 비례함.
반환값:
- 전달된 패러미터에 해당하는 함수 값을 반환합니다.
모든 경우에 가상 함수 func()는 PowellsMethod 클래스에서 파생된 클래스에서 재정의되어야 합니다. func() 함수는 검색 알고리즘을 적용할 때 함수에 의해 반환되는 최소값에 해당하는 인수를 찾는 목적 함수입니다.
파월법의 구현에는 각 패러미터에 대한 검색 방향을 결정하기 위해 브렌트의 일변량 포물선 보간법이 사용됩니다. 이들 메소드의 정확도와 최대 허용 시행 횟수 수는 각각 SetItMaxPowell, SetFtolPowell, SetItMaxBrent 그리고 SetFtolBrent를 호출하는 것으로 세팅 가능합니다.
해당 알고리즘의 기본 특성이 이런 식으로 바뀔 수 있습니다. 이 기능은 특정 목표 함수로 설정된 기본 정확도가 너무 높고 알고리즘이 검색 프로세스에서 너무 많은 반복을 필요로 할 때 유용합니다. 필요한 정확도 값의 변경은 다양한 범주의 객관적 함수와 관련하여 검색을 최적화할 수 있습니다.
파월법을 채용한 알고리즘의 복잡성에도 불구하고 사용이 상당히 간단합니다.
예시를 하나 복습해봅시다. 우리가 함수 하나가 있다고 가정하고
그리고 우리는 패러미터 값을 찾아야하고 
그리고 
어떤 함수가 최소값을 가질지를 찾아야합니다.
이 문제를 해결할 방법을 시연하는 스크립트를 작성해봅시다.
//----------------------------------------------------------------------------------- // PM_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- class PM_Test:public PowellsMethod { public: void PM_Test(void) {} private: virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- double PM_Test::func(const double &p[]) { double f,r1,r2; r1=p[0]-0.5; r2=p[1]-6.0; f=r1*r1*4.0+r2*r2; return(f); } //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { int it; double p[2]; p[0]=8; p[1]=9; // Initial point PM_Test *pm = new PM_Test; it=pm.Optimize(p); Print("Iter= ",it," Fret= ",pm.GetFret()); Print("p[0]= ",p[0]," p[1]= ",p[1]); delete pm; } //-----------------------------------------------------------------------------------
이 스크립트를 작성할 때 p[0] 및 p[1] 패러미터의 전달값을 사용하여 주어진 테스트 함수의 값을 계산하는 PM_Test 클래스의 멤버로 func() 함수를 먼저 만듭니다. 그 후 OnStart() 함수 본체에 필수 패러미터에 초기 값을 부여합니다. 이 값들부터 탐색하기 시작할 것입니다.
추가적으로 PM_Test 클래스의 복사본이 생성되어 필수 값 p[0] 및 p[1]은 Optimize 메소드를 호출하는 것으로 탐색을 시작합니다. 부모 클래스 PowellsMethod 클래스는 재정의된 func() 함수를 호출할 것입니다. 검색이 완료되면 최소 지점에서의 시행 횟수, 함수 값, 얻어진 패러미터 값 p[0]=0.5 및 p[1]=6이 로그에 추가됩니다.
PowellsMethod.mqh 그리고 테스트 케이스 PM_Test.mq5가 이 문서의 끝에 첨부된 Files.zip 아카이브 내에 있습니다. PM_Test.mq5를 컴파일 하려면 이 파일은 PowellsMethod.mqh와 같은 폴더 내에 위치하여야합니다.
9. 모델 패러미터 값 최적화
이 문서의 초반부에서는 최소 함수를 찾는 메소드 구현을 다루었으며, 함수 사용에 대한 간단한 예를 제시했습니다. 이제 부터는지수 평활 모델 패러미터의 최적화와 관련된 문제를 다뤄보겠습니다.
우선, 시즌성을 고려한 모델은 이 글에서 더 이상 고려되지 않을 것이기 때문에 시즌성 성분과 관련된 모든 요소를 제외함으로써 앞서 소개한 AdditiveES 클래스를 최대한 단순화해 보겠습니다. 이렇게 하면 클래스의 소스 코드를 훨씬 더 쉽게 이해하고 계산 수를 줄일 수 있습니다. 또한 감쇠 고려 중인 선형 성장 모델의 패러미터 최적화에 대한 접근 방식을 쉽게 시연하는 목적으로, 예측 신뢰도 구간의 예측 및 계산과 관련된 모든 계산도 제외할 것입니다.
//----------------------------------------------------------------------------------- // OptimizeES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- // Class OptimizeES //----------------------------------------------------------------------------------- class OptimizeES:public PowellsMethod { protected: double Dat[]; // Input data int Dlen; // Data lenght double Par[5]; // Parameters int NCalc; // Number of last elements for calculation public: void OptimizeES(void) {} int Calc(string fname); private: int readCSV(string fnam,double &dat[]); virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- // Calc //----------------------------------------------------------------------------------- int OptimizeES::Calc(string fname) { int i,it; double relmae,naiv,s,t,alp,gam,phi,e,ae,pt; if(readCSV(fname,Dat)<0){Print("Error."); return(-1);} Dlen=ArraySize(Dat); NCalc=200; // number of last elements for calculation if(NCalc<0||NCalc>Dlen-1){Print("Error."); return(-1);} Par[0]=Dat[Dlen-NCalc]; // initial S Par[1]=0; // initial T Par[2]=0.5; // initial Alpha Par[3]=0.5; // initial Gamma Par[4]=0.5; // initial Phi it=Optimize(Par); // Powell's optimization s=Par[0]; t=Par[1]; alp=Par[2]; gam=Par[3]; phi=Par[4]; relmae=0; naiv=0; for(i=Dlen-NCalc;i<Dlen;i++) { e=Dat[i]-(s+phi*t); relmae+=MathAbs(e); naiv+=MathAbs(Dat[i]-Dat[i-1]); ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } relmae/=naiv; PrintFormat("%s: N=%i, RelMAE=%.3f",fname,NCalc,relmae); PrintFormat("Iter= %i, Fmin= %e",it,GetFret()); PrintFormat("p[0]= %.5f, p[1]= %.5f, p[2]= %.2f, p[3]= %.2f, p[4]= %.2f", Par[0],Par[1],Par[2],Par[3],Par[4]); return(0); } //----------------------------------------------------------------------------------- // readCSV //----------------------------------------------------------------------------------- int OptimizeES::readCSV(string fnam,double &dat[]) { int n,asize,fhand; fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI); if(fhand==INVALID_HANDLE) { Print("FileOpen Error!"); return(-1); } asize=512; ArrayResize(dat,asize); n=0; while(FileIsEnding(fhand)!=true) { dat[n++]=FileReadNumber(fhand); if(n+128>asize) { asize+=128; ArrayResize(dat,asize); } } FileClose(fhand); ArrayResize(dat,n-1); return(0); } //------------------------------------------------------------------------------------ // func //------------------------------------------------------------------------------------ double OptimizeES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 sse=0; for(i=Dlen-NCalc;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(NCalc*MathLog(k1*k2*k3*sse)); } //------------------------------------------------------------------------------------
OptimizeES 클래스는 PowellsMethod 클래스에서 상속되며 가상 함수 func()를 재정의하는 과정이 포함됩니다. 앞서 언급한 바와 같이, 최적화 과정에서 계산된 값이 최소화되는 패러미터는는 이 함수 입력시에 통과되어야 합니다.
최대우도법에 따라 func() 함수는 1단계 선행 예측 오류의 제곱의 합의 로그 값을 계산합니다. 오류는 루프 안에서 시퀀스 내 최신 값 NCalc 개만큼 계산됩니다.
모델의 안정성을 유지하기 위해 우리는 패러미터 변화의 범위에 제한을 설정할 것입니다. Alpha 및 Gamma 패러미터의 범위는 0.05에서 0.95이며, Phi 패러미터 값은 0.05에서 1.0입니다. 그러나 우리의 경우엔 최적화를 위해 우리는 목적 함수의 인수에 대한 제한의 사용을 의미하지 않는 제한 없는 최소값을 찾는 방법을 사용합니다.
검색 알고리즘을 변경하지 않고 패러미터에 부과되는 모든 제한을 고려할 수 있도록 한계가 있는 다변수 함수의 최소값을 찾는 문제를 제약 없는 최소값을 찾는 문제로 전환하려고 합니다. 이 목적을 달성하기 위해 흔히 페널티 함수 메소드라고 부르는 것을 이용할 것입니다. 이 메소드는 1차원 케이스에서는 쉽게 시연할 수 있습니다.
검색 프로세스에서 이 함수 패러미터에 값을 할당할 수 있는 알고리즘과 단일 인수(2.0~3.0 도메인)가 있다고 가정합니다. 이 경우, 검색 알고리즘이 최대 허용값을 초과하는 인수(예: 3.5)를 통과했다면, 3.0에 해당하는 인수에 대해 함수를 계산할 수 있으며, 얻은 결과에 최대값 초과에 비례하는 계수를 더 곱할 수 있습니다(예: k=1+(3.5-3)*200.2
최소 허용 값 미만으로 판명된 인수 값과 관련하여 유사한 연산을 수행한다면, 결과 목적 함수는 인수에서 허용되는 변경 범위를 벗어나 증가한다는 것을 보장합니다. 이와 같이 목적 함수의 결과 값이 인위적으로 증가하면 함수에 전달된 인수가 어떤 식으로든 제한적이었다는 사실을 검색 알고리즘이 인식하지 않고 결과 함수의 최소값이 인수의 설정된 한계 내에 있음을 보장할 수 있습니다. 그러한 어프로치는 몇가지 변수의 함수에 쉽게 적용할 수 있습니다.
OptimizeES 클래스의 메인 메소드는 Calc 메소드입니다. 이 메소드를 호출하면 파일에서 데이터를 읽고, 얻어진 메소드 값에 대해 RelMAE를 이용하여 모형의 최적 패러미터 값을 검색하고, 예측 정확도를 추정할 수 있습니다. 파일에서 읽은 시퀀스 값의 처리 수는 NCalc 변수에 설정된 경우입니다.
아래에 OptimizeES 클래스를 이용하는 Optimization_Test.mq5 스크립트의 예제가 있습니다.
//----------------------------------------------------------------------------------- // Optimization_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "OptimizeES.mqh" OptimizeES es; //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { es.Calc("Dataset\\USDJPY_M1_1100.TXT"); } //-----------------------------------------------------------------------------------
이 스크립트를 실행하면 다음과 같은 결과를 얻을 수 있습니다.
6번 그림. Optimization_Test.mq5 스크립트 결과
이제 모델의 최적 패러미터 값과 초기 값을 찾을 수 있지만, 간단한 도구를 사용하여 최적화할 수 없는 모수, 즉 최적화에 사용되는 시퀀스 값의 수가 있습니다. 큰 길이의 시퀀스를 최적화하기 위해 평균적으로 시퀀스 전체 길이에 대한 최소 오차를 보장하는 최적의 패러미터 값을 얻을 것입니다.
그러나 이 구간 내에서 시퀀스의 특성이 변화하면 일부 파편에 대해 얻은 값이 더 이상 최적이 아니게 됩니다. 반면에 시퀀스 길이가 극적으로 감소하면 짧은 간격에 대해 얻은 최적 모수가 더 긴 시간 지연에 대해 최적이라는 보장이 없습니다.
OptimizeES.mqh 그리고 Optimization_Test.mq5는 이 문서 끝에 있는 Files.zip 아카이브에 들어 있습니다. 컴파일 시에 OptimizeES.mqh 및 PowellsMethod.mqh가 컴파일 된 Optimization_Test.mq5와 같은 폴더 안에 있어야합니다. 상술한 예시에서 USDJPY_M1_1100.TXT 파일에 테스트 시퀀스가 들어있고 \MQL5\Files\Dataset\ 폴더에 들어있어야합니다.
테이블 2는 이 스크립트를 통해 RelMAE를 사용하여 얻은 예측 정확도의 추정치를 보여줍니다. 각 시퀀스의 마지막 100, 200 및 400 값을 사용하여 문서에서 앞서 언급한 8개의 테스트 시퀀스에 대해 예측을 시행하였습니다.
|
테이블 2. RelMAE를 이용해 추정한 예측 에러
알 수 있듯이 예측 오차 추정치는 통일성에 가깝지만 대부분의 경우 이 모델에서 주어진 순서에 대한 예측은 순진한 방법보다 더 정확합니다.
10. IndicatorES.mq5 인디케이터
AdditiveES.mqh 클래스에 기반한 AdditiveES_Test.mq5 인디케이터는 앞서 클래스를 리뷰할 때에 언급한 바 있습니다. 이 인디케이터의 평활화 패러미터들은 모두 직접 세팅되었습니다.
이제 모델 패러미터를 최적화할 수 있는 방법을 고려한 후 최적 패러미터 값과 초기 값이 자동으로 결정되고 처리된 샘플 길이만 수동으로 설정하면 되는 유사한 인디케이터를 만들 수 있습니다. 그리 되었으니 시즌성에 관련된 계산을 모두 제거하겠습니다.
인디케이터 제작에 사용한 CIndiсatorES 클래스는 아래 있습니다.
//----------------------------------------------------------------------------------- // CIndicatorES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- // Class CIndicatorES //----------------------------------------------------------------------------------- class CIndicatorES:public PowellsMethod { protected: double Dat[]; // Input data int Dlen; // Data lenght double Par[5]; // Parameters public: void CIndicatorES(void) { } void CalcPar(double &dat[]); double GetPar(int n) { if(n>=0||n<5)return(Par[n]); else return(0); } private: virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- // CalcPar //----------------------------------------------------------------------------------- void CIndicatorES::CalcPar(double &dat[]) { Dlen=ArraySize(dat); ArrayResize(Dat,Dlen); ArrayCopy(Dat,dat); Par[0]=Dat[0]; // initial S Par[1]=0; // initial T Par[2]=0.5; // initial Alpha Par[3]=0.5; // initial Gamma Par[4]=0.5; // initial Phi Optimize(Par); // Powell's optimization } //------------------------------------------------------------------------------------ // func //------------------------------------------------------------------------------------ double CIndicatorES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 sse=0; for(i=0;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(Dlen*MathLog(k1*k2*k3*sse)); } //------------------------------------------------------------------------------------
이 클래스는 CalcPar 및 GetPar 메소드를 가지고 있는데, 전자는 모델의 최적화 패러미터 값을 계산하도록 설계되었으며 후자는 해당 값들을 액세스하는 용도로 설계되었습니다. 한편, CIndicatorES 클래스 또한 가상 함수 func()를 재정의하는 과정이 포함되었습니다.
IndicatorES.mq5 인디케이터의 소스코드
//----------------------------------------------------------------------------------- // IndicatorES.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" // Forecast #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "ConfUp" // Confidence interval #property indicator_type3 DRAW_LINE #property indicator_color3 clrCrimson #property indicator_style3 STYLE_DOT #property indicator_width3 1 #property indicator_label4 "ConfDn" // Confidence interval #property indicator_type4 DRAW_LINE #property indicator_color4 clrCrimson #property indicator_style4 STYLE_DOT #property indicator_width4 1 input int nHist=80; // History bars, nHist>=24 #include "CIndicatorES.mqh" #define NFORE 12 double Hist[],Fore[],Conf1[],Conf2[]; double Data[]; int NDat; CIndicatorES Es; //----------------------------------------------------------------------------------- // Custom indicator initialization function //----------------------------------------------------------------------------------- int OnInit() { NDat=nHist; if(NDat<24)NDat=24; MqlRates rates[]; CopyRates(NULL,0,0,NDat,rates); // Load missing data ArrayResize(Data,NDat); SetIndexBuffer(0,Hist,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,Fore,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFORE); SetIndexBuffer(2,Conf1,INDICATOR_DATA); // Confidence interval PlotIndexSetString(2,PLOT_LABEL,"ConfUp"); PlotIndexSetInteger(2,PLOT_SHIFT,NFORE); SetIndexBuffer(3,Conf2,INDICATOR_DATA); // Confidence interval PlotIndexSetString(3,PLOT_LABEL,"ConfDN"); PlotIndexSetInteger(3,PLOT_SHIFT,NFORE); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } //----------------------------------------------------------------------------------- // Custom indicator iteration function //----------------------------------------------------------------------------------- int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,start; double s,t,alp,gam,phi,e,f,a,a1,a2,a3,var,ci; if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar start=rates_total-NDat; //----------------------- PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat); PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE); for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data Es.CalcPar(Data); // Optimization of parameters s=Es.GetPar(0); t=Es.GetPar(1); alp=Es.GetPar(2); gam=Es.GetPar(3); phi=Es.GetPar(4); f=(s+phi*t); var=0; for(i=0;i<NDat;i++) // History { e=Data[i]-f; var+=e*e; a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1; f=(s+phi*t); Hist[start+i]=f; } var/=(NDat-1); a1=1; a2=0; a3=1; for(i=rates_total-NFORE;i<rates_total;i++) { a1=a1*phi; a2+=a1; Fore[i]=s+a2*t; // Forecast ci=1.96*MathSqrt(var*a3); // Confidence intervals a=alp*(1+a2*gam); a3+=a*a; Conf1[i]=Fore[i]+ci; Conf2[i]=Fore[i]-ci; } return(rates_total); } //-----------------------------------------------------------------------------------
모든 새 바에서 지표는 모델 패러미터의 최적 값을 찾고, 주어진 막대 수 NHist에 대해 모델에서 계산을 수행하며, 예측을 작성하고, 예측 신뢰 한계를 정의합니다.
이 인디케이터의 유일한 패러미터는 처리된 시퀀스의 길이이며 최소값은 24 바로 제한됩니다. 이 인디케이터의 모든 계산은 open[] 값을 기반으로 이루어집니다. 예측 평선은 12 바 입니다. IndicatorES.mq5 인디케이터 및 CIndicatorES.mqh 파일 코드는 문서 끝에 위치한 Files.zip 아카이브 내에서 찾으실 수 있습니다.
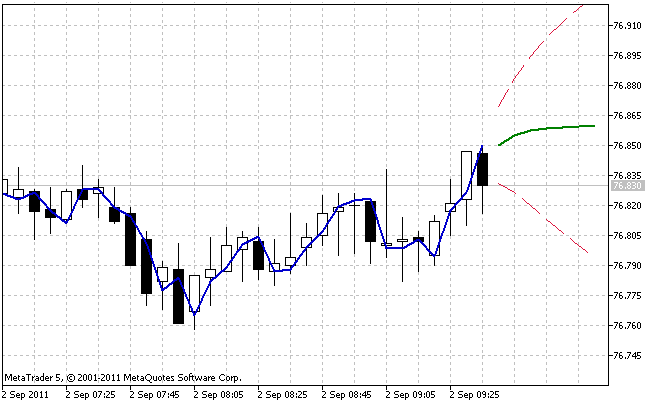
7번 그림. IndicatorES.mq5 인디케이터의 운용 결과
IndicatorES.mq5 인디케이터 운영 결과 예시를 7번 그림에서 확인하실 수 있습니다. 인디케이터 작동 과정에서 95% 예측 신뢰도 구간은 모형의 최적 패러미터 값에 해당하는 값을 취합니다. 평활 패러미터 값이 클 수록, 늘어나는 예측 선상에서 신뢰도 구간이 더욱 빠르게 커지게 됩니다.
간단한 개선만으로도 IndicatorES.mq5 인디케이터를 외환 시세 뿐만이 아니라 다양한 인디케이터나 재가공 데이터의 값을 예측하는 데에 쓸 수 있게 됩니다.
마치며
이 문서의 목적은 독자 여러분이 예측에서 쓰이는 지수 평활 모델에 친숙해지게 하는 것이었습니다. 실용적인 사례를 점검해보면서, 몇가지 이슈도 짚고 넘어갈 수 있게 되었습니다. 다만 이 문서에서 다룬 자료들은 기껏해야 예측과 관련된 방대한 폭의 문제와 그 해결법에 대한 입문에 지나지 않는다고 보셔야합니다.
이 문서에서 다뤄진 클래스, 함수, 스크립트, 인디케이터는 문서를 작성하는 과정에서 만들어졌으며, 주로 문서의 자료들에 대한 본보기가 되도록 설계되었다는 점에 주목해주셨으면 합니다. 안정성이나 오류를 깊게 체크해본 것 또한 아닙니다. 한 편, 문서에서 사용된 인디케이터는 관련된 메소드를 시연하는 용도라고 생각하셔야합니다..
기사에 소개된 IndicatorES.mq5 인디케이터를 통한 예측의 정확성은 적용된 모델에 변화를 줌으로서 향상될 수 있을 것이라고 봅니다. 시세의 특수성을 감안하면 그쪽이 더 적절할 것입니다. 이 인디케이터는 다른 모델들에 의해 강화될 수도 있습니다. 하지만 그 내용은 이 문서에서 다룰 내용을 아득이 넘어갑니다.
결론적으로, 지수 평활 모형을 통해 더욱 복잡하게 설계된 모형을 이용하여 얻은 예측과 동일한 수준의 정확도의 예측을 해낼 수 있었습니다. 이를 통하여 무작정 모형이 복잡한 것이 좋은 것이 아님을 증명하였습니다.
참조
- Everette S. Gardner Jr. Exponential Smoothing: The State of the Art – Part II. June 3, 2005.
- Rob J Hyndman. Forecasting Based on State Space Models for Exponential Smoothing. 29 August 2002.
- Rob J Hyndman et al. Prediction Intervals for Exponential Smoothing Using Two New Classes of State Space Models. 30 January 2003.
- Rob J Hyndman and Muhammad Akram. Some Nonlinear Exponential Smoothing Models Are Unstable. 17 January 2006.
- Rob J Hyndman and Anne B Koehler. Another Look at Measures of Forecast Accuracy. 2 November 2005.
- Yu. P. Lukashin. Adaptive Methods for Short-Term Forecasting of Time Series: Textbook. - М.: Finansy i Statistika, 2003.-416 pp.
- D. Himmelblau. Applied Nonlinear Programming. М.: Mir, 1975.
- Numerical Recipes in C. The Art of Scientific Computing. Second Edition. Cambridge University Press.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/318
인디케이터 및 통계적 매개 변수 분석하기
시계열 주요 특성의 분석
판별 분석을 이용한 매매 시스템 구축
MQL5에서의 진보된 적응형 인디케이터 이론 및 구현
