Üssel Düzeltme Kullanarak Zaman Serisi Tahmini
297
0
Giriş
Şu anda, yalnızca bir zaman sırasının geçmiş değerlerinin analizine dayanan çok sayıda iyi bilinen tahmin yöntemleri, yani normalde teknik analizde kullanılan ilkeleri kullanan yöntemleri, vardır. Bu yöntemlerin ana aracı, belirli bir zamanda tanımlanan sıra özelliklerinin sınırlarının ötesine geçtiği dış değer şemasıdır.
Aynı zamanda gelecekteki sıra özelliklerinin geçmiş ve şimdikiyle aynı olacağı varsayılır. Tahmin aralığındaki bu tür dinamikler açısından sıra özelliklerindeki değişikliklerin dinamiklerinin incelenmesini içeren daha karmaşık bir dış değer şeması tahminde daha az kullanılır.
Dış değere dayalı en iyi bilinen tahmin yöntemleri belki de özbağımlı entegre hareketli ortalama modeli (ARIMA) kullananlardır. Bu yöntemlerin popülaritesi öncelikle entegre ARIMA modeli öneren ve geliştiren Box-Jenkins'in çalışmalarından kaynaklanmaktadır. Box-Jenkins tarafından tanıtılan modeller dışında elbette başka modeller ve tahmin yöntemleri de vardır.
Bu makale kısaca - Box-Jenkins'in eserlerinin ortaya çıkmasından önce Holt ve Brown tarafından önerilen üssel düzeltme modellerini - daha basit modelleri kapsayacaktır.
Daha basit ve net matematiksel araçlara rağmen, üssel yumuşatma modelleri kullanılarak tahmin yapmak genellikle ARIMA modeli kullanılarak elde edilenlerle benzer sonuçlara ortaya çıkar. Bu, üssel düzeltme modelleri ARIMA modelinin özel bir durumu olduğu için pek şaşırtıcı değildir. Başka bir deyişle, bu makalede incelenmekte olan her üssel düzeltme modeline karşılık gelen eşdeğer bir ARIMA modeli vardır. Bu eşdeğer modeller makalede dikkate alınmayacaktır ve sadece bilgi için belirtilmiştir.
Her özel durumda tahminin bireysel bir yaklaşım gerektirdiği ve normalde birtakım prosedür içerdiği bilinmektedir.
Örneğin:
- Eksik ve aykırı değerler için zaman sırasının analizi. Bu değerlerin ayarlanması.
- Eğilimin ve türünün tanımlaması. Sıra periyodikliğin belirlenmesi.
- Sıranın sabitliğinin kontrolü.
- Sıralı ön işleme analizi (logaritma, farklılık vb. alma).
- Model seçimi.
- Model parametresi belirleme. Seçili modeli temel alan tahmin.
- Model tahmini doğruluk değerlendirmesi.
- Seçili modelin hatalarının analizi.
- Seçili modelin yeterliliğinin belirlenmesi ve gerekirse modelin değiştirilmesi ve önceki ögelere geri dönülmesi.
Bu, etkili tahmin için gereken eylemlerin tam listesi değildir.
Model parametresinin belirlenmesi ve tahmin sonuçlarının elde edilmesi genel tahmin sürecinin sadece küçük bir parçası olduğu vurgulanmalıdır. Ancak bir makalede tahminle ilgili tüm sorunları şu veya bu şekilde ele almak imkansızdır.
Bu nedenle, bu makalede yalnızca üssel düzeltme modelleri ele alınacak ve önceden işlenmemiş para birimi tekliflerini test sırası olarak kullanılacaktır. Eşlik eden sorunlar kesinlikle makalede tamamen önlenemez, ancak modellerin gözden geçirilmesi için gerekli oldukları sürece bunlara değinilecektir.
1. Sabitlik
Dış değer kavramı, incelenmekte olan sürecin gelecekteki gelişiminin geçmiş ve günümüzdeki gibi olacağı anlamına gelir. Başka bir deyişle, sürecin sabitliği ile ilgilidir. Sabit süreçler tahmin açısından çok çekicidir, ancak ne yazık ki, herhangi bir gerçek süreç gelişimi boyunca değiştiği için doğada bulunmaz.
Gerçek süreçlerin zaman içinde belirgin bir şekilde farklı beklentisi, varyansı ve dağılımı olabilir, ancak özellikleri çok yavaş değişen süreçler muhtemelen sabit süreçlere bağlanabilir. Bu durumda "çok yavaş", sonlu gözlem aralığındaki işlem özelliklerindeki değişikliklerin ihmal edilebilecek kadar önemsiz göründüğü anlamına gelir.
Mevcut gözlem aralığı (kısa örnek) ne kadar kısa olursa sürecin bir bütün olarak sabitliği konusunda yanlış karar verme olasılığı o kadar yüksek olur. Ancak daha sonra kısa vadeli bir tahmin yapmayı planlayan süreçle daha fazla ilgileniyorsak numune boyutundaki azalma bazı durumlarda bu tahminin doğruluğunun artmasına neden olabilir.
İşlem değişikliklere tabiyse gözlem aralığında belirlenen sıra parametreleri, sınırları dışında farklı olacaktır. Böylece tahmin aralığı ne kadar uzunsa sıra özelliklerinin değişkenliğinin tahmin hatası üzerindeki etkisi o kadar güçlüdür. Bu nedenle kendimizi sadece kısa vadeli bir tahminle sınırlamalıyız; tahmin aralığındaki önemli bir azalma, yavaş değişen sıra özelliklerinin önemli tahmin hatalarına neden olmayacağını düşünmemizi sağlar.
Ayrıca, sıra parametrelerinin değişkenliği, parametreler aralık içinde sabit kalmadığı için gözlem aralığına göre tahmin edilirken elde edilen değerin ortalama olmasına neden olur. Bu nedenle, elde edilen parametre değerleri bu aralığın son anında ilişkili olmayacak, ancak belirli bir ortalamasını yansıtacaktır. Ne yazık ki bu hoş olmayan fenomeni tamamen ortadan kaldırmak mümkün değildir, ancak model parametresi tahmininde (çalışma aralığı) yer alan gözlem aralığının uzunluğu mümkün olduğunca azaltılırsa azaltılabilir.
Bunun yanı sıra çalışma aralığı aşırı derecede azaltılırsa sıra parametresi tahmini doğruluğu da azalacağı için çalışma aralığı belirsiz olarak kısaltılamaz. Sıra özelliklerinin değişkenliği ile ilişkili hataların etkisi ile çalışma aralığındaki aşırı azalma nedeniyle artan hatalar arasında bir uzlaşma aranmalıdır.
Yukarıdakilerin tümü, süreçlerin sabitliği varsayımlarına dayandığı için ARIMA modelleri gibi üssel düzeltme modelleri kullanılarak tahmin için tamamen geçerlidir. Bununla birlikte basitlik adına, bundan sonra geleneksel olarak incelenen tüm sıraların parametrelerinin gözlem aralığı içinde değiştiğini, ancak bu değişikliklerin ihmal edilebilecek kadar yavaş bir şekilde olduğunu varsayacağız.
Bu nedenle, makale üssel düzeltme modelleri temelinde yavaş değişen özelliklere sahip sıraların kısa vadeli tahminiyle ilgili sorunları ele alacaktır. Bu durumda "kısa vadeli tahmin", genellikle ekonomide anlaşıldığı gibi bir yıldan daha kısa bir süre için tahminde etmek yerine bir, iki veya daha fazla zaman aralığı için tahmin anlamına gelmelidir.
2. Test Sıraları
Bu makaleyi yazarken M1, M5, M30 ve H1 için önceden kaydedilmiş EURRUR, EURUSD, USDJPY ve XAUUSD alıntıları kullanılmıştır. Kaydedilen dosyaların her biri 1100 "açık" değer içerir. "En eski" değer dosyanın başında ve "en son" değer dosyanın sonunda bulunur. Dosyaya kaydedilen son değer, dosyanın oluşturulduğu zamana karşılık gelir. Test sıralarını içeren dosyalar HistoryToCSV.mq5 komut dosyası kullanılarak oluşturulmuştur. Veri dosyaları ve oluşturuldukları komut dosyası, Files.zip arşivdeki makalenin sonunda bulunur.
Daha önce de belirtildiği gibi kaydedilen alıntılar bu makalede dikkatinizi çekmek istediğim bariz sorunlara rağmen ön işleme alınmadan kullanılmaktadır. Örneğin, gün içinde EURRUR_H1 alıntısı 12 ila 13 çubuk içerirken, XAUUSD alıntısı, Cuma günleri diğer günlere göre bir çubuk daha az içerir. Bu örnekler, alıntıların düzensiz örnekleme aralığıyla üretildiğini gösterir; bu, tekdüze bir nicelik aralığına sahip olmayı öneren doğru zaman sıralarıyla çalışmak için tasarlanmış algoritmalar için kabul edilmez.
Dış değer kullanılarak eksik alıntı değerleri yeniden üretilse bile hafta sonları alıntı eksikliğiyle ilgili sorunu açık kalır. Hafta sonları dünyada meydana gelen olayların dünya ekonomisi üzerinde hafta içi olaylarla aynı etkiye sahip olduğunu varsayabiliriz. Devrimler, doğa eylemleri, yüksek profilli skandallar, hükümet değişiklikleri ve bu tür diğer büyük olaylar her an meydana gelebilir. Cumartesi günü böyle bir olay olsaydı dünya pazarları üzerinde hafta içi meydana gelenden daha az etkiye sahip olmazdı.
Belki de bu olaylar, çalışma haftasının sonunda çok sık gözlemlenen alıntılarda boşluklara yol açar. Görünüşe göre FOREX çalışmasa bile dünya kendi kurallarına göre devam ediyor. Teknik analiz için tasarlanan hafta sonlarına karşılık gelen alıntılardaki değerlerin çoğaltılıp çoğaltılmayacağı ve ne gibi bir fayda sağlayabileceği hala belirsizdir.
Açıkçası bu konular, bu makalenin kapsamı dışındadır, ancak ilk bakışta herhangi bir boşluk içermeyen sıra, en azından döngüsel (dönemsel) bileşenlerin tespiti açısından analiz için daha uygundur.
Daha fazla analiz için verilerin ön hazırlığının önemi çok az tahmin edilebilirdir; bu, bizim durumumuzda alıntı olarak önemli bir bağımsız konudur, Terminal'de görünme şekli, genellikle teknik analiz için uygun değildir. Yukarıdaki boşlukla ilgili konuların dışında başka birçok sorun vardır.
Örneğin alıntıları oluştururken sabit zaman noktasına kendisine ait olmayan "aç" ve "kapat" değerleri atanır; bu değerler, seçilen bir zaman dilimi grafiğinin sabit bir an yerine, işaret oluşum süresine karşılık gelir; oysa işaretlerin genelde çok nadir olduğu bilinmektedir.
Kimse, bir dakika aralığında bile örnekleme oranının yukarıdaki teoremi (diğer büyük aralıklardan bahsedilmeden) karşıladığını garanti edemediği için başka bir örnek, örnekleme teoremini tamamen göz ardı ederek görülebilir. Ayrıca bazı durumlarda alıntı değerlerinin üzerine eklenebilen değişken bir yayılmanın varlığını akılda tutulmalıdır.
Ancak bu konuları, bu makalenin kapsamı dışında bırakalım ve öncelikli konumuza geri dönelim.
3. Üssel Düzeltme
Önce en basit modele bir göz atalım
,
burada:
- X(t) – incelenen (temsili) süreç,
- L(t) – değişken işlem düzeyi,
- r(t)– sıfır ortalama rastgele değişken.
Görüldüğü gibi bu model iki bileşenin toplamını içerir; özellikle L(t) işlem seviyesiyle ilgileniyoruz ve ayırmaya çalışacağız.
Rastgele bir sıranın ortalamasının, varyansın azalmasına, yani ortalamadan sapma aralığının azalmasına neden olabileceği iyi bilinmektedir. Bu nedenle, basit modelimiz tarafından açıklanan işlem ortalamaya (düzeltmeye) maruz kalırsa rastgele bileşen r(t)'den tamamen kurtulamayabiliriz, ancak en azından önemli ölçüde zayıflatabilir ve böylece hedef seviye L(t)’i ayırabiliriz.
Bu amaçla, basit bir üssel düzeltme (SES) kullanacağız.
Bu çok bilinen formülde düzeltme derecesi, 0'dan 1'e ayarlanabilen alfa katsayısı ile tanımlanır. Alfa sıfıra ayarlanırsa X giriş sırasının yeni gelen değerlerinin düzeltme sonucu üzerinde hiçbir etkisi olmaz. Herhangi bir zaman noktası için düzeltme sonucu sabit bir değer olacaktır.
Sonuç olarak bu gibi aşırı durumlarda rahatsız eden rastgele bileşen tamamen bastırılır, ancak incelenen işlem seviyesi düz bir yatay çizgiye düzeltilir. Alfa katsayısı bir olarak ayarlanırsa giriş sırası düzeltme işleminden etkilenmez. İncelenen düzey L(t) bu durumda bozulmaz ve rastgele bileşen de bastırılmaz.
Alfa değerini seçerken aynı anda çakışan gereksinimleri karşılamak zorundadır. Rastgele bileşeni r(t) etkili bir şekilde bastırmak için alfa değeri sıfıra yakın olmalıdır. Bunun yanı sıra ilgilendiğimiz L(t) bileşenini bozmamak için alfa değerini birliğe yakın ayarlamanız önerilir. En uygun alfa değerini elde etmek için bu değerin optimize edilebileceği bir kriter belirlememiz gerekir.
Bu tür bir kriteri belirledikten sonra bu makalenin sadece sıraların düzeltilmesiyle değil, tahminle de ilgili olduğunu unutmayın.
Bu durumda basit üssel düzeltme modeliyle ilgili olarak, belirli bir zamanda elde edilen 
değeri, ilerideki herhangi bir adım için bir tahmin olarak değerlendirmek gelenekseldir.
burada 
t zamanında yapılan m adım ilerisi tahminidir.
Bu nedenle t zamanında yapılan sıra değerinin tahmini, önceki adımda yapılan bir adım ilerisi tahmini olacaktır
Bu durumda, alfa katsayısı değerinin optimizasyonu için bir adım ilerisi tahmin hatası bir ölçüt olarak kullanılabilir
Böylece, bu hataların karelerinin toplamını tüm örnek üzerinde en aza indirerek belirli bir sıra için alfa katsayısının en uygun değerini belirleyebiliriz. En iyi alfa değeri elbette hataların karelerinin toplamının minimum olacağı değer olacaktır.
Şekil 1, bir adım ilerdeki tahmin hatalarının karelerinin toplamının bir grafiğini ve USDJPY M1 test sırasının bir parçası için alfa katsayı değerini gösterir.
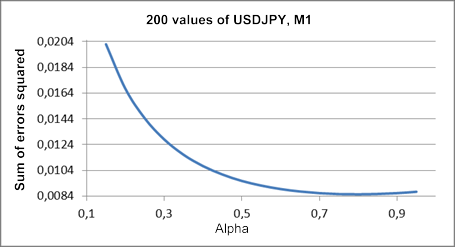
Şekil 1. Basit üssel düzeltme
Elde edilen çizimdeki minimum değerin fark edilmesi zordu ve 0,8 alfa değerine yakındır. Ancak bu tür bir resim, basit üssel düzeltme ile ilgili olarak her zaman böyle değildir. Makalede kullanılan test sırası parçaları için en uygun alfa değerini elde etmeye çalışırken sürekli olarak birliğe düşen bir grafik daha sık elde edeceğiz.
Düzeltme katsayısının bu tür yüksek değerleri, bu basit modelin test sıralarımızın (alıntıların) tanımlanması için yeterli olmadığını göstermektedir. L(t) işlem düzeyi ya çok hızlı değişir ya da işlemde bir eğilim vardır.
Başka bir bileşen ekleyerek modelimizi biraz karmaşıklaştıralım
,
burada:
- X(t) - incelenen (temsili) süreç;
- L(t) - değişken işlem düzeyi;
- T(t) - doğrusal eğilim;
- r(t) - sıfır ortalama rastgele değişken.
Doğrusal gerileme katsayıları bir sıranın çift düzeltmesiyle belirlenir:
Bu şekilde elde edilen a1 ve a2 katsayıları için, t zamanında m-step-ahead tahmini şuna eşit olacaktır;
Yukarıdaki formüllerde ilk ve tekrarlanan düzletme için aynı alfa katsayısının kullanılmıştır. Bu modele, doğrusal büyümenin katkılı tek parametre modeli denir.
Basit model ile doğrusal büyüme modeli arasındaki farkı gösterelim.
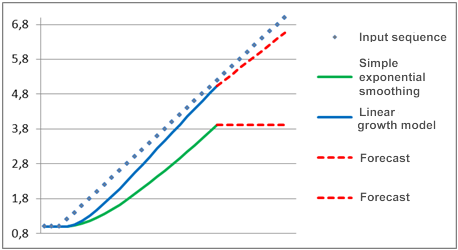
Uzun bir süre boyunca incelenen sürecin sabit bir bileşeni temsil ettiğini, yani grafikte düz bir yatay çizgi olarak göründüğünü, ancak bir noktada doğrusal bir eğilimin ortaya çıkmaya başladığını varsayalım. Bu işlem için yukarıda belirtilen modeller kullanılarak yapılan tahmin Şekil 2'de gösterilmiştir.
karşılaştırması
Şekil 2. Model karşılaştırması
Görüldüğü üzere basit üssel düzeltme modeli doğrusal olarak değişen giriş sırasının önemli ölçüde arkasındadır ve bu model kullanılarak yapılan tahmin daha da uzaklaşır. Doğrusal büyüme modeli kullanıldığında çok farklı bir model görebiliriz. Eğilim ortaya çıktığında bu model sanki doğrusal olarak değişen sırayı bulmaya çalışıyor ve model tahmini değişen giriş değerlerinin yönüne daha yakın gibi oluyor.
Verilen örnekteki düzeltme katsayısı daha yüksekse doğrusal büyüme modeli verilen süre içinde giriş sinyaline "ulaşabilirdi" ve tahmini giriş sırasıyla neredeyse çakışıyordu.
Doğrusal eğilim varken sabit durumdaki doğrusal büyüme modeli iyi sonuçlar vermesine rağmen eğimi "yakalamasının" biraz zaman aldığı kolayca görülebilir. Bu nedenle eğilimin yönü sık sık değişirse model ve giriş sırası arasında her zaman bir boşluk olacaktır. Ayrıca eğilim doğrusal olmayan bir şekilde büyür ama bunun yerine kare yasaya uymazsa doğrusal büyüme modeli ona "ulaşamaz". Ancak bu dezavantajlara rağmen bu model, doğrusal eğilimde basit üssel düzeltme modelinden daha faydalıdır.
Daha önce de belirtildiği gibi doğrusal büyümenin tek parametreli modelini kullandık. Test sırası USDJPY M1'in bir parçası için alfa parametresinin en uygun değerini bulmak için alfa katsayı değerine karşı bir adım öndeki tahmin hatalarının karelerinin toplamının grafiğini oluşturalım.
Şekil 1'dekiyle aynı sıra parçası temel alınarak oluşturulan bu çizime Şekil 3'te ulaşabilirsiniz.
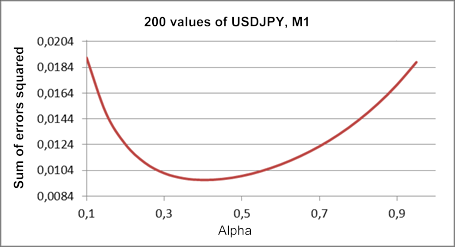
Şekil 3. Doğrusal büyüme modeli
Şekil 1'deki sonuçla karşılaştırıldığında alfa katsayısının optimal değeri bu durumda yaklaşık 0,4'e düşmüştür. Birinci ve ikinci düzeltme, teorik olarak değerleri farklı olsa da bu modelde aynı katsayılara sahiptir. İki farklı düzeltme katsayısına sahip doğrusal büyüme modeli daha detaylı incelenecektir.
İncelediğimiz her iki üssel düzeltme modelinin gösterge şeklindeki analogları MetaTrader 5'te bulunmaktadır. Bunlar tahmin için değil, sıra değerlerinin düzeltilmesi için tasarlanmış EMA ve DEMA iyi bilinmektedir.
DEMA göstergesini kullanırken tek adımlı tahmin değeri yerine a1 katsayısına karşılık gelen değerin görüntülendiği belirtilmelidir. a2 katsayısı (doğrusal büyüme modeli için yukarıdaki formüllere bakın) bu durumda hesaplanmaz veya kullanılmaz. Ayrıca düzeltme katsayısı eşdeğer dönem açısından n hesaplanır
Örneğin, 0,8'e eşit alfa, n'nin yaklaşık olarak 2'ye eşit olmasına karşılık gelir ve alfa 0,4 ise n 4'e eşittir.
4. Başlangıç Değerleri
Daha önce de belirtildiği gibi üssel düzeltme uygulanması üzerine öyle ya da böyle düzeltme katsayısı değeri elde edilecektir. Ancak bu, yetersiz olabilir. Üssel düzeltmede geçerli değer bir öncekine göre hesaplandığı için bu tür değerin sıfır zamanında daha olmadığı bir durum vardır. Başka bir deyişle, doğrusal büyüme modelinde S veya S1 ve S2'nin başlangıç değeri bir şekilde sıfır zamanında hesaplanacaktır.
Başlangıç değerlerini elde etme sorununu çözmek her zaman kolay değildir. Çok uzun (MetaTrader 5'te tırnak işareti kullanma durumunda olduğu gibi) geçmişimiz varsa üssel düzeltme eğrisi, ilk değerler yanlış belirlenmişse ilk hatamızı düzelterek mevcut noktaya kadar stabilize etmek için zamanımız olacaktır. Bu, düzeltme katsayısı değerine bağlı olarak yaklaşık 10 ila 200 (ve hatta bazen daha fazla) dönem gerektirecektir.
Bu durumda başlangıç değerlerini kabaca tahmin etmek ve hedef zaman diliminden 200-300 dönem önce üssel düzeltme işlemini başlatmak yeterli olacaktır. Ancak mevcut örnek yalnızca 100 değer içerdiğinde daha zor hale gelir.
Literatürde ilk değerlerin seçimi ile ilgili çeşitli öneriler vardır. Örneğin, basit üssel düzeltmedeki başlangıç değeri, sıradaki ilk ögeye eşitlenebilir veya rastgele aykırı değerleri düzeltmek için bir görünüme sahip sıradaki üç ila dört başlangıç ögesinin ortalaması olarak hesaplanabilir. Doğrusal büyüme modelinde S1 ve S2 başlangıç değerleri, tahmin eğrisinin başlangıç düzeyinin sıradaki ilk ögeye eşit olacağı ve doğrusal eğilimin eğiminin sıfır olacağı varsayımları temel alınarak belirlenebilir.
İlk değerlerin seçimiyle ilgili farklı kaynaklarda daha fazla öneri bulunabilir, ancak hiçbiri düzeltme algoritmasının erken aşamalarında gözle görülür hataların olmamasını sağlayamaz. Sabit bir duruma ulaşmak için çok sayıda dönem gerektiğinde düşük değerli düzeltme katsayılarının kullanılmasıyla özellikle fark edilir.
Bu nedenle, (özellikle kısa sıralar için) ilk değerlerin seçimiyle ilişkili sorunların etkisini en aza indirmek için bazen minimum tahmin hatasına neden olacak bu tür değerlerin aranmasını içeren bir yöntem kullanırız. Tüm sıra boyunca küçük artışlarla değişen başlangıç değerleri için bir tahmin hatası hesaplamasıdır.
Hata hesaplandıktan sonra ilk değerlerin olası tüm birleşimleri aralığında en uygun varyant seçilebilir. Ancak bu yöntem çok fazla hesaplama gerektirir ve çok zahmetlidir, doğrudan şeklinde neredeyse hiç kullanılmaz.
Açıklanan sorun, en iyi duruma getirme veya en az çok değişkenli işlev değeri arama ile ilgilidir. Bu tür sorunlar gerekli hesaplamaların kapsamını önemli ölçüde azaltmak için geliştirilen çeşitli algoritmalar kullanılarak çözülebilir. Birazdan tahminde parametrelerin ve başlangıç değerlerinin optimizasyonu sorunlarına geri döneceğiz.
5. Tahmin Doğruluğu Değerlendirmesi
Tahmin prosedürü ve modelin ilk değerlerinin veya parametrelerinin seçimi, tahmin doğruluğunu tahmin etme sorununa yol açtı. İki farklı modeli karşılaştırırken veya elde edilen tahminin tutarlılığını belirlerken doğruluğun değerlendirilmesi önemlidir. Tahmin doğruluğu değerlendirmesi için çok sayıda iyi bilinen tahmin vardır, ancak bunlardan herhangi birinin hesaplanması, her adımda tahmin hatasının bilinmesi gerekir.
Daha önce de belirtildiği gibi t zamanında bir adım önde tahmin hatası eşittir
burada:
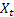– t zamanında giriş sırası değeri;
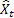– önceki adımda yapılan t zamanında tahmin.
Muhtemelen en yaygın tahmin doğruluğu tahmini ortalama kare hatasıdır (MSE):
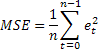
Burada n bir sıradaki ögelerin sayısıdır.
Büyük değerin arada sırada olan hatalarına karşı aşırı duyarlılık bazen MSE'nin bir dezavantajı olarak gösterilir. Bu, MSE hesaplanırken hata değerinin kareli olması yüzündendir. Alternatif olarak bu durumda ortalama mutlak hatanın (MAE) kullanılması önerilir.
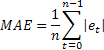
Buradaki kare hata, hatanın mutlak değeriyle değiştirilir. MAE kullanılarak elde edilen tahminler daha tutarlı olabilir.
Her iki tahmin örneğin, farklı model parametreleri veya farklı modeller kullanılarak aynı sıranın tahmin doğruluğunun değerlendirilmesi için oldukça uygundur, ancak farklı sıralarda alınan tahmin sonuçlarının karşılaştırılması için pek de kullanışlı değildir.
Ayrıca bu tahminlerin değerleri, tahmin sonucunun kalitesini önermez. Örneğin, elde edilen 0,03 MAE'nin mi yoksa başka bir değerin mi iyi veya kötü olduğunu söyleyemeyiz.
Farklı sıraların tahmin doğruluğunu karşılaştırabilmek için RelMSE ve RelMAE göreli tahminleri kullanabiliriz:
Burada, elde edilen tahmin doğruluğu tahminleri, tahmin test yöntemi kullanılarak elde edilen ilgili tahminlere bölünür. Bir test yöntemi olarak sürecin gelecekteki değerinin mevcut değere eşit olacağını öne süren saf yöntemi kullanmak uygundur.
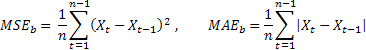
Tahmin hatalarının ortalaması saf yöntem kullanılarak elde edilen hataların değerine eşitse göreli tahmin değeri bire eşit olur. Göreli tahmin değeri birden küçükse ortalama olarak tahmin hata değerinin saf yöntemden daha küçük olduğu anlamına gelir. Başka bir deyişle tahmin sonuçlarının doğruluğu saf yöntemin doğruluğuna göre sıralar. Tam tersine göreli tahmin değeri birden büyükse tahmin sonuçlarının doğruluğu ortalama olarak saf tahmin yönteminden daha zayıftır.
Bu tahminler, iki veya daha fazla adım için tahmin doğruluğunun değerlendirilmesi için de uygundur. Hesaplamalardaki tek adımlı tahmin hatasının ilerideki uygun adım sayısı için tahmin hatalarının değeriyle değiştirilmesi yeterlidir.
Örneğin, aşağıdaki tablo doğrusal büyümenin tek parametreli modelinde RelMAE kullanılarak tahmin edilen bir adım ilerideki tahmin hatalarını içerir. Hatalar, her test sırasının son 200 değeri kullanılarak hesaplandı.
|
Tablo 1. RelMAE kullanılarak tahmin edilen bir adım ileri tahmin hataları
RelMAE tahmini, farklı sıraları tahmin ederken seçili yöntemin etkinliğini karşılaştırmayı sağlar. Tablo 1'deki sonuçlardan da anlaşılacağı gibi, tahminimiz hiçbir zaman saf yöntemden daha doğru olmamıştır - tüm RelMAE değeri birden fazladır.
6. Katkı Modelleri
Makalenin geçtiğimiz bölümlerinde işlem düzeyinin, doğrusal eğilimin ve rastgele bir değişkenin toplamını içeren bir model vardı. Yukarıdaki bileşenlere ek olarak döngüsel, dönemsel bir bileşen içeren başka bir model ekleyerek bu makalede incelenen modellerin listesini genişleteceğiz.
Toplam olarak tüm bileşenleri içeren üssel düzeltme modellerine katkı modelleri denir. Bu modellerin dışında bir tane, birçok veya tüm bileşenlerin bir ürün olarak oluştuğu çarpımsal modeller vardır. Katkı modelleri grubunu incelemeye devam edelim.
Bir adım ileri tahmin hatası, makalenin geçtiğimiz bölümlerinde defalarca belirtilmiştir. Bu hata, üssel düzeltmeye dayalı tahminle ilgili hemen hemen her uygulamada hesaplanmalıdır. Tahmin hatasının değeri bilinirse yukarıda tanıtılan üssel düzeltme modellerinin formülleri biraz farklı bir biçimde (hata düzeltme formu) sunulabilir.
Bizim durumumuzda kullanacağımız model gösteriminin şekli, ifadelerinde daha önce elde edilen değerlere kısmen veya tamamen eklenen bir hata içerir. Bu gösterime, ekleme hatası modeli denir. Üssel düzeltme modelleri, bu makalede kullanılmayacak olan çarpımsal hata formuyla da ifade edilebilir.
Katkılı üssel düzeltme modellerine bir göz atalım.
Basit üssel düzelme:
Eşdeğer model – ARIMA(0,1,1):
Katkılı doğrusal büyüme modeli:
Daha önce tanıtılan tek parametreli doğrusal büyüme modelinin aksine burada iki farklı düzeltme parametresi kullanılır.
Eşdeğer model – ARIMA(0,2,2): 
Sönümlemeli doğrusal büyüme modeli:
Bu tür bir sönümlemenin anlamı, eğilim eğiminin sönümleme katsayısının değerine bağlı olarak sonraki her tahmin adımında geri çekilmesidir. Bu etki Şekil 4'te gösterilmiştir.
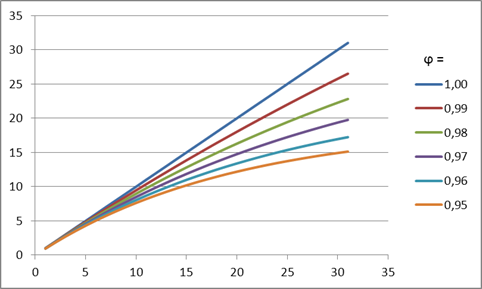
Şekil 4. Sönümleme katsayısı etkisi
Şekilde görüldüğü üzere, tahminde bulunarak sönümleme katsayısının azalan değeri, eğilimin daha hızlı güç kaybetmesine neden olacak, böylece doğrusal büyüme giderek daha fazla sönümlenecektir.
Eşdeğer model - ARIMA(1,1,2): 
Bu üç modelin her birine toplam olarak dönemsel bir bileşen ekleyerek üç model daha elde edeceğiz.
Katkı dönemselliği içeren basit model:
Katkı dönemselliği içeren doğrusal büyüme modeli:
Sönümlemeli ve katkı dönemselliği içeren doğrusal büyüme modeli:
Dönemsellik modeline eşdeğer ARIMA modelleri de vardır, ancak pratik bir öneme sahip olmayacakları için burada gösterilmeyecektir.
Sağlanan formüllerde kullanılan gösterimler aşağıdaki gibidir:
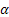- [0:1] sıra seviyesi için düzeltme parametresi;
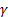- [0:1] eğim için düzeltme parametresi;
– dönemsel endeksler için düzeltme parametresi, [0:1];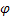
- sönüm parametresi [0:1];
- 
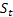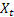olduktan sonra t zamanında hesaplanan sıranın düzleştirilmiş seviyesi;
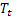- t zamanında hesaplanan düzleştirilmiş katkılı eğimi;
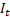– t zamanında hesaplanan düzleştirilmiş dönemsel endeks;
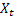- t zamanında sıranın değeri;- m - tahminin yapıldığı gelecek adımların sayısı;
- p – dönemsel döngüdeki dönem sayısı;
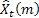- t zamanında yapılan m adım ilerisi tahmini;
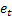- t zamanında bir adım ilerisi tahmini hatası, 
.
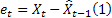Sağlanan son modelin formüllerinin incelenen altı varyasyonun tümünü içerdiği kolayca görülür.
Sönümleme ve katkı dönemselliği ile doğrusal büyüme modeli formüllerinde
,
tahminde dönemsellik göz ardı edilecektir. Ayrıca, 
olduğunda doğrusal bir büyüme modelinin üretilir ve 
olduğunda sönümleme ile doğrusal bir büyüme modeli elde edilir.
Basit üssel düzeltme modeli 
'a karşılık gelecektir.
Dönemsellik içeren modeller kullanılırken döngünün ve döngünün döneminin varlığı, bu verileri dönemsel endekslerin değerlerinin başlatılması için daha fazla kullanma amacıyla mevcut herhangi bir yöntem kullanılarak belirlenmelidir.
Tahminlerin kısa zaman aralıklarında yapıldığı bizim durumumuzda kullanılan test sıralarının parçalarında önemli ölçüde kararlı bir döngüsellik tespit edemedik. Bu nedenle, bu makalede ilgili örnekler vermeyeceğiz ve dönemsellikle ilişkili özellikleri genişletmeyeceğiz.
İncelenen modellerle ilgili olasılık tahmin aralıklarını kararlaştırmak için kaynakta bulunan analitik türevleri kullanacağız [3]. n boyutundaki tüm örneklerde hesaplanan bir adım ilerideki tahmin hatalarının karelerinin toplamının ortalaması, bu tür hataların tahmini farkı olarak kullanılacaktır.
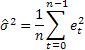
İncelenen modeller için 2 ve daha fazla adım ileriye yönelik tahmindeki tahmini varyansının kararlaştırılması için aşağıdaki ifade doğru olacaktır:
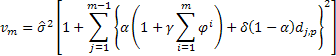
Burada j modulo p sıfırsa 
bire eşittir, aksi takdirde 
sıfırdır.
Her adım m için tahmin tahmini varyansı hesapladığında % 95 tahmin aralığının sınırlarını bulabiliriz:
Bu tahmin aralığını, tahmin güven aralığı olarak adlandıracağız.
Üssel düzeltme modelleri için sağlanan ifadeleri MQL5 ile yazılmış bir sınıfta uygulayalım.
7. AdditiveES Sınıfının Uygulanması
Sınıfın uygulanması, sönümlemeli ve katkı dönemsellikli doğrusal büyüme modeli için ifadelerin kullanımını içerir.
Daha önce de belirtildiği gibi, diğer modeller uygun bir parametre seçimi ile türetilebilir.
//----------------------------------------------------------------------------------- // AdditiveES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //----------------------------------------------------------------------------------- // Forecasting. Exponential smoothing. Additive models. // References: // 1. Everette S. Gardner Jr. Exponential smoothing: The state of the art – Part II. // June 3, 2005. // 2. Rob J Hyndman. Forecasting based on state space models for exponential // smoothing. 29 August 2002. // 3. Rob J Hyndman et al. Prediction intervals for exponential smoothing // using two new classes of state space models. 30 January 2003. //----------------------------------------------------------------------------------- class AdditiveES:public CObject { protected: double Alpha; // Smoothed parameter for the level of the series double Gamma; // Smoothed parameter for the trend double Phi; // Autoregressive or damping parameter double Delta; // Smoothed parameter for seasonal indices int nSes; // Number of periods in the seasonal cycle double S; // Smoothed level of the series, computed after last Y is observed double T; // Smoothed additive trend double Ises[]; // Smoothed seasonal indices int p_Ises; // Pointer for Ises[] shift register double F; // Forecast for 1 period ahead from origin t public: AdditiveES(); double Init(double s,double t,double alpha=1,double gamma=0, double phi=1,double delta=0,int nses=1); double GetS() { return(S); } double GetT() { return(T); } double GetF() { return(F); } double GetIs(int m); void IniIs(int m,double is); // Initialization of smoothed seasonal indices double NewY(double y); // Next calculating step double Fcast(int m); // m-step ahead forecast double VarCoefficient(int m); // Coefficient for calculating prediction intervals }; //----------------------------------------------------------------------------------- // Constructor //----------------------------------------------------------------------------------- void AdditiveES::AdditiveES() { Alpha=0.5; Gamma=0; Delta=0; Phi=1; nSes=1; ArrayResize(Ises,nSes); ArrayInitialize(Ises,0); p_Ises=0; S=0; T=0; } //----------------------------------------------------------------------------------- // Initialization //----------------------------------------------------------------------------------- double AdditiveES::Init(double s,double t,double alpha=1,double gamma=0, double phi=1,double delta=0,int nses=1) { S=s; T=t; Alpha=alpha; if(Alpha<0)Alpha=0; if(Alpha>1)Alpha=1; Gamma=gamma; if(Gamma<0)Gamma=0; if(Gamma>1)Gamma=1; Phi=phi; if(Phi<0)Phi=0; if(Phi>1)Phi=1; Delta=delta; if(Delta<0)Delta=0; if(Delta>1)Delta=1; nSes=nses; if(nSes<1)nSes=1; ArrayResize(Ises,nSes); ArrayInitialize(Ises,0); p_Ises=0; F=S+Phi*T; return(F); } //----------------------------------------------------------------------------------- // Calculations for the new Y //----------------------------------------------------------------------------------- double AdditiveES::NewY(double y) { double e; e=y-F; S=S+Phi*T+Alpha*e; T=Phi*T+Alpha*Gamma*e; Ises[p_Ises]=Ises[p_Ises]+Delta*(1-Alpha)*e; p_Ises++; if(p_Ises>=nSes)p_Ises=0; F=S+Phi*T+GetIs(0); return(F); } //----------------------------------------------------------------------------------- // Return smoothed seasonal index //----------------------------------------------------------------------------------- double AdditiveES::GetIs(int m) { if(m<0)m=0; int i=(int)MathMod(m+p_Ises,nSes); return(Ises[i]); } //----------------------------------------------------------------------------------- // Initialization of smoothed seasonal indices //----------------------------------------------------------------------------------- void AdditiveES::IniIs(int m,double is) { if(m<0)m=0; if(m<nSes) { int i=(int)MathMod(m+p_Ises,nSes); Ises[i]=is; } } //----------------------------------------------------------------------------------- // m-step-ahead forecast //----------------------------------------------------------------------------------- double AdditiveES::Fcast(int m) { int i,h; double v,v1; if(m<1)h=1; else h=m; v1=1; v=0; for(i=0;i<h;i++){v1=v1*Phi; v+=v1;} return(S+v*T+GetIs(h)); } //----------------------------------------------------------------------------------- // Coefficient for calculating prediction intervals //----------------------------------------------------------------------------------- double AdditiveES::VarCoefficient(int m) { int i,h; double v,v1,a,sum,k; if(m<1)h=1; else h=m; if(h==1)return(1); v=0; v1=1; sum=0; for(i=1;i<h;i++) { v1=v1*Phi; v+=v1; if((int)MathMod(i,nSes)==0)k=1; else k=0; a=Alpha*(1+v*Gamma)+k*Delta*(1-Alpha); sum+=a*a; } return(1+sum); } //-----------------------------------------------------------------------------------
AdditiveES sınıfının yöntemlerini kısaca inceleyelim.
Init yöntemi
Giriş parametreleri:
- double s - düzeltilmiş seviyenin başlangıç değerini ayarlar;
- double t - düzeltilmiş eğilimin başlangıç değerini ayarlar;
- double alpha=1 - sıra düzeyi için düzeltme parametresini ayarlar;
- double gamma=0 - eğilim için düzeltme parametresini ayarlar;
- double phi=1 - sönümleme parametresini ayarlar;
- double delta=0 - dönemsel endeksler için düzeltme parametresini ayarlar;
- int nses=1 - dönem döngüsündeki dönem sayısını ayarlar.
Dönüş değeri:
- Ayarlanan ilk değerler temel alınarak hesaplanan bir adım ilerideki tahmine döner.
Init yöntemi ilk etapta kullanılmalıdır. Bu, düzeltme parametrelerini ve başlangıç değerlerini ayarlamak için gereklidir. Init yönteminin dönemsel endekslerin rasgele değerlerde başlatıldığını unutmayınız; bu yöntemi kullanırken dönemsel endeksler her zaman sıfır olarak ayarlanır.
IniIs yöntemi
Giriş parametreleri:
- Int m - dönemsel endeks numarası;
- double is - m numarasının dönemsel sıra değerini ayarlar.
Dönüş değeri:
- Hiçbiri
IniIs(...) yöntemi, dönemsel endekslerin başlangıç değerleri sıfırdan farklıysa kullanılır. Sezon endeksler, Init(...) yöntemi kullanıldıktan hemen sonra başlatılmalıdır.
NewY yöntemi
Giriş parametreleri:
- double y – giriş sırasının yeni değeri
Dönüş değeri:
- Sıranın yeni değerine göre hesaplanan bir adım ilerideki tahmine döner
Bu yöntem, giriş sırasına her yeni değer girildiğinde bir adım ilerideki tahmini hesaplamak için tasarlanmıştır. Yalnızca Init ve -gerektiğinde- IniIs yöntemleri tarafından sınıf başlatıldıktan sonra kullanılmalıdır.
Fcast yöntemi
Giriş parametreleri:
- int m – 1,2,3,... döneminin tahmin ufku;
Dönüş değeri:
- M-adım ileri tahmin değerine döner.
Bu yöntem, düzeltme işleminin durumunu etkilemeden yalnızca tahmin değerini hesaplar. Genellikle NewY yöntemini kullanıldıktan sonra kullanılır.
VarCoefficient yöntemi
Giriş parametreleri:
- int m – 1,2,3,... döneminin tahmin ufku;
Dönüş değeri:
- Tahmin farkını hesaplamak için katsayı değerine döner.
Bu katsayı değeri, bir adım ilerideki tahmin varyansına kıyasla m-adım ilerideki tahmin varyansındaki artışı gösterir.
GetS, GetT, GetF, GetIs yöntemleri
Bu yöntemler sınıfın korumalı değişkenlerine erişim sağlar. GetS, GetT ve GetF sırayla, düzeltilmiş seviyenin, düzeltilmiş eğilimin ve bir adım ilerideki tahmin değerlerine döner. GetIs yöntemi, dönemsel endekslere erişim sağlar ve giriş bağımsız değişkeni olarak m endeks numarasının belirtilmesini gerektirir.
İncelediğimiz en karmaşık model, AdditiveES sınıfının oluşturulduğu sönümlemeli ve katkı dönemsellikli doğrusal büyüme modelidir. Bu, çok makul olan - kalan daha basit modellere ne gerek olduğu sorusunu gündeme getiriyor.
Daha karmaşık modellerin görünüşte daha basit olanlara göre açık bir avantajı olması gerekmesine rağmen her zaman böyle değildir. Daha az parametreye sahip daha basit modeller, vakaların büyük çoğunluğunda tahmin hatalarının daha az varyansı olmasını sağlar, yani çalışmaları daha istikrarlı olacaktır. Bu, en basitinden en karmaşık olanlara kadar mevcut tüm modellerin eşzamanlı paralel çalışmasına dayalı tahmin algoritmaları oluşturmada kullanılır.
Sıra tam olarak işlendikten sonra parametrelerinin sayısı (yani karmaşıklığı), verilen en düşük hatayı gösteren bir tahmin modeli seçilir. Bu amaçla geliştirilen bir dizi kriter vardır, örneğin Akaike’nin Bilgi Kriteri(AIC). En istikrarlı tahmini üretmesi beklenen bir modelin seçilmesini sağlayacaktır.
AdditiveES sınıfının kullanımını göstermek için tüm düzeltme parametreleri manuel olan basit bir gösterge oluşturuldu.
AdditiveES_Test.mq5 göstergesinin kaynak kodu aşağıda verilmiştir.
//----------------------------------------------------------------------------------- // AdditiveES_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" // Forecast #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "PInterval+" // Prediction interval #property indicator_type3 DRAW_LINE #property indicator_color3 clrCadetBlue #property indicator_style3 STYLE_SOLID #property indicator_width3 1 #property indicator_label4 "PInterval-" // Prediction interval #property indicator_type4 DRAW_LINE #property indicator_color4 clrCadetBlue #property indicator_style4 STYLE_SOLID #property indicator_width4 1 double HIST[]; double FORE[]; double PINT1[]; double PINT2[]; input double Alpha=0.2; // Smoothed parameter for the level input double Gamma=0.2; // Smoothed parameter for the trend input double Phi=0.8; // Damping parameter input double Delta=0; // Smoothed parameter for seasonal indices input int nSes=1; // Number of periods in the seasonal cycle input int nHist=250; // History bars, nHist>=100 input int nTest=150; // Test interval, 50<=nTest<nHist input int nFore=12; // Forecasting horizon, nFore>=2 #include "AdditiveES.mqh" AdditiveES fc; int NHist; // history bars int NFore; // forecasting horizon int NTest; // test interval double ALPH; // alpha double GAMM; // gamma double PHI; // phi double DELT; // delta int nSES; // Number of periods in the seasonal cycle //----------------------------------------------------------------------------------- // Custom indicator initialization function //----------------------------------------------------------------------------------- int OnInit() { NHist=nHist; if(NHist<100)NHist=100; NFore=nFore; if(NFore<2)NFore=2; NTest=nTest; if(NTest>NHist)NTest=NHist; if(NTest<50)NTest=50; ALPH=Alpha; if(ALPH<0)ALPH=0; if(ALPH>1)ALPH=1; GAMM=Gamma; if(GAMM<0)GAMM=0; if(GAMM>1)GAMM=1; PHI=Phi; if(PHI<0)PHI=0; if(PHI>1)PHI=1; DELT=Delta; if(DELT<0)DELT=0; if(DELT>1)DELT=1; nSES=nSes; if(nSES<1)nSES=1; MqlRates rates[]; CopyRates(NULL,0,0,NHist,rates); // Load missing data SetIndexBuffer(0,HIST,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,FORE,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFore); SetIndexBuffer(2,PINT1,INDICATOR_DATA); PlotIndexSetString(2,PLOT_LABEL,"Conf+"); PlotIndexSetInteger(2,PLOT_SHIFT,NFore); SetIndexBuffer(3,PINT2,INDICATOR_DATA); PlotIndexSetString(3,PLOT_LABEL,"Conf-"); PlotIndexSetInteger(3,PLOT_SHIFT,NFore); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } //----------------------------------------------------------------------------------- // Custom indicator iteration function //----------------------------------------------------------------------------------- int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,j,init,start; double v1,v2; if(rates_total<NHist){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated>rates_total||prev_calculated<=0||(rates_total-prev_calculated)>1) {init=1; start=rates_total-NHist;} else {init=0; start=prev_calculated;} if(start==rates_total)return(rates_total); // New tick but not new bar //----------------------- if(init==1) // Initialization { i=start; v2=(open[i+2]-open[i])/2; v1=(open[i]+open[i+1]+open[i+2])/3.0-v2; fc.Init(v1,v2,ALPH,GAMM,PHI,DELT,nSES); ArrayInitialize(HIST,EMPTY_VALUE); } PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFore); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFore); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFore); for(i=start;i<rates_total;i++) // History { HIST[i]=fc.NewY(open[i]); } v1=0; for(i=0;i<NTest;i++) // Variance { j=rates_total-NTest+i; v2=close[j]-HIST[j-1]; v1+=v2*v2; } v1/=NTest; // v1=var j=1; for(i=rates_total-NFore;i<rates_total;i++) { v2=1.96*MathSqrt(v1*fc.VarCoefficient(j)); // Prediction intervals FORE[i]=fc.Fcast(j++); // Forecasting PINT1[i]=FORE[i]+v2; PINT2[i]=FORE[i]-v2; } return(rates_total); } //-----------------------------------------------------------------------------------
Göstergenin kullanılması veya tekrarlanan başlatılması üssel düzeltme başlangıç değerlerini ayarlar
Bu göstergede dönemsel endeksler için başlangıç ayarları yoktur, bu nedenle başlangıç değerleri her zaman sıfıra eşittir. Bu tür bir başlatmayla birlikte dönemselliğin tahmin sonucu üzerindeki etkisi, yeni gelen değerlerin tanıtılmasıyla kademeli olarak sıfırdan belirli bir sabit değere yükselir.
Sabit durumlu çalışma durumuna ulaşmak için gereken döngü sayısı, dönemsel endeksler için düzeltme katsayısının değerine bağlıdır: Düzeltme katsayı değeri ne kadar düşük olursa o kadar fazla zaman gerektirecektir.
Varsayılan ayarlara sahip AdditiveES_Test.mq5 göstergesinin işlem sonucu Şekil 5'te gösterilmiştir.
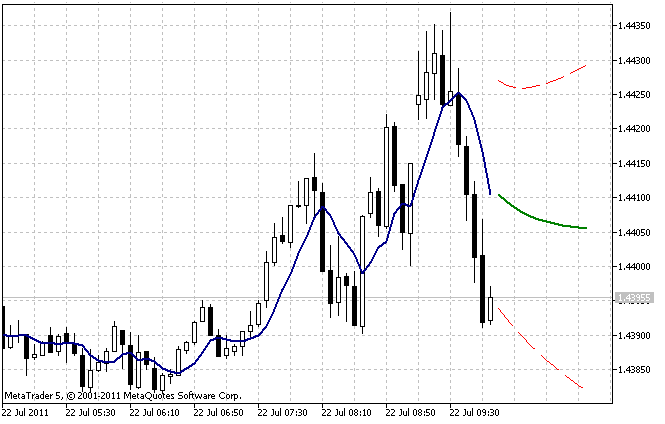
Şekil 5. AdditiveES_Test.mq5 göstergesi
Gösterge, tahmin dışında %95 tahmin güven aralığının sırasının geçmiş değerleri ve sınırları için tek adımlı tahmine karşılık gelen ek bir satır görüntüler.
Güven aralığı, bir adım ilerideki hatanın tahmini farkına dayanır. Seçilen başlangıç değerleri yanlışlığının etkisini azaltmak için tahmini varyans, tüm nHist uzunluğu boyunca hesaplanmaz, ancak sadece giriş parametresi nTest'te belirtilen son çubuklara göre hesaplanır.
Makalenin sonundaki Files.zip arşivi, AdditiveES.mqh ve AdditiveES_Test.mq5 dosyalarını içerir. Gösterge derlendiğinde, AdditiveES.mqh dosyasının AdditiveES_Test.mq5 ile aynı dizinde bulunması gerekir.
AdditiveES_Test.mq5 göstergesi oluşturulduğu zaman başlangıç değerlerini seçme sorunu bir dereceye kadar çözülürken, düzeltme parametrelerinin en uygun değerlerini seçme sorunu açık kalır.
8. En Uygun Parametre Değerlerinin Seçimi
Basit üssel düzeltme modeli, tek bir düzeltme parametresine sahiptir ve en uygun değeri, basit numaralandırma yöntemi kullanılarak bulunabilir. Tüm sıra üzerinden tahmin hata değerleri hesaplanmasından sonra parametre değeri küçük bir artışta değiştirilir ve tam hesaplama yeniden yapılır. Bu prosedür, tüm olası parametre değerleri numaralandırılana kadar tekrarlanır. Şimdilik sadece en küçük hata değeriyle sonuçlanan parametre değerini seçmemiz gerekiyor.
0,05 artışlarla 0,1 ila 0,9 aralığındaki düzeltme katsayısının en uygun değerini bulmak için tahmin hata değerinin tam hesaplamasının on yedi kez yapılması gerekir. Görüldüğü gibi gerekli hesaplama sayısı çok büyük değildir. Ancak sönümlemeli doğrusal büyüme modeli, üç düzeltme parametresinin optimizasyonunu içerir ve bu durumda tüm kombinasyonlarını aynı aralıkta ve aynı 0,05 artışlarla numaralandırmak için 4913 hesaplama çalıştırılması gerekir.
Tüm olası parametre değerlerinin numaralandırılması için gereken tam çalıştırma sayısı, parametre sayısındaki artış, numaralandırma aralığının artışı ve genişlemesindeki azalma ile hızla artar. Düzeltme parametrelerine ek olarak modellerin başlangıç değerlerini daha fazla optimize etmek gerekliyse basit numaralandırma yöntemini kullanarak yapmak oldukça zor olacaktır.
Birkaç değişkenin işlevinin minimumunu bulmakla ilgili sorunlar iyi incelenmiştir ve bu tür algoritmalardan oldukça fazla vardır. Kaynakta fonksiyonun minimumunu bulmak için çeşitli yöntemlerin tanımı ve karşılaştırması bulunabilir [7]. Tüm bu yöntemler öncelikle nesnel işlevin kullanılma sayısını azaltmaya, yani minimumu bulma sürecindeki hesaplama çabalarını azaltmaya yöneliktir.
Farklı kaynaklar genellikle quasi-Newton methods of optimization’a referans içerir. Büyük olasılıkla bunun yüksek verimlilikleriyle ilgilidir, ancak daha basit bir yöntemin uygulanması da tahminin optimizasyonuna yönelik bir yaklaşımın gösterilmesi için yeterli olmalıdır. Powell yönteminiele alalım. Powell yöntemi, nesnel işlev türevlerinin hesaplanmasını gerektirmez ve arama yöntemlerindendir.
Bu yöntem, diğer yöntemler gibi programlı olarak çeşitli şekillerde uygulanabilir. Nesnel işlev değerinin belirli bir doğruluğa veya bağımsız değişken değerine ulaşıldığında arama tamamlanmalıdır. Ayrıca belirli bir uygulama, izin verilen işlev parametresi değişiklikleri aralığında sınırlamalar kullanma olasılığını içerebilir.
Bizim durumumuzda, Powell yöntemini kullanarak kısıtlanmamış bir minimum bulma algoritması PowellsMethod.class'da uygulanmaktadır. Algoritma, nesnel işlev değerinin verilen doğruluğa ulaşıldığında aramayı durdurur. Bu yöntemin uygulanmasında kaynakta [8] bulunan bir algoritma prototip olarak kullanılmıştır.
Aşağıda PowellsMethod sınıfının kaynak kodu verilmiştir.
//----------------------------------------------------------------------------------- // PowellsMethod.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #define GOLD 1.618034 #define CGOLD 0.3819660 #define GLIMIT 100.0 #define SHFT(a,b,c,d) (a)=(b);(b)=(c);(c)=(d); #define SIGN(a,b) ((b) >= 0.0 ? fabs(a) : -fabs(a)) #define FMAX(a,b) (a>b?a:b) //----------------------------------------------------------------------------------- // Minimization of Functions. // Unconstrained Powell’s Method. // References: // 1. Numerical Recipes in C. The Art of Scientific Computing. //----------------------------------------------------------------------------------- class PowellsMethod:public CObject { protected: double P[],Xi[]; double Pcom[],Xicom[],Xt[]; double Pt[],Ptt[],Xit[]; int N; double Fret; int Iter; int ItMaxPowell; double FtolPowell; int ItMaxBrent; double FtolBrent; int MaxIterFlag; public: void PowellsMethod(void); void SetItMaxPowell(int n) { ItMaxPowell=n; } void SetFtolPowell(double er) { FtolPowell=er; } void SetItMaxBrent(int n) { ItMaxBrent=n; } void SetFtolBrent(double er) { FtolBrent=er; } int Optimize(double &p[],int n=0); double GetFret(void) { return(Fret); } int GetIter(void) { return(Iter); } private: void powell(void); void linmin(void); void mnbrak(double &ax,double &bx,double &cx,double &fa,double &fb,double &fc); double brent(double ax,double bx,double cx,double &xmin); double f1dim(double x); virtual double func(const double &p[]) { return(0); } }; //----------------------------------------------------------------------------------- // Constructor //----------------------------------------------------------------------------------- void PowellsMethod::PowellsMethod(void) { ItMaxPowell= 200; FtolPowell = 1e-6; ItMaxBrent = 200; FtolBrent = 1e-4; } //----------------------------------------------------------------------------------- void PowellsMethod::powell(void) { int i,j,m,n,ibig; double del,fp,fptt,t; n=N; Fret=func(P); for(j=0;j<n;j++)Pt[j]=P[j]; for(Iter=1;;Iter++) { fp=Fret; ibig=0; del=0.0; for(i=0;i<n;i++) { for(j=0;j<n;j++)Xit[j]=Xi[j+n*i]; fptt=Fret; linmin(); if(fabs(fptt-Fret)>del){del=fabs(fptt-Fret); ibig=i;} } if(2.0*fabs(fp-Fret)<=FtolPowell*(fabs(fp)+fabs(Fret)+1e-25))return; if(Iter>=ItMaxPowell) { Print("powell exceeding maximum iterations!"); MaxIterFlag=1; return; } for(j=0;j<n;j++){Ptt[j]=2.0*P[j]-Pt[j]; Xit[j]=P[j]-Pt[j]; Pt[j]=P[j];} fptt=func(Ptt); if(fptt<fp) { t=2.0*(fp-2.0*(Fret)+fptt)*(fp-Fret-del)*(fp-Fret-del)-del*(fp-fptt)*(fp-fptt); if(t<0.0) { linmin(); for(j=0;j<n;j++){m=j+n*(n-1); Xi[j+n*ibig]=Xi[m]; Xi[m]=Xit[j];} } } } } //----------------------------------------------------------------------------------- void PowellsMethod::linmin(void) { int j,n; double xx,xmin,fx,fb,fa,bx,ax; n=N; for(j=0;j<n;j++){Pcom[j]=P[j]; Xicom[j]=Xit[j];} ax=0.0; xx=1.0; mnbrak(ax,xx,bx,fa,fx,fb); Fret=brent(ax,xx,bx,xmin); for(j=0;j<n;j++){Xit[j]*=xmin; P[j]+=Xit[j];} } //----------------------------------------------------------------------------------- void PowellsMethod::mnbrak(double &ax,double &bx,double &cx, double &fa,double &fb,double &fc) { double ulim,u,r,q,fu,dum; fa=f1dim(ax); fb=f1dim(bx); if(fb>fa) { SHFT(dum,ax,bx,dum) SHFT(dum,fb,fa,dum) } cx=bx+GOLD*(bx-ax); fc=f1dim(cx); while(fb>fc) { r=(bx-ax)*(fb-fc); q=(bx-cx)*(fb-fa); u=bx-((bx-cx)*q-(bx-ax)*r)/(2.0*SIGN(FMAX(fabs(q-r),1e-20),q-r)); ulim=bx+GLIMIT*(cx-bx); if((bx-u)*(u-cx)>0.0) { fu=f1dim(u); if(fu<fc){ax=bx; bx=u; fa=fb; fb=fu; return;} else if(fu>fb){cx=u; fc=fu; return;} u=cx+GOLD*(cx-bx); fu=f1dim(u); } else if((cx-u)*(u-ulim)>0.0) { fu=f1dim(u); if(fu<fc) { SHFT(bx,cx,u,cx+GOLD*(cx-bx)) SHFT(fb,fc,fu,f1dim(u)) } } else if((u-ulim)*(ulim-cx)>=0.0){u=ulim; fu=f1dim(u);} else {u=cx+GOLD*(cx-bx); fu=f1dim(u);} SHFT(ax,bx,cx,u) SHFT(fa,fb,fc,fu) } } //----------------------------------------------------------------------------------- double PowellsMethod::brent(double ax,double bx,double cx,double &xmin) { int iter; double a,b,d,e,etemp,fu,fv,fw,fx,p,q,r,tol1,tol2,u,v,w,x,xm; a=(ax<cx?ax:cx); b=(ax>cx?ax:cx); d=0.0; e=0.0; x=w=v=bx; fw=fv=fx=f1dim(x); for(iter=1;iter<=ItMaxBrent;iter++) { xm=0.5*(a+b); tol2=2.0*(tol1=FtolBrent*fabs(x)+2e-19); if(fabs(x-xm)<=(tol2-0.5*(b-a))){xmin=x; return(fx);} if(fabs(e)>tol1) { r=(x-w)*(fx-fv); q=(x-v)*(fx-fw); p=(x-v)*q-(x-w)*r; q=2.0*(q-r); if(q>0.0)p=-p; q=fabs(q); etemp=e; e=d; if(fabs(p)>=fabs(0.5*q*etemp)||p<=q*(a-x)||p>=q*(b-x)) d=CGOLD*(e=(x>=xm?a-x:b-x)); else {d=p/q; u=x+d; if(u-a<tol2||b-u<tol2)d=SIGN(tol1,xm-x);} } else d=CGOLD*(e=(x>=xm?a-x:b-x)); u=(fabs(d)>=tol1?x+d:x+SIGN(tol1,d)); fu=f1dim(u); if(fu<=fx) { if(u>=x)a=x; else b=x; SHFT(v,w,x,u) SHFT(fv,fw,fx,fu) } else { if(u<x)a=u; else b=u; if(fu<=fw||w==x){v=w; w=u; fv=fw; fw=fu;} else if(fu<=fv||v==x||v==w){v=u; fv=fu;} } } Print("Too many iterations in brent"); MaxIterFlag=1; xmin=x; return(fx); } //----------------------------------------------------------------------------------- double PowellsMethod::f1dim(double x) { int j; double f; for(j=0;j<N;j++) Xt[j]=Pcom[j]+x*Xicom[j]; f=func(Xt); return(f); } //----------------------------------------------------------------------------------- int PowellsMethod::Optimize(double &p[],int n=0) { int i,j,k,ret; k=ArraySize(p); if(n==0)N=k; else N=n; if(N<1||N>k)return(0); ArrayResize(P,N); ArrayResize(Xi,N*N); ArrayResize(Pcom,N); ArrayResize(Xicom,N); ArrayResize(Xt,N); ArrayResize(Pt,N); ArrayResize(Ptt,N); ArrayResize(Xit,N); for(i=0;i<N;i++)for(j=0;j<N;j++)Xi[i+N*j]=(i==j?1.0:0.0); for(i=0;i<N;i++)P[i]=p[i]; MaxIterFlag=0; powell(); for(i=0;i<N;i++)p[i]=P[i]; if(MaxIterFlag==1)ret=-1; else ret=Iter; return(ret); } //-----------------------------------------------------------------------------------
Optimize yöntemi, sınıfın ana yöntemidir.
Optimize yöntemi
Giriş parametreleri:
- double &p[] - girişte en uygun değerlerin bulunacağı parametrelerin başlangıç değerlerini içeren dizi; bu parametrelerin elde edilen en uygun değerleri dizinin çıktısıdır.
- int n=0 - p[] sırasındaki bağımsız değişken sayısı. Burada n=0, parametre sayısı, p[] sırasının boyutuna eşit olarak kabul edilir.
Dönüş değeri:
- Algoritmanın çalışması için gereken yineleme sayısına veya izin verilen maksimum sayıya ulaşıldıysa -1’e döner.
En uygun parametre değerleri aranırken nesnel işlevin minimumuna yinelemeli bir yaklaşım oluşur. Optimize yöntemi, verilen doğrulukla işlev minimumuna ulaşmak için gereken yineleme sayısına döner. Nesnel işlev her yinelemede birkaç kez kullanılır, yani nesnel işlevin kullanılma sayısı, Optimize yöntemi tarafından yineleme sayısından önemli ölçüde (on ve hatta yüz kat) daha büyük olabilir.
Sınıfın diğer yöntemleri.
SetItMaxPowell yöntemi
Giriş parametreleri:
- Int n - Powell'ın yönteminde izin verilen maksimum yineleme sayısı. Varsayılan değer 200'dür.
Dönüş değeri:
- Yok.
İzin verilen en fazla yineleme sayısını ayarlar; bu sayıya ulaşıldıktan sonra, belirli bir doğrulukla nesnel işlevin en azının bulunup bulunmadığına bakılmaksızın arama sona erer. Ve ilgili bir mesaj günlüğe eklenir.
SetFtolPowell yöntemi
Giriş parametreleri:
- double er - doğruluk. Nesnel işlevin en küçük değerinden bu sapma değerine ulaşılması durumunda Powell yöntemi aramayı durdurur. Varsayılan değer 1e-6'dır.
Dönüş değeri:
- Yok.
SetItMaxBrent yöntemi
Giriş parametreleri:
- Int n - yardımcı Brent yöntemi için izin verilen maksimum yineleme sayısı. Varsayılan değer 200'dür.
Dönüş değeri:
- Yok.
İzin verilen en fazla yineleme sayısını ayarlar. Sayıya ulaşıldıktan sonra yardımcı Brent'in yöntemi aramayı durdurur ve günlüğe ilgili bir mesaj ekler.
SetFtolBrent yöntemi
Giriş parametreleri:
- double er – doğruluk. Bu değer yardımcı Brent'in yöntemi için minimumun aranmasında doğruluğu tanımlar. Varsayılan değer 1e-4'dür.
Dönüş değeri:
- Yok.
GetFret yöntemi
Giriş parametreleri:
- Yok.
Dönüş değeri:
- Elde edilen nesnel işlevin minimum değerine döner.
GetIter yöntemi
Giriş parametreleri:
- Yok.
Dönüş değeri:
- Algoritmanın çalışması için gereken yineleme sayısına döner.
Sanal işlev func(const double &p[])
Giriş parametreleri:
- const double &p[] – en iyi duruma getirilmiş parametreleri içeren dizinin adresi. Dizinin boyutu işlev parametrelerinin sayısına karşılık gelir.
Dönüş değeri:
- Ona geçirilen parametrelere karşılık gelen işlev değerine döner.
Sanal işlev func(), her özel durumda PowellsMethod sınıfından türetilen sınıfta yeniden tanımlanacaktır. func() işlevi, arama algoritması uygulanırken işlev tarafından dönülen minimum değere karşılık gelen bağımsız değişkenlerin bulunacağı nesnel işlevdir.
Powell yönteminin bu uygulaması, her parametreyle ilgili arama yönünü belirlemek için Brent'in tek değişkenli parabolik enterpolasyon yöntemini kullanmaktadır. Bu yöntemler için doğruluk ve izin verilen maksimum yineleme sayısı SetItMaxPowell, SetFtolPowell, SetItMaxBrent ve SetFtolBrent çağrılarak ayrı olarak ayarlanabilir.
Böylelikle algoritmanın varsayılan özellikleri değiştirilebilir. Bu, belirli bir nesnel işleve ayarlanan varsayılan doğruluk çok yüksek olduğunda ve algoritma arama işleminde çok fazla yineleme gerektirdiğinde faydalı olabilir. Gerekli doğruluğun değerindeki değişiklik, farklı nesnel işlev kategorilerine göre aramayı optimize edebilir.
Powell yöntemini kullanan algoritmanın karmaşık görünmesine rağmen kullanımı oldukça basittir.
Örneği gözden geçirelim. Diyelim ki bir işlevimiz var
ve işlevin en küçük değere sahip olacağı parametrelerin değerlerini 
ve 
bulmalıyız.
Bu soruna çözüm gösteren bir senaryo yazalım.
//----------------------------------------------------------------------------------- // PM_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- class PM_Test:public PowellsMethod { public: void PM_Test(void) {} private: virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- double PM_Test::func(const double &p[]) { double f,r1,r2; r1=p[0]-0.5; r2=p[1]-6.0; f=r1*r1*4.0+r2*r2; return(f); } //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { int it; double p[2]; p[0]=8; p[1]=9; // Initial point PM_Test *pm = new PM_Test; it=pm.Optimize(p); Print("Iter= ",it," Fret= ",pm.GetFret()); Print("p[0]= ",p[0]," p[1]= ",p[1]); delete pm; } //-----------------------------------------------------------------------------------
Bu komut dosyasını yazarken önce, p[0] ve p[1] parametrelerinin geçen değerlerini kullanarak verilen test işlevinin değerini hesaplayan PM_Test sınıfının bir üyesi olarak func() işlevini oluştururuz. Daha sonra OnStart() işlevinin gövdesinde, başlangıç değerleri gerekli parametrelere atanır. Arama bu değerlerden başlayacaktır.
Ayrıca PM_Test sınıfının bir kopyası oluşturulur ve p[0] ve p[1] gerekli değerlerini aramak, Optimize yöntemi kullanılarak başlar; üst PowellsMethod sınıfının yöntemleri yeniden tanımlanan func() işlevini kullanır. Arama tamamlandıktan sonra yineleme sayısı, minimum noktadaki işlev değeri ve elde edilen parametre değerleri p[0]=0.5 ve p[1]=6 günlüğe eklenir.
PowellsMethod.mqh ve PM_Test.mq5 test çalışması, Files.zip arşivdeki makalenin sonunda bulunur. PM_Test.mq5 derlemek için PowellsMethod.mqh ile aynı dizinde bulunmalıdır.
9. Model Parametre Değerlerinin Optimize Edilmesi
Makalenin önceki bölümünde işlevi minimum bulma yönteminin uygulanması ele alındı ve bunun kullanımına basit bir örnek verdi. Şimdi, üssel düzeltme modeli parametrelerinin optimizasyonu ile ilgili konulara devam edeceğiz.
İlk olarak dönemselliği dikkate alan modeller, bu makalede daha fazla incelenmeyeceği için dönemsel bileşenle ilişkili tüm unsurları hariç tutarak daha önce bahsedilen AdditiveES sınıfını maksimuma basitleştirelim. Bu, sınıfın kaynak kodunun anlaşılmasını ve hesaplama sayısını azaltmayı çok daha kolay hale getirir. Buna ek olarak, dikkate alınan sönümlemeli doğrusal büyüme modeli parametrelerinin optimizasyonuna yönelik yaklaşımın kolay gösterimi için tahmin güven aralıklarının tahmin ve hesaplamalarıyla ilgili tüm hesaplamaları hariç tutacağız.
//----------------------------------------------------------------------------------- // OptimizeES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- // Class OptimizeES //----------------------------------------------------------------------------------- class OptimizeES:public PowellsMethod { protected: double Dat[]; // Input data int Dlen; // Data lenght double Par[5]; // Parameters int NCalc; // Number of last elements for calculation public: void OptimizeES(void) {} int Calc(string fname); private: int readCSV(string fnam,double &dat[]); virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- // Calc //----------------------------------------------------------------------------------- int OptimizeES::Calc(string fname) { int i,it; double relmae,naiv,s,t,alp,gam,phi,e,ae,pt; if(readCSV(fname,Dat)<0){Print("Error."); return(-1);} Dlen=ArraySize(Dat); NCalc=200; // number of last elements for calculation if(NCalc<0||NCalc>Dlen-1){Print("Error."); return(-1);} Par[0]=Dat[Dlen-NCalc]; // initial S Par[1]=0; // initial T Par[2]=0.5; // initial Alpha Par[3]=0.5; // initial Gamma Par[4]=0.5; // initial Phi it=Optimize(Par); // Powell's optimization s=Par[0]; t=Par[1]; alp=Par[2]; gam=Par[3]; phi=Par[4]; relmae=0; naiv=0; for(i=Dlen-NCalc;i<Dlen;i++) { e=Dat[i]-(s+phi*t); relmae+=MathAbs(e); naiv+=MathAbs(Dat[i]-Dat[i-1]); ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } relmae/=naiv; PrintFormat("%s: N=%i, RelMAE=%.3f",fname,NCalc,relmae); PrintFormat("Iter= %i, Fmin= %e",it,GetFret()); PrintFormat("p[0]= %.5f, p[1]= %.5f, p[2]= %.2f, p[3]= %.2f, p[4]= %.2f", Par[0],Par[1],Par[2],Par[3],Par[4]); return(0); } //----------------------------------------------------------------------------------- // readCSV //----------------------------------------------------------------------------------- int OptimizeES::readCSV(string fnam,double &dat[]) { int n,asize,fhand; fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI); if(fhand==INVALID_HANDLE) { Print("FileOpen Error!"); return(-1); } asize=512; ArrayResize(dat,asize); n=0; while(FileIsEnding(fhand)!=true) { dat[n++]=FileReadNumber(fhand); if(n+128>asize) { asize+=128; ArrayResize(dat,asize); } } FileClose(fhand); ArrayResize(dat,n-1); return(0); } //------------------------------------------------------------------------------------ // func //------------------------------------------------------------------------------------ double OptimizeES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 sse=0; for(i=Dlen-NCalc;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(NCalc*MathLog(k1*k2*k3*sse)); } //------------------------------------------------------------------------------------
OptimizeES sınıfı PowellsMethod sınıfından türemiştir ve sanal işlev func()’ın yeniden tanımlamasını içerir. Daha önce de belirtildiği gibi, optimizasyon sırasında hesaplanan değeri minimuma indirilecek parametreler, bu işlevin girişine geçirilecektir.
Maksimum olasılık yöntemine uygun olarak func() işlevi, bir adım ilerideki tahmin hatalarının karelerinin toplamının logaritmasını hesaplar. Hatalar, sıranın NCalc son değerleriyle ilgili olarak bir döngüde hesaplanır.
Modelin istikrarını korumak için model parametrelerindeki değişiklik aralığına sınırlamalar getirmeliyiz. Alfa ve Gama parametreleri için bu aralık, 0,05 ila 0,95 ve Phi parametresi için - 0,05 ila 1,0 olacaktır. Ancak bizim durumumuzda optimizasyon için nesnel işlevin bağımsız değişkenlerin sınırlamaların kullanıldığı anlamına gelmeyen, kısıtlanmamış minimum bulmak için yöntem kullanırız.
Sınırlı çok değişkenli fonksiyonun minimumunu bulma sorununu, sınırsız bir minimum bulma sorununa dönüştürmeye, arama algoritmasını değiştirmeden parametrelere uygulanan tüm sınırlamaları dikkate almaya çalışacağız. Bu amaçla ceza fonksiyonu adı verilen yöntem kullanılacaktır. Bu yöntem tek boyutlu bir durum için kolayca gösterilebilir.
Tek bir (etki alanı 2,0 ila 3,0 olan) bağımsız değişkenin işlevine ve arama işleminde bu işlev parametresine, herhangi bir değer atayabilecek algoritmaya sahip olduğumuzu varsayalım. Bu durumda şöyle yapabiliriz: arama algoritması, izin verilen maksimum değeri aşan bir bağımsız değişkeni geçtiyse örneğin, 3.5, işlev 3.0'a eşit bağımsız değişken için hesaplanabilir ve elde edilen sonuç, örneğin, k=1+(3.5-3)*200 gibi maksimum değerin fazlalığıyla orantılı bir katsayı ile daha çarpılır.
İzin verilen minimum değerin altında olduğu ortaya çıkan bağımsız değişken değerlerine göre benzer işlemler yapılırsa elde edilen nesnel işlevin, bağımsız değişkeninde izin verilen değişiklik aralığının dışında artacağı garanti edilir. Nesnel işlevin elde edilen değerindeki bu yapay artış, arama algoritmasının işleve iletilen bağımsız değişkenin herhangi bir şekilde sınırlı olduğundan habersiz kalmasını ve elde edilen işlevin minimumunun bağımsız değişkenin belirlenen sınırların içinde olmasını sağlar. Bu tür yaklaşım birkaç değişkenin işlevine kolayca uygulanır.
OptimizeES sınıfının ana yöntemi Calc yöntemidir. Bu yöntemin kullanımı, dosyadan veri okumaktan, modelin en uygun parametre değerlerini aramaktan ve elde edilen parametre değerleri için RelMAE kullanarak tahmin doğruluğunu tahmin etmekten sorumludur. Bir dosyadan okunan sıranın işlenen değerlerinin sayısı bu durumda NCalc değişkeninde ayarlanır.
Aşağıda OptimizeES sınıfını kullanan Optimization_Test.mq5 komut dosyası örneği verilmiştir.
//----------------------------------------------------------------------------------- // Optimization_Test.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "OptimizeES.mqh" OptimizeES es; //----------------------------------------------------------------------------------- // Script program start function //----------------------------------------------------------------------------------- void OnStart() { es.Calc("Dataset\\USDJPY_M1_1100.TXT"); } //-----------------------------------------------------------------------------------
Bu komut dosyasının yürütülmesinden sonra elde edilen sonuç aşağıda gösterildiği gibi olacaktır.
Şekil 6. Optimization_Test.mq5 komut dosyası sonucu
Modelin en uygun parametre değerlerini ve başlangıç değerlerini bulabilsek de basit araçlar -optimizasyonda kullanılan sıra değerlerinin sayısı- kullanılarak optimize edilemeyen bir parametre kalır. Büyük uzunluktaki sırayla ilgili optimizasyonda, ortalama olarak sıranın tüm uzunluğu boyunca minimum hata sağlayan en uygun parametre değerlerini elde edeceğiz.
Ancak sıranın niteliği bu aralık içinde değiştiyse bazı parçaların elde edilen değerleri artık en uygun olmayacaktır. Öte yandan, sıra uzunluğu önemli ölçüde azalırsa bu kadar kısa bir aralık için elde edilen en uygun parametrelerin daha uzun bir gecikmede en uygunu olacağının garantisi yoktur.
OptimizeES.mqh ve Optimization_Test.mq5, Files.zip arşivindeki makalenin sonunda bulunur. Derleme yaparken OptimizeES.mqh ve PowellsMethod.mqh'un derlenmiş Optimization_Test.mq5 ile aynı dizinde bulunması gerekir. Verilen örnekte test sırasını içeren ve \MQL5\Files\Dataset\ dizininde bulunması gereken USDJPY_M1_1100.TXT dosya kullanılır.
Tablo 2, bu komut dosyasıyla RelMAE kullanılarak elde edilen tahmin doğruluğunun tahminlerini gösterir. Tahmin, test sıraların her birinin son 100, 200 ve 400 değerleri kullanılarak makalede daha önce belirtilen sekiz test sırasıyla ilgili olarak yapılmıştır.
|
Tablo 2. RelMAE kullanılarak tahmin edilen tahmin hataları
Görüldüğü gibi tahmin hatası tahminleri birliğe yakındır, ancak çoğu durumda, bu modelde verilen sıralar için tahmin sade yöntemden daha doğrudur.
10. IndicatorES.mq5 Göstergesi
AdditiveES.mqh sınıfına dayalı AdditiveES_Test.mq5 göstergesi, sınıfın gözden geçirilmesi üzerine daha önce belirtilmiştir. Bu göstergedeki tüm düzeltme parametreleri manuel olarak ayarlandı.
Şimdi model parametrelerini optimize etmeye izin verme yöntemini ele aldıktan sonra, en uygun parametre değerlerinin ve başlangıç değerlerinin otomatik olarak kararlaştırılacağı ve sadece işlenmiş numune uzunluğunun manuel olarak ayarlanacağı benzer bir gösterge oluşturabiliriz. Bununla birlikte dönemsellikle ilgili tüm hesaplamaları hariç tutacağız.
Gösterge oluşturulurken kullanılan CIndiсatorES sınıfının kaynak kodu aşağıda verilmiştir.
//----------------------------------------------------------------------------------- // CIndicatorES.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include "PowellsMethod.mqh" //----------------------------------------------------------------------------------- // Class CIndicatorES //----------------------------------------------------------------------------------- class CIndicatorES:public PowellsMethod { protected: double Dat[]; // Input data int Dlen; // Data lenght double Par[5]; // Parameters public: void CIndicatorES(void) { } void CalcPar(double &dat[]); double GetPar(int n) { if(n>=0||n<5)return(Par[n]); else return(0); } private: virtual double func(const double &p[]); }; //----------------------------------------------------------------------------------- // CalcPar //----------------------------------------------------------------------------------- void CIndicatorES::CalcPar(double &dat[]) { Dlen=ArraySize(dat); ArrayResize(Dat,Dlen); ArrayCopy(Dat,dat); Par[0]=Dat[0]; // initial S Par[1]=0; // initial T Par[2]=0.5; // initial Alpha Par[3]=0.5; // initial Gamma Par[4]=0.5; // initial Phi Optimize(Par); // Powell's optimization } //------------------------------------------------------------------------------------ // func //------------------------------------------------------------------------------------ double CIndicatorES::func(const double &p[]) { int i; double s,t,alp,gam,phi,k1,k2,k3,e,sse,ae,pt; s=p[0]; t=p[1]; alp=p[2]; gam=p[3]; phi=p[4]; k1=1; k2=1; k3=1; if (alp>0.95){k1+=(alp-0.95)*200; alp=0.95;} // Alpha > 0.95 else if(alp<0.05){k1+=(0.05-alp)*200; alp=0.05;} // Alpha < 0.05 if (gam>0.95){k2+=(gam-0.95)*200; gam=0.95;} // Gamma > 0.95 else if(gam<0.05){k2+=(0.05-gam)*200; gam=0.05;} // Gamma < 0.05 if (phi>1.0 ){k3+=(phi-1.0 )*200; phi=1.0; } // Phi > 1.0 else if(phi<0.05){k3+=(0.05-phi)*200; phi=0.05;} // Phi < 0.05 sse=0; for(i=0;i<Dlen;i++) { e=Dat[i]-(s+phi*t); sse+=e*e; ae=alp*e; pt=phi*t; s=s+pt+ae; t=pt+gam*ae; } return(Dlen*MathLog(k1*k2*k3*sse)); } //------------------------------------------------------------------------------------
Bu sınıf, CalcPar ve GetPar yöntemlerini içerir; birincisi modelin en uygun parametre değerlerinin hesaplanması için, ikincisi ise bu değerlere erişmek için tasarlanmıştır. Ayrıca CIndicatorES sınıfı, sanal işlev func() yeniden tanımlanmasını içerir.
IndicatorES.mq5 göstergesinin kaynak kodu:
//----------------------------------------------------------------------------------- // IndicatorES.mq5 // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #property indicator_chart_window #property indicator_buffers 4 #property indicator_plots 4 #property indicator_label1 "History" #property indicator_type1 DRAW_LINE #property indicator_color1 clrDodgerBlue #property indicator_style1 STYLE_SOLID #property indicator_width1 1 #property indicator_label2 "Forecast" // Forecast #property indicator_type2 DRAW_LINE #property indicator_color2 clrDarkOrange #property indicator_style2 STYLE_SOLID #property indicator_width2 1 #property indicator_label3 "ConfUp" // Confidence interval #property indicator_type3 DRAW_LINE #property indicator_color3 clrCrimson #property indicator_style3 STYLE_DOT #property indicator_width3 1 #property indicator_label4 "ConfDn" // Confidence interval #property indicator_type4 DRAW_LINE #property indicator_color4 clrCrimson #property indicator_style4 STYLE_DOT #property indicator_width4 1 input int nHist=80; // History bars, nHist>=24 #include "CIndicatorES.mqh" #define NFORE 12 double Hist[],Fore[],Conf1[],Conf2[]; double Data[]; int NDat; CIndicatorES Es; //----------------------------------------------------------------------------------- // Custom indicator initialization function //----------------------------------------------------------------------------------- int OnInit() { NDat=nHist; if(NDat<24)NDat=24; MqlRates rates[]; CopyRates(NULL,0,0,NDat,rates); // Load missing data ArrayResize(Data,NDat); SetIndexBuffer(0,Hist,INDICATOR_DATA); PlotIndexSetString(0,PLOT_LABEL,"History"); SetIndexBuffer(1,Fore,INDICATOR_DATA); PlotIndexSetString(1,PLOT_LABEL,"Forecast"); PlotIndexSetInteger(1,PLOT_SHIFT,NFORE); SetIndexBuffer(2,Conf1,INDICATOR_DATA); // Confidence interval PlotIndexSetString(2,PLOT_LABEL,"ConfUp"); PlotIndexSetInteger(2,PLOT_SHIFT,NFORE); SetIndexBuffer(3,Conf2,INDICATOR_DATA); // Confidence interval PlotIndexSetString(3,PLOT_LABEL,"ConfDN"); PlotIndexSetInteger(3,PLOT_SHIFT,NFORE); IndicatorSetInteger(INDICATOR_DIGITS,_Digits); return(0); } //----------------------------------------------------------------------------------- // Custom indicator iteration function //----------------------------------------------------------------------------------- int OnCalculate(const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[]) { int i,start; double s,t,alp,gam,phi,e,f,a,a1,a2,a3,var,ci; if(rates_total<NDat){Print("Error: Not enough bars for calculation!"); return(0);} if(prev_calculated==rates_total)return(rates_total); // New tick but not new bar start=rates_total-NDat; //----------------------- PlotIndexSetInteger(0,PLOT_DRAW_BEGIN,rates_total-NDat); PlotIndexSetInteger(1,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(2,PLOT_DRAW_BEGIN,rates_total-NFORE); PlotIndexSetInteger(3,PLOT_DRAW_BEGIN,rates_total-NFORE); for(i=0;i<NDat;i++)Data[i]=open[rates_total-NDat+i]; // Input data Es.CalcPar(Data); // Optimization of parameters s=Es.GetPar(0); t=Es.GetPar(1); alp=Es.GetPar(2); gam=Es.GetPar(3); phi=Es.GetPar(4); f=(s+phi*t); var=0; for(i=0;i<NDat;i++) // History { e=Data[i]-f; var+=e*e; a1=alp*e; a2=phi*t; s=s+a2+a1; t=a2+gam*a1; f=(s+phi*t); Hist[start+i]=f; } var/=(NDat-1); a1=1; a2=0; a3=1; for(i=rates_total-NFORE;i<rates_total;i++) { a1=a1*phi; a2+=a1; Fore[i]=s+a2*t; // Forecast ci=1.96*MathSqrt(var*a3); // Confidence intervals a=alp*(1+a2*gam); a3+=a*a; Conf1[i]=Fore[i]+ci; Conf2[i]=Fore[i]-ci; } return(rates_total); } //-----------------------------------------------------------------------------------
Her yeni çubukta gösterge, model parametrelerinin en uygun değerlerini bulur, belirli sayıda NHist çubukları için modelde hesaplamalar yapar, tahmin oluşturur ve tahmin güven sınırlarını tanımlar.
Göstergenin tek parametresi, minimum değeri 24 çubukla sınırlı olan işlenmiş sıranın uzunluğudur. Göstergedeki tüm hesaplamalar, açık[] değerlere göre yapılır. Tahmin süresi 12 bardır. IndicatorES.mq5 göstergesinin ve CIndicatorES.mqh dosyasının kodu, Files.zip arşivinde makalenin sonunda bulunmaktadır.
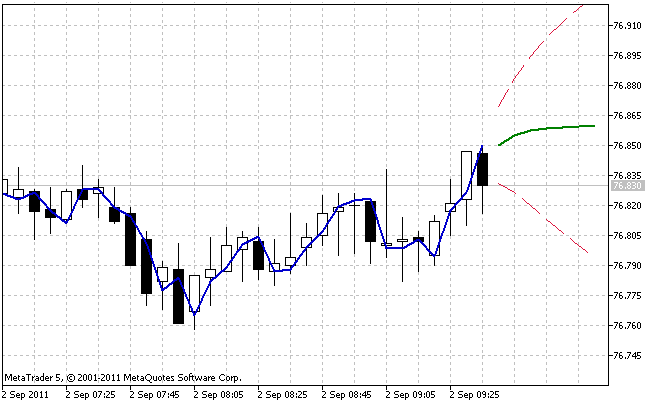
Şekil 7. IndicatorES.mq5 göstergesinin çalışma sonucu
IndicatorES.mq5 göstergesinin çalışma sonucuna bir örnek Şekil 7'de gösterilmiştir. Göstergenin çalışması sırasında %95 tahmin güven aralığı, modelin elde edilen en uygun parametre değerlerine karşılık gelen değerleri alacaktır. Düzeltme parametre değerleri ne kadar büyükse artan tahmin ufkunda güven aralığındaki artış o kadar hızlı olur.
Basit bir iyileştirmeyle IndicatorES.mq5 göstergesi, sadece döviz tekliflerini tahmin etmek için değil, ayrıca çeşitli göstergelerin veya önceden işlenmiş verilerin değerlerini tahmin etmek için de kullanılabilir.
Sonuç
Makalenin temel amacı, okuyucuya tahminde kullanılan katkılı üssel düzeltme modellerini tanıtmaktı. Pratik kullanımlarını gösterirken beraberindeki bazı sorunlar da ele alındı. Ayrıca makalede verilen materyaller, yalnızca tahminle ilgili çok çeşitli sorunlara ve çözümlere giriş olarak kabul edilebilir.
Verilen sınıfların, işlevlerin, senaryoların ve göstergelerin makalenin yazım sürecinde oluşturulduğuna ve öncelikle makalenin materyallerine örnek teşkil edecek şekilde tasarlandığı hususlarına dikkatinizi çekmek isterim. Bu nedenle stabilite ve hatalar için ciddi bir test yapılmadı. Ayrıca makalede belirtilen göstergeler, sadece ilgili yöntemlerin uygulanmasının bir göstergesi olarak düşünülmelidir.
Makalede tanıtılan IndicatorES.mq5 göstergesinin tahmin doğruluğu, incelenen alıntıların özellikleri açısından daha yeterli olan, uygulanan modelin değişiklikleri kullanılarak büyük olasılıkla geliştirilebilir. Gösterge, diğer modeller tarafından da yükseltilebilir. Ancak bu konular, bu makalenin kapsamının dışındadır.
Sonuç olarak, üssel düzeltme modellerinin belirli durumlarda, daha karmaşık modeller uygulanarak elde edilen tahminlerle aynı doğrulukta tahminler üretebileceği ve böylece en karmaşık modelin bile her zaman en iyi olmadığını bir kez daha kanıtladığı belirtilmelidir.
Referanslar
- Everette S. Gardner Jr. Exponential Smoothing: The State of the Art – Part II. 3 Haziran 2005.
- Rob J Hyndman. Forecasting Based on State Space Models for Exponential Smoothing. 29 Ağustos 2002.
- Rob J Hyndman et al. Prediction Intervals for Exponential Smoothing Using Two New Classes of State Space Models. 30 Ocak 2003.
- Rob J Hyndman ve Muhammad Akram. Some Nonlinear Exponential Smoothing Models Are Unstable. 17 Ocak 2006.
- Rob J Hyndman ve Anne B Koehler. Another Look at Measures of Forecast Accuracy. 2 Kasım 2005.
- Yu. P. Lukashin. Adaptive Methods for Short-Term Forecasting of Time Series: Textbook. - М.: Finansy i Statistika, 2003.-416 pp.
- D. Himmelblau. Applied Nonlinear Programming. М.: Mir, 1975.
- Numerical Recipes in C. The Art of Scientific Computing. İkinci Baskı. Cambridge University Press.
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/318
Göstergelerin İstatistiksel Parametrelerini Analiz Etme
Zaman Serisinin Temel Özelliklerinin Analizi
Alım Satım Sistemleri Geliştirmek İçin Diskriminant Analizini Kullanma
MQL5'te Gelişmiş Uyarlanabilir Göstergeler Teorisi ve Uygulaması
- Ücretsiz ticaret uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz