ボックスーコックス変換

MetaTrader 5 — 統計と分析 | 28 10月 2015, 08:22

2 391

はじめに

PCの能力が向上する一方、FOREXトレーダーやアナリストは、かなりのCPU資源を要する複雑で高度な数学的アルゴリズムを使用する可能性を得るようになりました。しかし、CPU資源の妥当性は、トレーダーの問題を単独では解決できません。市場価格の分析における効果的なアルゴリズムも必要なのです。

現在、数学的な統計の分野や経済学、計量経済学は、数多くのメソッド、モデルや、市場分析にてトレーダーにより使用されるよく機能するアルゴリズムを提供しています。多くは、リサーチされるシーケンスの安定性や、分布則の標準生を想定して作成された標準パラメーターメソッドです。

しかし、FOREXの取引価格は、安定してたり、正規分布則を持つものとして分類することができないシーケンスです。したがって、取引価格を分析する際に数学的統計や軽量経済学などの「標準の」パラーメターメソッドは使用できません。

"Box-Cox Transformation and the Illusion of Macroeconomic Series "Normality" [1]（ボックスーコックス変換と、マクロ経済学シリーズ”正規性”の錯覚）という記事では、A.NPorunovは以下のように記述しました：

"経済アナリストは、なぜか正規性のテストを通過しない統計データを扱う必要があります。この場合、二つの選択肢があります：かなりの数学的な訓練を要するパラメーターでないメソッドに頼るか、元の「正常な」統計において「異常な統計」を変換する特別なテクニックです、ただこれは複雑なタスクになります。”

A.N.Porunovの引用が経済アナリストを言及しているにもかかわらず、数学的統計や計量経済学のパラメーターメソッドを使用した「異常な」FOREX価格の分析の試みに完全に依存しています。これらのメソッドの大半は、正規分布則を持つシーケンスを分析するために開発されました。しかし、多くの場合、「異常な」初期データの事実は単に無視されます。さらに、言及されたメソッドは、正規分布のみではなく、初期のシーケンスの定常性も必要とします。

後退、拡散 (ANOVA) そして、いくつかの種類の分析は、初期データの正規性を要する「標準」メソッドと呼びます。正規分布則をに関連する制限を持つパラメーターメソッドを全てリスト化することは、非パラメーターメソッド以外の計量経済学の全ての分野を占めるため、不可能です。

「標準」パラメーターメソッドは、正規値からの初期データの拡散則の偏差に対して異なる感性を持っています。したがって、これらのメソッド使用中における「正規」からの偏差は、破滅的な結果には必ずしもつながりませんが、もちろん、取得された結果の信頼性や正確性は向上させません。

すべては、取引価格を分析・予想する非パラメーターメソッドへの変更の必要性に関する疑問を沸きたてます。しかし、パラメーターメソッドは依然とても魅力的です。これは、その普及度や、十分な量のデータや、アルゴリズム、その適用によっては、説明されません。これらのメソッドを適切に使用するために、少なくとも初期のシーケンス、不安定性と「異常性」に関連する二つの問題を処理する必要があります。

初期シーケンスの安全性に影響を与えることはできませんが、標準のものに近い分布則を持ってくることはできます。この問題を解決するために、様々な変換が存在します。よく知られたものは、"The Use of Box-Cox Transformation Technique in Economic and Statistical Analyses" [2]（ボックスーコックス変換技術の経済、統計的分析での使用）という記事にて簡単に述べられています。この記事では、ボックスーコックス変換 [1], [2], [3]のうち１つのみを扱います。

その他の種類と同様、ボックス-コックス変換の使用は、初期のシーケンスの分布則を多かれ少なかれ、標準に近づけることができると強調したいと思います。それは、この変換を使用することは、結果のシーケンスが標準の分布則を持つことを保証しません。

1. ボックスーコックス変換

Nの大きさでのXシーケンスに関して、

１パラメーターでのボックス-コックス変換は以下のようになります：

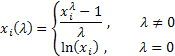
そこでは.

ご覧の通り、この変換は、１つのパラメーターーlanbdaのみを持ちます。もしラムダ値が０であれば、初期シーケンスの対数の変換が実行され、ラムダ値が０とは違う場合、変換は、指数法則です。もしラムダパラメーターが１に等しければ、それぞれの値から引かれるようにシーケンスはシフトしますが、初期シーケンスの分布則は変化しません。

ラムダ値に応じて、ボックス-コックス変換は、以下の特別なケースを持ちます；

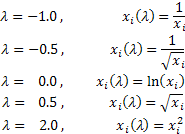
ボックス-コックス変換を使用すると、全ての入力シーケンス値が正の数であり、０とは異なることが要されます。もし入力シーケンスがこれらの必要性を満たさなければ、すべての値が正であることを保証する量によって正の区域に移動されます。

１パラメーターのボックス-コックス変換を、適切な方法で入力データを準備し、試してみましょう。負の数や０の値を避けるために、入力シーケンスの最低値を見て、1e-5の小さいシフトを追加で実行しながら、シーケンスの各要素からそれを引きます。そのような追加のシフトは、最低値が０に等しい場合、保証されたシーケンスの正の区域への置換を行います。

実際この置換を「正」のシーケンスに適用する必要はありません。しかし、変換中に累乗時に、かなりの大きい値を取得する可能性を排除するため同じアルゴリズムを使用します。したがって、入力シーケンスは、シフト後正の区域に位置し、０に近い最低値を持ちます。

図1 はボックス-コックス変換がラムダパラメーターの異なる値によりカーブすることを示します。図1 "Box-Cox Transformations（ボックス-コックス変換）" [3]のものです。チャートの水平のグリッドは、対数の規模について提供されています。

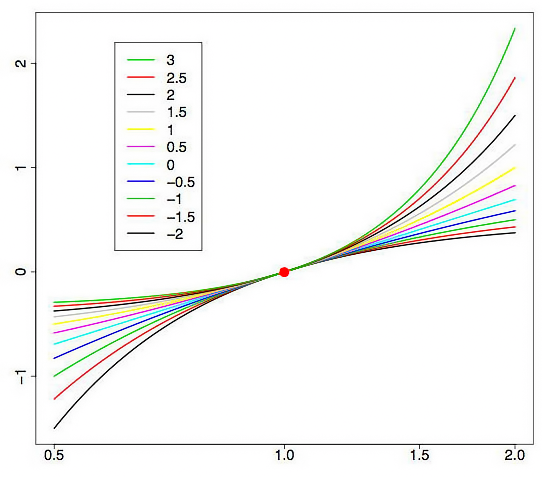
図1. ラムダパラメーターの様々な値におけるボックス-コックス変換

ご覧の通り、初期の分布の裏は、「伸ばされる」か「すぼめられる」のです。図1の上方のカーブは、ラムダ=3に一致し、下方は、ラムダ=2に一致します。

結果のシーケンスの分布則が正規則にできる限り近づくために、ラムダパラメーターの最適値が選択されなければばりません。

このパラメーターの最適値を決定する方法は、起こりうる関数の対数を最大化することです。

where

この関数が最大値に達する地点でのラムダパラメーターを選択する必要があるということです。

"Box-Cox Transformations" [3]（ボックス-コックス変換）という記事では、分類された変換済みシーケンスと正規分布関数の量との間での相関係数の最大値を探すことに基づいたこのパラメーターの最適値の別の決定方法を扱っています。おそらく、ラムダパラメーターの最適化メソッドを見つけることはできますが、まずは、起こりうる関数の対数の最大値の検索について議論しましょう。

いくつかの異なる方法があります。例えば、単純探索です。このためには、低ピッチでのラムダパラメーターを変化させる選択された範囲内での起こりうる関数値を計算する必要があります。また、可能背のある関数が最も高い値を持つ際の最適なラムダパラメーターを選択します。

そのピッチ間の距離は、ラムダパラメーターの最適な値の計算の正確性を決定します。計算の必要な量が比例して増えますが、ピッチが低くなれば、正確性は増します。関数の最大/最小を探す様々なアルゴリズム、遺伝アルゴリズムや、その他のメソッドは、計算の効果を向上させます。

2. 正規分布則への変換

ボックス-コックス変換の重要なタスクの一つは、入力シーケンスの分布則の「正規」形式への変化です。そのような問題がこの変換の助けにより、いかに解決されるのか理解しましょう。

不必要な繰り返しなどを避けるために、Powellのメソッドによる関数最小値の探索アルゴリズムを使用します。このアルゴリズムはすでに"Time Series Forecasting Using Exponential Smoothing"記事'指数平滑法を用いた時系列予測'）（にて紹介され、 "Time Series Forecasting Using Exponential Smoothing (continued)"記事'指数平滑法を用いた時系列予測'続き）でも言及されています。

変換パラメーター値の探索のためのCBoxCoxクラスを作成します。このクラスでは、上記の関数が客観的なものとして実現されています。PowellsMethod クラス[4]、 [5]は、探索アルゴリズムを直接実現する基礎として使用されます。

//+------------------------------------------------------------------+
//|                                                      CBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| CBoxCox class                                                    |
//+------------------------------------------------------------------+
class CBoxCox:public PowellsMethod
  {
protected:
   double            Dat[];          // Input data
   double            BCDat[];        // Box-Cox data
   int               Dlen;          // Data size
   double            Par[1];         // Parameters
   double            LnX;            // ln(x) sum
public:
   void   CBoxCox(void) { }
   void              CalcPar(double &dat[]);
   double GetPar(int n) { return(Par[n]); }
private:
   virtual double    func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CBoxCox::CalcPar(double &dat[])
  {
   int i;
   double a;
   //--- Lambda initial value
   Par[0]=1.0;                
   Dlen=ArraySize(dat);
   ArrayResize(Dat,Dlen);
   ArrayResize(BCDat,Dlen);
   LnX=0;
   for(i=0;i<Dlen;i++)
     {
    //--- input data
      a=dat[i]; Dat[i]=a;
     //--- ln(x) sum
     LnX+=MathLog(a);        
     }
    //--- Powell optimization
    Optimize(Par);            
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CBoxCox::func(const double &p[])
  {
   int i;
   double a,lamb,var,mean,k,ret;

   lamb=p[0]; var=0; mean=0; k=0;
   if(lamb>5.0){k=(lamb-5.0)*400; lamb=5.0;}         // Lambda >  5.0
   else if(lamb<-5.0){k=-(lamb+5.0)*400; lamb=-5.0;} // Lambda < -5.0

   //--- Lambda != 0.0
   if(lamb!=0)                                     
     {
      for(i=0;i<Dlen;i++)
        {
          //--- Box-Cox transformation
         BCDat[i]=(MathPow(Dat[i],lamb)-1.0)/lamb;  
          //--- average value calculation
         mean+=BCDat[i]/Dlen;
        }
     }
    //--- Lambda == 0.0
    else                                            
     {
      for(i=0;i<Dlen;i++)
        {
          //--- Box-Cox transformation
         BCDat[i]=MathLog(Dat[i]);
          //--- average value calculation
         mean+=BCDat[i]/Dlen;
        }
     }
   for(i=0;i<Dlen;i++)
     {
      a=BCDat[i]-mean;
       //--- variance
      var+=a*a/Dlen;
     }
   //--- log-likelihood
   ret=Dlen*MathLog(var)/2.0-(lamb-1)*LnX;         
   return(k+ret);
  }
//------------------------------------------------------------------------------------

ラムダパラメーターの最適値を見つけるためにすべきことは、入力データを含む配列へのリンクを提供することで言及されたクラスのCalcParメソッドを参照することです。取得されたパラメーターの最適値を、GetParメソッドを参照することで取得できます。以前述べられた通り、入力データは、正の数である必要があります。

PowellsMethodクラスは、変数のロットの関数最小値の探索アルゴリズムを実行しますが、この場合、シングルパラメーターが最適化されます。それは、Par[]配列の次元が１に等しいということにつながります。その配列は、一つの値のみ持つということを意味します。理論的に、パラメーター配列の代わりに標準変数を使用できますが、これは、PowellsMethod基礎クラスコードへの変更の実行を要します。想定するに、もしMQL5コードを一つの要素のみの配列を使用してコンパイルしても問題はありません。

CBoxCox::func()関数が、ラムダパラメーター許容値の範囲の制限を含むという事実にも注意してください。この場合、範囲は、-5から5の値に限られます。これは、入力データをラムダのレベルに上げる際に、大きすぎる、または小さすぎる値を取得することを避けるために行われます。

さらに、もし大きすぎるか、小さすぎるラムダの値を最適化中に取得すれば、シーケンスが選択された変換型において役に立たないということを意味します。したがって、ラムダ値の計算時に、妥当な範囲を超えないようにすることが賢い方法です。

3. ランダムシーケンス

擬似ランダムシーケンスのボックスーコックス変換を実行するテストスクリプトをCBoxCoxクラスを用いて作成しましょう。

以下が、そのスクリプトのソースコードです。

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest1.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- data size
   n=1600;
//--- input array preparation
   ArrayResize(dat,n);
//--- transformed data array
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- random sequence generation
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Exp();

//--- input data shift
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- optimization by lambda  
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- input data
//--- bcdat[] <-- transformed data
  }
//-----------------------------------------------------------------------------------

分布の指数則の擬似ランダムシーケンスは、入力データとして使用されます。シーケンスの長さは変数nにセットされ、1600値に等しいです。

RNDXor128クラス (George Marsaglia, Xorshift RNG)は擬似ランダムシーケンスの生成に使用されます。このクラスは、 "Analysis of the Main Characteristics of Time Series" [6]（'時系列の主な特徴の分析）にて記載されています。BoxCoxTest1.mq5スクリプトコンパイルにおいて、必要なファイルはBox-Cox-Tranformation_MQL5.zip アーカイブに保存されています。これらのファイルは、成功したコンパイルのために一つのディレクトリに位置しています。

そのスクリプトが実行された際、その入力シーケンスは形成され、正の値域に移動され、ラムダパラメーターの再t系値の探索が実行されます。それから、取得されたラムダ値や探索アルゴリズムの通貨数に関するメッセージが表示されます。変換済みのシーケンスは、bdat[]アウトプット配列に結果として作成されます。

現在の形式でのこのスクリプトは、さらなる使用のために変換済みのシーケンスのみを準備可能にし、その他の変更は実行しません。この記事を書く際、"Analysis of the Main Characteristics of Time Series" [6]（'時系列の主な特徴の分析）にて記載されている分析種類は、変換結果の評価のために選択されました。それに使用されるスクリプトは、行数を減らすためにこの記事は記載されていません。すでに出来上がった分析グラフ結果が以下に示されています。

図2は、BoxCoxTest1.mq5スクリプトにて使用された指数法則を持つランダムシーケンスのための正規分布規模により提供されたチャートとヒストグラムを表示しています。Jarque-Bera test result JB=3241.73, p= 0.000. ご覧の通り、入力シーケンスは「正規」ではなく、期待していた通り、その分布は指数のものと類似しています。

図 2

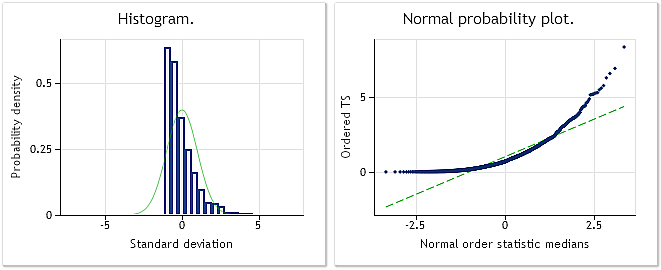
図 2. 指数分布則に沿った擬似ランダムシーケンスJarque-Bera test JB=3241.73, р=0.000.

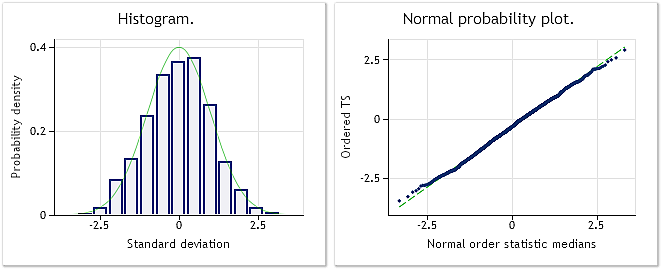
図3. 変換済みシーケンスLambda parameter=0.2779, Jarque-Bera test JB=4.73, р=0.094

図3は、変換済みシーケンス分析の結果(BoxCoxTest1.mq5 script, bcdat[] array).を示します。変換済みシーケンスの分布則は、正規分布のものとかなり近く、Jarque-Bera テスト結果 JB=4.73, p=0.094によっても確認されます。取得されたラムダパラメーター値=0.2779.

ボックスーコックス変換は、この例で適しているということが証明されました。結果のシーケンスは、より「正規」のものに近く、Jerue-Beraテスト結果はJB=3241.73から JB=4.73に下がりました。選択されたシーケンスは、この変換の種類に適しているため驚くべきことではありません。

擬似ランダムシーケンスのボックスーコックス変換の他の例を見てみましょう。ボックスーコックス変換において"適した"入力シーケンスを指数法則を考慮し作成する必要があります。このために、擬似ランダムシーケンス（すでに正規のもと近い分布則を持っています）を保証し、すべての値を0.35の乗数にあげることで変化させなければなりません。ボックスーコックス変換は、元の正規分布を正確に入力シーケンスに返すことを期待できます。

以下は、BoxCoxTest2.mq5テキストスクリプトのソースコードです。

このスクリプトは、その他の入力シーケンスがそれに生成されたという事実により以前のものと異なります。

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest2.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
#include  "RNDXor128.mqh"
CBoxCox   Bc;
RNDXor128 Rnd;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
//--- data size
   n=1600;
//--- input data array
   ArrayResize(dat,n);
//--- transformed data array
   ArrayResize(bcdat,n);
   Rnd.Reset();
//--- random sequence generation
   for(i=0;i<n;i++)dat[i]=Rnd.Rand_Norm();

//--- input data shift
   min=dat[ArrayMinimum(dat)]-1e-5;

   for(i=0;i<n;i++)dat[i]=dat[i]-min;
   for(i=0;i<n;i++)dat[i]=MathPow(dat[i],0.35);

//--- optimization by lambda
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);

   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0) { for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;   }
   else          { for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);  }     // Lambda == 0.0

//-- dat[]   <-- input data
//-- bcdat[] <-- transformed data
  }
//-----------------------------------------------------------------------------------

正規分布則の入力擬似ランダムシーケンスは、示されたスクリプトにて生成されます。それは、正の区域にシフトされ、このシーケンスのすべての要素は0.35乗にあげられます。このスクリプトの処理の終了後、dat[]配列は、入力シーケンスを含み、一方bcdat[]配列は、変換済みのものを含みます。

図4 は、0.35乗にまであげたため元の正規分布を失った入力シーケンスの特徴を示します。その場合、Jarque-BeraテストはJB=3609.29, p= 0.000と示します。」

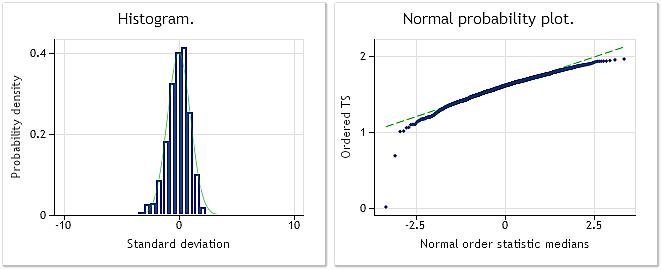
図4. 入力擬似ランダムシーケンスJarque-Bera テスト JB=3609.29, p=0.000.

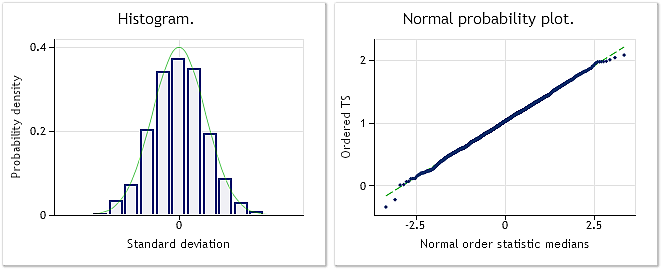
図5. 変換済みシーケンスラムダパラメーター=2.9067, Jarque-Beraテスト JB=0.30, p=0.859

図5で示されるように、変換済みシーケンスは、正規分布に近い分布則を持ち、Jarque-Bera テスト値 JB=0.30, p=0.859によって示されます。

これらのボックスーコックス変換の使用例は、よい結果を示しています。しかし、双方において、この変換において最も都合のよいシーケンスを扱ったことを忘れてはいけません。したがって、これらの結果は、作成したアルゴリズムのパフォーマンスを確認するものとしてみることができ間sう。

4. 取引価格

ボックスーコックス変換を実行するアルゴリズムのパフォーマンスを確認した後、正規のものに近づけるためそれを実際のFOREX取引価格に適用しましょう。

"Time Series Forecasting Using Exponential Smoothing (continued)"（'時系列の主な特徴の分析：続） [5] にて記載されたシーケンスをテスト価格として使用します。Box-Cox-Tranformation_MQL5.zipアーカイブの\Dataset2ディレクトリに位置しており、1200値は、適切なファイルに保存されています。これらのファイルへのアクセスを提供するため、\Dataset2 フォルダは、ターミナルの\MQL5\Filesディレクトリに位置する必要があります。

これらの価格が定常のシーケンスではないと想定しましょう。したがって、その分析結果をいわゆる一般的な母集団に拡大しませんが、この特有の限られた長さのシーケンスの特徴として考えましょう。

さらに、もし定常性がなければ、同じ通貨ペアの異なる価格が様々な分布則に従うことが言及されなければなりません。

ファイルからシーケンス値を読むためのスクリプトを作成し、ボックスコックス変換を実行しましょう。テストスクリプトから、入力シーケンスの生成方法においてのみ異なります。以下は、そのスクリプトのソースコードです。BoxCoxTest3.mq5スクリプトは添付アーカイブにあります。

//+------------------------------------------------------------------+
//|                                                  BoxCoxTest3.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"
#include  "CBoxCox.mqh"
CBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],bcdat[],lambda,min;
   string fname;
//--- input data file
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- data reading
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- data size
   n=ArraySize(dat);
//--- transformed data array
   ArrayResize(bcdat,n);

//--- input data array
   min=dat[ArrayMinimum(dat)]-1e-5;
   for(i=0;i<n;i++)dat[i]=dat[i]-min;

//--- lambda parameter optimization
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   PrintFormat("Iterations= %i,   lambda= %.4f",Bc.GetIter(),lambda);

   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(dat[i],lambda)-1.0)/lambda;}
   else         {for(i=0;i<n;i++)bcdat[i]=MathLog(dat[i]);}     // Lambda == 0.0

//--- dat[]   <-- input data
//--- bcdat[] <-- transformed data
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//-----------------------------------------------------------------------------------

すべての値（この場合、1200あります）は、このスクリプトのdat[]配列にfname変数に名前がセットされた取引価格ファイルからインポートされます。さらに、最適なパラメーター値を探索する初期シーケンスのシフトと、ボックスーコックス変換が実行され、上記に記述された方法で行われます。スクリプトが実行されたのち、変換結果は、bcdat[]配列に位置します。

示されているソースコードをご覧の通り、EURUSD M1取引価格シー券sうは、変換のスクリプトが選択されます。もとの変換されるシーケンス分析結果は、図６、７に示されています。

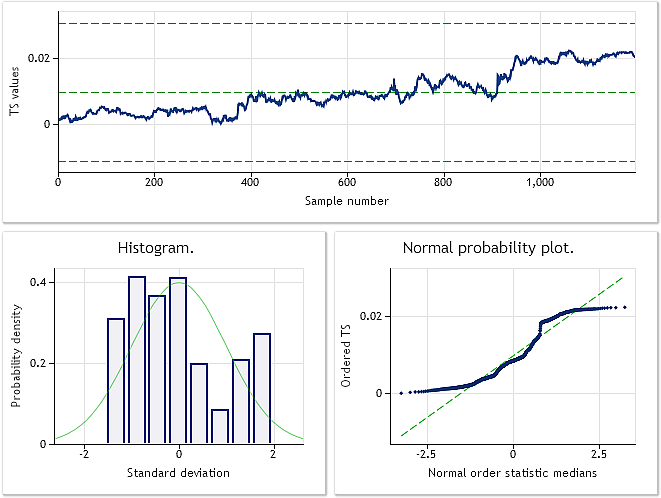
図6. EURUSD M1 入力シーケンスJarque-Bera テスト JB=100.94, p=0.000.

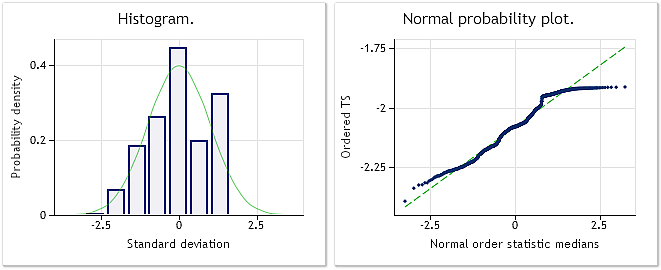
図7. 変換済みシーケンスラムダパラメーター=0.4146, Jarque-Bera テスト JB=39.30, p=0.000

図７で示されている特徴によると、EURUSD M1取引価格変換の結果は、擬似ランダムシーケンスの結果ほど驚嘆するものではありません。ボックスーコックス変換は、普遍的なものであると考えられていますが、入力シーケンスのすべての種類を扱うことはできません。例えば、指数法則の変換からツートップの分布を正規分布に変換することを期待することはできません。

図７で示された分布則が正規のものではないですが、以下の例のようなJarque-Beraテスト値の減少をみることができます。一方、もとのシーケンスにおいて JB=100.94、JB-39.30を変換後示します。分布則は、正規の値にある程度、変換後近づくようにできたということを意味します。

おおよそ、同じ結果がその他の取引価格の断片を変換した際に取得されます。ボックスーコックス変換が分布則を正規に近づけます。しかし、正規には必ずなりません。

様々な取引価格における一連の実験により、かなり予測のできる結論を導きだすことができます。ボックスーコックス変換は、Forex価格の分布則を正規のものに近づけますが、変換データの分布則の真の正規性を約束しません。

元のシーケンスを正規のものにする変換を実行することが合理的でしょうか？この質問に対して明確な答えはありません。各特定のケースにおいて、ボックスーコックス変換における必要性移管して個別の決定を行う必要があります。この場合、価格分析にて使用されるパラメーターメソッドの種類や、正規分布則からの初期データの偏差に対するこれらのメソッドの敏感性に依存していました。

5. トレンド除去

図6の上部は、BCTransform.mq5スクリプトに使用されているEURUSD M1シーケンスのチャートを表示しています。その値はすべてのシーケンスにおいて単一で向上していることがわかります。最初の接近値では、そのシーケンスが線形トレンドを持つと結論づけることができます。そのような「流行」の存在は、様々な変換の実行や取得されたシーケンスの分析前にトレンドを排除しようとすることを意味します。

分析された入力シーケンスからのトレンドの除去は、おそらくすべての場合において適切なメソッドとして考えられません。しかし、周期的なコンポーネントを見つけるために図６にて示されるシーケンスの分析を行うことを想定しましょう。この場合、トレンドのパラメーターを定義したのち、入力シーケンスから線形トレンドを引くことができます。

線形トレンドの除去は、周期的なコンポーネントの発見に影響を与えません。それは役に立つ可能性があり、選択された分析メソッドに応じて、そのような分析の結果をより正確で信頼のできるものにある程度変化させることができます。

もしトレンドの除去は、いくつかの場合において役に立つと決定すれば、おろらく、いかにボックスーコックス変換がトレンドが除去された後に、シーケンスを処理するかを知ることが妥当かもしれません。

どのような状況においても、トレンドを除去する際、どのような曲線がトレンドの近似において使用されるべきか決定しなければなりません。これは直線、より高い注文の曲線、移動平均です。この場合、最適な曲線の選択の問題により注意が背けられないように極端なバージョンを選択しましょう。元のシーケンスの上昇、すなわち、現在と以前の値の違いを元のシーケンスの代わりに使用します。

成長分析について議論するや否や、関連するポイントについてコメントせずにはいられません。

様々な記事やフォーラムにおいて、成長分析への移行の必要性は、そのようなものの属性について間違った印象を残すような形で正当化されます。成長分析への移行は、元のシーケンスを定常のものに変えるか、分布則を正規化することのできる変換の一種だと紹介されます。しかし、本当でしょうか？この質問を答えてみましょう。

成長分析への移行の本質は、元のシーケンスを二つに分割するというとてもシンプルなアイディアに成り立っているという事実から始める必要があります。以下のように示すことができます。

入力シーケンスを持っていると想定します。

そして、それをいかなる理由においてもトレンドと、元のシーケンス要素からトレンド値を引いた後に現れるその他残る要素に分割することに決定しました。トレンドの近似における二つのシーケンス要素に等しい平滑化期間とのシンプルな移動平均を使用するとします。

そのような移動平均は、二つに分けれらた二つの近隣のシーケンス要素の合計として計算されます。そのような場合、元のシーケンスからの平均引き算からの残りは、二つで分けられた同じ近隣の要素の違いに等しいです。

上記の平均値Sを示しましょう。一方、残りはDになります。より分かりやすくするために等式の左側に永久ファクター２を移動させる場合、以下のようになります：

簡単な変換を終了させた後、元のシーケンスを二つのコンポーネントに分割しました。その内の一つは、近隣のシーケンス値の合計であり、もう一方は、その差を示します。これらはインクリメントと呼ぶシーケンスであり、一方合計がトレンドを形成します。

この点に関して、元のシーケンスのある部分をインクリメントとして考えることが妥当です。したがって、もし成長分析に移るなら、合計により定義されたそのシーケンスの他の部分は個別に分析しない限り単純に無視されます。

シーケンスの分割によりどのような利点が得られるのかについて理解する最も容易い方法は、スペクトルメソッドを適用することです。

上記で示された数式から、Sコンポーネントは、h=1.1の特徴を持つ低頻度フィルターの使用による元のシーケンス濾過作用の結果であると言えます。したがって、Dコンポーネントは、 h=-1.1.の特徴を持つ高頻度フィルターの使用による濾過の結果です。図8 フィルターの頻度特徴を表示しています

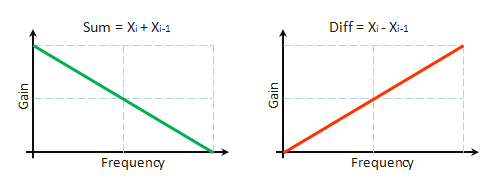
図8. 振幅周波数特徴

シーケンスの直接の分析から差異の分析へ移ったとしましょう。どのようなことが期待できるでしょうか？その場合において様々なオプションがあります。それらのいくつかを簡単に見ていきましょう。

分析プロセスの基礎的なエネルギーは、元のシーケンスの低頻度区域に集中している場合、差異分析への移行はそのエネルギーを抑制し、より複雑に、分析を続けることができないようにします。
分析プロセスの基礎的なエネルギーは、元のシーケンスの高頻度区域に集中している場合、干渉する低頻度コンポーネントの濾過のため差異分析への移行は肯定的な効果につながります。しかし、これは、そのような濾過が分析プロセスに影響を与えない限り可能です。
分析プロセスのエネルギーが単一にすべてのシーケンスの頻度範囲に分散された場合を言及できます。その場合、低頻度部分を抑制することで、差異の分析への移行後のプロセスを変化させます。

同様に、その他のトレンドの組み合わせ、短期間のトレンド、干渉ノイズなどにおける差異分析への移行の結果についての結論を導くこともできます。しかし、差異分析への移行は、分析プロセスの定常形式に繋がらず、分布プロセスを正規化しません。

上記に基づき、シーケンスは、差異分析の移行後、自動的に向上しないと結論づけることができます。いくつかの場合、入力シーケンスとその差異の両方を、近隣の値の合計と共に分析する方が、入力シーケンスについてより詳しい知識を得るためには良い方法で、一方、このシーケンスの属性についての最終的な結論は、取得された結果の検査に基づき導かれます。

この記事の主題に戻り、ボックスーコックス変換が図６で示したようなEURUSD M1シーケンスの成長分析への移行時にどのように動作するか見てみましょう。このためには、BoxCoxTest3.mq5スクリプトを使用します、そちらでは、シーケンスの値と差異をファイルからのシーケンスの値を計算後、置換します。そのスクリプトコードへの変化が実装されていないため、こちらで記載する必要はありません。その分析の結果を記します。

EURUSD M1 インクリメントJarque-Bera テスト JB=32494.8, p=0.000

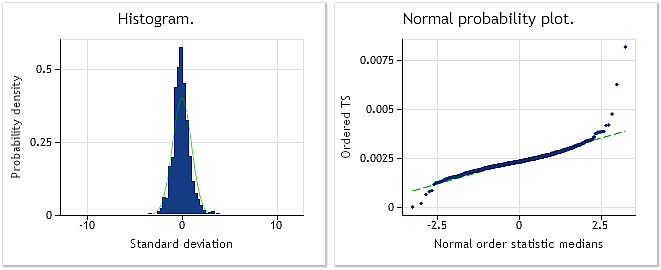
図9. EURUSD M1 インクリメントJarque-Bera テスト JB=32494.8, p=0.000

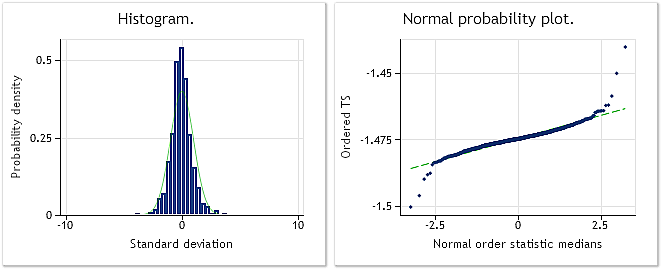
図10. 変換済みシーケンスラムダパラメーター=0.6662, Jarque-Bera テスト JB=10302.5, p=0.000

図９は、EURUSD M1インクリメント（差異）から成るシーケンスの特徴を示し、一方図１０は、ボックスーコックス変換の後、取得された特徴を示します。Jarque-Beraテスト値は、JB = 32494.8からJB = 10302.5へ３分の１ほど減少するにもかかわらず、変換後、変換されたシーケンスの分布則は、以前正規のものではありません。

しかし、ボックスーコックス変換がインクリメントの変換を適切に扱えないと早急に結論づけるべきではありません。特別な場合を考えました。その他の入力シーケンスを扱う差異、完全に異なる結果を取得する可能性があります。

6. 引用例

すべての引用されたボックスーコックス変換の例は、元のシーケンスの分布則が正規のもに変化されるか、正規にできる限り近いものに変化されるというケースに関連しています。冒頭で言及されたように、そのような変換は、正規のものからのシーケンスの分布則の偏差に敏感であるパラメーター分析メソッドを使用する差異に必要になります。

変換後すべての場合において、Jarque-Beraのテスト結果によると、実は元のシーケンスに比較するとより近い正規のものと分布則を持つシーケンスを取得したと例が示しています。この事実は、ボックスーコックス変換の多才や効果を示しています。

しかし、ボックスーコックス変換の可能性を課題評価すべきではなく、いかなる入力シーケンスは厳格に正規のものに変化されると想定します。上記の例からわかる通り、これは真実ではありません。元のシーケンスや変換されたシーケンスは実際の取引価格の正規のものと考えられません。

ボックスーコックス変換は、今の所より視覚的なワンパラメーターの形式にて考えられています。これは、それに対する最初の対応を単純化するためです。このアプローチは、この変換の能力を示すために正当化されていますが、実際的な目的において、より一般的な表示形式を使用することが良いでしょう。

7. ボックスーコックス変換の一般的な形式

ボックスーコックス変換は、正の０ではない値を持つシーケンスにのみ適用されます。この要件は、正の区域へのシーケンスのシフトにより満たされますが、正の区域のシフトの強度は、変換結果に直接影響を与えることができます。

したがって、そのシフト値は、追加の変換パラメーターとしてみなされ、ラムダパラメーターと共に最適化し、シーケンス値が負の区域に入らないようにします。

Nの長さでの元のシーケンスXにおいて：

二つのパラメーターのボックスーコックス変換の一般的な形式を決定する表現は、以下のものになります；

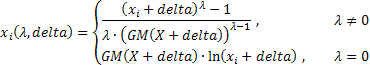
where:

;

GM() - 幾何学上の平均

シーケンスの幾何学上の平均値は以下のように計算されます。

ご覧の通り、二つのパラメーターが、すでに以下の等式にて使用されていますーラムダとデルタです。今、これらのパラメーターの双方を変換中に同時に最適化しなければなりません。そのアルゴリズムのわずかなコンパイルにもかかわらず、追加パラメーターの導入は変換の効果を向上しています。さらに、追加の正規化要因が、以前使用された変換と比較し等式に現れました。この要因により、その変換結果は、ラムダパラメーターの変更中に大きさを維持することができます。

ボックスーコックス変換についてのさらなる情報は、 [7], [8]でご覧になれます。同じタイプのその他の変換は、[8]にて記載されています。

現在のより一般的な形式の主な機能があります。

その変換は、入力シーケンスから正の値を含む必要があります。追加デルタパラメーターの錯覚は、自動的にいくつかの条件を満たす差異に、シーケンスの必要なシフトを実行します。
デルタパラメーターの最適値を選択する際、その大きさは、すべてのシーケンス値が「正の数」であると保証します。
その変換は、ラムダパラメーターの改変、そして０値の変更の場合では、継続される。
変換結果は、ラムダパラメーターの値の改変の場合、規模を維持します。

可能性のある関数の対数基準は、以前引用された例にてラムダパラメーターの最適値を検索する際に使用されました。もちろん、これは変換パラメーターの最適値を評価する唯一の方法ではありせん。

例として、パラメーターの最適化メソッドを言及でき、その昇順でソートされた変換済みのシーケンスと正規分布関数の量におけるシーケンスとの相関係数の最大値が、その時点で検索されます。そのバリアントは以前この記事にて述べられています。正規分布量の値は、James J. Filliben [9]が提唱した等式に沿って計算できます。

二つのパラメーターの変換の一般的な形式を決める数式は、確実に、以前のものより扱いにくいです。おそらく、これは、そのような変換は数学的、統計的なパッケージにて使用sあれないという事実によるものです。引用された等式は、MQL5にて、より一般的な形式のボックスーコックス変換を使用できるように実現されました。

CFullBoxCox.mqhファイルは、CFulBoxCoxクラスのソースコードを含んでおり、それは、変換パラメーターの最適値の探索を実行します。すでに述べられている通り、最適化プロセスは、相関係数の計算に基づきます。

//+------------------------------------------------------------------+
//|                                                  CFullBoxCox.mqh |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+

#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include "PowellsMethod.mqh"
//+------------------------------------------------------------------+
//| CFullBoxCox class                                                |
//+------------------------------------------------------------------+
class CFullBoxCox:public PowellsMethod
  {
protected:
  int    Dlen;                     // data size
  double Dat[];                    // input data array
  double Shift[];                  // input data array with the shift
  double BCDat[];                  // transformed data (Box-Cox)
  double Mean;                     // transformed data average value
  double Cdf[];                    // Quantile of the distribution cumulative function
  double Scdf;                     // Square root of summ of Quantile^2
  double R;                        // correlation coefficient 
  double DeltaMin;                 // Delta minimum value
  double DeltaMax;                 // Delta maximum value
  double Par[2];                   // parameters array
public:
  void   CFullBoxCox(void)       { }
  void   CalcPar(double &dat[]);
  double GetPar(int n)           { return(Par[n]); }
private:
  double ndtri(double y0);         // the function opposite to the normal distribution function
  virtual double func(const double &p[]);
  };
//+------------------------------------------------------------------+
//| CalcPar                                                          |
//+------------------------------------------------------------------+
void CFullBoxCox::CalcPar(double &dat[])
  {
  int i;
  double a,max,min;
  
  Dlen=ArraySize(dat);
  ArrayResize(Dat,Dlen);
  ArrayResize(Shift,Dlen);
  ArrayResize(BCDat,Dlen);
  ArrayResize(Cdf,Dlen);
//--- copy the input data array
  ArrayCopy(Dat,dat);
  
  Scdf=0;
  a=MathPow(0.5,1.0/Dlen);
  Cdf[Dlen-1]=ndtri(a); Scdf+=Cdf[Dlen-1]*Cdf[Dlen-1];
  Cdf[0]=ndtri(1.0-a); Scdf+=Cdf[0]*Cdf[0];
  a=Dlen+0.365;
  for(i=1;i<(Dlen-1);i++)
    {
    //--- calculation of the distribution cumulative function Quantile
    Cdf[i]=ndtri((i+0.6825)/a);
    //--- calculation of the sum of Quantile^2
    Scdf+=Cdf[i]*Cdf[i];
    }

//--- square root of the sum of Quantile^2
  Scdf=MathSqrt(Scdf);             
  
  min=dat[0]; max=min;
  for(i=0;i<Dlen;i++)
    {
//--- copy the input data
    a=dat[i]; Dat[i]=a;
    if(min>a)min=a;
    if(max<a)max=a;
    }
  
//--- Delta minimum value
  DeltaMin=1e-5-min;
//--- Delta maximum value
  DeltaMax=(max-min)*200-min;
//--- Lambda initial value
  Par[0]=1.0;
//--- Delta initial value
  Par[1]=(max-min)/2-min;
//--- optimization using Powell method
  Optimize(Par);             
  }
//+------------------------------------------------------------------+
//| func                                                             |
//+------------------------------------------------------------------+
double CFullBoxCox::func(const double &p[])
  {
  int i;
  double a,b,c,lam,del,k1,k2,gm,gmpow,mean,ret;
  
  lam=p[0]; del=p[1]; k1=0; k2=0;
  if (lam>5.0){k1=(lam-5.0)*400; lam=5.0;}                    // Lambda >  5.0
  else if(lam<-5.0){k1=-(lam+5.0)*400; lam=-5.0;}             // Lambda < -5.0
  if (del>DeltaMax){k2=(del-DeltaMax)*400; del=DeltaMax;}    // Delta > DeltaMax
  else if(del<DeltaMin){k2=(DeltaMin-del)*400; del=DeltaMin; // Delta < DeltaMin
  
  gm=0;
  for(i=0;i<Dlen;i++)
    {
    Shift[i]=Dat[i]+del;
    gm+=MathLog(Shift[i]);
    }

//--- geometric mean
  gm=MathExp(gm/Dlen);
  gmpow=lam*MathPow(gm,lam-1);
  mean=0;
//--- Lambda != 0.0
   if(lam!=0)                                  
    {
    for(i=0;i<Dlen;i++)
      {
      a=(MathPow(Shift[i],lam)-1.0)/gmpow;
       //--- transformed data (Box-Cox)
      BCDat[i]=a;
       //--- average value
      mean+=a;
      }
    }
  //--- Lambda == 0.0
  else                                        
     {
    for(i=0;i<Dlen;i++)
      {
      a=gm*MathLog(Shift[i]);
       //--- transformed data (Box-Cox)
      BCDat[i]=a;
      //--- average value
      mean+=a;
      }
    }
  mean=mean/Dlen;
  //--- sorting of the transformed data array
  ArraySort(BCDat);
  a=0; b=0;
  for(i=0;i<Dlen;i++)
    {
    c=(BCDat[i]-mean);
    a+=Cdf[i]*c;
    b+=c*c;
    }
  //--- correlation coefficient
  ret=a/(Scdf*MathSqrt(b)); 
  return(k1+k2-ret);
  }
//+------------------------------------------------------------------+
//| The function opposite to the normal distribution function        |
//| Prototype:                                                       |
//| Cephes Math Library Release 2.8: June, 2000                      |
//| Copyright 1984, 1987, 1989, 2000 by Stephen L. Moshier           |
//+------------------------------------------------------------------+
double CFullBoxCox::ndtri(double y0)
  {
  static double s2pi =2.50662827463100050242E0; // sqrt(2pi)
  static double P0[5]={-5.99633501014107895267E1,  9.80010754185999661536E1,
                       -5.66762857469070293439E1,  1.39312609387279679503E1,
                       -1.23916583867381258016E0};
  static double Q0[8]={ 1.95448858338141759834E0,  4.67627912898881538453E0,
                        8.63602421390890590575E1, -2.25462687854119370527E2,
                        2.00260212380060660359E2, -8.20372256168333339912E1,
                        1.59056225126211695515E1, -1.18331621121330003142E0};
  static double P1[9]={ 4.05544892305962419923E0,  3.15251094599893866154E1,
                        5.71628192246421288162E1,  4.40805073893200834700E1,
                        1.46849561928858024014E1,  2.18663306850790267539E0,
                       -1.40256079171354495875E-1,-3.50424626827848203418E-2,
                       -8.57456785154685413611E-4};
  static double Q1[8]={ 1.57799883256466749731E1,  4.53907635128879210584E1,
                        4.13172038254672030440E1,  1.50425385692907503408E1,
                        2.50464946208309415979E0, -1.42182922854787788574E-1,
                       -3.80806407691578277194E-2,-9.33259480895457427372E-4};
  static double P2[9]={ 3.23774891776946035970E0,  6.91522889068984211695E0,
                        3.93881025292474443415E0,  1.33303460815807542389E0,
                        2.01485389549179081538E-1, 1.23716634817820021358E-2,
                        3.01581553508235416007E-4, 2.65806974686737550832E-6,
                        6.23974539184983293730E-9};
  static double Q2[8]={ 6.02427039364742014255E0,  3.67983563856160859403E0,
                        1.37702099489081330271E0,  2.16236993594496635890E-1,
                        1.34204006088543189037E-2, 3.28014464682127739104E-4,
                        2.89247864745380683936E-6, 6.79019408009981274425E-9};
  double x,y,z,y2,x0,x1,a,b;
  int i,code;
  if(y0<=0.0){Print("Function ndtri() error!"); return(-DBL_MAX);}
  if(y0>=1.0){Print("Function ndtri() error!"); return(DBL_MAX);}
  code=1; y=y0;
  if(y>(1.0-0.13533528323661269189)){y=1.0-y; code=0;}  // 0.135... = exp(-2)
  if(y>0.13533528323661269189)                         // 0.135... = exp(-2)
    {
    y=y-0.5; 
    y2=y*y;
    a=P0[0]; for(i=1;i<5;i++)a=a*y2+P0[i];
    b=y2+Q0[0]; for(i=1;i<8;i++)b=b*y2+Q0[i];
    x=y+y*(y2*a/b);
    x=x*s2pi; 
    return(x);
    }
  x=MathSqrt(-2.0*MathLog(y));
  x0=x-MathLog(x)/x;
  z=1.0/x;
//--- y > exp(-32) = 1.2664165549e-14
  if(x<8.0)
    {
    a=P1[0]; for(i=1;i<9;i++)a=a*z+P1[i];
    b=z+Q1[0]; for(i=1;i<8;i++)b=b*z+Q1[i];
    x1=z*a/b;
    }
  else
    {
    a=P2[0]; for(i=1;i<9;i++)a=a*z+P2[i];
    b=z+Q2[0]; for(i=1;i<8;i++)b=b*z+Q2[i];
    x1=z*a/b;
    }
  x=x0-x1;
  if(code!=0)x=-x;
  return(x);
  }
//------------------------------------------------------------------------------------

最適化中に、いくつかの制限が変換パラメーターの変更範囲に適用されます。ラムダパラメーターの値は、5.0から-5.0の値に制限されています。デルタパラメーターにおける制限は、入力シーケンスの最小値に関連して明記されます。このパラメーターは、DeltaMin=(0.00001-min) と、DeltaMax=(max-min)*200-min値、最小値と最大値が入力シーケンス要素の最小・最大値の地点で制限されます。

FullBoxCoxTest.mq5スクリプトは、CFullBoxCoxクラスの使用を紹介します。このスクリプトのソースコードは以下に示されています。

//+------------------------------------------------------------------+
//|                                               FullBoxCoxTest.mq5 |
//|                                                    2012, victorg |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "2012, victorg"
#property link      "https://www.mql5.com"

#include  "CFullBoxCox.mqh"
CFullBoxCox   Bc;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int i,n;
   double dat[],shift[],bcdat[],lambda,delta,gm,gmpow;
   string fname;

//--- input file name
   fname="Dataset2\\EURUSD_M1_1200.txt";
//--- reading the data
   if(readCSV(fname,dat)<0){Print("Error."); return;}
//--- data size
   n=ArraySize(dat);
//--- shifted input data array
   ArrayResize(shift,n);
//--- transformed data array
   ArrayResize(bcdat,n);

//--- lambda and delta parameters optimization
   Bc.CalcPar(dat);
   lambda=Bc.GetPar(0);
   delta=Bc.GetPar(1);

   PrintFormat("Iterations= %i,   lambda= %.4f,   delta= %.4f",
               Bc.GetIter(),lambda,delta);
   gm=0;
   for(i=0;i<n;i++)
     {
      shift[i]=dat[i]+delta;
      gm+=MathLog(shift[i]);
     }
//--- geometric mean
   gm=MathExp(gm/n);
   gmpow=lambda*MathPow(gm,lambda-1);
   if(lambda!=0){for(i=0;i<n;i++)bcdat[i]=(MathPow(shift[i],lambda)-1.0)/gmpow;}
   else         {for(i=0;i<n;i++)bcdat[i]=gm*MathLog(shift[i]);}
//--- dat[]   <-- input data
//--- shift[] <-- input data with the shift
//--- bcdat[] <-- transformed data
  }
//+------------------------------------------------------------------+
//| readCSV                                                          |
//+------------------------------------------------------------------+
int readCSV(string fnam,double &dat[])
  {
   int n,asize,fhand;

   fhand=FileOpen(fnam,FILE_READ|FILE_CSV|FILE_ANSI);
   if(fhand==INVALID_HANDLE)
     {
      Print("FileOpen Error!");
      return(-1);
     }
   asize=512;
   ArrayResize(dat,asize);
   n=0;
   while(FileIsEnding(fhand)!=true)
     {
      dat[n++]=FileReadNumber(fhand);
      if(n+128>asize)
        {
         asize+=128;
         ArrayResize(dat,asize);
        }
     }
   FileClose(fhand);
   ArrayResize(dat,n-1);
   return(0);
  }
//------------------------------------------------------------------------------------

入力シーケンスは、dat[]配列にそのファイルからスクリプトの開始時にアップロードされ、変換パラメーターの最適値の探索が実行されます。それから、その変換は、取得されたパラメーターの使用とともに実行されます。結果として、dat[]配列は、元のシーケンスを含み、shift[]配列は、デルタ値によりシフトされた元のシーケンスを含み、bcdat[]配列は、ボックスーコックス変換の結果を含みます。

FullBoxCoxTest.mq5 スクリプトのコンパイルにて必要なすべてのファイルは、Box-Cox-Tranformation_MQL5.zipアーカイブに位置しています。

テストシーケンスの変換は、 FullBoxCoxTest.mq5スクリプトの助けにより実行されます。予想された通り、取得されたデータの分析中、この二つのパラメーターの変換種類は、１パラメータータイプと比較し多少より良い結果を示します。例えば、 EURUSD M1シーケンスにおいて、図６にて示された Jarque-BeraJB=100.94. テスト値の分析結果は、ワンパラメーター変換（図７）の後のJB=39.30 になりますが、二つのパラメーターの変換の後、(FullBoxCoxTest.mq5 スクリプト)この値はJB=37.49にまで下がります。

結論

この記事では、ボックスーコックス変換パラメーターしかし、実際そのケースはボックスーコックス変換が異なる方法で使用される際に起こります。例えば、以下のアルゴリズムは、時間シーケンスの予測時に使用できます：

ボックスーコックス変換パラメーター値と予測モデルの予備的な値が選択されます；
入力データのボックスコックス変換が実行されます;
予測は、現在のパラメーターに沿って実行されます;
リバースボックスーコックス変換は、予測結果において実行されます;
予測エラーは、入力未変換シーケンスによって評価されます;
パラメーター値は、予測エラーを最小化するために変更され、そのアルゴリズムは、ステップ２に戻ります。

そのアルゴリズムにおいて、予測モデルと同様、その変換パラメーターは、予測エラー最小基準により最小化されます。この場合、ボックスーコックス変換の目的は、すでに入力シーケンスの正規分布則への変換ではありません。

それでは、最小予測エラーを提供する分布則を受け取るために入力シーケンスを変換する必要があります。選択された予測メソッドに依存し、この分布則は必ずしも正規である必要はありません。

ボックスーコックス変換は、正の数と非０の値を持つシーケンスのみ適用されます。入力シーケンスのシフトは、すべてのケースにおいて実行される必要があります。この変換の特徴は、欠点の一つであると言われています。しかし、これにも関わらず、ボックスーコックス変換は、その他同じ種類の変換において最も多才で効果的なツールです。

参照元リスト

А.N. Porunov. マクロ経済学シリーズ : ボックスーコックス変換と、正規性の錯覚 "ビジネス情報科学"誌 , №2(12)-2010, pp. 3-10.
Mohammad Zakir Hossain, 経済・統計的分析におけるボックスーコックス変換技術の使用経済学・経営科学における新興トレンド誌 (JETEMS) 2(1):32-39.
ボックスーコックス変換
記事「指数平滑方を用いた時系列分析」
記事「指数平滑方を用いた時系列分析」（続）
時系列の主な特徴の分析
乗数変換
Draper N.R. とH. Smith, 景気後退分析第三版., 1998, John Wiley & Sons, New York.
Q-Q plot

MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/363

添付されたファイル |

ZIPをダウンロード

box-cox-transformation_mql5.zip (91.48 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

初めてのお客様へのアドバイス

有名人の格言ではよくこう言われます。「失敗を恐れる者はなにもなしえない。」怠慢自体が誤りであることを認めなければ、この言葉を語るのは難しいでしょう。しかし、将来の過ちを最小にするために過去の過ち（自分自身または他者の）を分析することは常に可能です。これから、同じ名前のサービスにおけるジョブ実行中に再発生可能性な状況を検証していこうと思います。

自作 DLL の排除

MQL5 言語機能がタスク遂行に十分でなければMQL5 プログラマーは別のツールを使用する必要があります。別のプログラム言語によって仲介DLL を作成する必要があります。MQL5 にはさまざまなデータタイプを表示し、それを API に転送する機能がありますが、残念ながら MQL5 は受け付けられたポインタからデータを抽出することに関する問題を解決することはできません。本稿ではすべての "i" にドットを打ち、複雑なデータタイプを交換し、それと連携するメカニズムを示していきます。

重回帰分析ストラテジージェネレータ兼ストラテジーテスタ

本稿ではトレーディングシステム開発のために重回帰分析を利用する方法を述べます。戦略検索自動化のための回帰分析の利用法を示します。例としてプログラミングに高い技能を要求せず作成され統合される回帰式を提供します。

2013 年第三四半期 MetaTrader AppStore 実績

また四半期が経過したところで、 MetaTrader AppStore の実績を集計することにしました。MetaTrader AppStore は MetaTrader の売買ロボットおよびテクニカルインディケータの最大ストアです。報告対象四半期の終わりまでに「マーケット」には 500 人以上の開発者が 1,200 以上のプロダクツを出しました。