
取引における様々な移動平均の比較
目次
はじめに
移動平均(MA)は、外国為替市場で最も人気のあるテクニカル指標の1つです。ここでの目的は、市場に出入りする均等な条件の下で、様々なMAを検討し、取引内でそれらを比較することです。
移動平均、適応移動平均、二重指数移動平均、フラクタル適応移動平均、三重指数移動平均、可変インデックス動的平均、およびNick Rypock移動平均の7種類の移動平均を考えてみましょう。
移動平均の種類
このセクションには、関連する移動平均を計算するための簡単な説明と数式が含まれています。
移動平均テクニカル指標
移動平均は、最も広く普及しているテクニカル指標の1つで、一定期間の銘柄価格の平均値を表します。MA指標には異なる変種が存在します。
- 単純移動平均(SMA)
- 指数移動平均(EMA)
- 平滑移動平均(SMMA)
- 線形加重移動平均(LWMA)
移動平均指標の各変種の計算式を以下に示します。
| 移動平均指標の変種 | 計算式 | コメント |
|---|---|---|
| 単純移動平均(SMA) | 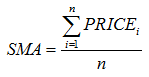 |
|
| 指数移動平均(EMA) |
| |
| 平滑移動平均(SMMA) |
| |
| 線形加重移動平均(LWMA) |
|
移動平均指標の異なる変種の価格チャートでの表示を検討してみましょう。図1は、12月の移動平均指標の変種を、終値で計算して示しています。
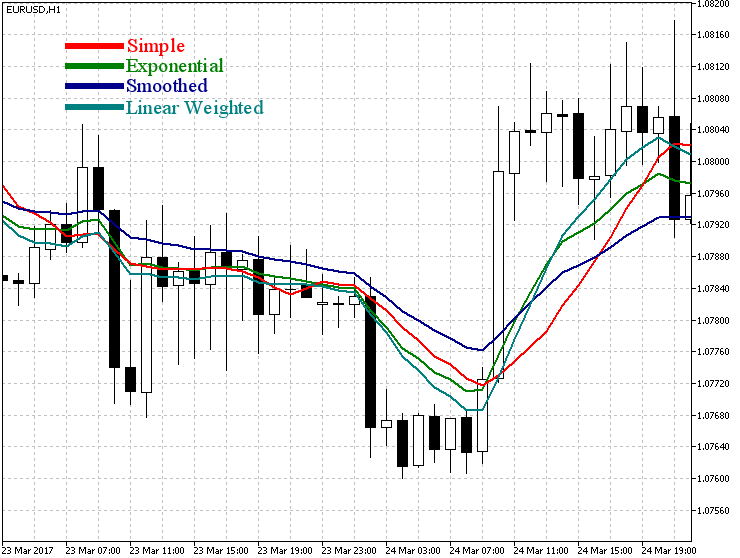
図1 移動平均指標の変種
図が示すように、単純移動平均はフラットでわずかに変動し、誤った取引シグナルをもたらす可能性があります。平滑移動平均は、その名前からわかるように、よりスムーズに見えます。指数移動平均および線形加重移動平均は、フラットでも同様に動作します。線形加重移動平均はSMMAやEMAとは異なり、以前の値には依存しないので、トレンドがある時は他のラインよりも価格に近くなります。
指数移動平均(EMA) に基づくテクニカル指標
指数移動平均(EMA)は、他の多くのテクニカル指標の基礎となります。
| 指標 | 説明 | 計算式 | 計算式の説明 |
|---|---|---|---|
適応移動平均(AMA) | ノイズに対する感度の低いMAです。他の移動平均と比較すると、この指標では動向の反転と変化を判断する際の遅れが最小限に抑えられます。価格スパイクでは、それは強い変動をもたらさないので、誤った取引シグナルを呼び出すことはありません。 |
| |
二重指数移動平均 | 価格や他の指標値を平滑にするために使われます。 主な利点は、価格がジグザグ様式で動いている時に偽のシグナルがないことです。強い動向の期間中にポジションを維持し、通常のEMAと比較してシグナルの遅れを減少させます。 |
|
|
三重指数移動平均 | 一重、二重および三重指数MAを合成したものです。全体的な遅れは、それらのMA個別のものに対してにはるかに少ないです。 価格チャートと他の指標値を平滑化するために、従来の移動平均の代わりに適用されます。 |
| |
フラクタル適応移動平均 | 平滑化係数は、現在の価格系列のフラクタル次元に基づいて計算されます。指標の優位性は、強い動向を辿り、保合期間中に大幅に減速することです。 |
|
|
可変インデックス動的平均 | これは平均化期間が動的に変化し、市場のボラティリティに依存するEMAです。 市場のボラティリティはChandeモメンタムオシレータ(CMO)によって測定され、一定期間(CMO期間)の正と負の増分の合計の比率を測定します。CMO値は、EMA平滑化係数の係数です。従って、指標では、CMOオシレータ周期とEMA平滑化期間の2つのパラメータが設定されます。 |
| |
Nick Rypock移動平均 | この指標は普通のMetaTrader 5ディストリビューションの一部ではありません。その主な利点は、フラットでほとんど変動がないことです。 それは厳密に動向を辿ります。 |
|
|
通常のEMAとの指標の差
上記の指標を通常のEMAと比較してみましょう。図2は以下を示します。
- 適応移動平均(期間 - 12、高速EMA - 2、低速EMA - 30、シフト - 0)
- 二重指数移動平均(期間 - 12、シフト - 0)
- フラクタル適応移動平均(期間 - 12、シフト - 0)
- 指数移動平均(期間 - 12、シフト - 0)
- 三重指数移動平均(期間 - 12、シフト - 0)
- 可変インデックス動的平均(CMO期間 - 12、EMA期間 - 12、シフト - 0)
- Nick Rypock移動平均(平均方法 - SMA、平滑化の深さ-3、平滑化パラメータ-15(SMAには未使用)、Kf-1、Fast-12、Sharp-2、垂直および水平シフト-0)
すべての指標は終値を基準にしています。
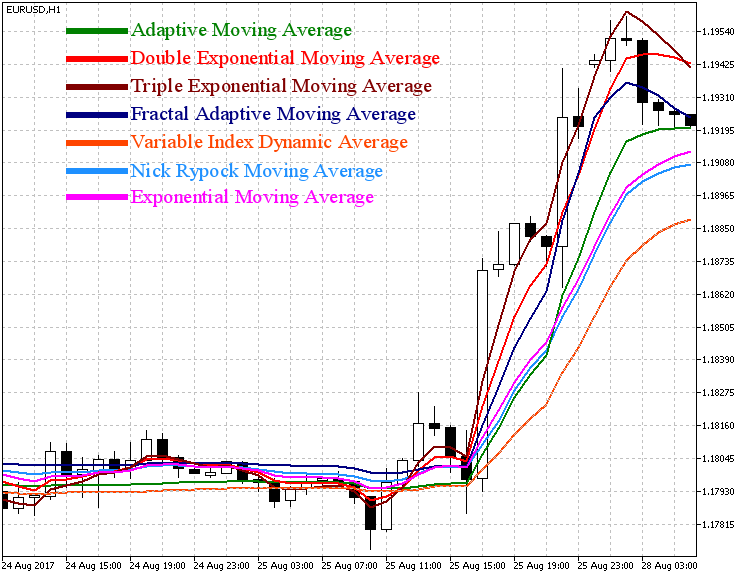
図2 指数移動平均(EMA)に基づいた指標の比較
図2に示すように、DEMAとTEMAは通常のEMAと比較して、より正確に価格の動きに従います。 しかし、フラットでは変動し、偽の取引シグナルを与える可能性があります。残りの指標(FRAMA、AMA、VIDYA、NRMA)はフラットではほとんど変動せず、小規模な価格変動には反応しません。トレンドでは、ほとんどすべての指標が同じように振る舞い、TEMAとFRAMAはトレンド方向の変化に他の指標より速く反応しました。
様々な移動平均の比較
上記の考慮されたテクニカル指標の取引戦略と市場への出入りの均等条件を比較してみましょう。
取引戦略仕様
指標をテストするために、市場への出入りの明らかな条件を備えた単純な戦略が選択されました。
市場エントリの条件
- 予備的な買いシグナル:指標線が強気ローソク足の実体を横切る。その後、指標の現在値と以前の値との差が指定された[Growth factor]パラメータ(指標の伸び)よりも大きい場合に買い取引を始める。
- 予備的な売りシグナル:指標線が弱気ローソク足の実体を横切る。その後、指標の現在値と以前の値との差が、指定された[Growth factor]パラメータ(指標の下降)よりも大きい場合に売り取引を始める。
市場江グジットの条件
- TakeProfitまたはStopLossレベルに達した後
- 買い取引が開かれ、指標線が弱気ローソク足の実体を越えたとき
- 買い取引が開かれ、指標線が強気ローソク足の実体を越えたとき
図3と図4はそのような戦略での取引例を示します。
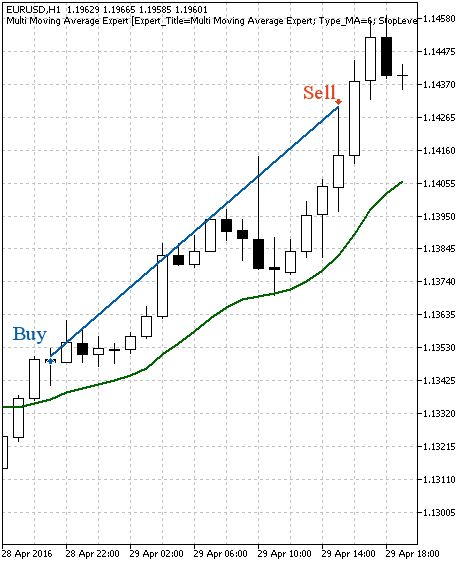
図3 買い取引の例
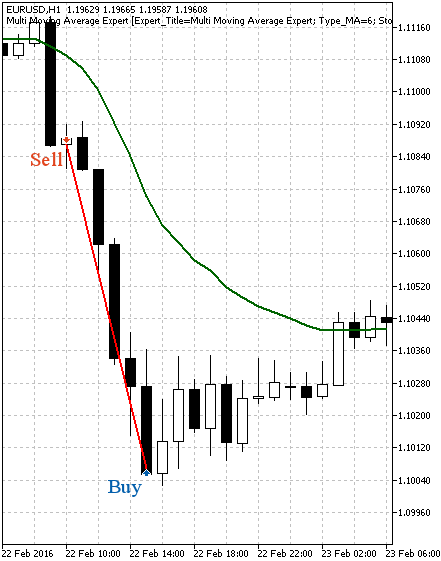
図4 売り取引の例
MetaTrader 5ターミナルナビゲータにある移動平均エキスパートアドバイザーでも同様の取引戦略が実現しています。
エキスパートアドバイザーの作成
上記の特定の戦略での取引のためのエキスパートアドバイザーを作成しましょう。MA(単純、指数関数、平滑化、直線加重法)、DEMA、TEMA、FRAMA、AMA、VIDYA、NRMAテクニカル指標の1つを選択する機能が実装されます。選択した指標がチャートに描画されます。また、指標入力パラメータ、TakeProfitとStopLossのサイズ、取引のためのロットのサイズ、指標成長係数(成長因子)の値を指定することができます。各ティックの代わりに新しいバーで市場への出入りの条件を確認します。最初にポジションの利用可能性が確認されます(この目的のために、SelectPosition関数がエキスパートアドバイザーに提供されます)。そのようなポジションがない場合、エントリ条件(CheckForOpen関数)を確認し、可能であればエグジット条件(CheckForClose関数)を確認します。
本稿には完全なエキスパートアドバイザーコードが添付されています(MultiMovingAverageExpert.mq5ファイル)。市場への出入りの条件を実現することだけを考えてみましょう。入力条件は、CheckForOpen関数で次のように確認されます。
if(rt[0].open>ma[0] && rt[0].close<ma[0]) // 弱気ローソク足実体を交差したかの確認 { if(BuyCross) BuyCross=false; // 買いの前提条件を削除する(それ以前にラインが強気ローソク足を交差した場合) SellCross=true; // 売りの前提条件を設定する } else if(rt[0].open<ma[0] && rt[0].close>ma[0]) // 強気ローソク足実体を交差したかの確認 { if(SellCross) SellCross=false; // 売りの前提条件を削除する(それ以前にラインが弱気ローソク足を交差した場合) BuyCross=true; // 買いの前提条件を設定する } if(SellCross && ma[0]>ma[1] && ma[0]-ma[1]>GFactor) { signal=ORDER_TYPE_SELL; // 指標が下降すると売り条件が発生する SellCross=false; // 売り取引前提条件を削除する } else if(BuyCross && ma[1]>ma[0] && ma[1]-ma[0]>GFactor) { signal=ORDER_TYPE_BUY; // 指標が成長すると買い条件が発生する BuyCross=false; // 買い取引前提条件を削除する }
- Arrayrt[]には価格履歴が保存されます。
- Array ma[]には指標値が保存されます。
- rt[0].close、rt[0].openは1つ前の終値と始値です。
- ma[0]は1つ前の指標値です。
- ma[1]は現在の指標値です。
- GFactorは指標の伸びの係数です。
- 変数シグナルが、売買要求を形成するためにさらに使用されます。
エグジット条件は下記のようにCheckForClose関数で確認されます。
bool signal=false; long type=PositionGetInteger(POSITION_TYPE); if(type==(long)POSITION_TYPE_BUY && rt[0].open>ma[0] && rt[0].close<ma[0]) // 買いポジションが開いていて // 指標線が弱気ローソク足の実体を横切る signal=true; // 約定シグナル if(type==(long)POSITION_TYPE_SELL && rt[0].open<ma[0] && rt[0].close>ma[0]) // 買いポジションが開いていて // 指標線が強気ローソク足の実体を横切る signal=true; // 約定シグナル if(signal) { if(TerminalInfoInteger(TERMINAL_TRADE_ALLOWED) && Bars(_Symbol,_Period)>100) ExtTrade.PositionClose(_Symbol,3); // 約定 }
エキスパートアドバイザーのテストとパフォーマンス
エキスパートアドバイザーは、H1時間枠で、通貨ペアEUR USD、GBPUSD、USDJPY、USDCAD、AUDUSDでテストされます(決済指値 - 80ポイント、決済逆指値は - 0ポイント、取引ロット量 - 0.1、預金 - 10,000USD、テストモード - 全てのティック、レバレッジ - 1:100、5桁クオーツ、 MetaQuotes-Demo サーバ使用)。
テスト期間は01.01.2016から09.09.2017までです。
各指標について、期間(変動範囲-5〜50、ペース1)および[Growth factor]パラメータ(変動範囲0,0001〜0,0001、ペース0,001)が最適化されました。
可変インデックス動的平均については、EMA期間(指標計算期間)とCMOオシレータ期間(変動範囲 - 5 - 50、ペース1)が最適化されました。
Nick Rypock移動平均については、指標計算の期間を決定するFactパラメータが最適化されました。
指標値は、横と縦のシフトなしで終値に基づいて計算されます。一部の指標には追加パラメータがあります。
| 移動平均の名前 | パラメータ値 |
|---|---|
| 適応移動平均 |
|
| Nick Rypock移動平均 |
|
EURUSD通貨ペアでのテスト結果
EURUSD 通貨ペアでのテスト結果(最大純利益合計が最大のもの)は、以下の表に示されています。
| 移動平均の名前 | 最適化されたパラメータとその値 | 取引数 | 総純利益 | 利益率 | 回復率 | シャープレシオ | バランスドローダウン最大値 | エクイティドローダウン 最大値 |
|---|---|---|---|---|---|---|---|---|
| 移動平均(平均化の手法 - 単純) | Period —15、Growth factor - 0.0002 | 383 | 1309.82 | 1.32 | 3.14 | 0.1 | 397.29 (3.81%) | 417.26 (3.99%) |
| 移動平均(平均化の手法 - 指数) | Period —11、Growth factor - 0.0003 | 405 | 1109.72 | 1.22 | 3.02 | 0.08 | 346.35 (3.39%) | 367.45 (3.6%) |
| 移動平均(平均化の手法 - 平滑) | Period —6、Growth factor - 0.0003 | 405 | 1109.72 | 1.22 | 3.02 | 0.08 | 346.35 (3.39%) | 367.45 (3.6%) |
| 移動平均(平均化の手法 - 加重) | Period —22、Growth factor - 0.0002 | 351 | 1505.35 | 1.34 | 3.65 | 0.11 | 383.71 (3.41%) | 412.88 (3.91%) |
| 適応移動平均 | Period —14、Growth factor - 0.0001 | 384 | 1024.19 | 1.19 | 1.63 | 0.07 | 600.06 (5.41%) | 627.36 (5.64%) |
| 二重指数移動平均 | Period —28、Growth factor - 0.0003 | 366 | 1676.43 | 1.39 | 3.49 | 0.12 | 460.33 (4.39%) | 481.03 (4.58%) |
| 三重指数移動平均 | Period —44、Growth factor - 0.0002 | 482 | 1842.81 | 1.35 | 5.31 | 0.11 | 321.07 (3.14%) | 347.27 (3.39%) |
| フラクタル適応移動平均 | Period —16、Growth factor - 0.0007 | 174 | 766.52 | 1.37 | 2.69 | 0.12 | 252.4 (2.5%) | 285.08 (2.78%) |
| 可変インデックス動的平均 | Period EMA - 12、period CMO - 2、Growth factor - 0.0003 | 333 | 1237.31 | 1.26 | 2.86 | 0.09 | 385.44 (3.43%) | 432.81 (3.84%) |
| Nick Rypock移動平均 | Period —15、Growth factor - 0.0001 | 295 | 1669.62 | 1.42 | 4.14 | 0.14 | 376.22 (3.5%) | 403.52 (3.75%) |
テスト結果に基づいて以下の結論を下すことができます。
- 三重指数移動平均は総純利益と回復率の最良の指標です。他の指標にはそれほど良くありませんが、良好な結果は二重指数移動平均とNick Rypock移動平均でも示されています。
- 利益率、回復率、シャープレシオ、およびエクイティと残高の最大ドローダウンの最悪の指数は、適応移動平均によって示されます。
テスト結果をより鮮明に比較するために、純利益、利益率、シャープレシオ、回復率、残高およびエクイティドローダウンの指数を次の公式で正規化します。
![]()
ここで
- nValue - 0から1までの区間内の正規化されたパラメータ値
- Value - 現在のパラメータ値
- MaxValue - 最大のパラメータ値
- MinValue - 最小のパラメータ値
です。結果は表に示されています(最良の結果は黄色、最悪の結果は赤色)。
| 移動平均の名前 | 総純利益 | 利益率 | 回復率 | シャープレシオ | バランスドローダウン最大値 | エクイティドローダウン最大値 | ドローダウンを除いた指標の合計 | ドローダウンを含む指標の合計 |
|---|---|---|---|---|---|---|---|---|
| 移動平均(平均化の手法 - 単純) | 0.50479 | 0.56522 | 0.41033 | 0.42857 | 0.41676 | 0.38618 | 1.9089 | 1.10597 |
| 移動平均(平均化の手法 - 指数) | 0.31887 | 0.13043 | 0.37772 | 0.14286 | 0.27024 | 0.24065 | 0.96988 | 0.459 |
| 移動平均(平均化の手法 - 平滑) | 0.31887 | 0.13043 | 0.37772 | 0.14286 | 0.27024 | 0.24065 | 0.96988 | 0.459 |
| 移動平均(平均化の手法 - 加重) | 0.68646 | 0.65217 | 0.54891 | 0.57143 | 0.3777 | 0.37338 | 2.45898 | 1.7079 |
| 適応移動平均 | 0.23941 | 0 | 0 | 0 | 1 | 1 | 0.23941 | -1.76059 |
| 二重指数移動平均 | 0.84541 | 0.86957 | 0.50543 | 0.71429 | 0.59808 | 0.57248 | 2.9347 | 1.76413 |
| 三重指数移動平均 | 1 | 0.69565 | 1 | 0.57143 | 0.19572 | 0.18169 | 3.26708 | 2.88787 |
| フラクタル適応移動平均 | 0 | 0.78261 | 0.28804 | 0.71429 | 0 | 0 | 1.78494 | 1.78494 |
| 可変インデックス動的平均 | 0.43742 | 0.29631 | 0.33361 | 0.27656 | 0.38267 | 0.43161 | 1.34419 | 0.52992 |
| Nick Rypock移動平均 | 0.83909 | 1 | 0.68207 | 1 | 0.35615 | 0.34603 | 3.52115 | 2.81897 |
表の最後の列では、指標を合計すると、バランスとエクイティドローダウンの最大値が負の符号で取られます(ドローダウンが少ないほど戦略が良好です)。したがって、考えられる戦略の最良の結果は、三重指数移動平均、Nick Rypock移動平均および二重指数移動平均(表中の黄色)によって示されます。TEMA、NRMAおよびDEMAのテスト結果は図 5-10に示されています。
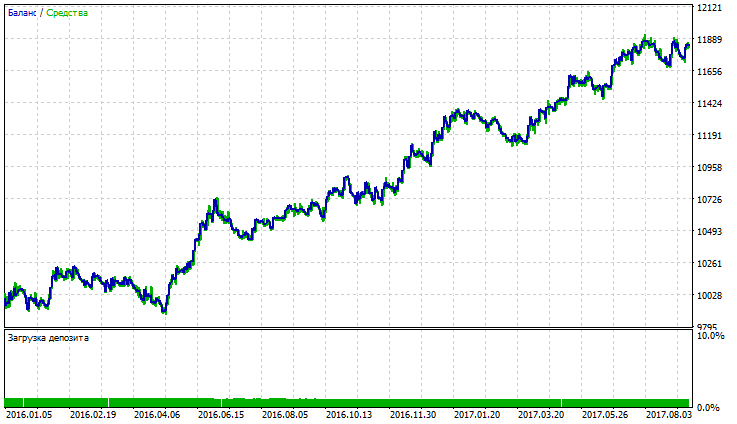
図5 三重指数移動平均のバランス(エクイティ)チャート
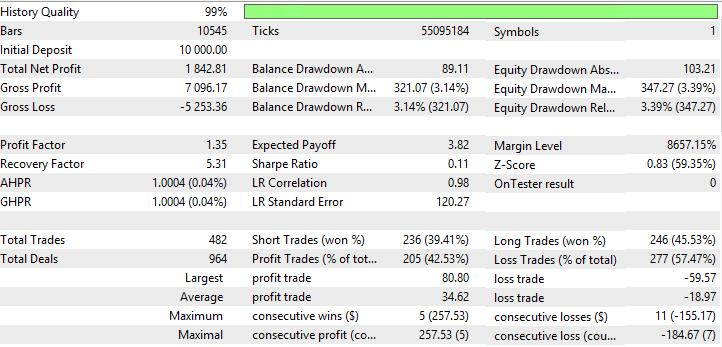
図6 三重指数移動平均のレポート
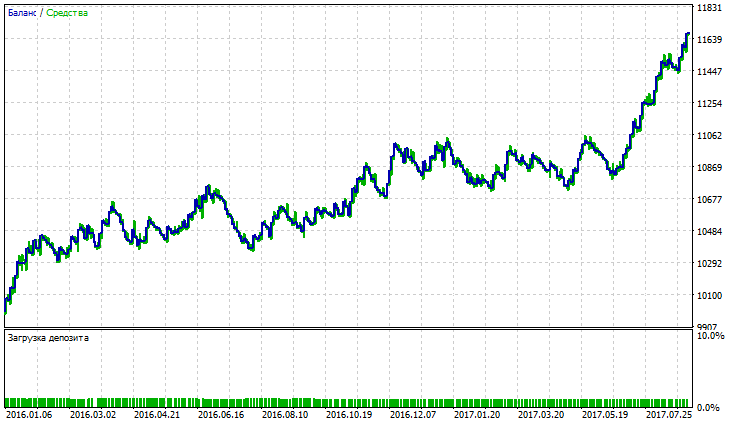
図7 Nick Rypock移動平均のバランス(エクイティ)チャート
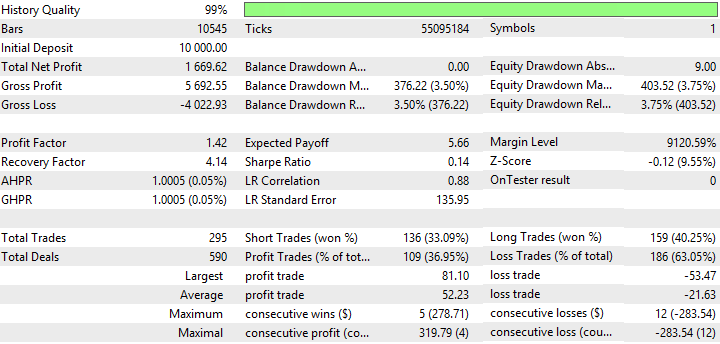
図8 Nick Rypock移動平均のレポート
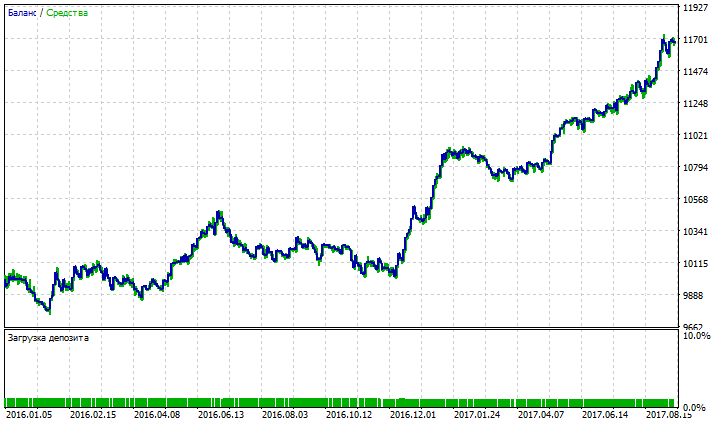
図9 二重指数移動平均のバランス(エクイティ)チャート
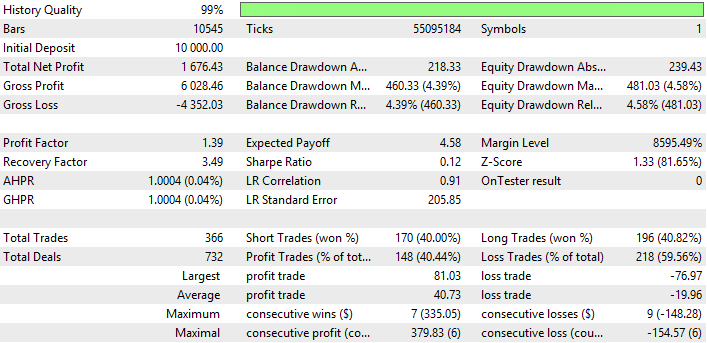
図10 二重指数移動平均のレポート
図5、7、9は、TEMAのバランス(エクイティ)チャートには わずかなドローダウンがありますが、NRMAやDEMAよりも安定していることを示しています。NRMAのバランス(エクイティ)チャートでは、過去3ヶ月間の取引での利益の急上昇が観測されます。DEMAのチャートでは、利益(少量のドローダウン)は2016年12月から伸び始めます。
GBPUSD通貨ペアでのテスト結果
GBPUSD通貨ペアでのテスト結果は以下の表に示されています。
| 移動平均の名前 | 最適化されたパラメータとその値 | 取引数 | 総純利益 | 利益率 | 回復率 | シャープレシオ | バランスドローダウン最大値 | エクイティ ドローダウン最大値 |
|---|---|---|---|---|---|---|---|---|
| 移動平均(平均化の手法 - 単純) | Period —38、Growth factor - 0.0005 | 52 | 1013.56 | 1.98 | 3.82 | 0.32 | 207.04 (2.7%) | 265.06 (2.65%) |
| 移動平均(平均化の手法 - 指数) | Period —41、Growth factor - 0.0002 | 219 | 787.12 | 1.14 | 1.23 | 0.07 | 576.96 (5.21%) | 639.44 (5.75%) |
| 移動平均(平均化の手法 - 平滑) | Period —42、Growth factor - 0.0003 | 48 | 817.42 | 1.71 | 3.85 | 0.26 | 151.32 (1.51%) | 212.24 (2.04%) |
| 移動平均(平均化の手法 - 加重) | Period —50、Growth factor - 0.0001 | 328 | 1086.08 | 1.17 | 1.26 | 0.07 | 818.34 (7.45%) | 861.04 (7.82%) |
| 適応移動平均 | Period —21、Growth factor - 0.001 | 100 | 1102.16 | 1.61 | 4.61 | 0.21 | 176.46 (1.71%) | 239.12 (2.28%) |
| 二重指数移動平均 | Period —23、Growth factor - 0.0007 | 263 | 1070.88 | 1.21 | 1.96 | 0.08 | 466.24 (4.42%) | 547.58 (5.16%) |
| 三重指数移動平均 | Period —30、Growth factor - 0.0009 | 214 | 1443.90 | 1.39 | 4.11 | 0.14 | 322.76 (3.02%) | 351.14 (3.28%) |
| フラクタル適応移動平均 | Period —38、Growth factor - 0.0001 | 819 | 651.54 | 1.05 | 0.85 | 0.02 | 747.98 (7.12%) | 764.88 (7.28%) |
| 可変インデックス動的平均 | Period EMA - 35、period CMO - 7、Growth factor - 0.0004 | 73 | 1606.98 | 1.99 | 5.20 | 0.34 | 251.94 (2.52%) | 309 (3.08%) |
| Nick Rypock移動平均 | Fact - 45、Growth factor - 0.0005 | 53 | 978.30 | 1.80 | 3.86 | 0.29 | 200.64 (1.99%) | 253.58 (2.51%) |
以下の表には正規化された結果が示されています(最良の結果は黄色、最悪の結果は赤色)。
| 移動平均の名前 | 総純利益 | 利益率 | 回復率 | シャープレシオ | バランスドローダウン最大値 | エクイティドローダウン最大値 | ドローダウンを除いた指標の合計 | ドローダウンを含む指標の合計 |
|---|---|---|---|---|---|---|---|---|
| 移動平均(平均化の手法 - 単純) | 0.3789 | 0.98929 | 0.68343 | 0.91799 | 0.08354 | 0.08141 | 2.96961 | 2.80467 |
| 移動平均(平均化の手法 - 指数) | 0.1419 | 0.09351 | 0.08718 | 0.13465 | 0.63812 | 0.65845 | 0.45724 | -0.8393 |
| 移動平均(平均化の手法 - 平滑) | 0.17416 | 0.70302 | 0.69032 | 0.74598 | 0 | 0 | 2.31347 | 2.31347 |
| 移動平均(平均化の手法 - 加重) | 0.45481 | 0.12036 | 0.09417 | 0.14629 | 1 | 1 | 0.81562 | -1.1844 |
| 適応移動平均 | 0.47164 | 0.58999 | 0.86402 | 0.57613 | 0.03769 | 0.04143 | 2.50177 | 2.42265 |
| 二重指数移動平均 | 0.4389 | 0.17142 | 0.25383 | 0.1936 | 0.47213 | 0.51686 | 1.05774 | 0.06875 |
| 三重指数移動平均 | 0.82931 | 0.36161 | 0.74969 | 0.36845 | 0.25702 | 0.21409 | 2.30906 | 1.83795 |
| フラクタル適応移動平均 | 0 | 0 | 0 | 0 | 0.89452 | 0.85179 | 0 | -1.7463 |
| 可変インデックス動的平均 | 1 | 1 | 1 | 1 | 0.15085 | 0.14914 | 4 | 3.70001 |
| Nick Rypock移動平均 | 0.342 | 0.79826 | 0.69126 | 0.82047 | 0.07394 | 0.06372 | 2.65199 | 2.51433 |
表が示唆しているように、可変インデックス動的平均の指標が最良で、Nick Rypock移動平均と単純な平均化手法を持った移動平均でかなり良い結果が得られました。VIDYA、NRMA及びSMAのテスト結果は図11-16に示されています。
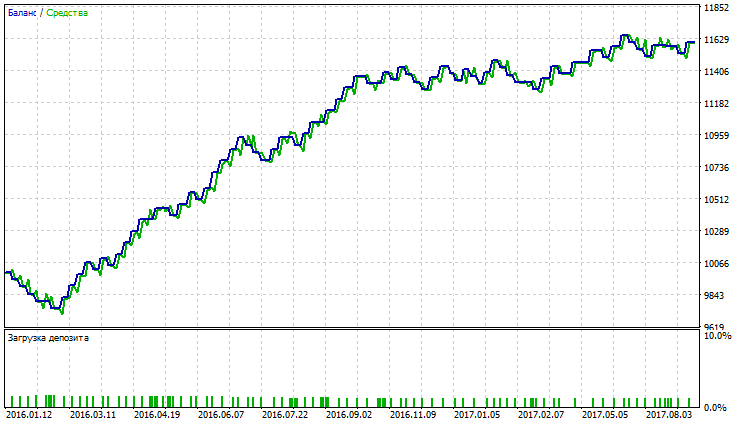
図11 可変インデックス動的平均のバランス(エクイティ)チャート
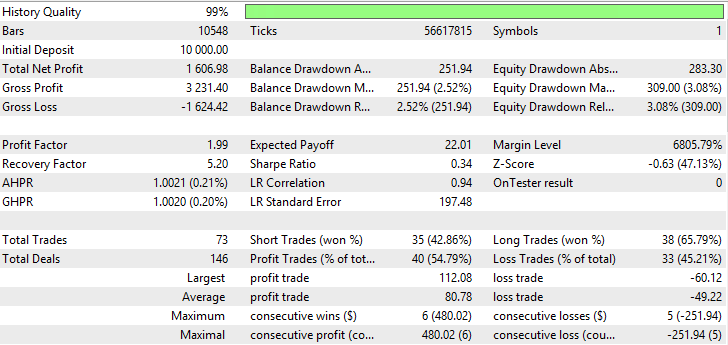
図12 可変インデックス動的平均のレポート
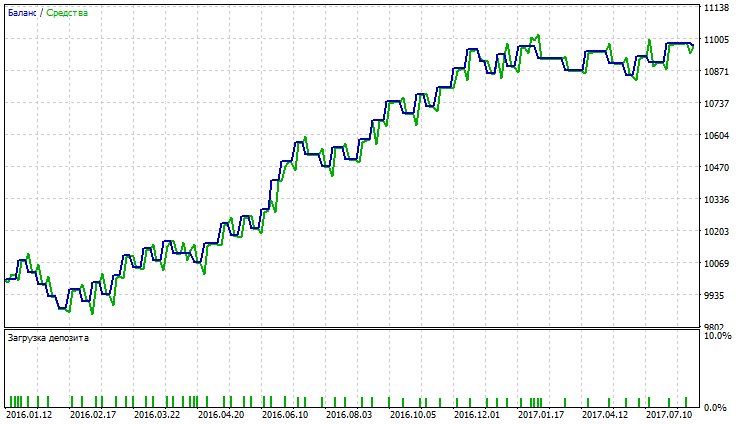
図13 Nick Rypock移動平均のバランス(エクイティ)チャート
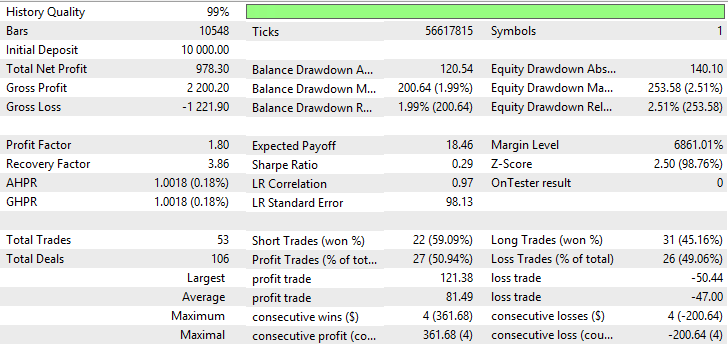
図14 Nick Rypock移動平均のレポート
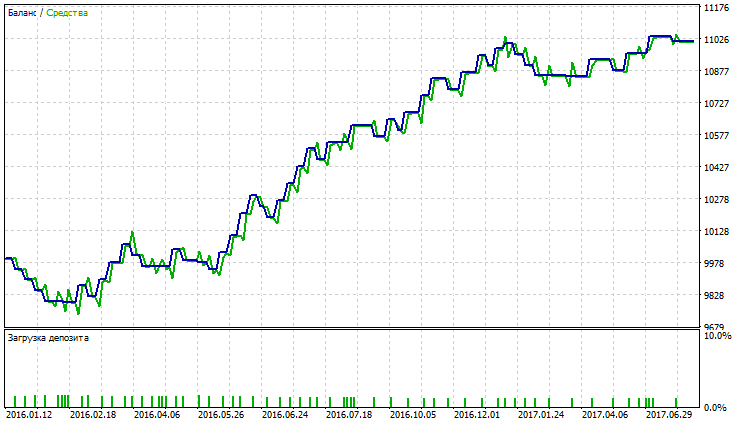
図15 単純移動平均のバランス(エクイティ)チャート
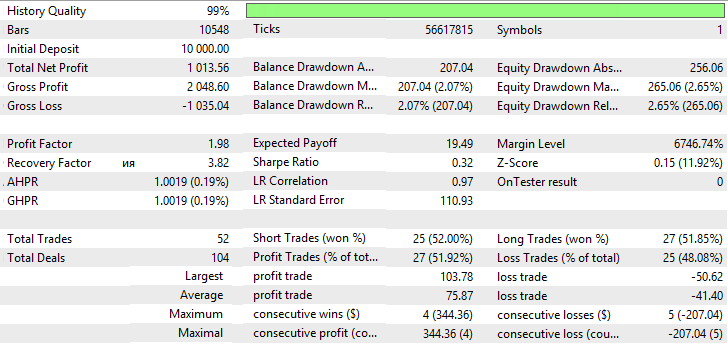
図16 単純移動平均のレポート
図11~16は、取引開始時に若干ドローダウンが観察された場合にはVIDYA、NRMAおよびSMAが幾分同じように見えることを示しています。 さらにチャートが伸び、VIDYAの取引数はNRMAやSMAよりも多くなります。VIDYAの収益性の高い取引の割合は、NRMAとSMAのものを上回ります。
USDJPY通貨ペアでのテスト結果
USDJPY 通貨ペアでのテスト結果は以下の表に示されています。
| 移動平均の名前 | 最適化されたパラメータとその値 | 取引数 | 総純利益 | 利益率 | 回復率 | シャープレシオ | バランスドローダウン最大値 | エクイティ ドローダウン最大値 |
|---|---|---|---|---|---|---|---|---|
| 移動平均(平均化の手法 - 単純) | Period —34、Growth factor - 0.0004 | 451 | 1784.95 | 1.32 | 3.69 | 0.1 | 465.52 (4.17%) | 483.34 (4.32%) |
| 移動平均(平均化の手法 - 指数) | Period —42、Growth factor - 0.0007 | 465 | 1135.23 | 1.20 | 2.21 | 0.07 | 461.52 (4.08%) | 514.61 (4.53%) |
| 移動平均(平均化の手法 - 平滑) | Period —33、Growth factor - 0.0008 | 372 | 1702.94 | 1.36 | 5.15 | 0.12 | 296.57 (2.58%) | 330.6 (2.87%) |
| 移動平均(平均化の手法 - 加重) | Period —50、Growth factor - 0.0005 | 477 | 1892.24 | 1.33 | 4.66 | 0.10 | 384.06 (3.68%) | 406.1 (3.88%) |
| 適応移動平均 | Period —46、Growth factor - 0.0006 | 403 | 1460.51 | 1.26 | 2.56 | 0.09 | 527.75 (4.77%) | 569.67 (5.13%) |
| 二重指数移動平均 | Period —18、Growth factor - 0.001 | 1062 | 1459.18 | 1.15 | 3.55 | 0.05 | 366.24 (3.30%) | 410.56 (3.69%) |
| 三重指数移動平均 | Period —50、Growth factor - 0.0003 | 657 | 1115.86 | 1.15 | 1.87 | 0.05 | 537.18 (4.68%) | 597.71 (5.18%) |
| フラクタル適応移動平均 | Period —24、Growth factor - 0.0008 | 1030 | 615.92 | 1.06 | 0.8 | 0.02 | 734.03 (6.58%) | 766.01 (6.85%) |
| 可変インデックス動的平均 | Period EMA - 18、period CMO - 42、Growth factor - 0.001 | 238 | 2338.68 | 1.64 | 5.14 | 0.21 | 417.66 (3.62%) | 454.69 (3.93%) |
| Nick Rypock移動平均 | Fact —28、Growth factor - 0.0002 | 435 | 1465.32 | 1.27 | 3.00 | 0.09 | 456.65 (4.02%) | 488.7 (4.29%) |
以下の表には正規化された結果が示されています(最良の結果は黄色、最悪の結果は赤色)。
| 移動平均の名前 | 総純利益 | 利益率 | 回復率 | シャープレシオ | バランスドローダウン最大値 | エクイティドローダウン最大値 | ドローダウンを除いた指標の合計 | ドローダウンを含む指標の合計 |
|---|---|---|---|---|---|---|---|---|
| 移動平均(平均化の手法 - 単純) | 0.67858 | 0.45316 | 0.66457 | 0.4324 | 0.38621 | 0.3508 | 2.22871 | 1.49171 |
| 移動平均(平均化の手法 - 指数) | 0.30144 | 0.25001 | 0.32251 | 0.25216 | 0.37706 | 0.42261 | 1.12612 | 0.32645 |
| 移動平均(平均化の手法 - 平滑) | 0.63098 | 0.51885 | 1 | 0.50010 | 0 | 0 | 2.64993 | 2.64993 |
| 移動平均(平均化の手法 - 加重) | 0.74086 | 0.46535 | 0.88693 | 0.42881 | 0.2 | 0.1734 | 2.52195 | 2.14855 |
| 適応移動平均 | 0.49025 | 0.34559 | 0.40481 | 0.36951 | 0.52846 | 0.54907 | 1.61017 | 0.53264 |
| 二重指数移動平均 | 0.48948 | 0.15054 | 0.63263 | 0.14711 | 0.15926 | 0.18364 | 1.41976 | 1.07686 |
| 三重指数移動平均 | 0.2902 | 0.15141 | 0.2445 | 0.15928 | 0.55002 | 0.61347 | 0.84538 | -0.3181 |
| フラクタル適応移動平均 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | -2 |
| 可変インデックス動的平均 | 1 | 1 | 0.99825 | 1 | 0.2768 | 0.285 | 3.99825 | 3.43645 |
| Nick Rypock移動平均 | 0.49305 | 0.36549 | 0.50479 | 0.37182 | 0.36593 | 0.36311 | 1.73515 | 1.00611 |
表が示すように、可変インデックス動的平均および移動平均は平滑化および線形加重平均化手法で最も優れた指標を示します。総純利益、利益率、VIDYAとのシャープレシオの指標は、SMMAとLWMAを上回っていますが、SMMAとLWMA は、バランスとエクイティドローダウンが最も少ないです。VIDYA, SMMA及びLWMAのテスト結果は図17~22に示されています。
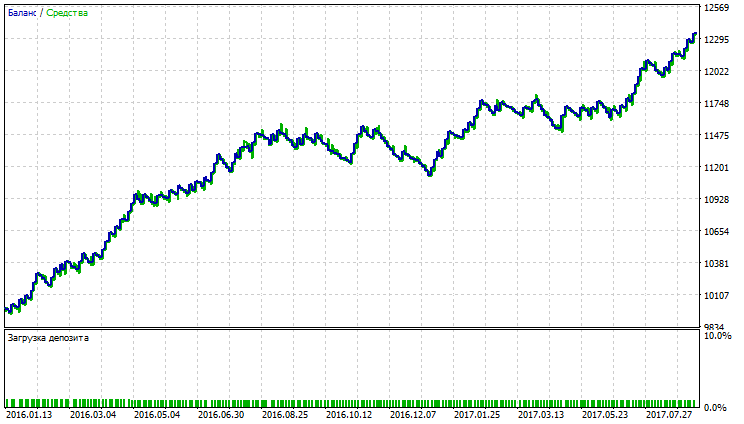
図17 可変インデックス動的平均のバランス(エクイティ)チャート
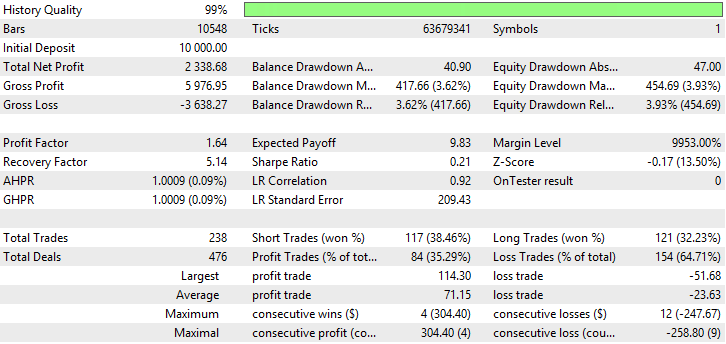
図18 可変インデックス動的平均のレポート
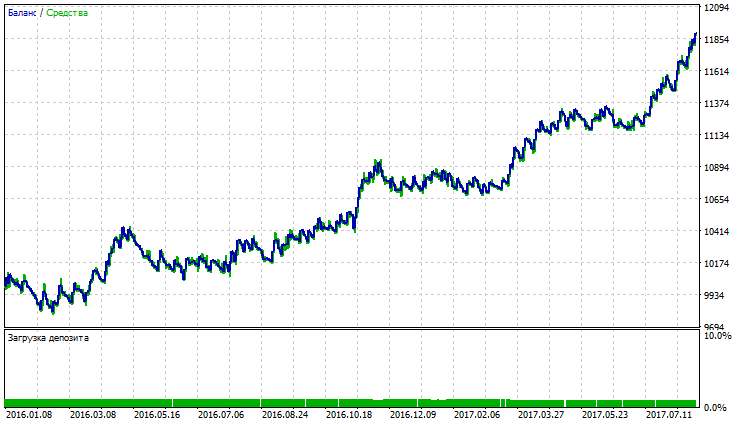
図19 線形加重移動平均のバランス(エクイティ)チャート
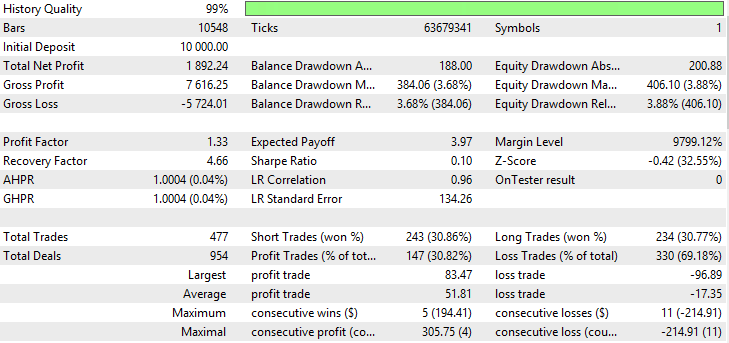
図20 線形加重移動平均のレポート
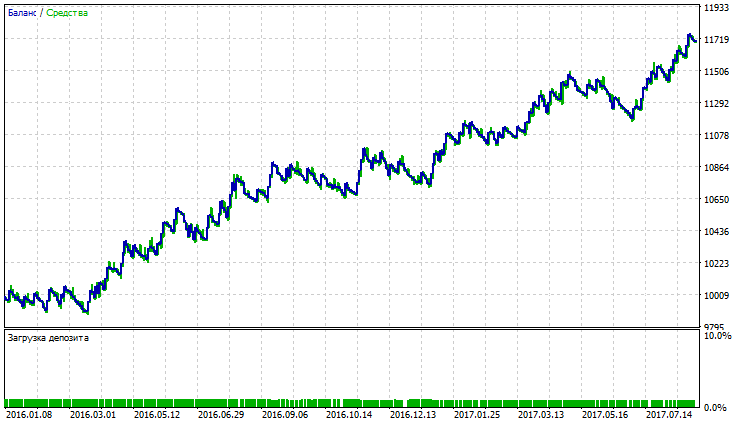
図21 平滑移動平均のバランス(エクイティ)チャート
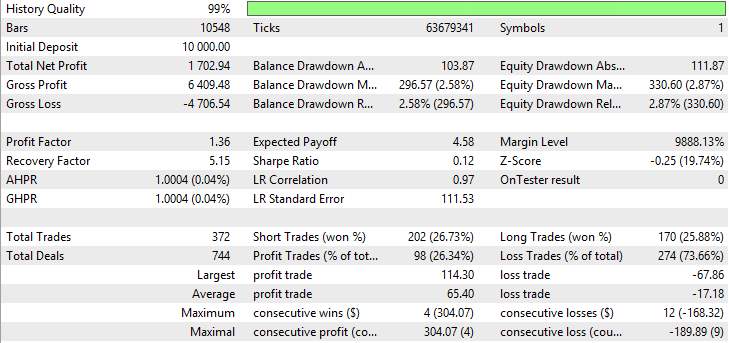
図22 平滑移動平均のレポート
図17~22は、収益性の低い取引の割合が低いにもかかわらず、指標が総純利益が高いことを示しています。 これは通貨ペアUSDJPYのボラティリティが高いという事実と結びついています。
USDCAD通貨ペアでのテスト結果
USDCAD通貨ペアでのテスト結果は以下の表に示されています。
| 移動平均の名前 | 最適化されたパラメータとその値 | 取引数 | 総純利益 | 利益率 | 回復率 | シャープレシオ | バランスドローダウン最大値 | エクイティ ドローダウン最大値 |
|---|---|---|---|---|---|---|---|---|
| 移動平均(平均化の手法 - 単純) | Period —39、Growth factor - 0,0004 | 59 | 110 | 2.30 | 7.11 | 0.40 | 133.44 (1.25%) | 154.92 (1.45%) |
| 移動平均(平均化の手法 - 指数) | Period —31、Growth factor - 0.0005 | 76 | 951.88 | 1.74 | 3.01 | 0.27 | 278.08 (2.56%) | 316.57 (2.91%) |
| 移動平均(平均化の手法 - 平滑) | Period —50、Growth factor - 0.0001 | 121 | 1262.26 | 1.57 | 3.07 | 0.22 | 343.76 (3.19%) | 411.32 (3.81%) |
| 移動平均(平均化の手法 - 加重) | Period —46、Growth factor - 0.0005 | 46 | 903.64 | 2.34 | 5.31 | 0.42 | 128.97 (1.22%) | 170.05 (1.61%) |
| 適応移動平均 | Period —38、Growth factor - 0.0009 | 41 | 990.44 | 3.18 | 8.62 | 0.55 | 77.57 (0.73%) | 114.96 (1.09%) |
| 二重指数移動平均 | Period —44、Growth factor - 0.0007 | 73 | 941.93 | 2.07 | 5.33 | 0.32 | 137.28 (1.28%) | 176.6 (1.64%) |
| 三重指数移動平均 | Period —49、Growth factor - 0.0009 | 76 | 559.18 | 1.62 | 3.28 | 0.20 | 122.21 (1.2%) | 170.57 (1.66%) |
| フラクタル適応移動平均 | Period —15、Growth factor - 0.0009 | 185 | 504.26 | 1.27 | 2.44 | 0.09 | 197.12 (1.95%) | 206.37 (2.04%) |
| 可変インデックス動的平均 | Period EMA - 34、period CMO - 9、Growth factor - 0.0002 | 111 | 1563.99 | 1.86 | 6.17 | 0.30 | 185.64 (1.70%) | 253.36 (2.32%) |
| Nick Rypock移動平均 | Fact - 41、Growth factor —0.0004 | 81 | 594.91 | 1.39 | 1.74 | 0.16 | 309.02 (2.88%) | 342.16 (3.18%) |
以下の表には正規化された結果が示されています(最良の結果は黄色、最悪の結果は赤色)。
| 移動平均の名前 | 総純利益 | 利益率 | 回復率 | シャープレシオ | バランスドローダウン最大値 | エクイティドローダウン最大値 | ドローダウンを除いた指標の合計 | ドローダウンを含む指標の合計 |
|---|---|---|---|---|---|---|---|---|
| 移動平均(平均化の手法 - 単純) | 0.56352 | 0.53776 | 0.78104 | 0.67198 | 0.20989 | 0.13484 | 2.5543 | 2.20957 |
| 移動平均(平均化の手法 - 指数) | 0.42239 | 0.24419 | 0.18441 | 0.37529 | 0.75326 | 0.68029 | 1.22628 | -0.2073 |
| 移動平均(平均化の手法 - 平滑) | 0.71528 | 0.15751 | 0.19342 | 0.26924 | 1 | 1 | 1.33545 | -0.6646 |
| 移動平均(平均化の手法 - 加重) | 0.37687 | 0.55859 | 0.5199 | 0.69827 | 0.1931 | 0.18589 | 2.15363 | 1.77465 |
| 適応移動平均 | 0.45878 | 1 | 1 | 1 | 0 | 0 | 3.45878 | 3.45878 |
| 二重指数移動平均 | 0.413 | 0.42112 | 0.52277 | 0.48957 | 0.22431 | 0.20799 | 1.84645 | 1.41415 |
| 三重指数移動平均 | 0.05182 | 0.18256 | 0.22388 | 0.23681 | 0.1677 | 0.18764 | 0.69508 | 0.33974 |
| フラクタル適応移動平均 | 0 | 0 | 0.10249 | 0 | 0.44912 | 0.30844 | 0.10249 | -0.6551 |
| 可変インデックス動的平均 | 1 | 0.30606 | 0.64482 | 0.43945 | 0.40599 | 0.467 | 2.39033 | 1.51734 |
| Nick Rypock移動平均 | 0.08554 | 0.06124 | 0 | 0.14059 | 0.86949 | 0.76664 | 0.28737 | -1.3488 |
表が示すように、単純化平均法と可変インデックス動的平均を用いた適応移動平均、移動平均が最良の指標を示しています。可変インデックス動的平均は、利益率、回復率、シャープレシオの最良の指標を示していますが、バランスとエクイティを最小限に抑えています。変動指数動的平均が最大の総純利益を有しますが、他の指標は最高ではありません。 AMA, SMA及びVIDYAのテスト結果は図23~28に示されています。
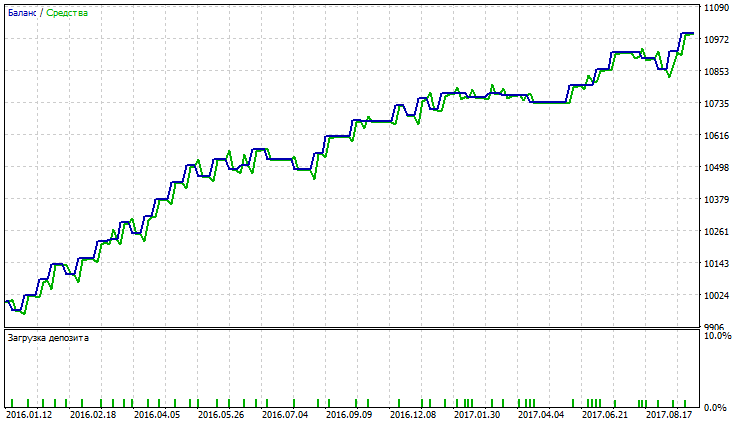
図23 適応移動平均のバランス(エクイティ)チャート
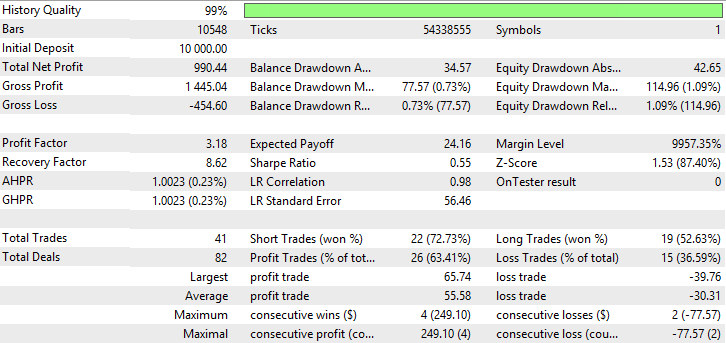
図24 適応移動平均のレポート
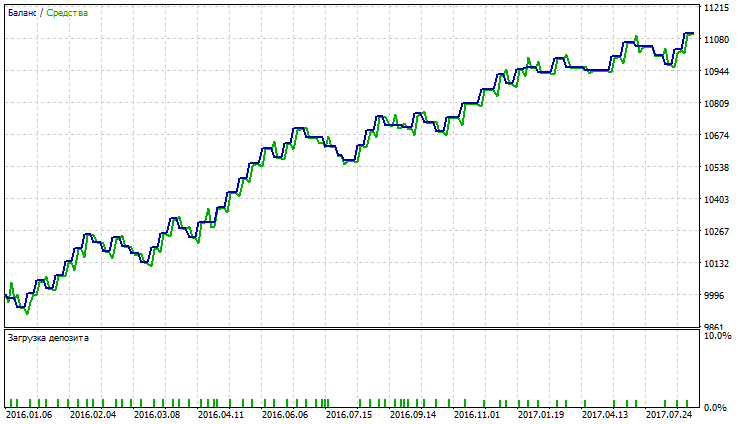
図25 単純移動平均のバランス(エクイティ)チャート
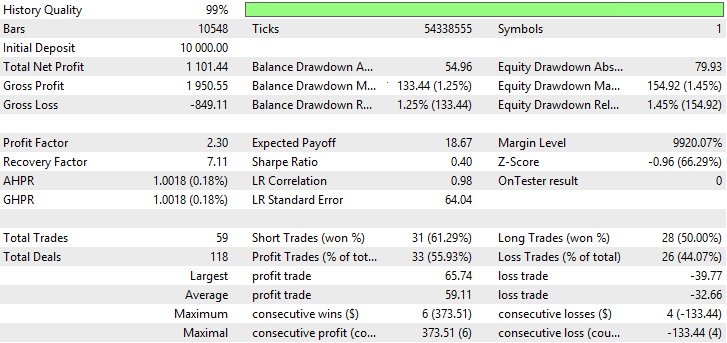
図26 . 単純移動平均のレポート
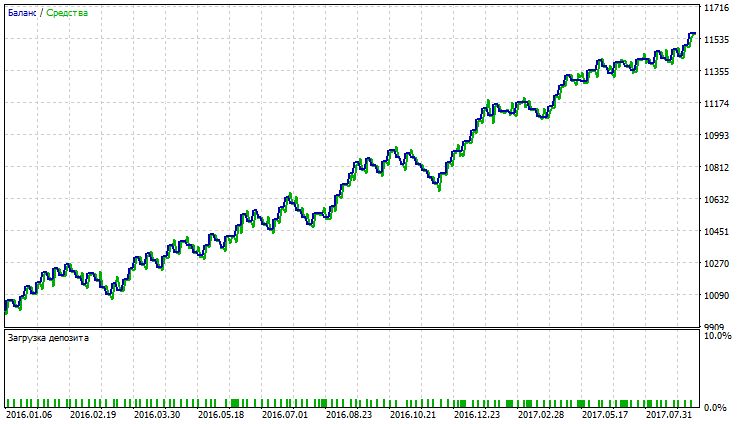
図27 可変インデックス動的平均のバランス(エクイティ)チャート
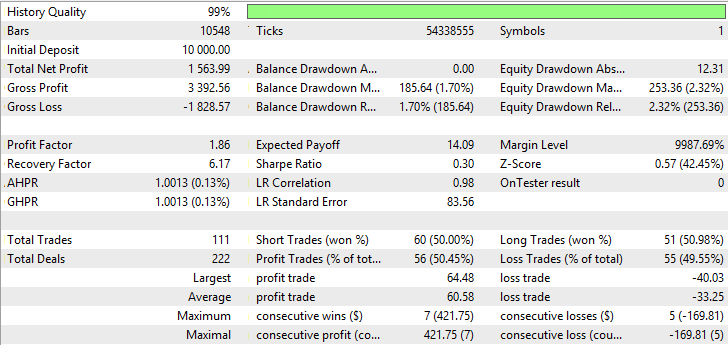
図28 可変インデックス動的平均のレポート
図23~28は、AMAの取引量が最も少なく、収益性の高い取引の割合が最も高いことを示しています。SMAとVIDYAは、より多くの取引量のアカウントで最も高い利益を得ていますが、収益性の高い取引数は、その損失を超えています。AMA、SMA及びVIDYAチャートでは大規模のドローダウンは観測されません。
AUDUSD通貨ペアでのテスト結果
AUDUSD 通貨ペアでのテスト結果は以下の表に示されています。
| 移動平均の名前 | 最適化されたパラメータとその値 | 取引数 | 総純利益 | 利益率 | 回復率 | シャープレシオ | バランスドローダウン最大値 | エクイティ ドローダウン最大値 |
|---|---|---|---|---|---|---|---|---|
| 移動平均(平均化の手法 - 単純) | Period —7、Growth factor - 0.0009 | 78 | 262.48 | 1.36 | 1.23 | 0.11 | 175.85 (1.74%) | 214.18 (2.11%) |
| 移動平均(平均化の手法 - 指数) | Period —40、Growth factor - 0.0004 | 24 | 652.88 | 2.62 | 2.82 | 0.47 | 206.76 (1.93%) | 231.76 (2.16%) |
| 移動平均(平均化の手法 - 平滑) | Period —21、Growth factor - 0.0004 | 24 | 651.18 | 2.61 | 2.81 | 0.47 | 206.76 (1.93%) | 231.76 (2.16%) |
| 移動平均(平均化の手法 - 加重) | Period —32、Growth factor - 0.0005 | 24 | 383.64 | 1.97 | 2.25 | 0.30 | 116.38 (1.11%) | 170.24 (1.62%) |
| 適応移動平均 | Period —21、Growth factor - 0.0007 | 58 | 252.39 | 1.30 | 0.54 | 0.11 | 392.15 (3.80%) | 464.47 (4.48%) |
| 二重指数移動平均 | Period —40、Growth factor - 0.0006 | 39 | 296.15 | 1.70 | 1.53 | 0.20 | 156.62 (1.51%) | 193.02 (1.86%) |
| 三重指数移動平均 | Period —21、Growth factor - 0.001 | 69 | 273.12 | 1.35 | 1.05 | 0.11 | 228.5 (2.20%) | 259.71 (2.50%) |
| フラクタル適応移動平均 | Period —38、Growth factor - 0.0007 | 83 | 109.01 | 1.11 | 0.55 | 0.04 | 142.85 (1.42%) | 196.47 (1.94%) |
| 可変インデックス動的平均 | Period EMA - 26、period CMO - 5、Growth factor - 0.0006 | 23 | 697.59 | 2.99 | 2.96 | 0.53 | 151.35 (1.41%) | 235.38 (2.19%) |
| Nick Rypock移動平均 | Period —22、Growth factor - 0.0006 | 34 | 509.27 | 1.90 | 2.55 | 0.28 | 94.58 (0.9%) | 200 (1.89%) |
以下の表には正規化された結果が示されています(最良の結果は黄色、最悪の結果は赤色)。
| 移動平均の名前 | 総純利益 | 利益率 | 回復率 | シャープレシオ | バランスドローダウン最大値 | エクイティドローダウン最大値 | ドローダウンを除いた指標の合計 | ドローダウンを含む指標の合計 |
|---|---|---|---|---|---|---|---|---|
| 移動平均(平均化の手法 - 単純) | 0.26075 | 0.12921 | 0.28183 | 0.13463 | 0.27311 | 0.14934 | 0.80642 | 0.38397 |
| 移動平均(平均化の手法 - 指数) | 0.92404 | 0.80629 | 0.93942 | 0.86552 | 0.37699 | 0.20909 | 3.53527 | 2.94919 |
| 移動平均(平均化の手法 - 平滑) | 0.92115 | 0.8006 | 0.93639 | 0.86226 | 0.37699 | 0.20909 | 3.5204 | 2.93433 |
| 移動平均(平均化の手法 - 加重) | 0.4666 | 0.45691 | 0.70658 | 0.52861 | 0.07326 | 0 | 2.1587 | 2.08544 |
| 適応移動平均 | 0.2436 | 0.10105 | 0 | 0.13347 | 1 | 1 | 0.47812 | -1.5219 |
| 二重指数移動平均 | 0.31795 | 0.31405 | 0.40942 | 0.31848 | 0.20849 | 0.07742 | 1.3599 | 1.07399 |
| 三重指数移動平均 | 0.27882 | 0.12776 | 0.20999 | 0.14014 | 0.45005 | 0.30408 | 0.75672 | 0.00259 |
| フラクタル適応移動平均 | 0 | 0 | 0.00473 | 0 | 0.16221 | 0.08915 | 0.00473 | -0.2466 |
| 可変インデックス動的平均 | 1 | 1 | 1 | 1 | 0.19078 | 0.22139 | 4 | 3.58783 |
| Nick Rypock移動平均 | 0.68004 | 0.42124 | 0.82757 | 0.48773 | 0 | 0.10115 | 2.41659 | 2.31545 |
表が示唆するように、可変インデックス動的平均と移動平均は、指数関数及び平滑平均化手法で最良の指標で、VIDYAは、総純利益、利益率、回収率、シャープレシオの最良指標を示しています。EMAとSMMAには、ほぼ等しい指標と取引数があります。 VIDYA、EMA、およびSMMAのテスト結果は図29~34に示されています。
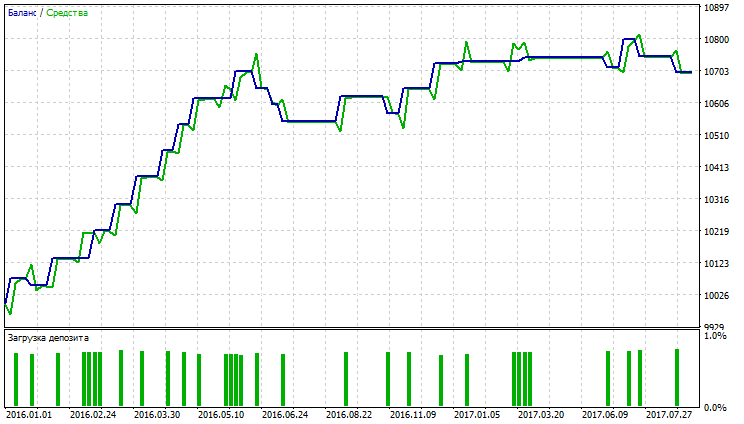
図29 可変インデックス動的平均のバランス(エクイティ)チャート
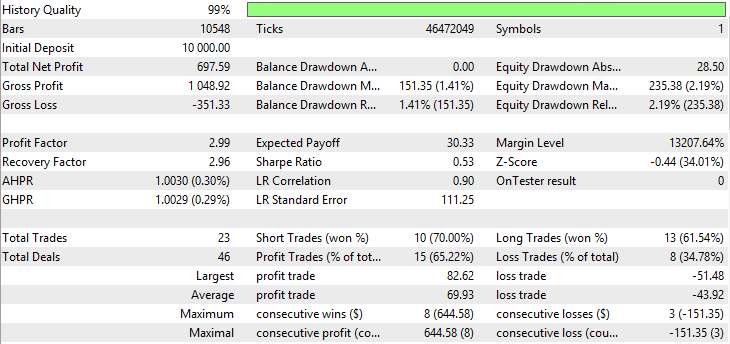
図30 可変インデックス動的平均のレポート
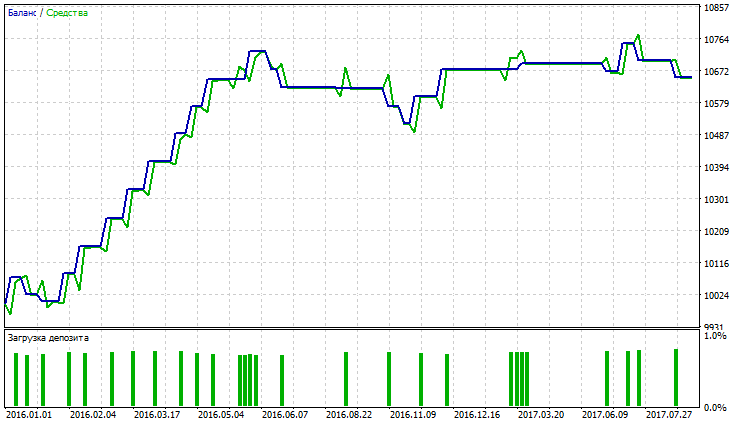
図31 指数移動平均のバランス(エクイティ)チャート
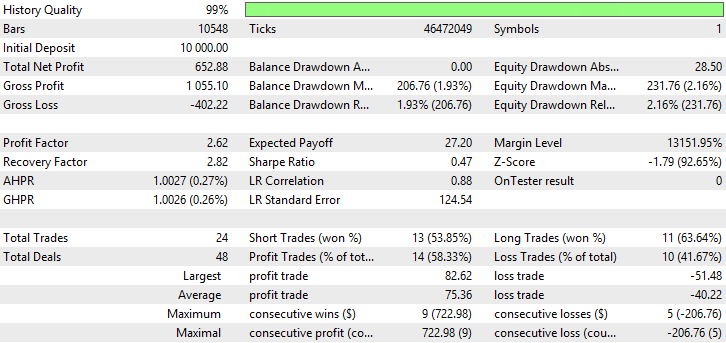
図32 指数移動平均のレポート
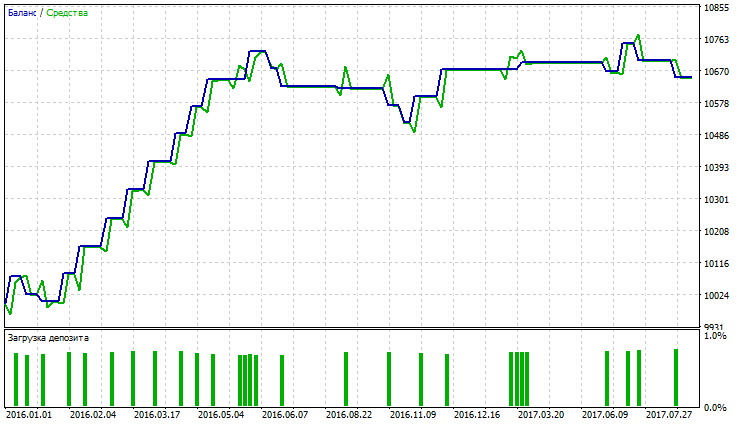
図33 平滑移動平均のバランス(エクイティ)チャート
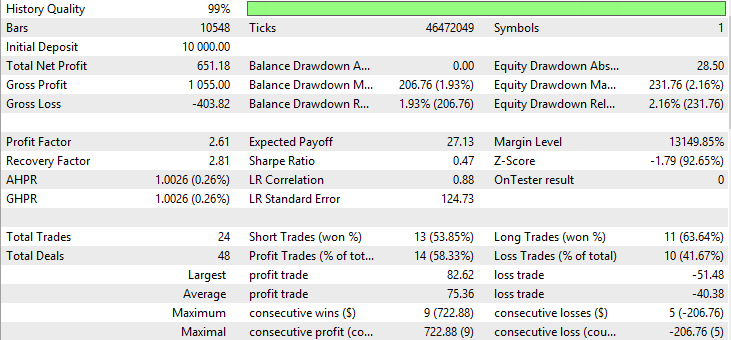
図34 平滑移動平均のレポート
図29~34は、VIDYA、EMA、SMMAのバランス(エクイティ)チャートがほぼ等しいことを示しています。VIDYAはEMAやSMMAよりも収益性の高い取引数が多いです。得られた結果が通貨ペアAUDUSDのボラティリティの低さによって説明されています。
通貨ペアEUR、GBPUSD、USDJPY、USDCAD、AUDUSDのテスト結果に基づいて、以下の結論を下すことができます。
- 高ボラティリティ( GBPUSD、USDJPY)と低ボラティリティ( AUDUSD)を持つ通貨ペアで最良の結果は可変インデックス動的平均によって示された
- 適応移動平均は、通貨ペアUSDCADでは最良の指数を示したが、通貨ペアEURUSDでは最悪の結果を示した。
- 通貨ペアEUR USDでは、最良の指数は三重指数移動平均によって示された。
- 通貨ペアGBPUSD、USDJPY、USDCAD、AUDUSDの最悪の結果は、フラクタル適応移動平均によって示された。
- 様々な平均期間での標準的移動平均の結果は有望です。
終わりに
異なる移動平均(MA、単純、指数、平滑、直線加重法)、DEMA、TEMA、FRAMA、AMA、VIDYA、NRMA)を考慮し、それぞれのMAについて計算の手順を説明しました。移動平均は市場への出入りの等しい条件での取引において比較されて最適化されました。
得られた結果に基づいて、以下の結論を下すことができます。
- 収益性のある戦略は、考察された移動平均のいずれかのパラメータを最適化することによっても獲得できる。
- 移動平均の大部分はEMA指標の変種である。
- EMAベースの移動平均の主な利点は、フラットでの誤シグナルの減少及び傾向変化に対するより高速な応答である。
- 最良の結果は可変インデックス動的平均によって示され、高ボラティリティ及び低ボラティリティ通貨ペアと、平均的ボラティリティ通貨ペアで使用することができる。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/3791
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 インジケーターへのエントリの解決
インジケーターへのエントリの解決
 戦略バランス曲線の品質評価としての R 乗
戦略バランス曲線の品質評価としての R 乗
 カルマンフィルタを用いた価格方向予測
カルマンフィルタを用いた価格方向予測
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
過去数本の平均値を示す棒グラフが、どうして価格の行方を示すのでしょうか?
正確には、上昇したのだから、今後も上昇し続けるだろう、というようなものだ。
素晴らしい )))まずこの期間でパラメータ・フィッティングを行い、それからテストする ))前方最適化とテストを行ってみてください。
そうですね。バック・オプティマイゼーションとフォワード・テストの方が現実的でしょう。私はEURUSDで TEMA、NRMA、DEMAについてそのような最適化とテストを行った(彼らは記事で最高の結果を出した)。
バック最適化。期間2016.01.01-04.11.2016(先にテストした時間間隔の半分)。
フォワードテスト。期間2016.11.05-2017.09.09。
結果を表にまとめた:
(最適化)
(テスト)
(最適化)
(テスト)
NRMAについては、テスト結果は記事よりも悪かった。TEMAとDEMAは良い結果を示した。