知っておくべきMQL5ウィザードのテクニック（第62回）：強化学習TRPOでADXとCCIのパターンを活用する

はじめに

今回は、価格変動の異なる側面を追跡するテクニカル指標を、機械学習においてどのように組み合わせるかを引き続き検討します。前回の記事では、多層パーセプトロン(MLP)による教師あり学習が、価格変動予測の基盤をどのように形成するかを確認しました。MLPの入力を「特徴量」、予測出力を「状態」と呼びます。前回の記事では、特徴量の定義を第57回～第60回の手法とは少し異なる形でおこない、より連続的な入力ベクトルを使用することを目指しました。これは、以前使用していた離散的オプションからの移行です。連続データと回帰への移行、そして離散データと分類からの脱却は、AIトレンドを考察すると最も説得力を持って説明できるかもしれません。

かつては、コンピュータプログラムに実用的な応答をさせるためには、その応答をプログラムに手動で組み込む必要がありました。本質的に、多くのプログラムでは「if文」がコアでした。そして考えてみれば、if文への依存は、ユーザー入力やプログラムが処理するデータが特定のカテゴリに分類されていることを前提としていました。つまり、データは離散的である必要がありました。このため、私たちが離散データを開発し使用してきた背景は、データや解くべき問題そのものに起因するのではなく、プログラミングの制約に応じた結果であったと言えます。

しかし、2023年秋にOpenAIが最初の公開GPTを発表したことで、状況は一変しました。TransformerネットワークやGPTの開発は一夜にしておこなわれたわけではなく、最初のパーセプトロンは1960年代後半に開発されましたが、ChatGPTの登場は重要なマイルストーンであったと言えます。大規模言語モデルが広く採用される中で、トークン化、単語埋め込み、そしてSelf-Attention（自己注意）が、モデルの処理能力を拡張する上で重要な要素であることが明らかになりました。もはやif文に依存する必要はありません。このような背景のもと、ネットワーク入力を可能な限り連続的にするためのトークン化や単語埋め込みの手法を応用し、教師あり学習MLPの入力も「より連続的」に設計しました。

これを具体的に示すために、第2の特徴量、Feature_1はPythonからMLPに対して以下のように表現されます。

def feature_1(adx_df, cci_df):
    """
    Creates a modified 3D signal array with:
    1. ADX > 25 (1 when above 25, else 0)
    2. CCI crosses from below 0 to above +50 (1 when condition met, else 0)
    3. CCI crosses from above 0 to below -50 (1 when condition met, else 0)
    """
    # Initialize empty array with 3 dimensions
    feature = np.zeros((len(adx_df), 5))
    
    # Dimension 1: ADX above 25 (continuous, not just crossover)
    feature[:, 0] = (adx_df['adx'] > 25).astype(int)
    
    # Dimension 2: CCI crosses from <0 to >+50
    feature[:, 1] = (cci_df['cci'] > 50).astype(int)
    feature[:, 2] = (cci_df['cci'].shift(1) < 0).astype(int)
    
    # Dimension 3: CCI crosses from >0 to <-50
    feature[:, 3] = (cci_df['cci'] < -50).astype(int)
    feature[:, 4] = (cci_df['cci'].shift(1) > 0).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    feature[0, :] = 0
    
    return feature

第57回～第60回までで使用していた手法に従っていた場合、処理は次のようにおこなわれていたでしょう。

def feature_1(adx_df, cci_df):
    """
    """
    # Initialize empty array with 3 dimensions and same length as input
    feature = np.zeros((len(dem_df), 3))
    
    # Dimension 1:
    feature[:, 0] = (adx_df['adx'] > 25).astype(int)
    feature[:, 1] = ((cci_df['cci'] > 50) &
                     (cci_df['cci'].shift(1) < 0)).astype(int)
    feature[:, 2] = ((cci_df['cci'] < -50) &
                     (cci_df['cci'].shift(1) > 0)).astype(int)
    
    # Set first row to 0 (no previous values to compare)
    feature[0, :] = 0
    
    return feature

このアプローチは、出力ベクトルの2番目の要素が強気（ブル）シグナルの特徴量のみを捉え、3番目の要素が弱気（ベア）シグナルの特徴量のみを捉えるため、通常期待される強気・弱気のパターンに沿ってシグナルを分類する傾向があります。そのため、既に強気または弱気として定義されたパターンに従うことで、このアプローチは分類器的であり、離散的になりやすいと言えます。とはいえ、テスト結果では、2020年1月1日から2024年1月1日までに訓練/テストした10パターンのうち、2024年1月1日から2025年1月1日までフォワードウォークに成功したのはわずか3パターンでした。使用した通貨ペアはEUR/USDで、時間枠は日足です。

したがって、今回使用した比較的長い時間枠と学習期間を考慮すると、初期のMLPにおいてより離散的な入力データを使うことには妥当性があるように思われます。また、この点はLLMの入力を考慮するとさらに支持されます。確かに、トークン化や単語埋め込みにより入力データはより連続的になりますが、LLMの「秘密兵器」であるSelf-Attentionは本質的に離散的です。これは、プロンプトに与えられた各単語に相対的な重みを付与しようとするためです。

私たちはこれと同様のことをおこなっていないため、これが説明の一つになり得ます。MQL5のソースコードがすべて添付されているので、読者の皆さんは自由に入力フォーマットを変更してテストできます。私たちは、このアプローチを維持し、強化学習でどのような結果が得られるかを確認していく予定です。

強化学習

前回の記事で扱った教師あり学習モデルを基に、今回は行動と報酬を導入します。前回は、MLPへの入力として特徴量を用い、出力として状態（価格変動の予測）を得ていました。この段階での行動は、MLPが予測した結果に対して何をすべきかを表します。たとえば、価格が下落すると予測された場合、売り指値、売り逆指値、または即時成行売りといった行動が考えられます。このような意思決定を洗練させるために、ポリシーネットワーク（方策ネットワーク）を構築し、学習させることが有効です。

通常、前述のように複数の売り注文タイプを選択する場合、ポリシーネットワークの出力ベクトルのサイズは可能な行動の数と一致します。この場合、指値注文、逆指値注文、成行注文の3つの選択肢があるため、出力ベクトルのサイズは3となります。この設定で学習させると、パフォーマンスに差が生じることが期待されます。読者の皆様も自由に探索できます。私たちの場合、行動は単次元ベクトルとして扱い、前回のMLPからの状態出力ベクトルを本質的にコピーした形にしています。この場合の目的は何でしょうか。これは、教師あり学習ネットワークによるロング/ショート予測の確認として機能します。

さらに、報酬は各取引の利益の大きさを評価するために用いられます。報酬はバリューネットワーク（価値ネットワーク）の出力であり、今回は単次元ベクトルとして評価していますが、もちろん多次元化も可能です。これは、取引後の解析で利益/損失だけでなく、価格の変動幅も考慮できるためです。変動幅には有利なものと不利なものがあるため、報酬ベクトルは不利な変動・有利な変動・純利益の3次元ベクトルとしても表現できます。

TRPO（Trust Region Policy Optimization、信頼領域方策最適化)

TRPOは、方策の改善に特化した強化学習アルゴリズムです。この手法では、ポリシーネットワークの重みやバイアスを反復的に更新しつつ、常に現在の方策の「信頼領域」内に収めることを重視します。

TRPOの実装における主要な要素は、ポリシーネットワーク、信頼領域、およびKLダイバージェンス（KL距離）です。ポリシーネットワークは、状態から可能な行動の確率分布へのマッピングをおこなうニューラルネットワークで、行動選択を表現します。信頼領域は、各反復で方策が変化できる範囲に制約を設ける仕組みです。これにより、新しい方策が古い方策から大きく逸脱することを防ぎ、学習の不安定化を避けます。最後に、KLダイバージェンスは新しい方策と信頼される方策の確率分布の差を測る指標で、信頼領域の制約を定義する役割を果たします。

TRPOの学習プロセスは、まず現在の方策を用いて軌跡を収集することから始まります。このデータを基に、各状態-行動ペアについてアドバンテージ関数を推定し、特定の行動が平均的な行動よりどれだけ有利であるかを評価します。その後、KLダイバージェンス制約の下で報酬を最大化するように、方策およびバリューネットワークの重みとバイアスを最適化する問題を定式化します。最適化は勾配降下法などの手法によって解かれ、最後に方策とバリューネットワークの重みが更新されます。このプロセスを繰り返すことで、新しい方策は安定的に改善されていきます。

TRPOの主な利点としては、まず単調改善が挙げられます。これは、方策改善が保証されることを意味します。また、信頼領域により方策が不必要に大きく変化して不安定になることを防ぐため、学習の安定性も確保されます。さらに、TRPOは他の方策勾配法に比べて少ないサンプルで効果的に学習できるため、効率性にも優れています。要するに、TRPOの核心的な考え方は、新しい方策が古い方策に比べて期待アドバンテージを最大化することにあります。ただし、方策がどの程度変化できるかには制約があり、これが信頼領域の役割を果たします。この考え方は以下の式に表されます。

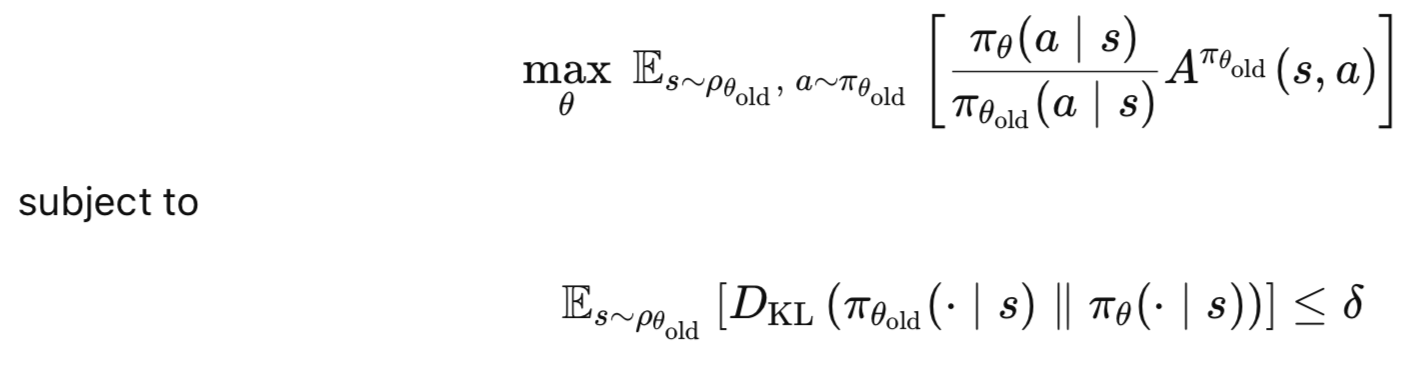
ここで

• θ：新しい方策パラメータ
• θold：更新前の古い方策パラメータ
• πθ(a∣s)：新しい方策πθ下での行動aの確率
• πθold(a∣s)：古い方策πθold下での行動aの確率
• Aπθold(s,a)：アドバンテージ関数（状態sにおける平均行動よりもaがどれだけ優れているかを推定）
• ρθold (s)：古い方策による状態訪問の配分
• DKL：カルバック・ライブラー情報量（古い方策と新しい方策の違いを測定）
• δ：信頼領域制約（小さな正の値）

ポリシーネットワーク

ポリシーネットワークとバリューネットワークをPythonで次のように実装します。

class PolicyNetwork(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_size=64, discrete=False):
        super(PolicyNetwork, self).__init__()
        self.discrete = discrete
        
        self.fc1 = nn.Linear(state_dim, hidden_size)
        self.fc2 = nn.Linear(hidden_size, hidden_size)

        self.export_mode = False
        
        if self.discrete:
            self.fc3 = nn.Linear(hidden_size, action_dim)
        else:
            self.mean = nn.Linear(hidden_size, action_dim)
            self.log_std = nn.Parameter(torch.zeros(action_dim))
    
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        
        if self.discrete:
            action_probs = F.softmax(self.fc3(x), dim=-1)
            dist = Categorical(action_probs)
        else:
            mean = self.mean(x)
            std = torch.exp(self.log_std)
            
            if self.export_mode:
                return mean, std  # return raw tensors
            
            cov_mat = torch.diag_embed(std).unsqueeze(dim=0)
    
            dist = MultivariateNormal(mean, cov_mat)
        
        return dist

ポリシーネットワークはnn.Moduleを継承しており、これによりPyTorchのネットワークモジュールとして機能します。このネットワークは、入力状態空間の次元を示すstate-dimension、行動空間の次元を示すaction-dimension、および隠れ層のサイズを指定するhidden-sizeをパラメータとして受け取ります。隠れ層のサイズはデフォルトで64に設定しています。また、discreteというブールフラグを入力として受け取り、行動空間が離散か連続かを設定します。このフラグは最終的に出力層の構造や使用される分布の種類にも影響します。

この設定により、ネットワークは離散および連続の行動空間の両方に対応可能となり、RL環境での汎用性が高まります。たとえば、CartPoleのようなゲームではdiscreteをTrueに設定し、取引やロボティクスのケースではFalseに設定します。TRPOにおいてポリシーネットワークはエージェントの方策を定義し、状態から行動へのマッピングをおこないます。そのため、異なる種類の行動空間を扱える柔軟性は、一般的な適用性において重要です。トレーダーの場合、前述の3種類の注文（指値、逆指値、成行）に行動を制限したい場合、discreteはtrueに設定されます。 

実装の際には、state-dimensionとaction-dimensionが環境や使用データセットの仕様に一致していることを確認することが重要です。discreteフラグも環境の行動空間タイプと一致させる必要があります。隠れ層サイズの64は調整可能なハイパーパラメータであり、環境やデータセットの複雑さに応じて増加させたり、隠れ層を追加したりすることが考えられます。

ネットワークアーキテクチャは、2つの全結合線形層（fc1とfc2）で構成されています。fc1は入力状態を隠れ層にマッピングし、fc2は同じサイズの別の隠れ層にマッピングします。export_modeは、ネットワークが生のテンソルを返すか、学習やサンプリング用の分布を返すかを制御するフラグです。 

これらの層は、ポリシーネットワークの骨格を形成しており、入力状態を適切な行動の高次表現に変換します。2層構造でReLU活性化を用いることで、モデルを軽量に保ちながら十分な表現力を確保しています。TRPOではポリシーネットワークが微分可能であることが必須であり、これは方策更新の勾配計算に必要です。2つの線形層により、この要件は満たされます。 

デフォルト設定として隠れ層2層、サイズ64は妥当ですが、入力状態が複雑化したり、特徴量が増えたりすると、層数やサイズを増やす必要があります。たとえば、複数のインジケーターを組み合わせて特徴量パターンを作る場合や、より複雑な状態をポリシーネットワークに入力する場合には、隠れ層のサイズを増やしたり、層を追加する必要があります。 

ネットワークが離散モードかどうかによって、最終出力層は単一ネットワークか2つのネットワークかに分かれます。離散行動の場合、fc3の出力は各行動のロジットを表します。一方、連続行動の場合(discrete=false)、2つのネットワークがそれぞれ別のベクトルを出力します。1つは各action-dimensionのガウス分布の平均、もう1つはaction-dimensionのガウス分布の対数標準偏差です。

これは重要で、なぜならこの分岐により異なる種類の行動空間をモデル化できるからです。discrete-onモードでは、ネットワークはあらかじめ設定された行動数に対する確率分布を出力します。連続モード(discrete-off)の場合は、多変量ガウス分布を出力します。これは単純に2つのベクトルで表され、1つは平均ベクトルで各行動の代表値および重み付けを示し、もう1つは対数標準偏差ベクトルで各平均値予測に対する信頼度や分布の広がりを示します。

TRPOでは、この方策分布を用いて環境とのインタラクション中に行動をサンプリングし、方策勾配の更新に必要な対数確率を計算します。そのため、離散か連続かの設定は計算量やネットワークの効率に直接影響します。対数確率の標準偏差は学習可能なパラメータであり、学習中に探索の幅や活用のバランスを調整する役割を果たします。これは探索と開発のバランスをとるために重要です。

離散行動の場合、action-dimensionは可能な行動数と一致させる必要があります。現在は連続変数を扱うため単次元ベクトルを使用していますが、後の章では離散行動オプションを再度扱う予定です。連続行動の場合は、log_stdの初期化が非常に重要です。Torch.zeros(action_dim)で初期化すると標準偏差はexp(0)=1となり、行動スケールによっては広すぎたり狭すぎたりする可能性があります。そのため、環境に応じた適切なスケーリング方法を用いる必要があります。

さらに、TRPOでは方策の対数確率が目的関数やKLダイバージェンス制約で使用されるため、分布内での数値的安定性を確保することが重要です。環境が行動範囲を制限している場合、ネットワーク出力が意図した範囲外になることがあり、この場合は平均出力をクリップしたりスケーリングしたりして調整する必要があります。

ポリシーネットワークへのフォワードパスでは、入力状態xがポリシーネットワークに渡され、fc1とfc2を通過し、ReLU活性化関数によって非線形性が加えられます。行動が離散的であれば、fc3の出力はsoftmaxを通して各行動の確率へと変換されます。一方、行動が連続的である場合、平均はmean層によって計算され、標準偏差はexp(log_std)を取ることで正の値が保証されます。export_modeがTrueであれば標準偏差は生のテンソルとして返され、export_modeがFalseであれば対角共分散行列(cov_mat)が構築され、多変量正規分布が作られて対数確率のサンプリングに用いられます。

フォワードパスは、方策が状態をどのように行動分布へとマッピングするかを定義するものであり、これは強化学習エージェントの意思決定の中核です。TRPOにおいて方策分布は、環境との相互作用の際に行動をサンプリングし、方策勾配目的関数のために対数確率を計算し、信頼領域制約を評価します。離散型のカテゴリ分布と連続型の多変量正規分布を利用することにより、PyTorchのtorch.distributionsなど標準的なRLライブラリとの互換性が確保されます。さらに、export_modeオプションは実運用上も便利であり、生の出力を返すことで、その後必要に応じて後処理をおこなうことが可能です。

離散の場合にsoftmaxを用いるのは、確率の総和が1になるよう保証するためです。ただし、ロジット内で数値的不安定性が生じやすいため、NaNを監視しTorch.Clampを適宜用いる必要があります。連続行動においては、対角共分散行列が各行動次元を独立と仮定しています。一方で行動が相関している場合には完全な共分散行列を用いるべきですが、その場合は計算コストが増加します。TRPOでは、方策の対数確率は共役勾配法やラインサーチのステップで使用されるため、効率的かつ正確に計算されなければなりません。

バリューネットワーク

バリューネットワークを以下のように実装します。

class ValueNetwork(nn.Module):
    def __init__(self, state_dim, hidden_size=64):
        super(ValueNetwork, self).__init__()
        self.fc1 = nn.Linear(state_dim, hidden_size)
        self.fc2 = nn.Linear(hidden_size, hidden_size)
        self.fc3 = nn.Linear(hidden_size, 1)
    
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

バリューネットワークとポリシーネットワークの設計と実装には、かなりの重複があるため、その大部分はここでは割愛します。ただし原則として、バリューネットワークはアドバンテージ（あるいは報酬）の計算や分散削減のために状態価値を推定します。構造としてはポリシーネットワークと同様にシンプルなアーキテクチャを採用しており、出力は単一のスカラーです。このネットワークは、正確な報酬推定を通じてTRPOにおける安定したポリシー更新を可能にする上で不可欠です。

TRPOエージェント

TRPOエージェントクラスをPythonで次のように実装します。

class TRPO_Agent:
    def __init__(self, state_dim, action_dim, discrete=False, 
                 hidden_size=64, lr_v=0.001, gamma=0.99, 
                 delta=0.01, lambda_=0.97, max_kl=0.01, cg_damping=0.1, 
                 cg_iters=10, device='cpu'):
        
        self.policy = PolicyNetwork(state_dim, action_dim, hidden_size, discrete).to(device)
        self.value_net = ValueNetwork(state_dim, hidden_size).to(device)
        self.value_optimizer = optim.Adam(self.value_net.parameters(), lr=lr_v)
        
        self.gamma = gamma
        self.delta = delta
        self.lambda_ = lambda_
        self.max_kl = max_kl
        self.cg_damping = cg_damping
        self.cg_iters = cg_iters
        
        self.discrete = discrete
        self.device = device
        self.state_dim = state_dim
    
    def get_action(self, state):
        # Convert state to tensor and add batch dimension
        state = torch.FloatTensor(state).unsqueeze(0).to(self.device)
        
        # Get action distribution from policy
        dist = self.policy(state)
        
        # Sample action from distribution
        action = dist.sample()
        
        # Get log probability BEFORE converting to numpy/item
        log_prob = dist.log_prob(action)
        
        # Convert action to appropriate format
        if self.discrete:
            action = action.item()  # For discrete actions
        else:
            action = action.detach().cpu().numpy()[0]  # For continuous actions
        
        # Clip continuous actions to [-1, 1] range (optional for discrete)
        if not self.discrete:
            action = np.clip(action, -1, 1)
        
        return action, log_prob
        
    def update_value_net(self, states, targets):
        # Convert inputs to proper tensor format
        if torch.is_tensor(states):
            states = states.detach().cpu().numpy()
        if torch.is_tensor(targets):
            targets = targets.detach().cpu().numpy()
        
        states = np.array(states, dtype=np.float32)
        targets = np.array(targets, dtype=np.float32)
        
        # Ensure proper shapes
        if len(states.shape) == 1:
            states = np.expand_dims(states, 0)
        if len(targets.shape) == 0:
            targets = np.expand_dims(targets, 0)
        
        states_tensor = torch.FloatTensor(states).to(self.device)
        targets_tensor = torch.FloatTensor(targets).to(self.device)
        
        # Forward pass
        self.value_optimizer.zero_grad()
        values = self.value_net(states_tensor)
        
        # Ensure matching shapes for loss calculation
        values = values.view(-1)
        targets_tensor = targets_tensor.view(-1)
        
        loss = F.mse_loss(values, targets_tensor)
        loss.backward()
        self.value_optimizer.step()

    def update_policy(self, states, actions, old_log_probs, advantages):
        # Handle tensor conversion safely
        def safe_convert(x):
            if torch.is_tensor(x):
                return x.detach().cpu().numpy()
            return np.array(x, dtype=np.float32)
        
        states = safe_convert(states)
        actions = safe_convert(actions)
        old_log_probs = safe_convert(old_log_probs)
        advantages = safe_convert(advantages)
        
        # Convert to tensors with proper shapes
        states_tensor = torch.FloatTensor(states).to(self.device)
        actions_tensor = torch.FloatTensor(actions).to(self.device)
        old_log_probs_tensor = torch.FloatTensor(old_log_probs).to(self.device)
        advantages_tensor = torch.FloatTensor(advantages).to(self.device)
        
        # Get old distribution
        with torch.no_grad():
            old_dist = self.policy(states_tensor)
        
        # Compute gradient of surrogate loss
        def get_loss():
            dist = self.policy(states_tensor)
            if self.discrete:
                log_probs = dist.log_prob(actions_tensor.long())
            else:
                log_probs = dist.log_prob(actions_tensor)
            return -self.surrogate_loss(log_probs, old_log_probs_tensor, advantages_tensor)
        
        # Rest of the TRPO update remains the same...
        loss = get_loss()
        grads = torch.autograd.grad(loss, self.policy.parameters(), create_graph=True)
        flat_grad = torch.cat([grad.view(-1) for grad in grads]).detach()
        
        step_dir = self.conjugate_gradient(states_tensor, old_dist, flat_grad, nsteps=self.cg_iters)
        
        shs = 0.5 * torch.dot(step_dir, self.hessian_vector_product(states_tensor, old_dist, step_dir))
        step_size = torch.sqrt(self.max_kl / (shs + 1e-8))
        full_step = step_size * step_dir
        
        old_params = torch.cat([param.view(-1) for param in self.policy.parameters()])
        
        def line_search():
            for alpha in [0.5**x for x in range(10)]:
                new_params = old_params + alpha * full_step
                self.set_policy_params(new_params)
                
                with torch.no_grad():
                    new_dist = self.policy(states_tensor)
                    new_loss = get_loss()
                    kl = self.kl_divergence(old_dist, new_dist)
                
                if kl <= self.max_kl and new_loss < loss:
                    return True
            return False
        
        if not line_search():
            self.set_policy_params(old_params)
    
    def set_policy_params(self, flat_params):
        prev_idx = 0
        for param in self.policy.parameters():
            flat_size = param.numel()
            param.data.copy_(flat_params[prev_idx:prev_idx + flat_size].view(param.size()))
            prev_idx += flat_size
    
    def compute_advantages(self, rewards, values, dones):
        advantages = np.zeros_like(rewards)
        last_advantage = 0
        
        for t in reversed(range(len(rewards))):
            if dones[t]:
                delta = rewards[t] - values[t]
                last_advantage = delta
            else:
                delta = rewards[t] + self.gamma * values[t+1] - values[t]
                last_advantage = delta + self.gamma * self.lambda_ * last_advantage
            advantages[t] = last_advantage
        
        advantages = (advantages - advantages.mean()) / (advantages.std() + 1e-8)
        return advantages
    
    def surrogate_loss(self, new_probs, old_probs, advantages):
        ratio = torch.exp(new_probs - old_probs)
        return torch.mean(ratio * advantages)
    
    def kl_divergence(self, old_dist, new_dist):
        if self.discrete:
            return torch.mean(torch.sum(old_dist.probs * (torch.log(old_dist.probs) - torch.log(new_dist.probs)), dim=1))
        else:
            return torch.distributions.kl.kl_divergence(old_dist, new_dist).mean()
    
    def hessian_vector_product(self, states, old_dist, vector):
        kl = self.kl_divergence(old_dist, self.policy(states))
        
        # First compute gradient of KL
        grads = torch.autograd.grad(kl, self.policy.parameters(), create_graph=True)
        flat_grad_kl = torch.cat([grad.view(-1) for grad in grads])
        
        # Compute gradient of (grad_KL * vector)
        grad_vector_product = torch.sum(flat_grad_kl * vector)
        grad_grad = torch.autograd.grad(grad_vector_product, self.policy.parameters(), retain_graph=True)
        flat_grad_grad = torch.cat([grad.contiguous().view(-1) for grad in grad_grad])
        
        return flat_grad_grad + self.cg_damping * vector
    
    def conjugate_gradient(self, states, old_dist, b, nsteps=10, residual_tol=1e-10):
        x = torch.zeros_like(b)
        r = b.clone()
        p = b.clone()
        rdotr = torch.dot(r, r)
        
        for i in range(nsteps):
            Avp = self.hessian_vector_product(states, old_dist, p)
            alpha = rdotr / torch.dot(p, Avp)
            x += alpha * p
            r -= alpha * Avp
            new_rdotr = torch.dot(r, r)
            if new_rdotr < residual_tol:
                break
            beta = new_rdotr / rdotr
            p = r + beta * p
            rdotr = new_rdotr
        
        return x

TRPOエージェントクラスは、連続行動空間と離散行動空間の両方に対応しており、ポリシーネットワークを用いて行動を選択し、バリューネットワークを用いて各状態に対する報酬を推定します。ここでの重要な違いは、TRPOのバリューネットワークでは入力が状態のみであり、他のRLアルゴリズムでよくあるように行動を含まない点です。TRPOは、KLダイバージェンスで定義される信頼領域内に収まるように制約を課しつつ、代理目的関数を最大化することで方策を最適化します。このクラスには、行動選択、価値関数の更新、方策最適化、報酬推定、その他の計算処理をおこなうメソッドが含まれています。

__init__関数は、ポリシーネットワークとバリューネットワーク、オプティマイザ、およびTRPO特有の信頼領域最適化用ハイパーパラメータを初期化します。入力として渡すハイパーパラメータの中には、max_klやcg_dampingのようにTRPO特有のものもあれば、gammaやlambdaといったRL全般に共通するものもあります。これらのチューニングにおいては、max_kl=0.01、cg_damping=0.1、lambda=0.97といったデフォルト値が妥当とされますが、環境やデータセットに依存します。

高次元データセットのような複雑な環境に対しては、より厳格な制約を課すためにmax_klを0.005程度に小さくしたり、共役勾配法の収束を改善するためにcg_itersを20程度に増やすことが適しています。バリューネットワークのオプティマイザにはAdamを使うのが標準ですが、ポリシーネットワークはTRPO特有のカスタムアップデートをいおこなうためオプティマイザは使用しません。また、バリューネットワークの学習率は十分に小さく設定し、学習の安定性を高めることが推奨されます。

get_action関数は、入力された状態をPyTorchのテンソルに変換し、ポリシーネットワークに通して行動分布を得ます。そして、その分布から行動をサンプリングし、その対数確率を計算したうえで、環境に適合する形式に変換します。離散行動の場合はスカラー値に、連続行動の場合はクリッピングされたNumPy配列になります。 

この関数はエージェントの環境とのインターフェイスを担っており、方策に基づいた行動選択を可能にします。特に対数確率は、代理損失の計算に用いられるため、TRPOの勾配計算において非常に重要です。連続行動を[-1,1]の範囲にクリッピングすることで、ポリシーネットワークの出力が環境のバウンディングと一致するようにします。さらに連続行動の場合には、標準偏差を監視して分布が退化しないようにする必要があります。現在の実装では単一状態入力を想定していますが、ベクトル化や多次元状態を扱う場合には拡張が必要です。

バリューネットワークの更新処理では、入力状態をQ値、すなわちポリシーネットワークの予測に基づく報酬に変換します。そのうえで、ターゲットとの平均二乗誤差(MSE)損失を計算し、Adamオプティマイザを用いて誤差逆伝播によりネットワークを更新します。正確な価値推定は、方策勾配の分散を削減し、TRPOの安定性を高めます。MSE損失により、バリューネットワークは期待割引報酬を予測するよう学習し、RLの目的と整合します。なお、学習ターゲットの計算にはTD誤差を用いた時系列差分が使われますが、この推定が不正確だと方策更新が不安定になるため、精度が重要です。

損失関数は標準的にはMSEを用いますが、分散が大きい環境やデータセットに対しては外れ値に強いHuber損失を検討することも有効です。形状補正のロジックも実装されていますが、大規模データセットでは対応が難しい場合があり、その場合は事前に入力の形状を最適化する必要があります。また、勾配クリッピングをtorch.nn.utils.clip_grad_norm_といったモジュールで取り入れることで、大きすぎる更新を抑制し、学習の安定性を高められます。

update_policy関数は、状態、行動、古い対数確率、報酬をそれぞれ適切な形状のテンソルに変換します。そして古い方策分布を計算してKLダイバージェンスを算出し、代理損失関数を定義します。代理損失は、新しい方策と古い方策の下での期待報酬を比較するものです。さらに、この関数では方策勾配を計算し、共役勾配法で探索方向を求め、max_klで定められた信頼領域制約に基づいてステップサイズを決定します。その後、ラインサーチを実行して新しい方策がKL制約を満たし代理損失を改善することを確認し、失敗した場合は古いパラメータに戻します。 

この処理こそがTRPOの中核であり、ポリシー改善と安定性を両立させるトラストリージョン最適化を実現しています。代理損失は方策勾配の目的関数を推定し、KLダイバージェンス制約は大きな方策変化を防いで性能の劣化を抑えます。共役勾配法は探索方向を効率的に解き、ラインサーチが堅牢な更新を保証します。

TRPOにおいて、max_klは極めて重要なパラメータです。0.005未満のように小さすぎる値は更新を過度に制限し、学習が非常に遅くなる一方、0.05を超えるような大きすぎる値は更新を不安定化させ、TRPOが解決しようとする問題を再び引き起こします。また、cg_iters（共役勾配の反復回数）は十分な大きさが必要で、収束性を確保しなければなりません。さらに、残差を監視して解の精度を検証することも重要です。

set_policy_params関数は、平坦化されたベクトルからパラメータをコピーし、それぞれのサイズにリシェイプしてポリシーネットワークを更新します。これにより、共役勾配とラインサーチで計算されたフラットなベクトルをそのままパラメータ更新に反映でき、ポリシーネットワークが更新後の最適化済みパラメータを保持することを保証します。

報酬計算、すなわちコード内でcompute_advantageと呼ばれる処理は、Generalized Advantage Estimation (GAE)を用いておこなわれます。これは各タイムステップにおけるTD誤差を計算し、lambdaを用いてバイアスと分散のバランスを取るものです。さらに、dones[t]パラメータによってエピソード終了を検知し、その都度アドバンテージをリセットします。最後に、これらの報酬を正規化して平均0、分散1にします。

surrogate_loss関数は、確率比πnew(a|s)/πold(a|s)にアドバンテージを掛け合わせた期待値として代理損失を計算します。代理損失は、方策の変化が期待される報酬にどのように影響するかを測定することで、方策勾配目的を推定します。TRPOでは、この損失を最大化することを目的とし、そのためget-lossでは符号を反転させます。これは信頼領域制約の範囲内でおこなわれます。

kl_divergence関数は、新しい方策分布と古い方策分布がどの程度離れているかを測定します。行動が離散の場合はカテゴリ分布の解析的な式が使われ、連続行動の場合はPyTorchの多変量正規分布が使われます。これらの測定値はTRPOの信頼領域制約を実装する助けになります。

hessian_vector_product関数は、その名の通り共役勾配法におけるKLダイバージェンスのためのヘッセ積を計算します。計算では、KLダイバージェンスの勾配を求め、それを入力ベクトルに掛け合わせ、さらに二階微分を計算します。数値安定性を改善するためにダンピングを加えます。フィッシャー情報行列のベクトルに対する作用を近似することで、TRPOにおける探索方向の効率的な計算を可能にします。減衰項はヘッセ行列を正定に保ち、共役勾配法の収束を保証します。

最後に、conjugate_gradient関数はHx=gを解く方法を実装します。ここでHはhessian_vector_product関数によって近似されたフィッシャー行列、gは方策勾配です。この関数は解x、すなわち探索方向を、収束するか、あるいは所定の反復回数に達するまで繰り返し改善します。

テスト実行

前回の記事でフォワードウォークに成功した3つの特徴量パターン（Feature_2、3、4）のみを対象にフォワードウォークをおこなうと、以下のレポートが得られました。テスト対象はEUR/USDペアで、期間は2020.01.01から2025.01.01までです。訓練はPython上でおこなわれ、その期間の80%にあたる2020.01.01から2024.01.01までのデータを使用しました。 

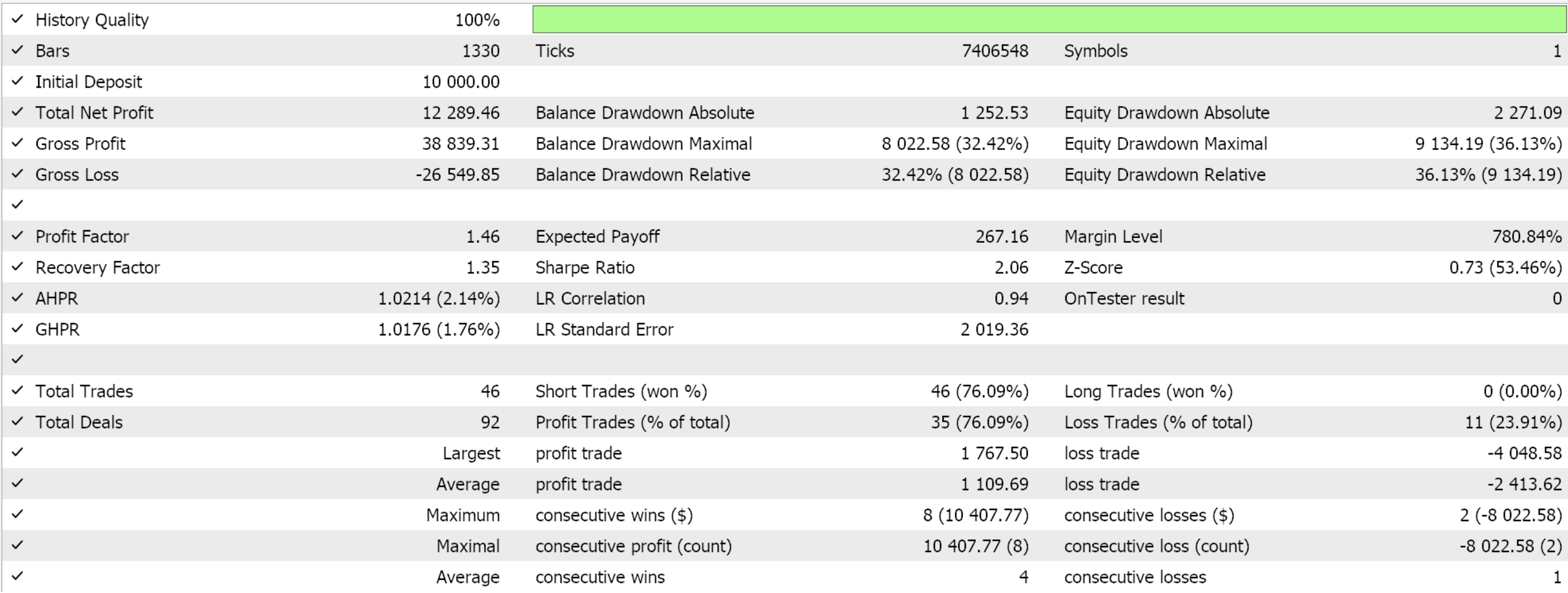
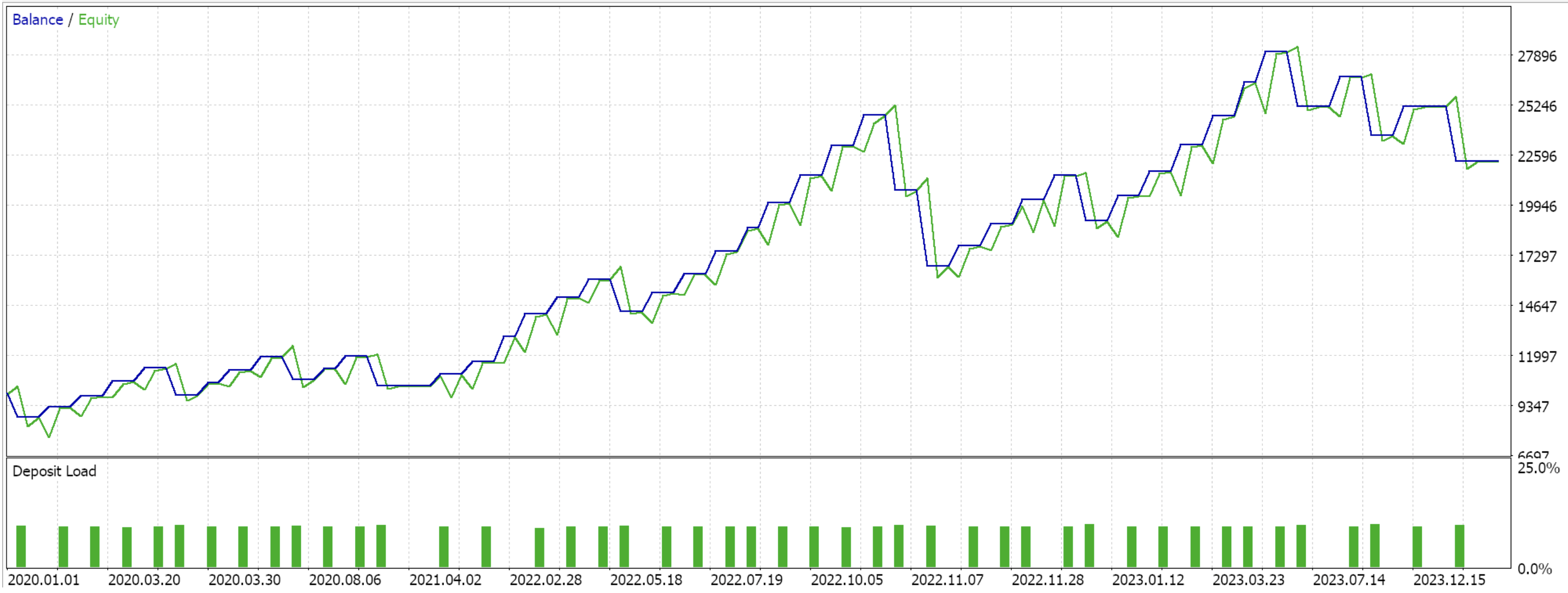
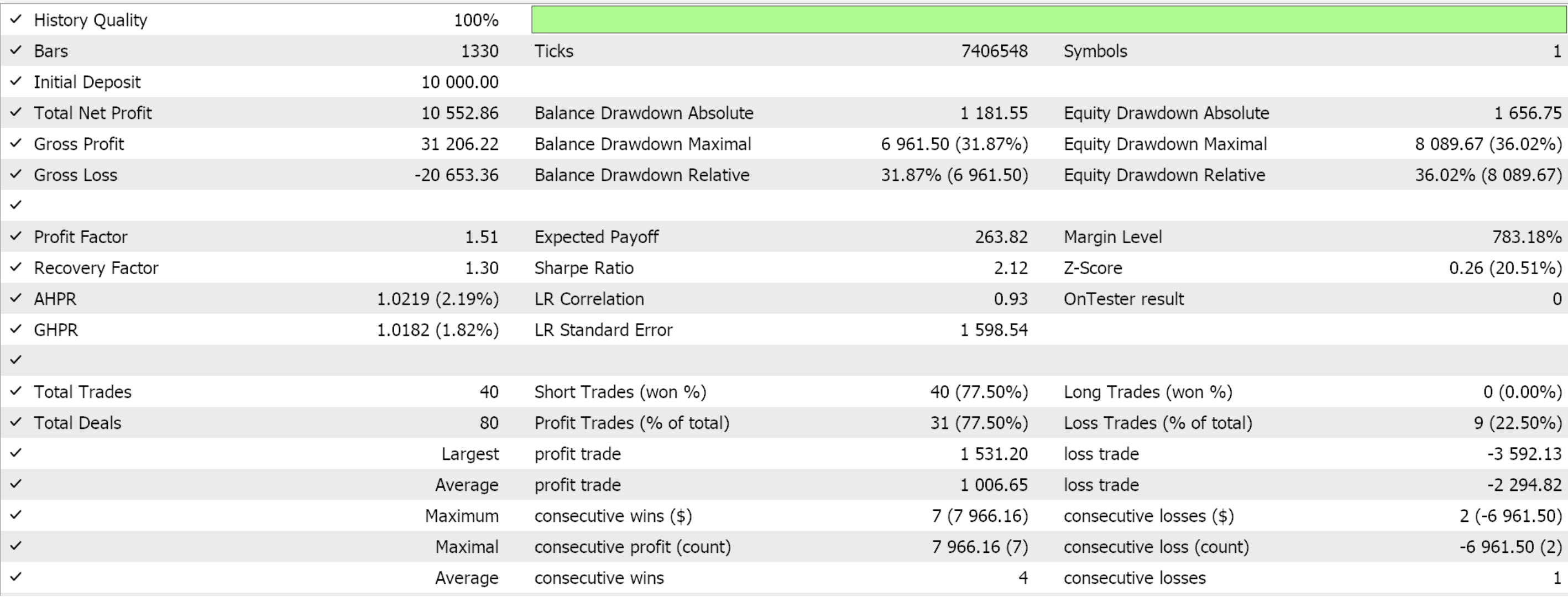
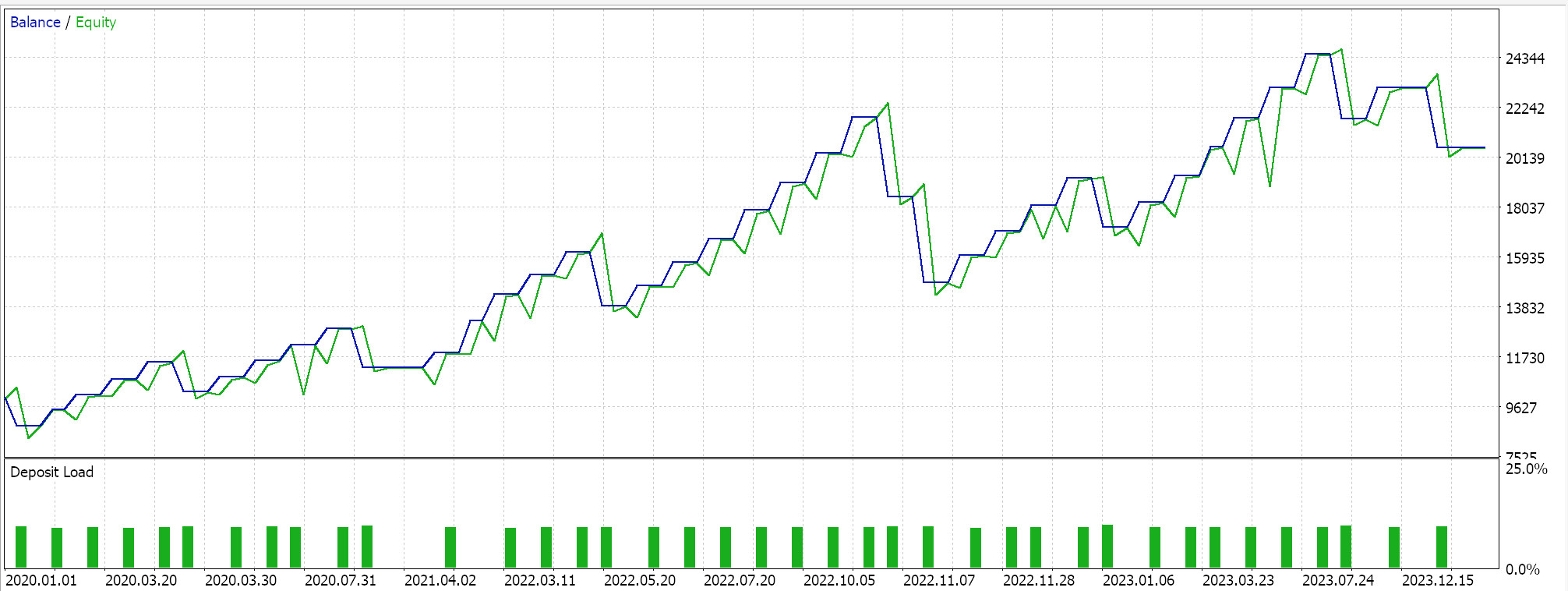
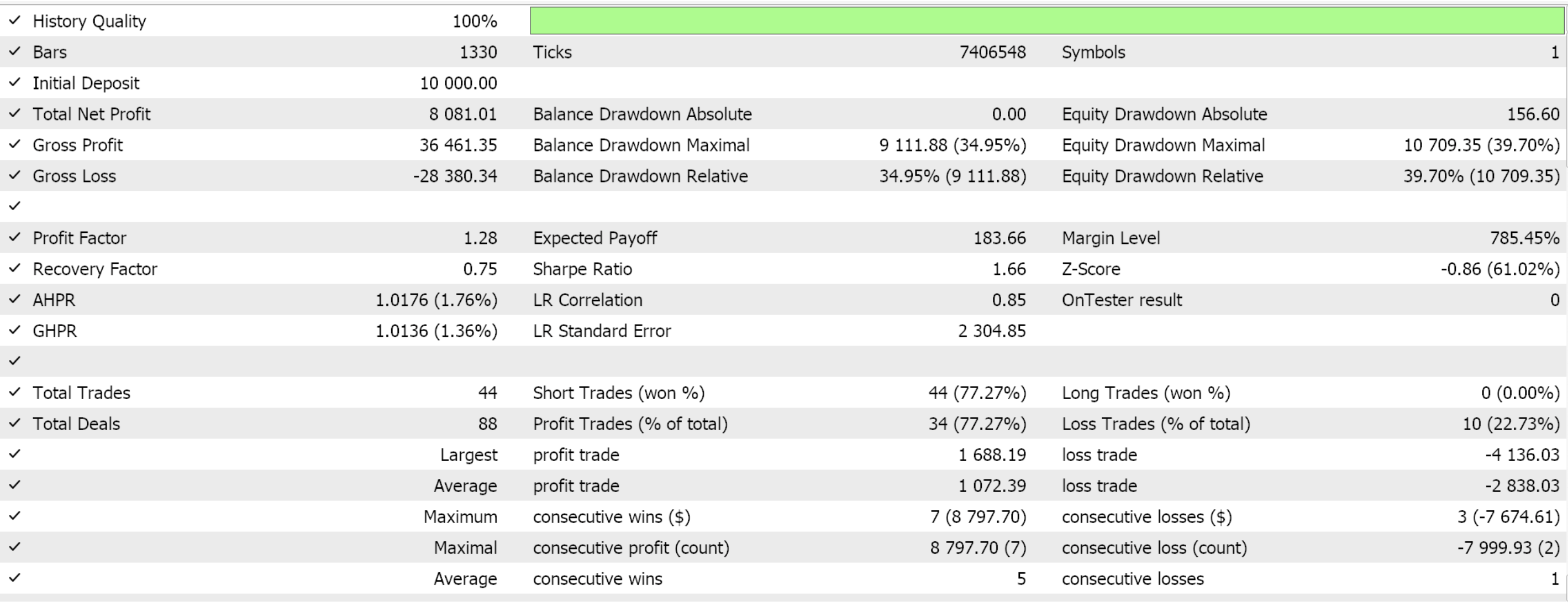
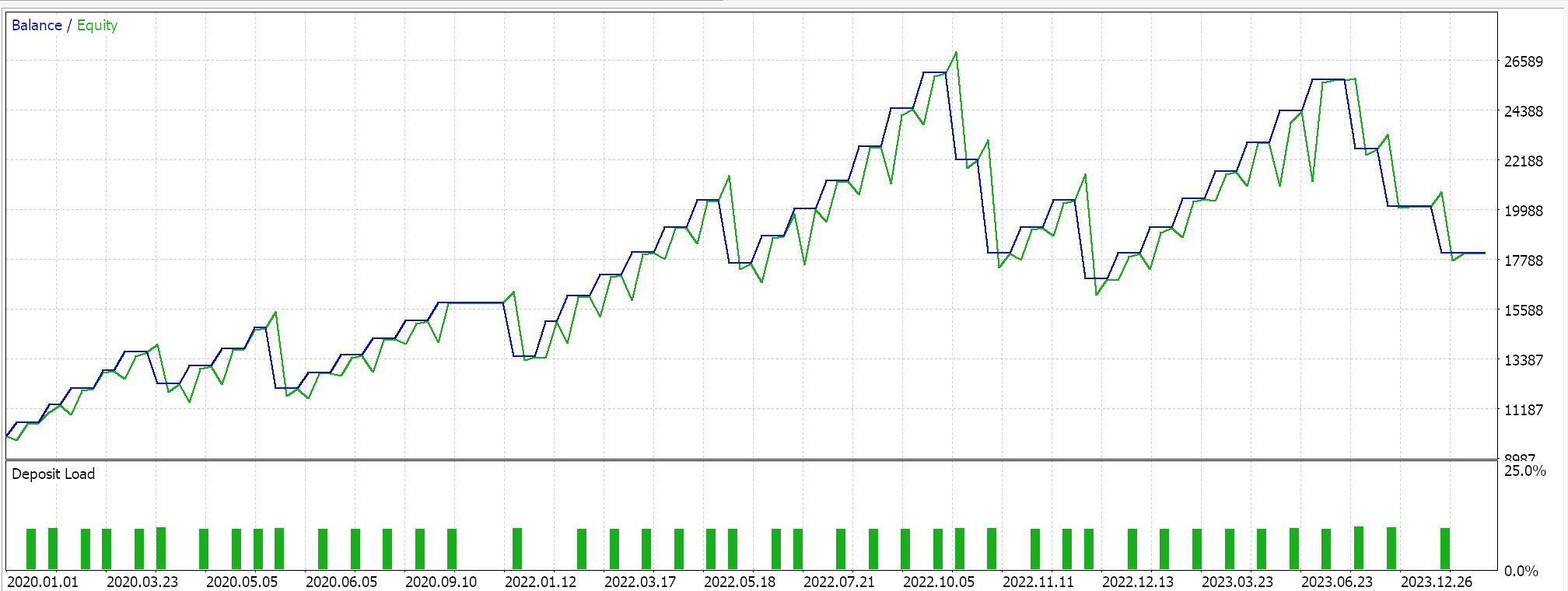
フォワードウォークの期間を2024年の1年間だけと考えるならば、フォワードウォークが可能であったのはパターン2とパターン3だけのようです。いつものことながら、多くの要因が関与しており、この記事で共有されているコードや資料を使用する前には、必ず独自に十分な検証をおこなうことをお勧めします。上記のテストで使用したようなエキスパートアドバイザー(EA)を組み立てて使うには、添付されたコードのファイルをMQL5ウィザードと一緒に使用する必要があります。新しい読者のために、その方法についてのガイダンスがこちらとこちらにあります。

結論

前回の記事では、ADXとCCIのパターンを入力として受け取り、それをEAに発展させる教師あり学習モデルの作り方を紹介しました。本記事では同じインジケーターを用いながらも、強化学習を適用しました。強化学習は、以前に開発されたEAを、学習ウィンドウを慎重に拡張することによってより堅牢にすることを目指しています。

これらのインジケーターパターンを対象とした一連の記事のまとめとして、本来は推論に焦点を当てた記事を予定していました。ここでいう推論とは、監督学習や強化学習で学習された内容を要約し、「アーカイブ」する手段として適用するものです。このアプローチの例示はこの記事にあります。ただし、推論の活用については読者に委ねることにし、私たちは再びシンプルな記事形式に戻り、いくつかの機械学習のアイデアを交互に取り上げていく予定です。 

名前	説明
wz_62.mq5	ヘッダにインクルードファイルを示すファイルを示すウィザード組み立てEA
SignalWZ_62.mqh	カスタムシグナルクラスファイル
61_2.onnx	Feature_2 ONNX教師あり学習モデル
61_3.onnx	Feature_3 ONNX教師あり学習モデル
61_4.onnx	Feature_4 ONNX教師あり学習モデル
62_policy_2.onnx	Feature_2強化版Actor学習
62_policy_3.onnx	Feature_3強化版Actor学習
62_policy_4.onnx	Feature_4強化版Actor学習
62_value_2.onnx	Feature_2強化版Critic学習
62_value_3.onnx	Feature_3強化版Critic学習
62_value_4.onnx	Feature_4強化版Critic学習