知っておくべきMQL5ウィザードのテクニック（第60回）：移動平均とストキャスティクスパターンを用いた推論（ワッサースタインVAE）

はじめに

MAとストキャスティクスの組み合わせから生じるパターンを検証するにあたり、この記事では機械学習を活用してアプローチの体系化を目指します。機械学習における主なネットワーク訓練の手法には、教師あり学習、強化学習、そして推論の3つが挙げられます。これらの学習方法は、モデルやネットワークの開発過程に応じて使い分けることが可能であり、それぞれの特性を活かして組み合わせることで、より高度で洗練されたモデルの構築が可能になると考えられます。

簡単な振り返り

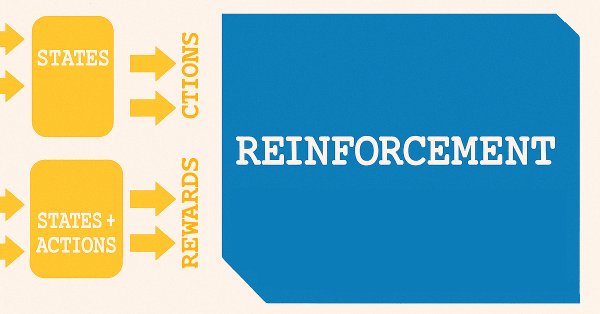
簡単に復習すると、以前の教師あり学習の記事では、特徴量(feature)を状態(state)にモデリングしました。特徴量とはMAとストキャスティクス両方のインジケーターパターンのことで、状態とはインジケーターのパターンに遅れて現れる価格変動の予測値を指し、これをモデルやネットワークが予測します。以下の簡単な図がこれを説明するのに役立ちます。

 

価格変動の予測に「状態」という用語を用いるのは都合よく、教師あり学習から強化学習への自然な橋渡しとなります。強化学習においては、「状態」が訓練プロセスの出発点として非常に重要な役割を果たし、その流れは下図に示す構造とよく似ています。

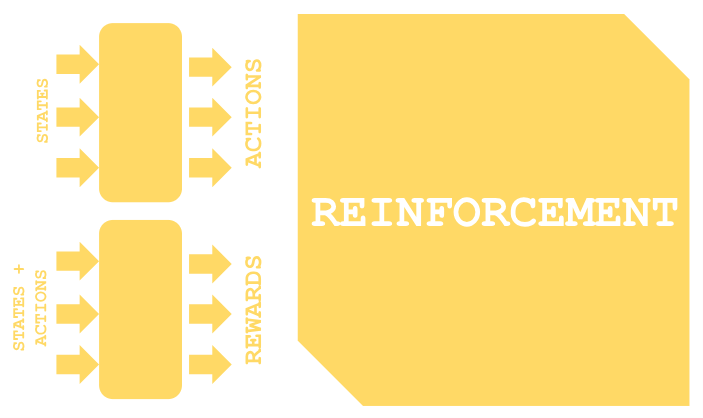
強化学習には使用されるアルゴリズムによっていくつかのバリエーションがありますが、ほとんどの場合、原理として2つのネットワークを使用します。図の上側に示されているのが方策ネットワーク、下側に示されているのが価値ネットワークです。

強化学習はモデルやシステムの単独の訓練方法として使うこともできますが、前回の記事では、実運用されているモデルに対してより活用されるべきだと主張しました。その場合、探索と活用のバランスが、すでに訓練済みのモデルが変化する市場環境に適応するためにより重要になります。それだけでなく、ロングやショートの判断がどのようにさらに処理され、予測された状態に対して必要な行動の種類を選択するかについても検討しました。

推論

ここで話は、推論、あるいは教師なし学習と呼ばれる領域へと移ります。では、推論の目的とは何でしょうか。最初にこのテーマについて考え始めたとき、私は、ある状況で訓練されたネットワークやモデルを、多少の調整やチューニングによって別の環境に適用できるのではないかと考えていました。トレーダーの観点から言えば、それは、EUR/USDで訓練されたモデルを微調整してEUR/JPYに応用する、といった発想に相当します。しかし、多くのトレーダーが証言しているように、複数の通貨ペアを同時に取引可能な非裁定のEAを開発することは非常に難しく、リスクとリターンのバランスが大きな課題となるプロセスです。

加えて、複数の通貨ペアに対応した個別のモデルを訓練するための計算コストは、かつてほど大きな制約ではなくなってきています。これは、高速なGPUの登場や、クラウドインフラの普及によって、多くのユーザーが高度な計算環境を利用できるようになったためです。こうした状況は、理論的には、多数のモデルの構築がより現実的となった要因となっています。ストレージコストも低下しており、数百万のパラメータを持つような大規模モデルですら、通常のコンピュータファイルとして保存できることを考えれば、エンコーダを活用した推論は、こうした知識を圧縮し、「より保存しやすい形にする」ことの重要性を示しています。

もっとも、ストレージのコストがきわめて低いため、特別な保存手段は不要だと考える人もいるでしょう。特に、すでに教師あり学習によってモデルが訓練され、さらに強化学習システムによってモデルが最新の状態に保たれている場合、推論にどのような意味があるのか疑問に思うかもしれません。ここで強調したいのは、すべてのデータが連続した時系列として存在しているわけではないということです。 

たとえば、過去の古いデータが、現在進行中の事象と何らかの形で類似している場合、推論は、その類似性をノイズを抑えながらマッピングする助けになります。ここで言うマッピングとは、以下の図に示される構成を指しています。

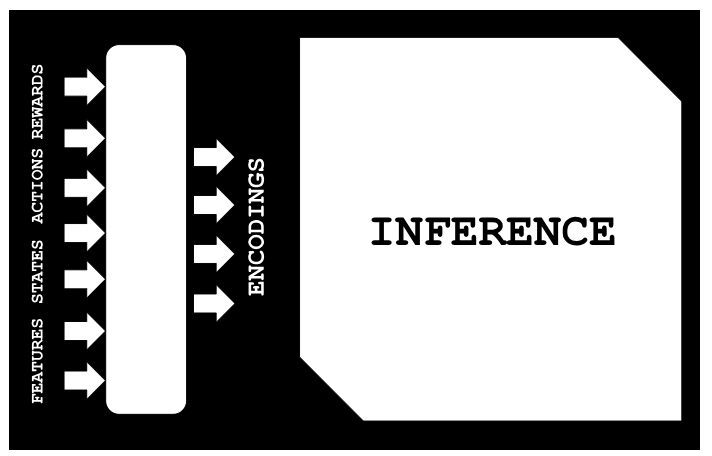
過去のデータの特徴量が利用できる状況において、以下では、教師なし学習（ここでは線形回帰）によって、それぞれの状態・行動・報酬を推論する方法を示します。この手法が可能なのは、変分オートエンコーダを使って、特徴量、状態、行動、報酬(FSAR: Feature, Status, Action, Reward)を潜在層（エンコーディング）に対応づけるように事前に学習させているためです。私たちは、FSARとエンコーディングのペアからなるデータセットを用いて線形回帰モデルを適合させることで、FSARデータセットの欠損部分を補完できるようにしています。これが本記事で探究する主要な応用例です。

さらに、もしここで一歩引いて教師あり学習と強化学習のプロセス全体を振り返ってみると、時間の経過とともに、それらで得られた知識をより包括的に統合していく必要が高まることに気づかされます。このような場合に、改めて長期間のデータに対して教師あり学習をおこない、その後に強化学習を再度適用するという選択肢もありますが、よりスケーラブルかつ全体的な代替手段として推論アプローチが適していると考えられます。

導入のまとめとして推論とは何かを簡単に定義しておくと、推論とは、観測されたデータから隠れた変数を推定することです。ベイズモデルにおいては、可視層のデータセットを与えられたときに、隠れ変数の事後分布を計算するプロセスが、一般に「推論」と呼ばれます。したがって、数学的には以下のように定義されます。

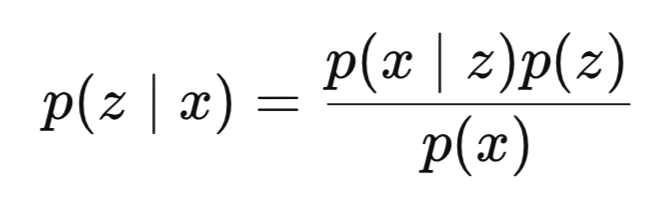
ここで

• zは潜在変数またはエンコーディング
  
  
• xは観測データ（本稿ではFSAR）
  
  
• p(z∣x)は事後分布（私たちが学びたいもの、つまりxが観測されたときにzが起こる確率）
  
  
• p(x∣z)は尤度（zが与えられたときにxが観測される確率）
  
  
• p(z)は事前分布
  
  
• p(x)は証拠（周辺尤度）

P(x)は、多くの場合、扱いにくく、計算が困難です。

なぜ困難なのでしょうか。分母であるp(x)は、すべての潜在変数にわたる積分を含むためです。

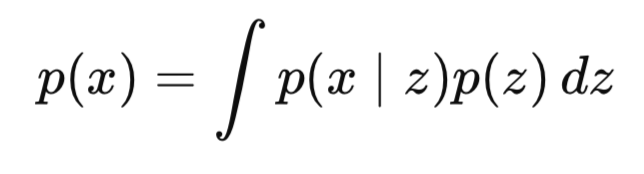
高次元になるほど、つまり潜在変数の次元が大きくなるほど、この計算は一般に計算的に扱いが困難になります。

では、VAEはどのように役立つのでしょうか。VAEは近似推論の問題を最適化問題に変換します。これはエンコーダ（推論ネットワーク）とデコーダ（生成ネットワーク）を導入することで実現されます。エンコーダは外部の事後分布を学習で近似したq(z|x)に答え、デコーダネットワークは潜在コード（エンコーディング）からデータ（本ケースではFSAR）を再構築するp(x|z)を扱います。

しかし、VAEの最大の革新は、事後分布を正確に計算する代わりに、変分下限(ELBO: Evidence Lower Bound Optimization)を最適化する点にあります。ELBOは真のデータ分布を近似しつつ、モデルが有意義な潜在表現を学習し、ノイズを減らすことを保証する目的関数であり、VAEの訓練に用いられます。この目的関数に対する直感的な解釈は、以下の通りです。

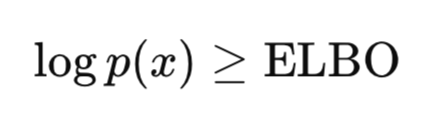
前述のように、p(x)の計算は非常に困難で扱いにくいですが、p(x)またはlog p(x)がある値以上であることを示すことは可能であり、扱いやすいです。私たちの目標はp(x)を最大化することであるため、下限を最大化することは結果的にp(x)を高めることになります。VAEはデータから潜在構造を推論することを学習し、勾配降下法でエンドツーエンドに訓練されます。したがって、VAEは償却推論と生成モデリングの両方を1つのフレームワークで実現しています。

なぜVAEが推論の哲学において中心的なのか。それはVAEがエンコーダを通じて推論を学習するからです。つまり、新しいデータセットが来るたびに推論問題を解く代わりに、共有されたエンコーダを使うことができます。これを償却推論とも呼びます。これは忠実性と規則性のトレードオフを評価するための優れたツールであり、一般的に潜在変数が生成構造をどのように表現するかを理解する助けにもなります。

本記事では、VAEの実装にあたり、従来のカルバック・ライブラー情報量の代わりにワッサースタイン距離を用いて分布を比較します。その理由は主に探索的なもので、将来的な記事でカルバック・ライブラー情報量を検討する可能性もあります。ただし、カルバック・ライブラー情報量は潜在空間を過度に制約し、posterior collapse（事後崩壊）を引き起こす可能性があると指摘されています。これに対して、ワッサースタイン距離は、特に比較対象の分布がほとんど重なりを持たない場合において、より柔軟な分布比較の指標であるとされています。

ワッサースタイン距離の核心的な考え方は、一つの確率分布を別の確率分布に「変換するコスト」を測ることにあります。そのため「アースムーバー距離」とも呼ばれます。これは次の式で表されます。

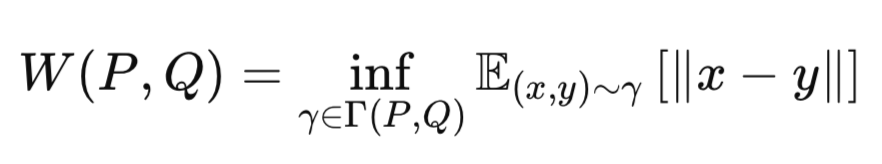
ここで

• P：真のデータ分布（例：ガウス事前分布p(z)）

• 質問：近似分布（例：エンコーダの出力q(z∣x)）

• γ：結合分布。PとQの間で定義される同時分布

• Γ(P,Q)：PとQのすべての可能な結合分布の集合

• ∥x−y∥:距離関数（例：ユークリッド距離）

• inf：（下限・劣限）：可能な輸送コストの中で最小のもの（最小下界）

ワッサースタイン距離は、分布Qの質量をPに一致させるために必要な「労力」の最小値を計算します。そのため、ワッサースタインVAE (WVAE)は、よりシャープなサンプルを生成し、より表現力のある潜在表現を得ることができる重要なモデルとされています。また、特定の条件下では、学習がより安定しやすいと一般に考えられています。

ワッサースタインVAEには主に2つの代表的な実装方法があります。WVAE-MMDとWVAE-GANです。前者は、最大平均差(MMD: Maximum Mean Discrepancy)を用いて、p(z)とq(z)の分布を比較します。本記事ではこのMMDベースの手法を採用します。一方、後者のWVAE-GANでは、潜在分布を整合させるために敵対的損失を使用します。こちらの実装についても、今後の記事で取り上げる可能性があります。最大平均差異は次の式で表されます。

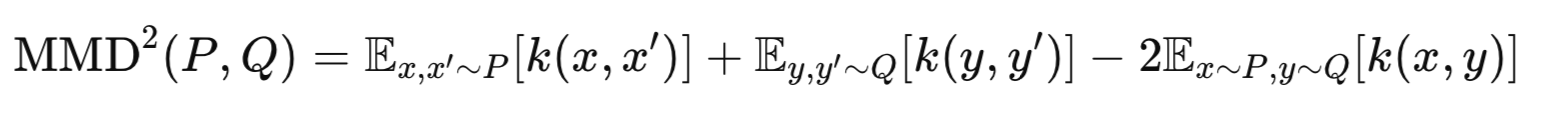
ここで

• P：真の事前分布（例：p(z)=N(0,I)）

• Q：エンコーダによって得られる分布（例：q(z∣x)）。

• k(⋅,⋅)：カーネル関数（例：ガウスRBFカーネル）

• x、x′：分布Pからの2つの独立したサンプル

• y、y′：分布Qからの2つの独立したサンプル

MMDは、再生核ヒルベルト空間(RKHS)における分布PとQの平均埋め込み(mean-embedding)を比較する指標です。この空間において、両分布の平均ベクトルが近ければ近いほど、2つの分布は類似していると判断されます。

VAEの実装

まず、モデル/ネットワークの実装をPythonで始めます。これは、MQL5の生コードに比べて、Pythonの方が訓練を迅速に行えるためです。MQL5でもOpenCLを利用することで、このパフォーマンス差をある程度埋める回避策は存在しますが、本連載内ではまだそこまで扱っていません。ここでは、ワッサースタインVAEのクラスをPythonで実装していきます。

class WassersteinVAEUnsupervised(nn.Module):
    def __init__(self, feature_dim, encoding_dim, k_neighbors=5):
        super().__init__()
        self.encoding_dim = encoding_dim
        self.k_neighbors = k_neighbors
        
        # Feature encoder
        self.feature_encoder = nn.Sequential(
            nn.Linear(feature_dim, 256),
            nn.ReLU(),
            nn.Linear(256, 128),
            nn.ReLU(),
            nn.Linear(128, encoding_dim * 2)  # mean and logvar
        )
        
        # Buffer for storing training references
        self.register_buffer('ref_encoding', torch.zeros(1, encoding_dim))
        self.register_buffer('ref_states', torch.zeros(1, 1))
        self.register_buffer('ref_actions', torch.zeros(1, 1))
        self.register_buffer('ref_rewards', torch.zeros(1, 1))
        self._references_loaded = False
    
    def encode(self, features):
        h = self.feature_encoder(features)
        z_mean, z_logvar = torch.chunk(h, 2, dim=1)
        return z_mean, z_logvar
    
    def reparameterize(self, mean, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mean + eps * std
    
    def update_references(self, encoding_vectors, states, actions, rewards):
        """Store reference data for unsupervised prediction"""
        self.ref_encoding = encoding_vectors.detach().clone()
        self.ref_states = states.detach().clone().unsqueeze(-1)
        self.ref_actions = actions.detach().clone().unsqueeze(-1)
        self.ref_rewards = rewards.detach().clone().unsqueeze(-1)
        self._references_loaded = True
    
    def knn_predict(self, z, ref_values):
        # z shape: [batch_size, encoding_dim]
        # ref_values shape: [ref_size, 1] or [ref_size]
        
        # Ensure ref_values is properly shaped
        ref_values = ref_values.view(-1)  # Flatten to [ref_size]
        
        # Calculate distances between z and reference encodings
        distances = torch.cdist(z, self.ref_encoding)  # [batch_size, ref_size]
        
        # Get top-k nearest neighbors
        _, indices = torch.topk(distances, k=self.k_neighbors, largest=False)  # [batch_size, k]
        
        # Gather corresponding reference values
        neighbor_values = torch.gather(
            ref_values.unsqueeze(0).expand(indices.size(0), -1),  # [batch_size, ref_size]
            1,
            indices
        )  # [batch_size, k]
        
        # Average the nearest values
        predictions = neighbor_values.mean(dim=1, keepdim=True)  # [batch_size, 1]
        
        return predictions
    
    def gaussian_predict(self, z, ref_values):
        # Input validation
        assert z.dim() == 2, "z must be 2D [batch, encoding]"
        assert ref_values.dim() == 2, "ref_values must be 2D"
        
        # Calculate distances (Euclidean)
        distances = torch.cdist(z, self.ref_encoding)  # [batch, ref_size]
        
        # Convert to similarities (Gaussian weights)
        weights = torch.softmax(-distances, dim=1)  # [batch, ref_size]
        
        # Prepare reference values
        ref_values = ref_values.squeeze(-1) if ref_values.size(1) == 1 else ref_values
        ref_values = ref_values.unsqueeze(0) if ref_values.dim() == 1 else ref_values
        
        # Ensure proper shapes
        ref_values = ref_values.view(-1, 1)  # Force [792, 1] shape
        
        # Calculate distances
        distances = torch.cdist(z, self.ref_encoding)  # [batch_size, 792]
        
        # Convert to weights
        weights = torch.softmax(-distances, dim=1)  # [batch_size, 792]
        
        # Matrix multiplication Weighted combination
        predictions = torch.matmul(weights, ref_values)  # [batch, 1]
        
        return predictions.unsqueeze(-1) if predictions.dim() == 1 else predictions
    
    def linear_predict(self, z, ref_values):
        """Linear regression prediction using normal equations"""
        # Add bias term
        X = torch.cat([self.ref_encoding, torch.ones_like(self.ref_encoding[:, :1])], dim=1)
        y = ref_values
        
        # Compute closed-form solution
        XtX = torch.matmul(X.T, X)
        Xty = torch.matmul(X.T, y)
        theta = torch.linalg.solve(XtX, Xty)
        
        # Predict with new z values
        X_new = torch.cat([z, torch.ones_like(z[:, :1])], dim=1)
        return torch.matmul(X_new, theta)

    def predict_from_encoding(self, z):
        if not self._references_loaded:
            raise RuntimeError("Reference data not loaded")
            
        # Validate reference shapes
        self.ref_states = self.ref_states.view(-1, 1)
        self.ref_actions = self.ref_actions.view(-1, 1)
        self.ref_rewards = self.ref_rewards.view(-1, 1)
        
        states = self.knn_predict(z, self.ref_states)
        actions = self.gaussian_predict(z, self.ref_actions)
        rewards = self.linear_predict(z, self.ref_rewards)
        
        return states, actions, rewards
    
    def forward(self, features, states=None, actions=None, rewards=None):
        z_mean, z_logvar = self.encode(features)
        z = self.reparameterize(z_mean, z_logvar)
        
        if states is not None and actions is not None and rewards is not None:
            return {
                'z': z,
                'z_mean': z_mean,
                'z_logvar': z_logvar
            }
        else:
            pred_states, pred_actions, pred_rewards = self.predict_from_encoding(z)
            return {
                'states': pred_states,
                'actions': pred_actions,
                'rewards': pred_rewards
            }

上記のワッサースタインVAEの実装は、主に4つの構成要素から成り立っています。特徴量エンコーダ、参照バッファ、予測メソッド、そして訓練と推論の両方に対応するデュアルモードのフォワードパスです。特徴量エンコーダは3層の多層パーセプトロン(MLP)で構成されており、入力を潜在空間のパラメータ(z、z-mean、z-logvar)に圧縮する役割を果たします。参照バッファは、事前に学習させたFSARの入力と、それに対応する潜在エンコーディングを保持します。予測メソッド群は、特徴量しか与えられていない不完全なデータセットに対して、状態・行動・報酬を推定するために使われます。使用されている手法は、K近傍法(K-NN)、ガウス重み付き回帰、そして線形回帰の3つです。これらはすべて、潜在空間上でエンコーディングをSAR（状態・行動・報酬）にマッピングすることで機能します。フォワードパスは、訓練と推論の両モードに対応するよう設計されています

機能面での中核となるのは、エンコーディング処理、参照システム、予測機構、そして推論フローです。エンコーディング処理では、FSARの入力がエンコーダネットワークを通過し、出力では、これらの入力がz、z-mean、z-log-varの「エンコーディング」に分割されます。この過程において、リパラメトリゼーショントリックを利用することで、勾配に対応したサンプリングが可能になります。参照システムでは、エンコードされた出力をその対応するFSAR入力とともに保存し、後の推論時に参照できるようにします。これには、update_references関数による明示的な初期化が必要です。

3つの予測手法は、それぞれ状態、行動、報酬の推定を目的としています。モデルは、特徴量が常に利用可能であるという前提に基づいており、状態・行動・報酬のいずれかが欠損している場合に、潜在空間における近傍情報をもとに補完をおこないます。状態の予測にはK-NNクラスタリング、行動の予測にはガウス過程回帰、報酬の予測には線形回帰が用いられます。推論フローにおいては、まず入力された特徴量が潜在空間へとエンコードされ、その後、各入力に対して適切な予測手法が選択され、状態、行動、報酬の各推定値が返されます。

この実装には、今後いくつかの改善の余地があります。これらの改善点は、大きく分けて3つのカテゴリに分類できます。すなわち、アーキテクチャの拡張、訓練プロセスの改善、そしてロバスト性の強化です。アーキテクチャの改善としては、リプシッツ連続性を保証するためのスペクトル正規化の追加、ガウス過程回帰における温度パラメータの学習化、参照バッファのメモリ管理（FIFOや間引きの導入）、および不確実性の推定を目的としたモンテカルロサンプリングの追加などが挙げられます。 訓練プロセスの改善としては、ワッサースタイン制約を満たすための勾配ペナルティの導入、MMDやカバレッジ項を用いた潜在空間の正則化、入力ごとに適応的に予測手法を選択する仕組みの追加、さらには複数の予測手法の重み付けによるアンサンブル化が考えられます。

ロバスト性に関しては、やや抽象的ではありますが、分布外データの検出能力の導入、参照の品質をスコア化するシステム、近傍サイズを動的に最適化する機構、入力に応じてノイズのスケーリングを変化させる手法などが検討可能です。

MMD損失の実装

今回実装しているワッサースタインVAEの形式はMMD損失(Maximum Mean Discrepancy Loss)に基づくものです。この形式のVAEにおいて使用される2つの損失関数は、以下の通りです。

def mmd_loss(y_true, y_pred, kernel_mul=2.0, kernel_num=5):
    """
    MMD loss using Gaussian RBF kernel.
    Args:
        y_true: Ground truth samples (shape: [batch_size, dim])
        y_pred: Predicted samples (shape: [batch_size, dim])
        kernel_mul: Multiplier for kernel bandwidths
        kernel_num: Number of kernels to use
    Returns:
        MMD loss (scalar)
    """
    batch_size = y_true.size(0)
    
    # Combine real and predicted samples
    xx = y_true
    yy = y_pred
    xy = torch.cat([xx, yy], dim=0)
    
    # Compute pairwise distances
    distances = torch.cdist(xy, xy, p=2)
    
    # Compute MMD using multiple RBF kernels
    loss = 0.0
    for sigma in [kernel_mul ** k for k in range(-kernel_num, kernel_num + 1)]:
        if sigma == 0:
            continue
        kernel_val = torch.exp(-distances ** 2 / (2 * sigma ** 2))
        k_xx = kernel_val[:batch_size, :batch_size]
        k_yy = kernel_val[batch_size:, batch_size:]
        k_xy = kernel_val[:batch_size, batch_size:]
        
        # MMD formula: E[k(x,x)] + E[k(y,y)] - 2*E[k(x,y)]
        loss += (k_xx.mean() + k_yy.mean() - 2 * k_xy.mean())
    
    return loss / (2 * kernel_num)

def compute_loss(predictions, batch):
    # Ensure shapes match (squeeze if needed)
    pred_states = predictions['states'].squeeze(-1)  # [B, 1] → [B]
    pred_actions = predictions['actions'].squeeze(-1)
    pred_rewards = predictions['rewards'].squeeze(-1)
    
    # MMD Loss (distributional matching)
    mmd_state = mmd_loss(batch['states'], pred_states)
    mmd_action = mmd_loss(batch['actions'], pred_actions)
    mmd_reward = mmd_loss(batch['rewards'], pred_rewards)
    
    # Combine losses (adjust weights as needed)
    total_loss = mmd_state + mmd_action + mmd_reward
    
    return {
        'loss': total_loss,
        'mmd_state': mmd_state,
        'mmd_action': mmd_action,
        'mmd_reward': mmd_reward
    }

mmd_loss関数の入力パラメータはy_trueとy_predであり、これらはそれぞれ、Ground Truthデータと生成されたサンプルを表しています。両者の次元が整合していることが重要で、整合していないと比較ができません。入力kernel_mulおよびkernel_numは、RBFカーネルのバンド幅（カーネル幅）を制御するためのハイパーパラメータであり、そのため、分布の違いにおけるさまざまなスケールに対する感度に影響を与えます。

実際のサンプルと生成サンプルは、xyという結合データとしてまとめられ、これによってすべてのペアワイズ距離（全組み合わせの距離）を一括して計算できるようになります。このやり方はメモリ効率が高く、距離の計算も一貫性を保てるため非常に実用的です。距離の計算には、p=2（ユークリッド距離）が用いられており、これはMMDの標準的な選択です。この選択は、分布の違いに対する感度に直接影響を与えます。距離の計算部分、すなわちcdistの処理は、数式的に見るとこの損失関数の中心的な演算であり、MMDがペアワイズな比較に依存していることを考えると、その重要性は極めて高いです。

さらに、この実装ではマルチカーネル手法を採用しており、これは複数の異なるスケール(kernel_mul^k)で分布を観察するために、幾何学的に間隔を取った複数のカーネルバンド幅を用いています。このアプローチにより、バンド幅が0に近づいてゼロ除算が発生するといった数値的不安定性を回避できます。複数のカーネルの結果は平均化されて最終的な損失値となり、各カーネルが同等に寄与します。MMDの計算では、分布間の差異を定量化する基本式(k_xx + k_yy - 2k_xy)が使用されます。平均演算によって有限サンプルから期待値を推定し、カーネル数による正規化によって、異なる構成でも損失のスケールが一貫性を保ちます。

このMMDにはいくつかの改善点があります。まずカーネルに関しては、サンプル統計量に基づく適応的なバンド幅選択の導入、非RBFカーネルを評価してデータタイプに最適なカーネルを見極めること、そしてバンド幅に対する自動関連性判別(ARD: Automatic Relevance Determination)の実装などが挙げられます。数値計算の安定化策としては、分母に小さなイプシロンを加えること、非常に小さなカーネル値に対して対数空間で演算をおこなうこと、極端な距離値をクリッピングしてオーバーフローを防ぐことなどが考えられます。その他にも、計算効率の向上やVAEとの統合に関する改善もあります。 

この推論を実行するためには多くのコードが必要ですが、ここではそのすべてを明示的に取り上げているわけではありません。 ただし、FASRの入力データの生成は、以前の移動平均とストキャスティクスに関する2つの記事で実行されたコードに基づいている点は注目に値します。教師あり学習の記事では、VAEの入力となる特徴量と状態のコンポーネントが提供されており、強化学習の記事のコードでは行動と報酬が得られます。

線形回帰の実装

推論モデルを利用するにあたっては、VAEネットワーク自体ではなく、潜在層から欠損入力をマッピングする回帰関数のみを使用します。これは、これまでの記事でおこなってきたように、訓練済みネットワークをONNXファイルとしてエクスポートしていた手法とは対照的です。 

このような構成となる理由は、私たちが訓練済みのVAEに対して、入力データセットを補完することに関心があるためです。

以降では、利用可能なデータとして特徴量のみが存在します。したがって、「これらの特徴量に基づく状態、行動、報酬は何か？」という問いに答える必要があります。この問いに答えるために、EAの初期化時に、特徴量エンコーディング、状態エンコーディング、行動エンコーディング、報酬エンコーディングのペアからなるデータセットを用いて、線形回帰モデルを訓練（または適合）する必要があります。線形回帰モデルが訓練された後は、新たなデータの特徴量に対してそのエンコーディングを取得し、その同じモデルを通じて、対応する状態・行動・報酬をマッピングすることができます。

このエンコーディングの対応関係を取得する適合プロセスは、教師なし学習を用いておこなわれます。以下に、MQL5における線形回帰の実装を示します。

//+------------------------------------------------------------------+
// Linear Regressor (unchanged from previous implementation)         |
//+------------------------------------------------------------------+
class LinearRegressor
{
private:
   vector m_coefficients;
   double m_intercept;

   matrix m_coefficients_2d;
   vector m_intercept_2d;

public:
   void Fit(const matrix &X, const vector &y)
   {  int n = (int)X.Rows();
      int p = (int)X.Cols();
      matrix X_with_bias(n, p + 1);
      for(int i = 0; i < n; i++)
      {  for(int j = 0; j < p; j++)
            X_with_bias[i][j] = X[i][j];
         X_with_bias[i][p] = 1.0;
      }
      matrix Xt = X_with_bias.Transpose();
      matrix XtX = Xt.MatMul(X_with_bias);
      matrix XtX_inv = XtX.Inv();
      vector y_col = y;
      y_col.Resize(n, 1);
      vector beta = XtX_inv.MatMul(Xt.MatMul(y_col));
      m_coefficients = beta;
      m_coefficients.Resize(p);
      m_intercept = beta[p];
   }

   void Fit2d(const matrix &X, const matrix &Y)
   {  int n = (int)X.Rows();    // Number of samples
      int p = (int)X.Cols();    // Number of input features
      int k = (int)Y.Cols();    // Number of output encodings
      // Add bias term (column of 1s) to X
      matrix X_with_bias(n, p + 1);
      for(int i = 0; i < n; i++)
      {  for(int j = 0; j < p; j++)
            X_with_bias[i][j] = X[i][j];
         X_with_bias[i][p] = 1.0;
      }
      // Calculate coefficients using normal equation: (X'X)^-1 X'Y
      matrix Xt = X_with_bias.Transpose();
      matrix XtX = Xt.MatMul(X_with_bias);
      matrix XtX_inv = XtX.Inv();
      matrix beta = XtX_inv.MatMul(Xt.MatMul(Y));
      // Split coefficients and intercept
      m_coefficients_2d.Resize(p, k);  // Coefficients for each output encodings
      m_intercept_2d.Resize(k);        // Intercept for each input feature
      for(int j = 0; j < p; j++)
      {  for(int d = 0; d < k; d++)
         {  m_coefficients_2d[j][d] = beta[j][d];
         }
      }
      for(int d = 0; d < k; d++)
      {  m_intercept_2d[d] = beta[p][d];
      }
   }

   double Predict(const vector &x)
   {  return m_intercept + m_coefficients.Dot(x);
   }

   vector Predict2d(const vector &X) const
   {  int p = (int)X.Size();    // Number of input features
      int k = (int)m_intercept_2d.Size(); // Number of output encodings
      vector predictions(k);  // vector to store predictions
      for(int d = 0; d < k; d++)
      {  // Initialize with intercept for this output dimension
         predictions[d] = m_intercept_2d[d];
         // Add contribution from each feature
         for(int j = 0; j < p; j++)
         {  predictions[d] += m_coefficients_2d[j][d] * X[j];
         }
      }
      return predictions;
   }
};

コア構造では、1次元データ(m_coefficients / m_intercept)と2次元データ(m_coefficients_2d / m_intercept_2d)に対して、係数を個別に保持する設計となっています。バッチ処理の効率化のために行列演算（線形代数）を用いており、単一出力と複数出力の両方の回帰に対応しています。適合処理では、正規方程式を用い、(X'X)^-1X'y を直接解くことでモデルを訓練します。バイアス項（切片）の処理は、入力特徴量に1の列を追加することで対応しています。このクラスは、2次元データに特化した処理により、複数の出力を行列演算を通じて同時に扱うことができます。

予測処理には内積を用いた実装が採用されており、これは入力と重みとの線形結合を効率的に実行する方法です。単一出力・複数出力のいずれのケースでも次元の取り扱いが適切におこなわれており、結果ベクトルの事前メモリ確保によって処理効率も確保されています。状態・行動・報酬の予測には、擬似的なワッサースタインVAEクラスを使用して呼び出し・実装をおこなっています。この処理は、MQL5では次のように記述されています。

//+------------------------------------------------------------------+
// Wasserstein VAE Predictors Implementation (unchanged)             |
//+------------------------------------------------------------------+
class WassersteinVAEPredictors
{
private:
   LinearRegressor m_feature_predictor;
   LinearRegressor m_state_predictor;
   LinearRegressor m_action_predictor;
   LinearRegressor m_reward_predictor;
   bool m_predictors_trained;

public:
   WassersteinVAEPredictors() : m_predictors_trained(false) {}

   void FitPredictors(const matrix &features,
                      const vector &states,
                      const vector &actions,
                      const vector &rewards,
                      const matrix &encodings)
   {  m_feature_predictor.Fit2d(features, encodings);
      m_state_predictor.Fit(encodings, states);
      m_action_predictor.Fit(encodings, actions);
      m_reward_predictor.Fit(encodings, rewards);
      m_predictors_trained = true;
   }

   void PredictFromFeatures(const vector &y, vector &z)
   {  if(!m_predictors_trained)
      {  Print("Error: Predictors not trained yet");
         return;
      }
      z = m_feature_predictor.Predict2d(y);
   }

   void PredictFromEncodings(const vector &z, double &state, double &action, double &reward)
   {  if(!m_predictors_trained)
      {  Print("Error: Predictors not trained yet");
         return;
      }
      state = m_state_predictor.Predict(z);
      action = m_action_predictor.Predict(z);
      reward = m_reward_predictor.Predict(z);
   }
};

また、カスタムシグナルクラス内では、予測を処理するためにInfer関数を使用するようになりました。具体的には以下の通りです。

//+------------------------------------------------------------------+
//| Inference Learning Forward Pass.                                 |
//+------------------------------------------------------------------+
vector CSignal_WVAE::Infer(int Index, ENUM_POSITION_TYPE T)
{  vectorf _f = Get(Index, m_time.GetData(X()), m_close, m_ma, m_ma_lag, m_sto);
   vector _features;
   _features.Init(_f.Size());
   _features.Fill(0.0);
   for(int i = 0; i < int(_f.Size()); i++)
   {  _features[i] = _f[i];
   }
// Make a prediction
   vector _encodings;
   _encodings.Init(__ENCODINGS);
   _encodings.Fill(0.0);
   double _state = 0.0, _action = 0.0, _reward = 0.0;
   if(Index == 1)
   {  m_vae_1.PredictFromFeatures(_features, _encodings);
      m_vae_1.PredictFromEncodings(_encodings, _state, _action, _reward);
   }
   else if(Index == 2)
   {  m_vae_2.PredictFromFeatures(_features, _encodings);
      m_vae_2.PredictFromEncodings(_encodings, _state, _action, _reward);
   }
   else if(Index == 5)
   {  m_vae_5.PredictFromFeatures(_features, _encodings);
      m_vae_5.PredictFromEncodings(_encodings, _state, _action, _reward);
   }
   vector _inference;
   _inference.Init(3);
   _inference[0] = _state;
   _inference[1] = _action;
   _inference[2] = _reward;
   //
   if(T == POSITION_TYPE_BUY)
   {  if(_state > 0.5)
      {  _inference[0] -= 0.5;
         _inference[0] *= 2.0;
         if(_action < 0.0)
         {  _inference[0] = 0.0;
         }
      }
      else
      {  _inference[0] = 0.0;
      }
   }
   else if(T == POSITION_TYPE_SELL)
   {  if(_state < 0.5)
      {  _inference[0] -= 0.5;
         _inference[0] *= -2.0;
         if(_action > 0.0)
         {  _inference[0] = 0.0;
         }
      }
      else
      {  _inference[0] = 0.0;
      }
   }
   return(_inference);
}

新しい読者のために、MQL5ウィザードでEAを組み立てる方法についてのガイドは、こちらとこちらにあります。前回の記事では、最初に取り上げた10のパターンのうち、フォワードウォークに耐えたのはパターン1、2、および5のみでした。そのため、今回のエキスパートアドバイザーにおけるロング条件およびショート条件の関数では、これら3つのパターンのみを処理対象としています。本モデルでは、状態、行動、報酬の3つの値を予測します。状態は0から1の範囲に正規化されており、行動も同様の範囲に収まる設計です。報酬については-1から+1の範囲となっています。ニューラルネットワークの学習と運用にある程度の経験がある方であれば、ターゲット値に制約された範囲を持つように学習させたとしても、推論（テストまたは運用）時に出力が必ずしもその範囲内に収まるとは限らないことをご存じでしょう。そのため、推論後に何らかの正規化処理が必要になることがよくあります。

本稿では正規化処理を行っていませんが、訓練済みネットワークを本番運用に導入する際には、この点に留意しておくべきであることを読者に注意喚起しておきます。EUR/USDの日足データ2年分をPythonにアップロードし、VAEを用いて「特徴量—状態—行動—報酬」のエンコーディング対応データセットを生成・学習させます。このデータセットは、線形回帰モデルへのフィッティングに使用され、新たな特徴量に対して状態・行動・報酬を推定するために活用されます。このデータは、MetaTrader 5のPythonモジュールを用いて取り扱い、80%を学習用、残りの20%をテスト用として分割しています。

使用したデータ期間は2023年1月1日から2025年1月1日までで、フォワードウォークに相当する期間は2025年1月1日以前の約5か月間となります。今回は、これをやや広げた2024年7月1日から2025年1月1日までの6か月間でテストをおこない、以下のレポート結果が得られました。

パターン1

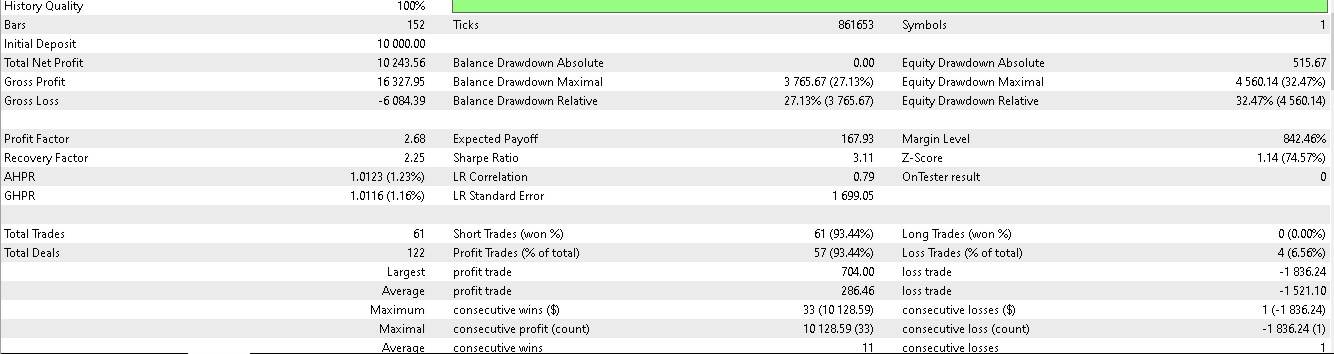
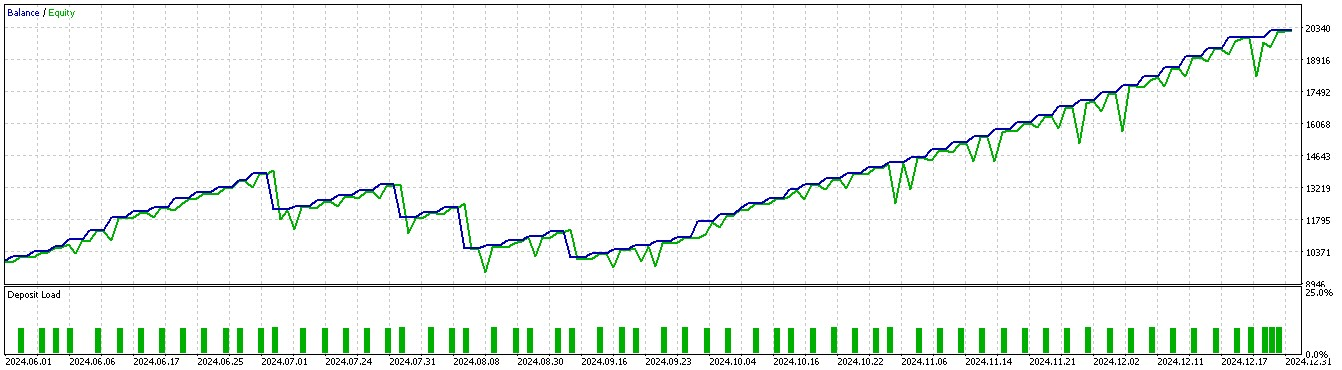
パターン2

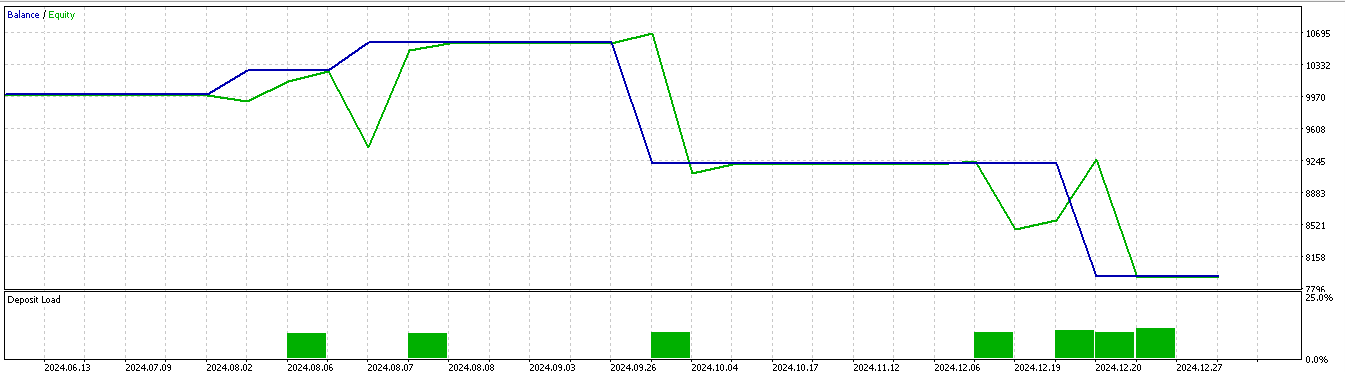
パターン5

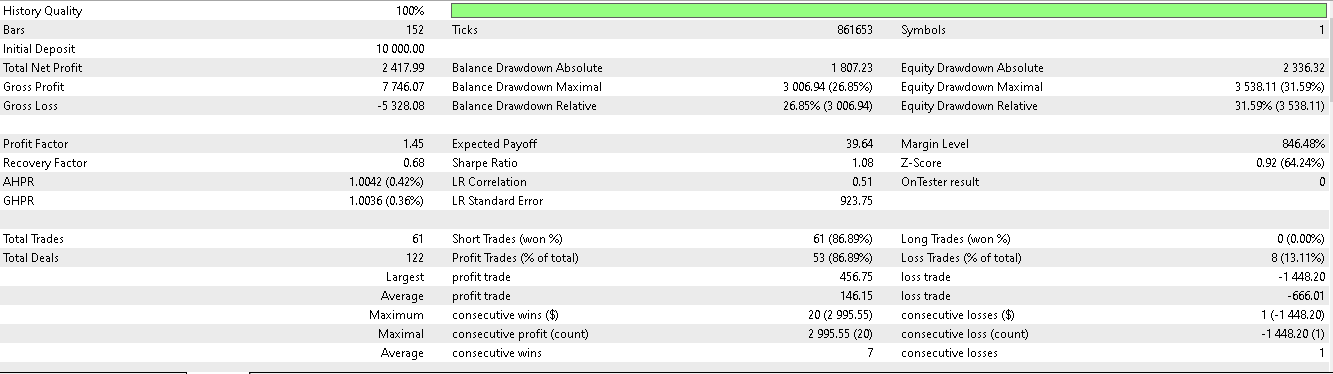
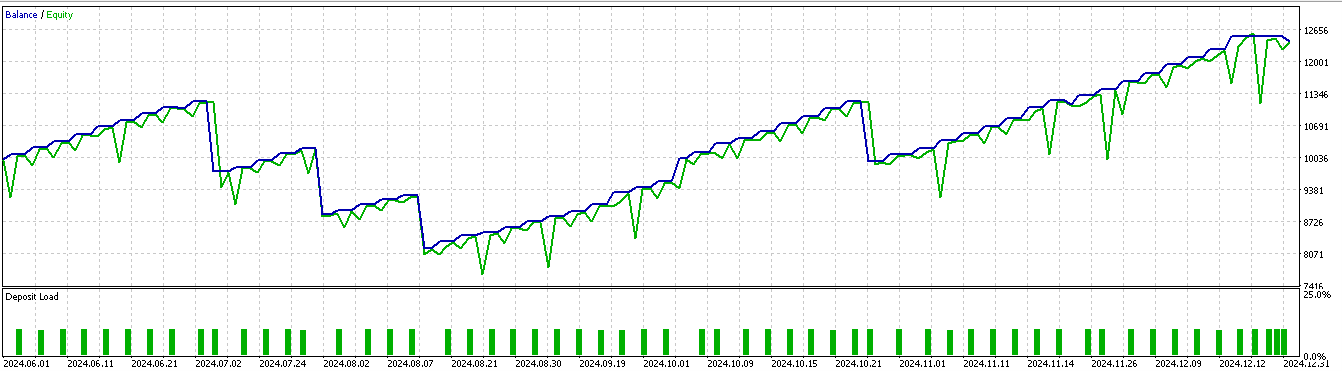
どうやら、短期間（2年間）の学習・テスト期間に基づく推論において有効性を発揮できたのは、パターン1とパターン5のみであるようです。

結論

本稿では、移動平均とストキャスティクス・オシレーターのパターンを機械学習と組み合わせて活用する取り組みの締めくくりとして、推論のユースケースを取り上げました。教師あり学習が完了し、さらに強化学習が実環境でのテストとして導入された後においても、これらの学習成果をより包括的に統合・蓄積するアプローチが依然として求められるという前提に基づき、推論の実装方法の一例を提示しました。私は、推論がこの役割を果たすにふさわしく、また適していると考えています。なぜなら、その学習手法は、すでに使用してきた教師あり学習や強化学習と重複するものではなく、それらを補完する形で機能し得るからです。

名前	説明
wz_60.mq5	ウィザードで組み立てたEA。必要なアセンブリファイルを示すヘッダーのみが含まれており、ファイルの説明は省略されている
SignalWZ_60.mqh	シグナルクラスファイル
60_vae_1.onnx	パターン1のVAE ONNXモデル（EAには必要なし）
60_vae_2.onnx	パターン2のVAE ONNXモデル（EAには必要なし）
60_vae_5.onnx	パターン5のVAE ONNXモデル（EAには必要なし）