Anwendung der Nash'schen Spieltheorie mit HMM-Filterung im Handel

Einführung

Die Anwendung mathematischer Theorien kann einen strategischen Vorteil bieten. Eine dieser Theorien ist das Nash-Gleichgewicht, das von dem bekannten Mathematiker John Forbes Nash Jr. entwickelt wurde. Bekannt für seine Beiträge zur Spieltheorie, hat Nashs Arbeit in verschiedenen Bereichen, einschließlich der Wirtschaftswissenschaften und darüber hinaus, einen großen Einfluss gehabt. In diesem Artikel wird untersucht, wie die Gleichgewichtstheorie von Nash effektiv auf den Handel angewendet werden kann. Durch den Einsatz von Python-Skripten und fortschrittlichen statistischen Modellen wollen wir die Prinzipien der Nash'schen Spieltheorie nutzen, um Handelsstrategien zu optimieren und fundiertere Entscheidungen auf dem Markt zu treffen.

Nash

Wer ist John Forbes Nash Jr.?

Wikipedia sagt über ihn:

John Forbes Nash, Jr. (* 13. Juni 1928 in Bluefield, West Virginia; † 23. Mai 2015 in Monroe Township, New Jersey) war ein US-amerikanischer Mathematiker, der besonders in den Bereichen Spieltheorie und Differentialgeometrie sowie auf dem Gebiet der partiellen Differentialgleichungen arbeitete. Im Jahr 1994 erhielt er zusammen mit Reinhard Selten und John Harsanyi den Alfred-Nobel-Gedächtnispreis für Wirtschaftswissenschaften für die gemeinsamen Leistungen auf dem Gebiet der Spieltheorie. Damit war Nash einer der wenigen Mathematiker, die diesen Preis erhielten. 2015 erhielt er mit dem Abelpreis auch noch einen der wichtigsten Wissenschaftspreise auf dem Gebiet der Mathematik.

Nach einem vielversprechenden Start seiner mathematischen Karriere erkrankte Nash im Alter von 30 Jahren an Schizophrenie. Von der Krankheit erholte sich Nash zu Beginn der 1990er Jahre.

Seine Geschichte ist Ende 2001 einem breiteren Publikum durch den preisgekrönten Spielfilm „A Beautiful Mind“ bekannt geworden.  Wir werden seine Spieltheorie auf den Handel mit MQL5 anwenden.

Wie werden wir die Nash'sche Spieltheorie in den Handel einführen?

Theorie des Nash-Gleichgewichts

Das Nash-Gleichgewicht ist ein Konzept in der Spieltheorie, bei dem davon ausgegangen wird, dass jeder Spieler die Gleichgewichtsstrategien der anderen Spieler kennt und kein Spieler etwas zu gewinnen hat, wenn er nur seine eigene Strategie ändert.

In einem Nash-Gleichgewicht ist die Strategie eines jeden Spielers optimal, wenn die Strategien aller anderen Spieler berücksichtigt werden. Ein Spiel kann mehrere Nash-Gleichgewichte oder gar keins haben.

Das Nash-Gleichgewicht ist ein grundlegendes Konzept der Spieltheorie, benannt nach dem Mathematiker John Nash. Sie beschreibt einen Zustand in einem nicht-kooperativen Spiel, in dem jeder Spieler eine Strategie gewählt hat und kein Spieler davon profitieren kann, wenn er seine Strategie einseitig ändert, während die anderen Spieler ihre Strategie unverändert lassen.

Formale Definition:

Sei (N, S, u) ein Spiel mit:

• N Spieler: N = {1, 2, ..., n}
• Strategie-Sets für jeden Spieler: S = (S₁, S₂, ..., Sₙ)
• Nutzenfunktion für jeden Spieler: u = (u₁, u₂, ..., uₙ)

Ein Strategieprofil s* = (s₁*, s₂*, ..., sₙ*) ist ein Nash-Gleichgewicht, wenn für jeden Spieler i und für alle Alternativstrategien sᵢ ∈ Sᵢ gilt:

uᵢ(s₁*, ..., sᵢ*, ..., sₙ*) ≥ uᵢ(s₁*, ..., sᵢ, ..., sₙ*)

Mit anderen Worten: Kein Spieler i kann seinen Nutzen einseitig verbessern, indem er von seiner Gleichgewichtsstrategie sᵢ* zu einer anderen Strategie sᵢ abweicht, vorausgesetzt, alle anderen Spieler behalten ihre Gleichgewichtsstrategien bei.

Für ein Spiel mit zwei Spielern können wir dies noch knapper ausdrücken:

(s₁*, s₂*) ist ein Nash-Gleichgewicht, wenn:

1. u₁(s₁*, s₂*) ≥ u₁(s₁, s₂*) für alle s₁ ∈ S₁
2. u₂(s₁*, s₂*) ≥ u₂(s₁*, s₂) für alle s₂ ∈ S₂

Diese Formulierung unterstreicht, dass die Strategie eines jeden Spielers die beste Antwort auf die Strategie des anderen Spielers im Gleichgewicht ist.

Es ist wichtig, das zu beachten:

1. Nicht alle Spiele haben ein Nash-Gleichgewicht in reinen Strategien.
2. Einige Spiele können mehrere Nash-Gleichgewichte haben.
3. Ein Nash-Gleichgewicht ist nicht notwendigerweise pareto-optimal oder das wünschenswerteste Ergebnis für alle Spieler zusammen.

Das Konzept des Nash-Gleichgewichts hat weitreichende Anwendungen in der Wirtschaft, der Politikwissenschaft und anderen Bereichen, in denen strategische Interaktionen zwischen rationalen Akteuren untersucht werden.

Obwohl in einem Nash-Gleichgewicht niemand seine Position einseitig verbessern kann, ohne dass andere sich anpassen, sind die Finanzmärkte in der Praxis dynamisch und befinden sich selten im perfekten Gleichgewicht. Möglichkeiten, Geld zu verdienen, ergeben sich aus vorübergehenden Ineffizienzen, Informationsvorteilen, besserem Risikomanagement und der Fähigkeit, schneller als andere Akteure zu reagieren. Darüber hinaus können externe und unvorhersehbare Faktoren das Gleichgewicht stören und neue Chancen für diejenigen schaffen, die darauf vorbereitet sind.

Als erstes müssen wir die Währungen auswählen (wir werden das Nash-Gleichgewicht durchführen, also brauchen wir zwei Symbole, wir werden negativ korrelierte Symbole wählen), wir werden dafür Python verwenden. Dies ist das verwendete Skript:

import MetaTrader5 as mt5
import pandas as pd
from scipy.stats import pearsonr
from statsmodels.tsa.stattools import coint
import numpy as np
import datetime

# Connect with MetaTrader 5
if not mt5.initialize():
    print("Failed to initialize MT5")
    mt5.shutdown()

# Get the list of symbols
symbols = mt5.symbols_get()
symbols = [s.name for s in symbols if s.name.startswith('EUR') or s.name.startswith('USD') or s.name.endswith('USD')]  # Filter symbols by example

# Download historical data and save in dictionary
data = {}
for symbol in symbols:
    start_date = "2020-01-01"
    end_date = "2023-12-31"
    timeframe = mt5.TIMEFRAME_H4
    start_date = datetime.datetime.strptime(start_date, "%Y-%m-%d")
    end_date = datetime.datetime.strptime(end_date, "%Y-%m-%d")
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    
    if rates is not None:
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        data[symbol] = df.set_index('time')['close']

# Close connection with MT5
mt5.shutdown()

# Calculate the Pearson coefficient and test for cointegration for each pair of symbols
cointegrated_pairs = []
for i in range(len(symbols)):
    for j in range(i + 1, len(symbols)):
        if symbols[i] in data and symbols[j] in data:
            common_index = data[symbols[i]].index.intersection(data[symbols[j]].index)
            if len(common_index) > 30:  # Ensure there are enough data points
                corr, _ = pearsonr(data[symbols[i]][common_index], data[symbols[j]][common_index])
                if abs(corr) > 0.8:  # Strong correlation
                    score, p_value, _ = coint(data[symbols[i]][common_index], data[symbols[j]][common_index])
                    if p_value < 0.05:  # P-value less than 0.05
                        cointegrated_pairs.append((symbols[i], symbols[j], corr, p_value))

# Filter and show only cointegrated pairs with p-value less than 0.05
print(f'Total pairs with strong correlation and cointegration: {len(cointegrated_pairs)}')
for sym1, sym2, corr, p_val in cointegrated_pairs:
    print(f'{sym1} - {sym2}: Correlation={corr:.4f}, P-Cointegration value={p_val:.4f}')

Dieses Skript initialisiert zunächst den MetaTrader 5 und ruft dann alle Symbole ab, die mit EUR oder USD beginnen oder auf USD enden. Danach werden die Daten von diesen Symbolen heruntergeladen und der MetaTrader 5 wird beendet. Er vergleicht alle Symbole und lässt nur die stark korrelierten durch, um dann einen weiteren Filter für die stark kointegrierten Paare zu erstellen. Am Ende werden im Terminal die verbleibenden Symbole angezeigt.

Die Korrelation misst, wie zwei Dinge miteinander in Beziehung stehen. Stell dir vor, du und dein bester Freund gehen samstags immer zusammen ins Kino. Dies ist ein Beispiel für eine Korrelation: Wenn Sie ins Kino gehen, ist Ihr Freund auch dort. Wenn die Korrelation positiv ist, bedeutet dies, dass bei einem Anstieg des einen Wertes auch der andere Wert steigt. Wenn sie negativ ist, nimmt die eine zu, während die andere abnimmt. Ist die Korrelation gleich Null, bedeutet dies, dass es keinen Zusammenhang zwischen beiden gibt.

Kointegration ist ein statistisches Konzept, das eine Situation beschreibt, in der zwei oder mehr Variablen in einer langfristigen Beziehung zueinander stehen, auch wenn sie kurzfristig unabhängig voneinander schwanken können. Stellen Sie sich zwei Schwimmer vor, die mit einem Seil aneinander gebunden sind: Sie können frei im Becken schwimmen, aber sie können sich nicht weit voneinander entfernen. Kointegration bedeutet, dass diese Variablen trotz vorübergehender Unterschiede immer wieder zu einem gemeinsamen langfristigen Gleichgewicht oder Trend zurückkehren werden.

Der Pearson-Koeffizient misst die lineare Verbundenheit von zwei Variablen. Liegt der Koeffizient nahe bei +1, so deutet dies auf eine direkte Abhängigkeit hin, denn wenn eine Variable zunimmt, nimmt auch die andere zu. Ein Koeffizient nahe bei -1 bedeutet, dass der eine Wert steigt und der andere sinkt, was auf eine umgekehrte Beziehung hindeutet. Ein Wert von 0 bedeutet keine lineare Verbindung. Die Messung der Temperatur und der Anzahl der verkauften Kaltgetränke kann zum Beispiel helfen zu verstehen, wie diese Faktoren mit Hilfe des Pearson-Koeffizienten zusammenhängen.

Die Ergebnisse des Skripts sollten wie diese aussehen (dies sind die Ergebnisse, die für die Anfangsbedingungen des Skripts erzielt wurden):

    start_date = "2020-01-01"
    end_date = "2023-12-31"
    timeframe = mt5.TIMEFRAME_H4

Total pairs with strong correlation and cointegration: 40
USDJPY - EURCHF: Correlation=-0.9416, P-Cointegration value=0.0165
USDJPY - EURN.NASDAQ: Correlation=0.9153, P-Cointegration value=0.0008
USDCNH - USDZAR: Correlation=0.8474, P-Cointegration value=0.0193
USDRUB - USDRUR: Correlation=0.9993, P-Cointegration value=0.0000
AUDUSD - USDCLP: Correlation=-0.9012, P-Cointegration value=0.0280
AUDUSD - USDILS: Correlation=-0.8686, P-Cointegration value=0.0026
NZDUSD - USDNOK: Correlation=-0.9353, P-Cointegration value=0.0469
NZDUSD - USDILS: Correlation=-0.8514, P-Cointegration value=0.0110
...
EURSEK - XPDUSD: Correlation=-0.8200, P-Cointegration value=0.0269
EURZAR - USDP.NASDAQ: Correlation=-0.8678, P-Cointegration value=0.0154
USDMXN - EURCNH: Correlation=-0.8490, P-Cointegration value=0.0389
EURL.NASDAQ - EURSGD: Correlation=0.9157, P-Cointegration value=0.0000
EURN.NASDAQ - EURSGD: Correlation=-0.8301, P-Cointegration value=0.0358

Mit all den Ergebnissen werden wir diese beiden Symbole wählen (eine negative Korrelation bedeutet, dass, wenn eine nach oben geht, die andere nach unten geht und umgekehrt, und eine positive Korrelation bedeutet, dass die Symbole eine wie die andere gehen), werde ich USDJPY-Symbol wählen, weil, wie in Nash-Gleichgewicht erklärt, könnten wir den Vorteil des USD als Motor des Forex und die anderen korreliert könnte hinter ihm zu bewegen:

USDJPY - EURCHF: Correlation=-0.9416, P-Cointegration value=0.0165

Ich habe MetaTrader 5 mit einem Demo-Konto für den Erhalt aller Daten erhalten und Backtesting der EA verwendet.

HMM (Hidden Markov Model)

Das Hidden Markov Model (HMM) ist ein statistisches Modell zur Beschreibung von Systemen, die sich im Laufe der Zeit teilweise zufällig und teilweise abhängig von verborgenen Zuständen verändern. Stellen Sie sich einen Prozess vor, bei dem wir nur bestimmte Ergebnisse beobachten können, die aber von zugrunde liegenden Faktoren (oder Zuständen) beeinflusst werden, die wir nicht direkt sehen können.

HMM wird im Handel eingesetzt, um ein Modell zu haben, das anhand von Daten aus der Vergangenheit Muster des Marktes vorhersagt.

Wir werden ein Python-Skript verwenden, um das HMM-Modell zu erhalten. Dabei müssen wir den verwendeten Zeitrahmen (er sollte derselbe sein wie im EA), die verborgenen Zustände und die Anzahl der Daten berücksichtigen, aus denen die Vorhersage erfolgen soll (je größer, desto besser).

Das Python-Skript gibt 3 Matrizen (in einer .txt-Datei) und drei Diagramme zurück, die wir für den Expert Advisor verwenden werden.

Dies ist das .py-Skript:

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
from hmmlearn import hmm
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import datetime
import os
import sys

# Number of models to train
n_models = 10

# Redirect stdout to a file
def redirect_output(symbol):
    output_file = f"{symbol}_output.txt"
    sys.stdout = open(output_file, 'w')

# Connect to MetaTrader 5
if not mt5.initialize():
    print("initialize() failed")
    mt5.shutdown()

# Get and process data
def get_mt5_data(symbol, timeframe, start_date, end_date):
    """Get historical data from MetaTrader 5."""
    start_date = datetime.datetime.strptime(start_date, "%Y-%m-%d")
    end_date = datetime.datetime.strptime(end_date, "%Y-%m-%d")
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    return df

def calculate_features(df):
    """Calculate important features like returns, volatility, and trend."""
    df['returns'] = df['close'].pct_change()
    df['volatility'] = df['returns'].rolling(window=50).std()
    df['trend'] = df['close'].pct_change(periods=50)
    return df.dropna()

# Main script
symbol = "USDJPY"
timeframe = mt5.TIMEFRAME_H4
start_date = "2020-01-01"
end_date = "2023-12-31"
current_date = datetime.datetime.now().strftime("%Y-%m-%d")

# Redirect output to file
redirect_output(symbol)

# Get historical data for training
df = get_mt5_data(symbol, timeframe, start_date, end_date)
df = calculate_features(df)

features = df[['returns', 'volatility', 'trend']].values
scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)

# Lists to store the results of each model
state_predictions = np.zeros((scaled_features.shape[0], n_models))
strategy_returns = np.zeros((scaled_features.shape[0], n_models))
transition_matrices = np.zeros((10, 10, n_models))
means_matrices = np.zeros((n_models, 10, 3))
covariance_matrices = np.zeros((n_models, 10, 3, 3))

# Train multiple models and store the results
for i in range(n_models):
    model = hmm.GaussianHMM(n_components=10, covariance_type="full", n_iter=10000, tol=1e-6, min_covar=1e-3)
    X_train, X_test = train_test_split(scaled_features, test_size=0.2, random_state=i)
    model.fit(X_train)

    # Save the transition matrix, emission means, and covariances
    transition_matrices[:, :, i] = model.transmat_
    means_matrices[i, :, :] = model.means_
    covariance_matrices[i, :, :, :] = model.covars_

    # State prediction
    states = model.predict(scaled_features)
    state_predictions[:, i] = states

    # Generate signals and calculate strategy returns for this model
    df['state'] = states
    df['signal'] = 0
    for j in range(10):
        df.loc[df['state'] == j, 'signal'] = 1 if j % 2 == 0 else -1
    df['strategy_returns'] = df['returns'] * df['signal'].shift(1)
    strategy_returns[:, i] = df['strategy_returns'].values

# Average of matrices
average_transition_matrix = transition_matrices.mean(axis=2)
average_means_matrix = means_matrices.mean(axis=0)
average_covariance_matrix = covariance_matrices.mean(axis=0)

# Save the average matrices in the output file in appropriate format
print("Average Transition Matrix:")
for i, row in enumerate(average_transition_matrix):
    for j, val in enumerate(row):
        print(f"average_transition_matrix[{i}][{j}] = {val:.8f};")

print("\nAverage Means Matrix:")
for i, row in enumerate(average_means_matrix):
    for j, val in enumerate(row):
        print(f"average_means_matrix[{i}][{j}] = {val:.8f};")

print("\nAverage Covariance Matrix:")
for i in range(10):  # For each state
    for j in range(3):  # For each row of the covariance matrix
        for k in range(3):  # For each column of the covariance matrix
            print(f"average_covariance_matrix[{i}][{j}][{k}] = {average_covariance_matrix[i, j, k]:.8e};")

# Average of state predictions and strategy returns
average_states = np.round(state_predictions.mean(axis=1)).astype(int)
average_strategy_returns = strategy_returns.mean(axis=1)

# Store the average results in the original dataframe
df['average_state'] = average_states
df['average_strategy_returns'] = average_strategy_returns

# Calculate cumulative returns using the average strategy
df['cumulative_market_returns'] = (1 + df['returns']).cumprod()
df['cumulative_strategy_returns'] = (1 + df['average_strategy_returns']).cumprod()

# Plot cumulative returns (training)
plt.figure(figsize=(7, 6))
plt.plot(df.index, df['cumulative_market_returns'], label='Market Returns')
plt.plot(df.index, df['cumulative_strategy_returns'], label='Strategy Returns (Average)')
plt.title('Cumulative Returns with Average Strategy')
plt.xlabel('Date')
plt.ylabel('Cumulative Returns')
plt.legend()
plt.grid(True)
plt.savefig(f'average_strategy_returns_{symbol}.png')
plt.close()

# Additional plots for averages
fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(12, 15), sharex=True)

# Plot closing price and average HMM states
ax1.plot(df.index, df['close'], label='Closing Price')
scatter = ax1.scatter(df.index, df['close'], c=df['average_state'], cmap='viridis', s=30, label='Average HMM States')
ax1.set_ylabel('Price')
ax1.set_title('Closing Price and Average HMM States')
ax1.legend(loc='upper left')

# Add color bar for states
cbar = plt.colorbar(scatter, ax=ax1)
cbar.set_label('Average HMM State')

# Plot returns
ax2.bar(df.index, df['returns'], label='Market Returns', alpha=0.5, color='blue')
ax2.bar(df.index, df['average_strategy_returns'], label='Average Strategy Returns', alpha=0.5, color='red')
ax2.set_ylabel('Return')
ax2.set_title('Daily Returns')
ax2.legend(loc='upper left')

# Plot cumulative returns
ax3.plot(df.index, df['cumulative_market_returns'], label='Cumulative Market Returns')
ax3.plot(df.index, df['cumulative_strategy_returns'], label='Cumulative Average Strategy Returns')
ax3.set_ylabel('Cumulative Return')
ax3.set_title('Cumulative Returns')
ax3.legend(loc='upper left')

# Adjust layout
plt.tight_layout()
plt.xlabel('Date')

# Save figure
plt.savefig(f'average_returns_{symbol}.png')
plt.close()

# Calculate cumulative returns for each average state
state_returns = {}
for state in range(10):  # Assuming 10 states
    state_returns[state] = df[df['average_state'] == state]['returns'].sum()

# Create lists for states and their cumulative returns
states = list(state_returns.keys())
returns = list(state_returns.values())

# Create bar chart
plt.figure(figsize=(7, 6))
bars = plt.bar(states, returns)

# Customize chart
plt.title('Cumulative Returns by Average HMM State', fontsize=7)
plt.xlabel('State', fontsize=7)
plt.ylabel('Cumulative Return', fontsize=7)
plt.xticks(states)

# Add value labels above each bar
for bar in bars:
    height = bar.get_height()
    plt.text(bar.get_x() + bar.get_width()/2., height,
             f'{height:.4f}',
             ha='center', va='bottom')

# Add horizontal line at y=0 for reference
plt.axhline(y=0, color='r', linestyle='-', linewidth=0.5)

# Adjust layout and save chart
plt.tight_layout()
plt.savefig(f'average_bars_{symbol}.png')
plt.close()

# Get recent data to test the model
df_recent = get_mt5_data(symbol, timeframe, end_date, current_date)
df_recent = calculate_features(df_recent)

# Apply the same scaler to recent data
scaled_recent_features = scaler.transform(df_recent[['returns', 'volatility', 'trend']].values)

# Lists to store the results of each model for recent data
recent_state_predictions = np.zeros((scaled_recent_features.shape[0], n_models))
recent_strategy_returns = np.zeros((scaled_recent_features.shape[0], n_models))

# Apply the trained model to recent data
for i in range(n_models):
    model = hmm.GaussianHMM(n_components=10, covariance_type="full", n_iter=10000, tol=1e-4, min_covar=1e-3)
    X_train, X_test = train_test_split(scaled_features, test_size=0.2, random_state=i)
    model.fit(X_train)
    
    recent_states = model.predict(scaled_recent_features)
    recent_state_predictions[:, i] = recent_states

    df_recent['state'] = recent_states
    df_recent['signal'] = 0
    for j in range(10):
        df_recent.loc[df_recent['state'] == j, 'signal'] = 1 if j % 2 == 0 else -1
    df_recent['strategy_returns'] = df_recent['returns'] * df_recent['signal'].shift(1)
    recent_strategy_returns[:, i] = df_recent['strategy_returns'].values

# Average of state predictions and strategy returns for recent data
average_recent_states = np.round(recent_state_predictions.mean(axis=1)).astype(int)
average_recent_strategy_returns = recent_strategy_returns.mean(axis=1)

# Store the average results in the recent dataframe
df_recent['average_state'] = average_recent_states
df_recent['average_strategy_returns'] = average_recent_strategy_returns

# Calculate cumulative returns using the average strategy on recent data
df_recent['cumulative_market_returns'] = (1 + df_recent['returns']).cumprod()
df_recent['cumulative_strategy_returns'] = (1 + df_recent['average_strategy_returns']).cumprod()

# Plot cumulative returns (recent test)
plt.figure(figsize=(7, 6))
plt.plot(df_recent.index, df_recent['cumulative_market_returns'], label='Market Returns')
plt.plot(df_recent.index, df_recent['cumulative_strategy_returns'], label='Strategy Returns (Average)')
plt.title('Cumulative Returns with Average Strategy (Recent Data)')
plt.xlabel('Date')
plt.ylabel('Cumulative Returns')
plt.legend()
plt.grid(True)
plt.savefig(f'average_recent_strategy_returns_{symbol}.png')
plt.close()

# Close MetaTrader 5
mt5.shutdown()


# Assign descriptive names to the hidden states
state_labels = {}
for state in range(10):  # Assuming 10 states
    if state in df['average_state'].unique():
        label = f"State {state}: "  # You can customize this description based on your observations
        if state_returns[state] > 0:
            label += "Uptrend"
        else:
            label += "Downtrend"
        state_labels[state] = label
    else:
        state_labels[state] = f"State {state}: Not present"

# Print the states and their descriptive labels
print("\nDescription of Hidden States:")
for state, label in state_labels.items():
    print(f"{label} (State ID: {state})")

# Close MetaTrader 5 connection
mt5.shutdown()

# Finally, close the output file
sys.stdout.close()
sys.stdout = sys.__stdout__

Dieses Skript mit diesen Anfangsbedingungen hat zu diesen Ergebnissen geführt:

timeframe = mt5.TIMEFRAME_H4
start_date = "2020-01-01"
end_date = "2023-12-31"

Average Transition Matrix:
average_transition_matrix[0][0] = 0.15741321;
average_transition_matrix[0][1] = 0.07086962;
average_transition_matrix[0][2] = 0.16785905;
average_transition_matrix[0][3] = 0.08792403;
average_transition_matrix[0][4] = 0.11101073;
average_transition_matrix[0][5] = 0.05415263;
average_transition_matrix[0][6] = 0.08019415;
.....
average_transition_matrix[9][3] = 0.13599698;
average_transition_matrix[9][4] = 0.12947508;
average_transition_matrix[9][5] = 0.06385211;
average_transition_matrix[9][6] = 0.09042617;
average_transition_matrix[9][7] = 0.16088280;
average_transition_matrix[9][8] = 0.06588065;
average_transition_matrix[9][9] = 0.04559230;

Average Means Matrix:
average_means_matrix[0][0] = 0.06871601;
average_means_matrix[0][1] = 0.14572210;
average_means_matrix[0][2] = 0.05961646;
average_means_matrix[1][0] = 0.06903949;
average_means_matrix[1][1] = 1.05226034;
.....
average_means_matrix[7][2] = 0.00453701;
average_means_matrix[8][0] = -0.38270747;
average_means_matrix[8][1] = 0.86916742;
average_means_matrix[8][2] = -0.58792329;
average_means_matrix[9][0] = -0.16057267;
average_means_matrix[9][1] = 1.17106076;
average_means_matrix[9][2] = 0.18531821;

Average Covariance Matrix:
average_covariance_matrix[0][0][0] = 1.25299224e+00;
average_covariance_matrix[0][0][1] = -4.05453267e-02;
average_covariance_matrix[0][0][2] = 7.95036804e-02;
average_covariance_matrix[0][1][0] = -4.05453267e-02;
average_covariance_matrix[0][1][1] = 1.63177290e-01;
average_covariance_matrix[0][1][2] = 1.58609858e-01;
average_covariance_matrix[0][2][0] = 7.95036804e-02;
average_covariance_matrix[0][2][1] = 1.58609858e-01;
average_covariance_matrix[0][2][2] = 8.09678270e-01;
average_covariance_matrix[1][0][0] = 1.23040552e+00;
average_covariance_matrix[1][0][1] = 2.52108300e-02;
....
average_covariance_matrix[9][0][0] = 5.47457383e+00;
average_covariance_matrix[9][0][1] = -1.22088743e-02;
average_covariance_matrix[9][0][2] = 2.56784647e-01;
average_covariance_matrix[9][1][0] = -1.22088743e-02;
average_covariance_matrix[9][1][1] = 4.65227101e-01;
average_covariance_matrix[9][1][2] = -2.88257686e-01;
average_covariance_matrix[9][2][0] = 2.56784647e-01;
average_covariance_matrix[9][2][1] = -2.88257686e-01;
average_covariance_matrix[9][2][2] = 1.44717234e+00;

Description of Hidden States:
State 0: Not present (State ID: 0)
State 1: Downtrend (State ID: 1)
State 2: Uptrend (State ID: 2)
State 3: Downtrend (State ID: 3)
State 4: Uptrend (State ID: 4)
State 5: Uptrend (State ID: 5)
State 6: Uptrend (State ID: 6)
State 7: Downtrend (State ID: 7)
State 8: Uptrend (State ID: 8)
State 9: Not present (State ID: 9)

Um sie zu nutzen, müssen wir nur das Symbol, von dem die Daten stammen, die Anzahl der Zustände und die Daten, von denen die Daten stammen, ändern. Wir müssen auch in der EA anpassen und in beiden Python-Skripte verwenden den Zeitraum (Zeitrahmen) (alle Skripte und die EA mit dem gleichen).

Dieses Skript wird 10 Modelle haben, und es wird den Durchschnitt von ihnen machen, um ein robustes Modell zu erhalten (wenn wir nur zwei Modelle gemacht haben, würden beide Gruppen von Matrizen unterschiedlich sein) (Es wird einige Zeit dauern, um die Matrizen zu erstellen). Am Ende haben wir die Matrizen, drei Graphen (ich werde jetzt erklären, warum sie wichtig sind), eine Beschreibung der verborgenen Zustände und eine .txt-Datei mit den Matrizen.

Die Ergebnisse

Im ersten Bild sehen wir das Ergebnis eines Backtestings mit dem durchschnittlichen HMM-Modell. Sie können den Preiswert und die Strategie mit HMM-Ergebnissen für das Backtesting in diesem Zeitraum sehen.

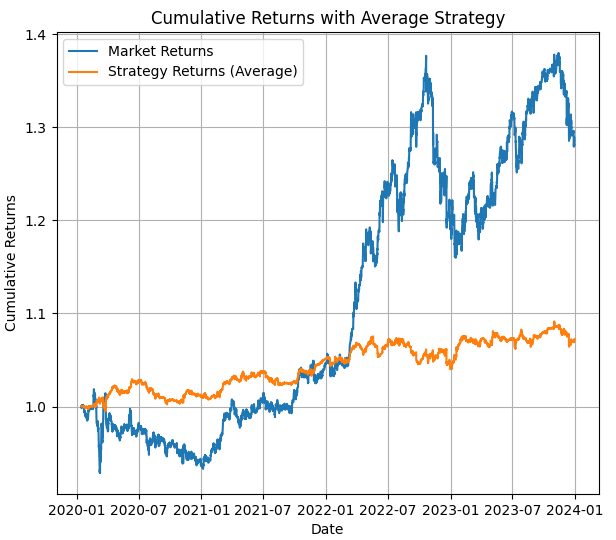
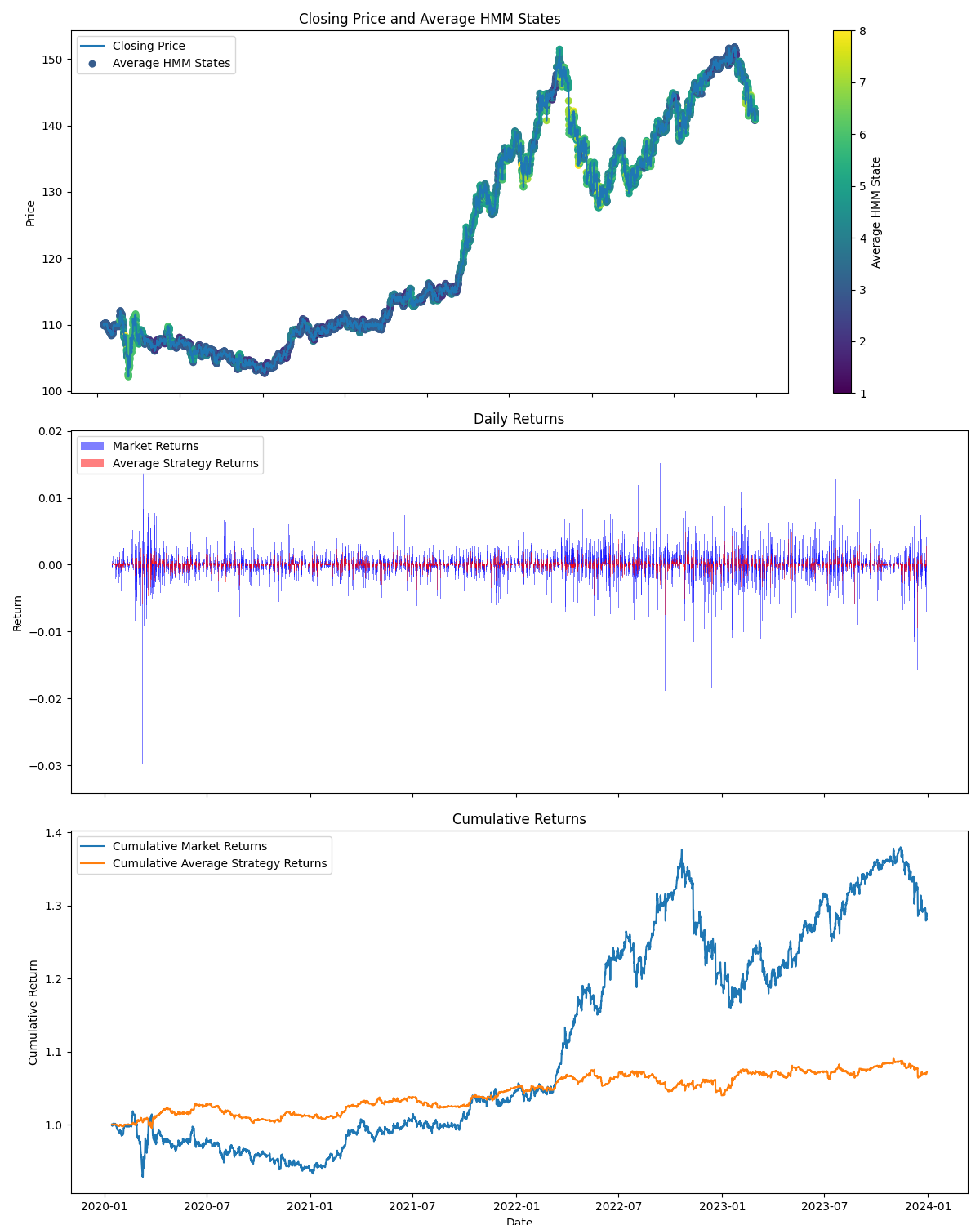
Im zweiten Bild sehen wir die Ergebnisse des Backtestings in der Testperiode und ein wichtiges Bild, das zeigt, wo die versteckten Zustände verwendet werden (Sie können sehen, wo sie einen Aufwärtstrend oder einen Abwärtstrend oder sein Schwanken oder neutral bekommen haben).

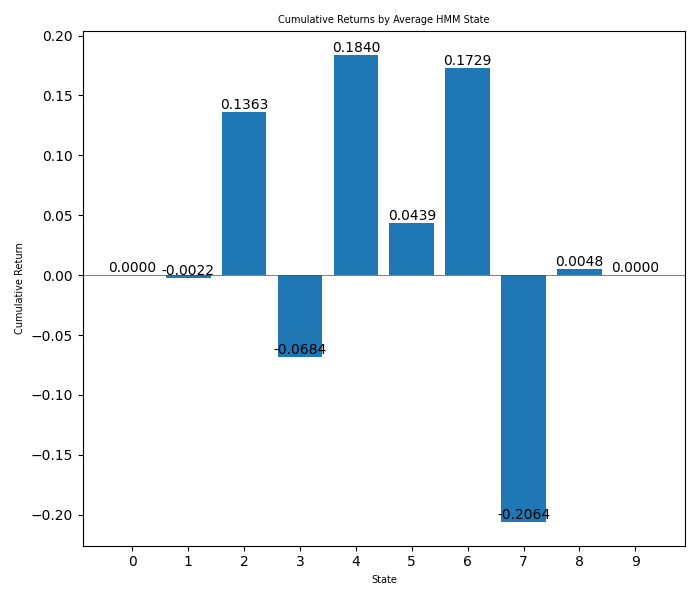
Auf dem dritten Bild sehen Sie die Gewinne für jeden verdeckten Zustand als Balken.

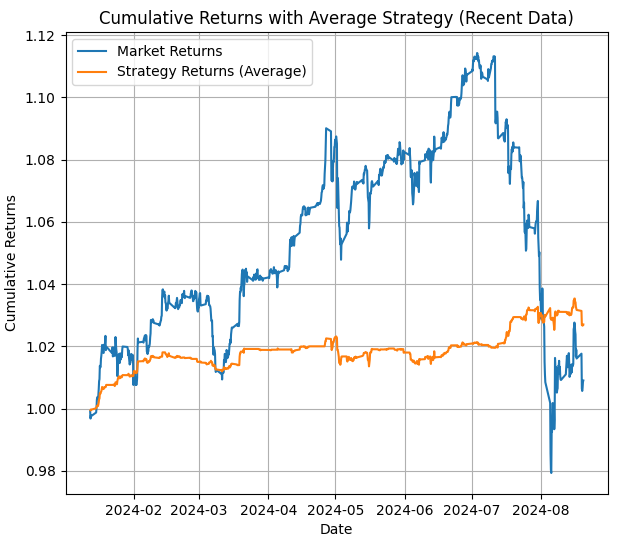
Es gibt ein viertes Bild mit den durchschnittlichen Erträgen für die Strategie während des Zeitraums zwischen dem letzten Datum und heute (dies ist, was wir von der Strategie im MetaTrader 5 Backtesting erwarten sollten, wenn wir die Zustände nicht anpassen).

Nun, da wir alle diese Informationen haben, können wir diese verwenden, um auszuwählen, welche versteckten Statistiken wir verwenden werden, und wir können wissen, ob ein versteckter Zustand entsteht, wenn er einen Trend aufweist (mit dem zweiten Bild) und auch Gewinne (mit den Balken). Mit all dem werden wir die Zustände im EA umschalten.

Aus den Balken können wir ersehen, dass die verborgenen Zustände, die wir verwenden wollen, folgende sind: 2, 3 und 7, das entspricht wahrscheinlich dem Bereich, Aufwärtstrend und Abwärtstrend bzw. könnte ein hoher Trend sein. Wir können nun die Strategie im EA einrichten und dabei berücksichtigen, dass die anderen versteckten Zustände nicht profitabel waren (wir können viele Backtests durchführen, um herauszufinden, welche Strategie am besten geeignet ist).

Alle Python-Skripte haben Python 3.10 verwendet.

Wir könnten die Matrizen zum EA hinzufügen (Komponente für Komponente, da Python eine andere Art hat, Matrizen darzustellen), aber da wir nicht viel arbeiten wollen, werden wir dieses nächste Skript verwenden, um die Matrix in eine MQl5-Form zu bringen, die wir für den EA verwenden werden. Dies ist der EA, den wir für die Matrixformatierung verwenden können:

import re
import os

def read_file(filename):
    if not os.path.exists(filename):
        print(f"Error: The file {filename} does not exist.")
        return None
    try:
        with open(filename, "r") as file:
            return file.read()
    except Exception as e:
        print(f"Error reading the file: {str(e)}")
        return None

def parse_matrix(file_content, matrix_name):
    pattern = rf"{matrix_name}\[(\d+)\]\[(\d+)\]\s*=\s*([-+]?(?:\d*\.\d+|\d+)(?:e[-+]?\d+)?)"
    matches = re.findall(pattern, file_content)
    matrix = {}
    for match in matches:
        i, j, value = int(match[0]), int(match[1]), float(match[2])
        if i not in matrix:
            matrix[i] = {}
        matrix[i][j] = value
    return matrix

def parse_covariance_matrix(file_content):
    pattern = r"average_covariance_matrix\[(\d+)\]\[(\d+)\]\[(\d+)\]\s*=\s*([-+]?(?:\d*\.\d+|\d+)(?:e[-+]?\d+)?)"
    matches = re.findall(pattern, file_content)
    matrix = {}
    for match in matches:
        i, j, k, value = int(match[0]), int(match[1]), int(match[2]), float(match[3])
        if i not in matrix:
            matrix[i] = {}
        if j not in matrix[i]:
            matrix[i][j] = {}
        matrix[i][j][k] = value
    return matrix

def format_matrix(matrix, is_3d=False):
    if not matrix:
        return "{     };"
    
    formatted = "{\n"
    for i in sorted(matrix.keys()):
        if is_3d:
            formatted += "        {  "
            for j in sorted(matrix[i].keys()):
                formatted += "{" + ", ".join(f"{matrix[i][j][k]:.8e}" for k in sorted(matrix[i][j].keys())) + "}"
                if j < max(matrix[i].keys()):
                    formatted += ",\n           "
            formatted += "}"
        else:
            formatted += "        {" + ", ".join(f"{matrix[i][j]:.8f}" for j in sorted(matrix[i].keys())) + "}"
        if i < max(matrix.keys()):
            formatted += ","
        formatted += "\n"
    formatted += "     };"
    return formatted

def main():
    input_filename = "USDJPY_output.txt"
    output_filename = "formatted_matrices.txt"
    content = read_file(input_filename)
    
    if content is None:
        return

    print(f"Input file size: {len(content)} bytes")
    print("First 200 characters of the file:")
    print(content[:200])

    transition_matrix = parse_matrix(content, "average_transition_matrix")
    means_matrix = parse_matrix(content, "average_means_matrix")
    covariance_matrix = parse_covariance_matrix(content)

    print(f"\nElements found in the transition matrix: {len(transition_matrix)}")
    print(f"Elements found in the means matrix: {len(means_matrix)}")
    print(f"Elements found in the covariance matrix: {len(covariance_matrix)}")

    output = "Transition Matrix:\n"
    output += format_matrix(transition_matrix)
    output += "\n\nMeans Matrix:\n"
    output += format_matrix(means_matrix)
    output += "\n\nCovariance Matrix:\n"
    output += format_matrix(covariance_matrix, is_3d=True)

    try:
        with open(output_filename, "w") as outfile:
            outfile.write(output)
        print(f"\nFormatted matrices saved in '{output_filename}'")
    except Exception as e:
        print(f"Error writing the output file: {str(e)}")

    print(f"\nFirst lines of the output file '{output_filename}':")
    output_content = read_file(output_filename)
    if output_content:
        print("\n".join(output_content.split("\n")[:20]))  # Display the first 20 lines

if __name__ == "__main__":
    main()

Wir können auch Sockets verwenden (Sockets sind eine gute Möglichkeit, mit mt5 über externe Daten zu interagieren), um die Matrizen zu importieren. Sie können dies tun, wie es in diesem Artikel erklärt wird:  Stimmungsanalyse auf Twitter mit Sockets und sogar Sentiment Analysis hinzufügen (wie in diesem Artikel erklärt), um bessere Trend-Positionen zu erhalten.

Mit diesem Skript erhalten wir eine .txt-Datei, die etwas Ähnliches wie das hier zeigt:

Transition Matrix:
{
        {0.15741321, 0.07086962, 0.16785905, 0.08792403, 0.11101073, 0.05415263, 0.08019415, 0.12333382, 0.09794255, 0.04930020},
        {0.16646033, 0.11065086, 0.10447035, 0.13332935, 0.09136784, 0.08351764, 0.06722600, 0.09893912, 0.07936700, 0.06467150},
        {0.14182826, 0.15400641, 0.13617941, 0.08453877, 0.09214389, 0.04040276, 0.09065499, 0.11526167, 0.06725810, 0.07772574},
        {0.15037837, 0.09101998, 0.09552059, 0.10035540, 0.12851236, 0.05000596, 0.09542873, 0.12606514, 0.09394759, 0.06876588},
        {0.15552336, 0.08663776, 0.15694344, 0.09219379, 0.08785893, 0.08381830, 0.05572122, 0.10309824, 0.08512219, 0.09308276},
        {0.19806868, 0.11292565, 0.11482367, 0.08324432, 0.09808519, 0.06727817, 0.11549253, 0.10657752, 0.06889919, 0.03460507},
        {0.12257742, 0.11257625, 0.11910078, 0.07669820, 0.16660657, 0.04769350, 0.09667861, 0.12241177, 0.04856867, 0.08708823},
        {0.14716725, 0.12232022, 0.11135735, 0.08488571, 0.06274817, 0.07390905, 0.10742571, 0.12550373, 0.11431005, 0.05037277},
        {0.11766333, 0.11533807, 0.15497601, 0.14017237, 0.11214274, 0.04885795, 0.08394306, 0.12864406, 0.06945878, 0.02880364},
        {0.13559147, 0.07444276, 0.09785968, 0.13599698, 0.12947508, 0.06385211, 0.09042617, 0.16088280, 0.06588065, 0.04559230}
     };

Means Matrix:
{
        {0.06871601, 0.14572210, 0.05961646},
        {0.06903949, 1.05226034, -0.25687024},
        {-0.04607112, -0.00811718, 0.06488246},
        {-0.01769149, 0.63694700, 0.26965491},
        {-0.01874345, 0.58917438, -0.22484670},
        {-0.02026370, 1.09022869, 0.86790417},
        {-0.85455759, 0.48710677, 0.08980023},
        {-0.02589947, 0.84881170, 0.00453701},
        {-0.38270747, 0.86916742, -0.58792329},
        {-0.16057267, 1.17106076, 0.18531821}
     };

Covariance Matrix:
{
        {  {1.25299224e+00, -4.05453267e-02, 7.95036804e-02},
           {-4.05453267e-02, 1.63177290e-01, 1.58609858e-01},
           {7.95036804e-02, 1.58609858e-01, 8.09678270e-01}},
        {  {1.23040552e+00, 2.52108300e-02, 1.17595322e-01},
           {2.52108300e-02, 3.00175953e-01, -8.11027442e-02},
           {1.17595322e-01, -8.11027442e-02, 1.42259217e+00}},
        {  {1.76376507e+00, -7.82189996e-02, 1.89340073e-01},
           {-7.82189996e-02, 2.56222155e-01, -1.30202288e-01},
           {1.89340073e-01, -1.30202288e-01, 6.60591043e-01}},
        {  {9.08926052e-01, 3.02606081e-02, 1.03549625e-01},
           {3.02606081e-02, 2.30324420e-01, -5.46541678e-02},
           {1.03549625e-01, -5.46541678e-02, 7.40333449e-01}},
        {  {8.80590495e-01, 7.21102489e-02, 3.40982555e-02},
           {7.21102489e-02, 3.26639817e-01, -1.06663221e-01},
           {3.40982555e-02, -1.06663221e-01, 9.55477387e-01}},
        {  {3.19499555e+00, -8.63552078e-02, 5.03260281e-01},
           {-8.63552078e-02, 2.92184645e-01, 1.03141313e-01},
           {5.03260281e-01, 1.03141313e-01, 1.88060098e+00}},
        {  {3.22276957e+00, -6.37618091e-01, 3.80462477e-01},
           {-6.37618091e-01, 4.96770891e-01, -5.79521882e-02},
           {3.80462477e-01, -5.79521882e-02, 1.05061090e+00}},
        {  {2.16098355e+00, 4.02611831e-02, 3.01261346e-01},
           {4.02611831e-02, 4.83773367e-01, 7.20003108e-02},
           {3.01261346e-01, 7.20003108e-02, 1.32262495e+00}},
        {  {4.00745050e+00, -3.90316434e-01, 7.28032792e-01},
           {-3.90316434e-01, 6.01214190e-01, -2.91562862e-01},
           {7.28032792e-01, -2.91562862e-01, 1.30603500e+00}},
        {  {5.47457383e+00, -1.22088743e-02, 2.56784647e-01},
           {-1.22088743e-02, 4.65227101e-01, -2.88257686e-01},
           {2.56784647e-01, -2.88257686e-01, 1.44717234e+00}}
     };

Dies ist das Format für die Matrix, die wir im EA verwenden werden.

Jetzt haben wir zwei Symbole, die negativ korreliert und kointegriert sind. Wir haben ein HMM für eines dieser Symbole erstellt (wir brauchen nur eines davon, weil wir wissen, dass beide Symbole korreliert sind), und da sie negativ korreliert sind, werden wir, wenn wir annehmen, dass eines der Symbole steigen wird (mit dem HMM), Nash anwenden, und wenn alles richtig ist, werden wir das andere Symbol verkaufen.

Wir könnten dies mit mehreren Symbolen tun (wenn sie korreliert sind, kaufen Sie in dieselbe Richtung oder verkaufen Sie, wenn sie negativ korreliert sind).

Aber zuerst habe ich ein Skript in Python erstellt, um zu zeigen, wie die Ergebnisse aussehen würden und um mit den versteckten Zuständen zu spielen. Dies ist das Skript:

import MetaTrader5 as mt5
import numpy as np
import pandas as pd
from hmmlearn import hmm
import matplotlib.pyplot as plt
from datetime import datetime

# Function to load matrices from the .txt file
def parse_matrix_block(lines, start_idx, matrix_type="normal"):
    matrix = []
    i = start_idx
    while i < len(lines) and not lines[i].strip().startswith("};"):
        line = lines[i].strip().replace("{", "").replace("}", "").replace(";", "")
        if line:  # Ensure the line is not empty
            if matrix_type == "covariance":
                # Split the line into elements
                elements = [float(x) for x in line.split(',') if x.strip()]
                matrix.append(elements)
            else:
                row = [float(x) for x in line.split(',') if x.strip()]  # Filter out empty values
                matrix.append(row)
        i += 1
    return np.array(matrix), i

def load_matrices(file_path):
    with open(file_path, 'r') as file:
        lines = file.readlines()
    
    transition_matrix = []
    means_matrix = []
    covariance_matrix = []
    
    i = 0
    while i < len(lines):
        line = lines[i].strip()
        
        if line.startswith("Transition Matrix:"):
            transition_matrix, i = parse_matrix_block(lines, i + 1)
            i += 1  # Move forward to avoid repeating the same block

        elif line.startswith("Means Matrix:"):
            means_matrix, i = parse_matrix_block(lines, i + 1)
            i += 1

        elif line.startswith("Covariance Matrix:"):
            covariance_matrix = []
            i += 1
            while i < len(lines) and not lines[i].strip().startswith("};"):
                block, i = parse_matrix_block(lines, i, matrix_type="covariance")
                covariance_matrix.append(block)
                i += 1
            covariance_matrix = np.array(covariance_matrix)
            covariance_matrix = covariance_matrix.reshape(-1, 3, 3)

        i += 1
    
    return transition_matrix, means_matrix, covariance_matrix

# Load the matrices from the .txt file
transition_matrix, means_matrix, covariance_matrix = load_matrices('formatted_matrices.txt')

# Connect to MetaTrader 5
if not mt5.initialize():
    print("initialize() failed, error code =", mt5.last_error())
    quit()

# Set parameters to retrieve data
symbol = "USDJPY"  # You can change to your desired symbol
timeframe = mt5.TIMEFRAME_H4  # You can change the timeframe
start_date = datetime(2024, 1, 1)
end_date = datetime.now()

# Load data from MetaTrader 5
rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
mt5.shutdown()

# Convert the data to a pandas DataFrame
data = pd.DataFrame(rates)
data['time'] = pd.to_datetime(data['time'], unit='s')
data.set_index('time', inplace=True)

# Use only the closing prices column
prices = data['close'].values.reshape(-1, 1)

# Create and configure the HMM model
n_components = len(transition_matrix)
model = hmm.GaussianHMM(n_components=n_components, covariance_type="full")
model.startprob_ = np.full(n_components, 1/n_components)  # Initial probabilities
model.transmat_ = transition_matrix
model.means_ = means_matrix
model.covars_ = covariance_matrix

# Fit the model using the loaded prices
model.fit(prices)

# Predict hidden states
hidden_states = model.predict(prices)

# Manual configuration of states
bullish_states = [2,4,5,6,8]  # States considered bullish
bearish_states = [1,3,7]  # States considered bearish
exclude_states = [0,9]  # States to exclude (neither buy nor sell)

# HMM strategy:
hmm_returns = np.zeros_like(prices)
for i in range(1, len(prices)):
    if hidden_states[i] in bullish_states:  # Buy if the state is bullish
        hmm_returns[i] = prices[i] - prices[i-1]
    elif hidden_states[i] in bearish_states:  # Sell if the state is bearish
        hmm_returns[i] = prices[i-1] - prices[i]
    # If the state is in exclude_states, do nothing

# Buy and hold strategy (holding)
holding_returns = prices[-1] - prices[0]

# Plot results
plt.figure(figsize=(7, 8))
plt.plot(data.index, prices, label='Price of '+str(symbol), color='black', linestyle='--')
plt.plot(data.index, np.cumsum(hmm_returns), label='HMM Strategy', color='green')
plt.axhline(holding_returns, color='blue', linestyle='--', label='Buy and Hold Strategy (Holding)')
plt.title('Backtesting Comparison: HMM vs Holding and Price')
plt.legend()
plt.savefig("playground.png")

# Print accumulated returns of both strategies
print(f"Accumulated returns of the HMM strategy: {np.sum(hmm_returns)}")
print(f"Accumulated returns of the Holding strategy: {holding_returns[0]}")

Schauen wir uns dieses Skript an. Es öffnet die .txt-Datei mit den Matrizen, lädt die Daten vom MetaTrader 5 für dieses Symbol herunter und verwendet Daten vom letzten Datum, das wir in den anderen Skripten verwendet haben, bis heute, um zu sehen, wie das HMM funktioniert. Die Ergebnisse werden in einer .png-Datei angezeigt, und wir können die Zustände ändern. Schauen wir uns die Ergebnisse an, wenn wir alle Zustände verwenden, wie es das zweite Skript vorschreibt:

Aus dem zweiten Skript:

Description of Hidden States:
State 0: Not present (State ID: 0)
State 1: Downtrend (State ID: 1)
State 2: Uptrend (State ID: 2)
State 3: Downtrend (State ID: 3)
State 4: Uptrend (State ID: 4)
State 5: Uptrend (State ID: 5)
State 6: Uptrend (State ID: 6)
State 7: Downtrend (State ID: 7)
State 8: Uptrend (State ID: 8)
State 9: Not present (State ID: 9)

Hier ist das Ergebnis:

Accumulated returns of the HMM strategy: -1.0609999999998365
Accumulated returns of the Holding strategy: 5.284999999999997

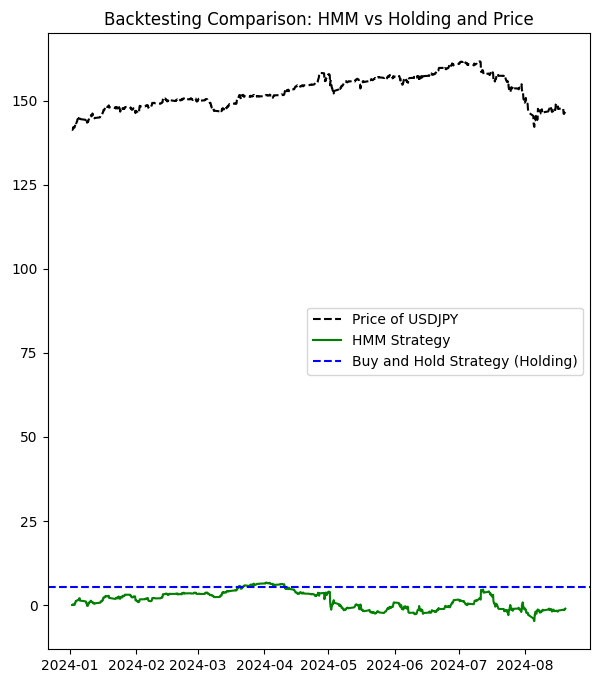
Wie Sie sehen können, ist diese Strategie nicht wirklich gut. Spielen wir also mit den ausgeblendeten Zuständen (die wir mithilfe des Balkendiagramms auswählen, wobei wir den siebten Zustand ausschließen):

# Manual configuration of states
bullish_states = [2,4,5,6,8]  # States considered bullish
bearish_states = [1,3]  # States considered bearish
exclude_states = [0,7,9]  # States to exclude (neither buy nor sell)

Accumulated returns of the HMM strategy: 7.978000000000122
Accumulated returns of the Holding strategy: 5.284999999999997

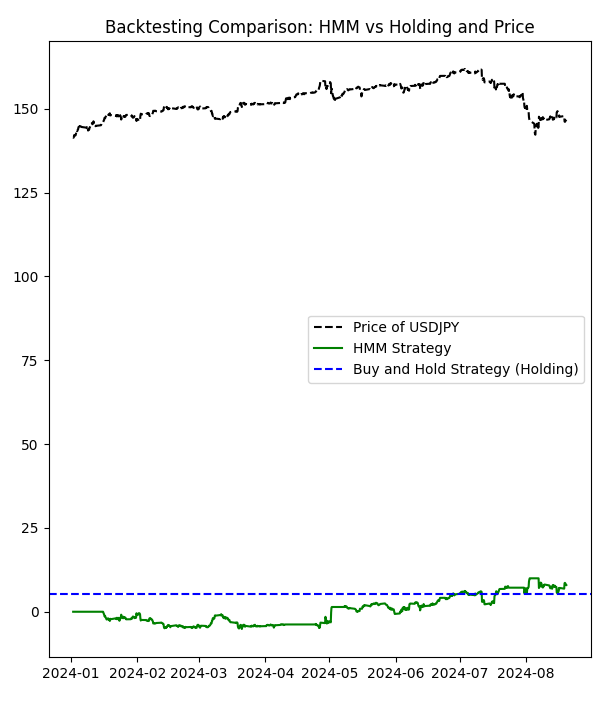
Daraus haben wir gelernt, dass wir eine profitablere Strategie verfolgen können, wenn wir nicht die schlechtesten versteckten Zustände verwenden.

Auch hier könnte die Anwendung von Deep Learning helfen, mehr Muster des Ausgangssymbols (in diesem Fall USDJPY) zu erkennen. Vielleicht können wir damit ein anderes Mal experimentieren.

Implementation in MQL5

Der Nash Expert Advisor (EA) ist ein hochentwickeltes algorithmisches Handelssystem, das für die Plattform MetaTrader 5 entwickelt wurde. Im Kern verwendet der EA einen Multi-Strategie-Ansatz, der Hidden-Markov-Modelle (HMM), Log-Likelihood-Analysen, Trendstärkebewertungen und Nash-Gleichgewichtskonzepte einbezieht, um Handelsentscheidungen auf dem Devisenmarkt zu treffen.

Der EA beginnt mit der Initialisierung wichtiger Parameter und Indikatoren. Es richtet die wesentlichen gleitenden Durchschnitte (EMAs), den Relative Strength Index (RSI), die Average True Range (ATR) und die Bollinger Bänder ein. Diese technischen Indikatoren bilden die Grundlage für die Marktanalyse des EA. Der Initialisierungsprozess umfasst auch die Einstellung der Parameter des Hidden Markov Model, die für die Vorhersagefähigkeiten des EA von zentraler Bedeutung sind.

Eines der wichtigsten Merkmale des EA ist sein System zur Erkennung von Marktregimen. Dieses System nutzt sowohl die HMM- als auch die Log-Likelihood-Methode, um den aktuellen Marktzustand in drei Kategorien zu klassifizieren: Aufwärtstrend, Abwärtstrend, oder nicht vorhanden (neutral). Der Prozess der Regimeerkennung umfasst komplexe Berechnungen von Emissionswahrscheinlichkeiten und Zustandsübergängen, die einen differenzierten Blick auf die Marktbedingungen ermöglichen.

Der EA implementiert vier verschiedene Handelsstrategien: HMM-basiert, Log-Likelihood-basiert, Trendstärke und Nash-Equilibrium. Jede Strategie erzeugt ihr eigenes Handelssignal, das dann gewichtet und zu einer umfassenden Handelsentscheidung kombiniert wird. Die Strategie des Nash-Gleichgewichts zielt insbesondere darauf ab, ein optimales Gleichgewicht zwischen den anderen Strategien zu finden, was zu robusteren Handelsentscheidungen führen kann.

Das Risikomanagement ist ein wichtiger Aspekt der Nash EA. Es umfasst Funktionen wie die dynamische Losgröße auf der Grundlage von Kontostand und Strategieperformance, Stop-Loss- und Take-Profit-Levels sowie einen Trailing-Stop-Mechanismus. Diese Instrumente des Risikomanagements zielen darauf ab, das Kapital zu schützen und gleichzeitig potenzielle Gewinne unter günstigen Marktbedingungen zu ermöglichen.

Der EA enthält auch eine Backtesting-Funktion, die es Händlern ermöglicht, seine Leistung anhand historischer Daten zu bewerten. Diese Funktion berechnet verschiedene Leistungskennzahlen für jede Strategie, einschließlich Gewinn, Gesamtzahl der Trades, Gewinntrades und Gewinnrate. Dank dieser umfassenden Testmöglichkeiten können Händler die Parameter des EAs für eine optimale Leistung feinabstimmen.

In seiner Hauptoperationsschleife verarbeitet der Nash EA bei jedem neuen Kursbalken Marktdaten. Es berechnet Marktregime neu, aktualisiert Strategiesignale und trifft Handelsentscheidungen auf der Grundlage des kollektiven Outputs aller aktivierten Strategien. Der EA ist so konzipiert, dass er Positionen in Paaren eröffnet und möglicherweise gleichzeitig mit dem Primärsymbol und dem EURCHF handelt, was Teil einer Absicherungs- oder Korrelationsstrategie sein könnte.

Schließlich enthält der EA robuste Funktionen zur Fehlerbehandlung und -protokollierung. Es prüft kontinuierlich, ob die Indikatorwerte gültig sind, stellt sicher, dass der Handel gemäß den Terminal- und Experteneinstellungen zulässig ist, und erstellt detaillierte Protokolle über seine Operationen und Entscheidungsprozesse. Dieses Maß an Transparenz erleichtert die Fehlersuche und Leistungsanalyse.

Wir werden uns nun einige wichtige Funktionen und Nash-Gleichgewichte ansehen:

Die wichtigsten Funktionen, die zur Umsetzung des Nash-Gleichgewichtskonzepts in diesem Expert Advisor (EA) verwendet werden, sind:

1. CalculateStrictNashEquilibrium()

Dies ist die Hauptfunktion zur Berechnung des strengen Nash-Gleichgewichts. Hier ist die Umsetzung:

void CalculateStrictNashEquilibrium()
{
   double buySignal = 0;
   double sellSignal = 0;

   // Sum the weighted signals of the enabled strategies
   for(int i = 0; i < 3; i++) // Consider only the first 3 strategies for Nash equilibrium
   {
      if(strategies[i].enabled)
      {
         buySignal += strategies[i].weight * (strategies[i].signal > 0 ? 1 : 0);
         sellSignal += strategies[i].weight * (strategies[i].signal < 0 ? 1 : 0);
      }
   }

   // If there's a stronger buy signal than sell signal, set Nash Equilibrium signal to buy
   if(buySignal > sellSignal)
   {
      strategies[3].signal = 1; // Buy signal
   }
   else if(sellSignal > buySignal)
   {
      strategies[3].signal = -1; // Sell signal
   }
   else
   {
      // If there's no clear signal, force a decision based on an additional criterion
      double closePrice = iClose(_Symbol, PERIOD_CURRENT, 0);
      double openPrice = iOpen(_Symbol, PERIOD_CURRENT, 0);
      strategies[3].signal = (closePrice > openPrice) ? 1 : -1;
   }
}

Erläuterung:

• Diese Funktion berechnet Kauf- und Verkaufssignale auf der Grundlage der gewichteten Signale der ersten drei Strategien.
• Er vergleicht die Kauf- und Verkaufssignale, um das Nash-Gleichgewicht zu bestimmen.
• Wenn die Signale gleich sind, trifft er eine Entscheidung auf der Grundlage der aktuellen Kursrichtung.

2. SimulateTrading()

Diese Funktion ist zwar nicht ausschließlich für das Nash-Gleichgewicht gedacht, implementiert aber die Handelslogik, die das Nash-Gleichgewicht beinhaltet:

void SimulateTrading(MarketRegime actualTrend, datetime time, string symbol)
{
   double buySignal = 0;
   double sellSignal = 0;

   for(int i = 0; i < ArraySize(strategies); i++)
   {
      if(strategies[i].enabled)
      {
         if(strategies[i].signal > 0)
            buySignal += strategies[i].weight * strategies[i].signal;
         else if(strategies[i].signal < 0)
            sellSignal -= strategies[i].weight * strategies[i].signal;
      }
   }

   // ... (code to simulate trades and calculate profits)
}

Erläuterung:

• Diese Funktion simuliert den Handel auf der Grundlage von Signalen aus allen Strategien, einschließlich der Nash-Gleichgewichtsstrategie.
• Es berechnet gewichtete Kauf- und Verkaufssignale für alle aktivierten Strategien.

3. OnTick()

In der Funktion OnTick() ist die Logik zur Ausführung von Handelsgeschäften auf der Grundlage des Nash-Gleichgewichts implementiert:

void OnTick()
{
   // ... (other code)

   // Check if the Nash Equilibrium strategy has generated a signal
   if(strategies[3].enabled && strategies[3].signal != 0)
   {
      if(strategies[3].signal > 0)
      {
         OpenBuyOrder(strategies[3].name);
      }
      else if(strategies[3].signal < 0)
      {
         OpenSellOrder(strategies[3].name);
      }
   }

   // ... (other code)
}

Erläuterung:

• Diese Funktion prüft, ob die Strategie des Nash-Gleichgewichts (die 3. Strategie im Strategien-Array) aktiviert ist und ein Signal erzeugt hat.
• Liegt ein Kaufsignal vor (Signal > 0), wird ein Kaufauftrag eröffnet.
• Liegt ein Verkaufssignal vor (Signal < 0), wird ein Verkaufsauftrag eröffnet.

Zusammenfassend lässt sich sagen, dass das Nash-Gleichgewicht als eine der Handelsstrategien in diesem EA implementiert ist. Die Funktion CalculateStrictNashEquilibrium() bestimmt das Nash-Gleichgewichtssignal auf der Grundlage der Signale von anderen Strategien. Dieses Signal wird dann in der Funktion OnTick() verwendet, um Handelsentscheidungen zu treffen. Bei der Umsetzung wird versucht, ein Gleichgewicht zwischen verschiedenen Strategien zu finden, um solidere Handelsentscheidungen zu treffen.

Dieser Ansatz zur Umsetzung eines Nash-Gleichgewichts in einer Handelsstrategie ist eine interessante Anwendung der Spieltheorie auf die Finanzmärkte. Es wird versucht, eine optimale Strategie zu finden, indem die Wechselwirkungen zwischen verschiedenen Handelssignalen berücksichtigt werden, was der Suche nach einem Gleichgewicht in einem Spiel mit mehreren Spielern entspricht, bei dem jeder „Spieler“ eine andere Handelsstrategie vertritt.

DetectMarketRegime Funktion: Diese Funktion ist für den Entscheidungsprozess der EA von entscheidender Bedeutung. Sie analysiert die aktuellen Marktbedingungen anhand technischer Indikatoren und komplexer statistischer Modelle, um die Marktordnung zu bestimmen.

void DetectMarketRegime(MarketRegime &hmmRegime, MarketRegime &logLikelihoodRegime)
{
    // Calculate indicators
    double fastEMA = iMAGet(fastEMAHandle, 0);
    double slowEMA = iMAGet(slowEMAHandle, 0);
    double rsi = iRSIGet(rsiHandle, 0);
    double atr = iATRGet(atrHandle, 0);
    double price = SymbolInfoDouble(_Symbol, SYMBOL_BID);

    // Calculate trend strength and volatility ratio
    double trendStrength = (fastEMA - slowEMA) / slowEMA;
    double volatilityRatio = atr / price;

    // Normalize RSI
    double normalizedRSI = (rsi - 50) / 25;

    // Calculate features for HMM
    double features[3] = {trendStrength, volatilityRatio, normalizedRSI};

    // Calculate log-likelihood and HMM likelihoods
    double logLikelihood[10];
    double hmmLikelihoods[10];
    CalculateLogLikelihood(features, symbolParams.emissionMeans, symbolParams.emissionCovs);
    CalculateHMMLikelihoods(features, symbolParams.emissionMeans, symbolParams.emissionCovs, symbolParams.transitionProb, 10, hmmLikelihoods);

    // Determine regimes based on maximum likelihood
    int maxLogLikelihoodIndex = ArrayMaximum(logLikelihood);
    int maxHmmLikelihoodIndex = ArrayMaximum(hmmLikelihoods);

    logLikelihoodRegime = InterpretRegime(maxLogLikelihoodIndex);
    hmmRegime = InterpretRegime(maxHmmLikelihoodIndex);

    
    // ... (confidence calculation code)
}

Diese Funktion kombiniert technische Indikatoren mit Hidden-Markov-Modellen und Log-Likelihood-Analysen, um das aktuelle Marktregime zu bestimmen. Es handelt sich dabei um einen ausgefeilten Ansatz zur Marktanalyse, der einen differenzierten Blick auf die Marktbedingungen ermöglicht.

CalculateStrategySignals Funktion: Diese Funktion berechnet Handelssignale für jede der EA-Strategien auf der Grundlage des aktuellen Marktregimes und technischer Indikatoren.

void CalculateStrategySignals(string symbol, datetime time, MarketRegime hmmRegime, MarketRegime logLikelihoodRegime)
{
    if(strategies[0].enabled) // HMM Strategy
    {
        CalculateHMMSignal();
    }
    
    if(strategies[1].enabled) // LogLikelihood Strategy
    {
        CalculateLogLikelihoodSignal();
    }
    
    if(strategies[2].enabled) // Trend Strength
    {
        double trendStrength = CalculateTrendStrength(PERIOD_CURRENT);
        strategies[2].signal = NormalizeTrendStrength(trendStrength);
    }
    
    if(strategies[3].enabled) // Nash Equilibrium
    {
        CalculateStrictNashEquilibrium();
    }
}

Diese Funktion berechnet Signale für jede aktivierte Strategie und integriert verschiedene Analysemethoden, um eine umfassende Handelsentscheidung zu treffen.

SimulateTrading Funktion: Diese Funktion simuliert den Handel auf der Grundlage der berechneten Signale und aktualisiert die Leistungskennzahlen der einzelnen Strategien.

void SimulateTrading(MarketRegime actualTrend, datetime time, string symbol)
{
    double buySignal = 0;
    double sellSignal = 0;

    for(int i = 0; i < ArraySize(strategies); i++)
    {
        if(strategies[i].enabled)
        {
            if(strategies[i].signal > 0)
                buySignal += strategies[i].weight * strategies[i].signal;
            else if(strategies[i].signal < 0)
                sellSignal -= strategies[i].weight * strategies[i].signal;
        }
    }

    // Simulate trade execution and calculate profits
    // ... (trade simulation code)

    // Update strategy performance metrics
    // ... (performance update code)
}

Diese Funktion ist für das Backtesting und die Bewertung der Leistung des EAs von entscheidender Bedeutung. Es simuliert den Handel auf der Grundlage der berechneten Signale und aktualisiert die Leistungskennzahlen der einzelnen Strategien.

CalculateHMMLikelihoods Funktion: Diese Funktion berechnet die Wahrscheinlichkeiten der verschiedenen Marktzustände unter Verwendung des Hidden Markov Model.

void CalculateHMMLikelihoods(const double &features[], const double &means[], const double &covs[], const double &transitionProb[], int numStates, double &hmmLikelihoods[])
{
    // Initialize and calculate initial likelihoods
    // ... (initialization code)

    // Forward algorithm to calculate HMM likelihoods
    for(int t = 1; t < ArraySize(features) / 3; t++)
    {
        // ... (HMM likelihood calculation code)
    }

    // Normalize and validate likelihoods
    // ... (normalization and validation code)
}

Diese Funktion implementiert den Vorwärtsalgorithmus von Hidden Markov Modellen, um die Wahrscheinlichkeit verschiedener Marktzustände zu berechnen. Dabei handelt es sich um eine hochentwickelte Methode zur Vorhersage des Marktverhaltens auf der Grundlage beobachteter Merkmale.

Diese Funktionen bilden den Kern der Analyse- und Entscheidungsprozesse des Nash Expert Advisors. Die Stärke des EA liegt in der Kombination von traditioneller, technischer Analyse mit fortschrittlichen, statistischen Methoden wie Hidden Markov Models und Nash Equilibrium Konzepten. Dieser Multi-Strategie-Ansatz, gepaart mit robusten Backtesting- und Risikomanagement-Funktionen, macht es zu einem potenziell leistungsstarken Tool für den algorithmischen Handel auf dem Devisenmarkt.

Der wichtigste Aspekt von diesem EA ist der adaptiver Charakter. Durch die kontinuierliche Bewertung der Marktbedingungen und die Anpassung der Strategiegewichtung auf der Grundlage der Performance soll die Effektivität unter verschiedenen Marktbedingungen erhalten bleiben. Es ist jedoch wichtig zu wissen, dass solche Systeme zwar hochentwickelt sind, aber eine sorgfältige Überwachung und regelmäßige Neukalibrierung erfordern, um sicherzustellen, dass sie in einem sich ständig verändernden Marktumfeld effektiv bleiben.

Ergebnisse

Mit diesen Einstellungen

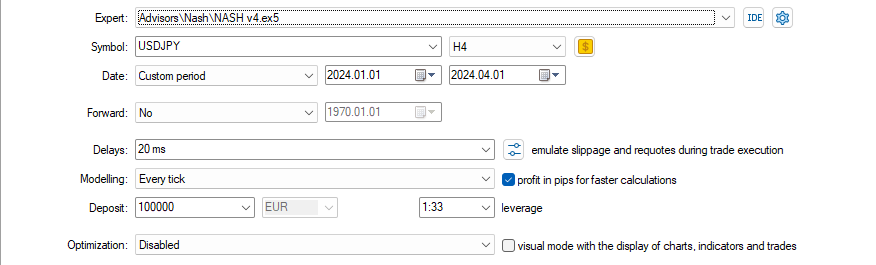
und diese Eingaben

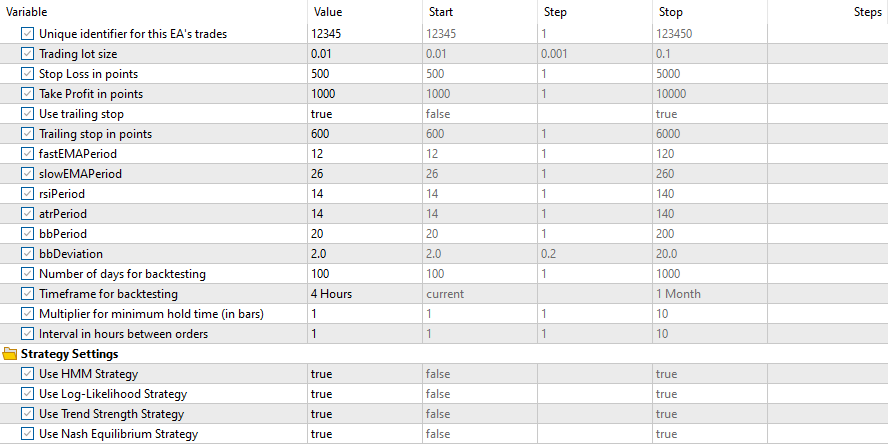
Die Ergebnisse für alle Strategien waren wie folgt:

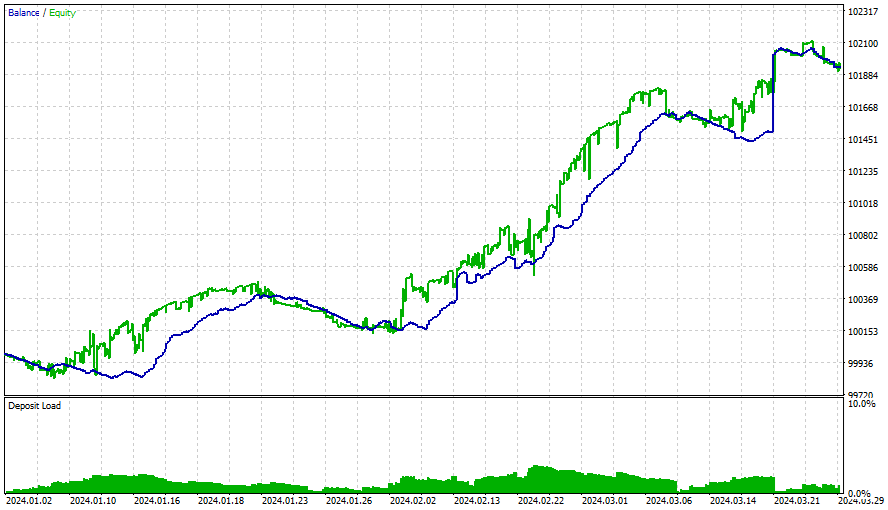
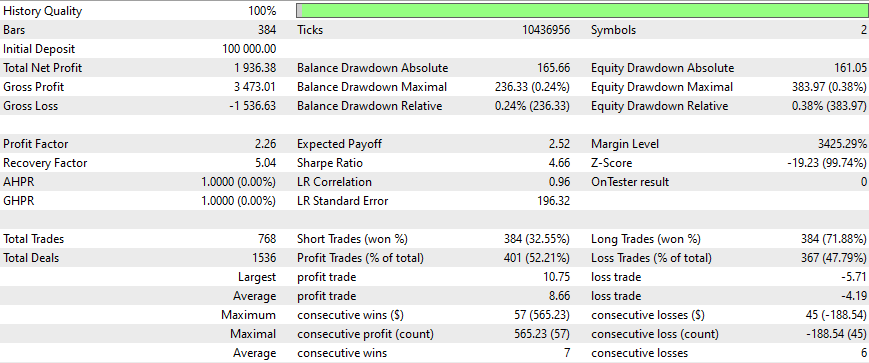
Nach diesem Zeitraum gingen die Gewinne zurück, und die Optimierung hätte alle 3 Monate durchgeführt werden müssen (mit all diesen Ausgangsbedingungen). Die Strategien sind einfach und verwenden einen Trailing-Stop (der sehr einfach und fest ist). Bessere Ergebnisse können mit mehr Optimierungen, mit neueren Matrizen und mit besseren und ausgefeilteren Strategien erzielt werden. Wir müssen auch in Betracht ziehen, diesen EA um Sentiment-Analyse und Deep Learning zu erweitern, ohne dabei das zuvor Gesagte zu vergessen.

Alle Strategien brauchen Nash, um zu funktionieren.

Schlussfolgerung

Die Überschneidung von Spieltheorie und Handel bietet spannende Möglichkeiten zur Verbesserung von Marktstrategien. Durch die Anwendung der Nash-Gleichgewichtstheorie können Händler kalkuliertere Entscheidungen treffen, indem sie die möglichen Aktionen anderer Marktteilnehmer berücksichtigen. Dieser Artikel beschreibt, wie diese Konzepte mit Python und MetaTrader 5 umgesetzt werden können, und bietet damit ein leistungsstarkes Instrumentarium für alle, die ihren Handelsansatz verbessern möchten. Da sich die Märkte weiter entwickeln, könnte die Integration mathematischer Theorien wie des Nash-Gleichgewichts ein entscheidendes Unterscheidungsmerkmal für den beständigen Erfolg im Handel sein.

Ich hoffe, es hat Ihnen Spaß gemacht, diesen Artikel zu lesen oder wiederzugeben, und ich hoffe, dass er für Ihren eigenen EA hilfreich sein wird. Es ist ein interessantes Thema, und ich hoffe, dass es Ihre Erwartungen erfüllt hat und Ihnen so gut gefällt, wie mir die Erstellung des Artikels gefallen hat.