知っておくべきMQL5ウィザードのテクニック（第55回）：PER付きSAC

ニューラルネットワークモデルの複雑さが増している背景には、大量のデータを処理する能力の進化があります。従来の機械学習は効率性に課題がありますが、DeepSeek、Grok、ChatGPTのようなプラットフォームに代表されるニューラルネットワークは、非常に強力なソリューションを提供しています。

しかし、こうしたモデルの訓練には課題もあります。特に履歴データが限られている場合には、過学習のリスクが高まり、モデルが意味のあるパターンではなくノイズを学習してしまう可能性があります。従来の学習手法では損失関数の最小化が優先されがちで、それが汎化性能の低下につながることがあります。

強化学習(RL)はこれに対して、活用（重みの最適化）と探索（代替手段の試行）のバランスを取ることで対応します。PERのような手法は、学習の効率性を高め、データが希少な状況（たとえば経済指標が月次でしか発表されないような取引分野）においても効果を発揮します。

強化学習を成功させるための鍵となるのは、効果的な報酬関数の設計、適切なアルゴリズムの選択、および価値ベース（Q-Learning、DQNなど）と方策ベース（PPO、TRPOなど）のどちらを使うかの判断です。Actor-Critic系の手法（例：A3C、SAC）は、安定性と効率性のバランスをとります。オンポリシー手法（PPO、A3Cなど）は安定した学習を可能にし、オフポリシー手法（DQN、SACなど）はデータ効率を最大化します。

強化学習の適応性は、従来の機械学習パイプラインに対する有効な補完手段となります。特に、限られたデータで複雑なモデルを訓練する場合には、損失最小化よりも重みの更新を優先することで、より良い汎化性能とロバスト性を実現できます。

Prioritized Experience Replay

Prioritized Experience Replay (PER)バッファと、ランダムサンプリング用の一般的なリプレイバッファは、どちらもDQNやSACといったオフポリシーの強化学習アルゴリズムで使用されます。これらは、過去の経験を保存し、そこからサンプリングする仕組みを提供する点では共通していますが、PERは過去の経験をどのように優先付けしてサンプリングするかという点で一般的なリプレイバッファと異なります。 

一般的なリプレイバッファでは、経験は一様かつランダムにサンプリングされます。つまり、過去のどの経験も、その重要性や学習への貢献度にかかわらず、同じ確率で選ばれるということです。一方、PERでは、過去の経験はその「優先度」に基づいてサンプリングされます。この優先度は、時間差分誤差の大きさによって定量化されることが一般的です。この誤差は、学習における「重要性」の指標と見なされ、高い誤差値を持つ経験は、より頻繁にサンプリングされます。この優先度の割り当ては、比例型または順位型のアプローチで実装されることがあります。

一方で、一般的なリプレイバッファはバイアスを導入しませんが、PERはこの優先度付けによってバイアスを導入します。このバイアスが学習過程を不公平に歪めてしまう可能性があるため、PERでは重要度サンプリング重みを使用して、各サンプルが学習に与える影響を補正します。一般的なリプレイバッファは、内部処理が少ないためサンプル効率が高いという利点があります。それに対して、PERはより多くの処理を必要としますが、より焦点を絞った意味のある学習を実現する点で優れています。

このように、PERの実装は一般的なリプレイバッファに比べて複雑であることは言うまでもありません。ここで強調すべきは、PERが「sum-tree」と呼ばれる優先度付きキューを管理するための追加クラスを必要とする点です。このデータ構造を用いることで、優先度に応じた効率的な経験のサンプリングが可能になります。PERは、より情報量が多い、あるいは難易度の高い経験に焦点を当てることで、より早い収束と高い性能をもたらす傾向があります。

モデルでの実装

私たちのPERクラス（Pythonで実装）では、初期化時にコンストラクタのパラメータ、特にmodeパラメータの検証をおこなっています。これはC言語やMQL5では標準的に実現できない機能だと記憶しています。この__init__関数は次のように宣言します。

        def __init__(self, capacity, alpha=0.6, beta=0.4, beta_increment=0.001, mode='proportional'):
                self.capacity = capacity
                self.alpha = alpha
                self.beta = beta
                self.beta_increment = beta_increment
                self.mode = mode

                if mode == 'proportional':
                        self.tree = SumTree(capacity)
                elif mode == 'rank':
                        self.priorities = []
                        self.data = []
                else:
                        raise ValueError("Invalid mode. Choose 'proportional' or 'rank'.")

クラスを定義したら、そこに含めるべき重要な関数の1つが、経験をバッファに追加するためのメソッドです。この機能は、以下のように実装しています。 

    def add(self, error, sample):
        p = self._get_priority(error)
        if self.mode == 'proportional':
            self.tree.add(p, sample)
        elif self.mode == 'rank':
            heapq.heappush(self.priorities, -p)
            if len(self.data) < self.capacity:
                self.data.append(sample)
            else:
                heapq.heappop(self.priorities)
                heapq.heappush(self.data, sample)

この経験の追加処理において重要なのは、サンプリングのモードです。なぜなら、誤差に基づいた比例サンプリングをおこなう場合には、単にその経験をsum-treeに追加するだけでよいのに対し、誤差の大きさによるランクを基に選択する場合は、heapqモジュールを用いてヒープ構造を更新する必要があるからです。これは、先述の通り上記のサンプルでおこなっています。したがって、sum-treeクラスは比例サンプリングで使用され、ランクベースのサンプリングでは使用されません。実装方法は次のとおりです。

class SumTree:
    def __init__(self, capacity):
        self.capacity = capacity
        self.tree = np.zeros(2 * capacity - 1)
        self.data = np.zeros(capacity, dtype=object)
        self.write = 0
        self.n_entries = 0

    def _propagate(self, idx, change):
        parent = (idx - 1) // 2
        self.tree[parent] += change
        if parent != 0:
            self._propagate(parent, change)

    def _retrieve(self, idx, s):
        left = 2 * idx + 1
        right = left + 1

        if left >= len(self.tree):
            return idx

        if s <= self.tree[left]:
            return self._retrieve(left, s)
        else:
            return self._retrieve(right, s - self.tree[left])

    def total(self):
        return self.tree[0]

    def add(self, p, data):
        idx = self.write + self.capacity - 1

        self.data[self.write] = data
        self.update(idx, p)

        self.write += 1
        if self.write >= self.capacity:
            self.write = 0

        if self.n_entries < self.capacity:
            self.n_entries += 1

    def update(self, idx, p):
        change = p - self.tree[idx]
        self.tree[idx] = p
        self._propagate(idx, change)

    def get(self, s):
        idx = self._retrieve(0, s)
        data_idx = idx - self.capacity + 1
        return (idx, self.tree[idx], self.data[data_idx])

この重要なクラスが定義されたことで、次に不可欠なのは、PERクラスに含まれるsample関数、すなわちサンプリング処理そのものです。 

def sample(self, batch_size):
        batch = []
        idxs = []
        segment = self.tree.total() / batch_size if self.mode == 'proportional' else len(self.data) / batch_size
        priorities = []

        self.beta = np.min([1., self.beta + self.beta_increment])

        for i in range(batch_size):
            a = segment * i
            b = segment * (i + 1)

            if self.mode == 'proportional':
                s = random.uniform(a, b)
                (idx, p, data) = self.tree.get(s)
                priorities.append(p)
                batch.append(data)
                idxs.append(idx)
            elif self.mode == 'rank':
                idx = random.randint(0, len(self.data) - 1)
                priorities.append(-self.priorities[idx])
                batch.append(self.data[idx])
                idxs.append(idx)

        sampling_probabilities = np.array(priorities) / self.tree.total() if self.mode == 'proportional' else np.array(priorities) / sum(self.priorities)
        is_weights = np.power(len(self.data) * sampling_probabilities, -self.beta)
        is_weights /= is_weights.max()

        return batch, idxs, is_weights

ここでも再び重要になるのが、サンプリングのモード（比例ベースか順位ベースか）です。この2つのアプローチは、いずれもTD誤差を考慮して各経験に優先度を割り当てますが、その扱い方には微妙な違いがあります。比例サンプリングではTD誤差の「大きさ」が用いられ、ランクベースサンプリングではTD誤差の「順位」が使用されます。TD誤差とは、ある経験の出力と実際または目標の値との違いのことを指します。この誤差は生のままでは重み付けに使われず、代わりに優先度の値に変換されて使用されます。その変換は以下のコードで示されています。

def _get_priority(self, error):
        return (error + 1e-5) ** self.alpha

この優先度の値こそが、比例サンプリングではその大きさ、ランクサンプリングではその順位として使用され、モデルを訓練するために経験を選択する際に用いられます。PERは、Shaulらによって2015年に提案されました。  優先度の高い経験は、より頻繁にサンプリングされるため、強化学習環境においてサンプル効率と学習速度の向上が期待できます。なお、これらの優先度は学習後に更新されます。また、優先度に基づく非一様なサンプリングによって生じるバイアスを補正するために、重要度サンプリング重みが使われます。これは、先述したPERクラスのsample関数の中で示されています。それでは、これら2種類のサンプリングモードについて詳しく見ていきましょう。

比例優先度付け

上述の通り、優先度は時間差分誤差(|δ|)に比例します。したがって、ある経験iの優先度pₖは次のように計算されます。

pᵢ = |δᵢ| + ε

ここでε > 0は小さな定数であり、すべての経験がゼロの優先度にならないようにするために加えられます。このとき、経験iのサンプリング確率は以下のように定義されます。

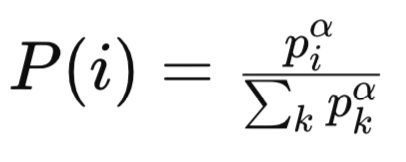
ここで

• pᵢは、リプレイバッファ内のi番目の経験に割り当てられた優先度であり、通常はその経験のTD誤差の絶対値に基づきます。TD誤差が大きいほど「学習に重要である」と見なされ、より高い優先度が付けられます。

• αは優先度の強さを調整するハイパーパラメータです。αが0のとき、すべての経験が一様にサンプリングされ（＝通常のリプレイバッファ）、αが1に近づくにつれて、優先度に強く依存したサンプリングがおこなわれるようになります。

• Σₖ pₖ^αは正規化項であり、リプレイバッファ内のすべての経験に対する優先度をα乗したものの総和です。この項によって、サンプリング確率の合計が1になるように調整されます。

• P(i)はi番目の経験がサンプリングされる確率であり、その経験の優先度(pᵢ^α)に比例し、全体の優先度(pₖ^α)の総和によって正規化された値です。

Sum Treeあるいは同様のデータ構造を用いることで、pᵢ^αに比例して経験を効率的にサンプリングすることが可能になります。比例優先度付けにおけるサンプリング分布は連続的であり、TD誤差の大きさに直接結びついています。TD誤差が大きい経験は非常に高い優先度を持つ傾向があり、その結果として重い尾を持つ分布が形成されます。

この性質は、ある特定の経験が（もしそのTD誤差が外れ値であれば）過剰に頻繁にサンプリングされるという問題を引き起こす可能性があります。一方で、誤差の小さな経験はほとんどサンプリングされないという事態にもつながります。訓練中の誤差に対する感度はタスクやフェーズによって異なる可能性がありますが、TD誤差の外れ値に対する脆弱性は比例サンプリングの課題です。大きな値がサンプリング分布を支配してしまうのです。

たとえば、ある経験の出力とターゲットの差が1000で、他のすべての経験ではその差が1だったとしましょう。このような場合、当然ながらその大きな値を持つ経験は不均衡に頻繁にサンプリングされることになります。この特性は、報酬やQ値にばらつきの大きいデータ環境では、ノイズや外れ値に過剰に適応してしまうリスクがあります。これを緩和する手段として考えられるのが、TD誤差のクリッピングや正規化です。以下にその一例を示します。

pᵢ = min( |δᵢ|, δₘₐₓ ) + ε

本質的には、この式では各経験の優先度が「その経験自身のTD誤差」と「サンプル区間内におけるすべての経験の最大TD誤差」のうち小さい方に、さらにゼロにならないように小さな正の値εを加えたものに設定されます。Sum Treeを使った場合の動作における計算量は明快で、経験ごとの優先度の計算はO(1)、サンプリングや優先度の更新操作はO(log n)（nはバッファサイズ）となります。ソートやランク付けの追加コストが不要なため、更新処理において計算効率に優れます。

一方で、比例優先度付け(Proportional Prioritization: PP)は、訓練段階においてTD誤差の変動が大きい場合、サンプリング分布が急激に変化してしまうため、学習が不安定になる可能性があります。また、ハイパーパラメータに対しても敏感であるため、αやεの値は、探索と活用のバランスを考慮しながら慎重に調整する必要があります。PPは、TD誤差が「良好な性質」を持ち、かつそれが学習価値を正しく反映しているようなタスクでは、高速な収束が期待できる一方で、ノイズの多い環境や非定常な環境ではうまく機能しづらくなります。

PPは、TD誤差が良好に分布しており、その大きさが学習の可能性や価値を直接的に示しているタスクに適しています。ノイズが少なく、Q値が安定していて、TD誤差が重要な経験を正確に反映している環境では、PPは非常に効果的です。たとえば、報酬構造が安定しているAtariゲームや、価値関数が滑らかな連続制御タスクなどがその例です。

しかし、PPのサンプリング分布は裾が重くなりやすいため、重要度サンプリング重みに大きなばらつきが生じます。サンプリング確率P(i)が小さい経験には、対応する補正重みwᵢが大きくなりがちで、これが勾配を過剰に強調してしまい、学習を不安定にする可能性があります。したがって、バイアス補正と安定性のバランスを保つには、βの値を慎重に調整する必要があります。

要するに、PPはTD誤差がよく制御され、学習のポテンシャルと強く相関している場合に特に適しています。ソートやランク付けの処理が不要なため、計算効率にも優れており、大規模なタスクにおいて有利です。ただし、外れ値の影響やα、β、εといったハイパーパラメータへの感度が高いため、安定した性能を引き出すには丁寧なチューニングが欠かせません。

ランクベースの優先順位付け

このモードでは、優先度はTD誤差を大きさ順に並べたリスト内でのランク（順位）に基づいて決定されます。経験iの順位は、すべての経験をTD誤差の絶対値の降順で並べ替えることによって設定されます。なぜ降順かというと、直感的にこの並びが経験の重要度を示しているからです。リストの上位にあるほど、その経験はより重要と見なされます。次に計算の観点からも、訓練で最も参照される経験がヒープ内で低いインデックスに位置するほうが効率的であり、アルゴリズムがヒープ全体を探索せずに重要な経験にアクセスできるため合理的です。経験iの優先度は通常、次のように計算されます。

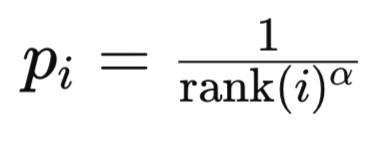
ここで

rank(i)は経験iの順位

αは優先度の強さを制御するハイパーパラメータ

サンプリング確率は、先に説明した比例優先度付けの場合と類似した式を用います。

ランクベース優先度付け(RP)では、サンプリング分布は離散的でランクに基づいています。これによりTD誤差の絶対的なスケールへの感度が低くなります。経験は誤差の大きさではなくランクに基づいて選ばれるため、経験間の優先度の差が「標準化」されており（例：1/1、1/2、1/3、…）、より均一な分布になります。さらに、RPは最高優先度が常に1/1に固定されるため、誤差の大きい外れ値に過剰適合するリスクが低く、ロバスト性があります。ただし、このロバスト性は、ランクベースの優先度関数が急速に減衰する場合に、非常に大きなTD誤差を持つ重要な経験が十分にサンプリングされないことによるアンダーサンプリングの問題により相殺されることがあります。

しかしながら、重要な経験のアンダーサンプリングのリスクに加え、RPの最大の欠点は計算コストの高さにあります。全バッファをソートしてランクを決定するには、サイズnのバッファに対して計算量はO(n log n)となります。実際には、二分探索木やヒープのような整列済みのデータ構造を用いてソートを回避できますが、優先度の更新には依然として経験ごとにO(log n)の計算が必要です。サンプリングと更新も比例優先度付けと同様にO(log n)でおこなわれます。つまり、RPはPPと比較して計算負荷がかなり高くなります。

学習時には、RPはサンプリング分布がTD誤差の変動に対して鈍感であるため、より安定した訓練を提供します。また、ランクは相対的でノイズや外れ値の影響が小さいため、時間を通じて一貫したサンプリング確率を保ちやすいです。絶対的なTD誤差が訓練に非常に重要なタスクでは、RPは大きな誤差を積極的に優先しないため、収束が遅くなることがあります。ハイパーパラメータの調整も比較的容易で、これはランクベースの優先度関数がスケールに対してあまり敏感でないためです。

RPは報酬がまばらな環境や、遅延報酬、高い報酬分散を持つタスクに適しています。安定性とバランスの取れたサンプリングが重要で、収束速度が多少遅くても問題ない場合に推奨されます。

PPとRPはいずれも非一様なサンプリング方法を用いるためバイアスを導入します。これは先に示したサンプリング関数の中で示されている通りで、基本的な補正式は次のとおりです。

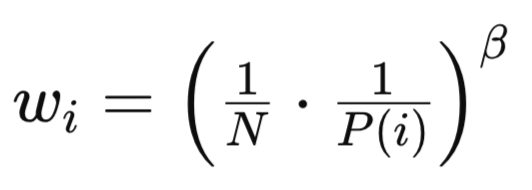
ここで

Nはリプレイバッファ内の経験総数

P(i)は経験iのサンプリング確率

βは重要度サンプリング補正の強さを制御するハイパーパラメータ(β∈[0,1])

似た式を使うものの、RPとPPの補正重みwᵢは重要な点で異なります。RPでは分布の歪みが小さいため、wᵢの分散が小さくなり、より安定した学習が可能でβに対する感度も低くなります。また、ランクベースの分布は本質的にバランスが取れているため、バイアス補正も管理しやすくなります。

シグナルクラスのテスト

先述のコードを用いて、前回の記事のSACモデルコードを単純なリプレイバッファの代わりにPERに変更すれば、モデルを訓練してその重み付きネットワークをONNXファイルとしてエクスポートすることが可能になります。このエクスポート方法については前回の記事で解説しており、PythonからONNXモデルをエクスポートするためのガイダンスもこちらにあります。ONNXモデルはMQL5でコンパイル時にリソースとして埋め込む形で利用されます。 

MQL5側では、IDE内でカスタムシグナルクラスを構築しますが、厳密には前回のSAC記事で扱ったものと違いはありません。MQL5ウィザードでの組み立て方法については、新規読者向けにこちらとこちらにガイドがあります。2023年の日足時間枠におけるUSD/JPYの非交差検証テストの結果は以下の通りです。

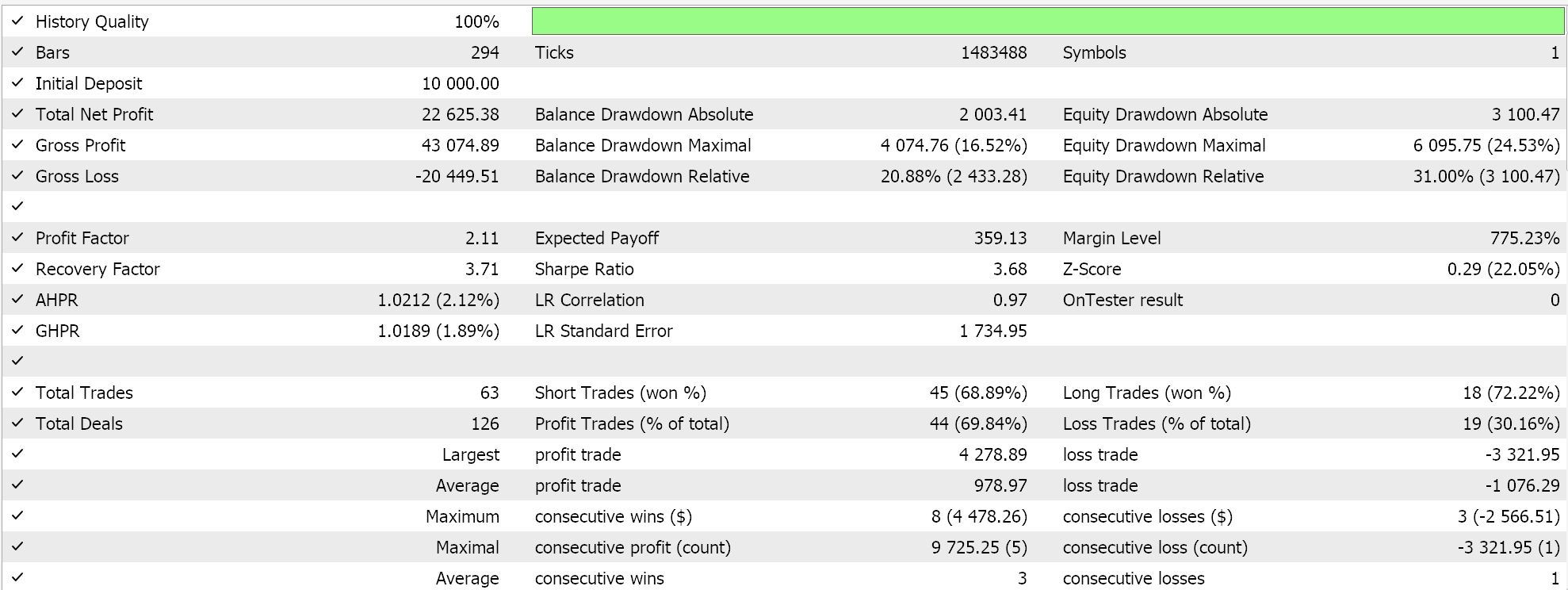
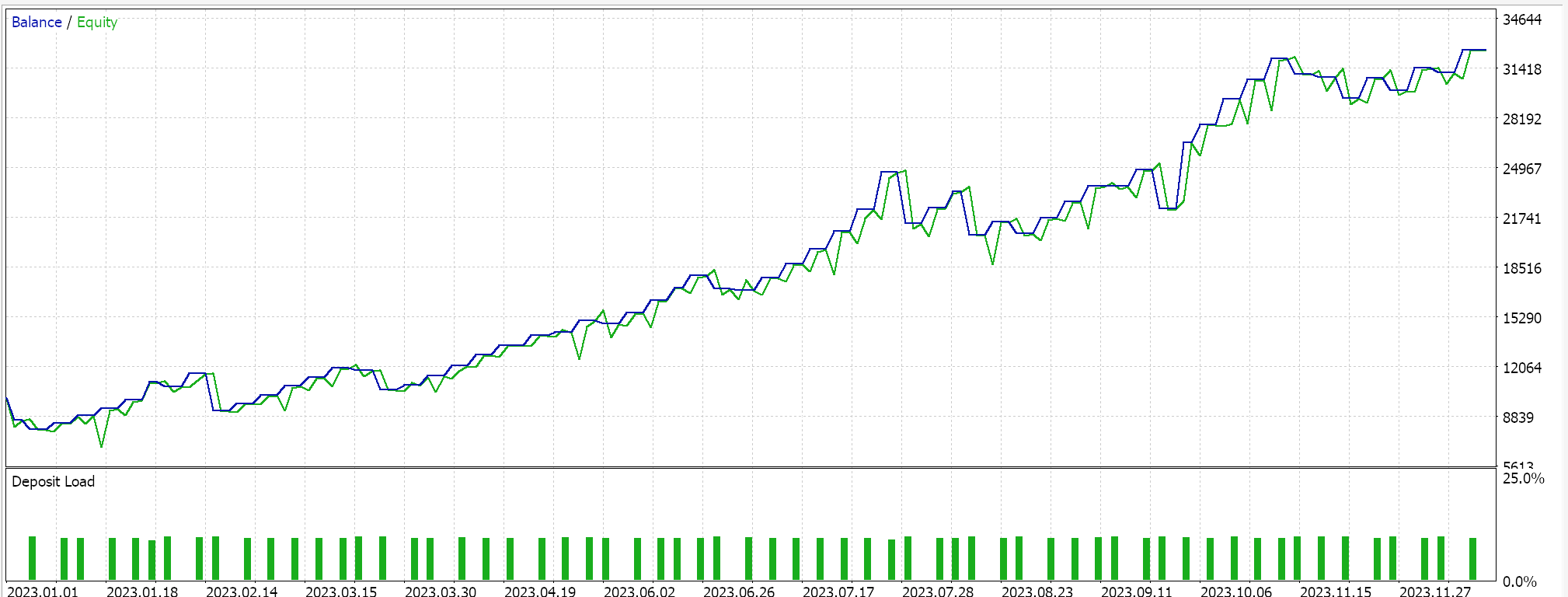
今後は、Pythonでのモデルの交差検証が非常に効率的におこなえるため、将来的にはこれらの記事にも取り入れていくかもしれません。ただし、いつものように過去の成績が将来の結果を保証するものではなく、ここで紹介したシステムを利用または導入する前に、導入前には、読者自身による追加検証と十分な確認を強く推奨します。

結論

強化学習の重要性を再検討し、今日の複雑なモデルと限られた過去のテストデータの状況においては、単に損失関数の低いスコアを追求するのではなく、適切なネットワーク重みを導き出す過程そのものが非常に重要であることを改めて強調しました。そしてその目的のために、強化学習における代替的なリプレイバッファとしてPrioritized Experience Replay (PER)バッファを取り上げました。このバッファは、単に最新の経験を保持して訓練時にサンプリングするだけでなく、ネットワークが学習すべき度合いや関連性に応じて経験を比例的にサンプリングする特徴を持っています。

ファイル	詳細
wz_55.mq5	使用されたファイルを表示するヘッダーを備えた、ウィザードで組み立てられたEA
SignlWZ_55.mqh	カスタムシグナルクラスファイル
USDJPY.onnx	ONNXネットワークファイル