От начального до среднего уровня: Операторы

Введение

Представленные здесь материалы предназначены исключительно для изучения. Ни в коем случае не стоит рассматривать его как окончательное приложение, или использовать приложение с иной целью, кроме изучения представленных здесь концепций

В предыдущей статье "От начального до среднего уровня: Переменные (III)", мы узнали немного о предопределенных переменных и продемонстрировали интересный способ интерпретации функций. Однако всё, о чем говорилось до сих пор, сталкивается с критической проблемой, которая как раз и является одной из самых больших трудностей для начинающих программистов, особенно для тех, кто хочет реализовать небольшие проекты для личного пользования. Данная сложность возникает из-за существования различных типов данных.

Как уже было объяснено в статье "От начального до среднего уровня: Переменные (II)", в MQL5 есть классификация данных по типам, которую можно использовать. Однако для того, чтобы правильно объяснить типы данных, нужно учитывать определенный контекст. Именно это и является основной темой этой статьи: базовые операторы, которые обеспечивают необходимый контекст для разговора о типах данных.

Я знаю, что многие посчитают, что тема слишком проста и нет смысла ее обсуждать. Однако, именно то, что тема проста, и делает ее незаменимой. Многие ошибки в коде связаны с непониманием сути данного вопроса.

Давайте приступим к первой теме данной статьи.

Типы данных и операторы

В нетипизированных языках разговоры об операторах и типах данных часто совершенно излишни. Такая операция, как деление 10 на 3, выдаст соответствующий результат независимо от контекста. Однако в типизированном языке MQL5, как и в C и C++, эта же операция деления имеет не один ответ, а два совершенно разных. В некоторых случаях количество ответов может быть и больше двух, но этот вопрос будет решен в свое время. В рамках нашего обсуждения мы можем сосредоточиться на варианте с двумя ответами.

Подождите секунду. Что значит "с двумя ответами"? Вы сошли с ума или бредите? Потому что каждый раз, когда мы делим 10 на 3, результат равен 3,3333... И никак иначе. Ну что ж, если вы так думаете, то эта статья определенно для вас. Именно поэтому она и была создана: чтобы объяснить, что в программировании всё не так, как многие думают.

Для начала мы сделаем кое-что попроще: сгенерируем значение, которое является периодической десятичной дробью. Но даже в этом случае оно может дать два совершенно разных ответа. Чтобы проиллюстрировать это, давайте рассмотрим довольно простой код. Его можно увидеть ниже:

1. //+------------------------------------------------------------------+
2. #property copyright "Daniel Jose"
3. //+------------------------------------------------------------------+
4. void OnStart(void)
5. {
6.     Print(5 / 2);
7. }
8. //+------------------------------------------------------------------+

Код 01

Код 01 очень простой, и послужит иллюстрацией к чему-то очень интересному, хотя и вызовет большую путаницу. Я так полагаю, что вы должны знать результат операции, который реализуется в шестой строке. Но я сомневаюсь, что вы знаете, какое значение будет отображаться на самом деле. А это связано с тем, что существует зависимость от типа данных, используемых в ответе. Естественно, ожидаемый результат - 2,5. Однако если мы запустим код 01, то увидим, что терминал выведет значение 2. Почему? Разве компьютер не знает, как вычислить это простое выражение? На самом деле, ответ - нет, компьютер не умеет выполнять вычисления, он очень хорошо справляется со сложением, но плохо - со всеми остальными операциями.

Вы скажете: слушай, друг, не пытаешься ли ты нас обмануть? Этого не может быть. Да, это может показаться шуткой, но это реальный факт. Компьютеры НЕ умеют выполнять никаких других операций, кроме сложения. И всё же проблема существует. Потому что, если мы попросим его сложить две дроби, он, скорее всего, не сможет выдать нам правильный результат. И всё это связано с тем, как значения представлены в памяти компьютера.

Компьютеры понимают только нули и единицы. И они либо включены, либо выключены. Они не знают разницы между двумя и тремя или любым другим числом, они работают только с хорошо известной булевой логикой. И, делая это определенным образом, выполняют вычисления, которые мы от них требуем. Хорошо, но если я наберу на калькуляторе 5, и делю на 2, то получу 2,5. Однако я не понимаю, почему, если делать это здесь, в MQL5, я получаю в качестве ответа два, а не 2,5.

Именно здесь, в игру вступает тип данных. В этом случае оба вида данных имеют тип integer. Поэтому компилятор будет считать, что генерируемый ответ также должен быть типа integer. Однако для калькулятора ответ может быть целочисленным типом или типом, известным в программировании как плавающая точка. Именно здесь для многих возникают сложности, поскольку в нетипизированных языках мы всегда получаем один и тот же ответ, а в типизированных языках мы можем получить более одного ответа. От нас, как от программистов, зависит, какой тип будет использоваться в ответе.

Поэтому один из способов исправить код 01 так, чтобы ответ был 2,5, - это использовать следующий код:

1. //+------------------------------------------------------------------+
2. #property copyright "Daniel Jose"
3. //+------------------------------------------------------------------+
4. void OnStart(void)
5. {
6.     Print((double)(5 / 2));
7. }
8. //+------------------------------------------------------------------+

Код 02

Если внести указанные изменения в код 02, ответ будет уникальным. Данный процесс известен как TYPECASTING или преобразование типов. Всю информацию об этом можно найти в документации по MQL5, как и по другим языкам программирования.

В случае с MQL5 можно ознакомиться с объяснением, задав поиск "Преобразование типов". Вы найдете изображения, которые помогут вам понять, как это неявно выполняется преобразование в более сложный тип. В данном случае все они склоняются к типу double. Одно из таких изображений показано ниже:

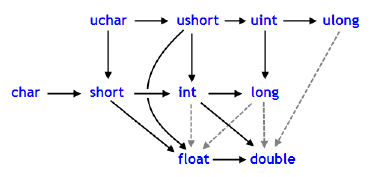
Рисунок 01

Поскольку данный вопрос очень хорошо объясняется в документации, по крайней мере, с точки зрения масштабирования данных по отношению друг к другу, нет необходимости подробно останавливаться на том, что там описано. Однако у людей, желающих разобраться в деталях этой конвертации курса, может возникнуть вопрос: почему это происходит?

Поняв это, можно будет понять и многое другое. Например, почему, выполняя операцию между двумя значениями, мы иногда получаем не правильный ответ, а ответ, который не имеет особого смысла? В других случаях, даже если ответ правильный, когда мы пытаемся его использовать, он кажется неправильным.

Подобные моменты действительно имеют место и напрямую связаны с тем, как данные представлены в памяти компьютера. Чтобы всё это объяснить как следует, давайте перейдем к следующей теме.

Ширина битов

В конце статьи "От начального до среднего уровня: Переменные (II)", мы представили небольшую таблицу, показывающую границы каждого значения, которое может быть представлено в памяти компьютера. Однако есть один важный момент: значения с плавающей точкой, такие как double и float, представляются не так, как целочисленные значения int или ushort. Поэтому то, что будет описано ниже, относится только к целочисленным значениям. Значения с плавающей точкой мы рассмотрим в другой раз, поскольку их работа требует более подробного объяснения, чтобы понять их функционирование и почему опасно слепо полагаться на значение, вычисленное компьютером, когда мы имеем дело с этим типом данных.

Для начала давайте разберемся, что такое целочисленные значения. Все они могут быть сведены к самой простой единице: битам. Наибольшее значение, которое может быть представлено типом данных, равно двум, возведенным на количество битов, используемых для его представления. Например, если используется четыре бита, то можно представить 16 различных значений. Если у нас 10 бит, можно представить 1024 значения, и так далее.

Однако это относится только к положительным значениям, к отрицательным значениям в этом подсчете применяется небольшая корректировка. При работе с отрицательными значениями диапазон, который можно представить, находится в пределах от двух до количества битов минус один и того же отрицательного значения минус один. Это может показаться немного запутанным, но на практике очень просто. Например, с помощью тех же четырех битов, но представляющих как положительные, так и отрицательные значения, мы можем перейти от -8 к 7. С помощью 10 бит мы можем перейти от -512 к 511. Но подождите минутку. Если не обращать внимания на то, что значение отрицательное, и сложить их вместе, то 8 плюс 7 будет не 15, а 16, как уже говорилось выше. Аналогично, 512 плюс 511 - это 1023, а не 1024. Почему же возникает такая разница? Ответ кроется в нуле, дорогой читатель. Когда мы прибавляем 8 к 7, мы рассматриваем только возможные значения, но ноль не учитывается в этой сумме, поэтому он занимает самостоятельную позицию.

Чтобы окончательно прояснить этот вопрос, нам нужно понять, как отрицательные значения представляются в памяти. Для этого нам надо обратиться к изображению ниже, чтобы более наглядно объяснить эту концепцию:

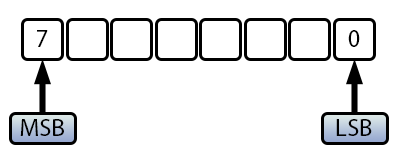
Рисунок 02

Здесь у нас значение типа uchar или char, поскольку отображается 8 бит. Однако разница между значением uchar и char заключается именно в том, что представлено в MSB-бите, или старшем бите. В случае со значениями uchar, где все значения положительные (благодаря префиксу u, обозначающему unsigned), MSB не является проблемой, поскольку значения всегда будут положительными. Поэтому, мы можем считать от 0 до 255, что составляет 256 возможных значений. С другой стороны, при использовании типа char, MSB указывает, является ли значение отрицательным или положительным. Если MSB равен единице, то значение отрицательное, а если MSB равен нулю, то значение положительное. По этой причине мы можем считать положительные значения от 0 до 127. Однако, поскольку ноль беззнаковый и это единственный случай, когда MSB включен, а другие биты отсутствуют, он интерпретируется как -128, "отрицательного нуля" не существует. Это также объясняет, почему при отрицательных значениях счет всегда имеет дополнительное значение по сравнению с половиной возможных значений.

Интересно, не правда ли? Но теперь всё становится только лучше. Если вы разобрались в приведенном объяснении, то уже понимаете, как функция ABS или MathAbs, присутствующая во многих языках программирования, может преобразовать отрицательное значение в положительное и наоборот. Для выполнения данного преобразования достаточно изменить состояние MSB.

Однако, если не обращать внимания на то, что мы делаем, с нами может случиться неожиданное. Например, если сложить два положительных значения, скажем 100 и 40, можно получить отрицательное значение. Вы можете подумать, какие безумные вещи он говорит? Как можно сложить два положительных значения и получить отрицательное? Это абсурд! Логика подсказывает, что ответ всегда должен быть положительным. В результате такой суммы мы никогда не сможем получить отрицательное значение. А вот в компьютерном мире истина иногда не совпадает со здравым смыслом. Чтобы прояснить это, давайте посмотрим на следующий код:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     char    value1 = 100,
07.             value2 = 40,
08.             Result;
09. 
10.     Result = value1 + value2;
11.     Print(value1, " + ", value2, " = ", Result);
12. }
13. //+------------------------------------------------------------------+

Код 03

После выполнения данного кода на экране появится следующий результат:

Рисунок 03

Господи! Что это такое? Это НЕВОЗМОЖНО. Нет, это точно не невозможно. Это как раз объясняет необходимость написания данной статьи. Вы обязательно должны понимать, что в типизированных языках правильный выбор типа данных напрямую влияет на результат вычислений. Многие люди испытывают серьезные трудности при программировании именно потому что не понимают того, что здесь объясняется здесь. И многие обманываются, потому что не знают об этих вопросах, которые, хотя и кажутся простыми, без должного понимания дают вам обманчивые обещания безопасности.

Хорошо. В этом случае можно подумать: отлично, мы используем тип, который может представлять до 127 для положительных значений и -128 для отрицательных. Разве не идеально было бы использовать тип побольше, например int, который вместо 8 бит использует 32 бита? Да, уважаемый читатель. Но проблема здесь не в этом, а в том, что в какой-то момент будет достигнут предел значений, которые можно представить. И когда это произойдет, счет так или иначе даст сбой. И всё же мы по-прежнему работаем только с целочисленными типами. Значения с плавающей точкой еще более сложны для понимания.

Поэтому прежде, чем переходить к работе с плавающей запятой, необходимо хорошо разобраться в целочисленных числах. Однако есть одна проблема, о которой нужно упомянуть: невозможность всегда работать с более мощным типом. Это очень часто случается при работе со строками. Именно здесь всё становится сложнее. Текстовые строки, или последовательности символов, могут использовать либо 16, либо 8 бит. Обычно, за исключением самых редких случаев, компьютеры используют так называемую таблицу ASCII. Эта 8-битная таблица была создана на заре компьютерной техники. Однако, поскольку она не подходила для представления некоторых символов, пришлось разработать другие типы таблиц. Поэтому некоторые программы используют 16 бит для записи текста. Но использование 16 бит изменяет только MSB на бит номер 15, но не создает бесконечного числа возможностей. Оно просто позволяет перейти от 256 значений к 65 536 различным значениям.

В любом случае, строка - это не что иное, как массив более простых значений, но с возможностью представления большего диапазона значений. Например, с помощью MQL5 можно создать 128-битное значение, хотя изначально наибольшее возможное значение - 64-битное с типом ulong. Как сделать нечто подобное? Всё очень просто. Если вы знаете значения, которые представляют каждый бит, включенный или выключенный в битовой последовательности, тогда нужно будет только сложить значения битов, которые включены. Когда сделаете это, произойдет нечто волшебное: можно будет представить любое значение, которое только можно себе представить.

Поэтому при сложении 100 с 40, как это было сделано в коде 03, мы получим значение -116. Это происходит, потому что значение -116 на самом деле является положительным значением 140, что на первый взгляд кажется довольно абсурдным. Но если посмотреть на значения в двоичном виде, то увидим следующее:

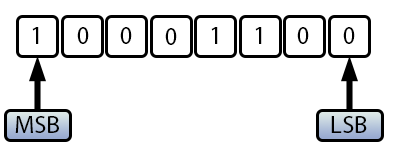
Рисунок 04

Другими словами, то же самое значение, которое интерпретируется как положительное в одном случае, интерпретируется как отрицательное в другом, именно из-за MSB. Поэтому нужно действовать осторожно, особенно при создании циклов. Именно из-за этого может возникнуть такая ситуация. Без должного внимания, как вычисления, так и циклы могут привести к нестабильному поведению нашей программы. Даже если (казалось бы) всё рассчитывается правильно, неправильный выбор типа данных или допустимых границ, которые он поддерживает, может вывести всё из-под контроля.

Хорошо, но в какой-то момент упомянулось, что мы можем использовать тип побольше для решения этой же проблемы. Почему в одних случаях данный тип решения работает, а в других - нет? Это происходит, потому что MSB будет смещаться, как можно видеть на изображении ниже:

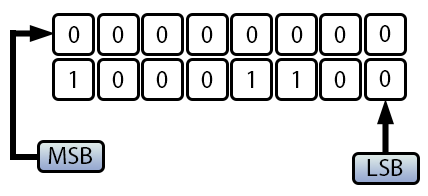
Рисунок 05

Это несложно для понимания, не так ли? Хорошо. То, что касается основных операций - на данный момент мы высказались, но всё, что обсуждалось до сих пор, связано с использованием арифметических операторов. Однако существует еще одна категория: логические операторы. Чтобы объяснить и правильно разделить эти понятия, мы перейдем к новой теме.

Логические операторы

Логический оператор работает с битами. Однако, в логических операциях, иногда мы можем использовать байты или целые наборы битов. Вообще, данный тип операторов должен быть задуман, по крайней мере, изначально, как ориентированный на работу с битами, а не байтами. Это может показаться немного запутанным, но со временем вы поймете, что в этом есть смысл. Это связано с тем, что в отличие от арифметических операторов, которые предназначены для вычисления, логические операторы предназначены для доказательства чего-либо. Эти тесты обычно выполняются для того, чтобы проверить, соответствуют ли значения определенному условию. Поскольку данные операторы имеют больше смысла при использовании в сочетании с другими командами, мы просто предложим краткий обзор, чтобы вы были готовы к тому, что мы увидим в ближайшее время.

Однако, несмотря на то, что они логичнее в сочетании с другими командами, с помощью логических операторов можно выполнять и небольшие операции. На самом деле, любая операция на процессоре включает в себя больше логики, чем арифметики. Хотя основная и самая важная часть CPU называется ALU (arithmetic and logic unit). Это связано с тем, что она отвечает за работу процессора.

В принципе, среди логических операторов есть операции AND, OR, NOT и, во многих языках (не во всех), XOR. В дополнение к ним у нас есть операции смещения вправо и влево. С помощью этих простых операций мы можем делать множество вещей. Честно говоря, мы можем сделать всё, что нам придет в голову. Фактически, на этих операциях основано ALU, которое является ядром CPU.

В этот момент вы, возможно, смотрите на документацию по MQL5 или какому-то другому языку и думаете: «Но есть и другие логические операторы, такие как «больше чем» и «меньше чем» среди прочих, присутствующих в некоторых языках». Да, в некоторых языках реализовано больше типов операторов или функций логического сравнения. Однако на уровне ALU многие из этих операций гораздо проще, чем они выглядят в реализациях на языке высокого уровня. И не поймите меня неправильно, не то чтобы я считал их неправильными или ненужными. Всё наоборот, они реализованы именно для того, чтобы упростить некоторые аспекты работы программиста. Например, если мы хотим сравнить одно значение с другим, то самым простым способом будет вычесть одно из другого. Но есть и другой способ: применять операцию XOR побитно. Если все биты равны, то конечный результат будет равен нулю. А если какой-либо бит отличается, то одно из значений может быть больше или меньше другого. Однако, когда выполняется вычитание и анализируется MSB, мы можем определить, равен ли результат нулю, меньше нуля или больше нуля. В зависимости от данного результата мы узнаем, является ли значение больше, меньше или равно другому.

Чтобы было понятнее, давайте рассмотрим простой пример сравнения, и определим, больше, меньше или равно одно значение другому. Для этого мы используем приведенный ниже код:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     short   value1 = 230,
07.             value2 = 250;
08. 
09.     Print("Result #1: ", value1 - value2);
10.     Print("Result #2: ", value2 - value1);
11.     Print("Result #3: ", value2 ^ value1);
12. }
13. //+------------------------------------------------------------------+

Код 04

Это типичная и простая система анализа значений. Когда мы запустим этот код, в терминале появится следующий результат:

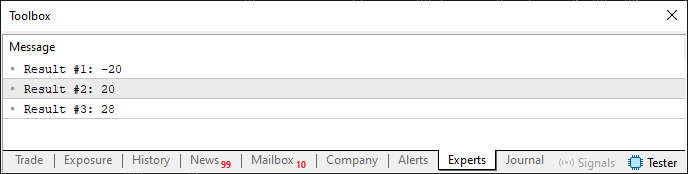
Рисунок 06

Теперь будьте внимательны, чтобы понять приведенное выше объяснение для определения того, является ли значение больше, меньше или равно. Чтобы было интереснее, мы используем 16-битный тип данных. Это позволяет нам обрабатывать 65 536 различных значений. Но поскольку это значение со знаком, то есть оно может принимать как отрицательные, так и положительные значения, диапазон составляет от -32 768 до 32 767. Если мы ограничимся анализом значений в 8-битном диапазоне, для нас будет несложно определить, больше, меньше или равно одно значение другому. Однако, в отличие от возможностей при использовании исключительно 8 бит, здесь мы можем работать со значениями в диапазоне от -255 до 255, что просто замечательно. Однако есть способы оптимизировать этот потенциал еще больше. Мы не будем вдаваться в подробности, так как вам потребуется знание некоторых понятий, которые еще не были объяснены. Тем не менее, код 04 довольно интересен.

Сейчас мы посмотрим, что произошло здесь. Поскольку value1 явно меньше value2, при вычитании одного из другого исходный результат будет отрицательным, что говорит о том, что value1 действительно меньше. Это делается в девятой строке кода 04. Однако при вычитании value2 из value1, как это сделано в десятой строке, результат будет положительным, что указывает на то, что value2 больше value1. То же самое происходит в одиннадцатой строке, но в этом случае проверяется, являются ли значения равными. Поскольку результат отличается от нуля, мы точно знаем, что значения не равны.

Данный вид упражнений очень интересен. И это становится еще удивительнее, когда мы понимаем, что ALU не содержит операции вычитания. На самом деле любая операция, выполняемая с ним, всегда будет сложением, в сочетании с другими логическими операциями. Даже сама операция сложения сводится, в самой своей сути, к логическим операциям.

Однако, чтобы продемонстрировать это, нам потребуется использовать некоторые функции управления. И поскольку мы еще не объяснили ни одной функции управления кодом, мы не будем показывать в этой статье, как данный процесс происходит в блоке арифметико-логической обработки (ALU). Но скоро мы сможем это сделать, ведь понимание этого, позволит нам использовать MQL5 для чего-то еще более впечатляющего, чем создание индикаторов, скриптов и советников.

Я пока не уверен, покажу ли я как реализовать нечто подобное. Цель - чисто дидактическая, но я буду иметь это в виду.

Согласен, операторам смещения по-прежнему не хватает должного представления, поскольку они практически не упоминаются в документации по MQL5. Однако у этих операторов очень специфическое назначение и они нацелены на выполнение конкретных задач. Именно поэтому они не находят широкого применения в большинстве распространенных кодов на MQL5, особенно в тех, которые предназначены для работы с индикаторами и советниками. Но при работе с изображениями в приложении, созданном на MQL5, эти операторы используются гораздо чаще.

Однако, если они предназначены для очень специфических занятий, их можно использовать и для других целей. Мы изучим один из них, как только расскажем, как работать с функциями управления.

Заключительные идеи

В этой статье мы рассмотрели некоторые моменты программирования, которые имеют значение при работе с языком, использующим типы для классификации данных. Однако, хотя мы и обсудили концепции, которые могут быть новыми для читателя, мы лишь поверхностно ознакомились с материалами эту тему. Поэтому, я рекомендую вам изучить базовую документацию по MQL5, чтобы лучше понять некоторые из объясняемых здесь концепций. Также настоятельно рекомендуем вам изучить немного булевой логики. Хотя она может показаться сложной, ее понимание поможет вам упростить многие расчеты, которые обычно приходится выполнять в кодах. Понимание того, когда значение является положительным или отрицательным, и умение работать с этими тонкостями помогут вам в долгосрочной перспективе.

Я включил в приложение три из четырех рассмотренных здесь кодов, чтобы вы могли изучить их более подробно. В следующей статье мы начнем обсуждать функции управления или операторов управления. Тогда всё станет намного интереснее, а веселье обретет форму и смысл. До скорой встречи!