From Basic to Intermediate: Operators

Introduction

The materials presented here are intended for educational purposes only. Under no circumstances should the application be viewed for any purpose other than to learn and master the concepts presented.

In the previous article "From Basic to Intermediate: Variables (III)", we explored predefined variables and an interesting way to interpret functions. However, everything discussed so far leads to a common challenge, one of the biggest difficulties faced by new programmers, especially those working on small personal projects. This challenge arises from the existence of different data types.

As briefly mentioned in "From Basic to Intermediate: Variables (II)", MQL5 classifies data into various types. However, in order to properly explain data types, we need to establish the right context. That context is precisely the main topic of this article: basic operators. Understanding these operators is essential before we can effectively discuss data types.

Some may feel that this topic is simple and unnecessary to cover. However, it is precisely because it appears trivial that it becomes essential. Many coding errors arise from a misunderstanding of this fundamental concept.

With that said, let's dive into the first topic of this article.

Data Types and Operators

In non-typed languages, discussing operators and data types is often unnecessary. For example, an operation like 10 divided by 3 will yield an expected result without issue. However, in a strongly typed language like MQL5, as well as C and C++, this simple division does not produce a single result but rather two different outcomes. And in some cases, even more, but we will explore those additional cases in a later discussion. For now, we will focus on the possibility of having two different results.

Wait a second. Two results? That doesn't make sense! You might be thinking: are you crazy? Every time we divide 10 by 3, we get 3.3333... There's no other possible answer! Well, if that's what you're thinking, then this article is definitely for you. The goal here is to clarify that, in programming, things don't always work as they might seem at first glance.

To begin, let's examine a case that is simpler than dealing with recurring decimals but still demonstrates how a single operation can yield two completely different results. Below, we'll look at a simple example in code. Here it is:

1. //+------------------------------------------------------------------+
2. #property copyright "Daniel Jose"
3. //+------------------------------------------------------------------+
4. void OnStart(void)
5. {
6.     Print(5 / 2);
7. }
8. //+------------------------------------------------------------------+

Code 01

This simple Code 01 will serve to illustrate an interesting concept that often causes significant confusion. You might think you already know the result of the operation performed on line six without even running the code in the MetaTrader 5 terminal. However, I challenge you: do you really know what value will be displayed? The answer may surprise you because it depends on the data type used for the calculation. Naturally, the expected result is 2.5. However, if you execute Code 01, you will see that the terminal prints 2 instead. But why? Does the computer not know how to calculate such a simple expression? In fact no, the computer does not inherently know how to perform arithmetic. In reality, computers are excellent at addition but terrible at most other mathematical operations.

"Wait, are you trying to trick us?" Not at all! Even though it may seem like a trick, this is a fundamental fact: computers can only perform addition. Even then, they struggle with fractions. If you ask a computer to add two fractional values, it might not always produce the correct result. This all comes down to how numbers are represented in the computer memory.

Computers only understand 0s and 1s, i.e. on and off states. They do not inherently recognize numbers like 2 or 3. Instead, they rely on Boolean logic to process data and perform calculations. And by doing this in a certain way, they perform the calculations that we require of them. But if I enter 5 divided by 2 into a calculator, I get 2.5. So why does MQL5 return 2 instead of 2.5?

This is precisely where data types come into play. On line six, both values are of the integer type. As a result, the compiler determines that the output must also be an integer. In contrast, a calculator allows results to be either integers or floating-point numbers (also known as decimals in programming). This is where many programmers, especially beginners, get confused. In dynamically typed languages, the result is always the same. However, in strongly typed languages like MQL5, multiple possible results exist depending on how you define the data type.

To fix Code 01 so that the correct result of 2.5 is displayed, we need to modify it as shown in the following example:

1. //+------------------------------------------------------------------+
2. #property copyright "Daniel Jose"
3. //+------------------------------------------------------------------+
4. void OnStart(void)
5. {
6.     Print((double)(5 / 2));
7. }
8. //+------------------------------------------------------------------+

Code 02

When we make the changes seen in Code 02, the result will now be unambiguous. This process is known as typecasting, or type conversion. The MQL5 documentation provides a detailed explanation of this concept, as do many other programming language references.

In the case of MQL5, you can refer to the Type Conversion section, where illustrations help clarify how implicit conversion works, always favoring a more complex type, typically double. One such illustration is shown below.

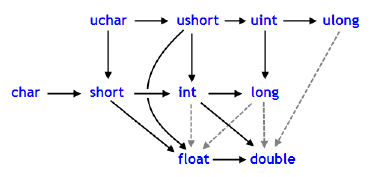
Figure 01

Since the documentation already explains how data types scale relative to each other, we won't go into those details here. However, curious readers may wonder: Why does this happen?

Understanding this will help you grasp many other concepts. For instance, why does performing a mathematical operation sometimes yield an incorrect or nonsensical result? Why does a value initially appear correct, but then seem incorrect when used later?

These inconsistencies stem from how data is represented in a computer's memory. To explain this properly, let’s introduce a new topic.

Bit Width

At the end of the article "From Basic to Intermediate: Variables (II)", we looked at a table showing the limits for different data types stored in memory. However, there's an important detail: floating-point types (double and float) are not represented in the same way as integer types (int, ushort, etc.). For now, we will focus solely on integer values. Floating-point numbers require a deeper explanation, which we'll cover later. This is crucial because blindly trusting a floating-point calculation can lead to serious inaccuracies.

First, let's break integer values down to their most fundamental unit: bits. The highest value a type can represent corresponds to 2 raised to the number of bits used. For example, with 4 bits, you can represent 16 distinct values. With 10 bits, you can represent 1024 values, and so on.

However, this applies only to positive values. Negative numbers require a small adjustment. In signed integers, the range is determined by 2 raised to (number of bits - 1), from the negative counterpart of that value minus one. This may sound confusing at first, but it's quite simple in practice. For example, using the same four bits, but representing both positive and negative values, we can go from -8 to 7. With 10 bits we can go from -512 to 511. But wait a minute. Shouldn't it be -8 to 8 or -512 to 512? After all, if we sum 8 and 7, we get 15, not 16, and if we sum 512 and 511, we get 1023, not 1024. Why is it so? The missing value is zero. The zero occupies one position in the range, which is why the count appears slightly off.

To clarify further, we need to understand how negative numbers are stored in memory. Let's look at the illustration below:

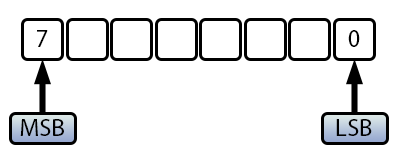
Figure 02

Here, we see an 8-bit value, which can represent either an unsigned char (uchar) or a signed char (char). The difference lies in the Most Significant Bit (MSB). For uchar (unsigned), where all values are positive (indicated by the u prefix), the MSB is not an issue, allowing values from 0 to 255 (256 total values). For char (signed), however, the MSB determines whether the value is positive or negative. If the MSB is one, the value is negative, and if the MSB is zero, the value is positive. For this reason, we can count positive values from 0 to 127. However, since zero is unsigned and this is the only case where the MSB is on and the other bits are not, it is interpreted as -128, there is no such thing as "negative zero". This also explains why, for negative values, the count always has an extra value compared to half of the possible values.

Interesting, isn't it? But now everything is only getting better. If you have understood the above explanation, then you already understand how the ABS or MathAbs function, present in many programming languages, can convert a negative value to a positive one and vice versa. To perform this transformation, we just need to change the state of the MSB.

However, if we do not pay attention to what we do, the unexpected can happen to us. For example, if you add two positive values, say 100 and 40, you can get a negative value. "Wait, what? If both numbers are positive, the sum must also be positive!" In everyday math, that's true. But in computing things don't always work as expected. Let's explore this phenomenon with the following code example. Look at the code below:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     char    value1 = 100,
07.             value2 = 40,
08.             Result;
09. 
10.     Result = value1 + value2;
11.     Print(value1, " + ", value2, " = ", Result);
12. }
13. //+------------------------------------------------------------------+

Code 03

After the execution of this code, the following result will appear on the screen:

Figure 03

Holy Virgin Mary! What is it? This is IMPOSSIBLE. No, dear reader, it is definitely not impossible. In fact, this is precisely why this article needed to be written. You must understand that in a strongly typed language, selecting the correct data type directly affects the calculated result. Many programmers struggle significantly because they fail to grasp this fundamental concept. Worse still, many are misled simply due to a lack of awareness of these seemingly simple issues. However, without proper understanding, you become vulnerable to false assurances of accuracy and security.

At this point, you might be thinking: "Alright, we're using a data type that can represent values up to 127 for positive numbers and -128 for negative numbers. Wouldn't it be better to use a larger type, such as an int, which uses 32 bits instead of 8?" Yes, dear reader, that would seem like a reasonable solution. However, that is not the real problem here. The issue is that at some point, the maximum representable value will be reached, and when that happens, the calculation will inevitably fail in some way. Keep in mind that we are still dealing only with integer types. Floating-point numbers introduce even more complexity.

Therefore, before delving into floating-point arithmetic, it is crucial to first understand integer operations. However, there is an important point to mention here: it is not always possible to use a larger data type at all times. This limitation is particularly evident when dealing with strings. This is where things get even more complicated. Strings, or sequences of characters, can use either 8-bit or 16-bit encoding. In most cases, computers rely on the ASCII table. It is an 8-bit encoding standard created in the early days of computing. However, since ASCII was inadequate for representing certain characters, additional encoding schemes had to be developed. This led to the introduction of 16-bit character encodings in some programs. Nevertheless, using 16-bit encoding does not create an infinite number of possibilities. It simply extends the range from 256 values to 65,536 values by shifting the Most Significant Bit (MSB) to position 15.

Even so, a string is ultimately nothing more than an array of simpler values, but one that allows for a much greater range of representation. For instance, in MQL5, you can create a 128-bit value, even though the largest predefined type (ulong) is limited to 64 bits. But how is this possible? It's actually quite simple. If you understand how each bit in a sequence contributes to a value when turned on or off, you can sum the corresponding values of the active bits. By doing so, something almost magical happens: you gain the ability to represent any value imaginable.

This is exactly why, when adding 100 and 40 in Code 03, the result is -116. That's because -116 in this context represents +140. At first, this may seem absurd, but when examining the values in binary, you would see the following:

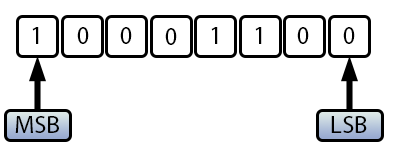
Figure 04

In other words, the same binary value can be interpreted as positive in one case and negative in another, solely because of how the MSB is handled. For this reason, you must be extremely cautious, especially when creating loops. If not managed properly, these type-related issues can cause both calculations and loops to behave unpredictably, even when everything appears to be functioning correctly. Errors in type selection or exceeding the maximum limit of a given type can cause an entire program to spiral out of control.

At one point, we mentioned that using a larger data type could resolve this issue. But why does this approach work in some cases and not in others? The answer lies in how the MSB is shifted. You can see this effect illustrated in the image below:

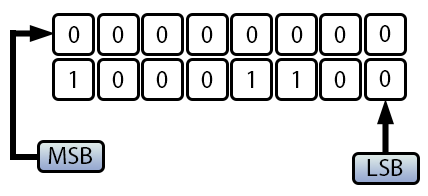
Figure 05

It’s a simple concept, isn't it? That covers the basics of arithmetic operations for now. However, everything we have discussed so far relates to arithmetic operators. There is another critical category of operators we need to explore next: logical operators. To explain and properly separate these concepts, we will move on to a new topic.

Logical Operators

Logical operators operate at the bit level. Although they can sometimes be applied to bytes or entire sets of bits, they are primarily designed to function at the bitwise level. At first, this may seem somewhat confusing, but over time, you’ll see that it makes sense. Unlike arithmetic operators, which are used for performing calculations, logical operators are used for evaluating conditions. Typically, logical operations test whether values meet specific conditions. Since these operators are most effective when used alongside control structures, we will only provide a brief overview here to prepare you for upcoming topics.

Even though logical operators are more meaningful when used with conditional statements, they can also be used to perform small-scale operations. In fact, every CPU operation is, in reality, more logical than arithmetic. Despite the fact that the Arithmetic Logic Unit (ALU) is named for both arithmetic and logic, logic operations are fundamental to CPU functionality.

In terms of logical operators, we primarily have AND, OR, NOT and in some but not all programming languages XOR. In addition to these, we have right and left shift operations. These simple operations serve as the foundation for all computational logic. In reality, anything can be built from these basic operations. This is the very principle on which the ALU, the "brain" of the CPU, operates.

At this point, you may be looking at the MQL5 documentation (or another programming language's reference) and wondering: "But there are more logical operators, such as greater than (>), less than (<), and others. Why aren't they included here?" Good question, dear reader. Some languages provide additional logical operators or comparison functions for convenience. However, at the hardware level, these operations are far simpler than the way they are presented in programming languages. To be clear, this is not a criticism of these implementations. In fact, they make programming significantly easier. For example, the simplest way to compare two values is through subtraction. However, an alternative method involves applying a bitwise XOR operation. If all bits match, the result is zero. If any bit differs, the values are not equal. When performing subtraction, we can analyze the MSB to determine whether the result is zero (equal), negative (less than), or positive (greater than). This allows us to establish numerical relationships without explicit comparison operators.

To make this concept clear, let's look at a simple example that determines whether one value is greater than, less than, or equal to another. For this, we'll use the following code snippet:

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. void OnStart(void)
05. {
06.     short   value1 = 230,
07.             value2 = 250;
08. 
09.     Print("Result #1: ", value1 - value2);
10.     Print("Result #2: ", value2 - value1);
11.     Print("Result #3: ", value2 ^ value1);
12. }
13. //+------------------------------------------------------------------+

Code 04

Here, we have a simple and typical value analysis system. When this code is executed, you will see the following result in the terminal:

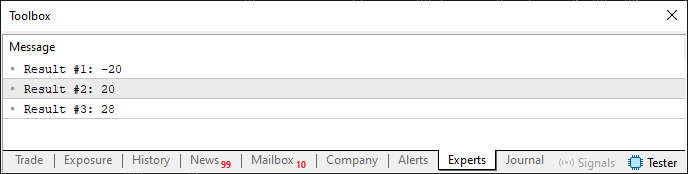
Figure 06

Now, pay attention to what was mentioned earlier regarding determining if one value is greater than, less than, or equal to another. To make things more interesting, we're using a 16-bit signed value, which allows us to represent 65,536 different values. However, since it is a signed value, meaning it can hold both negative and positive numbers, the range will vary from -32,768 to 32,767. If we stick to analyzing values within an 8-bit range, we won't have issues determining if one value is greater, smaller, or equal to another. But with 16-bit values, we can represent a much broader range, from -255 to 255, which is excellent. That being said, there are ways to make this even better. But we won't delve into that just yet, as there are a few concepts that need to be explained first. Still, Code 04 is quite fascinating and fun.

So, let's break down what's happening here. Since value1 is clearly less than value2, subtracting one from the other will result in a negative value, confirming that the first value is indeed smaller. This happens in line 9 of Code 04. On the other hand, when we subtract value1 from value2, as shown in line 10, the result is positive, indicating that value2 is greater than value1. Finally, in line 11, we perform a comparison to check if the values are equal. Since the result is non-zero, we can definitively conclude that the values are not the same.

This concept is quite interesting, and it becomes even more intriguing when you realize that there is no subtraction operation in the ALU. In fact, any operation performed in the ALU is essentially just a sum, combined with some logical operations. Even the addition operation, at its core, can be reduced to logical operations.

However, in order to demonstrate this properly, we would need to use some control functions. Since control functions have not yet been explained in this article, we won't be diving into how this would be implemented at the ALU level just yet. But don't worry, we'll cover that in future articles. Once you understand how to implement these techniques, you’ll be able to use MQL5 for much more advanced and exciting tasks beyond creating indicators, scripts, and Expert Advisors.

Whether or not I'll demonstrate this implementation is still uncertain, as the main goal here is purely educational. But I'll give it some thought.

I agree, shift operators still lack proper representation as they are hardly mentioned in MQL5 documentation. However, these operators have a very specific purpose and are aimed at performing specific tasks. This is why they are not widely used in most common MQL5 codes, especially when working with indicators and Expert Advisors. But when working with images in an application created in MQL5, these operators are used much more often.

However, if they are intended for very specific activities, they can be used for other purposes as well. One such task will be explored once we dive into control functions.

Final considerations

In this article, we covered some important details of programming that make a significant difference when working in a strongly typed language. While some of the concepts discussed might be new to many, we've only scratched the surface of what's available on this topic. So, dear reader, I advise you to take the time to study the basic MQL5 documentation to deepen your understanding of the concepts presented here. Additionally, I highly recommend exploring Boolean logic, which, despite its simplicity, will help simplify many of the calculations you will encounter in your coding tasks. Understanding how to work with positive and negative values and how these nuances play out makes a huge difference in the long run.

In the attached files, I will include three of the four codes discussed here so that you can study them at your own pace. In the next article, we will begin exploring control functions or operators. That's when things will get really exciting, and the real fun will begin. See you soon!