
Redes neuronales: así de sencillo (Parte 70): Mejoramos las políticas usando operadores de forma cerrada (CFPI)
Introducción
El enfoque de optimizar la política del Agente sujeto a restricciones sobre su comportamiento ha demostrado ser prometedor en tareas de aprendizaje por refuerzo offline. Usando transiciones históricas, la política de comportamiento del Agente se entrena para maximizar el valor de la función de valor.
Las restricciones de comportamiento ayudan a evitar cambios significativos en la distribución de las acciones del Agente, lo cual proporciona una seguridad razonable de que la estimación del valor de las acciones es correcta. En el artículo anterior, nos familiarizamos con el método SPOT, que explota este enfoque. Como continuación de este tema, me gustaría presentarles el algoritmo Closed-Form Policy Improvement (CFPI), que fue presentado en el artículo "Offline Reinforcement Learning with Closed-Form Policy Improvement Operators".
1. El algoritmo Closed-Form Policy Improvement (CFPI)
Una expresión de forma cerrada es una función matemática expresada mediante un número finito de operaciones estándar. Puede contener constantes, variables, operaciones estándar y funciones, pero normalmente no contiene límites ni expresiones diferenciales o de integración. Así, el método CFPI que estamos analizando introduce algunos puntos analíticos en el algoritmo de aprendizaje de la política del Agente.
La mayoría de los modelos existentes de aprendizaje por refuerzo offline usan el descenso estocástico del gradiente (SGD) para optimizar sus estrategias, lo cual puede provocar inestabilidad en el proceso de aprendizaje y exige un ajuste cuidadoso de la tasa de aprendizaje. Además, el rendimiento de las estrategias entrenadas offline puede depender del punto de evaluación específico. Y esto suele dar lugar a variaciones significativas en la fase final del aprendizaje. Esta inestabilidad supone un reto importante en el aprendizaje por refuerzo offline, ya que el acceso limitado a la interacción con el entorno dificulta el ajuste de los hiperparámetros. Además de la variación entre distintos puntos de evaluación, el uso de SGD para mejorar la estrategia puede provocar una variación significativa en el rendimiento bajo distintas condiciones iniciales aleatorias.
En el material presentado, los autores del método CFPI pretenden reducir la mencionada inestabilidad del aprendizaje RL offline. Así, desarrollan operadores estables de mejora de la estrategia. En particular, observan que la necesidad de limitar el desplazamiento distribucional motiva el uso de una aproximación de Taylor de primer orden, que produce una aproximación lineal de la función objetivo de la política del Agente que es precisa en una vecindad suficientemente pequeña de la estrategia de comportamiento. Basándose en esta observación clave, los autores del método construyen operadores de mejora de la estrategia que retornan soluciones de forma cerrada.
Al modelar las estrategias de comportamiento como una distribución gaussiana unitaria, el operador de mejora de la estrategia propuesto por los autores del CFPI desplaza de forma determinista la política de comportamiento en la dirección de la mejora del valor. Como resultado, el método de mejora de políticas de forma cerrada que proponen los autores evita la inestabilidad del aprendizaje de mejora de estrategias, ya que solo se utiliza el entrenamiento de estrategias básicas para el comportamiento de un conjunto de datos determinado.
Los autores del método CFPI también señalan que los conjuntos de datos prácticos suelen recopilarse usando estrategias heterogéneas. Esto puede dar lugar a una distribución multimodal de las acciones del Agente. Una vez más, una única distribución gaussiana no captaría muchos modos de la distribución subyacente, lo cual limitaría el potencial de mejora de la estrategia. Modelar las políticas de comportamiento como una mezcla de distribuciones gaussianas ofrece una mayor expresividad, pero conlleva una complejidad de optimización adicional. Los autores del método resuelven este problema usando el límite inferior LogSumExp y la desigualdad de Jensen, lo que también conduce a un operador de mejora de la estrategia de forma cerrada aplicable a estrategias de comportamiento multimodal.
Los autores también destacan las siguientes aportaciones del método Closed-Form Policy Improvement:
- Los operadores CFPI compatibles con estrategias de comportamiento monomodo y multimodo y capaces de mejorar las estrategias aprendidas por otros algoritmos.
- Las pruebas empíricas de las ventajas de modelar la estrategia de comportamiento como una mezcla de distribuciones gaussianas.
- Las variantes de un solo paso e iterativas del algoritmo propuesto superan a los algoritmos existentes anteriormente en la referencia estándar.
Los autores de CFPI crean un operador analítico para mejorar la estrategia sin aprendizaje con el fin de evitar la inestabilidad en escenarios offline. Asimismo, observan que la optimización con respecto a la función objetivo genera una estrategia que permite una desviación limitada de la estrategia de comportamiento de muestreo offline. Por ello, solo consultaremos el valor Q en las proximidades del comportamiento de la acción durante el entrenamiento. Naturalmente, esto motiva el uso de una aproximación lineal de primer orden.
En este caso, además, la evaluación de las acciones en la política actualizada proporciona una aproximación lineal precisa de la función de valor aprendida solo en una vecindad suficientemente pequeña de la distribución de la muestra de entrenamiento. Por consiguiente, la elección del par Estado-Acción de la muestra de entrenamiento resultará crucial en el resultado final del entrenamiento.
Para resolver el problema, los autores proponen resolver el siguiente problema aproximado para cualquier estado S:
![]()
Cabe señalar que D(•,•) no tiene por qué ser una función de divergencia definida matemáticamente. Se puede considerar cualquier D(•,•) general que pueda limitar la desviación de la acción de la política de comportamiento del Agente respecto a la distribución de la muestra de entrenamiento.
En general, el problema anterior no siempre tiene una solución de forma cerrada. Los autores del método CFPI analizan un caso especial:
- Utilizamos una estrategia gaussiana para recoger la muestra de entrenamiento.
- Luego aprendemos una política determinista del comportamiento del Agente.
- D(•,•) es una función de verosimilitud negativa.
En tal escenario, una opción razonable para el aprendizaje de políticas sería centrarse en torno a la distribución de la muestra de entrenamiento. Entonces, el problema de optimización propuesto podría representarse como una expresión de forma cerrada:
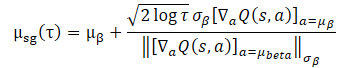
El uso de esta expresión de forma cerrada para mejorar la política del Agente aporta una beneficiosa eficiencia computacional, además de evitar la inestabilidad potencial causada por el SGD. No obstante, su aplicabilidad dependerá de la suposición de una única gaussiana para la estrategia de recogida de muestras de entrenamiento. En la práctica, los conjuntos de datos históricos suelen recopilarse usando estrategias heterogéneas con distintos niveles de experiencia. Una gaussiana unidimensional puede no captar la imagen completa de la distribución, por lo que parece razonable usar una mezcla de gaussianas para representar la política de recogida de datos.
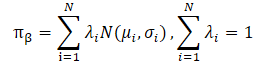
Sin embargo, la sustitución directa de una mezcla de gaussianas de las políticas de recogida de datos de entrenamiento viola la aplicabilidad del problema presentado anteriormente, ya que conduce a una función objetivo no convexa. Aquí nos enfrentamos a dos problemas principales a la hora de resolver la cuestión de la optimización.
En primer lugar, no está claro cómo seleccionar la acción adecuada a partir de la muestra de entrenamiento. Esto debería garantizar que la solución a la política objetivo se encuentre en una pequeña vecindad de la acción seleccionada.
En segundo lugar, el uso de una mezcla de gaussianas no permite la convexidad, lo cual presenta una dificultad en la optimización.
La aplicación de LogSumExp permite transformar el problema de optimización.
![]()
Que puede representarse como una expresión de forma cerrada.
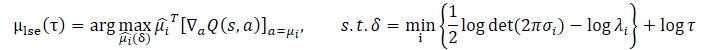
Usando la desigualdad de Jensen, se puede obtener el siguiente problema de optimización:
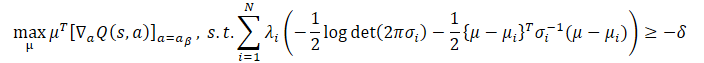
La forma cerrada de la solución para este problema es de la forma:
![]()
En comparación con el problema de optimización original, las dos adiciones propuestas imponen restricciones de intervalo de confianza más estrictas. Esto se logra proporcionando un límite inferior a las probabilidades logarítmicas de la mezcla de gaussianas por encima de un determinado valor umbral. Al mismo tiempo, el parámetro τ controla el tamaño del intervalo de confianza.
Ambas tareas de optimización tienen sus ventajas y desventajas. Cuando la distribución de la muestra de entrenamiento presenta una multimodalidad evidente, el límite inferior del logaritmo de la política de recogida de datos construido mediante la desigualdad de Jensen no puede captar los distintos modos debido a su concavidad, perdiendo la ventaja de modelar la política de recogida de datos como una mezcla de gaussianas. En este caso, el problema de optimización LogSumExp puede servir como sustituto razonable del problema de optimización original, puesto que el límite inferior de LogSumExp preserva la multimodalidad del logaritmo de la política de recogida de datos.
Cuando la distribución de la muestra de entrenamiento se reduce a una única gaussiana, la aproximación con la desigualdad de Jensen se convierte en una igualdad. Así, µjensen resuelve exactamente el problema de optimización que nos ocupa. Sin embargo, en este caso, el grado de precisión de la cota inferior LogSumExp depende en gran medida de los pesos λi=1...N.
Afortunadamente, podemos combinar las mejores cualidades de ambos enfoques y obtener un operador CFPI que tenga en cuenta todos los escenarios anteriores, que devuelva una política de comportamiento que seleccione la acción de mayor rango entre µlse y µjensen:
![]()
En el artículo del autor encontrará cálculos detallados y pruebas sobre la aplicabilidad de todas las expresiones presentadas.
Los autores del método CFPI señalan que el método propuesto también es aplicable a distribuciones no gaussianas de la muestra de entrenamiento. De esta forma, los operadores CFPI presentados ofrecen una plantilla genérica de aprendizaje offline con capacidad para derivar métodos de un solo paso, multipaso e iterativos.
Para evaluar las acciones se utiliza un modelo de Crítico previamente entrenado, que puede entrenarse con la muestra de entrenamiento de cualquier forma conocida. Lo cual supone, en esencia, el primer paso del algoritmo de entrenamiento del modelo.
Ahora le mostraremos un cierto paquete de Estados de la muestra de entrenamiento. Para este paquete se generarán acciones basadas en la política actual del Agente. A continuación, las acciones resultantes se evaluarán según los operadores CFPI propuestos anteriormente.
Basándose en los resultados de esta evaluación, se seleccionan los estados óptimos, sobre los que se realiza la actualización de la política del Agente.
En la construcción de métodos iterativos y de varios pasos, el proceso se repetirá.
Aunque el desarrollo de los operadores CFPI se inspira en el paradigma de restricciones políticas del Agentes de comportamiento, los enfoques propuestos son compatibles con los métodos básicos comunes de aprendizaje por refuerzo. El artículo del autor muestra ejemplos en los que los operadores de CFPI mejoraron la eficacia de las estrategias entrenadas mediante otros algoritmos.
2. Implementación con MQL5
Lo anterior supone una descripción teórica del método Closed-Form Policy Improvement. Estoy de acuerdo en que las fórmulas matemáticas presentadas pueden parecer bastante complejas, pero trataremos de abordarlas con más detalle en el proceso de aplicación de los planteamientos propuestos.
Debemos señalar de entrada que el algoritmo de entrenamiento del modelo propuesto por los autores del artículo implica el entrenamiento secuencial del Crítico y del Actor. En este caso, primero se entrenará el modelo del Crítico. Solo entonces procederemos a entrenar la política del Actor.
Con este enfoque, nuestra técnica en la que el Crítico utiliza el modelo del Actor para preprocesar los datos brutos se vuelve irrelevante. Al fin y al cabo, en la etapa de formación del Crítico, el modelo del Actor aún no ha sido entrenado. Obviamente, podríamos generar un modelo de Actor y utilizarlo como antes, pero entonces nos encontraríamos con el siguiente problema: en la fase de entrenamiento de la política, el algoritmo CFPI no prevé la actualización del modelo del Crítico, y cambiar los parámetros del Actor conllevará necesariamente cambiar también los parámetros del preprocesamiento inicial de datos, y en tal caso, se modificará la distribución en la entrada del Crítico, lo que generalmente conduce a una evaluación distorsionada de las acciones del Actor.
Para remediar la situación descrita anteriormente, podemos eliminar el codificador de estado de origen genérico o trasladarlo a un modelo separado.
No podemos mover el Codificador al modelo del Crítico, ya que la pasada directa del Crítico requiere acciones generadas por el Actor. Y para la pasada directa del Actor, necesitaremos los resultados del Codificador. El círculo se ha cerrado.
2.1 Arquitectura del modelo
En nuestra implementación, hemos decidido llevar el codificador de estado del entorno a un modelo separado, lo que se refleja en la arquitectura de los modelos. La arquitectura de los modelos se describe en el método CreateDescriptions. A pesar del entrenamiento coherente de los modelos de Actor y Crítico, no hemos dividido la descripción de la arquitectura de los modelos en 2 métodos. Por ello, en los parámetros, el método obtendrá los punteros a 3 arrays dinámicos de objetos para registrar la arquitectura de los modelos.
En el cuerpo del método, comprobaremos la relevancia de los punteros a los objetos recibidos y, si es necesario, crearemos nuevos ejemplares de objetos de array.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ bool CreateDescriptions(CArrayObj *actor, CArrayObj *critic, CArrayObj *encoder) { //--- CLayerDescription *descr; //--- if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!critic) { critic = new CArrayObj(); if(!critic) return false; } if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; }
El primero será una descripción de la arquitectura actual del codificador. La arquitectura del modelo comenzará con una capa de datos fuente, cuyo tamaño deberá ser suficiente para registrar la información sobre los movimientos de precio y las lecturas de los indicadores para toda la profundidad de la historia analizada.
//--- State Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1000; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Los datos "brutos" obtenidos se someten a un procesamiento primario en la capa de normalización por lotes.
A continuación viene el bloque de convolución, que reduce la dimensionalidad de los datos con la identificación paralela de patrones estables en ellos.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = HistoryBars; descr.window = BarDescr; descr.step = BarDescr; int prev_wout = descr.window_out = BarDescr / 2; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; prev_count = descr.count = prev_count; descr.window = prev_wout; descr.step = prev_wout; prev_wout = descr.window_out = 8; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 5 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronSoftMaxOCL; descr.count = prev_count; descr.step = prev_wout; descr.optimization = ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
Los resultados del bloque de convolución son procesados por 2 capas neuronales de convolución completa.
//--- layer 6 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.optimization = ADAM; descr.activation = LReLU; if(!encoder.Add(descr)) { delete descr; return false; } //--- layer 7 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Los datos procesados de este modo se complementan con información sobre el estado de la cuenta, que incluye asimismo los armónicos de la marca temporal.
//--- layer 8 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = 2 * LatentCount; descr.window = prev_count; descr.step = AccountDescr; descr.optimization = ADAM; descr.activation = SIGMOID; if(!encoder.Add(descr)) { delete descr; return false; }
A la salida del codificador, creamos estocasticidad. Así reducimos la posibilidad de sobreentrenamiento del modelo y aumentamos su estabilidad en un entorno externo estocástico.
//--- layer 9 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = LatentCount; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Ahora describiremos la arquitectura del Actor. Recibe como entrada los resultados del codificador del entorno descrito anteriormente.
//--- Actor actor.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Como podemos ver, el codificador ha hecho todo el trabajo preparatorio para preparar los datos en bruto. De este modo, el modelo Actor se mantiene lo más simple posible. Aquí crearemos 3 capas totalmente conectadas.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = 2 * NActions; descr.activation = None; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
Y sobre la salida del modelo, formaremos una política estocástica en un espacio de acción continuo.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronVAEOCL; descr.count = NActions; descr.optimization = ADAM; if(!actor.Add(descr)) { delete descr; return false; }
El modelo de Crítico también utiliza los resultados del codificador como entradas, pero a diferencia del modelo Actor, las complementa con un vector de Acciones evaluadas. Por lo tanto, después de la capa de datos de origen, utilizaremos una capa de concatenación que combine los 2 tensores de datos de origen.
//--- Critic critic.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; prev_count = descr.count = LatentCount; descr.activation = None; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConcatenate; descr.count = LatentCount; descr.window = prev_count; descr.step = NActions; descr.optimization = ADAM; descr.activation = LReLU; if(!critic.Add(descr)) { delete descr; return false; }
A continuación vendrá una unidad de toma de decisiones formada por capas neuronales totalmente conectadas.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = LatentCount; descr.activation = LReLU; descr.optimization = ADAM; if(!critic.Add(descr)) { delete descr; return false; } //--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; descr.count = NRewards; descr.optimization = ADAM; descr.activation = None; if(!critic.Add(descr)) { delete descr; return false; } //--- return true; }
Con esto concluimos la descripción de la arquitectura del modelo, por lo que podemos pasar a la construcción del algoritmo de entrenamiento del modelo.
Obviamente, tendremos que recoger una muestra de entrenamiento antes de empezar a entrenar los modelos. Y esta vez no podemos decir que los asesores de interacción con el entorno han trasladado en los artículos anteriores sin modificaciones. El cambio en la arquitectura del modelo en cuanto a la separación del codificador del entorno en un modelo externo también ha afectado a los algoritmos de estos asesores. Pero estos cambios son tan sutiles que le sugiero que se familiarice con ellos en los archivos "...\Experts\CFPI\Research.mq5" y "...\Experts\CFPI\Test.mq5". Encontrará los programas especificados en el anexo. Pasemos ahora a la construcción del algoritmo de aprendizaje del Crítico.
2.2 Entrenamiento del Crítico
El algoritmo de entrenamiento del modelo del Crítico se implementará en el asesor "...\Experts\CFPI\StudyCritic.mq5". Debemos decir que este asesor proporciona un entrenamiento paralelo de 2 modelos del Crítico. Como ya sabe, el uso de 2 Críticos puede mejorar la estabilidad y la eficacia del entrenamiento posterior de la política de comportamiento del Actor. Y junto con los modelos del Crítico, entrenaremos un codificador genérico de condiciones del entorno.
//+------------------------------------------------------------------+ //| Input parameters | //+------------------------------------------------------------------+ input int Iterations = 1e6; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ STrajectory Buffer[]; CNet StateEncoder; CNet Critic1; CNet Critic2;
En el método de inicialización del asesor, primero intentaremos cargar la muestra de entrenamiento.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
Y luego cargaremos los modelos que necesitamos. Cuando no podamos cargar los modelos preentrenados, generaremos otros nuevos con parámetros aleatorios.
//--- load models float temp; if(!StateEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new models"); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); CArrayObj *encoder = new CArrayObj(); if(!CreateDescriptions(actor, critic, encoder)) { delete actor; delete critic; delete encoder; return INIT_FAILED; } if(!Critic1.Create(critic) || !Critic2.Create(critic) || !StateEncoder.Create(encoder)) { delete actor; delete critic; delete encoder; return INIT_FAILED; } delete actor; delete critic; delete encoder; //--- }
Luego trasladaremos todos los modelos a un único contexto OpenCL, lo que nos permitirá intercambiar datos entre modelos sin transferir innecesariamente información hacia y desde la memoria principal del programa.
//---
OpenCL = Critic1.GetOpenCL();
Critic2.SetOpenCL(OpenCL);
StateEncoder.SetOpenCL(OpenCL);
Para evitar posibles errores de transferencia de datos entre modelos, comprobaremos que se ajusten a la misma disposición de los datos utilizados.
//--- StateEncoder.getResults(Result); if(Result.Total() != LatentCount) { PrintFormat("The scope of the State Encoder does not match the latent size count (%d <> %d)", LatentCount, Result.Total()); return INIT_FAILED; } //--- StateEncoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of State Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; } //--- Critic1.GetLayerOutput(0, Result); if(Result.Total() != LatentCount) { PrintFormat("Input size of Critic1 doesn't match State Encoder output (%d <> %d)", Result.Total(), LatentCount); return INIT_FAILED; } //--- Critic2.GetLayerOutput(0, Result); if(Result.Total() != LatentCount) { PrintFormat("Input size of Critic2 doesn't match State Encoder output (%d <> %d)", Result.Total(), LatentCount); return INIT_FAILED; }
Después de pasar con éxito todos los controles, inicializaremos el búfer de datos auxiliar.
//--- Gradient.BufferInit(AccountDescr, 0);
E inicializaremos un evento personalizado para iniciar el proceso de entrenamiento del modelo.
//--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
A continuación, finalizaremos el método de inicialización de asesor.
En el método de desinicialización del asesor, guardaremos los modelos entrenados y realizaremos una limpieza de memoria.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE)) { StateEncoder.Save(FileName + "Enc.nnw", 0, 0, 0, TimeCurrent(), true); Critic1.Save(FileName + "Crt1.nnw", Critic1.getRecentAverageError(), 0, 0, TimeCurrent(), true); Critic2.Save(FileName + "Crt2.nnw", Critic2.getRecentAverageError(), 0, 0, TimeCurrent(), true); } delete Result; delete OpenCL; }
El proceso inmediato de entrenamiento del modelo se llevará a cabo en el método Train. En el cuerpo del método, primero calcularemos las probabilidades ponderadas de seleccionar trayectorias del búfer de reproducción de experiencias.
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
A continuación declararemos las variables locales y organizaremos un ciclo de aprendizaje con el número de iteraciones que haya especificado el usuario en los parámetros externos del asesor.
vector<float> rewards, rewards1, rewards2, target_reward; uint ticks = GetTickCount(); //--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) {
En el cuerpo del ciclo de entrenamiento, muestrearemos la trayectoria y el estado en ella.
int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 3)); if(i < 0) { iter--; continue; }
Después, llenaremos los búferes de datos de origen. En primer lugar, llenaremos el búfer de descripción del entorno con los datos sobre los movimientos de precio y las lecturas de los indicadores analizados y el búfer de reproducción de experiencias.
//--- Q-function study
State.AssignArray(Buffer[tr].States[i].state);
A continuación, rellenaremos el búfer que describe el estado de la cuenta y las posiciones abiertas.
float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
Luego aumentaremos el búfer con armónicos de la marca temporal.
double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
Los datos recogidos serán suficientes para pasar directamente el codificador de estado del entorno.
//--- if(!StateEncoder.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Como ya hemos dicho, en esta fase no utilizaremos el modelo del Actor. Los críticos se entrenarán usando métodos de entrenamiento supervisados sobre la evaluación de las acciones reales y las recompensas del entorno que hemos almacenado previamente en la muestra de entrenamiento. Por lo tanto, utilizaremos los resultados del Codificador del entorno y el vector de acción de la muestra de entrenamiento para pasar directamente ambos Críticos.
//--- Actions.AssignArray(Buffer[tr].States[i].action); if(Actions.GetIndex() >= 0) Actions.BufferWrite(); //--- if(!Critic1.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actions)) || !Critic2.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actions))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Compruebe que las operaciones son correctas y cargue los resultados de la pasada directa de ambos Críticos.
//---
Critic1.getResults(rewards1);
Critic2.getResults(rewards2);
El siguiente paso consistirá en generar los valores objetivo para entrenar los modelos. Como ya hemos mencionado, entrenaremos con los valores reales de la muestra de entrenamiento. En este paso, utilizaremos la recompensa por una única transición a un nuevo estado. Y para mejorar la convergencia, corregiremos la dirección del vector de gradiente de error utilizando el método CAGrad.
Luego ajustaremos los parámetros de los modelos uno a uno. Primero ajustaremos los parámetros del primer Crítico y luego llamaremos al método de pasada inversa del Codificador de estado del entorno.
rewards.Assign(Buffer[tr].States[i + 1].rewards); target_reward.Assign(Buffer[tr].States[i + 2].rewards); rewards = rewards - target_reward * DiscFactor; Result.AssignArray(CAGrad(rewards - rewards1) + rewards1); if(!Critic1.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !StateEncoder.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
A continuación, repetiremos las operaciones para el segundo Crítico.
Result.AssignArray(CAGrad(rewards - rewards2) + rewards2); if(!Critic2.backProp(Result, GetPointer(Actions), GetPointer(Gradient)) || !StateEncoder.backPropGradient(GetPointer(Account), GetPointer(Gradient))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Tenga en cuenta que después de actualizar cada Crítico, se ajustarán los parámetros del Codificador. De este modo, intentaremos que la incorporación del estado del entorno sea lo más informativa y precisa posible.
Una vez actualizados con éxito los parámetros de los modelos, solo nos quedará informar al usuario sobre el progreso del entrenamiento y pasar a la siguiente iteración del ciclo.
//--- if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic1", iter * 100.0 / (double)(Iterations), Critic1.getRecentAverageError()); str += StringFormat("%-15s %5.2f%% -> Error %15.8f\n", "Critic2", iter * 100.0 / (double)(Iterations), Critic2.getRecentAverageError()); Comment(str); ticks = GetTickCount(); } }
Una vez completadas todas las iteraciones de nuestro ciclo de aprendizaje, borraremos el campo de comentarios del gráfico. Luego registraremos la información sobre los resultados del entrenamiento e iniciaremos la finalización del asesor.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic1", Critic1.getRecentAverageError()); PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Critic2", Critic2.getRecentAverageError()); ExpertRemove(); //--- }
Puede ver el código completo del programa en el archivo adjunto.
2.3 Entrenamiento de la política de comportamiento
Tras entrenar los críticos, pasaremos a la siguiente fase: el entrenamiento de la política de comportamiento del Actor. Implementaremos esta funcionalidad en el asesor "...\Expertos\CFPI\Estudio.mq5". Y lo primero que añadiremos a los parámetros externos es el tamaño del paquete en el que seleccionaremos el punto óptimo para el entrenamiento.
//+------------------------------------------------------------------+ //| Input parameters | //+------------------------------------------------------------------+ input int Iterations = 10000; input int BatchSize = 256;
En este asesor utilizaremos 4 modelos, pero entrenaremos solo el Actor.
CNet Actor; CNet Critic1; CNet Critic2; CNet StateEncoder;
En el método de inicialización del asesor, como antes, primero cargaremos la muestra de entrenamiento.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- ResetLastError(); if(!LoadTotalBase()) { PrintFormat("Error of load study data: %d", GetLastError()); return INIT_FAILED; }
Después cargaremos los modelos. En primer lugar, cargaremos los modelos preentrenados del codificador de estados del entorno y del Crítico. La ausencia de estos modelos no nos permitirá llevar más lejos el proceso de aprendizaje. Y cuando se produzca el error de carga de modelos, finalizaremos el asesor.
//--- load models float temp; if(!StateEncoder.Load(FileName + "Enc.nnw", temp, temp, temp, dtStudied, true) || !Critic1.Load(FileName + "Crt1.nnw", temp, temp, temp, dtStudied, true) || !Critic2.Load(FileName + "Crt2.nnw", temp, temp, temp, dtStudied, true)) { Print("Cann't load Critic models"); return INIT_FAILED; }
Pero en ausencia de un Actor preentrenado, inicializaremos un nuevo modelo lleno de parámetros aleatorios.
if(!Actor.Load(FileName + "Act.nnw", temp, temp, temp, dtStudied, true)) { Print("Init new models"); CArrayObj *actor = new CArrayObj(); CArrayObj *critic = new CArrayObj(); if(!CreateDescriptions(actor, critic, critic)) { delete actor; delete critic; return INIT_FAILED; } if(!Actor.Create(actor)) { delete actor; delete critic; return INIT_FAILED; } delete actor; delete critic; }
Trasladaremos todos los modelos al mismo contexto OpenCL y desactivaremos el modo de aprendizaje del Codificador y el Crítico.
OpenCL = Actor.GetOpenCL(); Critic1.SetOpenCL(OpenCL); Critic2.SetOpenCL(OpenCL); StateEncoder.SetOpenCL(OpenCL); //--- StateEncoder.TrainMode(false); Critic1.TrainMode(false); Critic2.TrainMode(false);
A continuación, comprobaremos que la arquitectura de los modelos sea adecuada y compatible.
//--- Actor.getResults(Result); if(Result.Total() != NActions) { PrintFormat("The scope of the actor does not match the actions count (%d <> %d)", NActions, Result.Total()); return INIT_FAILED; }
StateEncoder.GetLayerOutput(0, Result); if(Result.Total() != (HistoryBars * BarDescr)) { PrintFormat("Input size of State Encoder doesn't match state description (%d <> %d)", Result.Total(), (HistoryBars * BarDescr)); return INIT_FAILED; }
StateEncoder.getResults(Result); int latent_state = Result.Total(); Critic1.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Critic1 doesn't match output State Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
Critic2.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Critic2 doesn't match output State Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
Actor.GetLayerOutput(0, Result); if(Result.Total() != latent_state) { PrintFormat("Input size of Actor doesn't match output State Encoder (%d <> %d)", Result.Total(), latent_state); return INIT_FAILED; }
La superación exitosa del bloque de comprobaciones nos permitirá avanzar. Luego inicializaremos el búfer auxiliar y generaremos un evento personalizado para iniciar el proceso de entrenamiento.
Gradient.BufferInit(AccountDescr, 0); //--- if(!EventChartCustom(ChartID(), 1, 0, 0, "Init")) { PrintFormat("Error of create study event: %d", GetLastError()); return INIT_FAILED; } //--- return(INIT_SUCCEEDED); }
Esto completa las operaciones del método de inicialización del asesor. Como de costumbre, en el método de desinicialización, guardaremos el modelo entrenado y borraremos la memoria.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- if(!(reason == REASON_INITFAILED || reason == REASON_RECOMPILE)) Actor.Save(FileName + "Act.nnw", 0, 0, 0, TimeCurrent(), true); delete Result; delete OpenCL; }
El propio proceso de entrenamiento del modelo Actor se implementará en el método Train. En el cuerpo del método, primero determinaremos las probabilidades de seleccionar trayectorias de la muestra de entrenamiento.
//+------------------------------------------------------------------+ //| Train function | //+------------------------------------------------------------------+ void Train(void) { //--- vector<float> probability = GetProbTrajectories(Buffer, 0.9);
Después crearemos las variables locales necesarias,
//--- vector<float> rewards, rewards1, rewards2, target_reward; vector<float> action, action_beta; float Improve = 0; int bar = (HistoryBars - 1) * BarDescr; uint ticks = GetTickCount();
y crearemos un ciclo de entrenamiento del modelo con el número de iteraciones especificado en los parámetros externos del asesor.
//--- for(int iter = 0; (iter < Iterations && !IsStopped()); iter ++) {
En el cuerpo del ciclo, utilizaremos los planteamientos del método CFPI para entrenar la política de comportamiento del Actor. En primer lugar, muestrearemos el paquete de datos de la muestra de entrenamiento. Luego generaremos y evaluaremos las acciones de la actual política del Actor en los estados seleccionados. Para realizar estas operaciones, crearemos un ciclo anidado con un número de iteraciones igual al tamaño del paquete analizado. Guardaremos los resultados de las operaciones en la matriz local mBatch.
matrix<float> mBatch = matrix<float>::Zeros(BatchSize, 4); for(int b = 0; b < BatchSize; b++) { int tr = SampleTrajectory(probability); int i = (int)((MathRand() * MathRand() / MathPow(32767, 2)) * (Buffer[tr].Total - 2)); if(i < 0) { b--; continue; }
Las operaciones de muestreo serán similares a las realizadas anteriormente.
Luego rellenaremos los búferes de descripción de los estados del entorno con los datos de cada estado seleccionado.
//--- State
State.AssignArray(Buffer[tr].States[i].state);
Y el búfer para describir el estado de la cuenta.
float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
Después añadiremos los armónicos de la marca temporal,
double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); if(Account.GetIndex() >= 0) Account.BufferWrite();
e implementaremos el método de pasada directa del codificador de estado.
//--- State embedding if(!StateEncoder.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Tras generar la incorporación del estado del entorno, generamos las acciones del Agente dada la política actual.
//--- Action if(!Actor.feedForward(GetPointer(StateEncoder), -1, NULL, 1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Las acciones generadas serán evaluadas por ambos Críticos.
//--- Cost if(!Critic1.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor)) || !Critic2.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Una vez completadas con éxito todas las operaciones, descargaremos los resultados en vectores locales. E inmediatamente generaremos vectores de datos similares a partir de la muestra de entrenamiento.
Critic1.getResults(rewards1); Critic2.getResults(rewards2); Actor.getResults(action); action_beta.Assign(Buffer[tr].States[i].action); rewards.Assign(Buffer[tr].States[i + 1].rewards); target_reward.Assign(Buffer[tr].States[i + 2].rewards);
En nuestra matriz de resultados, almacenaremos las coordenadas del estado analizado como los índices de la trayectoria y del estado en ella. Y también conservaremos la desviación del vector de acción y su efecto en el resultado.
//--- Collect mBatch[b, 0] = float(tr); mBatch[b, 1] = float(i); mBatch[b, 2] = MathMin(rewards1.Sum(), rewards2.Sum()) - (rewards - target_reward * DiscFactor).Sum(); mBatch[b, 3] = MathSqrt(MathPow(action - action_beta, 2).Sum()); }
A continuación, pasaremos al muestreo y a la estimación del siguiente estado.
Tras procesar y recopilar los datos de todo el conjunto, tendremos que seleccionar el estado óptimo para optimizar la política de comportamiento del Actor. En este paso, deberemos seleccionar el estado con una estimación válida del Crítico y el máximo impacto en la salida del modelo.
En cuanto a la validez de la estimación de la acción, ya hemos dicho que la estimación de la acción del Crítico resultará más precisa con las desviaciones mínimas de la distribución de la muestra de entrenamiento. A medida que aumente la desviación, también disminuirá la precisión de la valoración de los Críticos. Siguiendo esta lógica, un criterio para la precisión de la evaluación de acciones podría ser la distancia entre acciones, que almacenaremos en la columna con el índice 3 de nuestra matriz de análisis.
Ahora deberemos elegir un intervalo de confianza. En su trabajo, los autores del método CFPI usaron la varianza de la distribución. Nosotros no podemos tomar la varianza para el vector de varianzas de acción. La cuestión es que la varianza se considera como la desviación estándar desde la mitad de la distribución. En nuestro caso, en cambio, conservaremos los valores absolutos de las desviaciones. Por tanto, la desviación cero, donde la estimación del Crítico es más precisa, solo puede ser un extremo. En cambio, la media de la distribución estará lejos de este punto. Por lo tanto, el uso de la varianza en este caso no nos garantizará la precisión deseada en las estimaciones de las acciones.
Pero aquí podemos usar la regla de las "3 sigmas": en una distribución normal, el 68% de los datos no se desviará de la esperanza matemática en más de 1 desviación estándar, lo cual significa que podremos utilizar una función cuantil para determinar el intervalo de confianza. Mediante sencillas operaciones matemáticas crearemos un vector de pesos con valores cero para las acciones con desviaciones superiores al intervalo de confianza y "1" para el resto.
action = mBatch.Col(3); float quant = action.Quantile(0.68); vector<float> weights = action - quant - FLT_EPSILON; weights.Clip(weights.Min(), 0); weights = weights / weights; weights.ReplaceNan(0);
Una vez determinado el intervalo de confianza, podremos seleccionar un conjunto de estados con estimaciones de acción adecuadas. Ahora tendremos que elegir el estado óptimo para optimizar la política de comportamiento del Actor. Para simplificar todo el algoritmo y acelerar el proceso de entrenamiento del modelo, hemos abandonado los métodos analíticos propuestos por los autores del CFPI, utilizando uno más sencillo.
Creo que resulta obvio que en nuestro caso la dirección más óptima de optimización será la que maximice el cambio en la rentabilidad de la política de comportamiento del Agente mientras minimiza el cambio en el subespacio de acciones. Al fin y al cabo, nuestro objetivo es maximizar el rendimiento de nuestras políticas, y unas desviaciones mínimas nos permitirán hablar de una evaluación más precisa de las acciones del Crítico. Huelga decir que existen desplazamientos positivos y negativos en nuestra matriz analítica de evaluación de las acciones. Al mismo tiempo, el aumento de la rentabilidad total se verá afectado por igual tanto por los mayores beneficios como por las menores pérdidas. Por lo tanto, utilizaremos el valor absoluto de la desviación de la recompensa de transición para calcular el criterio de selección óptimo.
rewards = mBatch.Col(2); weights = MathAbs(rewards) * weights / action;
En el vector resultante, seleccionaremos el elemento con el valor máximo. Su índice nos indicará el estado óptimo para utilizarlo en el algoritmo de optimización del modelo.
ulong pos = weights.ArgMax(); int sign = (rewards[pos] >= 0 ? 1 : -1);
Aquí almacenaremos el signo de la desviación de la recompensa en la variable local.
De cara al futuro, debemos decir que actualizaremos la política de comportamiento del Actor usando los gradientes de error transmitidos por el modelo del Crítico. En este modo de entrenamiento, no podremos contar el error de predicción del Actor. Y para controlar el proceso de entrenamiento, hemos introducido una medida del coeficiente de mejora media de los estados utilizados.
Improve = (Improve * iter + weights[pos]) / (iter + 1);
Lo que sigue es el conocido algoritmo para optimizar el modelo de política, solo que esta vez no utilizaremos un estado aleatorio, sino uno en el que podamos maximizar el rendimiento del modelo.
int tr = int(mBatch[pos, 0]); int i = int(mBatch[pos, 1]);
Al igual que antes, rellenaremos los búferes para describir el estado del entorno y el estado de la cuenta.
//--- Policy study State.AssignArray(Buffer[tr].States[i].state); float PrevBalance = Buffer[tr].States[MathMax(i - 1, 0)].account[0]; float PrevEquity = Buffer[tr].States[MathMax(i - 1, 0)].account[1]; Account.Clear(); Account.Add((Buffer[tr].States[i].account[0] - PrevBalance) / PrevBalance); Account.Add(Buffer[tr].States[i].account[1] / PrevBalance); Account.Add((Buffer[tr].States[i].account[1] - PrevEquity) / PrevEquity); Account.Add(Buffer[tr].States[i].account[2]); Account.Add(Buffer[tr].States[i].account[3]); Account.Add(Buffer[tr].States[i].account[4] / PrevBalance); Account.Add(Buffer[tr].States[i].account[5] / PrevBalance); Account.Add(Buffer[tr].States[i].account[6] / PrevBalance);
Luego añadiremos los armónicos de la marca temporal.
double time = (double)Buffer[tr].States[i].account[7]; double x = time / (double)(D'2024.01.01' - D'2023.01.01'); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_MN1); Account.Add((float)MathCos(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_W1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0)); x = time / (double)PeriodSeconds(PERIOD_D1); Account.Add((float)MathSin(x != 0 ? 2.0 * M_PI * x : 0));
Y generaremos una incorporación del estado del entorno.
//--- State if(Account.GetIndex() >= 0) Account.BufferWrite(); if(!StateEncoder.feedForward(GetPointer(State), 1, false, GetPointer(Account))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Acción del agente en vista de la política actual.
//--- Action if(!Actor.feedForward(GetPointer(StateEncoder), -1, NULL, 1)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Después estimaremos el coste de las acciones del Agente.
//--- Cost if(!Critic1.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor)) || !Critic2.feedForward(GetPointer(StateEncoder), -1, GetPointer(Actor))) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
Para optimizar la política de comportamiento del Agente, utilizaremos el Crítico con una estimación mínima. Y para mejorar la convergencia, corregiremos el vector de dirección del gradiente utilizando el método CAGrad.
Critic1.getResults(rewards1); Critic2.getResults(rewards2); //--- rewards.Assign(Buffer[tr].States[i + 1].rewards); target_reward.Assign(Buffer[tr].States[i + 2].rewards); rewards = rewards - target_reward * DiscFactor; CNet *critic = NULL; if(rewards1.Sum() <= rewards2.Sum()) { Result.AssignArray(CAGrad((rewards1 - rewards)*sign) + rewards1); critic = GetPointer(Critic1); } else { Result.AssignArray(CAGrad((rewards2 - rewards)*sign) + rewards2); critic = GetPointer(Critic2); }
Luego realizaremos secuencialmente la pasada inversa del Crítico y el Actor.
if(!critic.backProp(Result, GetPointer(Actor), -1) || !Actor.backPropGradient((CBufferFloat *)NULL)) { PrintFormat("%s -> %d", __FUNCTION__, __LINE__); break; }
En este punto quiero recordarles que en esta fase no estamos optimizando el modelo del Crítico. Por lo tanto, no será necesaria la pasada inversa del codificador de estado del entorno.
Con esto completaremos las operaciones de una iteración de actualización de la política de comportamiento del Agente. Después informaremos al usuario sobre el progreso del proceso de entrenamiento y pasaremos a la siguiente iteración de nuestro ciclo.
if(GetTickCount() - ticks > 500) { string str = StringFormat("%-15s %5.2f%% -> %15.8f\n", "Mean Improvement", iter * 100.0 / (double)(Iterations), Improve); Comment(str); ticks = GetTickCount(); } }
Una vez completadas todas las iteraciones del ciclo de entrenamiento, borraremos el campo de comentarios del gráfico, mostraremos la información sobre los resultados del entrenamiento en el registro e iniciaremos la finalización del asesor.
Comment(""); //--- PrintFormat("%s -> %d -> %-15s %10.7f", __FUNCTION__, __LINE__, "Mean Improvement", Improve); ExpertRemove(); //--- }
Aquí concluimos el análisis de los algoritmos de los programas utilizados en este artículo. Podrá leer su código completo en el archivo adjunto. Pasemos ahora a comprobar los resultados del trabajo realizado.
3. Simulación
Más arriba nos hemos familiarizado con el método Closed-Form Policy Improvement y hemos trabajado bastante para implementar sus enfoques utilizando MQL5. Quiero recordarles que hemos utilizado las ideas propuestas, pero el método analítico para seleccionar el estado óptimo se ha aplicado de forma distinta a la propuesta del artículo. Además, hemos utilizado nuestra experiencia previa en nuestro trabajo. Por lo tanto, los resultados obtenidos pueden diferir significativamente de los indicados por los autores del método en su artículo. Obviamente, nuestro entorno de pruebas será diferente de los experimentos mencionados en el artículo del autor.
Como siempre, el entrenamiento y las pruebas de los modelos se han realizado con los datos históricos del marco temporal EURUSD H1. Para entrenar los modelos, hemos utilizado los datos de los 7 primeros meses de 2023. Los modelos entrenados se han probado con los datos históricos de agosto de 2023. Los parámetros de todos los indicadores analizados se han utilizado por defecto.
La aplicación del método CFPI ha requerido algunos cambios en la arquitectura de los modelos, pero no ha afectado a la estructura de los datos originales. Por lo tanto, en la primera fase del entrenamiento podemos usar la muestra de entrenamiento creada anteriormente al probar uno de los algoritmos de aprendizaje que hemos comentado antes. En el artículo, hemos utilizado la muestra de entrenamiento del artículo anterior. Para ello, hemos creado una copia de un archivo llamado "CFPI.bd". Pero también podemos crear una muestra de entrenamiento completamente nueva utilizando uno de los métodos comentados anteriormente. En esta parte, el método CFPI no impone ninguna restricción,
aunque los cambios en la arquitectura nos han impedido aprovechar los modelos previamente entrenados. Por tanto, todo el proceso de aprendizaje ha partido de cero, por así decirlo.
En primer lugar, hemos entrenado los modelos del Codificador de estados y el Crítico utilizando el asesor "...{Experts\Experts\CFPI\StudyCritic.mq5".
L, muestra de entrenamiento que hemos utilizado tenía 500 trayectorias con 3591 estados en cada trayectoria. lo que nos da un total de unos 1,8 millones de conjuntos Estado-Acción-Recompensa. El entrenamiento inicial de los modelos de los Críticos se ha realizado durante 1 millón de iteraciones, lo que teóricamente permite analizar casi cada segundo estado. De acuerdo, para las trayectorias continuas, cuando no todas las nuevas condiciones del entorno conllevan cambios drásticos en la situación del mercado, no es un mal resultado. Y con el énfasis en las trayectorias de máximo rendimiento, esto permitirá a los Críticos explorar virtualmente dichas trayectorias y ampliar sus "horizontes" a pasadas menos rentables.
A continuación, entrenaremos la política de comportamiento del Actor en el asesor "...\Experts\CFPI\Study.mq5". En una pasada, realizamos 10 mil iteraciones de entrenamiento con un paquete de 256 estados. En total, esto nos permite analizar más de 2,5 millones de estados, lo cual supera nuestra muestra de entrenamiento.
Debo decir que ya después de la primera iteración del entrenamiento, en la pasada de prueba, podemos notar algunos requisitos previos para la creación de estrategias rentables. Los gráficos de balance pueden poner de relieve las áreas rentables. Durante la recopilación adicional de trayectorias de entrenamiento, de 200 pasadas, 3 de ellas han terminado con beneficios. Obviamente, esto podría ser tanto mi opinión subjetiva como el resultado de la confluencia de algunos factores independientes del método. Por ejemplo, hemos tenido suerte y la inicialización aleatoria de los modelos no ha ofrecido un mal resultado. Pero sin duda podemos afirmar que existe una clara tendencia al alza en el rendimiento medio y el factor de beneficio de las pasadas como resultado de las iteraciones posteriores de entrenamiento de los modelos y la recopilación de pasadas adicionales.
Tras varias iteraciones de entrenamiento del modelo, hemos obtenido una política de comportamiento del Actor capaz de generar beneficios tanto con los datos históricos de la muestra de entrenamiento como con los datos de prueba posteriores fuera de la muestra de entrenamiento. A continuación le mostramos los resultados de las pruebas del modelo.
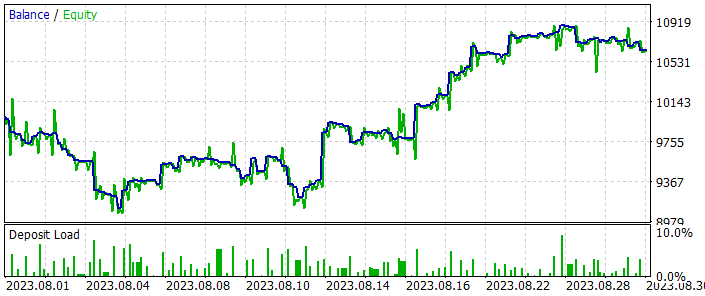
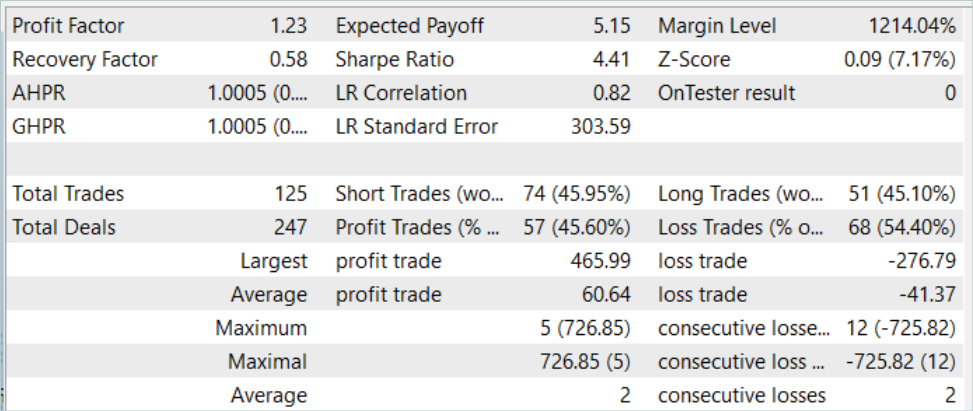
En el gráfico de balance, es posible que observe cierta reducción al principio del periodo de prueba. Pero más adelante, el modelo muestra una tendencia bastante plana de crecimiento del balance, lo cual nos permite tanto recuperar lo perdido como aumentar nuestros beneficios. En general, durante el periodo de prueba el modelo ha realizado 125 operaciones, de las que el 45,6% se han cerrado con beneficios. Cabe señalar aquí que la operación rentable máxima y la operación rentable media son un 50% superiores a las operaciones perdedoras similares. Y esto nos permite obtener un factor de beneficio de 1,23.
Conclusión
En este artículo, hemos introducido otro algoritmo para entrenar modelos, el Closed-Form Policy Improvement. Probablemente, la principal aportación de este método sea la adición de enfoques analíticos para seleccionar la dirección de optimización del modelo entrenado. Sí, este proceso requiere un coste computacional adicional, pero, curiosamente, este enfoque reduce el coste de entrenamiento del modelo en su conjunto. La cuestión es que no intentamos replicar por completo la mejor trayectoria presentada. En su lugar, concentramos las amplificaciones en los lugares de máxima eficacia y no perdemos el tiempo buscando la optimalidad en los fenómenos de ruido.
En la parte práctica de nuestro trabajo hemos aplicado las ideas propuestas por los autores del método CFPI, aunque desviándonos de los cálculos matemáticos de los autores. No obstante, hemos tenido una experiencia positiva y un buen resultado de las pruebas del trabajo realizado.
Mi opinión personal es que el método Closed-Form Policy Improvement tiene su mérito, y podemos utilizar sus planteamientos para construir nuestras estrategias comerciales.
Enlaces
Programas usados en el artículo
| # | Nombre | Tipo | Descripción |
|---|---|---|---|
| 1 | Research.mq5 | Asesor | Asesor de recopilación de datos |
| 2 | ResearchRealORL.mq5 | Asesor | Asesor de recopilación de ejemplos con el método Real-ORL |
| 3 | Study.mq5 | Asesor | Asesor de entrenamiento del Actor |
| 4 | StudyCritic.mq5 | Asesor | Asesor de entrenamiento del Crítico |
| 5 | Test.mq5 | Asesor | Asesor para la prueba de modelos |
| 6 | Trajectory.mqh | Biblioteca de clases | Estructura de descripción del estado del sistema. |
| 7 | NeuroNet.mqh | Biblioteca de clases | Biblioteca de clases para crear una red neuronal |
| 8 | NeuroNet.cl | Biblioteca | Biblioteca de código de programa OpenCL |
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/13982
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Redes neuronales: así de sencillo (Parte 71): Previsión de estados futuros basada en objetivos (GCPC)
Redes neuronales: así de sencillo (Parte 71): Previsión de estados futuros basada en objetivos (GCPC)
 GIT: ¿Pero qué es esto?
GIT: ¿Pero qué es esto?
 Algoritmos de optimización de la población: Algoritmo híbrido de optimización de forrajeo bacteriano con algoritmo genético (Bacterial Foraging Optimization - Genetic Algorithm, BFO-GA)
Algoritmos de optimización de la población: Algoritmo híbrido de optimización de forrajeo bacteriano con algoritmo genético (Bacterial Foraging Optimization - Genetic Algorithm, BFO-GA)
 Desarrollo de un sistema de repetición (Parte 42): Proyecto Chart Trade (I)
Desarrollo de un sistema de repetición (Parte 42): Proyecto Chart Trade (I)
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso