MQL5の圏論（第6回）：単射的引き戻しと全射的押し出し

MetaTrader 5 — トレーディングシステム | 1 6月 2023, 13:38

365

Stephen Njuki

はじめに

前回の記事では、圏論の等化子を使用して、サンプリングされたデータを使用してボラティリティの変化を推定する方法について説明しました。このフォローアップ記事では、最終的な解析結果におけるさまざまな錐の設定の重要性を探ることにより、圏論における構成と錐について詳しく掘り下げていきます。市場のいくつかの側面を予測したり説明したりするのに使用できる圏論の別の概念を検討しているのではなく、より具体的に圏論の構成と錐の感度分析をおこないます。

その前に、前回の記事の概念の双対である余等化子を見てみましょう。

余等化子

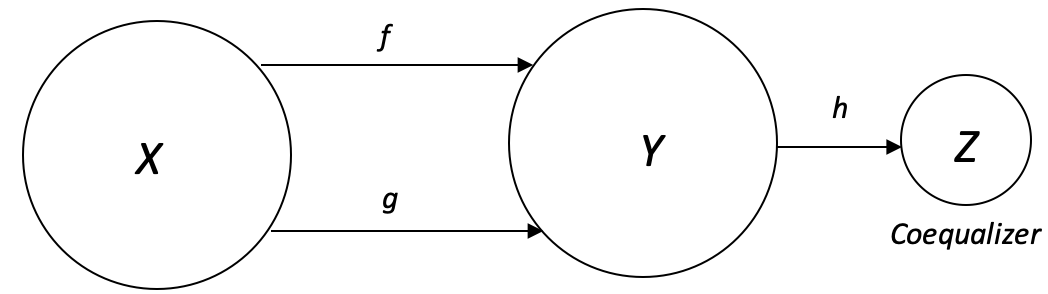
前の記事で説明した等化子の双対である余等化子は、通常は異なる余域から要素を取得する始域（類似した要素に焦点を当てた等化子を思い出してください）で、余等化子の射を通して、始域要素の差異ごとに1つの要素を生成します。新しい等化子始域内に作成された共通要素は、始域内の各要素に対しておこなわれます。通常、これは次のように描画されます。

したがって、関数hは商写像として機能します。始域（fまたはg）に応じて異なる値に写像される可能性がある始域内の各値dについて、余等化子始域の最終結果（要素）が同じであるからです。

値の配列に「共通の値の分子Z」を掛けて同じ値の配列で割ると、常に共通の値が得られます。したがって、Yの値の配列による除算は、Yの商のように機能します。これは、次のように表されることがよくあります。

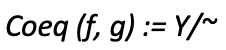
hを使用すると、商関数は次のように定義されます。

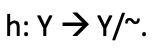
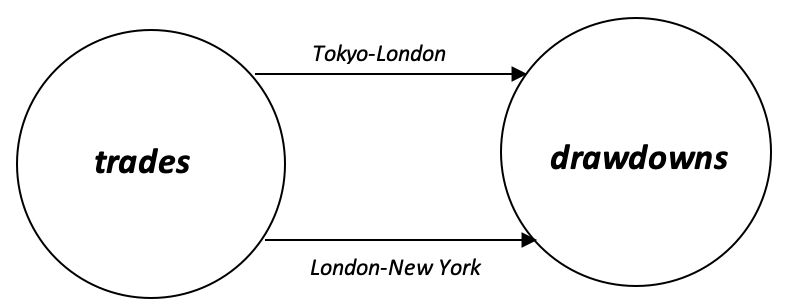
実世界で、トレーダーに最近の取引活動からの次のログがあるとします。

次の図が推測できます。

この図で、 Tokyo-London overlapで取引しているか、London-New York overlapで取引しているかに基づいてポジションサイズ設定をガイドする余等化子を考案することができます。ログに記録されたドローダウンに基づいてポジションサイズ設定を逆に重み付けすると、より悪いケースのシナリオに基づいた同等の余等化子が得られます。これは圏論を使わずにできます。圏理論が役立つのは、普遍性を適用することです。これはすでに2つの前の記事で強調されています。私たちの場合、ライブのドローダウン測定値を、ポートフォリオの重み付けされた（最悪の場合の）値と比較できます。現在の値が予想より悪い場合は、ポジションのサイズを適切に変更します。

単射的引き戻し

モニック射は、余域以下の基数の始域を持ち、その始域からのすべての射が余域内の個別の要素に写像される単射準同型写像です。圏論における引き戻しは、典型的な4始域の錐において、積始域の対角線上にある錐内の始域（別名ファイバー積）です。

これら2つの概念を組み合わせると、興味深い特性が得られます。以下の図を考えてみます。

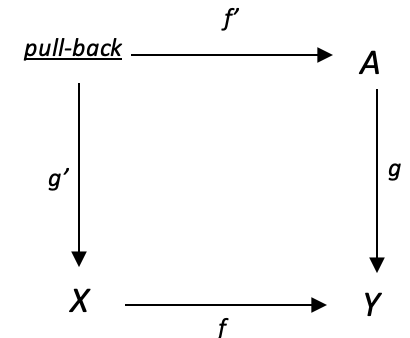
g:A-->Yがモニック射である場合、任意の関数f:X-->Yに対して、図の左辺の写像g’:pull-back-->Xもまた、可換である限りモニック射です。

これを説明するために、積始域Y、因子始域X、因子始域A、引き戻し始域を持つ錐（英語）を考えてみましょう。それぞれ、最新のNバーと以前のNバーのEURJPY、EURUSD、USDJPY、USDX（ドルインデックス）の相関値を持ちます。

Nの値は、フィボナッチ数列に従う分位値バケットから選択できます。この例では、3、5、8、13、21という5つの値を使用します。したがって、各始域には、これらの各期間を使用する相関関係が存在します。これらの値は時々変化するため、オントロジーログはこれらすべての値を毎回記録するのに役立ちます。したがって、オントロジーログには各期間の錐が存在します。

この記事ではオントロジーログは使用しませんが、6か月間にわたるさまざまな錐の値のテスターログを毎週の時間枠で計算して提示します。

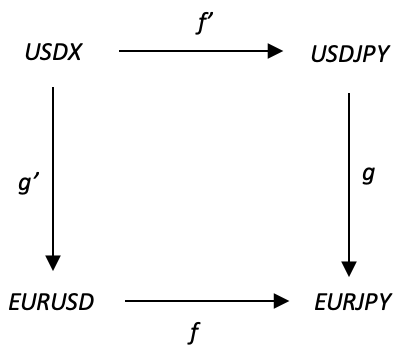
ただし、上の図を続けると、各始域には期間3、5、8、13、および21にわたる相関が含まれており、準同型写像f、g、f'、およびg'は、これらの期間ごとに始域全体で相関を単純にペアにします。したがって、USDXの最近5週間とその前の5週間の相関関係（f'の下）は、USDJPYの最近5週間とその前の5週間の相関関係とペアになります。

積始域EURJPYにも上記の5つの期間の相関値が含まれますが、その値は始域EURUSDとUSDJPYの間の積の結果になります。これら2つの積は、2つの始域の幾何平均になります。通常、幾何平均は2つの積の平方根です。ここでの場合、これらの積は2つの相関関係になります。これらの相関は負の値になる可能性があります。ここでは虚数については詳しく説明しませんが、相関値を-1.0～1.0ではなく0.0～2.0の範囲で正規化することが賢明です。平方根/幾何学値が取得されたら、-1.0～1.0の標準形式に戻すことができます。

したがって、正規化するには、幾何平均を計算する前に相関値に1.0を足します。平均値が得られたら、単に1.0を引いて標準に戻します。

制御目的で、特性を使用せずに、単に上記の期間分位バケットを使用して、毎週の時間枠で2021-07-01から2022-01-01（約26週間）までの期間の分位値バケットを使用して、最初に錐でテストを実行する場合、相関性が最も高いUSDXの期間のみを抽出すると、次の結果が得られます。

2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1)                        [,0]               [,1]               [,2]               [,3]               [,4]               [,5]
2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1)    [ 0,] " DATE "          ," N period "      ," EURUSD corr. "  ," USDJPY corr. "  ," geometric mean "," actual corr. "  
2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1)    [ 1,] "2021.07.04 00:00","13"              ,"0.49"            ,"0.90"            ,"0.69"            ,"0.25"            
2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1)    [ 2,] "2021.07.11 00:00","5"               ,"0.70"            ,"0.00"            ,"0.30"            ,"-0.00"           
2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1)    [ 3,] "2021.07.18 00:00","5"               ,"0.70"            ,"0.10"            ,"0.37"            ,"0.20"            
2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1)    [ 4,] "2021.07.25 00:00","5"               ,"0.50"            ,"-0.20"           ,"0.10"            ,"0.70"            
2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1)    [ 5,] "2021.08.01 00:00","5"               ,"0.80"            ,"0.10"            ,"0.41"            ,"0.50"            
2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1)    [ 6,] "2021.08.08 00:00","5"               ,"0.80"            ,"0.30"            ,"0.53"            ,"0.20"            
2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1)    [ 7,] "2021.08.15 00:00","5"               ,"0.90"            ,"0.30"            ,"0.57"            ,"0.70"            
2023.04.07 16:05:32.658 ct_6 (USDX-JUN23,W1)    [ 8,] "2021.08.22 00:00","5"               ,"0.40"            ,"0.50"            ,"0.45"            ,"0.90"            
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [ 9,] "2021.08.29 00:00","5"               ,"0.20"            ,"0.70"            ,"0.43"            ,"0.50"            
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [10,] "2021.09.05 00:00","5"               ,"-0.20"           ,"0.60"            ,"0.13"            ,"0.00"            
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [11,] "2021.09.12 00:00","21"              ,"0.69"            ,"0.27"            ,"0.46"            ,"-0.79"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [12,] "2021.09.19 00:00","5"               ,"0.60"            ,"-0.20"           ,"0.13"            ,"0.50"            
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [13,] "2021.09.26 00:00","5"               ,"0.30"            ,"0.20"            ,"0.25"            ,"0.60"            
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [14,] "2021.10.03 00:00","3"               ,"1.00"            ,"1.00"            ,"1.00"            ,"-0.50"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [15,] "2021.10.10 00:00","13"              ,"0.55"            ,"0.49"            ,"0.52"            ,"-0.29"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [16,] "2021.10.17 00:00","13"              ,"0.60"            ,"0.65"            ,"0.62"            ,"-0.36"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [17,] "2021.10.24 00:00","13"              ,"0.62"            ,"0.51"            ,"0.56"            ,"-0.45"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [18,] "2021.10.31 00:00","13"              ,"0.64"            ,"0.53"            ,"0.59"            ,"-0.55"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [19,] "2021.11.07 00:00","5"               ,"0.80"            ,"-0.50"           ,"-0.05"           ,"-0.10"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [20,] "2021.11.14 00:00","5"               ,"0.50"            ,"0.50"            ,"0.50"            ,"-0.70"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [21,] "2021.11.21 00:00","3"               ,"1.00"            ,"1.00"            ,"1.00"            ,"1.00"            
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [22,] "2021.11.28 00:00","3"               ,"0.50"            ,"0.50"            ,"0.50"            ,"1.00"            
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [23,] "2021.12.05 00:00","8"               ,"0.76"            ,"-0.62"           ,"-0.18"           ,"-0.02"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [24,] "2021.12.12 00:00","8"               ,"0.62"            ,"-0.52"           ,"-0.12"           ,"-0.12"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [25,] "2021.12.19 00:00","8"               ,"0.40"            ,"-0.05"           ,"0.16"            ,"-0.26"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [26,] "2021.12.26 00:00","3"               ,"0.50"            ,"0.50"            ,"0.50"            ,"0.50"

これらの結果では、幾何平均値と実際の値の間の相関は-0.07であり、USDXから最も高い相関期間を選択するという仮説がEURJPYの値の正確な予測につながらないことを意味します。

次に、上記のモニック射特性を見てみると、実装は始域が同じ基数を持たないことを意味します。当初、3、5、8、13、21などのフィボナッチ数列の一部に基づいて一連の期間を選択していました。上記のテスト実行ログから、ドルインデックス（USDX）との相関が最も高いものが選択されました。たとえば、2021-09-05の5つの選択期間は、現在の5つのUSDXバーと前の5つのUSDXバーの相関がすべての期間3、5、8、13、および21の中で最も高かったことになります。よってこれが選択され、EURUSDとUSDJPYの相関期間として使用されます。

ただし、たとえばUSDJPYとEURJPYおよびUSDXとEURUSDの平行な側面にある錐にモニック射特性を適用すると、より興味深い結果が得られる可能性があります。これを達成するために、始域の基数に焦点を当てます。錐はUSDXからEURJPYに向かって構成されており、モニック射は始域と比較した場合に等しいかそれより大きな余域を必要とするため、USDXからEURJPYに向かって始域サイズを増やし、余域内の同じ要素に写像される始域を避けることで、各準同型性が単射であることを簡単に保証できます。

始域サイズをスケーリングする単位は、各始域に割り当てる期間の長さの分位バケットです。したがって、前の記事で試みたように、始域ごとに分位バケットを作成する必要があります。したがって、これを錐のフローと組み合わせると、始域USDXのバケットが最も少なくなりますが、EURJPYに近づくにつれて、始域ごとの分位バケットの数が増加することがわかります。

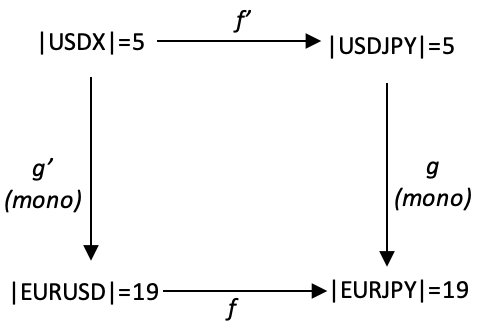
射g'とgの写像で使用する指標はRSIになります。周期的で0～100で簡単に正規化できるRSIは適格です。別の同様の指標を選択することもできますが、この場合、指標値によって余域のどの割合が関連するかが決まります。極値3および21は以前と同様に変更されませんが、値5はRSI測定値に正比例して4、5、6、7のいずれかに写像されます。

USDX内の同じ期間選択基準を使用して上記と同様のテストを実行すると、これらのログが得られます。

2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)                        [,0]               [,1]               [,2]               [,3]               [,4]               [,5]
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [ 0,] " DATE "          ," N period "      ," EURUSD corr. "  ," USDJPY corr. "  ," geometric mean "," actual corr. "  
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [ 1,] "2021.07.04 00:00","13"              ,"0.13"            ,"0.90"            ,"0.47"            ,"0.24"            
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [ 2,] "2021.07.11 00:00","5"               ,"-0.49"           ,"0.00"            ,"-0.28"           ,"-0.49"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [ 3,] "2021.07.18 00:00","5"               ,"0.37"            ,"0.10"            ,"0.23"            ,"-0.09"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [ 4,] "2021.07.25 00:00","5"               ,"0.20"            ,"-0.20"           ,"-0.02"           ,"-0.09"           
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [ 5,] "2021.08.01 00:00","5"               ,"0.43"            ,"0.10"            ,"0.25"            ,"0.14"            
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [ 6,] "2021.08.08 00:00","5"               ,"0.26"            ,"0.30"            ,"0.28"            ,"0.37"            
2023.04.07 16:05:32.659 ct_6 (USDX-JUN23,W1)    [ 7,] "2021.08.15 00:00","5"               ,"-0.20"           ,"0.30"            ,"0.02"            ,"0.09"            
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [ 8,] "2021.08.22 00:00","5"               ,"-0.71"           ,"0.50"            ,"-0.35"           ,"0.14"            
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [ 9,] "2021.08.29 00:00","5"               ,"-0.89"           ,"0.70"            ,"-0.56"           ,"-0.31"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [10,] "2021.09.05 00:00","5"               ,"-0.77"           ,"0.60"            ,"-0.40"           ,"-0.31"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [11,] "2021.09.12 00:00","21"              ,"0.68"            ,"0.27"            ,"0.46"            ,"-0.88"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [12,] "2021.09.19 00:00","5"               ,"-0.31"           ,"-0.20"           ,"-0.26"           ,"-0.09"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [13,] "2021.09.26 00:00","5"               ,"0.54"            ,"0.20"            ,"0.36"            ,"0.77"            
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [14,] "2021.10.03 00:00","3"               ,"-0.80"           ,"1.00"            ,"-0.37"           ,"-0.20"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [15,] "2021.10.10 00:00","13"              ,"0.16"            ,"0.49"            ,"0.32"            ,"-0.42"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [16,] "2021.10.17 00:00","13"              ,"0.43"            ,"0.65"            ,"0.53"            ,"-0.47"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [17,] "2021.10.24 00:00","13"              ,"0.68"            ,"0.51"            ,"0.59"            ,"-0.53"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [18,] "2021.10.31 00:00","13"              ,"0.78"            ,"0.53"            ,"0.65"            ,"-0.58"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [19,] "2021.11.07 00:00","5"               ,"0.89"            ,"-0.50"           ,"-0.03"           ,"0.71"            
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [20,] "2021.11.14 00:00","5"               ,"0.89"            ,"0.50"            ,"0.68"            ,"0.37"            
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [21,] "2021.11.21 00:00","3"               ,"-0.40"           ,"1.00"            ,"0.10"            ,"-0.20"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [22,] "2021.11.28 00:00","3"               ,"-0.40"           ,"0.50"            ,"-0.05"           ,"1.00"            
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [23,] "2021.12.05 00:00","8"               ,"0.33"            ,"-0.62"           ,"-0.29"           ,"-0.12"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [24,] "2021.12.12 00:00","8"               ,"0.43"            ,"-0.52"           ,"-0.17"           ,"-0.23"           
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [25,] "2021.12.19 00:00","8"               ,"0.60"            ,"-0.05"           ,"0.23"            ,"0.10"            
2023.04.07 16:05:32.660 ct_6 (USDX-JUN23,W1)    [26,] "2021.12.26 00:00","3"               ,"0.40"            ,"0.50"            ,"0.45"            ,"-0.80"

2つの結果セット間に有意な統計的差異はありません。そして、この結果-0.08は、ほぼ15%増加していることに変わりはありません。始域の錐とつながり、およびそのさまざまな要素（この場合は相関関係）は、それ自体では目立たないものの、取引において非常に決定的なパターンや傾向を研究する機会を確実に提供します。

全射的押し出し

エピ射は、余域よりも大きな基数を持つ始域を持ち、その始域からの射が余域内のすべての要素にマッピングされる、つまりリンクされていないものがないことを意味する全射準同型です。圏論における押し出し（英語）は、典型的な4始域の錐では余積始域の対角線上にある錐内の始域（別名ファイバー余積）です。

単射的引き戻しの場合と同様に、これら2つを組み合わせると、特性も得られます。これを次の図に示します。

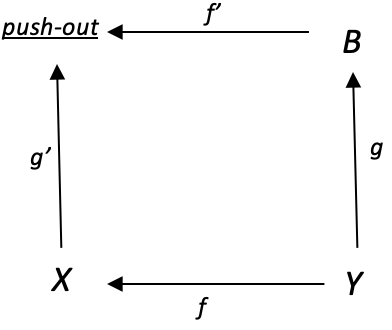
g:YàBは準同型であるため、任意の関数f:Y-->Xに対して、図の左辺の写像g':X-->push-ouも準同型です。これを調べるために、余積始域Yが任意の証券の入札価格のボリンジャーエンベロープ範囲値である錐をもう一度考えてみましょう。2つの余積因子始域（XおよびB）は、ボリンジャーバンドの上部エンベロープと下部エンベロープになります。これら2つの差（「余積和集合」）により、ボリンジャーエンベロープ範囲の予測が得られます。押し出し始域は、上下のエンベロープが導出されるボリンジャーバンドのベースライン移動平均になります。

上記の単射的引き戻しでさまざまな相関係数を計算するための変数として期間の長さを使用したのと同じように、さまざまなボリンジャーエンベロープを提供する各始域のさまざまな移動平均値を導出するためにも期間の長さを使用します。探索的テストでは、上記のように、期間3、5、8、13、21から開始できます。

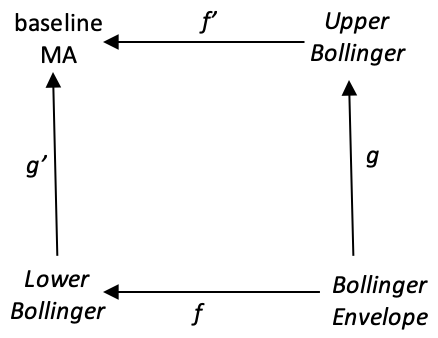
錐はボリンジャーエンベロープ始域からベースラインMA始域に向かって構成されます。これは、その頂点が以前のような積ではなく余積であるため、単射的押し出し上の最初の錐とは反対の方向に構成されます。射の矢印は準同型の方向を示します。各始域内の要素のリンクは、上記のようにそれぞれのN期間に従うだけです。

したがって、エピ射特性を適用する前に、最小標準偏差に基づいてベースラインMA始域の期間を選択してテストを実行すると、次のようなログが得られます。

2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)                        [,0]               [,1]               [,2]               [,3]               [,4]               [,5]               [,6]
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [ 0,] " DATE "          ," N period "      ," Baseline-MA "   ," Upper Bands "   ," Lower Bands "   ," Envelope Delta "," Actual Range "  
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [ 1,] "2021.07.04 00:00","8"               ,"103.425"         ,"105.548"         ,"101.301"         ,"4.248"           ,"0.850"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [ 2,] "2021.07.11 00:00","8"               ,"103.425"         ,"105.548"         ,"101.301"         ,"4.248"           ,"0.758"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [ 3,] "2021.07.18 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"0.691"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [ 4,] "2021.07.25 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"1.193"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [ 5,] "2021.08.01 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"1.030"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [ 6,] "2021.08.08 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"0.735"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [ 7,] "2021.08.15 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.270"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [ 8,] "2021.08.22 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.868"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [ 9,] "2021.08.29 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.854"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [10,] "2021.09.05 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.750"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [11,] "2021.09.12 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.912"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [12,] "2021.09.19 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.565"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [13,] "2021.09.26 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.325"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [14,] "2021.10.03 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.770"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [15,] "2021.10.10 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.811"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [16,] "2021.10.17 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.700"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [17,] "2021.10.24 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.035"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [18,] "2021.10.31 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.842"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [19,] "2021.11.07 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.400"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [20,] "2021.11.14 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"1.305"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [21,] "2021.11.21 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"0.933"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [22,] "2021.11.28 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.115"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [23,] "2021.12.05 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.747"           
2023.04.07 19:04:11.241 ct_6 (USDX-JUN23,W1)    [24,] "2021.12.12 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.077"           
2023.04.07 19:04:11.242 ct_6 (USDX-JUN23,W1)    [25,] "2021.12.19 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.685"           
2023.04.07 19:04:11.242 ct_6 (USDX-JUN23,W1)    [26,] "2021.12.26 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.778"

分析と実際の間の相関チェックは0.12であり、まだ有意ではありません。

これは、エピ射特性につながります。これを、たとえばLOWER-BOLLINGER-->BASELINE-MAおよびBOLLINGER-ENVELOPE-->UPPER-BOLLINGERの平行な側面にある錐に適用すると、異なる結果が得られる可能性があります。これを達成するために、始域の基数にもう一度焦点を当てます。錐は、BOLLINGER-ENVELOPEのBASELINE-MAに向けて構成されています。これは、以前の積ではなく共積であることを考慮しています。準同型性は余域と比較して等しいかそれより大きな始域を必要とするため、余域のサイズをBOLLINGER-ENVELOPEからBASELINE-MAに向かって増加させ、それぞれの余域内のすべての要素が写像されるようにすることで、各準同型性がエピ射であることを簡単に確認できます。

上記の場合と同様に、フィボナッチベースの分位値バケット化を適用したので、大きくしたい始域を単純に明示することができます。これは、上記と同様に、基数が| LOWER-BOLLINGER| = 19 and also | BOLLINGER-ENVELOPE | = 19になることを意味します。余積が与えられると組成が逆転するため、より大きな始域は頂点およびより低い因子始域に残ります。

これらの設定でテストを実行すると、次の結果が得られます。

2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)                        [,0]               [,1]               [,2]               [,3]               [,4]               [,5]               [,6]
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [ 0,] " DATE "          ," N period "      ," Baseline-MA "   ," Upper Bands "   ," Lower Bands "   ," Envelope Delta "," Actual Range "  
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [ 1,] "2021.07.04 00:00","8"               ,"103.425"         ,"105.548"         ,"101.301"         ,"4.248"           ,"0.850"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [ 2,] "2021.07.11 00:00","8"               ,"103.425"         ,"105.548"         ,"101.301"         ,"4.248"           ,"0.758"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [ 3,] "2021.07.18 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"0.691"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [ 4,] "2021.07.25 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"1.193"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [ 5,] "2021.08.01 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"1.030"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [ 6,] "2021.08.08 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"0.735"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [ 7,] "2021.08.15 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.270"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [ 8,] "2021.08.22 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.868"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [ 9,] "2021.08.29 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.854"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [10,] "2021.09.05 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.750"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [11,] "2021.09.12 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.912"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [12,] "2021.09.19 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.565"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [13,] "2021.09.26 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.325"           
2023.04.07 19:58:57.547 ct_6 (USDX-JUN23,W1)    [14,] "2021.10.03 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.770"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [15,] "2021.10.10 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.811"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [16,] "2021.10.17 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.700"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [17,] "2021.10.24 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.035"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [18,] "2021.10.31 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.842"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [19,] "2021.11.07 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.400"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [20,] "2021.11.14 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"1.305"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [21,] "2021.11.21 00:00","13"              ,"102.993"         ,"105.163"         ,"100.822"         ,"4.341"           ,"0.933"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [22,] "2021.11.28 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.115"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [23,] "2021.12.05 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.747"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [24,] "2021.12.12 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"1.077"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [25,] "2021.12.19 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.685"           
2023.04.07 19:58:57.548 ct_6 (USDX-JUN23,W1)    [26,] "2021.12.26 00:00","21"              ,"103.616"         ,"106.326"         ,"100.906"         ,"5.420"           ,"0.778"

ここでも結果は0.16と異なり、30%以上の変化を表します。

結論

結論として、指標や時系列を見ても必ずしも明らかではない方法で、その始域の錐構成をどのように関連付けて分析できるかを見てきました。圏論における錐は、ペアリング始域に多くの順列を示し、それ自体が複数の見方、解釈、したがって投影の方法につながります。具体的には、この記事では、単射的引き戻しと全射的押し出しを適用することで、錐の構成にわずかに制限的な調整をおこなうと、最終結果が15～30%変化する可能性があることを説明しました。重み付けやその他の変更を適用して射を観察すると、新しいエントリシグナルを開発できるだけでなく、熟練した資金管理システムを開発することもできます。読者の皆さんは、この記事に添付されているスクリプトファイルを使用してご自分の特定の指標や取引スタイルに合わせて微調整できます。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/12437

添付されたファイル |

ZIPをダウンロード

ct_6.mq5 (97.49 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

MetaTrader 5をPostgreSQLに接続する方法

この記事では、MQL5コードをPostgresデータベースに接続するための4つの方法について説明し、そのうちの1つであるREST APIの開発環境をWindows Subsystem For Linux (WSL)を使用して設定するためのステップバイステップのチュートリアルを提供します。APIのデモアプリが、データを挿入してそれぞれのテーブルにクエリを実行するための対応MQL5コード、このデータを使用するためのデモエキスパートアドバイザー(EA)とともに提供されます。

MQL5を使用してローソク足パターンを検出する方法

MQL5によって価格のローソク足パターンを自動的に検出する方法を学ぶ新しい記事です。

ニューラルネットワークの実験（第5回）：ニューラルネットワークに渡すための入力の正規化

ニューラルネットワークはトレーダーのツールキットの究極のツールです。この仮定が正しいかどうかを確認してみましょう。MetaTrader 5は、取引でニューラルネットワークを使用するための自立した媒体としてアプローチされています。簡単な説明が記載されています。

MQL5の圏論（第5回）等化子

圏論は、数学の多様かつ拡大を続ける分野であり、最近になってMQL5コミュニティである程度取り上げられるようになりました。この連載では、その概念と原理のいくつかを探索して考察することで、トレーダーの戦略開発におけるこの注目すべき分野の利用を促進することを目的としたオープンなライブラリを確立することを目指しています。