MetaTrader 5 / トレーディングシステム
English Русский 中文 Español Deutsch Português
preview
ニューラルネットワークの実験（第5回）：ニューラルネットワークに渡すための入力の正規化

ニューラルネットワークの実験（第5回）：ニューラルネットワークに渡すための入力の正規化

MetaTrader 5 — トレーディングシステム | 6 6月 2023, 09:41
848 0
Roman Poshtar
Roman Poshtar

はじめに

以前の実験の結果を少し振り返った後、以前に開発したエキスパートアドバイザー(EA)の訓練パフォーマンスと収益性を向上させる方法を考え始めました。

今日はシグナルの重要性、つまり将来の結果を分析および予測するためにニューラルネットワークにデータを送信することの重要性を強調します。おそらく、これがニューラルネットワークの最も重要なコンポーネントです。「最先端のライブラリを使ったのに動かなかった」といった厄介な誤解を避けるためにも、シグナルを理解することの重要性を読者に伝えたいと思っています。以前の記事では、いくつかの興味深い方法を適用しました。今回は、値を正規化して指標データを転送してみます。

いつものことですが、過度に複雑にならないようにしながらすべてを詳細に説明するつもりです。きっと誰もが理解できると思います。


ニューラルネットワークに渡す入力を正規化することの重要性

入力の正規化は、ニューラルネットワークを訓練するためのデータを準備する際の重要な手順です。このプロセスにより、入力を特定の範囲の値にして、訓練の収束の安定性と速度の向上に役立てることができます。

この記事では、正規化がニューラルネットワークの訓練において重要な手順である理由と、どのような正規化方法が使用できるかを見ていきます。

入力の正規化について

入力の正規化は、特定の範囲の値を持つように入力データを変換することで構成されます。正規化の2つの主な手法は、平均と標準偏差による正規化（Z-score化）と最小値と最大値による正規化（Min-Max法）です。

Z-score化では、平均と標準偏差を使用してデータを中心に配置し、スケールします。これを達成するには、各値を平均から引いて、標準偏差で割ります。Min-Max法では、最小値と最大値を使用して、データを特定の範囲にスケールします。

入力の正規化が重要な理由

入力の正規化は、訓練の収束の安定性と速度を向上させるために重要です。入力データが正規化されていない場合、一部のパラメータの値の範囲が大きくなり、ニューラルネットワークの訓練で問題が発生する可能性があります。たとえば、勾配が大きすぎたり小さすぎたりすると、最適化の問題や予測精度の低下につながる可能性があります。

正規化により、最適化アルゴリズムの収束が向上するため、訓練プロセスを高速化することもできます。適切に正規化されたデータは、入力データが十分に代表的でない場合に発生する可能性のある過学習問題を回避するのにも役立ちます。

使用できる正規化手法

正規化手法は、データの種類と解決しようとしている問題によって異なる場合があります。たとえば、画像の最も一般的な正規化方法は、Z-score化とMin-Max法です。ただし、オーディオシグナルやテキストデータなど、他の種類のデータの場合は、他の正規化方法を使用した方が効率的である場合があります。

たとえば、オーディオシグナルの場合、多くの場合、すべてのシグナル値が-1から1の間でスケールされる最大振幅正規化が使用されます。テキストデータの場合は、文内の単語または文字の数によって正規化すると便利です。

さらに、場合によっては、入力データだけでなく目的変数も正規化すると便利な場合があります。たとえば、目的変数の値の範囲が広い回帰問題では、目的変数を正規化して訓練の安定性と予測精度を向上させると役立つ場合があります。

入力の正規化は、ニューラルネットワークを訓練するためのデータを準備する際の重要な手順です。このプロセスにより、入力を特定の範囲の値にして、訓練の収束の安定性と速度の向上に役立てることができます。データのタイプと解決しようとしている問題に応じて、さまざまな正規化方法を使用できます。さらに、場合によっては、入力データだけでなく目的変数も正規化すると便利な場合があります。


正規化方法

Min-Max法

機械学習において、正規化は安定性と訓練の収束率を向上させる重要なデータ前処理手順です。最も一般的な正規化方法の1つはMin-Max法で、データ値を0から1の範囲に収めることができます。この記事では、時系列に対してMin-Max法を使用する方法を見ていきます。

時系列は、さまざまな時点で測定された一連の値です。時系列の例としては、気温、株価、商品の販売数などのデータが挙げられます。時系列を使用して、将来の値を予測したり、傾向やパターンを分析したり、異常を検出したりできます。

時系列の値の範囲は異なる場合があり、時間の経過に伴う変化は均一ではない場合があります。たとえば、株価は幅が広く、季節性、ニュース、その他の要因に基づいて変動する可能性があります。時系列の効果的な分析と予測をおこなうには、値を一定の範囲に収める必要があります。

Min-Max法は、最小値と最大値に従って値をスケーリングすることにより、値を0～1の範囲に正規化します。Min-Max法方程式は次のようになります。

x_norm = (x - x_min) / (x_max - x_min)

ここで、xはデータ値、x_minはデータセット全体の最小値、x_maxはデータセット全体の最大値、x_normは正規化された値です。

Min-Max法を時系列に適用すると、データを共通の値の範囲に収め、分析を簡素化することができます。たとえば、-30～+30度の範囲の温度データがある場合、Min-Max法を適用して値を0～1の範囲に収めることができます。これにより、さまざまな期間にわたる値を比較し、傾向や異常を特定できるようになります。

ただし、Min-Max法を時系列に適用する場合は、この方法の特徴とデータへの影響を考慮する必要があります。まず、Min-Max法を使用すると、範囲内の値の分布に関する情報が失われる可能性があります。たとえば、データセットに外れ値や極値がある場合、それらは0または1にキャストされ、分析では失われます。この場合、Z-score化などの代替の正規化方法を使用できます。

次に、Min-Max法を使用する場合は、データ変更のダイナミクスを考慮する必要があります。データの変化のダイナミクスが不均一である場合、正規化によって時間パターンの歪みや異常が発生する可能性があります。この場合、特定の期間内の各データグループの最小値と最大値が決定される局所正規化を適用できます。

第三に、Min-Max法を使用する場合、分析結果に対するサンプルの影響を考慮する必要があります。観測値のサンプルのバランスが取れていないまたはスパイクが含まれている場合、正規化によって誤った結論が導かれる可能性があります。この場合、スパイク除去やデータ平滑化などの代替データ処理方法を使用できます。

結論として、Min-Max法は機械学習で最も一般的な正規化手法の1つであり、時系列に効果的に適用して値を共通の範囲に収めることができます。ただし、この方法を使用する場合、時系列の分析と予測の歪みを避けるために、データの特徴を考慮し、追加の処理方法を適用する必要があります。

例：

int OnInit()
  {

// declare and initialize the array
double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6};

// find the minimum and maximum value in the array
double min_value = ArrayMinimum(data_array, 0, ArraySize(data_array)-1);
double max_value = ArrayMaximum(data_array, 0, ArraySize(data_array)-1);

// create an array to store the normalization result
double norm_array[ArraySize(data_array)];

// normalize the array
for(int i = 0; i < ArraySize(data_array); i++) {
    norm_array[i] = (data_array[i] - min_value) / (max_value - min_value);
}

// display the result
for(int i = 0; i < ArraySize(data_array)-1; i++) {
Print("Source array: ", data_array[i]);
Print("Min-Max normalization result: ", norm_array[i]);
}

return(INIT_SUCCEEDED);
}

このコードは、5つの浮動小数点数を含むdata_array配列を作成します。次に、次のコマンドを使用して配列内の最小値と最大値を見つけます。ArrayMinimum()およびArrayMinimum()関数は、正規化結果を格納するためにNorm_arrayという新しい配列を作成し、(data_array[i]-min_value)/(max_value-min_value)を要素ごとに計算してその配列を設定します。最後に、Print()関数を使用して結果が画面に表示されます。

結果：

2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Source array: 1.2
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Min-Max normalization result: 0.39999999999999997
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Source array: 2.3
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Min-Max normalization result: 0.7666666666666666
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Source array: 3.4
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Min-Max normalization result: 1.1333333333333333
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Source array: 4.5
2023.04.07 13:22:32.937 11111111111111 (EURUSD,H1)      Min-Max normalization result: 1.5


Z-score化

時系列は、特に経済学、金融、気象学、材料科学などの分野におけるデータ分析における重要なツールです。主要な時系列前処理方法の1つはZ-score化であり、データ分析の品質の向上に役立ちます。

Z-score化は、時系列のセンタリングとスケーリングをおこなう手法です。これは、時系列の平均値が0に等しく、標準偏差が1に等しくなるように時系列を変換することにあって、時系列を相互に比較したり、季節性や傾向の影響を除去したりするのに役立ちます。

時系列のZ-score化のプロセスには、次の手順が含まれます。

  1. 時系列の平均を計算します。
  2. 時系列の標準偏差を計算します。
  3. 時系列の各要素について、その値と時系列の平均値の差を計算します。
  4. それぞれの差を標準偏差で割ります。

結果の値の平均は0、標準偏差は1になります。

Z-score化の利点は次の通りです。

  1. データ分析品質の向上：Z-score化は、季節性や傾向の影響を取り除くのに役立ち、データ分析の品質を向上させることができます。
  2. 使いやすさ：使いやすく、さまざまな種類の時系列に適用できます。
  3. 時系列を比較するのに便利：異なるスケールや測定単位の影響が排除されるため、時系列を相互に比較することができます。

ただし、z-score化にはいくつかの制限もあります。

  1. 極端な値を含む時系列には不適：時系列に極端な値が含まれている場合、z-score化により結果が歪む可能性があります。
  2. 非定常時系列には不適：時系列が非定常である（つまり、傾向または季節性がある）場合、z-score化によってこれらの特性が排除されて不正確なデータ分析につながる可能性があります。
  3. 正規分布である保証なし：時系列の分布を正規化するのに役立ちますが、分布が正確に正規になることは保証されません。

これらの制限にもかかわらず、z-score化は、データ分析の品質の向上に役立つ重要な時系列前処理手法で、経済、金融、気象、材料科学などさまざまな分野で活用できます。

たとえば、経済学や金融では、z-score化を使用して、さまざまな資産やポートフォリオのパフォーマンスを比較したり、リスクやボラティリティを分析したりできます。

気象学では、z-score化は、気温や降水量などの気象データの分析から季節性や傾向を除去するのに役立ちます。

材料科学では、z-score化を使用して、熱膨張や磁気特性などの材料特性の時系列を分析できます。

結論として、z-score化は、さまざまな分野でのデータ分析の品質の向上に役立つ重要な時系列前処理手法です。いくつかの制限はありますが、z-score化は使いやすく、さまざまなタイプの時系列に適用できます。

例：

int OnInit()
  {

// declare and initialize the array
double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6};

// find the mean and standard deviation in the array
double mean_value = ArrayAverage(data_array, 0, ArraySize(data_array)-1);
double std_value = ArrayStdDev(data_array, 0, ArraySize(data_array)-1);

// create an array to store the normalization result
double norm_array[ArraySize(data_array)];

// normalize the array
for(int i = 0; i < ArraySize(data_array); i++) {
    norm_array[i] = (data_array[i] - mean_value) / std_value;
}

// display the result
for(int i = 0; i < ArraySize(data_array)-1; i++) {
Print("Source array: ", data_array[i]);
Print("Z-normalization result: ", norm_array[i]);
}

return(INIT_SUCCEEDED);
}

double ArrayAverage(double &array[], int start_pos=0, int count=-1)
{
    double sum = 0.0;
    int size = ArraySize(array);

    // Determine the last element index
    int end_pos = count < 0 ? size - 1 : start_pos + count - 1;
    end_pos = end_pos >= size ? size - 1 : end_pos;

    // Calculate the sum of elements
    for(int i = start_pos; i <= end_pos; i++) {
        sum += array[i];
    }

    // Calculate the average value
    double avg = sum / (end_pos - start_pos + 1);
    return (avg);
}

double ArrayStdDev(double &array[], int start_pos=0, int count=-1)
{
    double mean = ArrayAverage(array, start_pos, count);
    double sum = 0.0;
    int size = ArraySize(array);

    // Determine the last element index
    int end_pos = count < 0 ? size - 1 : start_pos + count - 1;
    end_pos = end_pos >= size ? size - 1 : end_pos;

    // Calculate the sum of squared deviations from the mean
    for(int i = start_pos; i <= end_pos; i++) {
        sum += MathPow(array[i] - mean, 2);
    }

    // Calculation of standard deviation
    double std_dev = MathSqrt(sum / (end_pos - start_pos + 1));
    return (std_dev);
}

このコードは、5つの浮動小数点数を含むdata_array配列を作成します。次に、次の式を使用して配列内の平均と標準偏差を見つけます。 ArrayAverage()関数とArrayStdDev()関数は、正規化結果を格納するためにNorm_arrayという新しい配列を作成し、(data_array[i]-means_value)/std_valueを計算してその配列を設定します。要素ごとに。最後に、Print()関数を使用して結果が画面に表示されます。

結果：

2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Source array: 1.2
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Z-normalization result: -1.3416407864998738
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Source array: 2.3
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Z-normalization result: -0.4472135954999581
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Source array: 3.4
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Z-normalization result: 0.44721359549995776
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Source array: 4.5
2023.04.07 13:51:57.501 11111111111111 (EURUSD,H1)      Z-normalization result: 1.3416407864998736


微分

時系列の微分はデータ分析の重要な方法であり、時系列から傾向や季節性を除去して、時系列をより定常的にすることができます。この記事では、微分とは何か、微分を適用する方法、微分がもたらすメリットについて説明します。

時系列微分について

微分は、時系列内の連続する値間の差異を見つけるプロセスです。見つける必要がある差異の数は、達成したい定常性の程度によって異なります。通常、傾向や季節性を排除するには、1つまたは2つの違いで十分です。1つの違いの手順は次のようになります。

y'(t) = y(t) - y(t-1)

ここで、y'(t)は系列の現在の値と前の値の差です。

系列が非定常である場合、微分後の値はよりランダムになり、目に見える傾向や季節性はなくなります。これは、サイクルやボラティリティなどの時系列のより明らかな特徴を強調するのに役立ちます。

時系列微分を適用するには？

時系列を区別するには、次の手順に従います。

  1. 系列が非定常かどうかを判断します。シリーズに傾向や季節性がある場合、それは非定常です。
  2. 定常性を得るために必要な差の数を決定します。トレンドだけを削除したい場合は、差異が1つあれば十分です。季節性を除去したい場合は、2つ以上の差異が必要になる場合があります。
  3. シリーズに差分変換を適用します。y'(t) = y(t) - y(t-1)を使用して、最初の差を見つけます。2番目の差を見つける必要がある場合は、方程式をy'(t)に適用します。
  4. シリーズが静止しているかどうかを確認します。これをおこなうには、ディッキーフラー検定などの定常性の統計検定を使用できます。
  5. 系列が非定常である場合は、系列が定常になるまで微分プロセスを繰り返します。

時系列を微分する利点は？

時系列を微分すると、次のようないくつかの利点が得られます。

  1. 改善の予測：時系列が静止している場合、時系列の統計的特性は時間の経過とともに変化しないため、予測が容易になります。
  2. トレンド除去：シリーズを微分すると線形傾向がなくなり、シリーズがより定常化し、分析が向上します。
  3. 季節性の削除：複数の差分手順を使用すると、時系列から季節性を除去し、時系列をより定常的にすることができます。
  4. ノイズ除去：シリーズを微分すると、低周波成分(傾向と季節性)が除去され、これらの成分によってもたらされるノイズを除去するのに役立ちます。
  5. 解釈の改善：シリーズが静止している場合、古典的な統計手法を使用して分析できるため、データの解釈がより簡単かつ理解しやすくなります。

ただし、微分にはデメリットも存在します。たとえば、系列を何度も微分すると、重要なシグナルが失われ、誤った結論が得られる可能性があります。さらに、微分により系列に追加のノイズが導入される可能性があります。

時系列微分は、系列から傾向や季節性を取り除き、系列をより定常的にする便利なデータ分析手法です。これにより、予測が改善され、ノイズが除去され、データの解釈が改善されます。ただし、微分には欠点がある場合もあるため、他のデータ分析方法と組み合わせて使用する場合には注意が必要です。

例：

int OnInit()
  {

// declare and initialize the array
double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6};

// create an array to store the result of differentiation
double diff_array[ArraySize(data_array)];

// differentiate the array
for(int i = 0; i < ArraySize(data_array)-1; i++) {
    diff_array[i] = data_array[i+1] - data_array[i];
}

// display the result
for(int i = 0; i < ArraySize(data_array)-1; i++) {
Print("Source array: ", data_array[i]);
Print("Differentiation result: ", diff_array[i]);
}

return(INIT_SUCCEEDED);
}

このコードは、5つの浮動小数点数を含むdata_array配列を作成します。次に、新しい配列diff_arrayを作成して微分の結果を保存し、 data_arrayのiから各要素i+1を減算して格納します。最後に、Print()関数を使用して結果が画面に表示されます。

結果：

2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Source array: 1.2
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Differentiation result: 1.0999999999999999
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Source array: 2.3
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Differentiation result: 1.1
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Source array: 3.4
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Differentiation result: 1.1
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Source array: 4.5
2023.04.07 13:13:50.650 11111111111111 (EURUSD,H1)      Differentiation result: 1.0999999999999996


対数変換

時系列の対数変換は、分析とモデリングの前に系列のプロパティを改善するために使用されるデータ変換手法です。この手法は、データの変動が大きい場合、または元の値が広い範囲にある場合に特に便利です。

対数変換について

対数変換は、時系列の各値に対数関数を適用するプロセスです。対数関数は、特に範囲が広い場合に、系列の値を圧縮するために使用されます。対数を使用すると、データの山と谷が平滑化され、目立たなくなるため、系列のばらつきが減少します。

対数変換が役立つシナリオは？

対数変換は次のような状況で役立ちます。

  1. データの変動性が高い場合、対数変換によってデータが平滑化され、予測可能になります。
  2. データが広範囲にわたる場合、対数変換によってデータが圧縮され、解釈を改善できます。
  3. データに指数関数的な傾向がある場合、対数変換によってデータを線形にすることができるため、分析とモデル化が容易になります。
  4. データが正規分布していない場合、対数変換によってデータを正規分布に近づけることができます。

対数変換を適用する例：

数年間にわたる店舗の毎日の売上高を表す時系列があるとします。売上は非常に変動し、斑点がある場合があるため、対数変換を適用してデータを平滑化し、予測しやすくすることができます。

例を続けると、売上時系列に対数変換を適用できます。これをおこなうには、系列内の各値に対数関数を適用します。

たとえば、一連の売上{100、200、300、400}がある場合、対数変換を適用して{log(100)、log(200)、log(300)、log(400)}または自然対数を使用すると、ちょうど{2,2.3,2.5,2.6}になります。

例からわかるように、対数変換により系列の値が圧縮され、分析とモデリングがより便利になります。これにより、販売傾向をより深く理解し、より正確な予測を立てることができます。

ただし、対数変換は普遍的な方法ではなく、常にすべてのデータ型に適しているわけではないことを忘れないでください。また、対数変換を適用する際は、必要に応じて元のデータスケールに戻すことを忘れないように注意してください。

結論として、対数変換は、分析やモデリングの前に時系列を変換してプロパティを改善するための有用な方法です。これは、変動性が高いデータや広範囲のデータに特に役立ちます。ただし、使用する場合は、その制限を認識し、結果を正しく解釈する必要があります。

例：

int OnInit()
  {

// declare and initialize the array
double data_array[] = {1.2, 2.3, 3.4, 4.5, 5.6};

// create an array to store the normalization result
double norm_array[ArraySize(data_array)];

// normalize the array
LogTransform(data_array, norm_array);

// display the result
for(int i = 0; i < ArraySize(data_array)-1; i++) {
Print("Source array: ", data_array[i]);
Print("Logarithmic transformation result: ", norm_array[i]);
}

return(INIT_SUCCEEDED);
}

void LogTransform(double& array1[], double& array2[])
{
    int size = ArraySize(array1);

    for(int i = 0; i < size; i++) {
        array2[i] = MathLog10(array1[i]);
    }
}

LogTransform()関数は、array1を対数変換し、結果をarray2に格納するために使用されます。

アルゴリズムは次のように機能します。MathLog10()関数を使用して、array1の各要素が常用対数に変換され、結果がarray2の対応する要素に格納されます。

LogTransform()関数は&を使用してデータ配列を参照によって受け入れます。これは、関数内でarray2に加えられた変更が、関数の呼び出し時に引数として渡された元の配列に反映されることを意味します。

結果：

2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Source array: 1.2
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Logarithmic transformation result: 0.07918124604762482
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Source array: 2.3
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Logarithmic transformation result: 0.36172783601759284
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Source array: 3.4
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Logarithmic transformation result: 0.5314789170422551
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Source array: 4.5
2023.04.07 14:21:22.374 11111111111111 (EURUSD,H1)      Logarithmic transformation result: 0.6532125137753437


時系列の分析と予測における歪みを回避するための追加の処理方法

時系列は、経済学、金融、気候科学などのさまざまな分野での分析と予測に広く使用されています。ただし、実際のデータには、時系列分析や予測の精度に影響を与える可能性のあるスパイク、欠損値、ノイズなどの歪みが含まれていることがよくあります。時系列の分析と予測における歪みを回避するのに役立つ追加の処理方法を検討してみましょう。

スパイクの除去

スパイクは、シリーズ内の他の値とは大きく異なる値です。これらは、測定エラー、データ入力エラー、または危機や事故などの予期せぬ出来事によって引き起こされる可能性があります。時系列からスパイクを削除すると、分析と予測の品質が向上します。

MQL5言語には、スパイクを除去するための関数がいくつか用意されています。たとえば、iqr()関数を使用して、四分位範囲を決定し、スパイク限界を計算できます。MODE_OUTLIERS関数を使用すると、決定層値に基づいてスパイクを決定できます。これらの関数は、他のスパイク除去機能と組み合わせて使用できます。

例：

void RemoveOutliers(double& array[])
{
    int size = ArraySize(array);
    double mean = ArrayAverage(array);
    double stddev = ArrayStdDev(array, mean);

    for(int i = 0; i < size; i++) {
        if(MathAbs(array[i] - mean) > 2 * stddev) {
            array[i] = mean;
        }
    }
}

double ArrayAverage(double &array[], int start_pos=0, int count=-1)
{
    double sum = 0.0;
    int size = ArraySize(array);

    // Determine the last element index
    int end_pos = count < 0 ? size - 1 : start_pos + count - 1;
    end_pos = end_pos >= size ? size - 1 : end_pos;

    // Calculate the sum of elements
    for(int i = start_pos; i <= end_pos; i++) {
        sum += array[i];
    }

    // Calculate the average value
    double avg = sum / (end_pos - start_pos + 1);
    return (avg);
}

double ArrayStdDev(double &array[], int start_pos=0, int count=-1)
{
    double mean = ArrayAverage(array, start_pos, count);
    double sum = 0.0;
    int size = ArraySize(array);

    // Determine the last element index
    int end_pos = count < 0 ? size - 1 : start_pos + count - 1;
    end_pos = end_pos >= size ? size - 1 : end_pos;

    // Calculate the sum of squared deviations from the mean
    for(int i = start_pos; i <= end_pos; i++) {
        sum += MathPow(array[i] - mean, 2);
    }

    // Calculation of standard deviation
    double std_dev = MathSqrt(sum / (end_pos - start_pos + 1));
    return (std_dev);
}

RemoveOutliers()関数は、平均と標準偏差を使用して、array内のスパイクを決定します。配列要素が平均から2標準偏差の範囲外にある場合、その要素はスパイクとみなされ、平均に置き換えられます。

RemoveOutliers()関数もまた、&を介して参照によってデータ配列を受け入れます。つまり、関数内で配列に加えられた変更は、関数の呼び出し時に引数として渡された元の配列に反映されます。


データの平滑化

データの平滑化は、時系列からノイズを除去することです。ノイズは、ランダムな変動や予期せぬ出来事によって発生する可能性があります。データの平滑化により、時系列の分析と予測に対するノイズの影響を軽減できます。

MQL5言語は、データを平滑化するための関数をいくつか提供します。たとえば、iMA()関数を使用して移動平均を計算できます。これにより、データを平滑化し、ノイズを低減し、傾向を検出することができます。iRSI()関数を使用すると、インデックスの相対的な強さを計算できます。また、この関数を使用して、データを平滑化し、傾向を特定することもできます。

例：

void SmoothData(double& array[], int period)
{
    int size = ArraySize(array);
    double smoothed[size];
    double weight = 1.0 / period;

    for(int i = 0; i < size; i++) {
        double sum = 0.0;
        for(int j = i - period + 1; j <= i; j++) {
            if(j >= 0 && j < size) {
                sum += array[j];
            }
        }
        smoothed[i] = sum * weight;
    }

    ArrayCopy(smoothed, array, 0, 0, size);
}

この関数は、単純な移動平均を使用して、array内のデータを平滑化します。periodは、各点の平均値を計算するために使用される要素の数を指定します。

関数内で、平滑化されたデータを保存するために新しい「平滑化」配列が作成されます。次に、arrayの各要素を反復処理し、periodで指定された期間の平均値を計算します。

最後に、ArrayCopy()関数を使用して、smoothed配列が配列にコピーされます。SmoothData()関数もまた、&を使用して参照によってデータ配列を受け入れます。つまり、関数内の配列に加えられた変更は、関数の呼び出し時に引数として渡された元の配列に反映されます。


欠損値

欠損値とは、時系列から欠落している値です。これは、データ入力エラーまたはデータ収集の問題が原因である可能性があります。欠損値は、時系列分析と予測に大きな影響を与える可能性があります。欠損値を処理するときは、欠損値を埋める方法を決定する必要があります。MQL5言語には、欠損値を処理するための関数がいくつか用意されています。

iBarShift()関数を使用すると、特定の日付に対応するバーインデックスを見つけることができます。特定の日付の時系列値が欠落している場合は、前のバーの値を使用するか、一定期間の時系列の平均値を入力できます。

例：

void FillMissingValues(double& array[])
{
    int size = ArraySize(array);
    double last_valid = 0.0;

    for(int i = 0; i < size; i++) {
        if(IsNaN(array[i])) {
            array[i] = last_valid;
        }
        else {
            last_valid = array[i];
        }
    }
}

この関数はfillingメソッドを使用します。これは、欠落している値をarray内の以前の有効な値に置き換えます。これをおこなうには、配列内の最後の有効な値を格納するlast_valid変数を作成し、配列の各要素をループします。現在の値が欠落している(NaN)場合は、last_validに置き換えます。値が欠落していない場合は、それをlast_validに保存し、反復を続けます。

FillMissingValues()関数もまた、&を使用して参照によってデータ配列を受け入れます。つまり、関数内で配列に加えられた変更は、関数の呼び出し時に引数として渡された元の配列に反映されます。


補間

補間は、2つの既知の値の間の欠損値が何らかの関数を使用して計算できることを前提とした、欠損値を埋める方法です。MQL5では、MathSpline()関数を使用して値を補間できます。

もちろん、時系列分析と予測の改善に役立つデータ処理手法は他にもあります。たとえば、時系列分解は、傾向、サイクル、季節要素を強調するのに役立ちます。クラスタ分析と因子分析は、時系列に影響を与える因子を特定するのに役立ちます。

結論として、追加のデータ処理方法を使用すると、時系列の分析と予測を大幅に改善できます。MQL5言語は、スパイクの除去、データの平滑化、欠損値の処理に使用できるさまざまなデータ処理関数を提供します。さらに、時系列の分析と予測を改善するために適用できる他のデータ処理方法もあります。

例：

double Interpolate(double& array[], double x)
{
    int size = ArraySize(array);
    int i = 0;

    // Find the two closest elements in the array
    while(i < size && array[i] < x) {
        i++;
    }

    if(i == 0 || i == size) {
        // x is out of the array range
        return 0.0;
    }

    // Calculate weights for interpolation
    double x0 = array[i-1];
    double x1 = array[i];
    double w1 = (x - x0) / (x1 - x0);
    double w0 = 1.0 - w1;

    // Interpolate value
    return w0 * array[i-1] + w1 * array[i];
}

Interpolate関数は、浮動小数点数の配列への参照と、補間されるx値の2つの引数を取ります。補間アルゴリズムは、配列内で最も近い2つの要素を見つけ、補間の重みを計算し、補間値を計算します。x値が配列の範囲外の場合、関数は0を返します。

Interpolate関数は、&を使用して参照によってデータ配列を受け入れるます。つまり、関数内で配列に加えられた変更は、関数の呼び出し時に引数として渡された元の配列に反映されます。


ニューラルネットワークへの送信に最適なシグナルの種類

シグナルはニューラルネットワークの動作にとって重要な要素です。これらは、処理と分析のためにニューラルネットワークに渡されるデータを表します。ニューラルネットワークに送信する適切な種類のシグナルを選択すると、その効率と精度に大きな影響を与えることができます。ここでは、ニューラルネットワークへの送信に最も適したタイプのシグナルを検討します。

数値シグナル

数値シグナルは、ニューラルネットワークで使用される最も一般的なタイプのシグナルです。これらはニューラルネットワークによって処理および分析できる数値です。数値シグナルは離散シグナルまたは連続シグナルのいずれかになります。離散シグナルは有限数の値を持ちますが、連続シグナルは無限数の値を持ちます。

画像

画像もニューラルネットワークで使用される一般的なシグナルの種類です。これらはニューラルネットワークで処理できるグラフィックイメージです。画像は白黒でもカラーでも構いません。画像をニューラルネットワークに転送するには、画像を数値形式に変換する必要があります。

テキストシグナル

テキストシグナルを使用して、ニューラルネットワークにデータを送信することもできます。これらは、ニューラルネットワークによって処理および分析できるテキスト文字列です。テキストシグナルは、自然言語と特殊なプログラミング言語の両方で使用できます。

オーディオシグナル

オーディオシグナルを使用して、ニューラルネットワークにデータを送信することもできます。これらは、ニューラルネットワークによって処理および分析できる音声シグナルです。オーディオシグナルは音声と音楽の両方です。

ビデオシグナル

ビデオシグナルは、ニューラルネットワークによって処理および分析できる一連の画像です。

感覚シグナル

感覚シグナルは、マシンビジョンやロボット工学の問題においてニューラルネットワークに送信される重要な種類のシグナルです。これらには、ジャイロスコープ、加速度センサー、距離センサーなどのセンサーからのデータが含まれる場合があります。このデータを使用してニューラルネットワークを訓練し、環境を分析して応答できるようにすることができます。

グラフィックシグナル

グラフィックシグナルは、ニューラルネットワークによって処理および分析できるベクトルまたはビットマップイメージです。文字や形状の認識、図面の自動作成など、グラフィックスやデザイン関連のタスクに使用できます。

時系列

時系列は、時間の経過とともに測定される一連の数値です。これらは、一時データの予測、傾向予測、分析に関連するタスクに使用できます。ニューラルネットワークを使用すると、時系列を処理して隠れたパターンを明らかにし、将来の値を予測できます。

ニューラルネットワークに送信する適切な種類のシグナルを選択するには？

ニューラルネットワークに送信する適切な種類のシグナルの選択は、特定のタスクと利用可能なデータによって異なります。一部のタスクでは、複数のシグナルタイプを同時に使用する必要がある場合があります。たとえば、音声認識タスクには、オーディオシグナルとテキストシグナルを同時に使用することが含まれる場合があります。

ニューラルネットワークに送信するシグナルの種類を選択するときは、サイズ、解像度、形式などの特性を考慮する必要があります。さらに、ニューラルネットワークによるデータ処理の最適な品質と精度を確保するには、正規化やフィルタリングなどの適切なデータ前処理をおこなう必要があります。

結論として、ニューラルネットワークに送信する適切な種類のシグナルを選択することは、機械学習タスクで最適な結果を達成するための重要な手順です。特定のタスクと利用可能なデータに応じて、さまざまなタイプのシグナルを使用してニューラルネットワークを訓練できます。シグナルタイプを正しく選択し、適切なデータ前処理をおこなうことで、ニューラルネットワークの最適な精度とパフォーマンスを確保できます。

ただし、コンピューティング能力とデータの可用性の制限も考慮する必要があります。シグナルの種類によっては、ニューラルネットワークでの処理がより困難になる場合があり、より多くの処理能力とより多くの訓練データが必要となる場合があります。したがって、ニューラルネットワーク訓練用のシグナルの種類を選択するときは、データの品質と可用性のバランスを取る必要があります。

一般に、ニューラルネットワークに送信する適切な種類のシグナルを選択することは、機械学習タスクで最適な結果を達成するための重要な手順です。ニューラルネットワークは、オーディオ、ビデオ、テキスト、感覚データ、グラフィックデータ、時系列など、さまざまな種類のシグナルを処理できます。シグナルタイプと適切なデータ前処理を正しく選択すると、特定のタスクにおけるニューラルネットワークの最適な精度とパフォーマンスを確保することができます。


実践

私たちのお気に入りのパーセプトロンに基づいたいくつかのEAを考えてみましょう。アクセラレータオシレータ指標の値を渡します。指標値を4つのローソク足に渡し、上記の正規化メソッドを適用してみましょう。詳細については、変換ありと変換なしのEAの結果を比較してみましょう。変換なしのEAでは、指標値を直接渡します。 

ここでは、本文中で繰り返さないように、最適化とフォワードテストのすべてのパラメータを提供します。

  • 外国為替
  • EURUSD
  • 時間枠： H1
  • ストップロス300とテイクプロフィット600
  • 「始値のみ」および「最大複合基準」の最適化およびテストモード：「最大複合基準」モードを使用することは非常に重要です。「最大収益性」と比較して、より安定した収益性の高い結果を示しました。
  • 最適化範囲3年：2019.04.06から2022.04.06まで。3年は信頼できる基準ではありません。このパラメータはご自分でいろいろとお試しください。
  • フォワードテスト範囲1年：2022.04.06から2023.04.06まで。私の「ニューラルネットワークの実験（第3回）：実用化）」稿で説明されているアルゴリズムに基づいてすべてを確認。これは、いくつかの最良の最適化結果の同時取引を意味します。
  • ここで最適化を40回実行します。以前のテストと比較して2倍に増やして、結果を見てみましょう。 
  • すべてのフォワードテストで、40の最適化結果を同時に使用。値は、以前のテストと比較して2倍に増加しています。
  • 「高速（遺伝的アルゴリズム）」パーセプトロンによるEAの最適化
  • 初回入金：10,000単位
  • レバレッジ：1:500

最適化のために、Delphiで開発した小さな自動クリッカープログラムを使用します。ここには掲載できませんが、必要な方には個別メッセージでお送りします。これは次のように機能します。

  1. 必要な最適化の数を入力する
  2. ストラテジーオプティマイザーの[開始]ボタンにマウスカーソルを合わせる
  3. 待つ

指定されたサイクルの後に最適化が終了し、プログラムが終了します。オートクリッカーは、スタートボタンの色の変化に反応します。プログラムは下のスクリーンショットに表示されています。 

オートクリッカー

EAパーセプトロンAC4SLTP

指標データは正規化を使用せずに直接渡されます。 

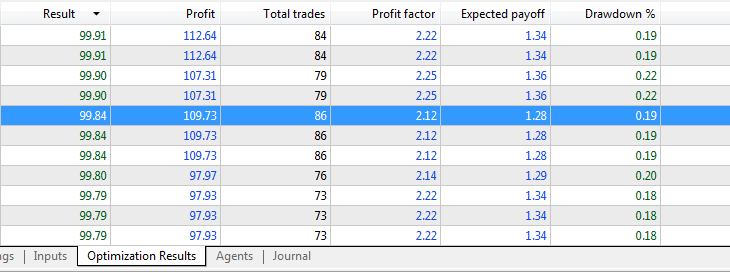
最適化結果：

最適化


最適化

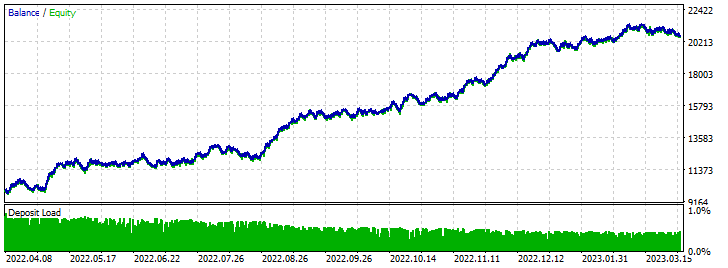
フォワードテスト結果：

テスト


EAパーセプトロンAC4(微分)SLTP

指標データはMin-Max法を使用して渡されます。 

最適化結果：

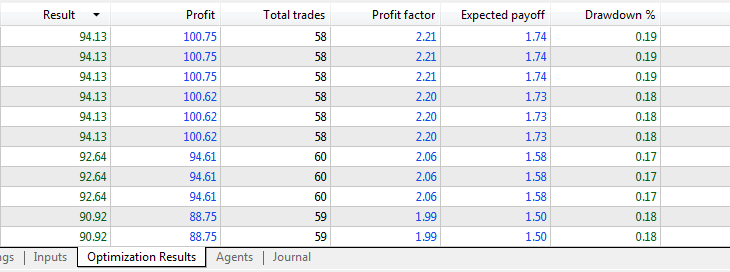
最適化


最適化

フォワードテスト結果：

テスト



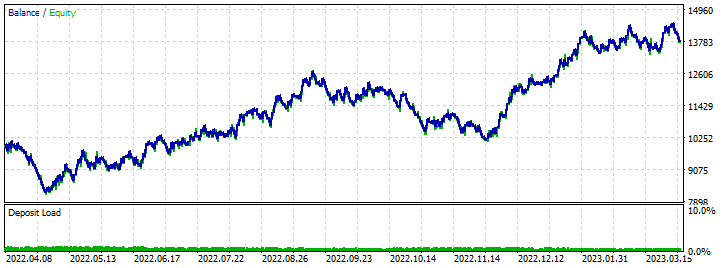
結論

添付ファイルのリスト：

  1. perceptron AC 4 SL TP - opt - 正規化をおこなわずにAC指標を最適化するパーセプトロンベースのEA
  2. perceptron AC 4 SL TP - trade - 正規化なしのAC指標に最適化されたパーセプトロンベースのEA
  3. perceptron AC 4 (Differentiation) SL TP - opt - 正規化に微分を使用したAC指標の最適化のためのパーセプトロンベースのEA
  4. perceptron AC 4 (Differentiation) SL TP - trade - 正規化に微分を使用してAC指標に最適化されたパーセプトロンベースのEA

正規化によりデータのスパイクの影響が軽減され、モデルの過学習の防止に役立ちます。適切に正規化されたデータにより、ネットワークはパラメータ間の関係をよりよく「理解」できるようになり、より正確な予測とモデルの品質の向上につながります。

この記事では、いくつかの正規化方法について説明しましたが、ニューラルネットワークの訓練を改善するためにデータを処理する方法はこれらだけではありません。それぞれの特定のケースには個別のアプローチが必要であり、データの特性と特定のタスクに応じて正規化方法を選択する必要があります。

一般に、入力パラメータの正規化は、ニューラルネットワークを訓練する際の重要な手順です。データが不適切に処理されると、結果が悪くなり、モデルのパフォーマンスに悪影響を及ぼす可能性があります。データを適切に正規化すると、訓練の安定性と収束率が向上し、より正確な予測とモデルの品質の向上につながります。

ご清聴ありがとうございました。



MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/12459

添付されたファイル |
ZIPをダウンロード
EA.zip (199.53 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
MQL5でJanus factorを実装する MQL5でJanus factorを実装する
ゲイリー・アンダーソンは、「Janus factor」と名付けた理論に基づく市場分析法を開発しました。この理論は、トレンドを明らかにし、市場リスクを評価するために使用できる一連の指標を記述するものです。今回は、これらのツールをMQL5で実装してみます。
MetaTrader 5をPostgreSQLに接続する方法 MetaTrader 5をPostgreSQLに接続する方法
この記事では、MQL5コードをPostgresデータベースに接続するための4つの方法について説明し、そのうちの1つであるREST APIの開発環境をWindows Subsystem For Linux (WSL)を使用して設定するためのステップバイステップのチュートリアルを提供します。APIのデモアプリが、データを挿入してそれぞれのテーブルにクエリを実行するための対応MQL5コード、このデータを使用するためのデモエキスパートアドバイザー(EA)とともに提供されます。
MetaTraderのMultibot：1つのチャートから複数のロボットを起動させる MetaTraderのMultibot：1つのチャートから複数のロボットを起動させる
今回は、個々のチャートにロボットの各インスタンスを設定する必要がなく、1つのチャートにのみ接続された状態で複数のチャートで使用できる汎用MetaTraderロボットを作成するための簡単なテンプレートについて考えてみます。
MQL5の圏論（第6回）：単射的引き戻しと全射的押し出し MQL5の圏論（第6回）：単射的引き戻しと全射的押し出し
圏論は、数学の多様かつ拡大を続ける分野であり、最近になってMQL5コミュニティである程度取り上げられるようになりました。この連載では、その概念と原理のいくつかを探索して考察することで、トレーダーの戦略開発におけるこの注目すべき分野の利用を促進することを目的としたオープンなライブラリを確立することを目指しています。