ペア取引における平均回帰による統計的裁定取引：数学で市場を攻略する

はじめに

「私は天体の動きは計算できるが、人々の狂気は計算できない。」— アイザック・ニュートン（70代で株式市場でほぼ全財産を失った後の言葉）

昨年の5月10日、世界はジェームズ・シモンズという偉大な人物を失いました。彼は、史上最も成功したヘッジファンドマネージャーとして知られています。

シモンズは著名な数学者であり、微分幾何学や暗号理論の分野で数々の業績を残し、学術的にも高く評価されてきました。しかし、彼の名が数学や金融に関心のない人々にも広く知られるようになったのは、定量的金融分析の分野における比類なき功績によるものでした。

彼の人生とキャリアは、数十冊の書籍、数百本のテレビ番組、そして世界中の何千もの記事やブログの題材となっており、いくつかの伝記も執筆されています。中でも最も有名なのが、『市場を解いた男：ジェームズ・シモンズはいかにしてクオンツ革命を始めたか』（原題：The Man Who Solved the Market: How Jim Simons Launched the Quant Revolution）です。

1980年代初頭、シモンズはルネサンス・テクノロジーズ(RenTech)を設立し、数学者、物理学者、信号処理の専門家、統計学者など、卓越した専門家たちを集め始めました。彼らは長年にわたり協力しながら研究を重ね、十分なデータと計算能力があれば、統計的なパターンとその中に潜む異常を見つけ出し、市場を「数学で攻略できる」ことを実証しました。

「1988年、同社は最も収益性の高いポートフォリオであるMedallion Fundを設立した。このファンドは、Leonard Baumの数理モデルを改良・拡張したものであり、代数学者James Axによるさらなる改善が加えられていた。これにより、同社は利益を生み出す相関関係を見出すことが可能になった。」（出典：Wikipedia）

Medallion Fundは1988年の設立以来、2018年までの30年間で年間平均リターン66％という驚異的な実績を記録し、累計で1,040億ドルを超える取引利益を生み出しました。現在もこのファンドは稼働を続けており、引き続き莫大な利益を上げています。当然ながら、多くの人々が彼らの運用手法や詳細、秘密のアルゴリズム、まるで「チートコード」のようなシステムの中身を知りたいと願っています。しかし、その「秘伝のソース」は極秘の企業契約として厳重に守られており、一般の人々がアクセスすることはできません。伝記の著者からMedallion Fundの運用戦略について問われた際、シモンズは、後の複数のインタビューでも繰り返すことになる、簡潔かつ象徴的な言葉でこう答えました：「ポートフォリオレベルの統計的アービトラージ」。さらに彼は、設立初期の段階から、市場の異常を検出するために「一種の機械学習」を用いていたことも明かしています。

統計的アービトラージという手法は、それ自体が非常に奥深く、大規模な研究領域です。ここに機械学習が加わると、高度な数学や統計の素養が求められ、一般のリテールトレーダー、ましてや初心者にとっては、容易に取り組めるものではなくなります。しかし一方で、「完全な機械学習搭載のポートフォリオレベル統計的アービトラージ戦略」の構築には確かに多大な困難とリソースが必要であるものの、「統計的アービトラージとは何か」「どのように機能するのか」を理解すること自体は、誰にでも可能です。そして、何より重要なのは、忍耐と努力、そしてある程度の時間をかけることで、小さな規模から始めて徐々に育てていくことも十分に可能であるという事実です。

本記事の目的は、RenTechやジェームズ・シモンズの運用モデルを再現することでも、彼らの「秘密のコード」を暴くことでもありません。それは先述のとおり、外部の人間には不可能です。ここでの狙いは、私自身の理解に基づき、彼らの成功を支えていた普遍的な原則を紹介することにあります。これらの原則は、たとえごく限られたリソースで運用されるリテールトレーダーの取引システムにおいても、十分に応用可能です。成果に違いが出るとすれば、それは投入可能な資金や技術、人材などの規模に由来するものです。

この記事の内容は、書籍、ビデオドキュメンタリー、専門コミュニティでのリサーチに加え、私自身の金融業界における数年間の実務経験（主にビジネスサイド、開発サイドではありません）をもとに構成しています。RenTechの戦略は巨大なシステムによって運用されていますが、ここで紹介するのはその縮小モデル、いわばスーパーヒーローのアクションフィギュアや高層ビルの縮小モデルのようなものです。 

本稿の目的は、MetaTrader 5プラットフォーム上で動作し、一般的なノートPCでも実行可能な、低コスト・軽量・開発容易な分析手法を紹介することです。この手法は、アルゴリズムトレーダーにとっても、裁量トレーダーにとっても、有用なものとなるはずです。私たちは、最も基本的な構成から始めます。それは、プロセスを説明するのに必要最小限のセットアップです。

モデルの基本的な概念を理解したのち、統計的アービトラージの最も単純な形に対応したミニマルなポートフォリオを構築し、それをエキスパートアドバイザー(EA)で自動運用します。その結果からいくつかの観察をおこない、最後に今後の発展に向けて必要となるステップについて考察していきます。私は、この経験が読者の皆さんにとって、この強力な取引手法への出発点となることを願っています。そしてやがては、この知識をもとにさらにスキルを深め、新たな銘柄をポートフォリオに追加したり、他のアルゴリズムを試したりしながら、各自のリソースと目標に応じたフル機能のStatArb戦略を構築できるようになることを心から期待しています。

モデルの背後にある一般的な概念

RenTechを創設する以前、ジェームズ・シモンズは冷戦時代に米国の諜報機関で暗号解読者として勤務していました。金融市場に足を踏み入れた当初、彼は株式や商品価格の将来を予測するという、一般的なアプローチを試みました。しかし、その試みはうまくいかず、やがて彼は大きな方針転換を決断します。彼はやがて、市場の未来を予測することなど不可能であるという現実を、受け入れざるを得ないと悟ったのです。市場とは、予測可能な対象ではなく、本質的に謎に満ちた存在であると認める必要がある――これが、彼の取引モデルの背後にある最初の重要な概念です。

次に挙げるのが、もうひとつの根本的な考え方です。それは、市場は常に変化し続けており、決して固定された状態にはならないという事実です。つまり、「強気相場」や「弱気相場」、「ローソク足/バーチャートのパターン」、「高い相関性を持つ銘柄」といったものは、本質的には存在しないということです。市場におけるすべては、常に、そして永遠に変化し続けているのです。

少し立ち止まって考えてみると、これら2つの前提は、多くのトレーダーや投資家が見過ごしがちな事実であることに気づくでしょう。

市場は謎である

市場は謎です。しかし、第二次世界大戦中にアラン・チューリングとそのチームが解読したエニグマ暗号とは異なり、市場の謎には逆解析や解読が可能な決定論的アルゴリズムは存在しません。入力と出力の間には予期せぬ出来事が起こりえます。たとえば、中央銀行の利上げは通常、その国の通貨を強くする方向に作用します。ところが、遠く離れた国で政治的な紛争が勃発すれば、その影響は通貨に対して逆方向に働き、利上げの効果を相殺、無効化、あるいは逆転させることすらあります。

市場が謎であるとされる本質的な理由は、入力と出力の間に介在する要素――経済主体の非合理性、政治の予測不能性、それら複雑な要素間のカオス的相互作用――にあります。たとえば、1年間続いた金の上昇トレンドと、翌週から始まる1か月にわたる急落。この間には、人間の行動が強く影響しています。この問題に取り組み、非合理な経済的意思決定を研究した心理学者ダニエル・カーネマンが、経済学のノーベル賞を受賞したのもまさにこのためです。彼は、「市場が合理的に動く」という前提を覆したのです。
それにもかかわらず、市場が非合理的な主体によって動き、混沌とした環境の中にあるにも関わらず、投資銀行は金融モデルに基づいて株を売買し、ヘッジファンドはブラック–ショールズ方程式を使ってオプションを評価し、そしてほぼすべての大手機関投資家が、数百万ドル規模の資金を投じてクオンツ戦略の開発に取り組んでいます。なぜでしょうか。もちろん、機能するからです。市場が予測不可能で、理不尽で、カオスに満ちているにも関わらず、なぜそれが機能するのでしょうか。
ジェームス・シモンズ、そして数千人に及ぶ成功したクオンツトレーダー、アルゴトレーダー、裁量トレーダーたちは、この問いに対して非常に率直な答えを持っています。そしてそれは、市場に参加するすべての志望トレーダーが、毎朝マントラのように唱えるべき教訓でもあります。

「取引における成功とは、常に正しいことではない。成功とは、利益を最大化し、損失を最小化することだ。」

これこそが、金融モデル、ブラック–ショールズ方程式、クオンツ取引戦略が目指す究極の目的なのです。すなわち、利益の最大化と損失の最小化です。これは新しい発見ではありません。市場という謎に対して成功したトレーダーたちが出した答えは、ローソク足チャートを発明した日本の米商人・本間宗久の時代よりも前から、すでに知られていた真理です。その答えこそが、リスク管理です。

しかし、金融モデルを使おうと使うまいと、どんな取引戦略であっても、ある一定期間は非常によく機能することがあります。その「うまく機能する期間」がどれだけ続くか――それは誰にも分かりません。1日かもしれませんし、1か月、あるいは1年かもしれません。私たちには知る術がないのです。ただ一つ言えるのは、その戦略が過去においてはうまく機能し、特定の銘柄、期間、パラメータ設定において利益を生んでいたという事実だけです。しかし、それが次の瞬間から通用しなくなる可能性もあります。初回のリアル運用で破綻するかもしれません。あるいは、運良く永続的に機能し続けるかもしれません。繰り返しますが、私たちにはわからないのです。それを知ることはできません。なぜなら、市場は謎だからです。この謎を解くことはできません。そこに破るべきコードなど存在しないのです。あるのはただ、絶え間なく変化し続ける状態だけです。

市場は常に変化し続けている状態にある

市場は常に変化しています。市場において唯一変わらないもの――それは「変化」そのものです。私たちが設定する戦略のパラメータは、「ある市場環境に最適だから」選ばれるのではなく、そのとき市場が経験していた変化に対して最も適していたからこそ選ばれるのです。たとえば、私たちが利益の出るポジションを取ったとき、そのエントリーから決済までの間に、市場は期待通りの方向へ変化していたということです。反対に損失が出た場合、それは市場が想定とは異なる方向へ変化したことを意味します。そして、最終的な損益に対してどの変化が最も大きく影響したかを正確に特定できなかったとしても、この原則は常に成り立ちます。

はっきりさせておきましょう。私たちは、「どの変化」が戦略を成功させたのか、あるいは失敗へと導いたのかを正確に知ることは決してできません。私たちにできるのは、将来似たような市場の変化に直面したとき、より高い確率で正しい判断ができるようにパターンを見出すことです。こうしたパターンを発見し、学び、理解していく――それが、経験を積んだトレーダーが、同じ資産や資産グループを何か月、あるいは何年にもわたって取引を重ねる中で身につけていくスキルです。そして、そのために私たちは取引日誌をつけるのです。市場がどのように動くと予測していたのか、実際にどう動いたのかを記録し、後から検証する。それによって予測の精度を高めていく――これが、継続的な成長の道です。

今日では、膨大な量のデータが利用可能となり、それを高速で処理できる計算機も手に入ります。その結果、かつては何年もかかっていたようなパターンの発見が、数時間、あるいは数分で可能になりました。私たちは、データの収集・分析・売買執行を自動化できます。テストやレポート作成すら自動化できます。さらには、どの銘柄や戦略を使うかといった判断自体を、包括的な機械学習モデルを訓練することで自動化することさえ可能です。もちろん、それには資金、人材、そして十分な時間といったリソースが必要です。しかし、それが実現可能な時代に私たちは生きています。

しかし、前述の通り、このノートの焦点は「平均的なリテールトレーダー」にあります。 この2つの単純ながら見落とされがちな原則を踏まえたうえで、StatArbとは何か、どのように機能するのかを理解する第一歩を踏み出していきましょう。

ポートフォリオの構築

市場が「常に変化し続ける謎」である以上、私たちは先入観を持たずにポートフォリオを構築します。自分たちが「正しい」と思い込んでいることを前提にせず、ポートフォリオは定期的に更新していきます。この更新の間隔は、使用する取引戦略によって決まり、利用可能な計算リソースによって制約されます。

そもそも、ポートフォリオの構築や管理は、それ自体が広く研究されている分野です。包括的な学術文献レビューによると、10年前の時点で、ペアトレーディングによる統計的アービトラージポートフォリオの構築には、距離法、共積、時系列分析、確率制御の少なくとも4つの主要なアプローチが存在していました。これらの主要な手法に加え、著者は、機械学習、予測の組み合わせ、コピュラ、主成分分析(PCA)のようなその他のアプローチも特定しています。

しかしここでは、シンプルさと基本的理解に焦点を当てるために、まずは単純なペアトレーディングポートフォリオから始めることにします。一部の著者にとっては、ペアトレーディングは統計的アービトラージの一部とされており、また別の見方では、ペアトレーディングは統計的アービトラージの祖先であると広く見なされているとされています。両者の違いは、ポートフォリオの規模と使用する統計アルゴリズムの複雑さにあります。その名前の通り、ペアトレーディングは2つの銘柄のみに限定されますが、統計的アービトラージは数十、あるいは数百の銘柄を監視し、場合によっては取引対象とすることができます。 

ペアトレーディングとは、ご存じの通り、相関性または共積性のある過去の価格データを持つ2つの銘柄を用いて、その価格差が一定の閾値を超えて拡大したときに、相対的に高くなっている銘柄を売り、相対的に安くなっている銘柄を買うという、非常にシンプルな戦略です。その根底にある前提は、価格は平均に回帰する、つまり価格差は過去の価格差に向かって収束するという考え方です。

フル機能の統計的アービトラージ戦略では、単に価格の相関や共積だけに限定される必要はありません。しかしこの記事の主な目的は、複雑な統計的アービトラージを、平均的なリテールトレーダーにも理解可能な形に単純化することにあります。そこでまずは、FX市場におけるシンプルなペアトレーディングポートフォリオを構築するために、過去のデータ収集から始めます。その後、他の市場や、価格の相関を超えた統計的関係へと拡張していくことができるでしょう。

取引銘柄のグループを選ぶ

この記事の執筆時点で、私のMetaTrader 5端末口座では、1万を超える銘柄が利用可能と表示されています。この記事での分析には、MetaTrader 5のPython連携機能を使用します。

print("Total symbols =",mt5.symbols_total()) # display all symbols
Total symbols = 10563

したがって、実際的な理由から、まずは利用可能なすべての銘柄の中からサブセットを選ぶ必要があります。まずは、XAUとの通貨ペアから始めましょう。

# get symbols containing XAU in their names
xau_symbols=mt5.symbols_get("*XAU*")
print('len(*XAU*): ', len(xau_symbols))
for s in xau_symbols:
    print(s.name)

len(*XAU*):  6
XAUUSD
XAUEUR
XAUAUD
* XAUG
XAUCHF
XAUGBP

* XAUGはETFであるため、今回は除外し、残りの5つのペアに注目することにします。それぞれがXAUUSD（米ドル建ての金価格）とどの程度相関しているかを確認してみましょう。

ここで、各ペアの過去の価格相関を計算する必要があります。現実のシナリオであれば、選択した銘柄間のあらゆる順列を検討することになるかもしれません。特に、数百の株式銘柄などを対象にする場合には、事前知識がないことを前提に、可能な限り幅広く調べることになるでしょう。しかし、ここでは対象を絞り、XAUUSDと、ユーロ、豪ドル、スイスフラン、英ポンドといった他通貨建ての金価格との相関関係のみに注目します。
必要なデータは、現在の日付から過去1年分の終値（日足）です。FX市場において1年はおおよそ250取引日に相当します。

# get 250 D1 bars from the current day
xauusd_rates = mt5.copy_rates_from_pos("XAUUSD", mt5.TIMEFRAME_D1, 0, 250)
xaueur_rates = mt5.copy_rates_from_pos("XAUEUR", mt5.TIMEFRAME_D1, 0, 250)
xauaud_rates = mt5.copy_rates_from_pos("XAUAUD", mt5.TIMEFRAME_D1, 0, 250)
xauchf_rates = mt5.copy_rates_from_pos("XAUCHF", mt5.TIMEFRAME_D1, 0, 250)
xaugbp_rates = mt5.copy_rates_from_pos("XAUGBP", mt5.TIMEFRAME_D1, 0, 250)

(...)

# calculate correlation coefficients
import numpy as np
usd_eur_corr = np.corrcoef(xauusd_close['close'], xaueur_close['close'])
usd_aud_corr = np.corrcoef(xauusd_close['close'], xauaud_close['close'])
usd_chf_corr = np.corrcoef(xauusd_close['close'], xauchf_close['close'])
usd_gbp_corr = np.corrcoef(xauusd_close['close'], xaugbp_close['close'])

これにより、次の結果が得られます。

	XAUUSD相関（ピアソン）
XAUEUR	0.9692368
XAUAUD	0.96677962
XAUCHF	0.8418827
XAUGBP	0.90490282

表1：2024年4月9日から2025年3月26日までの期間における、米ドル建ての金（XAUUSD）と、ユーロ建て、豪ドル建て、スイスフラン建て、英ポンド建ての金の日次終値の相関関係

以下のグラフでは、0.97に近い価格相関がどのようなものか視覚的に確認できます。

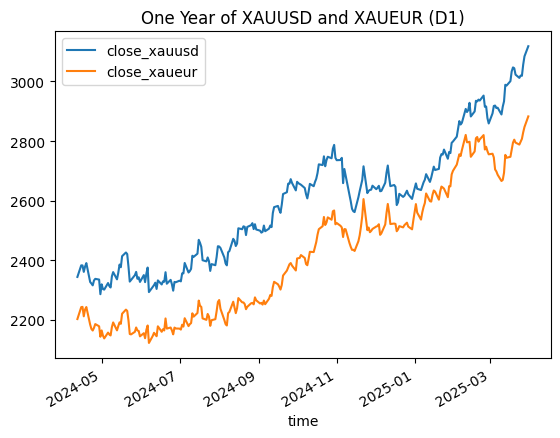
図1：米ドルとユーロで表示された金の1年間の終値

上のグラフは誤解を招く可能性があることに注意してください。ペア間の「スプレッドを取引する（トレードする）」ことを直感的に考えたくなりますが、それは実際のスプレッドとは異なります。そこで、XAUEURを、その日の為替レートに基づいて米ドルに換算しましょう。

adjusted_for_dollars = pd.concat([xauusd_close, xaueur_close['close'], eurusd_close['close']], join='inner', axis=1)
adjusted_for_dollars.columns = ['time', 'xauusd', 'xaueur', 'eurusd']
adjusted_for_dollars['xaueur_dollars'] = adjusted_for_dollars['xaueur'] * adjusted_for_dollars['eurusd']
adjusted_for_dollars['diff'] = abs(adjusted_for_dollars['xauusd'] - adjusted_for_dollars['xaueur_dollars'])

print(adjusted_for_dollars)

         time   xauusd   xaueur   eurusd  xaueur_dollars       diff
0   2024-04-12  2344.22  2202.92  1.06237     2340.316120   3.903880
1   2024-04-15  2383.10  2242.90  1.06181     2381.533649   1.566351
2   2024-04-16  2382.85  2243.81  1.06720     2394.594032  11.744032
3   2024-04-17  2361.16  2212.14  1.06425     2354.269995   6.890005
4   2024-04-18  2378.86  2234.79  1.06557     2381.325180   2.465180
..         ...      ...      ...      ...             ...        ...
245 2025-03-25  3019.81  2797.81  1.07918     3019.340596   0.469404
246 2025-03-26  3018.85  2807.50  1.07370     3014.412750   4.437250
247 2025-03-27  3056.42  2829.26  1.07975     3054.893485   1.526515
248 2025-03-28  3084.20  2847.12  1.08276     3082.747651   1.452349
249 2025-03-31  3118.19  2882.78  1.08152     3117.784226   0.405774

[250 rows x 6 columns]

adjusted_for_dollars.plot(title = 'One Year of XAUUSD and XAUEUR in US Dollars (D1)', x='time', y=['xauusd', 'xaueur_dollars'])
plt.show()

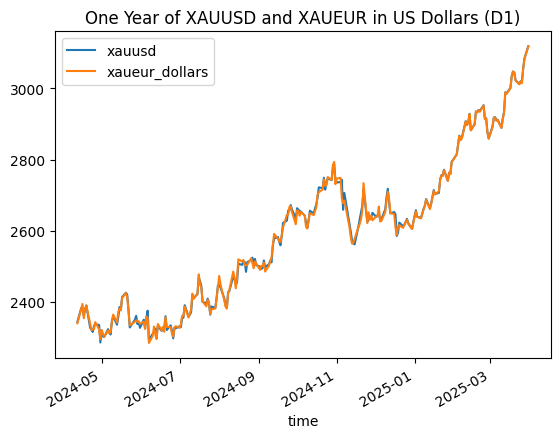
図2：米ドルとユーロで表示された金の1年間の終値（米ドル換算）

米ドル建ての金価格とユーロ建ての金価格の差を見てみると… 

print("median: ", adjusted_for_dollars['diff'].median())
adjusted_for_dollars['diff'].describe()

median:  4.052404150000029
count    250.000000
mean       5.894673
std        6.238511
min        0.050646
25%        1.279615
50%        4.052404
75%        8.587763
max       51.483719
median:  4.052404150000029

…この1年間の期間における実際の平均スプレッドは約5.9ドル、標準偏差は約6.2ドルであることがわかります。単純化して、両方の価格が現在の為替レートで換算された後の差はほぼゼロであるべきだと仮定すると、平均値を超えるスプレッドは、市場における取引可能な異常として考えることができます。 

統計的関係性の選択

私たちは、過去の約1年間（約250取引日）においてXAUUSDとXAUEURの間に高い相関が見られたことをもとに、統計的アービトラージポートフォリオの構築を始めることにしました。しかし、価格の相関は、本当に正しい、あるいはより良い統計的関係性なのでしょうか。

過去の価格における相関について話すとき、「相関」という言葉の一般的な使われ方と、統計学的な正しい意味との違いによって誤解が生じる可能性があります。この事実は、特にFX（外国為替）コミュニティにおいて顕著です。インターネットで「FX相関ペア」と検索すると、多くのリソースが、最も相関が高い/低い通貨ペアのリストや、それらをどう取引すべきかというヒントを紹介しています。ここでの私たちの目的は、特定のリソースやリスト、取引ヒントが正しいか間違っているかを判断することではありません。重要なのは、私たちがポートフォリオレベルの統計的アービトラージの基盤を築こうとしているという点であり、それはFXペアに限定されるものではないということです。代わりに、私たちのシステムはあらゆる資産クラス、市場、時間枠にも一般化できるものであるべきであり、市場中立性と検証可能性という要件だけが条件となります。

統計学者によれば、ピアソン相関係数は定常系列に対して用いるべき関数であり、価格の時系列は通常、非定常です。非定常な時系列に相関を計算すると、いわゆる「疑似相関」を得ることがあります。 

「非定常データは、原則として予測不可能であり、モデル化や予測ができません。非定常時系列を使って得られた結果は見せかけである可能性があり、実際には存在しない変数間の関係性を示すことがあります。信頼性のある一貫した結果を得るには、非定常データを定常データに変換する必要があります。」— Nason, G. P. (2006). Stationary and non-stationary time series. Investopedia)

したがって、統計的アービトラージポートフォリオを構築しようとするトレーダーとして、私たちは「疑似の相関」で十分とみなすのか、それとも、統計学的に正しい意味での相関を求めるのかという、一つの判断を下す必要があります。今のところ、私たちは完璧ではないが、簡易モデルにおいては十分であると判断し、この「見せかけの相関」を受け入れています。しかし、忘れてはならないのは、相関があるとされるペアであっても、スプレッドが広がり続ける可能性があるということです。つまり、一緒に上昇または下降しながら、長期間にわたって平均に戻らないこともあります。それでも統計的な相関は存在するということです。このような条件は、通貨ペアを扱う場合には例外的かもしれませんが、コモディティや先物、株価の時系列を扱う場合には非常に一般的な現象です。したがって、平均回帰戦略を取る場合には、ストップロスの設定とエントリータイミングの管理が必須となります。

取引のトリガーとする統計指標の選択

なぜ、過去のスプレッドを評価する際に平均や中央値を使うのでしょうか。統計学的には、外れ値が少ないデータには平均を使い、極端なピークを含むデータには中央値を使うべきだとされています。中央値はこうしたピークの影響を受けにくいためです。たとえば、重要な経済指標発表などによってスプレッドが大きく広がった値を除外したい場合は、中央値を選ぶのが適切でしょう。逆に、そうした高インパクトの出来事の影響もスプレッドに反映させたい場合は、平均を使う方が良いかもしれません。

つまり、「これが正解」という決まったレシピはありません。データと判断力に基づいて、自分自身で決めなければなりません。場合によっては、平均や中央値すら使わず、他の関係性を調査して、自分のケースに最適な方法を見つけるという選択もあります。 
ここでは、平均値を使うことにし、平均スプレッドの拡大をトリガーとする取引戦略のパラメータを設定します。たとえば、XAUUSDとXAUEURのスプレッドが平均値の50%以上に広がったとき、取引を発動します。その際は、パフォーマンスが劣っている方の銘柄を買い、上昇が早い方の銘柄を同時に売るという取引をおこないます。

では、どちらの銘柄が上昇し、どちらが下落しているのかはどう判断すればよいでしょうか。今回のように、両方のゴールド価格が為替換算後に等しくなると仮定しているケースでは、価格が高い方を「上昇しているペア」、もう一方を「下落しているペア」と見なすことができます。一方で、株価スプレッドの平均回帰を取引する場合などでは、非常に短期間の指数移動平均(EMA)を使い、EMAより上で取引されている銘柄を「上昇している」、下で取引されている銘柄を「下落している」と判断する、という手法も有効です。

bool IsRising(const int symbol)
  {
   switch(symbol)
     {
      case BASE_PAIR:
         //Print("Base pair is rising? ", quotes_base[0] > ema_base[0]);
         return quotes_base[0] > ema_base[0];
      case CORR_PAIR:
         //Print("Corr pair is rising? ", quotes_corr[0] > ema_corr[0]);
         return quotes_corr[0] > ema_corr[0];
      default:
         return false;
     }
  }

bool IsFalling(const int symbol)
  {
   switch(symbol)
     {
      case BASE_PAIR:
         //Print("Base pair is falling? ", quotes_base[0] < ema_base[0]);
         return quotes_base[0] < ema_base[0];
      case CORR_PAIR:
         //Print("Corr pair is falling? ", quotes_corr[0] < ema_corr[0]);
         return quotes_corr[0] < ema_corr[0];
      default:
         return false;
     }
  }

あるいは傾斜を使うこともできます。

void CalculateSlopes(double & slope_b[], double & slope_c[])
  {
   slope_b[0] = MathAbs((quotes_base[0] - quotes_base[SlopePeriod]) / SlopePeriod);
   slope_c[0] = MathAbs((quotes_corr[0] - quotes_corr[SlopePeriod]) / SlopePeriod);
  }

ここでは、単に最も高い価格の銘柄を使用しています。

if(quotes_base[0] > quotes_corr[0])

ポートフォリオの取引

仮説をバックテストで検証するために、シンプルなEAを構築しました。 

初期の価格はOnInit関数で取得し、その後OnTimer関数内で定期的に価格を更新しています。これは、OnTickは現在の銘柄/チャートに対してのみ呼び出されるため、OnTickイベントハンドラでは現在のチャート銘柄以外の通貨ペアの価格を安定して更新できないためです。多通貨（多銘柄）対応のEAを参照してください。

int OnInit()
  {
   ArrayResize(quotes_base, CountQuotes);
   ArrayResize(quotes_corr, CountQuotes);
   ArrayResize(quotes_conv, CountQuotes);
//--- Get start quotes for both pairs
   GetQuotes();
//--- EMA indicators
   EMA_Handle_Base = iMA(BasePair, _Period, EMAPeriod, 0, MODE_EMA, PRICE_CLOSE);
   EMA_Handle_Corr = iMA(CorrPair, _Period, EMAPeriod, 0, MODE_EMA, PRICE_CLOSE);
   if(EMA_Handle_Base == INVALID_HANDLE ||
      EMA_Handle_Corr == INVALID_HANDLE)
     {
      printf(__FUNCTION__ + ": EMA initialization failed");
      return(INIT_FAILED);
     }
//--- create timer
   EventSetTimer(5); // seconds
//---
   return(INIT_SUCCEEDED);
  }

bool GetQuotes()
  {
   if(CopyClose(BasePair, _Period, 0, CountQuotes, quotes_base) != CountQuotes)
     {
      Print(__FUNCTION__ + ": CopyClose failed. No data");
      //printf("Size quotes base pair %i ", ArraySize(quotes_base));
      return false;
     }
   if(CopyClose(CorrPair, _Period, 0, CountQuotes, quotes_corr) != CountQuotes)
     {
      Print(__FUNCTION__ + ": CopyClose failed. No data");
      //printf("Size quotes corr pair %i ", ArraySize(quotes_corr));
      return false;
     }
   if(CheckMode == PRICE)
     {
      if(CopyClose(ConvPair, _Period, 0, CountQuotes, quotes_conv) != CountQuotes)
        {
         Print(__FUNCTION__ + ": CopyClose failed. No data");
         //printf("Size quotes conv pair %i ", ArraySize(quotes_conv));
         return false;
        }
      //---
      for(int i = 0; i < CountQuotes; i++)
        {
         quotes_corr[i] *= quotes_conv[i];
        }
     }
   return true;
  }

void OnTimer()
  {
   UpdateQuotes();
   CalculateMeanSpread();
   if(CheckMode == EMA)
     {
      GetEMAs();
     }
  }

void UpdateQuotes()
  {
   ArrayRemove(quotes_base, ArraySize(quotes_base) - 1);
   double new_quote_base[1];
   CopyClose(BasePair, _Period, 0, 1, new_quote_base);
   ArrayInsert(quotes_base, new_quote_base, 0, 0);
//---
   ArrayRemove(quotes_corr, ArraySize(quotes_corr) - 1);
   double new_quote_corr[1];
   CopyClose(CorrPair, _Period, 0, 1, new_quote_corr);
   ArrayInsert(quotes_corr, new_quote_corr, 0, 0);
//---
   if(CheckMode == PRICE)
     {
      ArrayRemove(quotes_conv, ArraySize(quotes_conv) - 1);
      double new_quote_conv[1];
      CopyClose(ConvPair, _Period, 0, 1, new_quote_conv);
      ArrayInsert(quotes_conv, new_quote_conv, 0, 0);
      quotes_corr[0] *= quotes_conv[0];
     }
  }

平均スプレッドを計算します。

bool CalculateMeanSpread()
  {
   int sz_base_p = ArraySize(quotes_base);
   int sz_corr_p = ArraySize(quotes_corr);
   int sz_conv_p = ArraySize(quotes_conv);
   if(sz_base_p != sz_corr_p ||
      sz_corr_p != sz_conv_p)
     {
      Print(__FUNCTION__ + " Failed: Arrays must be of same size");
      return false;
     }
//---
   ArrayResize(pairs_spread, CountQuotes);
   for(int i = 0; i < sz_base_p; i++)
     {
      pairs_spread[i] = MathAbs(quotes_base[i] - quotes_corr[i]);
     }
   double max_spread = pairs_spread[ArrayMaximum(pairs_spread)];
   double min_spread = pairs_spread[ArrayMinimum(pairs_spread)];
   mean_spread = MathMean(pairs_spread);
//---
//printf("Last quote XAUUSD %f ", quotes_base[0]);
//printf("Last quote XAUEUR %f ", quotes_corr[0]);
//printf("Last spread %f ", pairs_spread[0]);
//printf("Max  spread %f ", max_spread);
//printf("Min  spread %f ", min_spread);
//printf("Mean spread %f ", mean_spread);
   return true;
  }

OnTickで取引シグナルを確認します。

void OnTick()
  {
//---
   CheckForClose();
   CheckForOpen();
  }

スプレッドが平均よりも設定したパーセンテージ以上に拡大した場合

bool HasSpreadTrigger()
  {
   double trigger_spread = mean_spread + (mean_spread * (PercentTrigger / 100.0));
//printf(" trigger spread %f ", trigger_spread);
   double current_spread = pairs_spread[0];
//printf(" current spread %f ", current_spread);
   return current_spread >= trigger_spread;
  }

価格が低い銘柄を買い、高い銘柄を売ります。この例では、この動作の切り替えはCheckMode列挙型によって実行されます。 

void CheckForOpen()
  {
   if(PositionsTotal() == 0 && HasSpreadTrigger())
     {
      switch(CheckMode)
        {
         case EMA:
            if(IsRising(BASE_PAIR) && IsFalling(CORR_PAIR))
              {
               OpenShort(BasePair);
               OpenLong(CorrPair);
              }
            if(IsFalling(BASE_PAIR) && IsRising(CORR_PAIR))
              {
               OpenLong(BasePair);
               OpenShort(CorrPair);
              }
            break;
         case SLOPE:
            CalculateSlopes(slope_base, slope_corr);
            if(slope_base[0] > slope_corr[0])
              {
               OpenShort(BasePair);
               OpenLong(CorrPair);
              }
            else
              {
               OpenLong(BasePair);
               OpenShort(CorrPair);
              }
            break;
         case PRICE:
            if(quotes_base[0] > quotes_corr[0])
              {
               OpenShort(BasePair);
               OpenLong(CorrPair);
              }
            else
              {
               OpenLong(BasePair);
               OpenShort(CorrPair);
              }
        }
     }
  }

ポジションは、ストップロス/テイクプロフィットまたは平均回帰によってCheckForCloseでクローズされます。

void CheckForClose()
  {
   int total = PositionsTotal();
   ulong ticket = 0;
   if(total > 0)
     {
      if(PositionSelect(BasePair) || PositionSelect(CorrPair))
        {
         for(int i = 0; i < total; i++)
           {
            ticket = PositionGetTicket(i);
            if(ticket == 0)
               continue;
            if(pairs_spread[0] <= mean_spread)
              {
               ExtTrade.PositionClose(ticket);
              }
           }
        }
     }
  }

バックテストにより、平均回帰戦略がペア取引に実行可能であることが確認されました。

図3：バックテスト資産曲線

バックテストによって私たちの仮説は検証されましたが、この特定のアルゴリズムには資本曲線を滑らかにするための改良が必要であることがわかります。たとえば、現在は取引量が最小の0.01ロット（マイクロロット）で固定されているため、動的なロットサイズの導入や、ストップロス/テイクプロフィット比率の最適化が考えられます。とはいえ、本記事においての主眼は「収益性」ではありません。その前提を踏まえたうえで、統計的アービトラージ取引において一般的に見られるとされる、興味深い結果をいくつか見ていきましょう（これは一部の著者によって報告されています）。

図4：バックテスト結果

取引回数は非常に多く、勝率と敗率の比率は小さい（約55％対45％）ものの、最大残高ドローダウンは比較的低く抑えられている

図5：バックテスト取引時間

特定の期間（時間帯、曜日など）に取引が集中する傾向があります。私たちのケースでは、取引の集中はアメリカ市場のオープン時間帯に見られ、2024年4月にピークを迎えました。

図6：バックテストポジションの保有時間×利益

多くの非常に短時間の取引が存在するという事実は、システムが市場の不安定な局面を利用し、勝ちトレードの直後に再エントリーしていることを示しています。

改善すべき点は何でしょうか。

ここで、ひとつ注意を促したいのは、取引戦略やセットアップを販売している人は、あなたの興味を引くために、可能な限り良い過去の結果だけを見せようとするということです。彼らは、最適化を繰り返して最も好成績を出したパラメータを選び出し（いわゆるチェリーピッキング）、潜在的な利益を強調し、損失のリスクを目立たなくする傾向があります。

ただし、統計的アービトラージの原理を理解して、小さく始めるという考えを除けば、私はここであなたに何かを「売ろう」としているわけではありません。むしろ、このバックテストが示しているのが改良が必要なアルゴリズムであるという事実に私は満足しています。なぜなら、それこそがすべての統計的アービトラージシステムの出発点だからです。

これまでのシンプルな自動売買では、リスク管理におけるパラメータを恣意的に決めていたに過ぎません。しかし、今後は次のような改善が求められます。

1. 各時点のリスク評価に基づいて、保有ポジション数を制御すること
2. ボラティリティを考慮した、変動的なスプレッドトリガー比率を導入すること
3. トリガースプレッド値およびその他の変数に基づき、利益確定/損切りの確率を導き出す、動的なストップロス/テイクプロフィット戦略を開発すること

これらは、今後このEAを改良していくためのアプローチの一部です。

縮小モデルの概要

1. 仮説から始める

相関のあるペア間のスプレッドは、平均に回帰する傾向があるというのが、私たちの仮説です。

トレーダーの視点から見れば、平均回帰の概念は非常にシンプルかつ直感的です。現在の価格が平均よりも下にある場合は上昇が見込まれ、現在の価格が平均よりも上にある場合は下落が見込まれます。ことわざにもあるように、価格は常に「平均を探している」のです。

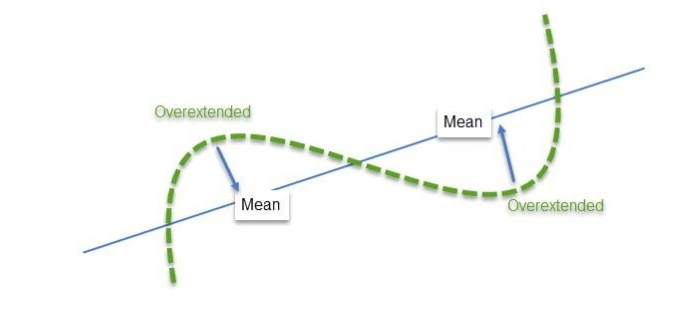
図7：買われ過ぎまたは売られ過ぎの証券は平均価格に戻る傾向がある（出典：ResearchGate CC BY 4.0）

トレンド相場では、平均値は上昇トレンドにおける動的なサポート、下降トレンドにおける動的なレジスタンスとして機能します。一方でレンジ相場では、平均値はチャネル内を推移し、最安値と最高値の中間点として振る舞う傾向があります。

この特徴は、通貨の為替レートにおいて短期足（タイムフレーム）でより顕著に観察されます。というのも、他の資産価格は理論的には無限に上昇・下落する可能性がある一方で、為替レートは各国間の貿易ルールなどによってある程度「上限・下限」が制限されているからです。 

以下はその代表例です。Apple社は1980年12月12日に1株22ドルで上場しました。その後5回の株式分割を経て、調整後のIPO価格は0.10ドルとなります。

本稿執筆時点でAppleの株価は192ドル（約875%上昇）です。そして、依然として上昇を続けています。理論的な上限は存在しません。

一方で、2つの通貨間の為替レートが50%も上昇あるいは下落することは、通常ではありえません。そのような極端な変動が起こるとすれば、それはハイパーインフレーションや大規模な戦争など、極端な要因を伴う場合のみです。通常の経済環境下では、為替市場で取引される通貨ペアの「価格」を定義する為替レートは、より早い段階で平均に回帰する傾向にあります。

2. 仮説を検証するためにデータのパターンを探す

XAUUSDとXAUEURの間のピアソン相関係数が0.97であることは、私たちのパターンを示しています。つまり、これら2つの銘柄の価格は同時に上昇または下降する傾向があるということです。

3. パターンの異常値を監視する

XAUUSDとXAUEURのスプレッドが平均から大きく乖離することが、私たちの異常値です。市場パターンの異常値を見つけることは、ポートフォリオレベルの統計的アービトラージにおける基本的な作業であり、シモンズのチームの運用でも用いられてきました。

4. 異常値を取引するための自動化を開発する

このシンプルなEAは自動化の一例ですが、前述のとおりアルゴリズムには多くの改善点があり、原理をより深く理解するためのツールにすぎません。さらに、EA自体にも通常必要なエラーチェックなどの処理が必要です。

結論

大手プレイヤーが実践するポートフォリオレベルの統計的アービトラージは、一般のリテールトレーダーにとってはほぼ不可能です。なぜなら、それには超高速取引(HFT)、高度なスキルを持つ専門チーム、高品質のビッグデータ、そして膨大な資金が必要だからです。私たちのスケールモデルをジェームズ・シモンズのヘッジファンド運用に近づけるには、冗談めかして言えば、以下の条件が求められます。

• 数百の資産銘柄を含むポートフォリオごとに、リアルタイムでサブ秒単位の粒度で市場分析をおこなうこと（かつてシモンズのチームは12の市場・地域で8,000以上の銘柄を扱っていました）
• 100万ドル単位の注文を出し、マイクロ秒単位で約定させること
• モデルを定期的に更新すること 

モデルの定期的な更新くらいは私たちにも始められそうです。🙂

しかし真面目な話、冒頭で引用したアイザック・ニュートンの言葉が示すように、「数学だけで金融市場で成功することは不十分」です。多くの数学者が失敗した場所で、シモンズは成功を収めましたが、それは数学だけを武器にしたからではありません。彼もまた、他のトレーダーと同じようにキャリアをスタートし、トレンドを追い、テクニカル分析や直感に頼りながら、利益を出したり損失を被ったりしました。多様な手法を試し、市場のルールを学び、プロのトレーダーと議論し協働する中で、持続可能な取引手法を模索していたのです。

それでもなお、彼の概念的枠組みは、正しいポートフォリオの選択、分析すべき特徴量の決定、パターンや異常値の探索、無料データでのプロトタイピング、そして有望なプロトタイプに対して高品質データを投入することで、最もバランスのとれたモデルを追求しようとする者には誰でも開かれています。世界中の多くのリテールトレーダーが、日々まさにその努力を続けています。彼らの多くは億万長者になるわけではありませんが、確実に多くの人が取引活動を持続可能なビジネスへと昇華させています。

さらに、機械学習を活用してパターンや異常値を発見する道も開かれています。これは一般の人にもアクセス可能で、すでに未来がここにあると言って差し支えありません。MetaTrader 5環境における機械学習活用に関する高品質な情報は数百件存在し、現在では低レベルの数学を知らなくとも、MQL5やPythonで高機能な機械学習ライブラリを用いて取引システムを構築できます。 

まとめると、本稿は限られたリソースのリテールトレーダーに向け、ポートフォリオレベルの統計的アービトラージの基礎原理を理解するための体系的な指針を提供しています。

ことわざにもある通り、「過去の結果は未来を保証しない」ものの、適切なツールと客観的なデータで過去の結果を分析すれば、より賢明な意思決定が可能になります。

添付ファイル	説明
pairs-trading.mq5	実験を再現するためのサンプルEAコードが含まれています。PairsTradingFunctions.mqhファイルをインクルードする必要があります。
PairsTradingFunctions.mqh	このリストの前のファイルに必要なインクルードであり、現時点では、EAがペア内の上昇/下降銘柄を識別するために使用するチェックモードの列挙体が1つだけ含まれています。
pairs-trading.ipynb	統計分析を実行するためのPythonコードを含むJupyter Notebookファイルです。
stat_arb_pairs_trading_GOLD_XAUEUR.ini	実験を再現するためのMetratrader 5テスターの構成設定です。