知っておくべきMQL5ウィザードのテクニック（第02回）：コホネンマップ

 

1. はじめに

1.1 MQL5ウィザードに関する連載を続けます。今回はコホネンマップを掘り下げます。ウィキペディアによると、これはデータのトポロジー構造を維持しながら、高次元のデータセットの低次元（通常は2次元）表現を生成するために使用される手法で、1980年代にTeuvo Kohonenによって発表されたものです。

簡単に言うと、コホネンマップ（別名：自己組織化マップ）は、要約されたものの明確さを失わずに複雑なものを要約するものです。要約は組織化の一形態として機能し、これが自己組織化という名前の由来です。再組織化されたデータや地図は2つの関連データになります。入力となる元の高次元データと、出力となる通常は（必ずしもではない）二次元で表現される要約（低次元データ）形式です。入力は既知のものであり、出力は未知のもの、この場合は「研究」されているものになります。

トレーダーのために、この記事の目的のために時間ベースの価格シリーズにのみ焦点を当てるならば、任意の時点で既知のもの（「フィードデータ」）はその時間から左側の価格で、未知のもの（「ファンクタデータ」）は右側の価格です。既知と未知をどのように分類するかによって、フィードデータとファンクタデータのそれぞれの次元数が決定されます。これは、トレーダーの相場に対する考え方やアプローチに大きく影響されるため、重要視されるべきことです。 

1.2 これらの地図でよくある誤解は、ファンクタのデータは画像か2次元であるべきだということです。以下のような画像は、どれも「コホネンマップ」を代表するものとしてよく共有されています。

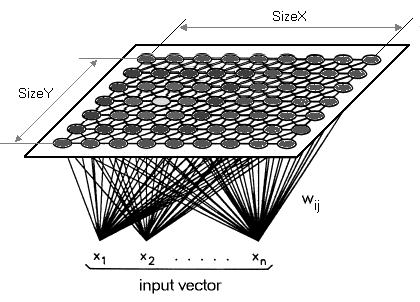
間違ってはいませんが、ファンクタは一次元でもいいし、おそらく（トレーダーにとっては）一次元であるべきだということを強調したいと思います。そこで、高次元のデータを2次元の地図に落とし込むのではなく、1本の線にマッピングすることにしました。 コホネンマップには次元を減らすという定義があるので、今回はこれを次の段階に進めたいと思います。 コホネンマップと通常のニューラルネットワークは、層数、アルゴリズムともに異なります。コホネンマップは、多層ではなく、単層（前述したように通常は線形2Dグリッド）ニューロンのセットです。ファンクタと呼んでいるこの層のすべてのニューロンはフィードに接続しますが、自分自身には接続しません。つまり、ニューロンは互いの重みの影響を直接受けず、フィードデータに対してのみ更新されます。 ファンクタデータ層は、多くの場合、フィードデータに応じて学習反復ごとに自己組織化するマップです。 そのため、訓練後、各ニューロンはファンクタ層で重み調整された次元を持ち、これにより、そのような任意の2つのニューロン間のユークリッド距離を計算することができます。

 

2. クラスの作成

2.1 クラス構成

2.1.1 ディメンション抽象クラスは、これから定義する最初のクラスです。このコードの大部分を別のファイルにして、それを参照するようにすればもっとすっきりするのですが、これについてはマネークラスやトレーリングクラスと合わせて次回に取り上げたいと思うので、とりあえずは前回と同様にすべてのコードをシグナルファイル内に記述することにします。このネットワークは出力に大きな影響を与えるため、次元は常に重要です。フィードデータ（入力）は、一般的なケースと同様に多次元となります。ファンクタデータ（出力）は、一般的なxとyとは逆に1次元となります。フィードとファンクタのデータがどちらも多次元であることから、理想的なデータ型はdouble配列です。

しかし、MQL5ライブラリの探索の流れに沿って、代わりにdouble型の配列リストを使用することにします。フィードデータは、前回の記事で使用したように、1本のバーの間の安値の変化から高値の変化を差し引いたものになります。原則として、入力はトレーダーの市場に対する洞察に基づいて選択されるのが望ましく、ライブ口座やテスト口座で誰もが採用・使用できるものではありません。各トレーダーは、自分の入力データを可能にするために、このコードを修正する必要があります。ファンクタデータは記載の通り1次元になります。しかし、リストでもあるため、カスタマイズして次元を増やすことも可能です。ただし、ここでは直近のバーの始値から終値までの変化に注目します。繰り返しになりますが、MQL5のウィザードでは、自分の時間枠を選択することで、バーが何であるかを設定することができます。ディメンションクラスは、MQL5コードライブラリのリストダブルインターフェイスを継承します。このクラスには、GetとSetという2つの関数が追加されます。その名が示すように、インデックスが提供されると、リスト内の値の取得と設定を支援します。

#include                        <Generic\ArrayList.mqh>
#include                        <Generic\HashMap.mqh>

#define                         SCALE 5

#define                         IN_WIDTH 2*SCALE
#define                         OUT_LENGTH 1

#define                         IN_RADIUS 100.0
#define                         OUT_BUFFER 10000

//
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cdimension                :  public CArrayList<double>
  {
    public:
        
      Cdimension()              {};
      ~Cdimension()             {};
        
     virtual double             Get(const int Index)                                    
                                {       
                                  double _value=0.0; TryGetValue(Index,_value); return(_value); 
                                };
     virtual void               Set(const int Index,double Value)       
                                {  
                                  Insert(Index,Value);                                                                                                                   
                                };
  };

2.1.2 フィードクラスは、上記で作成したディメンションクラスを継承しています。ここでは、特別な関数は追加されません。コンストラクタでリストの容量（配列のサイズに相当）を指定するだけです。フィードデータのリストのデフォルトのサイズは10になっています。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cfeed             : public Cdimension
 {
   public:
                
     Cfeed()            { Clear(); Capacity(IN_WIDTH);  };
     ~Cfeed()           {                               };
 };

2.1.3 ファンクタクラスは、フィードクラスと似ていますが、唯一の注意点はサイズです。前述の通り、ファンクタデータは通常の2次元ではなく1次元で考えるので、設定サイズは1になります。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cfunctor          : public Cdimension
 {
   public:
                
   Cfunctor()           { Clear(); Capacity(OUT_LENGTH); };
   ~Cfunctor()          {                                };
 };

2.1.4 ニューロンクラスは、コードが面白くなるところです。MQL5ライブラリのインターフェイスを継承したクラスとして宣言し、2つのカスタムデータ型を取ります。キーと値です。問題のテンプレートインターフェイスはHashMapです。 そして、私たちが使うカスタムデータの型は、上で宣言した2つのクラスになります。つまり、フィードクラスがキーで、ファンクタクラスが値となります。また、関数は持たず、フィードクラス、ファンクタクラス、同「Key-Value」クラスへのポインタのみとしています。このクラスの目的は、その名の通り、ニューロンを定義することです。ニューロンは、入力データ型（フィードデータ）と出力データ型（ファンクタデータ）の両方を含むので、データの単位となります。これは、ニューロンのフィードデータを、すでに訓練されたニューロンと照合して、ファンクタがどうなり得るかを予測するものです。また、マッピングされたニューロンは、新しいニューロンを学習するたびにファンクタデータが調整されます。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cneuron           : public CHashMap<Cfeed*,Cfunctor*>
 {
   public:
                
    double              weight;
                        
    Cfeed               *fd;
    Cfunctor            *fr;
                        
    CKeyValuePair
    <
    Cfeed*,
    Cfunctor*
    >                   *ff;
                        
    Cneuron()           {
                          weight=0.0;
                          fd = new Cfeed();
                          fr = new Cfunctor();
                          ff = new CKeyValuePair<Cfeed*,Cfunctor*>(fd,fr);
                          Add(ff);
                        };
                                                                        
   ~Cneuron()           {
                          ZeroMemory(weight);
                          delete fd;
                          delete fr;
                          delete ff;
                        };
 };

2.1.5 レイヤー抽象クラスは次に続くものです。ニューロンクラスのリストテンプレートを継承し、1つのオブジェクトであるニューロンポインタを持ちます。抽象クラスであるため、このニューロンポインタは、このクラスを継承するクラスで使用されることを想定しています。入力層と出力層という2つのクラスがあります。コホネンマップは、重みのあるフィードフォワードリンクと逆伝播を持たないので、厳密に言えばニューラルネットワークに分類されるべきものではありません。しかし、推進派の中には、ただ種類が違うだけだと感じる人もいます。 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Clayer            : public CArrayList<Cneuron*>
 {
   public:
                
    Cneuron             *n;
                
    Clayer()            { n = new Cneuron();     };
    ~Clayer()           { delete n;              };
 };

2.1.6 入力レイヤクラスは、抽象レイヤクラスを継承しています。ここにはネットワークが稼働しているときのライブのデータフィード値や最近のデータフィード値が保存されます。 複数のニューロンを持つ典型的な層ではなく、最新のフィードとファンクタのデータを持つ単一のニューロンを特徴とし、したがってそのサイズは1になります。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cinput_layer      : public Clayer
 {
   public:
                
   static const int     size;
                        
    Cinput_layer()      {
                          Clear();
                          Capacity(Cinput_layer::size);
                          for(int s=0; s<size; s++)
                          {
                            n = new Cneuron();
                            Add(n);
                          }
                        }
    ~Cinput_layer()     {};
 };
 const int Cinput_layer::size=1;

2.1.7 出力層クラスもレイヤークラスを継承していますが、ここには「訓練済み」ニューロンが格納されるため、マップとして機能します。この層のニューロンのファンクタデータ部分は、一般的なSOMの画像やマップに相当します。 その初期サイズは10,000で、新しいニューロンが訓練されると同じだけ増加されます。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Coutput_layer      : public Clayer
 {
   public:
                
    int                  index;
    int                  size;
                        
    Coutput_layer()      {
                           index=0;
                           size=OUT_BUFFER;
                           Clear();
                           Capacity(size);
                           for(int s=0; s<size; s++)
                           {
                             n = new Cneuron();
                             Add(n);
                           }
                         };
                                                                        
    ~Coutput_layer()     {
                           ZeroMemory(index);
                           ZeroMemory(size);
                         };
 };

2.1.8 ネットワーククラスもニューロンクラスと同様にHashMapテンプレートインターフェイスを継承しています。そのキーと値のデータ型は、入力層クラスと出力層クラスです。リストサイズの取得だけでなく、各層のニューロンを取得・更新する関数を最も多く（9個）備えています。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cnetwork           : public CHashMap<Cinput_layer*,Coutput_layer*>
 {
   public:
                
     Cinput_layer        *i;
     Coutput_layer       *o;
                        
     CKeyValuePair
     <
     Cinput_layer*,
     Coutput_layer*
     >                   *io;
                        
     Cneuron             *i_neuron;
     Cneuron             *o_neuron;
                        
     Cneuron             *best_neuron;
                        
     Cnetwork()          {
                           i = new Cinput_layer();
                           o = new Coutput_layer();
                           io = new CKeyValuePair<Cinput_layer*,Coutput_layer*>(i,o);
                           Add(io);
                                                                                
                           i_neuron = new Cneuron();
                           o_neuron = new Cneuron();
                                                                                
                           best_neuron = new Cneuron();
                         };
                                                                        
     ~Cnetwork()         {
                           delete i;
                           delete o;
                           delete io;
                           delete i_neuron;
                           delete o_neuron;
                           delete best_neuron;
                         };
                        
      virtual int        GetInputSize()
                         {
                           TryGetValue(i,o);
                           return(i.size);
                         };
                        
      virtual int        GetOutputIndex()
                         {
                           TryGetValue(i,o);
                           return(o.index);
                         };
                        
      virtual void       SetOutputIndex(const int Index)
                         {
                           TryGetValue(i,o);
                           o.index=Index;
                           TrySetValue(i,o);
                         };
                        
      virtual int        GetOutputSize()
                         {
                           TryGetValue(i,o);
                           return(o.size);
                         };
                        
      virtual void       SetOutputSize(const int Size)
                         {
                           TryGetValue(i,o);
                           o.size=Size;
                           o.Capacity(Size);
                           TrySetValue(i,o);
                         };
                        
      virtual void       GetInNeuron(const int NeuronIndex)
                         {
                           TryGetValue(i,o);
                           i.TryGetValue(NeuronIndex,i_neuron);
                         };
                        
      virtual void       GetOutNeuron(const int NeuronIndex)
                         {
                           TryGetValue(i,o);
                           o.TryGetValue(NeuronIndex,o_neuron);
                         };
                        
      virtual void       SetInNeuron(const int NeuronIndex)
                         {
                           i.TrySetValue(NeuronIndex,i_neuron);
                         };
                        
      virtual void       SetOutNeuron(const int NeuronIndex)
                         {
                           o.TrySetValue(NeuronIndex,o_neuron);
                         };
 };

2.1.9 地図クラスは、最終的なアンブレラクラスです。ネットワーククラスのインスタンスを呼び出し、ニューロンを訓練し、ネットワークに最適なニューロンを取得するための他の変数を含んでいます。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cmap
  {
    public:
                        
      Cnetwork               *network;
                        
      static const double     radius;
      static double           time;
                        
      double                  QE;       //proxy for Quantization Error
      double                  TE;       //proxy for Topological Error
                        
      datetime                refreshed;
                        
      bool                    initialised;
                        
      Cmap()                  {
                                network = new Cnetwork();
                                                                                        
                                initialised=false;
                                                                                        
                                time=0.0;
                                                                                        
                                QE=0.50;
                                TE=5000.0;
                                                                                        
                                refreshed=D'1970.01.05';
                               };
                                                                                
      ~Cmap()                  {
                                 ZeroMemory(initialised);
                                                                                        
                                 ZeroMemory(time);
                                                                                        
                                 ZeroMemory(QE);
                                 ZeroMemory(TE);
                                                                                        
                                 ZeroMemory(refreshed);
                               };
 };
 const double Cmap::radius=IN_RADIUS;
 double Cmap::time=10000/fmax(1.0,log(IN_RADIUS));

 

2.2.トポロジー

2.2.1 ニューロンの訓練は、出力層の既存ニューロンのファンクタの重みを調整し、新しいトレーナーニューロンを追加する競合学習プロセスです。これらの重みを調整する割合と、最も重要なのは、これらの重みを調整するために必要な反復回数で、ネットワークの有効性を決定する上で非常に重要なパラメータです。重みを調整する各反復で、新しい、より小さい半径が計算されます。私はこの半径をファンクタエラー（SOMトポロジカルエラーと混同しないように）と呼んでいますが、多くはユークリッド距離で測定した近傍半径と呼んでいます。「エラー」を選択したのは、より良いネットワーク結果を得るためには、このパラメータを最小化する必要があるからです。繰り返しの回数が多いほど、ファンクタエラーは小さくなります。  反復回数の他に、学習率を1に近い数値から0に向かって徐々に下げていく必要があります。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalKM::NetworkTrain(Cmap &Map,Cneuron &TrainNeuron)
  {
    Map.TE=0.0;

    int _iteration=0;
    double _training_rate=m_training_rate;

    int _err=0;
    double _functor_error=0.0;

    while(_iteration<m_training_iterations)
    {
      double _current_radius=GetTrainingRadius(Map,_iteration);

      for(int i=0; i<=Map.network.GetOutputIndex(); i++)
      {
        Map.network.GetOutNeuron(i);
        double _error = EuclideanFunctor(TrainNeuron,Map.network.o_neuron);

        if(_error<_current_radius)
        {
          _functor_error+=(_error);
          _err++;

          double _remapped_radius = GetRemappedRadius(_error, _current_radius);

          SetWeights(TrainNeuron,Map.network.o_neuron,_remapped_radius,_training_rate);

          Map.network.SetOutNeuron(i);
        }
      }

      _iteration++;
      _training_rate=_training_rate*exp(-(double)_iteration/m_training_iterations);
    }

    int
    _size=Map.network.GetOutputSize(),
    _index=Map.network.GetOutputIndex();
    Map.network.SetOutputIndex(_index+1);
    if(_index+1>=_size)
    {
      Map.network.SetOutputSize(_size+OUT_BUFFER);
    }

    Map.network.GetOutNeuron(_index+1);
    for(int w=0; w<IN_WIDTH; w++)
    {
      Map.network.o_neuron.fd.Set(w,TrainNeuron.fd.Get(w));
    }
    
    for(int l=0; l<OUT_LENGTH; l++)
    {
      Map.network.o_neuron.fr.Set(l,TrainNeuron.fr.Get(l));
    }

    Map.network.SetOutNeuron(_index+1);

    if(_err>0)
    {
      _functor_error/=_err;
      Map.TE=_functor_error*IN_RADIUS;
    }
  }

2.2.2 トポロジカルエラーはコホネンマップの重要な属性です。私は、これを出力層が長期的に意図した目標にどれだけ近づいているかを示す指標として捉えています。学習するたびに、出力層のニューロンは真の、あるいは意図した結果に適応していくので、問題はこの進捗をどのように測定するかです。この答えは、出力層をより温存していれば、この目標に近づくということです。この記事では、ファンクタエラーをその代理として機能させることにします。

2.3. 量子化

2.3.1 ニューロンマッピングは、フィードデータしか存在しないニューロンに対して、最も適合するファンクタの重みを求める処理です。これは、ファンクタデータが知られていないニューロンからフィードデータのユークリッド距離が最短の出力層のニューロンを見つけることによっておこなわれます。訓練のときと同様、この距離をフィードエラーと呼んでいます。 またですが、この値が小さいほど、ネットワークの信頼性が高いと言えます。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalKM::NetworkMapping(Cmap &Map,Cneuron *MapNeuron)
  {
    Map.QE=0.0;
    
    Map.network.best_neuron = new Cneuron();

    int _random_neuron=rand()%Map.network.GetOutputIndex();

    Map.network.GetInNeuron(0);
    Map.network.GetOutNeuron(_random_neuron);

    double _feed_error = EuclideanFeed(Map.network.i_neuron,Map.network.o_neuron);

    for(int i=0; i<Map.network.GetOutputIndex(); i++)
    {
      Map.network.GetOutNeuron(i);

      double _error = EuclideanFeed(Map.network.i_neuron,Map.network.o_neuron);

      if(_error < _feed_error)
      {
        for(int w=0; w<IN_WIDTH; w++)
        {
          Map.network.best_neuron.fd.Set(w,Map.network.o_neuron.fd.Get(w));
        }

        for(int l=0; l<OUT_LENGTH; l++)
        {
          Map.network.best_neuron.fr.Set(l,Map.network.o_neuron.fr.Get(l));
        }

        _feed_error = _error;
      }
    }

    Map.QE=_feed_error/IN_RADIUS;
}

2.3.2 量子化誤差コホネンマップにおけるもう1つの重要な属性は、私の意見では簡潔な定義を持っていません。私はこれを、高次元のデータを低次元の出力に変換する際に発生するエラーだと捉えています。ここでの場合、フィードをファンクタに変換する際のエラーとなります。この記事では、フィードエラーをその代理として機能させることにします。

 

3. MQL5ウィザードによる組み立て

3.1 ウィザードによる組み立ては直感的です。唯一の注意点は、まず大きな時間枠でテストを始めることです。というのも、1バーあたり理想的な10,000回の訓練反復には、かなりの期間にわたって訓練する場合、いくらか時間がかかるからです。 

 

 

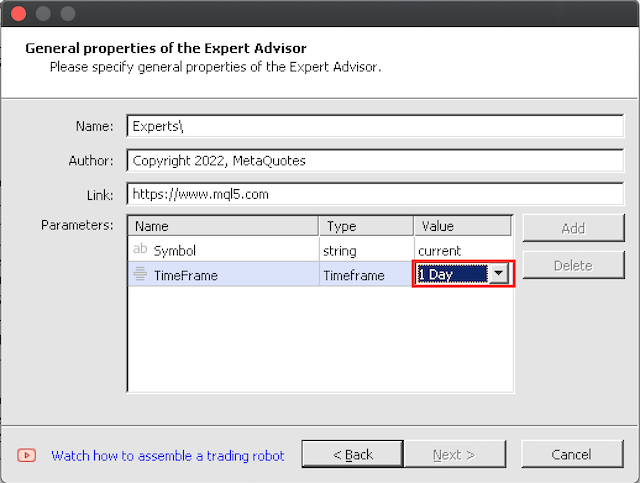
4.ストラテジーテスターでのテスト

4.1デフォルト入力テストでは、量子化エラープロキシ(QE)とトポロジカルエラープロキシ(TE)の感度を調査します。2つのシナリオを見ていきます。まず、QEとTEを0.5と12.5という非常に保守的な値でテストし、次にこれらの入力をそれぞれ0.75と25.0にしてテストしてみます。

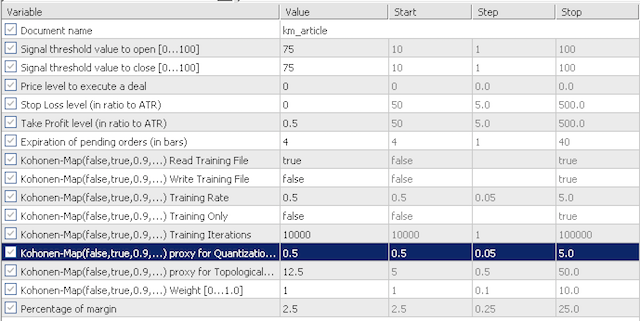
保守的オプション

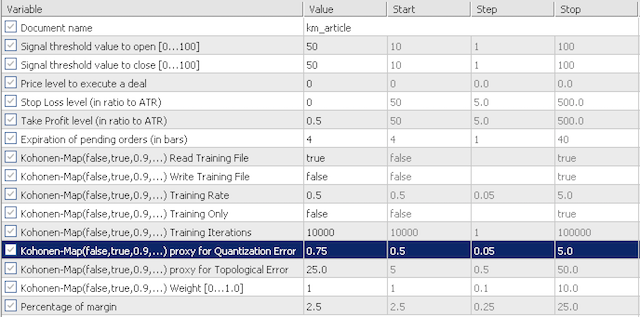
積極的オプション

 

 

入力はそれほど多くありません。初期化の前に訓練ファイルを読み込むかどうかを決める「training read」があります。EAはファイルがあるかどうかの検証をおこないません。また、「training write」は、その名の通り、EAが初期化されたときに学習ファイルを書き込むかどうかを決定するものです。訓練は常にEAが実行された後におこなわれます。訓練のみおこなって取引はおこなわないというオプションは、「training only」入力パラメータで設定します。コホネンマップの他の2つの重要なパラメータは、「training rate」（学習率とも呼ばれる）と「training iterations」（訓練の反復回数）です。一般に、この2つを高くすればするほど（学習率は1.0が上限）、より良いパフォーマンスが期待できますが、その分時間とCPUリソースが犠牲になります。 

EURJPYのV字型期間2018.10.01～2021.06.01でEAが学習し、学習終了日から現在までのフォワードテストがおこなわれました。

保守的な選択肢では次が方向されました。

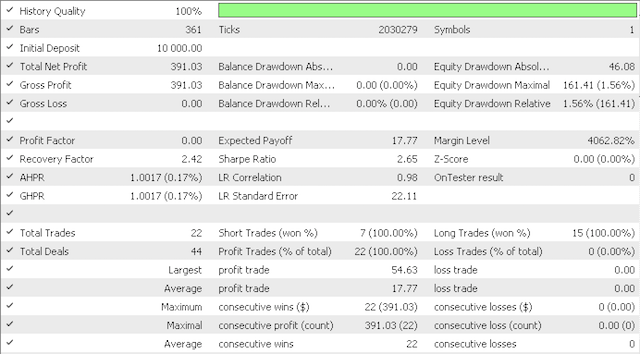
次はエクイティカーブです。

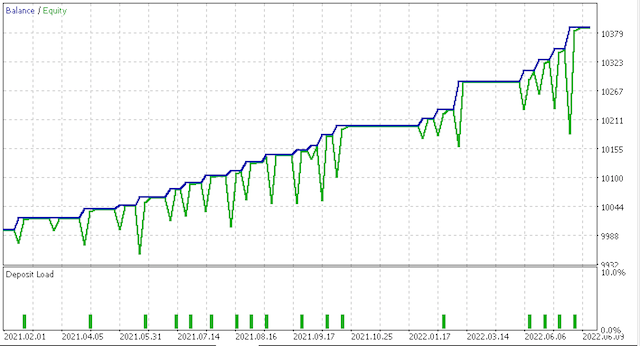
ただし、より積極的なオプションでは、こんな報告がありました。

 

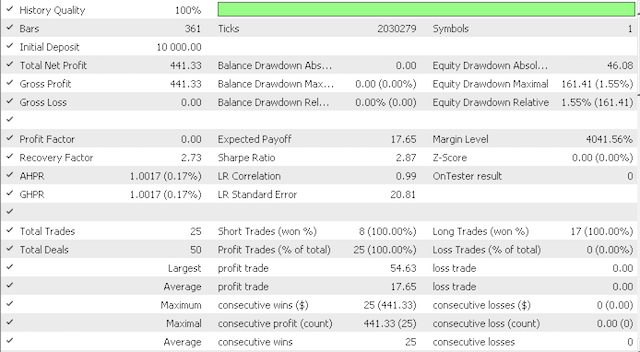
次はエクイティカーブです。

 

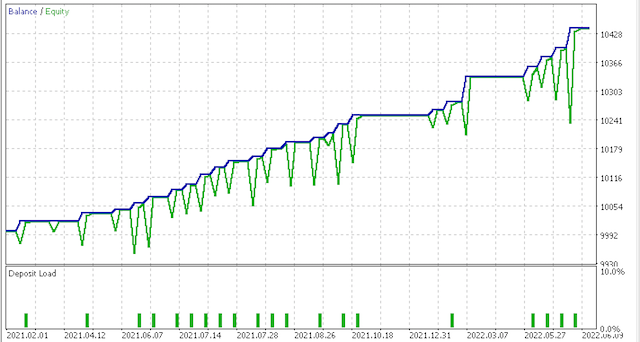
リスクとポジションサイジングについては、より多くのテストと微調整が必要であることは明らかですが、このように短期間に学習させたシステムとしては有望です。しかし、上記の2つのシナリオを比較すると、より保守的なオプションのシャープレシオの値が0.43で、より多くの取引の0.85のほぼ半分であることから、十分に報われていないように見えます。また、フィードやファンクタのデータを自分の取引スタイルに合わせてカスタマイズするだけでなく、導入前に必ず証券会社のリアルティックのデータで事前テストをおこなう必要があります。

 

5.結論

5.1MQL5ウィザードは、狭い時間枠の中で取引システムを組み立てるという点では、非常に機敏なツールであることは明らかです。今回は、価格時系列の多次元フィードデータを-1.0から1.0までの1次元に移植したコホネンマップという選択肢を検討しました。一般的ではありませんが、この方法は、複雑さを軽減し、意思決定を容易にするというコホネンマップの真髄を体現しています。また、配列リストやハッシュマップなど、MQLライブラリのより多くのコードを紹介しながら、これを実現しました。お気に召していただけたでしょうか。ご精読ありがとうございました。