MQL5 Wizard techniques you should know (Part 02): Kohonen Maps

 

1. Introduction    

1.1 Continuing with this series on the MQL5 wizard, we will delve into Kohonen-Maps for this one. These per Wikipedia are technique used to produce a low-dimensional (typically two-dimensional) representation of a higher dimensional data set while preserving the topological structure of the data. They were put forward by Teuvo Kohonen in the 1980s. 

In simple terms kohonen-maps (aka self-organizing maps) are away of summarizing complexity without losing the distinctness of what is summarized. The summary serves as a form of organizing hence the name self-organizing. With the re-organized data or maps we therefore have two sets of related data. The original high-dimensional data that serves as our input, and the summarized (lower-dimensional data) form that is usually, but not always, represented in two dimensions as the output. The inputs are the knowns while the outputs would be the unknown or in this case what is being ‘studied’.  

For a trader, if we are for the purpose of this article focus only on time-based price series, the knowns (that we’ll refer to as feed data) at any time are the prices left of that time with the unknowns (that we’ll call functor data) being those to the right. How we classify the knowns and unknowns determines the respective number of dimensions for both the feed and functor data. This is something traders should be critical-to because it is informed hugely by their outlook and approach to the markets.  

1.2  A Common misconception with these maps is that the functor data should be an image or 2 dimensional. Images such as the one below are all often shared as being representative of what Kohonen Maps are.

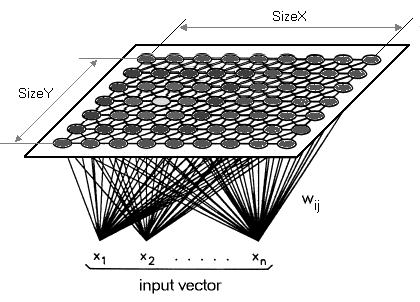
While not wrong, I want to highlight that the functor can and perhaps should (for traders) have a single dimension. So rather than reducing our high dimensional data to a 2D map, we will map it onto a single line. Kohonen maps by definition are meant to reduce dimensionality so I want us to take this to the next level for this article. The kohonen map is different from regular neural networks both in number of layers and the underlying algorithm. It is a single-layer (usually linear 2D grid as afore mentioned) set of neurons, instead of multiple layers. All the neurons on this layer which we are referring to as the functor connect to the feed, but not to themselves meaning the neurons are not influenced by each other’s weights directly, and only update with respect to the feed data. The functor data layer is often a “map” that organizes itself at each training iteration depending on the feed data. As such, after training, each neuron has weight adjusted dimension in the functor layer and this allows one to calculate the Euclidean distance between any two such neurons.

 

2. Creating the class

2.1  Class structure

2.1.1 Dimension abstract class is the first class we will define. This code would have been tidier if I had made most of it in a separate file and simply referenced it but I want to cover that together with the money and trailing classes in the next article, so for now like in the previous article all code will be in the signal file. The dimensions are always important in this network since they heavily influence the output. The feed data (the inputs) will be multi-dimensional as is typically the case. The functor data (the outputs) will have one dimension contrary to the typical x and y. Based on the multi-dimensionality of both the feed and functor data an ideal data type would be a double array.

However, keeping with the trend of exploring the MQL5 Library, we will use an array list of double type instead. The feed data will be changes in lows less changes in highs over a space of one bar as we had used in the previous article. As a rule inputs are better selected based on a trader’s insights on the market and should not be adopted and used by everyone on a live or even testing account. Every trader should modify this code to allow for his own input data. The functor data will be one dimensional as stated. However, since it is also a list, it can be customized to add more dimensions. For our purposes though, we will focus on the change between the most recent bar’s open and close. Once again, the MQL5 wizard allows you to set what a bar is by selecting your own timeframe. The dimension class will inherit from the list double interface in the MQL5 code library. Two functions will be added to this class, namely Get and Set. As their name suggests, they aid in retrieving and setting values in the list once an index is provided.

#include                        <Generic\ArrayList.mqh>
#include                        <Generic\HashMap.mqh>

#define                         SCALE 5

#define                         IN_WIDTH 2*SCALE
#define                         OUT_LENGTH 1

#define                         IN_RADIUS 100.0
#define                         OUT_BUFFER 10000

//
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cdimension                :  public CArrayList<double>
  {
    public:
        
      Cdimension()              {};
      ~Cdimension()             {};
        
     virtual double             Get(const int Index)                                    
                                {       
                                  double _value=0.0; TryGetValue(Index,_value); return(_value); 
                                };
     virtual void               Set(const int Index,double Value)       
                                {  
                                  Insert(Index,Value);                                                                                                                   
                                };
  };

2.1.2  Feed class will inherit from the dimension class just created above. No special functions will be added here. Only the constructor will specify the list capacity (analogous to array size) and default size of our feed data list will be 10.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cfeed             : public Cdimension
 {
   public:
                
     Cfeed()            { Clear(); Capacity(IN_WIDTH);  };
     ~Cfeed()           {                               };
 };

2.1.3  Functor class will be similar to the feed class with only caveat being the size. As stated, we will consider one (not the usual two) dimensions for our functor data, so the set size will be 1.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cfunctor          : public Cdimension
 {
   public:
                
   Cfunctor()           { Clear(); Capacity(OUT_LENGTH); };
   ~Cfunctor()          {                                };
 };

2.1.4   Neuron class is where our code gets interesting. We will declare it as a class that inherits from an interface in the MQL5 library that takes two custom data types. A key and a value. The template interface in question is the HashMap.  And the custom data typed we’ll use will be the two classes declared above. Namely the Feed class as our key and the Functor class as our value. We also have no functions but only pointers to the Feed class, Functor class and a ‘key-value’ class of the same. The purpose of this class as the name suggests is to define the neuron. The neuron is our unit of data since it includes both the inputs data-type (feed data) and output data-type (functor data). It is a neuron’s feed-data that is matched with already trained neurons in order to project what the functor could be. Also mapped neurons have their functor-data are adjusted whenever a new neuron is training.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cneuron           : public CHashMap<Cfeed*,Cfunctor*>
 {
   public:
                
    double              weight;
                        
    Cfeed               *fd;
    Cfunctor            *fr;
                        
    CKeyValuePair
    <
    Cfeed*,
    Cfunctor*
    >                   *ff;
                        
    Cneuron()           {
                          weight=0.0;
                          fd = new Cfeed();
                          fr = new Cfunctor();
                          ff = new CKeyValuePair<Cfeed*,Cfunctor*>(fd,fr);
                          Add(ff);
                        };
                                                                        
   ~Cneuron()           {
                          ZeroMemory(weight);
                          delete fd;
                          delete fr;
                          delete ff;
                        };
 };

2.1.5   Layer abstract class is what follows next. It inherits from a list template of the neuron class and has one object - a neuron pointer. Being an abstract class, this neuron pointer is meant to be used by classes that inherit from this class. There are two such classes, namely the input layer and the output layer. Strictly speaking, Kohonen maps should not be classified as neural networks as they do not have feed forward links with weights and back propagation. Some proponents though feel they are just a different type. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Clayer            : public CArrayList<Cneuron*>
 {
   public:
                
    Cneuron             *n;
                
    Clayer()            { n = new Cneuron();     };
    ~Clayer()           { delete n;              };
 };

2.1.6   Input Layer class inherits from the abstract layer class. It is where live and recent data feed values are stored when the network is running. Rather than being a typical layer with multiple neurons, it will feature a single neuron that has the most recent feed and functor data, therefore its size will be 1.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cinput_layer      : public Clayer
 {
   public:
                
   static const int     size;
                        
    Cinput_layer()      {
                          Clear();
                          Capacity(Cinput_layer::size);
                          for(int s=0; s<size; s++)
                          {
                            n = new Cneuron();
                            Add(n);
                          }
                        }
    ~Cinput_layer()     {};
 };
 const int Cinput_layer::size=1;

2.1.7  Output Layer class also inherits from the layer class but it serves as our map since ‘trained’ neurons are stored here. The functor-data portion of the neurons in this layer is equivalent to an image or map of your typical SOM. Its size will initially be 10,000 and will be incremented by the same amount as new neurons are trained.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Coutput_layer      : public Clayer
 {
   public:
                
    int                  index;
    int                  size;
                        
    Coutput_layer()      {
                           index=0;
                           size=OUT_BUFFER;
                           Clear();
                           Capacity(size);
                           for(int s=0; s<size; s++)
                           {
                             n = new Cneuron();
                             Add(n);
                           }
                         };
                                                                        
    ~Coutput_layer()     {
                           ZeroMemory(index);
                           ZeroMemory(size);
                         };
 };

2.1.8  Network class like the neuron class also inherits from the HashMap template interface. Its key and value data types are the input layer class and the output layer class. It has the most functions (9) for not only getting list size but also retrieving and updating neurons on the respective layers.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cnetwork           : public CHashMap<Cinput_layer*,Coutput_layer*>
 {
   public:
                
     Cinput_layer        *i;
     Coutput_layer       *o;
                        
     CKeyValuePair
     <
     Cinput_layer*,
     Coutput_layer*
     >                   *io;
                        
     Cneuron             *i_neuron;
     Cneuron             *o_neuron;
                        
     Cneuron             *best_neuron;
                        
     Cnetwork()          {
                           i = new Cinput_layer();
                           o = new Coutput_layer();
                           io = new CKeyValuePair<Cinput_layer*,Coutput_layer*>(i,o);
                           Add(io);
                                                                                
                           i_neuron = new Cneuron();
                           o_neuron = new Cneuron();
                                                                                
                           best_neuron = new Cneuron();
                         };
                                                                        
     ~Cnetwork()         {
                           delete i;
                           delete o;
                           delete io;
                           delete i_neuron;
                           delete o_neuron;
                           delete best_neuron;
                         };
                        
      virtual int        GetInputSize()
                         {
                           TryGetValue(i,o);
                           return(i.size);
                         };
                        
      virtual int        GetOutputIndex()
                         {
                           TryGetValue(i,o);
                           return(o.index);
                         };
                        
      virtual void       SetOutputIndex(const int Index)
                         {
                           TryGetValue(i,o);
                           o.index=Index;
                           TrySetValue(i,o);
                         };
                        
      virtual int        GetOutputSize()
                         {
                           TryGetValue(i,o);
                           return(o.size);
                         };
                        
      virtual void       SetOutputSize(const int Size)
                         {
                           TryGetValue(i,o);
                           o.size=Size;
                           o.Capacity(Size);
                           TrySetValue(i,o);
                         };
                        
      virtual void       GetInNeuron(const int NeuronIndex)
                         {
                           TryGetValue(i,o);
                           i.TryGetValue(NeuronIndex,i_neuron);
                         };
                        
      virtual void       GetOutNeuron(const int NeuronIndex)
                         {
                           TryGetValue(i,o);
                           o.TryGetValue(NeuronIndex,o_neuron);
                         };
                        
      virtual void       SetInNeuron(const int NeuronIndex)
                         {
                           i.TrySetValue(NeuronIndex,i_neuron);
                         };
                        
      virtual void       SetOutNeuron(const int NeuronIndex)
                         {
                           o.TrySetValue(NeuronIndex,o_neuron);
                         };
 };

2.1.9   Map class is the final umbrella class. It calls an instance of the network class and includes other variables for training neurons and getting the best matching neuron for the network. 

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class Cmap
  {
    public:
                        
      Cnetwork               *network;
                        
      static const double     radius;
      static double           time;
                        
      double                  QE;       //proxy for Quantization Error
      double                  TE;       //proxy for Topological Error
                        
      datetime                refreshed;
                        
      bool                    initialised;
                        
      Cmap()                  {
                                network = new Cnetwork();
                                                                                        
                                initialised=false;
                                                                                        
                                time=0.0;
                                                                                        
                                QE=0.50;
                                TE=5000.0;
                                                                                        
                                refreshed=D'1970.01.05';
                               };
                                                                                
      ~Cmap()                  {
                                 ZeroMemory(initialised);
                                                                                        
                                 ZeroMemory(time);
                                                                                        
                                 ZeroMemory(QE);
                                 ZeroMemory(TE);
                                                                                        
                                 ZeroMemory(refreshed);
                               };
 };
 const double Cmap::radius=IN_RADIUS;
 double Cmap::time=10000/fmax(1.0,log(IN_RADIUS));

 

2.2. Topology

2.2.1  Neuron training is the competitive learning process of adjusting the functor weights of existing neurons in the output layer and adding a new trainer neuron. The rate, at which these weights are adjusted and most importantly the number of iterations it takes to adjust these weights, are very sensitive parameters in determining the efficacy of the network. At each iteration of adjusting the weights, a new smaller radius is calculated. I refer to this radius as the functor-error (not to be confused with the SOM Topological-error) but most refer to it as the neighborhood radius as measured by Euclidean distance. I choose ‘error’ as this is a parameter that needs to be minimized for better network results. The more iterations one performs, the smaller will be the Functor-error.  Besides the number of iterations, the rate of learning needs to be reduced gradually from a number close to one towards zero.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalKM::NetworkTrain(Cmap &Map,Cneuron &TrainNeuron)
  {
    Map.TE=0.0;

    int _iteration=0;
    double _training_rate=m_training_rate;

    int _err=0;
    double _functor_error=0.0;

    while(_iteration<m_training_iterations)
    {
      double _current_radius=GetTrainingRadius(Map,_iteration);

      for(int i=0; i<=Map.network.GetOutputIndex(); i++)
      {
        Map.network.GetOutNeuron(i);
        double _error = EuclideanFunctor(TrainNeuron,Map.network.o_neuron);

        if(_error<_current_radius)
        {
          _functor_error+=(_error);
          _err++;

          double _remapped_radius = GetRemappedRadius(_error, _current_radius);

          SetWeights(TrainNeuron,Map.network.o_neuron,_remapped_radius,_training_rate);

          Map.network.SetOutNeuron(i);
        }
      }

      _iteration++;
      _training_rate=_training_rate*exp(-(double)_iteration/m_training_iterations);
    }

    int
    _size=Map.network.GetOutputSize(),
    _index=Map.network.GetOutputIndex();
    Map.network.SetOutputIndex(_index+1);
    if(_index+1>=_size)
    {
      Map.network.SetOutputSize(_size+OUT_BUFFER);
    }

    Map.network.GetOutNeuron(_index+1);
    for(int w=0; w<IN_WIDTH; w++)
    {
      Map.network.o_neuron.fd.Set(w,TrainNeuron.fd.Get(w));
    }
    
    for(int l=0; l<OUT_LENGTH; l++)
    {
      Map.network.o_neuron.fr.Set(l,TrainNeuron.fr.Get(l));
    }

    Map.network.SetOutNeuron(_index+1);

    if(_err>0)
    {
      _functor_error/=_err;
      Map.TE=_functor_error*IN_RADIUS;
    }
  }

2.2.2  Topological Error is a key attribute in Kohonen maps. I take it as a measure of how close the output layer is to its long-term intended goal. Remember, with each training the output layer neurons get adapted to the true or intended result so the question becomes how we measure this progress. The answer to this is if we are preserving the output layer more, then we are closer to this target. For the purposes of this article, I will have the functor-error act as a proxy for it.

2.3. Quantization

2.3.1   Neuron mapping is a process of finding the functor weights that would best fit a neuron for which only feed-data is present. This is done by finding the neuron in the output layer with the shortest feed-data Euclidean distance from the neuron, for which no functor data is known. Like with the training, I refer to this distance as the feed-error. Again, the smaller our value, the more reliable should be the network.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalKM::NetworkMapping(Cmap &Map,Cneuron *MapNeuron)
  {
    Map.QE=0.0;
    
    Map.network.best_neuron = new Cneuron();

    int _random_neuron=rand()%Map.network.GetOutputIndex();

    Map.network.GetInNeuron(0);
    Map.network.GetOutNeuron(_random_neuron);

    double _feed_error = EuclideanFeed(Map.network.i_neuron,Map.network.o_neuron);

    for(int i=0; i<Map.network.GetOutputIndex(); i++)
    {
      Map.network.GetOutNeuron(i);

      double _error = EuclideanFeed(Map.network.i_neuron,Map.network.o_neuron);

      if(_error < _feed_error)
      {
        for(int w=0; w<IN_WIDTH; w++)
        {
          Map.network.best_neuron.fd.Set(w,Map.network.o_neuron.fd.Get(w));
        }

        for(int l=0; l<OUT_LENGTH; l++)
        {
          Map.network.best_neuron.fr.Set(l,Map.network.o_neuron.fr.Get(l));
        }

        _feed_error = _error;
      }
    }

    Map.QE=_feed_error/IN_RADIUS;
}

2.3.2   Quantization Error is another critical attribute in Kohonen maps that does not have a concise definition in my opinion. My take is its the error in translating high dimensional data to the low dimensional output. In our case, here it would be the error in converting the feed to the functor. For the purposes of this article I will have the feed-error act as a proxy for it.

 

3. Assembling with MQL5 Wizard

3.1  Wizard assembly is straight forward. Only caution I have here is start testing on large timeframes first since the ideal 10,000 training iterations per bar will take some time when training over a significant period. 

 

 

4. Testing in Strategy Tester

4.1   Default inputs for our testing will investigate the sensitivity of our quantization error proxy (QE) and the topological error proxy (TE). We will look at the two scenarios. First, we will test with very conservative values with QE and TE at 0.5 and 12.5; then we will test these inputs at 0.75 and 25.0 respectively.

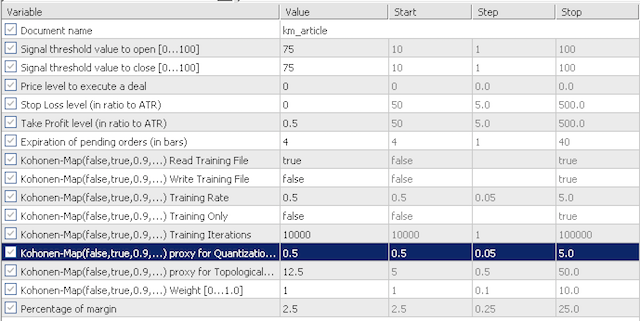
conservative options

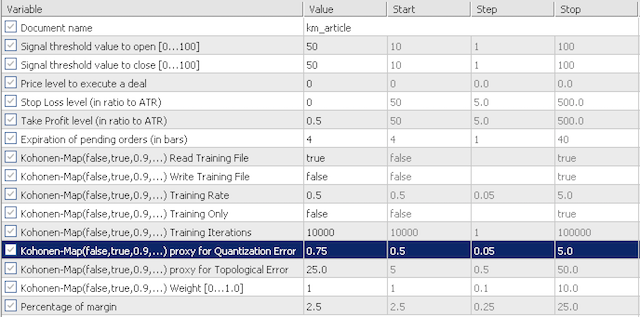
aggressive options

 

 

The inputs are not that many. We have 'training read' which determines whether or not we should read a training file prior to initialization. If this file is absent, the expert will not validate. We also have 'training write' which, as name suggests, determines whether a learning file should be written once the expert de-initializes. Training always takes place once the expert is running. The option to train only and not trade is set by the 'training only' input parameter. The other two significant parameters to Kohonen maps are the 'training rate' (also known as learning rate) and the training iterations. Generally the higher these two are (training rate is capped at 1.0), the better performance should one expect, however this will come at a cost of time and CPU resources. 

The expert was trained on EURJPY's V shaped period of 2018.10.01 to 2021.06.01 and forward tested from the training end date to present date.

The conservative option came to this report:

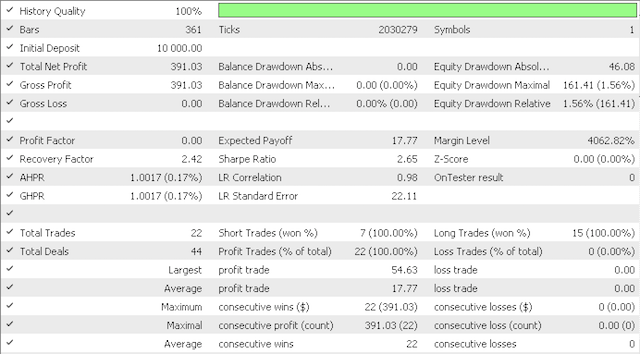
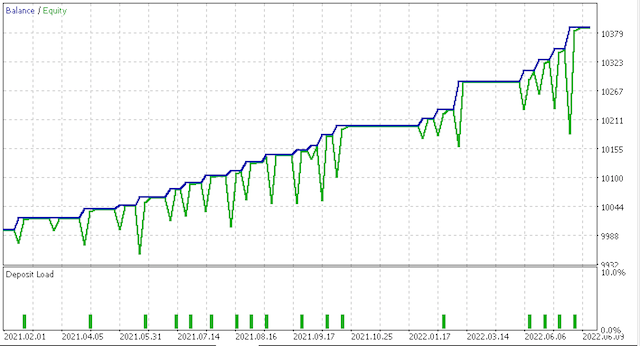
And this equity curve:

However, the more aggressive option had this report:

 

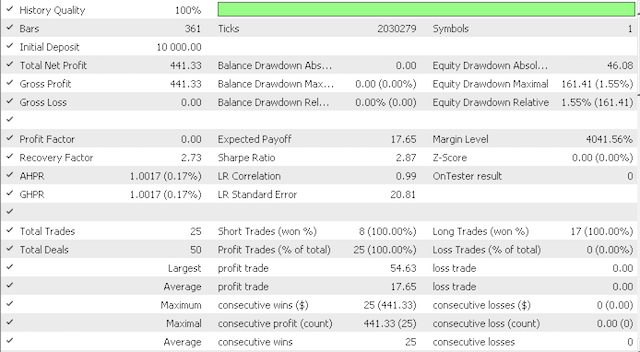
And this equity curve:

 

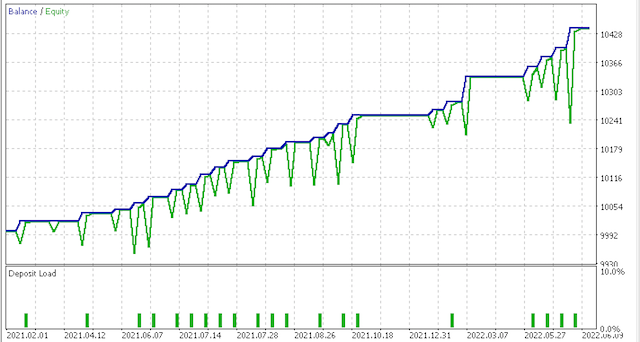
Clearly, more testing and fine-tuning is required regarding risk and position sizing but for a system that is trained over such a short period it is promising. Comparing the two scenarios above though, it appears the more conservative option is not sufficiently rewarded given its Sharpe ratio value of 0.43 is almost half the 0.85 value on more trades. More study is required here before use and as always besides customising the feed and functor data to one's style of how he trades; preliminary testing should always be done on your broker's real-ticks data over large significant periods of time before deployment.

 

5. Conclusion

5.1   MQL5 Wizard is clearly a very agile tool when it comes to assembling trading systems in a tight timeframe window. For this article, we explored the option of Kohonen maps that port multi-dimension feed data of price time series into a single dimension that ranges from -1.0 to 1.0. While not common practice, this approach does champion the very essence of Kohonen maps which is to reduce complexity and ease decision making. We have also done this while showcasing more code from the MQL library like array lists and hash maps. I hope, you liked it. Thanks for reading!