
Parallel Particle Swarm Optimization
As you know, MetaTrader 5 allows the optimization of trading strategies using the built-in Strategy Tester based on two algorithms: direct enumeration of input parameters and a genetic algorithm - GA. Genetic optimization is a type of evolutionary algorithm that provides a significant process speedup. However, GA results can significantly depend on the task and specifics of a certain GA implementation, in particular, of the one offered by the tester. That is why many traders who wish to extend the standard functionality try to create their own optimizers for MetaTrader. Here, possible fast optimization methods are not limited to the genetic algorithm. In addition to GA, there are other popular methods, such as Simulated Annealing and Particle Swarm Optimization.
In this article, we will implement the Particle Swarm Optimization (PSO) algorithm and will try to integrate it into the MetaTrader tester to run in parallel on available local agents. The objective optimization function will be the EA's trade performance metric selected by the user.
Particle Swarm Method
From an algorithmic point of view, the PSO method is relatively simple. The main idea is to generate a set of virtual "particles" in the space of the Expert Advisor's input parameters. The particles then move and change their speed depending on the EA's trading metrics at the corresponding points in space. The process is repeated many times until the performance stops improving. The pseudo-code of the algorithm is shown below:

Particle Swarm Optimization Pseudo-Code
According to this code, each particle has a current position, speed and memory of its "best" point in the past. Here, the "best" point means the point (a set of EA input parameters), where the highest value of the objective function for this particle was achieved. Let us describe this in a class.
class Particle { public: double position[]; // current point double best[]; // best point known to the particle double velocity[]; // current speed double positionValue; // EA performance in current point double bestValue; // EA performance in the best point int group; Particle(const int params) { ArrayResize(position, params); ArrayResize(best, params); ArrayResize(velocity, params); bestValue = -DBL_MAX; group = -1; } };
The size of all arrays is equal to the dimension of the optimization space, so it is equal to the number of the Expert Advisor parameters being optimized (passed to the constructor). By default, the larger the objective function value, the better the optimization. Therefore, initialize the bestValue field with the minimum possible -DBL_MAX number. One of the trading metrics is usually used as a criterion for evaluating an EA, such as profit, profit factor, Sharpe ratio, etc. If optimization is performed by the parameter whose lower values are considered better, such as for example drawdown, appropriate transformations can be made to maximize opposite values.
Arrays and variables are made public to simplify access and their recalculation code. Strict adherence to the OOP principles would require hiding them using the 'private' modifier and describing read and modify methods.
In addition to individual particles, the algorithm operates with so-called "topologies" or subsets of particles. They can be created according to different principles. "Social group topology" will be used in our case. Such a group stores information about the best position among all its particles.
class Group { private: double result; // best EA performance in the group public: double optimum[]; // best known position in the group Group(const int params) { ArrayResize(optimum, params); ArrayInitialize(optimum, 0); result = -DBL_MAX; } void assign(const double x) { result = x; } double getResult() const { return result; } bool isAssigned() { return result != -DBL_MAX; } };
By specifying a group name in the 'group' field of the Particle class, we indicate the group to which the particle belongs (see above).
Now, let us move on to coding the particle swarm algorithm itself. It will be implemented as a separate class. Let us start with arrays of particles and groups.
class Swarm { private: Particle *particles[]; Group *groups[]; int _size; // number of particles int _globals; // number of groups int _params; // number of parameters to optimize
For each parameter, we need to specify a range of values in which the optimization will be performed, as well as an increment (step).
double highs[]; double lows[]; double steps[];
In addition, the optimal set of parameters should be stored somewhere.
double solution[];
Since the class will have several different constructors, let us describe the unified initialization method.
void init(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { _size = size; _globals = globals; _params = params; ArrayCopy(highs, max); ArrayCopy(lows, min); ArrayCopy(steps, inc); ArrayResize(solution, _params); ArrayResize(particles, _size); for(int i = 0; i < _size; i++) // loop through particles { particles[i] = new Particle(_params); ///do ///{ for(int p = 0; p < _params; p++) // loop through all dimensions { // random placement particles[i].position[p] = (MathRand() * 1.0 / 32767) * (highs[p] - lows[p]) + lows[p]; // adjust it according to step granularity if(steps[p] != 0) { particles[i].position[p] = ((int)MathRound((particles[i].position[p] - lows[p]) / steps[p])) * steps[p] + lows[p]; } // the only position is the best so far particles[i].best[p] = particles[i].position[p]; // random speed particles[i].velocity[p] = (MathRand() * 1.0 / 32767) * 2 * (highs[p] - lows[p]) - (highs[p] - lows[p]); } ///} ///while(index.add(crc64(particles[i].position)) && !IsStopped()); } ArrayResize(groups, _globals); for(int i = 0; i < _globals; i++) { groups[i] = new Group(_params); } for(int i = 0; i < _size; i++) { // random group membership particles[i].group = (_globals > 1) ? (int)MathMin(MathRand() * 1.0 / 32767 * _globals, _globals - 1) : 0; } }
All arrays are distributed according to the given dimension and are filled with the transferred data. The initial position of the particles, their speed and group membership are determined randomly. There is something important commented out in the above code. We will get back to this a bit later.
Note that the classic version of the particle swarm algorithm is intended for optimizing functions defined on continuous coordinates. However, EA parameters are usually tested with a certain step. For example, a standard moving average cannot have a period of 11.5. That is why, in addition to a range of acceptable values for all dimensions, we set the step used to round off the particle positions. This will be done not only at the initialization phase, but also in calculations during optimization.
Now, we can implement a couple of constructors using init.
#define AUTO_SIZE_FACTOR 5 public: Swarm(const int params, const double &max[], const double &min[], const double &step[]) { init(params * AUTO_SIZE_FACTOR, (int)MathSqrt(params * AUTO_SIZE_FACTOR), params, max, min, step); } Swarm(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { init(size, globals, params, max, min, step); }
The first one uses a well-known rule of thumb to calculate the swarm size and the number of groups based on the number of parameters. The AUTO_SIZE_FACTOR constant, which is 5 by default, can be changed as desired. The second constructor allows the specification of all values explicitly.
The destructor releases the allocated memory.
~Swarm()
{
for(int i = 0; i < _size; i++)
{
delete particles[i];
}
for(int i = 0; i < _globals; i++)
{
delete groups[i];
}
}
Now it is time to write the main method of the class that directly performs optimization.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4)
The first parameter, Functor &f, is of particular interest. Obviously, the Expert Advisor will be called during the optimization process for various input parameters, in response to which an estimated number (profit, profitability, or another characteristic) will be returned. The swarm knows nothing (and it should not know anything) about the Expert Advisor. Its only task is to find the optimal value of an unknown objective function with an arbitrary set of numeric arguments. That is why we use an abstract interface, namely the Functor class.
class Functor { public: virtual double calculate(const double &vector[]) = 0; };
The only method received an array of parameters and returns a number (all types are double). In the future, the EA will have to somehow implement a class derived from Functor and to calculate the required variable inside the calculate method. Thus, the first parameter of the 'optimize' method will receive an object with a callback function provided by the trading robot.
The second parameter of the 'optimize' method is the maximum number of loops to run the algorithm. The following 3 parameters set the PSO coefficients: 'inertia' - keeping the particle's velocity (velocity usually decreases with the values less than 1), 'selfBoost' and 'groupBoost' determine how responsive the particle is when adjusting its direction to the best known positions in the participle/group history.
Now that we have considered all the parameters, we can proceed to the algorithm. Optimization loops almost completely reproduce pseudo-code, in a somewhat simplified form.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4) { double result = -DBL_MAX; ArrayInitialize(solution, 0); for(int c = 0; c < cycles && !IsStopped(); c++) // predefined number of cycles { for(int i = 0; i < _size && !IsStopped(); i++) // loop through all particles { for(int p = 0; p < _params; p++) // update particle position and speed { double r1 = MathRand() * 1.0 / 32767; double rg = MathRand() * 1.0 / 32767; particles[i].velocity[p] = inertia * particles[i].velocity[p] + selfBoost * r1 * (particles[i].best[p] - particles[i].position[p]) + groupBoost * rg * (groups[particles[i].group].optimum[p] - particles[i].position[p]); particles[i].position[p] = particles[i].position[p] + particles[i].velocity[p]; // make sure to keep the particle inside the boundaries of parameter space if(particles[i].position[p] < lows[p]) particles[i].position[p] = lows[p]; else if(particles[i].position[p] > highs[p]) particles[i].position[p] = highs[p]; // respect step size if(steps[p] != 0) { particles[i].position[p] = ((int)MathRound((particles[i].position[p] - lows[p]) / steps[p])) * steps[p] + lows[p]; } } // get the function value for the particle i particles[i].positionValue = f.calculate(particles[i].position); // update the particle's best value and position (if improvement is found) if(particles[i].positionValue > particles[i].bestValue) { particles[i].bestValue = particles[i].positionValue; ArrayCopy(particles[i].best, particles[i].position); } // update the group's best value and position (if improvement is found) if(particles[i].positionValue > groups[particles[i].group].getResult()) { groups[particles[i].group].assign(particles[i].positionValue); ArrayCopy(groups[particles[i].group].optimum, particles[i].position); // update the global maximum value and solution (if improvement is found) if(particles[i].positionValue > result) { result = particles[i].positionValue; ArrayCopy(solution, particles[i].position); } } } } return result; }
The method returns the found maximum value of the objective function. Another method is reserved for reading coordinates (parameter set).
bool getSolution(double &result[]) { ArrayCopy(result, solution); return !IsStopped(); }
This is almost the whole algorithm. I have previously mentioned that there are some simplifications. First of all, consider the following specific feature.
A Discrete World without Repetitions
The functor is called many times for dynamically recalculating parameter sets, but there is no guarantee that the algorithm will not hit the same point several times, especially considering the discreteness along the axes. To prevent such hitting, it is necessary to somehow identify already calculated points and to skip them.
Parameters are just numbers or a sequence of bytes. The most famous technique for checking data uniqueness is using a hash. The most popular way to get a hash is CRC. CRC is a check number (usually an integer, multi-bit) generated based on the data in such a way that the matching of two such characteristic numbers from data sets means with a high probability that the sets are identical. The more bits in CRC, the higher the probability of matching (up to almost 100%). A 64-bit CRC is probably enough for our task. If needed, it can be extended or changed to another hash function. CRC calculation implementation can be easily ported to MQL from C. One of the possible options is available in the crc64.mqh file attached below. The main working function has the following prototype.
ulong crc64(ulong crc, const uchar &s[], int l);
It accepts CRC from the previous data block (if they are more than one, or specify 0 if there is one block), an array of bytes and information on how many elements from it should be processed. The function returns a 64-bit CRC.
We need to input a set of parameters into this function. But this cannot be done directly, since each parameter is a double. To convert it to a byte array, let us use the TypeToBytes.mqh library (the file is attached to the article; however, it is better to check the codebase for its up-to-date version).
After including this library, a wrapper function can be created to calculate CRC64 from an array of parameters:
#include <TypeToBytes.mqh> #include <crc64.mqh> template<typename T> ulong crc64(const T &array[]) { ulong crc = 0; int len = ArraySize(array); for(int i = 0; i < len; i++) { crc = crc64(crc, _R(array[i]).Bytes, sizeof(T)); } return crc; }
†he following questions arise now: where to store hashes and how to check their uniqueness. The most suitable solution is a binary tree. It is a data structure that provides quick operations for adding new values and checking the existence of those already added. High speed is provided by a special tree property called balancing. In other words, the tree must be balanced (it must be constantly kept in a balanced state) in order to ensure the maximum speed of operations. The good fact is that we use the tree to store hashes. Here is the definition of hash.
The hash function (hash generation algorithm) generates for any input data a uniformly distributed output value. As a result, the addition of a hash to a binary tree statistically provides its state close to balanced, and thus leads to high efficiency.
A binary tree is a collection of nodes, each of which contains a certain value and two optional references to the so-called right and left node. The value in the left node is always less than the value in the parent node; the value in the right node is always greater than that in the parent. The tree starts filling from the root by comparing a new value with the node values. If the new value is equal to the value of the root (or other node), the sign of the value existence in the tree is returned. If the new value is less than the value in the node, go to the left node by reference and process its subtree in a similar way. If the new value is greater than the value in the node, follow right subtree. If any of the references is null (means there are no further branches), the search is completed without results. That is why, a new node with a new value should be created instead of a null reference.
A pair of template classes has been created to implement this logic: TreeNode and BinaryTree. Their full codes are provided in the attached header file.
template<typename T> class TreeNode { private: TreeNode *left; TreeNode *right; T value; public: TreeNode(T t): value(t) {} // adds new value into subtrees and returns false or // returns true if t exists as value of this node or in subtrees bool add(T t); ~TreeNode(); TreeNode *getLeft(void) const; TreeNode *getRight(void) const; T getValue(void) const; }; template<typename T> class BinaryTree { private: TreeNode<T> *root; public: bool add(T t); ~BinaryTree(); };
The 'add' method returns true if the value already exists in the tree. It returns false if it did not exist before but has just been added. Deletion of a root in the tree's destructor automatically leads to the deletion of all child nodes.
The implemented tree class is one of the simplest variants. There are other, more advanced trees, so you can try to embed them if you wish.
Let us add BinaryTree to the Swarm class.
class Swarm { private: BinaryTree<ulong> index;
The parts of the 'optimize' method in which we move particles to new positions should be extended.
double optimize(Functor &f, const int cycles, const double inertia = 0.8, const double selfBoost = 0.4, const double groupBoost = 0.4) { // ... double next[]; ArrayResize(next, _params); for(int c = 0; c < cycles && !IsStopped(); c++) { int skipped = 0; for(int i = 0; i < _size && !IsStopped(); i++) { // new placement of particles using temporary array next for(int p = 0; p < _params; p++) { double r1 = MathRand() * 1.0 / 32767; double rg = MathRand() * 1.0 / 32767; particles[i].velocity[p] = inertia * particles[i].velocity[p] + selfBoost * r1 * (particles[i].best[p] - particles[i].position[p]) + groupBoost * rg * (groups[particles[i].group].optimum[p] - particles[i].position[p]); next[p] = particles[i].position[p] + particles[i].velocity[p]; if(next[p] < lows[p]) next[p] = lows[p]; else if(next[p] > highs[p]) next[p] = highs[p]; if(steps[p] != 0) { next[p] = ((int)MathRound(next[p] / steps[p])) * steps[p]; } } // check if the tree contains this parameter set and add it if not if(index.Add(crc64(next))) { skipped++; continue; } // apply new position to the particle ArrayCopy(particles[i].position, next); particles[i].positionValue = f.calculate(particles[i].position); // ... } Print("Cycle ", c, " done, skipped ", skipped, " of ", _size, " / ", result); if(skipped == _size) break; // full coverage }
We have added the auxiliary array 'next', where the newly created coordinates are added first. CRC is calculated for them and the value uniqueness is checked. If the new position has not yet been encountered, it is added to the tree, copied to the corresponding particle, and all necessary calculations are performed for this position. If the position already exists in the tree (i.e., the functor has already been calculated for it), this iteration is skipped.
Testing Basic Functionality
Everything discussed above is the minimum necessary basis for running the first tests. Let us use the testpso.mq5 script to make sure that the optimization really works. The header file ParticleSwarmParallel.mqh header file used in this script contains not only already familiar classes, but also other improvements which we will consider below.
The tests are designed in the OOP style, which allows you to set your favorite objective functions. The base class for the tests is BaseFunctor.
class BaseFunctor: public Functor { protected: const int params; double max[], min[], steps[]; public: BaseFunctor(const int p): params(p) // number of parameters { ArrayResize(max, params); ArrayResize(min, params); ArrayResize(steps, params); ArrayInitialize(steps, 0); PSOTests::register(&this); } virtual void test(const int loop) // worker method { Swarm swarm(params, max, min, steps); swarm.optimize(this, loop); double result[]; swarm.getSolution(result); for(int i = 0; i < params; i++) { Print(i, " ", result[i]); } } };
All objects of derived classes will automatically register themselves at the time of creation, using the 'register' method in the PSOTests class.
class PSOTests { static BaseFunctor *testCases[]; public: static void register(BaseFunctor *f) { int n = ArraySize(testCases); ArrayResize(testCases, n + 1); testCases[n] = f; } static void run(const int loop = 100) { for(int i = 0; i < ArraySize(testCases); i++) { testCases[i].test(loop); } } };
The tests (optimization) are run by the 'run' method, which calls 'test' on all registered objects.
There are many popular benchmark functions, including "rosenbrock", "griewank", "sphere", which are implemented in the script. For example, a search scope and a 'calculate' method for a sphere can be defined as follows.
class Sphere: public BaseFunctor { public: Sphere(): BaseFunctor(3) // expected global minimum (0, 0, 0) { for(int i = 0; i < params; i++) { max[i] = 100; min[i] = -100; } } virtual void test(const int loop) { Print("Optimizing " + typename(this)); BaseFunctor::test(loop); } virtual double calculate(const double &vec[]) { int dim = ArraySize(vec); double sum = 0; for(int i = 0; i < dim; i++) sum += pow(vec[i], 2); return -sum; // negative for maximization } };
Pay attention that standard benchmark functions use minimization, while we implemented a maximization-based algorithm (because we aim to search for the maximum EA performance). Due to this, the calculation result will be used with a minus sign. Also, we don't use a discrete step here, and thus the functions are continuous.
void OnStart()
{
PSOTests::Sphere sphere;
PSOTests::Griewank griewank;
PSOTests::Rosenbrock rosenbrock;
PSOTests::run();
}
By running the script, you can see that it logs coordinate values close to the exact solution (extremum). Since the particles are randomly initialized, each run will produce slightly different values. The accuracy of the solution depends on the input parameters of the algorithm.
Optimizing PSOTests::Sphere PSO[3] created: 15/3 PSO Processing... Cycle 0 done, skipped 0 of 15 / -1279.167775306995 Cycle 10 done, skipped 0 of 15 / -231.4807406906516 Cycle 20 done, skipped 0 of 15 / -4.269510657558273 Cycle 30 done, skipped 0 of 15 / -1.931949742316357 Cycle 40 done, skipped 0 of 15 / -0.06018744740061506 Cycle 50 done, skipped 0 of 15 / -0.009498109984732127 Cycle 60 done, skipped 0 of 15 / -0.002058433538555499 Cycle 70 done, skipped 0 of 15 / -0.0001494176502579518 Cycle 80 done, skipped 0 of 15 / -4.141817579039349e-05 Cycle 90 done, skipped 0 of 15 / -1.90930142126799e-05 Cycle 99 done, skipped 0 of 15 / -8.161728746514931e-07 PSO Finished 1500 of 1500 planned calculations: true 0 -0.000594423827318461 1 -0.000484001094843528 2 0.000478096358862763 Optimizing PSOTests::Griewank PSO[2] created: 10/3 PSO Processing... Cycle 0 done, skipped 0 of 10 / -26.96927938978973 Cycle 10 done, skipped 0 of 10 / -0.939220906325796 Cycle 20 done, skipped 0 of 10 / -0.3074442362962919 Cycle 30 done, skipped 0 of 10 / -0.121905607345751 Cycle 40 done, skipped 0 of 10 / -0.03294107382891465 Cycle 50 done, skipped 0 of 10 / -0.02138355984774098 Cycle 60 done, skipped 0 of 10 / -0.01060479828529859 Cycle 70 done, skipped 0 of 10 / -0.009728742850384609 Cycle 80 done, skipped 0 of 10 / -0.008640623678293768 Cycle 90 done, skipped 0 of 10 / -0.008578769833161193 Cycle 99 done, skipped 0 of 10 / -0.008578769833161193 PSO Finished 996 of 1000 planned calculations: true 0 3.188612982502877 1 -4.435728146291838 Optimizing PSOTests::Rosenbrock PSO[2] created: 10/3 PSO Processing... Cycle 0 done, skipped 0 of 10 / -19.05855349617553 Cycle 10 done, skipped 1 of 10 / -0.4255148824156119 Cycle 20 done, skipped 0 of 10 / -0.1935391314277153 Cycle 30 done, skipped 0 of 10 / -0.006468452482022688 Cycle 40 done, skipped 0 of 10 / -0.001031992354315317 Cycle 50 done, skipped 0 of 10 / -0.00101322411502283 Cycle 60 done, skipped 0 of 10 / -0.0008800704421316765 Cycle 70 done, skipped 0 of 10 / -0.0005593151578155307 Cycle 80 done, skipped 0 of 10 / -0.0005516786893301249 Cycle 90 done, skipped 0 of 10 / -0.0005473814163781119 Cycle 99 done, skipped 0 of 10 / -7.255520122486163e-06 PSO Finished 982 of 1000 planned calculations: true 0 1.001858172119364 1 1.003524791491219
Note that the swarm size and the number of groups (written to the log in lines like PSO[N] created: X/G, where N is the space dimension, X is the number of particles, G is the number of groups) are automatically selected according to the programmed rules of thumb based on input data.
Moving on to a Parallel World
The first test is good. However, it has a nuance - the particle counting cycle is performed in one single thread, while the terminal allows utilizing all processor cores. Our ultimate goal is to write a PSO optimization engine that can be built into EAs for multithreaded optimization in the MetaTrader tester, and thus to provide an alternative to the standard genetic algorithm.
Calculations cannot be parallelized by mechanically transferring the algorithm inside an EA instead of script. This requires the modification of the algorithm.
If you look at the existing code, this task suggests selection of groups of particles to parallel calculations. Each group can be processed independently. A full cycle is performed for the specified number of times inside each group.
To avoid modification of the 'Swarm' class core, let us use a simple solution: instead of several groups inside a class, we will create several class instances, in each of which the number of groups will be degenerate, i.e. equal to one. In addition, we need to provide a code which will allow instances to exchange information, as each instance will be executed on its own testing agent.
First, let us add a new object initialization way.
Swarm(const int size, const int globals, const int params, const double &max[], const double &min[], const double &step[]) { if(MQLInfoInteger(MQL_OPTIMIZATION)) { init(size == 0 ? params * AUTO_SIZE_FACTOR : size, 1, params, max, min, step); } ...
According to the program operation in the optimization mode, set the number of groups equal to 1. The default swarm size is determined by a rule of thumb (unless the 'size' parameter is explicitly set to a value other than 0).
In the OnTester event handler, the Expert Advisor will be able to obtain the result of a mini-swarm (consisting of only one group) using the getSolution function and to send it in a frame to the terminal. The terminal can analyze passes and select the best one. Logically, the number of parallel swarms/groups should be equal to least the number of cores. However, it can be higher (though you should try to have it multiple of the number of cores). The larger the dimension of the space, the more groups may be required. But the number of cores should be enough for simple tests.
Data exchange between instances is required for calculating space without duplicate points. As you remember, the list of processed points in each object is stored in the 'index' binary tree. It could be sent to the terminal in a frame, similarly to the results, but the problem is that the hypothetical combined registry of these lists cannot be sent back to testing agents. Unfortunately, the tester architecture supports controlled data transfer only from agents to the terminal, but not back. Tasks from the terminal are distributed to agents in a closed format.
Therefore, I decided to use only local agents and to save each group indexes to files in a shared folder (FILE_COMMON). Each agent writes its own index and can read the indexes of all other passes at any time, as well as add them to its own index. This can be needed during pass initialization.
In MQL, changes in the written file can be read by other processes only when the file is closed. Flags FILE_SHARE_READ, FILE_SHARE_WRITE and the FileFlush functions do not help here.
Support for writing indexes is implemented using the well-known "visitor" pattern.
template<typename T> class Visitor { public: virtual void visit(TreeNode<T> *node) = 0; };
Its minimalist interface declares that we are going to perform some arbitrary operation with the passed tree node. A specific successor implementation has been created for working with files: Exporter. The internal value of each node is stored on a separate line in the file, in the order of traversing the entire tree by reference.
template<typename T> class Exporter: public Visitor<T> { private: int file; uint level; public: Exporter(const string name): level(0) { file = FileOpen(name, FILE_READ | FILE_WRITE | FILE_CSV | FILE_ANSI | FILE_SHARE_READ| FILE_SHARE_WRITE | FILE_COMMON, ','); } ~Exporter() { FileClose(file); } virtual void visit(TreeNode<T> *node) override { #ifdef PSO_DEBUG_BINTREE if(node.getLeft()) visit(node.getLeft()); FileWrite(file, node.getValue()); if(node.getRight()) visit(node.getRight()); #else const T v = node.getValue(); FileWrite(file, v); level++; if((level | (uint)v) % 2 == 0) { if(node.getLeft()) visit(node.getLeft()); if(node.getRight()) visit(node.getRight()); } else { if(node.getRight()) visit(node.getRight()); if(node.getLeft()) visit(node.getLeft()); } level--; #endif } };
The ordered tree traversal, which seems to be the most logical, can only be used for debugging purposes, if you need to receive sorted lines within files for contextual comparison. This method is surrounded by the PSO_DEBUG_BINTREE conditional compilation directive and is disabled by default. In practice, the statistical balancing of the tree is ensured by the addition of random, uniformly distributed values stored in the tree (hashes). If the tree elements are saved in a sorted form, then during its uploading from the file, we will get to the most sub-optimal and slow configuration (one long branch or a list). To avoid this, an uncertainty is introduced at the tree saving stage, concerning the sequence in which the nodes will be processed.
The special method saving the tree to the passed visitor can be easily added to the BinaryTree class, using the Explorer class.
template<typename T> class BinaryTree { ... void visit(Visitor<T> *visitor) { visitor.visit(root); } };
A new method in the Swarm class is also required to run the operation.
void exportIndex(const int id) { const string name = sharedName(id); Exporter<ulong> exporter(name); index.visit(&exporter); }
The 'id' parameter means a unique pass number (equal to the group number). This parameter will be used to configure optimization in the tester. The exportIndex method should be called immediately after execution two swarm methods: optimize and getSolution. This is performed by a calling code, because it may not always be required: our first "parallel" example (see further) does not need it. If the number of groups is equal to the number of cores, they will not be able to exchange any information, as they will be launched in parallel, and reading a file inside the loop is not efficient.
The sharedName helper function, mentioned inside exportIndex, allows the creation of a unique name based on the group number, EA name and the terminal folder.
#define PPSO_FILE_PREFIX "PPSO-" string sharedName(const int id, const string prefix = PPSO_FILE_PREFIX, const string ext = ".csv") { ushort array[]; StringToShortArray(TerminalInfoString(TERMINAL_PATH), array); const string program = MQLInfoString(MQL_PROGRAM_NAME) + "-"; if(id != -1) { return prefix + program + StringFormat("%08I64X-%04d", crc64(array), id) + ext; } return prefix + program + StringFormat("%08I64X-*", crc64(array)) + ext; }
If an identifier equal to -1 is passed to the function, the function will create a mask to find all files of this terminal instance. This feature is used when deleting old temporary files (from the previous optimization of this Expert Advisor), as well as when reading indexes of parallel streams. Here is how it is done, in general terms.
bool restoreIndex() { string name; const string filter = sharedName(-1); // use wildcards to merge multiple indices for all cores long h = FileFindFirst(filter, name, FILE_COMMON); if(h != INVALID_HANDLE) { do { FileReader reader(name, FILE_COMMON); reader.read(this); } while(FileFindNext(h, name)); FileFindClose(h); } return true; }
Each found file is passed to a new FileReader class for processing. The class is responsible for opening the file in read mode. It also sequentially loads all lines and immediately passes them to the Feed interface.
class Feed { public: virtual bool feed(const int dump) = 0; }; class FileReader { protected: int dump; public: FileReader(const string name, const int flags = 0) { dump = FileOpen(name, FILE_READ | FILE_CSV | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags, ','); } virtual bool isReady() const { return dump != INVALID_HANDLE; } virtual bool read(Feed &pass) { if(!isReady()) return false; while(!FileIsEnding(dump)) { if(!pass.feed(dump)) { return false; } } return true; } };
As you might guess, the Feed interface must be implemented directly in the swarm, because we passed this inside the FileReader.
class Swarm: public Feed { private: ... int _read; int _unique; int _restored; BinaryTree<ulong> merge; public: ... virtual bool feed(const int dump) override { const ulong value = (ulong)FileReadString(dump); _read++; if(!index.add(value)) _restored++; // just added into the tree else if(!merge.add(value)) _unique++; // was already indexed, hitting _unique in total return true; } ...
Using the variables _read, _unique and _restored, the method calculates the total number of elements read (from all files), the number of elements added to index and the number of elements that have not been added (which are already in the index). Since the groups operate independently, indices of different groups can have duplicates.
These statistics are important in determining the moment when the search space is fully explored or is close to being fully explored. In this case, the number of _unique approaches the number of possible parameter combinations.
As the number of completed passes increases, more and more unique points from the shared history will be loaded into local indexes. After the next execution of 'calculate', the index will receive new checked points, and the size of saved files will constantly grow. Gradually, overlapping elements in the files will start prevailing. This will require some extra costs, which are however less than recalculation of the EA's trading activity. This will lead to the acceleration of PSO cycles with the processing of each of the subsequent groups (tester tasks), as processing approaches full coverage of the optimization space.
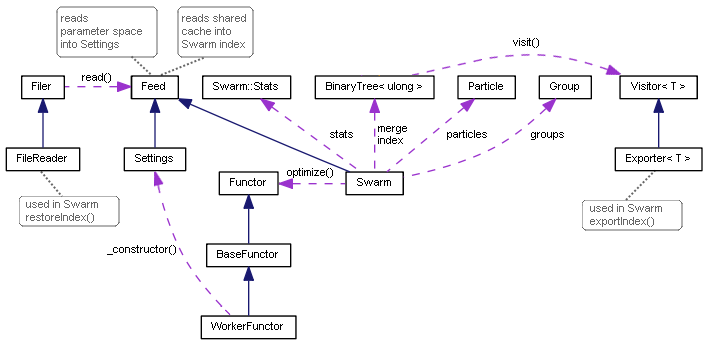
Particle Swarm Optimization Class Diagram
Parallel Computing Testing
To test the algorithm performance in multiple threads, let us transform the old script into the PPSO.mq5 Expert Advisor. It will run in the math calculation mode, since the trading environment is not needed yet.
The set of test objective functions is the same, as well as the classes that implement them are practically unchanged. A particular test will be selected in input variables.
enum TEST { Sphere, Griewank, Rosenbrock }; sinput int Cycles = 100; sinput TEST TestCase = Sphere; sinput int SwarmSize = 0; input int GroupCount = 0;
Here we can also specify the number of cycles, the swarm size and the number of groups. All of this is used in the functor implementation, in particular in the Swarm constructor. Default zero values mean auto-selection based on the dimension of the task.
class BaseFunctor: public Functor { protected: const int params; double max[], min[], steps[]; double optimum; double result[]; public: ... virtual void test() { Swarm swarm(SwarmSize, GroupCount, params, max, min, steps); optimum = swarm.optimize(this, Cycles); swarm.getSolution(result); } double getSolution(double &output[]) const { ArrayCopy(output, result); return optimum; } };
All calculations are started from the OnTester handler. The GroupCount parameter (by which tester iterations will be organized) is used as a randomizer to ensure instances in different threads contain different particles. A test functor is created depending on the TestCase parameter. Next, the functor.test() method is called, after which the results can be read using functor.getSolution() and can be sent in a frame to the terminal.
double OnTester() { MathSrand(GroupCount); // reproducible randomization BaseFunctor *functor = NULL; switch(TestCase) { case Sphere: functor = new PSOTests::Sphere(); break; case Griewank: functor = new PSOTests::Griewank(); break; case Rosenbrock: functor = new PSOTests::Rosenbrock(); break; } functor.test(); double output[]; double result = functor.getSolution(output); if(MQLInfoInteger(MQL_OPTIMIZATION)) { FrameAdd("PSO", 0xC0DE, result, output); } else { Print("Solution: ", result); for(int i = 0; i < ArraySize(output); i++) { Print(i, " ", output[i]); } } delete functor; return result; }
A bunch of functions OnTesterInit, OnTesterPass, OnTesterDeinit works in the terminal. It collects frames and determines the best solution from the sent ones.
int passcount = 0; double best = -DBL_MAX; double location[]; void OnTesterPass() { ulong pass; string name; long id; double r; double data[]; while(FrameNext(pass, name, id, r, data)) { // compare r with all other passes results if(r > best) { best = r; ArrayCopy(location, data); } Print(passcount, " ", id); const int n = ArraySize(data); ArrayResize(data, n + 1); data[n] = r; ArrayPrint(data, 12); passcount++; } } void OnTesterDeinit() { Print("Solution: ", best); ArrayPrint(location); }
The following data is written to log: the pass counter, its sequence number (may differ on complex tasks, when one thread overtakes another due to differences in data), the value of the objective function and the corresponding parameters. The final decision is made in OnTesterDeinit.
Let us also enable Expert Advisor running not only in the tester, but also on a regular chart. In this case, the PSO algorithm will execute in the regular single-threaded mode.
int OnInit() { if(!MQLInfoInteger(MQL_TESTER)) { EventSetTimer(1); } return INIT_SUCCEEDED; } void OnTimer() { EventKillTimer(); OnTester(); }
Let us see how it works. The following values of input parameters will be used:
- Cycles — 100;
- TestCase — Griewank;
- SwarmSize — 100;
- GroupCount — 10;
When launching an Expert Advisor on the chart, the following log will be written.
Successive PSO of Griewank PSO[2] created: 100/10 PSO Processing... Cycle 0 done, skipped 0 of 100 / -1.000317162069485 Cycle 10 done, skipped 0 of 100 / -0.2784790501384311 Cycle 20 done, skipped 0 of 100 / -0.1879188508394087 Cycle 30 done, skipped 0 of 100 / -0.06938172138150922 Cycle 40 done, skipped 0 of 100 / -0.04958694402304631 Cycle 50 done, skipped 0 of 100 / -0.0045818974357138 Cycle 60 done, skipped 0 of 100 / -0.0045818974357138 Cycle 70 done, skipped 0 of 100 / -0.002161613760466419 Cycle 80 done, skipped 0 of 100 / -0.0008991629607246754 Cycle 90 done, skipped 0 of 100 / -1.620636881582982e-05 Cycle 99 done, skipped 0 of 100 / -1.342285474092986e-05 PSO Finished 9948 of 10000 planned calculations: true Solution: -1.342285474092986e-05 0 0.004966759354110293 1 0.002079707592422949
Since test cases are calculated quickly (within a second or two), it makes no sense to measure the time. This will be added later for real trading tasks.
Now, select the EA in the tester, set "Math calculations" in the "Modeling" list, use the above parameters for the EA, except for GroupCount. This parameter will be used for optimization. So, set for it initial and final values, let's say 0 and 3, with a step of 1, to produce 4 groups (equal to the number of cores). The size of all groups will be 100 (SwarmSize, the entire swarm). With the number of processor cores is enough (if all groups work in parallel on agents), this should not affect the performance, but will increase the solution accuracy through additional checks of the optimization space. The following log can be received:
Parallel PSO of Griewank -12.550070232909 -0.002332638407 -0.039510275469 -3.139749741924 4.438437934965 -0.007396077598 3.139620588383 4.438298282495 -0.007396126543 0.000374731767 -0.000072178955 -0.000000071551 Solution: -7.1550806279852e-08 (after 4 passes) 0.00037 -0.00007
Thus, we made sure that the parallel modification of PSO algorithm became available in the tester in the optimization mode. But so far it has only been a test using math calculations. Next, let us adapt PSO to optimize Expert Advisors in a trading environment.
Expert Advisor Virtualization and Optimization (MQL4 API in MetaTrader 5)
To optimize Expert Advisors using the PSO engine, it is necessary to implement functors that can simulate trading on history based on a set of input parameters and calculate statistics.
This raises a dilemma faced by many application developers when writing their own optimizer over and/or instead of the standard one. How to provide a trading environment, including, first of all, quotes, as well as the state of the account and the archive of trades? If the math calculations mode is used, we need to somehow prepare and then pass the required data to the Expert Advisor (to agents). This requires the development of an API middle layer which "transparently" emulates many trading functions - this would allow the Expert Advisor to work similarly to the usual online mode.
To avoid this, I decided to use an existing virtual trading solution, created entirely in MQL and utilizing standard historical data structures, in particular ticks and bars. This is the Virtual library by fxsaber. It allows calculating a virtual pass of an Expert Advisor on the available history both online (for example, for periodic self-optimization on a chart) and in the tester. In the latter case, we can use any usual tick mode ("Every tick", "Every tick based on real ticks") or even "OHLC on M1" - for a quick, but more rough estimation of the system (it has only 4 ticks per minute).
After including the Virtual.mqh header file (it is downloaded with the necessary dependencies) into the EA code, a virtual test can be easily organized using the following lines:
MqlTick _ticks[]; // global array ... // copy/collect ticks[] VIRTUAL::Tester(_ticks, OnTick /*, TesterStatistics(STAT_INITIAL_DEPOSIT)*/ ); Print(VIRTUAL::ToString(INT_MAX)); // output virtual trades in the log const double result = TesterStatistics(STAT_PROFIT); // get required performance meter VIRTUAL::ResetTickets(); // optional VIRTUAL::Delete(); // optional
All operations are performed by the static VIRTUAL::Tester method. The following data should be passed to this method: a pre-filled array of ticks of the desired historical period and details, a pointer to the OnTick function (you can use a standard handler if it contains the logic of switching from online trading to virtual), and an initial deposit (it is optional - if the deposit is not specified, the current account balance will be used. If the above fragment is placed in the OnTester handler (we will place it there), the tester's initial deposit can be passed. To find out the result of virtual trading, call the familiar TesterStatistics function, which, after connecting the library, turns out to be actually "overlapped", like many other MQL API functions (you can check the source code if you wish). This "overlap" is smart enough to delegate calls to the original kernel function where the trading is actually performed. Please note that not all standard indicators from TesterStatistics are calculated in the library during virtual trading.
Pay attention that the library is based on the MetaTrader 4 trading API. In other words, it is only suitable for Expert Advisors which use "old" functions in their code, although they are written in MQL5. They can run in the MetaTrader 5 environment thanks to another well-known library by the same author -MT4Orders.
Testing will be performed using the ExprBot.mq5 EA modification, which was originally presented in the article Calculating Mathematical Expressions (Part 2). The EA is implemented using MT4Orders. A new version named ExprBotPSO.mq5 is available in the attachment.
The Expert Advisor uses a parser engine to calculate trading signals based on expressions. The benefits of this will be explained later. The trading strategy is the same: intersection of two moving averages, taking into account the specified divergence threshold. Here are the EA settings along with expressions for signals:
input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold"; input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold"; input string Variables = "Threshold=0.001"; input int Fast = 10; input int Slow = 21;
If you have any questions about how input variables are substituted into expressions and how the built-in EMA functions are integrated with the corresponding indicator, I recommend reading the mentioned article. The new robot uses the same principles. It will be slightly improved.
Please note that the parser engine has been updated to version v1.1 and is also included. Its old version will not work.
In addition to input parameters for signals, which we will discuss later, the EA has parameters for managing virtual testing and the PSO algorithm.
- VirtualTester — the flag enabling virtual testing and/or optimization; default is false which means normal operation.
- Estimator — the variable by which optimization is performed; default is STAT_PROFIT.
- InternalOptimization — flag enabling optimization in the virtual mode; default is false, which means single pass virtual trading. True initiates internal optimization by the PSO method.
- PSO_Enable — enable/disable PSO.
- PSO_Cycles — the number of PSO recalculation cycles in each pass; the larger the value, the better PSO search quality, but the single pass will be executed longer without a feedback (logging).
- PSO_SwarmSize — swarm size; 0 by default which means automatic empirical selection based on the number of parameters.
- PSO_GroupCount — number of groups; it is an incremental parameter for organizing multiple passes - start with a value from 0 to the number of cores/agents and then increase.
- PSO_RandomSeed — randomizer; the group number is added to it in each group, so they all initialize differently.
In the VirtualTester mode, the EA collects ticks in OnTick into an array. Then, in OnTester, the Virtual library trades using this array, calling the same OnTick handler with a special set flag allowing code execution with virtual operations.
So, a cycle of PSO_Cycles of recalculations of the swarm with a size of PSO_SwarmSize particles is executed for each incremented PSO_GroupCount value. Thus, we test PSO_GroupCount * PSO_Cycles * PSO_SwarmSize = N points in the optimization space. Each point is a virtual run of the trading system.
To obtain best results, find the suitable PSO parameters using trial and error. The number of components can be varied for the N number of tests. The final number of tests will be less than N because the same points can be hit (remember, the points are stored in a binary tree in swarm).
Agents exchange data only when the next task is sent. The tasks that are executed in parallel do not yet see each other's results and can also calculate several identical coordinates, with some probability.
Of course, the ExprBotPSO Expert Advisor includes functor classes, which are generally similar to those that we considered in previous examples. These include the 'test' method which creates a swarm instance, performs optimization in it and saves the results in member variables (optimum, result[]).
class BaseFunctor: public Functor { ... public: virtual bool test(void) { Swarm swarm(PSO_SwarmSize, PSO_GroupCount, params, max, min, steps); if(MQLInfoInteger(MQL_OPTIMIZATION)) { if(!swarm.restoreIndex()) return false; } optimum = swarm.optimize(this, PSO_Cycles); swarm.getSolution(result); if(MQLInfoInteger(MQL_OPTIMIZATION)) { swarm.exportIndex(PSO_GroupCount); } return true; } };
This is the first time we see the usage of restoreIndex and exportIndex methods described in previous sections. Expert Advisor optimization tasks usually require a lot of calculations (parameters and groups, each group is one tester pass), so the agents will need to exchange information.
Virtual EA testing is performed in the 'calculate' method according to the declared order. There is a new class used in the initialization of the optimization space - Settings.
class WorkerFunctor: public BaseFunctor { string names[]; public: WorkerFunctor(const Settings &s): BaseFunctor(s.size()) { s.getNames(names); for(int i = 0; i < params; i++) { max[i] = s.get<double>(i, SET_COLUMN_STOP); min[i] = s.get<double>(i, SET_COLUMN_START); steps[i] = s.get<double>(i, SET_COLUMN_STEP); } } virtual double calculate(const double &vec[]) { VIRTUAL::Tester(_ticks, OnTick, TesterStatistics(STAT_INITIAL_DEPOSIT)); VIRTUAL::ResetTickets(); const double r = TesterStatistics(Estimator); VIRTUAL::Delete(); return r; } };
The point is that to start an optimization, the user will configure EA's input parameters in the usual way. However, the swarm algorithm uses the tester only for parallelizing tasks (by incrementing the group number). Therefore, the EA should be able to read the settings of optimization parameters, save them to an auxiliary file transmitted to each agent, reset these settings in the tester and assign optimization by group number. The Settings class will read parameters from an auxiliary file. The file is "EA_name.mq5.csv", which should be connected using a directive.
#define PPSO_SHARED_SETTINGS __FILE__ + ".csv" #property tester_file PPSO_SHARED_SETTINGS
You can view the Settings class in the attachment. It reads a CSV file line by one. The file should have the following columns:
#define MAX_COLUMN 4 #define SET_COLUMN_NAME 0 #define SET_COLUMN_START 1 #define SET_COLUMN_STEP 2 #define SET_COLUMN_STOP 3
All of them are remembered in internal arrays and are available through 'get' methods by name or index. The isVoid() method returns an indication that there are no settings (the file could not be read, it is empty or has a wring format).
Settings are written to a file in the OnTesterInit handler (see below).
I recommend to manually create an empty file "EA_name.mq5.csv" in the MQL5/Files folder in advance. Otherwise, problems may arise with the first optimization tun.
Unfortunately, even though the creates this file automatically during the first start, it does not send the file to the agents, which is why the EA initialization on them ends with the INIT_PARAMETERS_INCORRECT error. A repeated optimization launch will not send it either, since the tester caches information about the connected resources and does not take into account the newly added file until the user re-selects the EA in the drop-down list of the tester settings. Only after that the file can be updated and sent to agents. Therefore, it is easier to create the file in advance.
string header[]; void OnTesterInit() { int h = FileOpen(PPSO_SHARED_SETTINGS, FILE_ANSI|FILE_WRITE|FILE_CSV, ','); if(h == INVALID_HANDLE) { Print("FileSave error: ", GetLastError()); } MqlParam parameters[]; string names[]; EXPERT::Parameters(0, parameters, names); for(int i = 0; i < ArraySize(names); i++) { if(ResetOptimizableParam<double>(names[i], h)) { const int n = ArraySize(header); ArrayResize(header, n + 1); header[n] = names[i]; } } FileClose(h); // 5008 bool enabled; long value, start, step, stop; if(ParameterGetRange("PSO_GroupCount", enabled, value, start, step, stop)) { if(!enabled) { const int cores = TerminalInfoInteger(TERMINAL_CPU_CORES); Print("PSO_GroupCount is set to default (number of cores): ", cores); ParameterSetRange("PSO_GroupCount", true, 0, 1, 1, cores); } } // remove CRC indices from previous optimization runs Swarm::removeIndex(); }
An additional function ResetOptimizableParam is used to search for parameters for which the optimization flag is enabled and to reset such flags. Also, in OnTesterInit, we remember the names of these parameters using the Expert library by fxsaber, which allows to display the results in a more visually clear manner. However, the library was needed primarily because the names should be known in advance in order to call the ParameterGetRange/ParameterSetRange standard functions, but the MQL API does not allow you to get the list of parameters. This will also make the code more universal, and thus you will be able to include this code into any EA without special modifications.
template<typename T> bool ResetOptimizableParam(const string name, const int h) { bool enabled; T value, start, step, stop; if(ParameterGetRange(name, enabled, value, start, step, stop)) { // disable all native optimization except for PSO-related params // preserve original settings in the file h if((StringFind(name, "PSO_") != 0) && enabled) { ParameterSetRange(name, false, value, start, step, stop); FileWrite(h, name, start, step, stop); // 5007 return true; } } return false; }
In the OnInit handler, which is executed on the agent, settings are read to the Settings global object as follows:
Settings settings; int OnInit() { ... FileReader f(PPSO_SHARED_SETTINGS); if(f.isReady() && f.read(settings)) { const int n = settings.size(); Print("Got settings: ", n); } else { if(MQLInfoInteger(MQL_OPTIMIZATION)) { Print("FileLoad error: ", GetLastError()); return INIT_PARAMETERS_INCORRECT; } else { Print("WARNING! Virtual optimization inside single pass - slowest mode, debugging only"); } } ... }
As you will see later, this object is passed to the created WorkerFunctor object in the OnTester handler, inside which all calculations and optimization are performed. Before starting calculations, we need to collect ticks. This is done in the OnTick handler.
bool OnTesterCalled = false; void OnTick() { if(VirtualTester && !OnTesterCalled) { MqlTick _tick; SymbolInfoTick(_Symbol, _tick); const int n = ArraySize(_ticks); ArrayResize(_ticks, n + 1, n / 2); _ticks[n] = _tick; return; // skip all time scope and collect ticks } ... // trading goes on here }
Why do we use the above method instead of the CopyTicksRange function call directly in OnTester? Firstly, this function works only in tick-by-tick modes, while we need to provide support for the fast OHLC M1 mode (4 ticks per minute). Secondly, the size of the returned array in the tick generation mode is limited to 131072 for some reason (there is no such restriction when working with real ticks).
The OnTesterCalled variable is initially equal to false and therefore the tick history is collected. OnTesterCalled is set to true later, in OnTester, before starting PSO. Then the Swarm object will start calculating the functor in a loop, in which VIRTUAL::Tester with a reference to the same OnTick is called. This time, OnTesterCalled will be equal to true and control will be transferred not to tick collection modes but to a trading logic mode. This will be considered a little later. In the future, as the PSO library further develops, mechanisms may appear simplifying integration into existing Expert Advisors by replacing the OnTick handler in the library header file.
Until then, OnTester (in a simplified form) is used.
double OnTester() { if(VirtualTester) { OnTesterCalled = true; // MQL API implies some limitations for CopyTicksRange function, so ticks are collected in OnTick const int size = ArraySize(_ticks); PrintFormat("Ticks size=%d error=%d", size, GetLastError()); if(size <= 0) return 0; if(settings.isVoid() || !InternalOptimization) // fallback to a single virtual test without PSO { VIRTUAL::Tester(_ticks, OnTick, TesterStatistics(STAT_INITIAL_DEPOSIT)); Print(VIRTUAL::ToString(INT_MAX)); Print("Trades: ", VIRTUAL::VirtualOrdersHistoryTotal()); return TesterStatistics(Estimator); } settings.print(); const int n = settings.size(); if(PSO_Enable) { MathSrand(PSO_GroupCount + PSO_RandomSeed); // reproducable randomization WorkerFunctor worker(settings); Swarm::Stats stats; if(worker.test(&stats)) { double output[]; double result = worker.getSolution(output); if(MQLInfoInteger(MQL_OPTIMIZATION)) { FrameAdd(StringFormat("PSO%d/%d", stats.done, stats.planned), PSO_GroupCount, result, output); } ArrayResize(output, n + 1); output[n] = result; ArrayPrint(output); return result; } } ... return 0; } return TesterStatistics(Estimator); }
The above code shows the creation of WorkerFunctor by a set of parameters from the 'settings' object and launch of a swarm using its 'test' method. The results obtained are sent in a frame to the terminal, where they are received to OnTesterPass.
The OnTesterPass handler is similar to the one in the PPSO test EA, except that the data received in frames is printed not to the log, but to a CSV file entitled PPSO-EA-name-date_time.
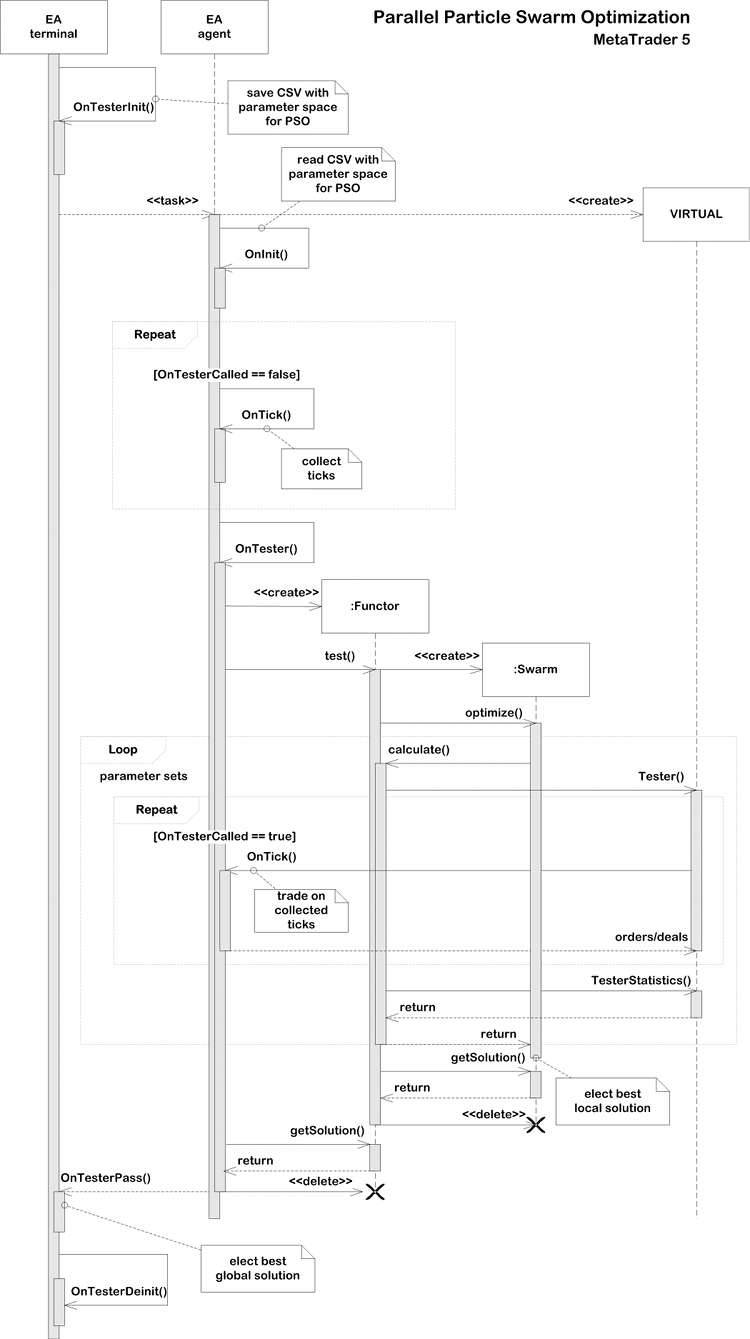
Parallel Particle Swarm Optimization Sequence Diagram
Let us finally get back to the trading strategy. It is almost the same as the one used in the article Calculating Mathematical Expressions (Part 2). However, some adjustments are needed to enable virtual trading. Former signal formulas calculate EMA indicators based on open prices on a zero bar:
input string SignalBuy = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) > 1 + Threshold"; input string SignalSell = "EMA_OPEN_{Fast}(0)/EMA_OPEN_{Slow}(0) < 1 - Threshold";
Now, they should be read from historical bars (because calculations are performed at the very end of the pass, from OnTester). The number of the "current" bar in the past can be easily determined: the Virtual library overrides the TimeCurrent system function, and therefore the following can be written in OnTick:
const int bar = iBarShift(_Symbol, PERIOD_CURRENT, TimeCurrent());
The current bar number should be added to the variable table of expressions, under a suitable name, for example, "Bar", and then the signal formulas can be rewritten as follows:
input string SignalBuy = "EMA_OPEN_{Fast}(Bar)/EMA_OPEN_{Slow}(Bar) > 1 + Threshold"; input string SignalSell = "EMA_OPEN_{Fast}(Bar)/EMA_OPEN_{Slow}(Bar) < 1 - Threshold";
The updated version of parsers has an intermediate call of the new 'with' method (also in OnTick) when changing the variable (bar number) and calculating the formula with this value:
const int bar = iBarShift(_Symbol, PERIOD_CURRENT, TimeCurrent()); // NEW bool buy = p1.with("Bar", bar).resolve(); // WAS: bool buy = p1.resolve(); bool sell = p2.with("Bar", bar).resolve(); // WAS: bool sell = p2.resolve();
Further, the OnTick trading code has no changes.
However, more modifications are needed.
The current formulas use the fixed EMA periods specified in the settings and converted to variables within expressions. However, the periods should be changed during the optimization process, which means using different instances of indicators. The problem is, the virtual optimization with parameter tuning by swarm is performed _inside_ the tester pass, at its very end, in the OnTester function. It is too late to create indicator handles here.
This is a global problem for any virtual optimization. There are three obvious solutions:
- do not use indicators at all; trading systems not utilizing any indicators have an advantage here;
- calculate indicators in a special way, independently within the EA; many use this method because this is the fastest way, even in comparison with standard indicators, but it is very labor-intensive;
- create in advance a set of indicators for all combinations of parameters from the settings; resource intensive; may require limiting the range of parameters.
The last method is questionable for systems that calculate signals on a tick-by-tick basis. Actually, all bars in the virtual history are already closed and indicators have already been calculated. In other words, only bar signals are available. If we run a system without controlling bar opening on such a history, this will produce much fewer trades with a lower quality, if compared with non-virtual ticks.
Our Expert Advisor trades by bars, so this is not a problem. This situation can be typical for some standard Expert Advisors in MetaTrader 5 - it is necessary to understand how a new bar opening event is detected. The method with a single tick volume control is not suitable for virtual history, because all bars are already filled with ticks. Therefore, it is recommended to define a new bar by comparing its time with the previous one.
The expression engine has been extended to solve the described problem using the third option. In addition to single MA indicator functions (MAIndicatorFunc), I have created MA Fan functions (MultiMAIndicatorFunc, see Indicators.mqh). Their name must begin with the "M_" prefix and must contain the minimum period, period step and maximum period, for example:
input string SignalBuy = "M_EMA_OPEN_9_6_27(Fast,Bar)/M_EMA_OPEN_9_6_27(Slow,Bar) > 1 + T"; input string SignalSell = "M_EMA_OPEN_9_6_27(Fast,Bar)/M_EMA_OPEN_9_6_27(Slow,Bar) < 1 - T";
Calculation method and price type are indicated in the name as before. Here an EMA fan is created based on OPEN prices with periods from 9 to 27 (inclusive), with a step of 6.
Another innovation in the expression library is a set of variables that provide access to trading statistics from TesterStatistics (see TesterStats.mqh). Based on this set, it is possible to add the Formula input to the EA, which allows setting the target value as an arbitrary expression. When this variable is filled, the Estimator is ignored. In particular, instead of STAT_PROFIT_FACTOR (which is undefined for zero losses) a 'smoother' indicator with a similar formula can be set in 'Estimator': "(GROSSPROFIT-(1/(TRADES+1)))/-(GROSSLOSS-1/(TRADES +1))".
Now, everything is ready to run virtual trading optimization using the PSO method.
Practical Testing
Let us prepare a tester. It should use slow optimization i.e. full iteration of all parameters. It will not be slow in our case, because only the group number is changed in each run, while the selective iteration of the EA's parameters is performed by a swarm within its cycle. Genetics cannot be used for three reasons. First, it does not guarantee that all combinations of parameters (a given number of groups in our case) will be calculated. Second, due to its specific nature, it will gradually "shift" towards the parameters which produced a more attractive result, not taking into account the fact that there is no dependence between the group number and its success, because the group number is only a randomizer of the PSO data structure. Third, the number of groups is usually not large enough to use genetic approach.
Optimization is performed by the maximum custom criterion.
First, optimize the Expert Advisor in a regular way, with the Virtual library disabled (ExprBotPSO-standard-optimization.set file). The number of parameter combinations for optimization is small for demonstration purposes. The Fast and Slow parameters variate from 9 to 45 with a step of 6, the T parameter - from 0 to 0.01 with a step of 0.0025 steps.
EURUSD, H1, range from the beginning of 2020, using real ticks. The following results can be obtained:
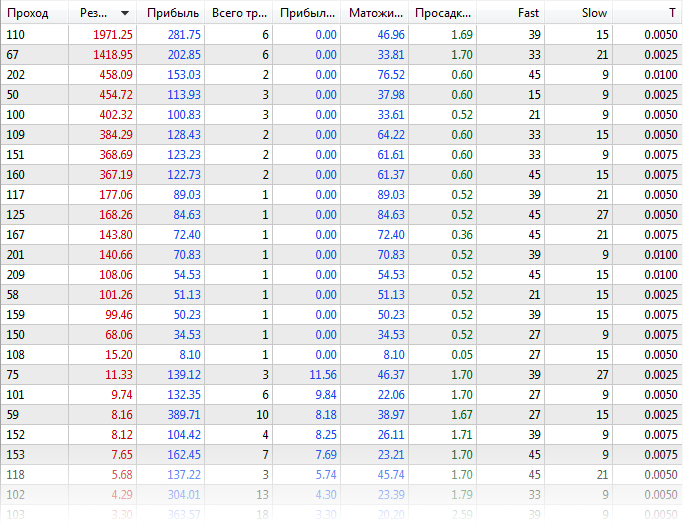
Standard optimization results table
According to logs, optimization on two agents tool almost 21 minutes.
Experts optimization frame expert ExprBotPSO (EURUSD,H1) processing started Tester Experts\ExprBotPSO.ex5 on EURUSD,H1 from 2020.01.01 00:00 to 2020.08.01 00:00 Tester complete optimization started ... Core 2 connected Core 1 connected Core 2 authorized (agent build 2572) Core 1 authorized (agent build 2572) ... Tester optimization finished, total passes 245 Statistics optimization done in 20 minutes 55 seconds Statistics shortest pass 0:00:05.691, longest pass 0:00:23.114, average pass 0:00:10.206
Now, optimize the Expert Advisor with virtual trading and PSO enabled (ExprBotPSO-virtual-pso-optimization.set). The number of groups equal to 4 is determined by iterating the PSO_GroupCount parameter from 0 to 3. Other operating parameters for which optimization is enabled will be forcibly disabled in standard optimization, but they are transferred to agents in CSV files for internal virtual optimization using the PSO algorithm.
Again, use simulation by real ticks, though it is also possible to use generated ticks or OHLC M1 for quick calculations. Mathematical calculations cannot be used here since ticks are collected in the tester for virtual trading.
The following can be obtained in tester logs:
Tester input parameter 'Fast' set to: enable=false, value=9, start=9, step=6, stop=45 Tester input parameter 'Slow' set to: enable=false, value=21, start=9, step=6, stop=45 Tester input parameter 'T' set to: enable=false, value=0, start=0, step=0.0025, stop=0.01 Experts optimization frame expert ExprBotPSO (EURUSD,H1) processing started Tester Experts\ExprBotPSO.ex5 on EURUSD,H1 from 2020.01.01 00:00 to 2020.08.01 00:00 Tester complete optimization started ... Core 1 connected Core 2 connected Core 2 authorized (agent build 2572) Core 1 authorized (agent build 2572) ... Tester optimization finished, total passes 4 Statistics optimization done in 4 minutes 00 seconds Statistics shortest pass 0:01:27.723, longest pass 0:02:24.841, average pass 0:01:56.597 Statistics 4 frames (784 bytes total, 196 bytes per frame) received
Each 'pass' is now a package of virtual optimizations, so it has become longer. But their total number is less and the total time is significantly reduced - only 4 minutes.
Messages from frames are received in logs (they show the best readings of each group). However, real and virtual trading results are slightly different.
22:22:52.261 ExprBotPSO (EURUSD,H1) 2 tmp-files deleted 22:25:07.981 ExprBotPSO (EURUSD,H1) 0 PSO75/1500 0 1974.400000000025 22:25:23.348 ExprBotPSO (EURUSD,H1) 2 PSO84/1500 2 402.6000000000062 22:26:51.165 ExprBotPSO (EURUSD,H1) 3 PSO70/1500 3 455.000000000003 22:26:52.451 ExprBotPSO (EURUSD,H1) 1 PSO79/1500 1 458.3000000000047 22:26:52.466 ExprBotPSO (EURUSD,H1) Solution: 1974.400000000025 22:26:52.466 ExprBotPSO (EURUSD,H1) 39.00000 15.00000 0.00500
The results will not exactly match (even if we had a tick-by-tick indicator-free strategy), because the tester has specific operation features that cannot be repeated in the MQL library. Here are just a few of them:
- limit orders near the market price can be triggered in different ways
- the margin is not calculated or is calculated not quite accurately
- commission is not calculated automatically (MQL API restriction), but it can be programmed through additional input parameters
- accounting of orders and trades in netting mode may differ
- only the current symbol is supported
For more information about the Virtual library, please refer to the relevant documentation and discussions.
For debugging purposes and for understanding the swarm operation, the test EA supports the virtual optimization mode on one core within a normal tester run. An example of settings is available in the ExprBotPSO-virtual-internal-optimization-single-pass.set file attached below. Do not forget to disable optimization in the tester.
Intermediate results are written in detail in the tester log. In each cycle, the position and value of the objective function of each particle are output from the given PSO_Cycles. If the particle hits already checked coordinates, the calculation is skipped.
Ticks size=15060113 error=0
[,0] [,1] [,2] [,3]
[0,] "Fast" "9" "6" "45"
[1,] "Slow" "9" "6" "45"
[2,] "T" "0" "0.0025" "0.01"
PSO[3] created: 15/3
PSO Processing...
Fast:9.0, Slow:33.0, T:0.0025, 1.31285
Fast:21.0, Slow:21.0, T:0.0025, -1.0
Fast:15.0, Slow:33.0, T:0.0075, -1.0
Fast:27.0, Slow:39.0, T:0.0025, 0.07673
Fast:9.0, Slow:9.0, T:0.005, -1.0
Fast:33.0, Slow:21.0, T:0.01, -1.0
Fast:39.0, Slow:45.0, T:0.0025, -1.0
Fast:15.0, Slow:15.0, T:0.0025, -1.0
Fast:33.0, Slow:21.0, T:0.0, 0.32895
Fast:33.0, Slow:39.0, T:0.0075, -1.0
Fast:33.0, Slow:15.0, T:0.005, 384.5
Fast:15.0, Slow:27.0, T:0.0, 2.44486
Fast:39.0, Slow:27.0, T:0.0025, 11.41199
Fast:9.0, Slow:15.0, T:0.0, 1.08838
Fast:33.0, Slow:27.0, T:0.0075, -1.0
Cycle 0 done, skipped 0 of 15 / 384.5000000000009
...
Fast:45.0, Slow:9.0, T:0.0025, 0.86209
Fast:21.0, Slow:15.0, T:0.005, -1.0
Cycle 15 done, skipped 13 of 15 / 402.6000000000062
Fast:21.0, Slow:15.0, T:0.0025, 101.4
Cycle 16 done, skipped 14 of 15 / 402.6000000000062
Fast:27.0, Slow:15.0, T:0.0025, 8.18754
Fast:39.0, Slow:15.0, T:0.005, 1974.40002
Cycle 17 done, skipped 13 of 15 / 1974.400000000025
Fast:45.0, Slow:9.0, T:0.005, 1.00344
Cycle 18 done, skipped 14 of 15 / 1974.400000000025
Cycle 19 done, skipped 15 of 15 / 1974.400000000025
PSO Finished 89 of 1500 planned calculations: true
39.00000 15.00000 0.00500 1974.40000
final balance 10000.00 USD
OnTester result 1974.400000000025
Since the optimization space is small, it was completely covered by 19 cycles. Of course, the situation will be different for real problems with millions of combinations. In such problems, it is extremely important to find the right combinations of PSO_Cycles, PSO_SwarmSize and PSO_GroupCount.
Do not forget that with PSO, one tester pass for each of PSO_GroupCount performs internally up to PSO_Cycles*PSO_SwarmSize virtual single passes, that is why the progress indication will be significantly slower than usual.
Many traders try to get the best results from the built-in genetic optimization by running it many times in a row. This collects various tests due to random initialization, and progress can be found after several runs. In the case of PSO, PSO_GroupCount acts as an analogue of multiple genetics launch. The number of single runs, which can reach 10000 in genetics, should be distributed in PSO between the two components of the product of PSO_Cycles*PSO_SwarmSize, for example, 100*100. PSO_Cycles is analogous to generations in genetics, and PSO_SwarmSize is the size of the population.
Virtualization of MQL5 API Expert Advisors
Until now, we have studied an example of an Expert Advisor written using the MQL4 trading API. This was connected with the Virtual library implementation specifics. However, I wanted to implement the possibility to use PSO for EAs with "new" MQL5 API functions. For this purpose, I have developed an experimental intermediate layer for redirecting MQL5 API calls to MQL4 API. It is available as the MT5Bridge.mqh file which requires the Virtual library and/or MT4Orders for operation.
#include <fxsaber/Virtual/Virtual.mqh> #include <MT5Bridge.mqh> #include <Expert\Expert.mqh> #include <Expert\Signal\SignalMA.mqh> #include <Expert\Trailing\TrailingParabolicSAR.mqh> #include <Expert\Money\MoneySizeOptimized.mqh> ...
After adding Virtual and MT5Bridge at the beginning of the code, before other #include, the MQL5 API functions are called through the redefined "bridge" functions, from which "virtual" MQL4 API functions are called. As a result, it is possible to virtually test and optimize the Expert Advisor. In particular, it is now possible to run PSO optimization similarly to the above ExprBotPSO example. This requires writing (partially copying) a functor and handlers for the tester. But the most resource and time intensive process concerns the adaptation of indicator signals for variable parameters.
MT5Bridge.mqh has an experimental status because its functionality has not been extensively tested. This is a Proof Of the Concept research. You can use source code for debugging and bug fixing.
Conclusion
We have considered the Particle Swarm Optimization algorithm and have implemented it in MQL, with support for multithreading using tester agents. The availability of open PSO settings allows greater flexibility in regulating the process, compared to using built-in genetic optimization. In addition to the settings provided in input parameters, it makes sense to try other adaptable coefficients, which we have used as arguments to the 'optimize' method with default values: inertia(0.8), selfBoost(0.4) and groupBoost(0.4). This will make the algorithm more flexible but will make the selection of settings for a specific task more difficult. The PSO library attached below can be used in the math calculations mode (if you have your own mechanism of virtual quotes, indicators and trades), as well as in tick-bar modes, using third-party ready-made trade emulation classes, such as Virtual.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/8321
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 Neural networks made easy (Part 3): Convolutional networks
Neural networks made easy (Part 3): Convolutional networks
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
With the tester_file directive, will this file be forwarded to the Agent during a job pack change?
If yes, it is possible to change the contents of this file during optimisation.
You can change the content, but it will have no effect - it seems that the information is cached/stored somewhere during the start of optimisation. At least it was so before.
What is the fastest way to load large amounts of data on each pass?
For local agents it is probably the fastest via a shared directory. For distributed agents there is not much choice.
There is little choice for the distributed.
Embed in source ZIP(MqlTick[]).
Embed in the source ZIP(MqlTick[]).
How will it differ from tester_file or more precisely from resource? Most likely, the access time will differ, but insignificantly.
How will it differ from tester_file or more precisely from resource? Most likely, the access time will be different, but insignificantly.
It will not sit in a sandbox and depend on FileLoad speed. You should measure it, in general.