Redes neuronales de propagación inversa del error en matrices MQL5

Entre las herramientas del tráder, el aprendizaje automático y, en concreto, las redes neuronales están presentes desde hace un tiempo considerable. A su vez, entre las redes neuronales, en la parte de su clasificación que combina los métodos denominados de "aprendizaje supervisado", las redes neuronales de propagación inversa del error o retropropagación (BPNN) ocupan un lugar especial. Existen muchas modificaciones diferentes de dichos algoritmos. Sobre su base se pueden construir, por ejemplo, redes neuronales profundas, recurrentes y convolucionales. Por ello, no debería sorprendernos la abundancia de materiales sobre este tema (así como el número de artículos en este sitio web). Hoy desarrollaremos dicho tema en una dirección relativamente nueva para MQL5. El asunto es que hace algún tiempo MQL5 introdujo nuevas funciones API diseñadas para trabajar con matrices y vectores. Estas permiten implementar cálculos en una red neuronal en el modo por paquetes, cuando los datos se procesan como un todo (o bloques), y no elemento por elemento.

Gracias a las operaciones matriciales, las instrucciones del programa que incorporan las fórmulas para la propagación hacia delante e inversa de las señales en la red se simplifican enormemente. De hecho, estas se convierten en expresiones de una sola línea. Debido a ello, podremos prestar atención a otros aspectos importantes para mejorar el algoritmo.

En este artículo, recordaremos brevemente la teoría de las redes de propagación inversa del error y crearemos clases universales para construir redes sobre esta base: las fórmulas anteriores se presentarán de forma "especular" en el código fuente. Por lo tanto, los principiantes podrán recorrer el "camino" completo para dominar esta tecnología sin recurrir a las publicaciones de terceros.

Si ya está familiarizado con la teoría, puede pasar con toda seguridad a la segunda parte del artículo, que analiza varios ejemplos sobre el uso de clases en la práctica: en un script, en un indicador y un asesor experto.

Introducción a la teoría de las redes neuronales

Recuerde que las redes neuronales (RN) constan de elementos informáticos simples: las neuronas, por regla general, se combinan lógicamente en capas y se conectan mediante conexiones (sinapsis) a través de las cuales "pasa" la señal. Una señal es una abstracción matemática que se puede usar para representar situaciones de cualquier área de aplicación, incluido el trading.

La sinapsis conecta la salida de una neurona con la entrada de otra y se caracteriza por un valor llamado peso wi. El estado actual de la neurona se obtiene como la suma ponderada de las señales recibidas en sus conexiones (entradas).

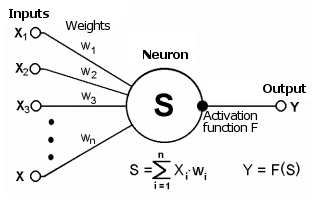
Esquema de una neurona

Este estado se procesa de forma adicional usando una función de activación no lineal que genera el valor de salida de una neurona en concreto desde la cual la señal irá más allá a lo largo de las sinapsis de las próximas neuronas conectadas (si las hay) o se convertirá en un componente de la "respuesta" de la red neuronal (si la neurona actual se encuentra en la última capa).

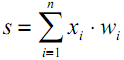	(1)

	(2)

La existencia de no linealidad mejora las capacidades computacionales de la red. Como funciones de activación se pueden usar, por ejemplo, la tangente hiperbólica o la logística (ambas se refieren a las llamadas funciones en forma de S o sigmoideas):

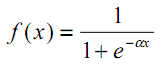	(3)

Como veremos a continuación, MQL5 ofrece un amplio conjunto de funciones de activación integradas. La elección de una función específica debe realizarse según las características específicas del problema (regresión, clasificación). Como regla general, resulta posible seleccionar varias funciones para cualquier tarea y luego encontrar experimentalmente la óptima.

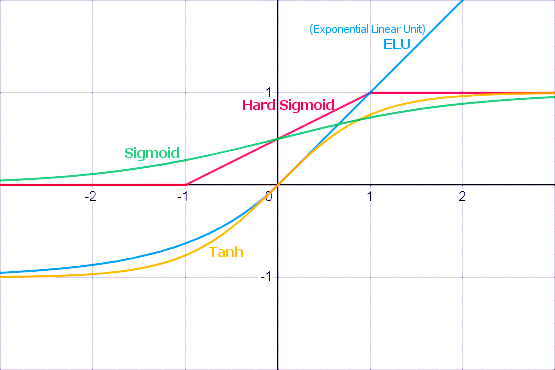
Funciones de activación populares

Las funciones de activación pueden tener diferentes rangos de valores: limitados o ilimitados. Concretamente, el sigmoide (3) asigna los datos al rango [0,+1] (mejor para problemas de clasificación), mientras que la tangente hiperbólica asigna los datos al rango [-1,+1] (mejor para problemas de regresión y pronóstico).

Una de las propiedades importantes de la función de activación es cómo se define su derivada por todo el eje. La presencia de una derivada finita distinta a cero es fundamental para el algoritmo de propagación inversa del error, que analizaremos más adelante. En particular, las funciones en forma de S cumplen con este requisito. Además, las funciones de activación estándar, por regla general, tienen una notación analítica bastante simple para la derivada, lo cual garantiza su cálculo eficiente. Por ejemplo, para el sigmoide (3) obtendremos:

	(4)

En la siguiente figura se muestra una red neuronal de una sola capa.

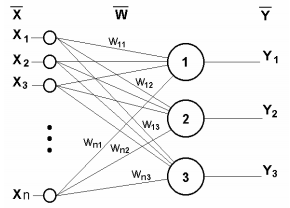
Red neuronal de una sola capa

La siguiente ecuación describe matemáticamente su principio de funcionamiento:

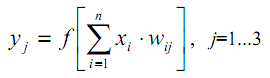	(5)

Obviamente, todos los coeficientes de peso de una capa se pueden reducir a una matriz W, en la que cada elemento wij indica el valor de la i-ésima conexión de la j-ésima neurona. Así, el proceso que ocurre en la RN se puede escribir en forma matricial:

Y = F(X W)	(6)

donde X e Y son los vectores de señal de entrada y salida, respectivamente, y F(V) es la función de activación aplicada elemento por elemento a los componentes del vector V.

El número de capas y el número de neuronas en cada capa de la red depende de los datos de entrada: su dimensionalidad, el tamaño de la muestra, la ley de distribución y muchos otros factores. Por regla general, el ajuste de la red se elige por ensayo y error.

Para ilustrar mejor este punto, aquí tenemos el esquema de una red de dos capas.

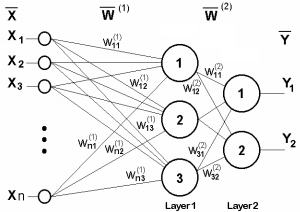
Red neuronal de dos capas

Ahora analizaremos un matiz omitido anteriormente. Por la figura de las funciones de activación, resulta obvio que hay algún valor de T, donde las funciones en forma de S tienen una inclinación máxima y transmiten bien las señales, mientras que otras funciones tienen un punto de ruptura característico (o varios de esos puntos). Por lo tanto, el trabajo principal de cada neurona ocurre en la proximidad de T. Usualmente T=0 o se encuentra cerca de 0, y por lo tanto resulta deseable tener un medio para cambiar automáticamente el argumento de la función de activación a T.

Este fenómeno no se ha reflejado en la fórmula (1), que debería haberse visto así:

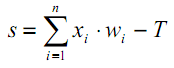	(7)

Tal desplazamiento generalmente se introduce añadiendo otra pseudo-entrada a la capa de neuronas, cuyo valor es siempre 1. Asignaremos a esta entrada el número 0. Entonces:

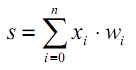	(8)

donde w0 = –T, x0 = 1.

El aprendizaje de la RN con aprendizaje supervisado presupone la presencia de datos de entrenamiento preparados de antemano y "marcados" por un experto humano. En estos datos, los vectores de salida necesarios se asocian con los vectores de entrada.

El entrenamiento en sí se realiza en las siguientes etapas.

1. Inicializamos los elementos de la matriz de pesos (normalmente pequeños valores aleatorios);

2. Aplicamos uno de los vectores a las entradas y calculamos la respuesta de la red; esta es la fase de propagación hacia delante de la señal, que también se utilizará durante el funcionamiento normal de una red ya entrenada;

3. Calculamos la diferencia entre los valores de salida ideales y los obtenidos, es decir, el error de red, y luego ajustamos los pesos según alguna fórmula (ver más abajo) dependiendo de este error;

4. Continuamos en un ciclo desde el paso 2 para todos los vectores de entrada del conjunto de datos hasta que el error resulte inferior al nivel mínimo indicado (finalización exitosa del entrenamiento) o se alcance el número máximo predefinido de ciclos de entrenamiento (la RN ha fallado).

Para el caso de una RN de una sola capa, la fórmula para modificar los pesos resulta bastante obvia:

	(9)

	(10)

donde δ es el error de la red (la diferencia entre la respuesta de la red obtenida y la ideal), t y t+1 son los números de las iteraciones actual y siguiente, respectivamente; ν es el coeficiente de la tasa de aprendizaje, 0<ν<1; i es el número de entrada; j es el número de la neurona en la capa.

No obstante, ¿qué debemos hacer cuando la red tenga varias capas? Aquí es donde llegamos a la idea de propagación inversa del error.

Algoritmo de propagación inversa del error

Entre las diversas estructuras de las redes neuronales, una de las más conocidas es la estructura multicapa, en la que cada neurona de una capa determinada está conectada a todas las neuronas de la capa anterior o, en el caso de la primera capa, a todas las entradas de la RN. Tales RN se conocen como redes neuronales completamente conectadas, y precisamente para su estructura se realiza la aclaración posterior. En muchos otros tipos de redes neuronales, en particular, en las redes convolucionales, las conexiones se establecen entre áreas limitadas de las capas, los llamados núcleos, lo cual complica un poco el direccionamiento de los elementos de la red, pero no influye en la aplicabilidad del método de propagación inversa del error.

Obviamente, la información sobre el error debe pasar de algún modo desde las salidas de la red hasta sus entradas, pasando gradualmente por todas las capas y teniendo en cuenta la "conductividad" de las mismas, es decir, los pesos.

Según el método de los mínimos cuadrados, la función objetivo del error de red que debemos minimizar será el valor siguiente:

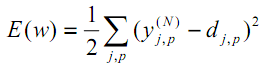	(11)

donde yjpᴺes el estado de salida real de la neurona j de la capa de salida N de la red neuronal cuando la imagen p-ésima se suministra a sus entradas; djp es el estado de salida ideal (deseado) de esta neurona.

La suma se efectúa sobre todas las neuronas de la capa de salida y sobre todas las imágenes procesadas. El coeficiente 1/2 se añade solo para obtener una derivada bonita de E (se anulan los doses), que se utilizará posteriormente para el entrenamiento (véase la ecuación (12)) y, en cualquier caso, se pondera a través de un parámetro importante del algoritmo: la velocidad (que puede duplicarse o modificarse dinámicamente según algunas condiciones).

Una de las formas más efectivas de minimizar una función se basa en que las mejores direcciones locales hacia los extremos indican las derivadas de esta función en un punto particular. Una derivada con signo más nos llevará hacia el máximo, mientras que una derivada con signo menos nos llevará hacia el mínimo. Obviamente, los máximos y mínimos pueden resultar locales, y es posible que se requieran trucos adicionales para "saltar" al mínimo global, pero dejaremos este problema fuera de plano por ahora.

El método descrito se denomina método de descenso de gradiente y consiste en ajustar los coeficientes de peso según la derivada de E, de la siguiente manera:

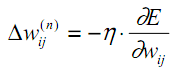	(12)

Aquí wij es el coeficiente de peso de la conexión que conecta la i-ésima neurona de la capa n-1 con la j-ésima neurona de la capa n, η es el coeficiente de velocidad de aprendizaje.

Vamos a recordar la estructura interna de la neurona y, usando esta como base, individualizaremos en la fórmula (12) cada etapa de los cálculos en una derivada parcial:

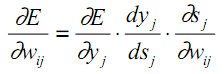	(13)

Aquí, por yj, como antes, se entiende la salida de la neurona j, mientras que por sj se entiende la suma ponderada de sus señales de entrada, es decir, el argumento de la función de activación. Como el factor dyj/ dsj es la derivada de esta función, de aquí se implica el requisito de que la función de activación sea diferenciable en todo el eje x para su uso en el algoritmo de propagación inversa del error que hemos considerado.

Por ejemplo, en el caso de la tangente hiperbólica, vemos que:

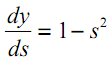	(14)

El tercer factor en (13) ∂sj/∂wij es igual a la salida de la neurona yi de la anterior capa (n-1). ¿Por qué esto es así? No olvidemos que en una red multicapa, la señal va desde la salida de la neurona de la capa anterior hasta la entrada de la neurona de la capa actual. Por consiguiente, la fórmula (1) para sjse puede reescribir de una forma más general de la siguiente manera:

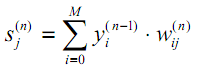	(15)

donde M es el número de neuronas en la capa n-1, considerando la neurona con un estado de salida constante +1, que establece el desplazamiento; yi(n-1)=xij(n) es la i-ésima entrada de la neurona j de la capa n, conectada a la salida de la i-ésima neurona de la (n-1)-ésima capa;

En cuanto al primer factor en (13), es lógico expandirlo en incrementos de error en la capa colindante más antigua (después de todo, los valores de error se propagan en la dirección opuesta):

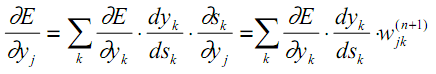	(16)

Aquí se efectúa la suma de k entre las neuronas de la capa n+1.

Podemos ver fácilmente que los dos primeros factores en (13) para una capa (con índices j en las neuronas) se repiten en (16) para la siguiente capa (con índices k) como un coeficiente frente al peso wjk.

Vamos a introducir una variable intermedia que incluye estos dos factores:

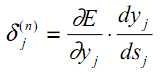	(17)

Como resultado, obtendremos una fórmula recursiva para calcular los valores δj(n) de la capa n a partir de los valores δk(n+1) de la capa más antigua n+1.

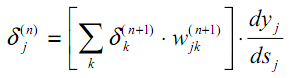	(18)

Para la capa de salida, la nueva variable, al igual que antes, se calcula según la diferencia entre el resultado de la red obtenido y el deseado.

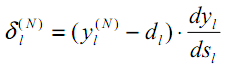	(19)

En comparación con (9), aquí, de una manera más estricta desde el punto de vista formal, se suma la derivada de la función de activación. Es cierto que en la capa de salida de la RN, dependiendo de la tarea, el AF puede estar ausente.

Ahora podemos escribir la fórmula (12) para corregir los pesos en el proceso de aprendizaje de forma más explícita:

	(20)

En ocasiones, para dotar al proceso de corrección de pesos de cierta inercia que suavice saltos bruscos en la derivada al moverse sobre la superficie de la función objetivo, la fórmula (20) se complementa con el valor del cambio de peso en la iteración anterior:

	(21)

donde µ es el coeficiente de inercia, y t es el número de la iteración actual.

Por lo tanto, el algoritmo completo de entrenamiento de la RN usando el procedimiento de propagación inversa del error se construye de la siguiente manera:

1. Inicializamos las matrices de pesos con pequeños números aleatorios.

2. Aplicamos uno de los vectores de datos a las entradas de la red y en el modo de funcionamiento normal, cuando las señales se propaguen de las entradas a las salidas, calculamos el resultado total de la RN capa a capa según las fórmulas de la suma ponderada (15) y la activación f:

	(22)

Además, las neuronas de la capa de entrada 0 se usan solo para suministrar las señales de entrada y no tienen sinapsis ni funciones de activación.

	(23)

Iq supone el q-ésimo componente del vector de entrada aplicado a la 0-ésima capa.

3. Si el error de red es inferior al valor pequeño dado, detendremos el proceso como exitoso. Si el error es significativo, continuaremos con los siguientes pasos.

4. Calculamos para la capa de salida N: δ usando la fórmula (19), y también los cambios en los pesos Δw usando las fórmulas (20) o (21).

5. Para todas las demás capas, en orden inverso, n=N-1,...1, calculamos δ y Δw usando las fórmulas (18) y (20) (o (18) y (21)) respectivamente.

6. Ajustamos todos los pesos en la RN para la iteración t según la iteración anterior t-1.

	(24)

7. Repetimos el proceso en un ciclo desde el paso 2.

El esquema de señales en la red durante el entrenamiento según el algoritmo de propagación inversa del error se muestra en la siguiente figura.

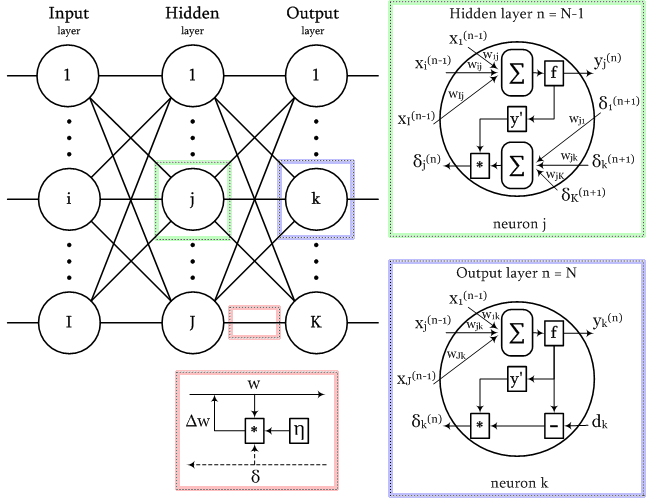
Esquema de señales en el algoritmo de propagación inversa del error

Todas las imágenes de entrenamiento se suministran alternativamente a la red para que no "olvide" una mientras memoriza otras. Esto generalmente se hace en orden aleatorio, pero debido a que colocaremos los datos en matrices y los calcularemos completamente como un solo conjunto, introduciremos otro elemento de aleatoriedad en nuestra implementación; lo discutiremos un poco más adelante.

El uso de matrices implica que los pesos de todas las capas, así como los datos de entrenamiento de entrada y objetivo, estarán representados por matrices, mientras que las fórmulas anteriores y, en consecuencia, los algoritmos recibirán una forma matricial. En otras palabras, no podremos trabajar con vectores separados de datos de entrada y entrenamiento, y el ciclo completo desde el paso 2 al 7 se calculará directamente para todo el conjunto de datos. Uno de esos ciclos se denomina época de aprendizaje.

Vista general de las funciones de activación

El artículo va acompañado del script AF.mq5 que muestra imágenes en miniatura de todas las funciones de activación admitidas en MQL5 (en azul) y sus derivados (en rojo) en el gráfico. El script escala automáticamente las miniaturas para que todas las funciones encajen en la ventana, por lo que, para obtener imágenes más detalladas, le recomendamos ampliar o maximizar la ventana de antemano. A continuación, le mostramos un ejemplo de una imagen generada por el script.

La elección correcta de la función de activación dependerá del tipo de red neuronal y el problema a resolver. Además, podemos usar varias funciones de activación diferentes en una red. Por ejemplo, SoftMax se diferencia de otras funciones en que procesa los valores de salida de la capa, pero no elemento a elemento, sino mediante vinculación mutua: los normaliza de tal forma que los valores pueden interpretarse como probabilidades (su suma es 1), lo cual se utiliza para la clasificación múltiple.

Este tema es tan extenso que requeriría un artículo o una serie de artículos aparte. Aquí nos limitaremos a advertir que todas las funciones tienen aspectos tanto positivos como negativos, lo cual puede conducir potencialmente a la inoperancia de la red. En particular, las funciones en forma de S se caracterizan por el llamado problema del "desvanecimiento de gradiente" ("vanishing gradient", cuando las señales comienzan a caer en los segmentos de "saturación" de la curva S y, por lo tanto, el ajuste de los pesos tiende a cero), mientras que las funciones que aumentan de forma monótona, presentan el problema del crecimiento explosivo del gradiente ("exploding gradient", es decir, el aumento constante de los pesos hasta el desbordamiento numérico y la obtención de NaN (Not A Number)). Ambos problemas se hacen más probables cuanto mayor sea el número de capas en la red. Para resolverlos, podemos usar varias técnicas, como la normalización de datos (incluidos no solo en la entrada, sino también en capas intermedias), algoritmos de adelgazamiento de red (descarte de neuronas ("dropout"), omisión de conexiones), el aprendizaje por paquetes de datos, el ruido y otras variantes de regularización, algunas de las cuales analizaremos e implementaremos más adelante.

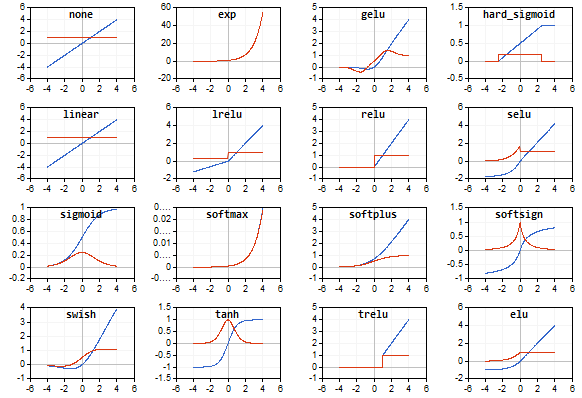
Script de demostración con todas las funciones de activación

Implementamos una red neuronal en la clase MatrixNet

Vamos a comenzar a escribir una clase de red neuronal basada en matrices MQL5. Como la red consta de capas, describiremos las matrices de los coeficientes de peso y los valores de salida de las neuronas de cada capa. El número de capas se almacenará en la variable n, mientras que los pesos de las neuronas en las capas y las señales a la salida de cada capa se almacenarán en las matrices de pesos y salidas, respectivamente. Tenga en cuenta que el término salidas se refiere a señales en las salidas de las neuronas de cualquier capa, no solo en la salida de la red. Entonces, outputs[i] describirán ambas capas intermedias, e incluso la capa 0, donde se suministran los datos de entrada.

La indexación de las matrices de los pesos y salidas se ilustra en el siguiente esquema (las conexiones de cada neurona a la fuente de desplazamiento +1 no se muestran para mayor simplicidad):

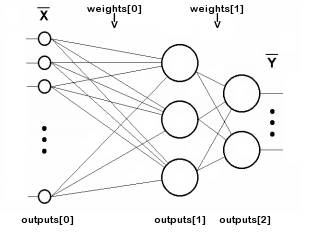
Esquema de indexación de matrices en una red de dos capas

El número n no incluye la capa de entrada porque esta no requiere pesos.

  class MatrixNet
  {
  protected:
     const int n;
     matrix weights[/* n */];
     matrix outputs[/* n + 1 */];
     ENUM_ACTIVATION_FUNCTION af;
     ENUM_ACTIVATION_FUNCTION of;
     double speed;
     bool ready;
     ...

Nuestra red admitirá 2 tipos de funciones de activación (el usuario puede elegirlas): una para todas las capas excepto la capa de salida (almacenada en la función de activación) y otra aparte para la capa de salida (en la variable of). En la variable speed se almacena la tasa de aprendizaje (coeficiente η de la fórmula (20)).

La variable ready contiene la señal de inicialización exitosa del objeto de red.

El constructor de la red adopta el array entero layers que define el número y el tamaño de todas las capas. El elemento 0 indica el tamaño de la pseudocapa de entrada, es decir, el número de características en cada vector de datos de entrada. El último elemento determina el tamaño de la capa de salida, todos los demás, las capas ocultas intermedias. El número de capas no puede ser menor a dos. Para asignar memoria para conjuntos de matrices, hemos escrito un método de asignación auxiliar (lo complementaremos más a medida que se expanda la clase).

  public:
     MatrixNet(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH,
        const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE):
        ready(false), af(f1), of(f2), n(ArraySize(layers) - 1)
     {
        if(n < 2) return;
        
        allocate();
        for(int i = 1; i <= n; ++i)
        {
           // NB: the weights matrix is transposed, i.e. indexes [row][column] specify [synapse][neuron]
           weights[i - 1].Init(layers[i - 1] + 1, layers[i]);
        }
        ...
     }
        
  protected:
     void allocate()
     {
        ArrayResize(weights, n);
        ArrayResize(outputs, n + 1);
        ...
     }

Para inicializar cada matriz de pesos, el tamaño de las capas layers[i - 1] anteriores se toma como el número de filas, y luego se le añade una sinapsis como fuente de desplazamiento ajustable constante +1. Como el número de columnas, se tomará el tamaño de la capa layers[i] actual. En cada matriz de pesos, el primer índice se refiere a la capa a la izquierda de la matriz, mientras que el segundo índice se refiere a la capa a la derecha.

Dicha numeración ofrece un registro simple de la multiplicación de vectores de señal por las matrices de las capas durante la propagación hacia delante (operación normal de la red). En la propagación inversa del error (en el modo de entrenamiento), deberemos multiplicar el vector de error de cada capa superior por su matriz de pesos transpuesta para recalcular los errores de la capa inferior.

En otras palabras, debido a que la información dentro de la red se mueve en dos direcciones opuestas (a saber, las señales de trabajo van de las entradas hacia las salidas, mientras que los errores van de las salidas hacia las entradas), las matrices de pesos en una de estas dos direcciones deberán utilizarse en su forma habitual, mientras que en la otra, se usarán transpuestas. Tomaremos como configuración normal este marcado de la matriz, lo cual facilitará el cálculo de la señal hacia delante.

Luego completaremos las matrices de salida directamente en el proceso de paso de la señal por la red. No obstante, los pesos deberán inicializarse aleatoriamente: para esto, llamaremos al método randomize al final del constructor.

  public:
     MatrixNet(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH,
        const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE):
        ready(false), af(f1), of(f2), n(ArraySize(layers) - 1)
     {
        ...
        ready = true;
        randomize();
     }
     
     // NB: set values with appropriate distribution for specific activation functions
     void randomize(const double from = -0.5, const double to = +0.5)
     {
        if(!ready) return;
        
        for(int i = 0; i < n; ++i)
        {
           weights[i].Random(from, to);
        }
     }

La presencia de matrices de pesos ya es suficiente para implementar la pasada hacia delante de señales desde la entrada de la red hacia la salida. El hecho de que aún no se hayan entrenado los pesos no resulta fundamental: nos ocuparemos del entrenamiento más adelante.

     bool feedForward(const matrix &data)
     {
        if(!ready) return false;
        
        if(data.Cols() != weights[0].Rows() - 1)
        {
           PrintFormat("Column number in data %d <> Inputs layer size %d",
              data.Cols(), weights[0].Rows() - 1);
           return false;
        }
        
        outputs[0] = data; // input the data to the network
        for(int i = 0; i < n; ++i)
        {
           // expand each layer (except the last one) with one neuron for the bias signal
           // (there is no weight matrix to the right of the last layer, since the signal does not go further)
           if(!outputs[i].Resize(outputs[i].Rows(), weights[i].Rows()) ||
              !outputs[i].Col(vector::Ones(outputs[i].Rows()), weights[i].Rows() - 1))
              return false;
           // forward the signal from i-th layer to the (i+1)-th layer: weighted sum
           matrix temp = outputs[i].MatMul(weights[i]);
           // apply the activation function, the result is received into outputs[i + 1]
           if(!temp.Activation(outputs[i + 1], i < n - 1 ? af : of))
              return false;
        }
        
        return true;
     }

El número de columnas en la matriz de entrada data deberá coincidir con el número de filas en la matriz de pesos 0 menos 1 (peso de la señal de desplazamiento).

El método getResults permite leer el resultado del funcionamiento regular de la red. Por defecto, retorna la matriz de estado de la capa de salida.

     matrix getResults(const int layer = -1) const
     {
        static const matrix empty = {};
        if(!ready) return empty;
        
        if(layer == -1) return outputs[n];
        if(layer < -1 || layer > n) return empty;
        
        return outputs[layer];
     }

Podemos evaluar la calidad actual del modelo utilizando el método test: tomaremos como entrada no solo la matriz de datos de entrada, sino también la matriz con la respuesta deseada de la red.

     double test(const matrix &data, const matrix &target, const ENUM_LOSS_FUNCTION lf = LOSS_MSE)
     { 
        if(!ready || !feedForward(data)) return NaN();
        
        return outputs[n].Loss(target, lf);
     }

Después de ejecutar un pasada hacia delante de la señal usando feedForward, aquí calcularemos una medida de la "pérdida" del tipo dado. Por defecto, este es el error cuadrático medio (LOSS_MSE) aplicado a los problemas de regresión y pronóstico. No obstante, si la red se utiliza para clasificar imágenes, deberemos elegir un tipo diferente de valoración, como la entropía cruzada LOSS_CCE.

En caso de error de cálculo, el método retornará "not a number" (NaN).

Ahora nos ocuparemos de la propagación inversa del error. El método backProp también comienza comprobando que coincidan el tamaño de los datos de destino y la capa de salida. Luego, para la capa de salida, se calcula la derivada de la función de activación (si la hubiera) y la "pérdida" de la red en la salida con respecto a los datos objetivo.

     bool backProp(const matrix &target)
     {
        if(!ready) return false;
     
        if(target.Rows() != outputs[n].Rows() ||
           target.Cols() != outputs[n].Cols())
           return false;
        
        // output layer
        matrix temp;
        if(!outputs[n].Derivative(temp, of))
           return false;
        matrix loss = (outputs[n] - target) * temp; // all data line by line

La matriz loss contiene los valores δ de la fórmula (19).

Además, para todas las capas excepto la de salida, se ejecuta el siguiente ciclo:

        for(int i = n - 1; i >= 0; --i) // all layers except the output in reverse order
        {
           // remove pseudo-losses in the last element which we added as an offset source
           // since it is not a neuron and further error propagation is not applicable to it
           // (we do it in all layers except the last one where the shift element was not added)
           if(i < n - 1) loss.Resize(loss.Rows(), loss.Cols() - 1);
           
           matrix delta = speed * outputs[i].Transpose().MatMul(loss);

En este caso, la fórmula (20) se aplica "de forma especular: obtenemos incrementos de peso basados en la tasa de aprendizaje η, δ de la capa actual y las salidas correspondientes de la capa anterior (menor).

A continuación, para cada capa, calculamos la fórmula (18), obteniendo recursivamente el δrestante: se usa nuevamente la derivada de la función de activación y la multiplicación del δ más antiguo por la matriz de pesos transpuesta. El índice i del array outputs[] corresponde a la capa con los pesos de la (i-1)-ésima matriz weights[], ya que la pseudocapa de entrada (outputs[0]) no tiene pesos. En otras palabras, en la propagación hacia delante, la matriz weights[0] se aplica a outputs[0] y genera outputs[1]; weights[1] genera outputs[2], y así sucesivamente. En cambio, en la propagación inversa del error, los índices son los mismos: por ejemplo, outputs[2] (tras la diferenciación) se multiplica por la traspuesta de weights[2].

           if(!outputs[i].Derivative(temp, af))
              return false;
           loss = loss.MatMul(weights[i].Transpose()) * temp;

Solo después de haber calculado loss δ para la capa más inferior, podremos ajustar los pesos de la matriz weights[i], es decir, corregirlos por el delta obtenido anteriormente.

           weights[i] -= delta;
        }
        return true;
     }

Ahora estamos casi listos para implementar un algoritmo de aprendizaje completo con un ciclo sobre las épocas y las llamadas a los métodos feedForward y backProp. No obstante, primero deberemos regresar a la teoría, porque antes hemos pospuesto algunos matices importantes.

Entrenamiento y regularización

La RN se entrena con los datos de entrenamiento actualmente disponibles. Usando como base estos datos, se selecciona la configuración de la red (número de capas, número de neuronas por capa, etc.), la tasa de aprendizaje y otras características. Por ello, en principio, siempre es posible construir una red lo suficientemente poderosa como para generar un error lo suficientemente pequeño en los datos de entrenamiento. Sin embargo, la principal fortaleza de las RN y el propósito de su uso es que funcionan bien con futuros datos desconocidos (con las mismas dependencias implícitas que el conjunto de entrenamiento).

El efecto cuando una red neuronal entrenada se ajusta demasiado bien a los datos de entrenamiento, pero no supera la "prueba forward", se denomina sobreajuste y debe ser erradicado de todas las formas posibles. Para este propósito, se usa la llamada regularización, añadiendo algunas condiciones adicionales al modelo o método de aprendizaje que evalúan la capacidad de generalización de la red. Hay muchas maneras diferentes de efectuar la regularización, concretamente:

• El análisis del funcionamiento de la red entrenada con un conjunto de datos de validación adicional (diferente al de entrenamiento);
• El descarte aleatorio de una parte de las neuronas o conexiones durante el entrenamiento;
• La poda (pruning) de la red después del entrenamiento;
• La introducción de ruido en los datos de entrada;
• La reproducción artificial de los datos;
• La disminución constante y débil en la amplitud de los pesos durante el entrenamiento;
• La selección experimental del volumen y configuración de la red a lo largo de una línea delgada, cuando la red aún puede aprender, pero ya no se reentrena con los datos disponibles;

Vamos a implementar algunos de ellos en nuestra clase.

Inicialmente, configuraremos el método de entrenamiento para que reciba no solo los datos de entrada y salida para el entrenamiento (parámetros «data» y «target», respectivamente), sino también de el conjunto de datos de validación (también consta de los vectores de entrada y de salida relevantes: «validation» y «check»).

A medida que avance el entrenamiento, el error de red en los datos de entrenamiento, por regla general, disminuirá de forma bastante monótona (usamos la palabra "generalmente" porque si seleccionamos incorrectamente la tasa de aprendizaje o la capacidad de la red, el proceso podría volverse inestable). Sin embargo, si el error de la red se calcula paralelamente con el conjunto de validación, también disminuirá al principio (mientras la red revela los patrones más importantes en los datos), y luego comenzará a aumentar a medida que se vuelva a entrenar (cuando la red se adapte a la características particulares del conjunto de entrenamiento, pero no del conjunto de validación). Por consiguiente, el proceso de aprendizaje deberá detenerse cuando el error de validación comience a aumentar. Este enfoque se llama "parada prematura".

Además de dos conjuntos de datos, el método de entrenamiento permite establecer el número máximo de épocas de entrenamiento («epochs»), la precisión deseada («accuracy», es decir, el error promedio mínimo suficiente para nosotros: en este caso, el entrenamiento también terminará con una señal de éxito) y el método de cálculo de errores (lf) .

La velocidad de la tasa de aprendizaje speed se establece igual a la precisión accuracy, pero para aumentar la flexibilidad de las configuraciones, pero podemos ajustarlas por separado si fuera necesario. Esto se debe a que, más adelante, admitiremos el ajuste de velocidad automático, y el valor aproximado inicial no será tan importante.

     double train(const matrix &data, const matrix &target,
        const matrix &validation, const matrix &check,
        const int epochs = 1000, const double accuracy = 0.001,
        const ENUM_LOSS_FUNCTION lf = LOSS_MSE)
     {
        if(!ready) return NaN();
        
        speed = accuracy;
        ...

Los valores de los errores de red en la época actual se almacenarán en las variables mse y msev: para los conjuntos de entrenamiento y validación. Sin embargo, para no reaccionar a las inevitables fluctuaciones aleatorias, deberemos promediar los errores durante un cierto periodo p, calculado a partir del número total dado de épocas. Los valores de error suavizados se almacenarán en las variables msema y msevma, mientras que sus valores anteriores se guardarán en las variables msemap y msevmap.

        double mse = DBL_MAX;
        double msev = DBL_MAX;
        double msema = 0;       // MSE averaging of the training set
        double msemap = 0;      // MSE averaging of the training set in the previous epoch
        double msevma = 0;      // MSE averaging of the validation dataset
        double msevmap = 0;     // MSE averaging of the validation dataset in the previous epoch
        double ema = 0;         // exponential smoothing factor
        int p = 0;              // EMA period
        
        p = (int)sqrt(epochs);  // empirically choose the period of the EMA averaging of errors
        ema = 2.0 / (p + 1);
        PrintFormat("EMA for early stopping: %d (%f)", p, ema);

A continuación, ejecutaremos un ciclo de épocas de entrenamiento. Permitiremos no proporcionar datos de validación, porque más adelante implementaremos otra forma de regularizar "dropout". Si el conjunto de validación no está vacío, calcularemos msev llamando al método test en él. En cualquier caso, calcularemos mse llamando a test en la muestra de entrenamiento. Recordemos que test llama al método feedForward y calcula el error del resultado de la red en relación con los valores objetivo.

        int ep = 0;
        for(; ep < epochs; ep++)
        {
           if(validation.Rows() && check.Rows())
           {
              // if there is validation, run it before normal pass/training
              msev = test(validation, check, lf);
              // smooth errors
              msevma = (msevma ? msevma : msev) * (1 - ema) + ema * msev;
           }
           mse = test(data, target, lf);  // enable feedForward(data) run
           msema = (msema ? msema : mse) * (1 - ema) + ema * mse;
           ...

En primer lugar, comprobaremos que el valor del error sea un número válido. De lo contrario, la red se habrá desbordado o habremos introducido datos incorrectos.

           if(!MathIsValidNumber(mse))
           {
              PrintFormat("NaN at epoch %d", ep);
              break; // will return NaN as error indication
           }

Si el nuevo error se ha vuelto mayor que el anterior con algún "margen" determinado a partir de la relación de los tamaños de las muestras de entrenamiento y validación, el ciclo se interrumpirá.

           const int scale = (int)(data.Rows() / (validation.Rows() + 1)) + 1;
           if(msevmap != 0 && ep > p && msevma > msevmap + scale * (msemap - msema))
           {
              // skip the first p epochs to accumulate values for averaging
              PrintFormat("Stop by validation at %d, v: %f > %f, t: %f vs %f", ep, msevma, msevmap, msema, msemap);
              break;
           }
           msevmap = msevma;
           msemap = msema;
           ...

Si el error continúa disminuyendo, o al menos no aumenta, almacenaremos los nuevos valores de error para realizar comparaciones en la próxima época.

Si el error ha alcanzado la precisión necesaria, consideraremos que el entrenamiento se ha completado y también saldremos del ciclo.

           if(mse <= accuracy)
           {
              PrintFormat("Done by accuracy limit %f at epoch %d", accuracy, ep);
              break;
           }

Asimismo, llamaremos en un ciclo el método virtual progress, que se puede redefinir en las clases derivadas de la red y usarse para interrumpir el entrenamiento en respuesta a algunas acciones del usuario. A continuación, mostraremos la implementación estándar de progress.

           if(!progress(ep, epochs, mse, msev, msema, msevma))
           {
              PrintFormat("Interrupted by user at epoch %d", ep);
              break;
           }

Finalmente, si el ciclo no ha sido interrumpido por ninguna de las condiciones anteriores, iniciaremos nuevamente la propagación inversa del error a través de la red usando backProp.

           if(!backProp(target))
           {
              mse = NaN(); // error flag
              break;
           }
        }
        
        if(ep == epochs)
        {
           PrintFormat("Done by epoch limit %d with accuracy %f", ep, mse);
        }
        
        return mse;
     }

El método progress propuesto por defecto registra la curva de aprendizaje una vez por segundo.

     virtual bool progress(const int epoch, const int total,
        const double error, const double valid = DBL_MAX,
        const double ma = DBL_MAX, const double mav = DBL_MAX)
     {
        static uint trap;
        if(GetTickCount() > trap)
        {
           PrintFormat("Epoch %d of %d, loss %.5f%s%s%s", epoch, total, error,
              ma == DBL_MAX ? "" : StringFormat(" ma(%.5f)", ma),
              valid == DBL_MAX ? "" : StringFormat(", validation %.5f", valid),
              valid == DBL_MAX ? "" : StringFormat(" v.ma(%.5f)", mav));
           trap = GetTickCount() + 1000;
        }
        return !IsStopped();
     }

Si el valor retornado es true, se proseguirá el entrenamiento, si es false, el ciclo se interrumpirá.

Además de la "parada prematura", la clase MatrixNet puede "deshabilitar" aleatoriamente algunas de las conexiones como lo hace "dropout".

El método "dropout" canónico implica la exclusión temporal de algunas neuronas seleccionadas aleatoriamente de la red. No obstante, no podemos implementar esto sin incurrir en gastos de recursos excesivos, ya que el algoritmo usa operaciones matriciales. Para excluir neuronas de la capa, deberíamos reformatear las matrices de pesos en cada iteración y copiarlas parcialmente. Resulta mucho más sencillo y eficiente establecer los pesos aleatorios en 0, es decir, interrumpir las conexiones. Obviamente, al inicio de cada época, el programa deberá restaurar los pesos temporalmente deshabilitados a su estado anterior y luego seleccionar algunos nuevos para deshabilitarlos en la siguiente época.

El número de enlaces que se restablecerán temporalmente se establece usando el método enableDropOut como un porcentaje de la cantidad total de los pesos de la red. Por defecto, la variable dropOutRate es igual a 0 y el modo estará deshabilitado.

     void enableDropOut(const uint percent = 10)
     {
        dropOutRate = (int)percent;
     }

El principio de funcionamiento de "dropout" consiste en guardar el estado actual de las matrices de pesos en algún repositorio adicional (implementado por la clase DropOutState) y restablecer las conexiones de red seleccionadas aleatoriamente. Tras entrenar la red con la forma modificada resultante durante una época, los elementos de la matriz puestos a cero restaurarán desde el repositorio y repetiremos el proceso: seleccionaremos otros pesos aleatorios, los pondremos a cero y la red se entrenará con ellos, y así sucesivamente. Proponemos al lector estudiar la construcción y el uso de la clase DropOutState por su cuenta.

Tasa de aprendizaje adaptativa

Hasta ahora, hemos asumido que estamos usando una tasa de aprendizaje constante (la variable speed), pero esto no es demasiado práctico (el aprendizaje puede resultar muy lento a velocidades bajas o bien "encabritarse" a velocidades altas).

Una de las variedades de adaptación de la tasa de aprendizaje se puede "mirar" en una modificación especial del algoritmo de propagación inversa del error llamada "rprop" (del inglés resilient propagation o propagación resiliente). La idea consiste en verificar para cada peso si el signo de los incrementos delta en la iteración anterior y actual es el mismo. La coincidencia del signo implicará que se conserva la dirección de la inclinación, y en este caso podremos aumentar la velocidad selectivamente para un peso dado. Para aquellos pesos en los que el signo de la inclinación ha cambiado, tendrá sentido, por el contrario, "disminuir la velocidad".

Como estamos calculando todos los datos a la vez en las matrices en cada época, el valor y el signo del gradiente para cada peso acumulan (y "promedian") el comportamiento de todo el paquete de datos. Por ello, más concretamente, la tecnología se llama "batch rprop".

Todas las líneas de código de la clase MatrixNet que implementan esta mejora están envueltas con las macros BATCH_PROP. Antes de incluir el archivo de encabezado MatrixNet.mqh en el código fuente, es recomendable habilitar la velocidad adaptativa usando la directiva:

  #define BATCH_PROP

Para empezar, tenga en cuenta que, en lugar de la variable speed, en este modo se utiliza el array de matrices speed, y también deberemos almacenar los incrementos de los pesos de la última época en el array de matrices deltas.

  class MatrixNet
  {
  protected:
     ...
     #ifdef BATCH_PROP
     matrix speed[];
     matrix deltas[];
     #else
     double speed;
     #endif

Además, los coeficientes de aceleración y deceleración, así como las velocidades máximas y mínimas, se establecen con 4 variables destinadas para ello.

     double plus;
     double minus;
     double max;
     double min;

La asignación de memoria para nuevas matrices y la configuración de los valores predeterminados para las nuevas variables se realiza en el método allocate que ya conocemos.

     void allocate()
     {
        ArrayResize(weights, n);
        ArrayResize(outputs, n + 1);
        ArrayResize(bestWeights, n);
        dropOutRate = 0;
        #ifdef BATCH_PROP
        ArrayResize(speed, n);
        ArrayResize(deltas, n);
        plus = 1.1;
        minus = 0.1;
        max = 50;
        min = 0.0;
        #endif
     }

Para establecer otros valores para estas variables antes de iniciar el entrenamiento, usaremos el método setupSpeedAdjustment.

En el constructor MatrixNet, los arrays de matrices speed y deltas se inicializan copiando el array de matrices weights; simplemente resulta más cómodo obtener las matrices de tamaños similares en las capas de la red. El rellenado de speed y deltas con valores significativos se realizará en pasos posteriores. En concreto, al inicio del método train, en lugar de simplemente asignar la precisión (accuracy) a la variable escalar speed, se rellenarán con este valor todas las matrices en el array speed.

     double train(const matrix &data, const matrix &target,
        const matrix &validation, const matrix &check,
        const int epochs = 1000, const double accuracy = 0.001,
        const ENUM_LOSS_FUNCTION lf = LOSS_MSE)
     {
        ...
        #ifdef BATCH_PROP
        for(int i = 0; i < n; ++i)
        {
           speed[i].Fill(accuracy); // adjust speeds on the fly
           deltas[i].Fill(0);
        }
        #else
        speed = accuracy;
        #endif
        ...
     }

Dentro del método backProp, la expresión con el cálculo de los incrementos ahora se refiere a la matriz de la capa correspondiente, y no a una escalar. Inmediatamente después de obtener los incrementos delta, llamaremos al método adjustSpeed (mostrado a continuación), transmitiendo el producto delta * deltas[i] para comparar las direcciones antiguas y nuevas. Finalmente, los nuevos incrementos de pesos se almacenarán en deltas[i] para que puedan ser analizados en la próxima época.

     bool backProp(const matrix &target)
     {
        ...
        for(int i = n - 1; i >= 0; --i) // all layers except the output in reverse order
        {
           ...
           #ifdef BATCH_PROP
           matrix delta = speed[i] * outputs[i].Transpose().MatMul(loss);
           adjustSpeed(speed[i], delta * deltas[i]);
           deltas[i] = delta;
           #else
           matrix delta = speed * outputs[i].Transpose().MatMul(loss);
           #endif
           ...
        }
        ...
     }

El método adjustSpeed es bastante simple. Un signo positivo en el elemento del producto matricial significará que se conserva el gradiente y que la velocidad aumentará en «plus» veces, pero no más que hasta el valor «max». Un signo negativo significará un cambio en la inclinación, y la velocidad disminuirá en «minus» veces, pero no menos que «min».

     void adjustSpeed(matrix &subject, const matrix &product)
     {
        for(int i = 0; i < (int)product.Rows(); ++i)
        {
           for(int j = 0; j < (int)product.Cols(); ++j)
           {
              if(product[i][j] > 0)
              {
                 subject[i][j] *= plus;
                 if(subject[i][j] > max) subject[i][j] = max;
              }
              else if(product[i][j] < 0)
              {
                 subject[i][j] *= minus;
                 if(subject[i][j] < min) subject[i][j] = min;
              }
           }
        }
     }

Almacenando y restaurando el mejor estado de la red entrenada

Bien, el entrenamiento de la red se lleva a cabo en un ciclo de iteraciones que conocemos por épocas: en cada época, por la red pasan todos los vectores del conjunto de entrenamiento colocados en una matriz en la que los registros se encuentran en filas, mientras que sus signos se hallan en columnas. Por ejemplo, cada registro puede almacenar una barra de cotizaciones, mientras que las columnas almacenan precios y volúmenes de OHLC.

El proceso de ajuste de los pesos, aunque se realiza por un gradiente, es aleatorio en el sentido de que, debido a la desigualdad de la función objetivo del problema que se resuelve y la velocidad variable, podemos llegar periódicamente a configuraciones "más pobres" antes de "descubrir" un nuevo mínimo del error de red. En principio, no tenemos ninguna garantía de que, con un aumento en el número de épocas, aumente la calidad del modelo entrenado y el error de red disminuya a ciencia cierta.

En relación con esto, tendrá sentido monitorear constantemente el error global de la red, y si después de la época actual el error actualiza el mínimo, deberemos almacenar los pesos encontrados. Para ello, definiremos otro array de matrices de pesos, así como una estructura con los indicadores de aprendizaje Stats.

  class MatrixNet
  {
     ...
  public:
     struct Stats
     {
        double bestLoss; // smallest error for all epochs
        int bestEpoch;   // index of the epoch with the minimum error
        int epochsDone;  // total number of completed epochs
     };
     
     Stats getStats() const
     {
        return stats;
     }
     
  protected:
     matrix bestWeights[];
     Stats stats;
     ...

Dentro del método train, antes de comenzar el ciclo por épocas, inicializaremos la estructura con estadísticas.

     double train(const matrix &data, const matrix &target,
        const matrix &validation, const matrix &check,
        const int epochs = 1000, const double accuracy = 0.001,
        const ENUM_LOSS_FUNCTION lf = LOSS_MSE)
     {
        ...
        stats.bestLoss = DBL_MAX;
        stats.bestEpoch = -1;
        DropOutState state(dropOutRate);

Dentro del propio ciclo, al detectarse un valor de error inferior al valor mínimo conocido, almacenaremos todas las matrices de pesos en bestWeights.

        int ep = 0;
        for(; ep < epochs; ep++)
        {
           ...
           const double candidate = (msev != DBL_MAX) ? msev : mse;
           if(candidate < stats.bestLoss)
           {
              stats.bestLoss = candidate;
              stats.bestEpoch = ep;
              // save best weights from 'weights'
              for(int i = 0; i < n; ++i)
              {
                 bestWeights[i].Assign(weights[i]);
              }
           }
        }
        ...

Después del entrenamiento, resultará sencillo consultar tanto los pesos finales de la red como los mejores pesos.

     bool getWeights(matrix &array[]) const
     {
        if(!ready) return false;
        
        ArrayResize(array, n);
        for(int i = 0; i < n; ++i)
        {
           array[i] = weights[i];
        }
        
        return true;
     }
     
     bool getBestWeights(matrix &array[]) const
     {
        if(!ready) return false;
        if(!n || !bestWeights[0].Rows()) return false;
        
        ArrayResize(array, n);
        for(int i = 0; i < n; ++i)
        {
           array[i] = bestWeights[i];
        }
        
        return true;
     }

Estos arrays de matrices se pueden guardar en un archivo para la posterior restauración de una red ya entrenada y lista para trabajar. Para ello hemos previsto un constructor aparte.

     MatrixNet(const matrix &w[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH,
        const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE):
        ready(false), af(f1), of(f2), n(ArraySize(w))
     {
        if(n < 2) return;
        
        allocate();
        for(int i = 0; i < n; ++i)
        {
           weights[i] = w[i];
           #ifdef BATCH_PROP
           speed[i] = weights[i];  // instead .Init(.Rows(), .Cols())
           deltas[i] = weights[i]; // instead .Init(.Rows(), .Cols())
           #endif
        }
        
        ready = true;
     }

Más adelante, mostraremos cómo almacenar y leer redes preparadas en uno de los ejemplos prácticos.

Visualizando el progreso del entrenamiento de la red

La presencia del método progress, que envía mensajes periódicos al diario de registro, no queda muy clara. Por consiguiente, el archivo MatrixNet.mqh también implementará la clase MatrixNetVisual derivada de MatrixNet, que muestra en la ventana un gráfico con los valores cambiantes de los errores de entrenamiento por épocas.

La visualización gráfica la proporciona la clase CGraphic estándar (suministrada con MetaTrader 5), o más bien, la pequeña clase CMyGraphic derivada de ella.

El objeto de esta clase forma parte de MatrixNetVisual. Además, dentro de la red "visualizada", se describen un array de 5 curvas y arrays de tipo double que se utilizan para mostrar las líneas.

  class MatrixNetVisual: public MatrixNet
  {
     CMyGraphic graphic;
     CCurve *c[5];
     double p[], x[], y[], z[], q[], b[];
     ...

Aquí:

p es el número de época (el eje X horizontal es común para todas las curvas);

x - error del conjunto de entrenamiento (Y);

y - error del conjunto de validación (Y);

z - error de validación suavizado (Y);

q - error de entrenamiento suavizado (Y);

b - punto (época) con el mínimo error (Y);

En el método graph, llamado desde los constructores MatrixNetVisual, se crea un objeto gráfico del tamaño de la ventana completa y se añaden las 5 curvas descritas anteriormente (CCurve).

   void graph()
   {
      ulong width = ChartGetInteger(0, CHART_WIDTH_IN_PIXELS);
      ulong height = ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS);

      bool res = false;
      const string objname = "BPNNERROR";
      if(ObjectFind(0, objname) >= 0) res = graphic.Attach(0, objname);
      else res = graphic.Create(0, objname, 0, 0, 0, (int)(width - 0), (int)(height - 0));
      if(!res) return;

      c[0] = graphic.CurveAdd(p, x, CURVE_LINES, "Training");
      c[1] = graphic.CurveAdd(p, y, CURVE_LINES, "Validation");
      c[2] = graphic.CurveAdd(p, z, CURVE_LINES, "Val.EMA");
      c[3] = graphic.CurveAdd(p, q, CURVE_LINES, "Train.EMA");
      c[4] = graphic.CurveAdd(p, b, CURVE_POINTS, "Best/Minimum");
      ...
   }

public:
   MatrixNetVisual(const int &layers[], const ENUM_ACTIVATION_FUNCTION f1 = AF_TANH,
      const ENUM_ACTIVATION_FUNCTION f2 = AF_NONE): MatrixNet(layers, f1, f2)
   {
      graph();
   }

En el método redefinido 'progress', los argumentos se añaden a las matrices double correspondientes, y luego se llama al método 'plot' para actualizar la imagen.

     virtual bool progress(const int epoch, const int total,
        const double error, const double valid = DBL_MAX,
        const double ma = DBL_MAX, const double mav = DBL_MAX) override
     {
        // fill all the arrays
        PUSH(p, epoch);
        PUSH(x, error);
        if(valid != DBL_MAX) PUSH(y, valid); else PUSH(y, nan);
        if(ma != DBL_MAX) PUSH(q, ma); else PUSH(q, nan);
        if(mav != DBL_MAX) PUSH(z, mav); else PUSH(z, nan);
        plot();
        
        return MatrixNet::progress(epoch, total, error, valid, ma, mav);
     }

El método plot efectúa el rellenado y la representación las curvas.

   void plot()
   {
      c[0].Update(p, x);
      c[1].Update(p, y);
      c[2].Update(p, z);
      c[3].Update(p, q);
      double point[1] = {stats.bestEpoch};
      b[0] = stats.bestLoss;
      c[4].Update(point, b);
      ...
      graphic.CurvePlotAll();
      graphic.Update();
   }

Proponemos al lector trabajar el aspecto técnico de la visualización por su propia cuenta. Qué aspecto tiene esto en la pantalla, lo veremos pronto.

Script de prueba

Las clases de la familia MatrixNet ya están listas para la primera prueba. De ello se encargará el script MatrixNet.mq5, en el que los datos iniciales se generan artificialmente usando como base un registro analítico conocido. La fórmula se toma del apartado de la guía de ayuda sobre aprendizaje automático, que proporciona un ejemplo nativo de entrenamiento con propagación inversa del error que no resulta tan versátil como nuestras clases y, por lo tanto, requiere una escritura de código significativa (compare la cantidad de filas con y sin usar la clase a continuación).

f = ((x + y + z)^2 / (x^2 + y^2 + z^2)) / 3

La única pequeña diferencia de nuestra fórmula es la división del valor por 3, lo cual le proporciona a la función un rango de 0 a 1.

La forma de la función se puede estimar usando la siguiente figura, donde se muestran las superficies (x<->y) para tres valores z diferentes: 0,05, 0,5 y 5,0.

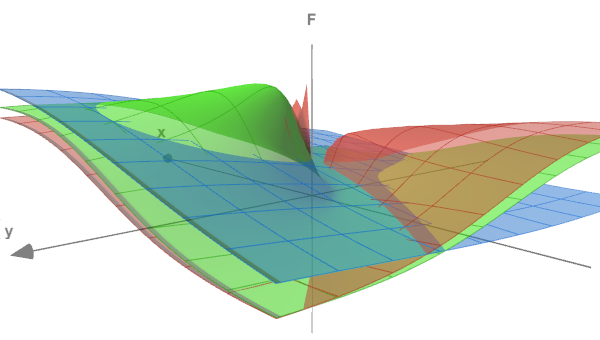
Función de prueba en 3 secciones

En las variables de entrada del script estableceremos el número de épocas de entrenamiento y la precisión (error terminal), así como la intensidad del ruido que podemos añadir de forma opcional a los datos generados (esto acercará el experimento a los problemas reales, y demostrará además cómo la presencia de ruido dificulta la identificación de dependencias). Por defecto, RandomNoise será 0 y no tendremos ruido.

  input int Epochs = 1000;
  input double Accuracy = 0.001;
  input double RandomNoise = 0.0;

La generación de datos experimentales será "gestionada" por la función CreateData. Sus parámetros matriciales 'data' y 'target' se rellenarán con puntos de la función descrita anteriormente, en un número equivalente a 'count'. El vector de entrada (fila de la matriz data) tiene 3 columnas (para x, y, z). El vector de salida (fila de la matriz target) es el valor único f. Los puntos (x, y, z) se generan aleatoriamente en un rango de -10 a +10.

  bool CreateData(matrix &data, matrix &target, const int count)
  { 
     if(!data.Init(count, 3) || !target.Init(count, 1))
        return false;
     data.Random(-10, 10);
     vector X1 = MathPow(data.Col(0) + data.Col(1) + data.Col(2), 2);
     vector X2 = MathPow(data.Col(0), 2) + MathPow(data.Col(1), 2) + MathPow(data.Col(2), 2);
     if(!target.Col(X1 / X2 / 3.0, 0))
        return false;
     if(RandomNoise > 0)
     {
        matrix noise;
        noise.Init(count, 3);
        noise.Random(0, RandomNoise);
        data += noise - RandomNoise / 2;
        
        noise.Resize(count, 1);
        noise.Random(-RandomNoise / 2, RandomNoise / 2);
        target += noise;
     }
     return true; 
  }

La intensidad del ruido en RandomNoise se establece como la amplitud de la dispersión adicional de las coordenadas correctas y el valor de función obtenido para las mismas. Como la función tiene un valor máximo de 1,0, este nivel de ruido la hará casi irreconocible.

Para usar la red neuronal, incluiremos el archivo de encabezado MatrixNet.mqh y definiremos la macro BATCH_PROP antes de esta directiva de preprocesador para activar el aprendizaje acelerado como una velocidad variable.

  #define BATCH_PROP
  #include <MatrixNet.mqh>

En la función principal del script, definiremos la configuración de la red (el número de capas y sus tamaños) utilizando la matriz layers transmitida al constructor MatrixNetVisual. Los conjuntos de datos de entrenamiento y validación los generaremos llamando a CreateData dos veces.

  void OnStart()
  {
     const int layers[] = {3, 11, 7, 1};
     MatrixNetVisual net(layers);
     matrix data, target;
     CreateData(data, target, 100);
     matrix valid, test;
     CreateData(valid, test, 25);
     ...

En la práctica, deberíamos normalizar los datos originales, limpiarlos de valores atípicos y verificar la independencia de los factores antes de enviarlos a la red, pero en este caso generamos los datos nosotros mismos.

El entrenamiento se realizará usando el método train con las matrices data y target. La parada prematura se realizará a medida que el rendimiento disminuya en el conjunto valid/test, pero en datos sin ruido es probable que alcancemos la precisión necesaria o el límite del ciclo, lo que suceda más rápido.

     Print("Training result: ", net.train(data, target, valid, test, Epochs, Accuracy));
     matrix w[];
     if(net.getBestWeights(w))
     {
        MatrixNet net2(w);
        if(net2.isReady())
        {
           Print("Best copy on training data: ", net2.test(data, target));
           Print("Best copy on validation data: ", net2.test(valid, test));
        }
     }

Tras el entrenamiento, solicitaremos las matrices de los mejores pesos encontrados y, para realizar la verificación, construiremos otro ejemplar de la red basado en ellos: el objeto net2, después de lo cual ejecutaremos de funcionamiento de la red en ambos conjuntos de datos y mostramos la magnitud del error para estos en el diario de registro.

Como el script utiliza una red con visualización del progreso del aprendizaje, iniciaremos un ciclo esperando el comando del usuario para completar el script y que el usuario pueda familiarizarse con el gráfico.

     while(!IsStopped())
     {
        Sleep(1000);
     }
  }

Al ejecutar el script con los parámetros por defecto, podremos obtener algo como la siguiente imagen (cada ejecución será diferente a las demás por la generación aleatoria de los datos y la inicialización de la red).

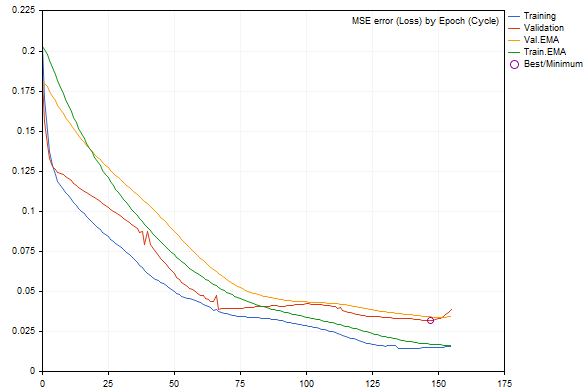
Dinámica del cambio del error de red durante el entrenamiento

Los errores en los conjuntos de entrenamiento y validación se muestran como líneas azules y rojas, respectivamente, mientras que sus versiones suavizadas son verdes y amarillas. Podemos ver claramente que a medida que avanza el entrenamiento, todos los tipos de error disminuyen, pero después de cierto momento, el error de validación se hace mayor que el error del conjunto de entrenamiento; más cerca del borde derecho del gráfico, se nota su aumento, y como resultado de ello, sucede una "parada prematura". La mejor configuración de la red se destaca con un círculo.

En el diario de registro veremos entradas como estas:

  EMA for early stopping: 31 (0.062500)
  Epoch 0 of 1000, loss 0.20296 ma(0.20296), validation 0.18167 v.ma(0.18167)
  Epoch 120 of 1000, loss 0.02319 ma(0.02458), validation 0.04566 v.ma(0.04478)
  Stop by validation at 155, v: 0.034642 > 0.034371, t: 0.016614 vs 0.016674
  Training result: 0.015707719706513287
  Best copy on training data: 0.015461956812387292
  Best copy on validation data: 0.03211748853774414

Si comenzamos a añadir ruido a los datos usando el parámetro RandomNoise, la tasa de aprendizaje disminuirá notablemente, y si hay demasiado ruido, el error de la red entrenada aumentará, o bien esta dejará de aprender por completo.

Por ejemplo, este será el gráfico con adición de ruido 3.0.

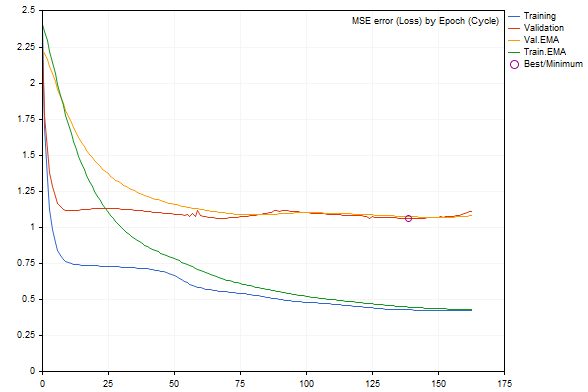
Dinámica de cambio del error de red durante el entrenamiento con ruido adicional

La tasa de error, según el diario de registro, es peor en un orden de magnitud.

  Epoch 0 of 1000, loss 2.40352 ma(2.40352), validation 2.23536 v.ma(2.23536)
  Stop by validation at 163, v: 1.082419 > 1.080340, t: 0.432023 vs 0.432526
  Training result: 0.4244786772678285
  Best copy on training data: 0.4300476339855798
  Best copy on validation data: 1.062895214094978

Tras asegurarnos de que el conjunto de herramientas de la RN funciona, vamos a pasar a ejemplos más prácticos: un indicador y un experto.

Indicador predictivo

Como ejemplo de un indicador predictivo basado en RN, analizaremos BPNNMatrixPredictorDemo.mq5: esta es una modificación de un indicador listo para usar del Code Base en la que una RN se implementa en MQL5 sin usar matrices, portando desde el lenguaje C++ otra versión anterior de la mismo indicador (con una descripción detallada, incluyendo partes relevantes de la teoría de RN).

El indicador funciona formando vectores de entrada de un tamaño determinado a partir de los incrementos pasados del precio medio de la EMA en los intervalos entre barras, separados entre sí por la secuencia de Fibonacci (1,2,3,5,8,13,21,34,55,89,144...). Usando como base esta información, deberemos predecir el incremento de precio en la siguiente barra (a la derecha de las barras históricas incluidas en el vector correspondiente). El tamaño del vector se determina mediante el tamaño indicado por el usuario de la capa de entrada de la RN (_numInputs). El número de capas (hasta 6) y sus tamaños se introducen en otras variables de entrada.

  input int _lastBar = 0;     // Last bar in the past data
  input int _futBars = 10;    // # of future bars to predict
  input int _smoothPer = 6;   // Smoothing period
  input int _numLayers = 3;   // # of layers including input, hidden & output (2..6)
  input int _numInputs = 12;  // # of inputs (that is neurons in input 0-th layer)
  input int _numNeurons1 = 5; // # of neurons in the 1-st hidden or output layer
  input int _numNeurons2 = 1; // # of neurons in the 2-nd hidden or output layer
  input int _numNeurons3 = 0; // # of neurons in the 3-rd hidden or output layer
  input int _numNeurons4 = 0; // # of neurons in the 4-th hidden or output layer
  input int _numNeurons5 = 0; // # of neurons in the 5-th hidden or output layer
  input int _ntr = 500;       // # of training sets / bars
  input int _nep = 1000;      // Max # of epochs
  input int _maxMSEpwr = -7;  // Error (as power of 10) for training to stop; mse < 10^this

También se indica el tamaño de la muestra de entrenamiento (_ntr), el número máximo de épocas (_nep) y el error MSE mínimo (_maxMSEpwr).

El periodo del promedio EMA del precio se establece en _smoothPer.

Por defecto, el indicador toma los datos de entrenamiento a partir de la última barra (_lastBar igual a 0) y hace un pronóstico para _futBars posteriores (obviamente, teniendo un pronóstico de 1 barra en la salida de la red, podemos "empujarlo" gradualmente en el vector de entrada para predecir varias barras posteriores). Si introducimos un número positivo en _lastBar, obtendremos un pronóstico partiendo del número correspondiente de barras en el pasado, lo cual nos permitirá evaluarlo visualmente (comparar con las cotizaciones existentes).

El indicador muestra 3 búferes:

• una línea verde claro con los valores objetivo de la muestra de entrenamiento;
• una línea azul con la salida de la red en el conjunto de entrenamiento;
• una línea roja con el pronóstico;

La parte aplicada del indicador para generar los conjuntos de datos y visualizar los resultados (tanto los datos iniciales como los pronósticos) no ha cambiado.

Las principales transformaciones han tenido lugar en dos funciones Train y Test: ahora delegan completamente el trabajo de la RN en los objetos de la clase MatrixNet. Train entrena la red según los datos recopilados y retorna una matriz con los pesos de la red (cuando se ejecuta en el simulador, el entrenamiento se realiza solo una vez, y cuando se ejecuta en línea, la apertura de una nueva barra provocará un nuevo entrenamiento; esto se puede cambiar fácilmente en el código fuente). Test recrea la red según los pesos y realiza un único cálculo de predicción normal. En principio, resultaría aún mejor guardar el objeto de la red entrenada y explotarlo sin necesidad de recreación. Haremos esto en el próximo ejemplo de asesor, y en el caso del indicador, dejaremos deliberadamente la estructura del código original de la versión anterior para que resulte más cómodo comparar los enfoques de codificación con y sin matrices. En particular, podemos prestar atención al hecho de que en la versión matricial no tenemos la necesidad de "ejecutar" los vectores a través de la red en un ciclo uno a uno y "remodelar" manualmente las matrices de datos según su dimensión.

Con la configuración por defecto, el indicador se verá así en el gráfico EURUSD,H1.

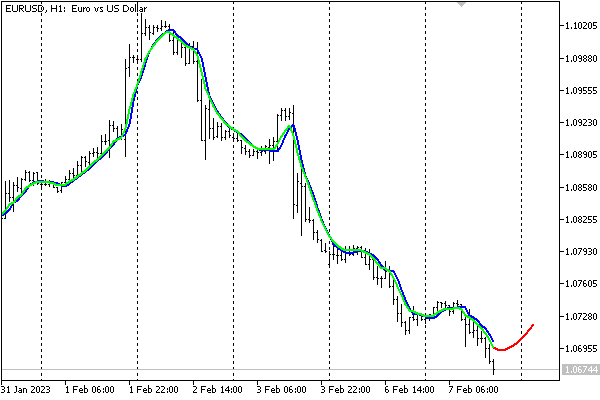
Predicción de indicador de red neuronal

Debemos señalar que el indicador solo supone una demostración del funcionamiento de la RN y no lo recomendamos en su forma simplificada actual para tomar decisiones comerciales.

Almacenamiento de las redes en archivos

Los datos originales que llegan del mercado pueden cambiar rápidamente, y algunos tráders consideran que merece la pena entrenar la red sobre la marcha (todos los días, cada sesión, etc.) con las muestras más recientes. No obstante, esto puede resultar costoso y no tan relevante para los sistemas comerciales a mediano y largo plazo que operan con días. En estos casos, resulta deseable guardar la red entrenada para su posterior carga y uso rápido.

Para ello, en el marco del artículo, hemos creado la clase MatrixNetStore, que se define en el archivo de encabezado MatrixNetStore.mqh. La clase tiene los métodos de plantilla save y load, que asumen cualquier clase de la familia MatrixNet como un parámetro de plantilla M (hasta ahora solo tenemos dos de ellos, considerando MatrixNetVisual, pero aquellos que lo deseen pueden ampliar el conjunto). Ambos métodos tienen un argumento con el nombre del archivo y trabajan con datos estándar de la RN: el número de capas, su tamaño, las matrices de pesos y las funciones de activación.

Aquí tenemos cómo se implementa el almacenamiento de la red

  class MatrixNetStore
  {
     static string signature;
  public:
     template<typename M> // M is a MatrixNet
     static bool save(const string filename, const M &net, Storage *storage = NULL, const int flags = 0)
     {
        // get the matrix of weights (the best weights, if any)
        matrix w[];
        if(!net.getBestWeights(w))
        {
           if(!net.getWeights(w))
           {
              return false;
           }
        }
        // open file
        int h = FileOpen(filename, FILE_WRITE | FILE_BIN | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags);
        if(h == INVALID_HANDLE) return false;
        // write network metadata
        FileWriteString(h, signature);
        FileWriteInteger(h, net.getActivationFunction());
        FileWriteInteger(h, net.getActivationFunction(true));
        FileWriteInteger(h, ArraySize(w));
        // write weight matrices
        for(int i = 0; i < ArraySize(w); ++i)
        {
           matrix m = w[i];
           FileWriteInteger(h, (int)m.Rows());
           FileWriteInteger(h, (int)m.Cols());
           double a[];
           m.Swap(a);
           FileWriteArray(h, a);
        }
        // if user data is provided, write it
        if(storage)
        {
          if(!storage.store(h)) Print("External info wasn't saved");
        }
        
        FileClose(h);
        return true;
     }
     ...
  };
     
  static string MatrixNetStore::signature = "BPNNMS/1.0";

Destacaremos un par de puntos. Al principio del archivo, se escribe una signatura para verificar con su ayuda que el formato del archivo sea correcto (la signatura se puede cambiar: la clase ofrece los métodos necesarios para ello). Además, el método save permite, de ser necesario, añadir cualquier dato adicional de usuario a la información estándar sobre la red: basta con transmitir el puntero al objeto de interfaz especial Storage.

  class Storage
  {
  public:
     virtual bool store(const int h) = 0;
     virtual bool restore(const int h) = 0;
  };

La red se puede restaurar a partir de un archivo de forma "especular".

  class MatrixNetStore
  {
     ...
     template<typename M> // M is a MatrixNet
     static M *load(const string filename, Storage *storage = NULL, const int flags = 0)
     {
        int h = FileOpen(filename, FILE_READ | FILE_BIN | FILE_SHARE_READ | FILE_SHARE_WRITE | FILE_ANSI | flags);
        if(h == INVALID_HANDLE) return NULL;
        // check the format by signature
        const string header = FileReadString(h, StringLen(signature));
        if(header != signature)
        {
           FileClose(h);
           Print("Incorrect file header");
           return NULL;
        }
        // read standard network metadata set
        const ENUM_ACTIVATION_FUNCTION f1 = (ENUM_ACTIVATION_FUNCTION)FileReadInteger(h);
        const ENUM_ACTIVATION_FUNCTION f2 = (ENUM_ACTIVATION_FUNCTION)FileReadInteger(h);
        const int size = FileReadInteger(h);
        matrix w[];
        ArrayResize(w, size);
        // read weight matrices
        for(int i = 0; i < size; ++i)
        {
           const int rows = FileReadInteger(h);
           const int cols = FileReadInteger(h);
           double a[];
           FileReadArray(h, a, 0, rows * cols);
           w[i].Swap(a);
           w[i].Reshape(rows, cols);
        }
        // read user data
        if(storage)
        {
           if(!storage.restore(h)) Print("External info wasn't read");
        }
        // create a network object
        M *m = new M(w, f1, f2);
        
        FileClose(h);
        return m;
     }

Ahora ya estamos listos para pasar al ejemplo final del artículo: el robot comercial.

Asesor predictivo

Como estrategia para el asesor predictivo TradeNN.mq5, tomaremos un principio bastante simple: comerciar en la dirección prevista de la siguiente barra. Para nosotros resulta importante mostrar las tecnologías de RN en acción y no explorar todos los factores previsibles para su aplicabilidad en el contexto de la rentabilidad.

Los datos iniciales serán los incrementos de precio en un número determinado de barras y, opcionalmente, podremos analizar no solo el símbolo actual, sino también otros adicionales, lo cual teóricamente nos permitirá identificar interdependencias (por ejemplo, si un ticker "sigue" indirectamente a otro o a sus combinaciones). La única salida de la red no se interpretará como un precio objetivo, sino que, para simplificar el sistema, se analizará el signo: positivo - compra, negativo - venta.

En otras palabras, el esquema de funcionamiento de la red será híbrido, en cierto sentido: por un lado, la red resolverá el problema de la regresión, pero por otro lado, la acción comercial se seleccionará entre dos, como en la clasificación. En un futuro, será posible aumentar la cantidad de neuronas en la capa de salida hasta la cantidad de situaciones comerciales y aplicar la función de activación SoftMax, no obstante, para entrenar dicha red, deberemos etiquetar automática o manualmente las cotizaciones según las situaciones.

La elección de la estrategia se hará deliberadamente lo más simple posible para centrarse en los parámetros de la red, no en la estrategia.

La enumeración de instrumentos a analizar se introducirá en el parámetro de entrada Symbols, usando comas para separarlos. El símbolo del gráfico actual deberá ir primero: con este símbolo se realizará el comercio.

  input string Symbols = "XAGUSD,XAUUSD,EURUSD";
  input int Depth = 5; // Vector size (bars)
  input int Reserve = 250; // Training set size (vectors)

La elección de los símbolos por defecto se condiciona al hecho de que la plata y el oro se consideran activos correlacionados, y hay relativamente pocas noticias perturbadoras (en comparación con las monedas), por lo que, en principio, podemos intentar analizar tanto la plata en relación al oro (como ahora), como el oro en relación a la plata. En lo que respecta a EURUSD, esta pareja ha sido añadida como base de todo el mercado, y en este caso, la presencia de noticias sobre ella no es importante, ya que funciona como un predictor, no como una variable predictiva.

Entre los otros parámetros más importantes se encuentra el número de barras (Depth) para cada instrumento, que forman el vector. Por ejemplo, si en la fila Symbols establecemos 3 tickers y en Depth establecemos 5 (valor predeterminado), el tamaño total del vector de entrada de la RN será de 15.

El parámetro Reserve nos permite establecer la longitud de la muestra (el número de vectores formados a partir de la historia de cotizaciones más próxima). El valor de 250 se elige por defecto, porque nuestra prueba utilizará el marco temporal de días y 250 supone aproximadamente 1 año. Como consecuencia, si Depth es igual a 5, tendremos una semana.

Obviamente, todas las configuraciones se pueden cambiar, al igual que el marco temporal, pero en marcos temporales mayores, como D1, los patrones fundamentales son supuestamente más pronunciados que las reacciones espontáneas del mercado ante circunstancias momentáneas.

También debemos recordar que cuando se inicia en el simulador, se carga aproximadamente 1 año de cotizaciones de antemano, por lo que aumentar la cantidad de datos de entrenamiento solicitados en D1+ requerirá omitir una cierta cantidad de barras iniciales, esperando que se acumule un número suficiente de ellas.

De forma similar a los ejemplos anteriores, deberemos especificar en los parámetros el número de épocas de entrenamiento y la precisión (que es también la velocidad inicial: más tarde la velocidad se seleccionará dinámicamente para cada sinapsis según "rprop").

  input int Epochs = 1000;
  input double Accuracy = 0.0001; // Accuracy (and training speed)

En este asesor experto, la RN obtendrá 5 capas: una de entrada, 3 ocultas y una salida. El tamaño de la capa de entrada determinará el vector de entrada, mientras que las capas segunda y la tercera se seleccionarán con el coeficiente HiddenLayerFactor. Para la penúltima capa, usaremos una fórmula empírica (mire el código fuente a continuación) para que su tamaño se encuentre entre la anterior y la de salida (único).

  input double HiddenLayerFactor = 2.0; // Hidden Layers Factor (to vector size)
  input int DropOutPercentage = 0; // DropOut Percentage

Además, usando esta RN como ejemplo, probaremos el método de regularización "dropout": el porcentaje de pesos seleccionados aleatoriamente para la reducción a cero se establecerá en el parámetro DropOutPercentage. Aquí no se contempla una muestra de validación, aunque si el lector lo desea, puede combinar ambos métodos: la clase lo permite.

El parámetro NetBinFileName se utiliza para cargar la red desde un archivo. Los archivos siempre se buscan en relación con la carpeta común de terminales, porque de lo contrario, para probar el asesor experto en el simulador, deberíamos especificar de antemano los nombres de todas las redes necesarias en el código fuente, en la directiva #property tester_file: esta es la única forma en que se enviarían al agente.

Cuando el parámetro NetBinFileName está vacío, el asesor entrena una nueva red y la guarda en un archivo con un nombre temporal único. Esto se hace incluso durante el proceso de optimización, lo cual permite generar una gran cantidad de configuraciones de red (para diferentes tamaños de vectores, capas, "dropout", profundidades de la historia).

  input string NetBinFileName = "";
  input int Randomizer = 0;

Además, el parámetro Randomizer hace posible inicializar el generador aleatorio de formas distintas y, por lo tanto, podemos entrenar muchos ejemplares de red para las mismas configuraciones. Recuerde que, debido a la aleatorización, cada red es única. Potencialmente, el uso de comités de RN de los que se extrae una decisión consolidada o regla de mayoría, supone otro tipo de regularización.

No obstante, configurar Randomizer en un valor específico nos permitirá replicar el mismo proceso de entrenamiento con fines de depuración.

El almacenamiento de la información sobre los precios según el símbolo se organiza usando la estructura Closes y un array de estructuras CC de este tipo: como resultado, obtendremos algo así como un array de arrays.

  struct Closes
  {
     double C[];
  };
     
  Closes CC[];

Los instrumentos de trabajo y sus cantidades se reservan para el array global 'S' y la variable 'Q': se rellenan en 'OnInit'.

  string S[];
  int Q;
     
  int OnInit()
  {
     Q = StringSplit(StringLen(Symbols) ? Symbols : _Symbol, ',', S);
     ArrayResize(CC, Q);
     MathSrand(Randomizer);
     ...
     return INIT_SUCCEEDED;
  }

La función Calc permite solicitar cotizaciones a una profundidad Depth específica establecida desde una barra concreta offset: aquí es donde se rellena el array CC. Un poco más adelante veremos cómo se llama esta función.

  bool Calc(const int offset)
  {
     const datetime dt = iTime(_Symbol, _Period, offset);
     for(int i = 0; i < Q; ++i)
     {
        const int bar = iBarShift(S[i], PERIOD_CURRENT, dt);
        // +1 for differences, +1 for model
        const int n = CopyClose(S[i], PERIOD_CURRENT, bar, Depth + 2, CC[i].C);
        
        for(int j = 0; j < n - 1; ++j)
        {
           CC[i].C[j] = (CC[i].C[j + 1] - CC[i].C[j]) /
              SymbolInfoDouble(S[i], SYMBOL_TRADE_TICK_SIZE) * SymbolInfoDouble(S[i], SYMBOL_TRADE_TICK_VALUE);
        }
        
        ArrayResize(CC[i].C, n - 1);
     }
     
     return true;
  }

Luego, para el array específico CC[i].C, la función especial Diff podrá calcular los incrementos de precio que se suministrarán a los vectores de entrada para la red. Una característica de la función es que escribe todos los incrementos, excepto el último, en el array «d» transmitido por referencia, mientras que el último incremento, que será el valor objetivo del pronóstico, se retornará directamente.

  double Diff(const double &a[], double &d[])
  {
     const int n = ArraySize(a);
     ArrayResize(d, n - 1); // -1 minus the "future" model
     double overall = 0;
     for(int j = 0; j < n - 1; ++j) // left (from old) to right (toward new)
     {
        int k = n - 2 - j;
        overall += a[k];
        d[j] = overall / sqrt(j + 1);
     }
     ... // additional normalization
     return a[n - 1];
  }

Cabe señalar aquí que, según la teoría de las series temporales del "paseo aleatorio", normalizaremos las diferencias usando la raíz cuadrada de la distancia en barras (proporcional al intervalo de confianza, si consideramos el pasado como un pronóstico ya resuelto). Esta no supone una técnica canónica, pero el trabajo con RN suele ser similar a una investigación.

El procedimiento completo de la selección de factores (por ejemplo, no solo precios, sino también indicadores, volúmenes) y la preparación de datos para la red (normalización, codificación) es un extenso tema aparte. Resulta vital facilitar el trabajo computacional de la RN tanto como sea posible, de lo contrario, puede que no logre hacer frente a la tarea.

En la función principal del asesor experto OnTick, todas las operaciones se realizan solo después de la apertura de una barra. Teniendo en cuenta que el asesor experto analiza cotizaciones de diferentes instrumentos, deberemos sincronizar sus barras antes de continuar con el trabajo regular. La sincronización se realiza con ayuda de la función Sync, que no se muestra aquí. Sin embargo, debemos notar que la sincronización aplicada basada en la función Sleep resulta adecuada incluso para realizar pruebas en el modo de precios de apertura, y usaremos este modo más adelante por razones de eficiencia.

  void OnTick()
  {
     ...
     static datetime last = 0;
     if(last == iTime(_Symbol, _Period, 0)) return;
     ...

El ejemplar de red se almacena en la variable de ejecución del tipo de puntero automático (archivo de encabezado AutoPtr.mqh), lo cual nos ahorra la necesidad de controlar la liberación de memoria. La variable «std» se usa para almacenar la varianza calculada con el conjunto de datos obtenidos de las funciones Calc y Diff discutidas anteriormente. Necesitaremos la varianza para normalizar los datos.

     static AutoPtr<MatrixNet> run;
     static double std;

Si el usuario ha indicado un nombre de archivo en NetBinFileName para cargar, el programa tratará de cargar la red usando LoadNet (ver más abajo). En caso de éxito, esta función retorna un puntero al objeto de red.

     if(NetBinFileName != "")
     {
        if(!run[])
        {
           run = LoadNet(NetBinFileName, std);
           if(!run[])
           {
              ExpertRemove();
              return;
           }
        }
     }

Si la red ya existe, ejecutaremos el pronóstico y realizaremos las operaciones comerciales: todo ello será gestionado por la función TradeTest (de la que hablaremos más adelante).

     if(run[])
     {
        TradeTest(run[], std);
     }
     else
     {
        run = TrainNet(std);      
     }
     
     last = iTime(_Symbol, _Period, 0);
  }

Si aún no tenemos una red, generaremos una muestra de entrenamiento y entrenaremos la red con ella llamando a TrainNet: esta función también retornará el puntero al nuevo objeto de red y, además, rellenará la variable «std» transmitida por referencia con la varianza calculada de los datos.

Tenga en cuenta que la red podrá entrenarse solo después de que la historia de todos los símbolos de trabajo contenga al menos el número solicitado de barras. Para un gráfico en línea, lo más probable es que esto suceda justo después de colocar el asesor experto (a menos que el usuario haya introducido un número exorbitante), y en el simulador, la historia precargada generalmente se limita a un año y, por lo tanto, podría ser necesario desplazar el inicio de la pasada hacia el pasado para que haya tiempo de acumular el número requerido de barras para el entrenamiento.

La verificación del número suficiente de barras se ha insertado al inicio de OnTick, pero no se ofrece en el presente artículo (consulte los códigos fuente completos).

Después de entrenar la red, el asesor comenzará a comerciar. Para el simulador, esto significará que conseguiremos una especie de prueba forward de la red entrenada. Los indicadores financieros obtenidos se pueden usar para la optimización con el fin de elegir la configuración de red más adecuada o seleccionar un comité de redes (de configuración idéntica).

Aquí tenemos la función TrainNet en sí (tenga en cuenta las llamadas Calc y Diff).

  MatrixNet *TrainNet(double &std)
  {
     double coefs[];
     matrix sys(Reserve, Q * Depth);
     vector model(Reserve);
     vector t;
     datetime start = 0;
    
     for(int j = Reserve - 1; j >= 0; --j) // loop through historical bars
     {
        // since close prices are used, we make +1 to the bar index
        if(!Calc(j + 1)) // collect data for all symbols starting with bar j to Depth bars
        {
           return NULL; // probably other symbols don't have enough history (wait)
        }
        // remember training sample start date/time
        if(start == 0) start = iTime(_Symbol, _Period, j);
      
        ArrayResize(coefs, 0);
      
        // calculate price difference for all symbols for Depth bars
        for(int i = 0; i < Q; ++i)
        {
           double temp[];
           double m = Diff(CC[i].C, temp);
           if(i == 0)
           {
              model[j] = m;
           }
           int dest = ArraySize(coefs);
           ArrayCopy(coefs, temp, dest, 0);
        }
      
        t.Assign(coefs);
        sys.Row(t, j);
     }
     
     // normalize
     std = sys.Std() * 3;
     Print("Normalization by 3 std: ", std);
     sys /= std;
     matrix target = {};
     target.Col(model, 0);
     target /= std;
    
     // the size of layers 0, 1, 2, 3 is derived from the data, always one output
     int layers[] = {0, 0, 0, 0, 1};
     layers[0] = (int)sys.Cols();
     layers[1] = (int)(sys.Cols() * HiddenLayerFactor);
     layers[2] = (int)(sys.Cols() * HiddenLayerFactor);
     layers[3] = (int)fmax(sqrt(sys.Rows()), fmax(sqrt(layers[1] * layers[3]), sys.Cols() * sqrt(HiddenLayerFactor)));
     
     // create and configure the network of the specified configuration
     ArrayPrint(layers);
     MatrixNetVisual *net = new MatrixNetVisual(layers);
     net.setupSpeedAdjustment(SpeedUp, SpeedDown, SpeedHigh, SpeedLow);
     net.enableDropOut(DropOutPercentage);

     // train the network and display the result (error)
     Print("Training result: ", net.train(sys, target, Epochs, Accuracy));
     ...

Usaremos una clase de red con visualización, como resultado de lo cual el progreso del aprendizaje se hará visible en el gráfico. Después del entrenamiento, podremos eliminar manualmente el objeto de imagen cuando ya no sea necesario. Al descargar el asesor experto, la imagen se eliminará automáticamente.

A continuación, deberemos leer las mejores matrices de pesos de la red. Además, verificaremos la capacidad de recrear con éxito la red utilizando estos pesos y probaremos su rendimiento con los mismos datos.

     matrix w[];
     if(net.getBestWeights(w))
     {
        MatrixNet net2(w);
        if(net2.isReady())
        {
           Print("Best result: ", net2.test(sys, target));
           ...
        }
     }
     return net;
  }

Finalmente, la red se almacenará en un archivo junto con una línea especialmente preparada que describirá las condiciones de entrenamiento: el intervalo de la historia, la lista de símbolos y el marco temporal, el tamaño de los datos, la configuración de la red.

        // the most important or all EA settings can be added to the network file
        const string context = StringFormat("\r\n%s %s %s-%s", _Symbol, EnumToString(_Period),
           TimeToString(start), TimeToString(iTime(_Symbol, _Period, 0))) + "\r\n" +
           Symbols + "\r\n" + (string)Depth + "/" + (string)Reserve + "\r\n" +
           (string)Epochs + "/" + (string)Accuracy + "\r\n" +
           (string)HiddenLayerFactor + "/" + (string)DropOutPercentage + "\r\n";
           
        // prepare a temporary file name
        const string tempfile = "bpnnmtmp" + (string)GetTickCount64() + ".bpn";
        
        // save the network and user data to a file
        MatrixNetStore store;                                   // main class unloading/loading the networks
        BinFileNetStorage writer(context, net.getStats(), std); // optional class wit hour information
        store.save(tempfile, *net, &writer);
        ...

La clase BinFileNetStorage mencionada aquí es específica de nuestro asesor experto y, al usar los métodos de almacenamiento/restauración redefinidos (la interfaz principal Storage), procesará nuestra descripción adicional, el valor de normalización (será necesario para el trabajo regular en nuevos datos), también como estadísticas de entrenamiento en forma de estructura MatrixNet::Stats (las mostramos arriba).

Además, el comportamiento del asesor dependerá de si funciona en el modo de optimización o no. Al realizar la optimización, enviaremos el archivo de red desde el agente al terminal usando el mecanismo de frames (ver código fuente). Estos archivos se almacenarán en la carpeta local MQL5/Files/, en la subcarpeta con el nombre del asesor.

        if(!MQLInfoInteger(MQL_OPTIMIZATION))
        {
           // set a new name in a more understandable time format, in the common folder
           string filename = "bpnnm" + TimeStamp((datetime)FileGetInteger(tempfile, FILE_MODIFY_DATE))
              + StringFormat("(%7g)", net.getStats().bestLoss) + ".bpn";
           if(!FileMove(tempfile, 0, filename, FILE_COMMON))
           {
              PrintFormat("Can't rename temp-file: %s [%d]", tempfile, _LastError);
           }
        }
        else
        {
           ... // the file will be sent from the agent to the terminal as a frame
        }

En los demás casos (pruebas simples o trabajo en línea), el archivo se trasladará a la carpeta común de los terminales. Esto se hace así para facilitar la carga posterior con ayuda del parámetro NetBinFileName. El hecho es que para trabajar en el simulador, necesitaríamos especificar la directiva #property tester_file en el código fuente con el nombre de archivo específico que planeamos introducir en el parámetro NetBinFileName y volver a compilar el asesor experto. Sin estas manipulaciones, el archivo de red no se copiará en el agente. Por consiguiente, resultará más práctico utilizar una carpeta compartida accesible desde todos los agentes locales.

La función LoadNet se implementará de la forma siguiente:

  MatrixNet *LoadNet(const string filename, double &std, const int flags = FILE_COMMON)
  {
     BinFileNetStorage reader; // optional user data
     MatrixNetStore store;     // general metadata
     MatrixNet *net;
     std = 1.0;
     Print("Loading ", filename);
     ResetLastError();
     net = store.load<MatrixNet>(filename, &reader, flags);
     if(net == NULL)
     {
        Print("Failed: ", _LastError);
        return NULL;
     }
     MatrixNet::Stats s[1];
     s[0] = reader.getStats();
     ArrayPrint(s);
     std = reader.getScale();
     Print(std);
     Print(reader.getDescription());
     return net;
  }

La función TradeTest llamará a Calc(0) para luego obtener el vector de los incrementos de precio reales.

  bool TradeTest(MatrixNet *net, const double std)
  {
     if(!Calc(0)) return false;
     double coefs[];
     for(int i = 0; i < Q; ++i)
     {
        double temp[];
        // difference on the 0th bar is ignored, it will be predicted
        /* double m = */Diff(CC[i].C, temp, true);
        ArrayCopy(coefs, temp, ArraySize(coefs), 0);
     }
      
     vector t;
     t.Assign(coefs);
      
     matrix data = {};
     data.Row(t, 0);
     data /= std;
     ...

Según el vector, la red deberá realizar un pronóstico, pero antes de ello, la posición abierta existente se cerrará forzosamente; aquí no se analizará la coincidencia de las direcciones nueva y antigua. El método ClosePosition usado para el cierre se mostrará a continuación. Luego, según los resultados de la pasada hacia delante de la red, abriremos una nueva posición en la dirección deseada.

     ClosePosition();
     
     if(net.feedForward(data))
     {
        matrix y = net.getResults();
        Print("Prediction: ", y[0][0] * std);
        
        OpenPosition((y[0][0] > 0) ? ORDER_TYPE_BUY : ORDER_TYPE_SELL);
        return true;
     }
     return false;
  }

Las funciones OpenPosition y ClosePosition se implementarán de manera similar. Mostraremos solo ClosePosition.

  bool ClosePosition()
  {
     // define an empty structure
     MqlTradeRequest request = {};
     
     if(!PositionSelect(_Symbol)) return false;
     const string pl = StringFormat("%+.2f", PositionGetDouble(POSITION_PROFIT));
     
     // fill in the required fields
     request.action = TRADE_ACTION_DEAL;
     request.position = PositionGetInteger(POSITION_TICKET);
     const ENUM_ORDER_TYPE type = (ENUM_ORDER_TYPE)(PositionGetInteger(POSITION_TYPE) ^ 1);
     request.type = type;
     request.price = SymbolInfoDouble(_Symbol, type == ORDER_TYPE_BUY ? SYMBOL_ASK : SYMBOL_BID);
     request.volume = PositionGetDouble(POSITION_VOLUME);
     request.deviation = 5;
     request.comment = pl;
     
     // send request
     ResetLastError();
     MqlTradeResult result[1];
     const bool ok = OrderSend(request, result[0]);
     
     Print("Status: ", _LastError, ", P/L: ", pl);
     ArrayPrint(result);
     
     if(ok && (result[0].retcode == TRADE_RETCODE_DONE
            || result[0].retcode == TRADE_RETCODE_PLACED))
     {
        return true;
     }
     
     return false;
  }

Ha llegado el momento de la investigación práctica. Ejecutaremos el asesor en el simulador con la configuración predeterminada, en el gráfico XAGUSD,D1, y en el modo de precios de apertura. Asimismo, estableceremos como fecha de inicio de la prueba el 01.01.2022. Esto significa que inmediatamente después de iniciar el asesor experto, la red comenzará a entrenarse con los precios del año anterior, el 2021, y luego comerciará según sus señales. Para ver el gráfico de cambios de error por épocas, el simulador deberá ejecutarse en el modo visual.

El diario de registro contendrá entradas del siguiente tipo relacionadas con el entrenamiento de la RN.

  Sufficient bars at: 2022.01.04 00:00:00
  Normalization by 3 std: 1.3415995381755823
  15 30 30 21  1
  EMA for early stopping: 31 (0.062500)
  Epoch 0 of 1000, loss 2.04525 ma(2.04525)
  Epoch 121 of 1000, loss 0.31818 ma(0.36230)
  Epoch 243 of 1000, loss 0.16857 ma(0.18029)
  Epoch 367 of 1000, loss 0.09157 ma(0.09709)
  Epoch 479 of 1000, loss 0.06454 ma(0.06888)
  Epoch 590 of 1000, loss 0.04875 ma(0.05092)
  Epoch 706 of 1000, loss 0.03659 ma(0.03806)
  Epoch 821 of 1000, loss 0.03043 ma(0.03138)
  Epoch 935 of 1000, loss 0.02721 ma(0.02697)
  Done by epoch limit 1000 with accuracy 0.024416
  Training result: 0.024416206367547762
  Best result: 0.024416206367547762
  Check-up of saved and restored copy: bpnnm202302121707(0.0244162).bpn
  Loading bpnnm202302121707(0.0244162).bpn
      [bestLoss] [bestEpoch] [trainingSet] [validationSet] [epochsDone]
  [0]      0.024         999           250               0         1000
  1.3415995381755823
     
  XAGUSD PERIOD_D1 2021.01.18 00:00-2022.01.04 00:00
  XAGUSD,XAUUSD,EURUSD
  5/250
  1000/0.0001
  2.0/0
     
  Best result restored: 0.024416206367547762

Por ahora, prestaremos atención a la magnitud del error final. Posteriormente, repetiremos la prueba con el modo "dropout" habilitado a diferentes intensidades y compararemos los resultados.

El informe comercial tiene el aspecto que sigue.

Ejemplo de informe comercial del pronóstico

Obviamente, durante la mayor parte de 2022, el comercio ha resultado insatisfactorio. No obstante, en el lado izquierdo, justo después de 2021 (que nos ha proporcionado la muestra de entrenamiento), hay un breve periodo rentable. Probablemente, los patrones encontrados por la red han continuado funcionando durante algún tiempo. Si esto es así, y si la configuración de la red o el conjunto de entrenamiento deben modificarse de alguna forma para mejorar el rendimiento, solo lo podremos averiguar para cada sistema comercial específico en el curso de una investigación exhaustiva. Hablamos de un trabajo muy minucioso que no está relacionado con la implementación interna de algoritmos de redes neuronales. Aquí nos limitaremos a un análisis mínimo.

El diario de registro nos comunica el nombre del archivo con la red entrenada. Lo introducimos en el simulador, en el parámetro NetBinFileName y ampliamos el tiempo de la prueba, a partir de 2021. En este modo, todos los parámetros de entrada, excepto los dos primeros (Symbols y Depth), no tienen importancia.

El comercio de prueba en un intervalo prolongado muestra la siguiente dinámica del balance (la muestra de entrenamiento está resaltada en amarillo).

Curva de balance al comerciar en un intervalo prolongado, incluida la muestra de entrenamiento

Como era de esperar, la red "ha aprendido" los detalles de un intervalo en particular, pero poco después de finalizar este deja de ser rentable.

Vamos a repetir el entrenamiento de la red dos veces: con un "dropout" de 25% y 50% (el parámetro DropOutPercentage deberá establecerse secuencialmente en 25 y luego en 50). Para iniciar el entrenamiento de las nuevas redes, borraremos el parámetro NetBinFileName, estableciendo nuevamente el inicio de la prueba en la fecha 2022.01.01.

Con un "dropout" del 25%, obtendremos un error notablemente mayor que en el primer caso. Pero esto era de esperar, ya que, volviendo el modelo más tosco, intentamos ampliar su aplicabilidad a los datos fuera de la muestra.

  Epoch 0 of 1000, loss 2.04525 ma(2.04525)
  Epoch 125 of 1000, loss 0.46777 ma(0.48644)
  Epoch 251 of 1000, loss 0.36113 ma(0.36982)
  Epoch 381 of 1000, loss 0.30045 ma(0.30557)
  Epoch 503 of 1000, loss 0.27245 ma(0.27566)
  Epoch 624 of 1000, loss 0.24399 ma(0.24698)
  Epoch 744 of 1000, loss 0.22291 ma(0.22590)
  Epoch 840 of 1000, loss 0.19507 ma(0.20062)
  Epoch 930 of 1000, loss 0.18931 ma(0.19018)
  Done by epoch limit 1000 with accuracy 0.182581
  Training result: 0.18258059873803228

Con un "dropout" del 50%, el error aumenta aún más.

  Epoch 0 of 1000, loss 2.04525 ma(2.04525)
  Epoch 118 of 1000, loss 0.54929 ma(0.55782)
  Epoch 242 of 1000, loss 0.43541 ma(0.45008)
  Epoch 367 of 1000, loss 0.38081 ma(0.38477)
  Epoch 491 of 1000, loss 0.34920 ma(0.35316)
  Epoch 611 of 1000, loss 0.30940 ma(0.31467)
  Epoch 729 of 1000, loss 0.29559 ma(0.29751)
  Epoch 842 of 1000, loss 0.27465 ma(0.27760)
  Epoch 956 of 1000, loss 0.25901 ma(0.26199)
  Done by epoch limit 1000 with accuracy 0.251914
  Training result: 0.25191436104184456

La siguiente imagen combina los gráficos de entrenamiento en las 3 opciones.

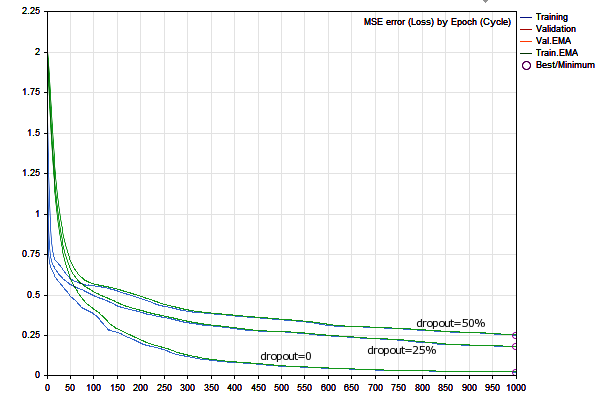
Dinámicas de aprendizaje con diferentes valores de dropout

Y aquí tenemos las curvas de balance (la muestra de entrenamiento está resaltada en amarillo).

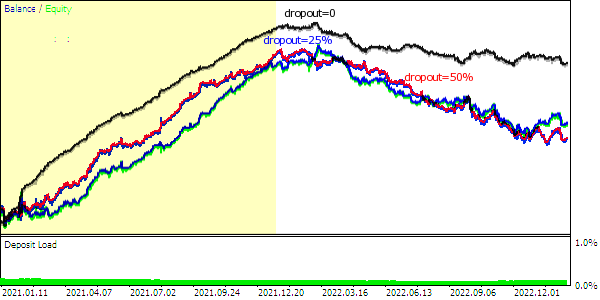
Curvas de balances comerciales según los pronósticos de las redes con diferente dropout

Debido a la desconexión aleatoria de los pesos durante el "dropout", la línea de balance durante el periodo de entrenamiento no es tan estable como en la red completa y, por supuesto, el beneficio total disminuye.

En este experimento, todas las opciones pierden rápidamente el contacto con el mercado (en un mes o dos), pero la esencia del experimento consistía en probar las herramientas de red neuronal creadas, no en desarrollar un sistema completo.

En general, el valor promedio de "dropout" del 25 % parece ser el óptimo, porque un menor grado de regularización nos lleva de vuelta al sobreajuste, mientras que un mayor grado destruye las capacidades computacionales de la red. No obstante, la conclusión principal que podemos sacar de forma preliminar es que el enfoque de red neuronal no representa una panacea capaz de "sacar adelante" cualquier sistema comercial. Los motivos del fracaso pueden provenir tanto de suposiciones incorrectas sobre la presencia de dependencias específicas como de los parámetros de diferentes módulos del algoritmo y la preparación de datos.

Antes de descartar este (o cualquier otro) sistema comercial, deberíamos probar varias formas de encontrar la mejor configuración para la red, como solemos hacer para las configuraciones de los asesores sin IA. Para sacar conclusiones bien condicionadas, necesitaríamos recopilar muchas más estadísticas.

En concreto, podemos buscar otros grupos de símbolos o marcos temporales, ejecutar la optimización con las variables públicas disponibles actualmente o expandir su lista (por ejemplo, según funciones de activación, métodos de generación de vectores, filtrado por días de la semana, etc.).

En este sentido, el uso de RN no libera de ninguna forma al tráder de la tarea de generar hipótesis, probar ideas y factores significativos. La única diferencia es que la optimización de la configuración del sistema comercial se complementará con los metaparámetros de la RN.

Como experimento, ejecutaremos optimizaciones en relación con el tamaño del vector, la cantidad de vectores, el factor de tamaño de la capa oculta y el "dropout". Además, incluiremos en la optimización el parámetro Randomizer; esto nos permitirá generar varios ejemplares de redes para cada combinación de otras configuraciones.

• Vector size (Depth) — 1 a 5
• Training set (Reserve) — de 50 a 400 en incrementos de 50
• Hidden Layer Factor — de 1 a 5
• DropOut — 0, 25%, 50%
• Randomizer — de 0 a 9

Adjuntamos un archivo con la configuración. El intervalo de fechas va del 01.01.2022 al 15.02.2023.

Elegiremos, por ejemplo, Profit Factor como criterio de optimización, aunque dado el pequeño número de combinaciones (6000) y su iteración completa (a diferencia de la genética), esto no resulta importante.

El análisis de los resultados de la optimización se puede realizar exportando la información a un archivo XML o directamente usando un archivo opt, por ejemplo, como se propone en el programa OLAP del artículo Análisis cuantitativo y visual de los informes del Simulador de estrategias o usando otros scripts (el formato opt es abierto).

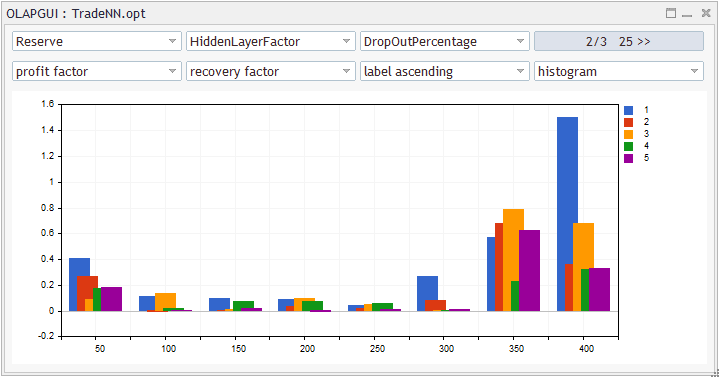
Análisis estadístico del informe de optimización

Para esta captura de pantalla, la adición de indicadores en las divisiones solicitadas (Reserve en X - eje horizontal, HiddenLayerFactor en Y - representado a color, y DropOutPercentage del 25% en Z) se ha realizado usando un cálculo específico del factor de beneficio (por celdas en los ejes X/Y/Z) a partir del factor de recuperación (de cada pasada del simulador en el contexto de la optimización). Esta medida artificial de la calidad no es perfecta, pero está disponible en formato "lista para usar".

Podemos calcular estadísticas similares o más familiares en Excel.

Estadísticamente, resulta más ventajoso un factor de capas ocultas de 1 (en lugar de 2, como estaba por defecto) y un tamaño de vector de 4 (en lugar de 5). En este caso, el valor de "dropout" recomendado será 25% o 50%, pero no 0%.

Además, como era de esperar, resulta preferible una historia más profunda (350 o 400 recuentos, y probablemente esté justificado un mayor aumento).

Vamos a resumir las configuraciones de trabajo encontradas:

• Vector size = 4
• Training set = 400
• Hidden Layer Factor = 1

Como el parámetro Randomizer ha estado involucrado en la optimización, tendremos 30 ejemplares de red entrenados con esta configuración: 10 redes para cada nivel de "dropout" (0%, 25%, 50%). Necesitaremos las del 25% y el 50%. Descargando el informe de optimización en XML, podremos filtrar las entradas necesarias y obtener una tabla (clasificada según la rentabilidad con un filtro mayor a 1):

Pass    Result  Profit  Expected Profit  Recovery Sharpe Custom  Equity Trades Depth  Reserve Hidden  DropOut Randomizer
			Payoff	 Factor	 Factor	 Ratio	 	 DD %			      LayerF	Perc
3838    1.35    336.02  2.41741  1.34991 1.98582 1.20187 1       1.61    139     4       400     1       25      6
838     1.23    234.40  1.68633  1.23117 0.81474 0.86474 1       2.77    139     4       400     1       25      1
3438    1.20    209.34  1.50604  1.20481 0.81329 0.78140 1       2.47    139     4       400     1       50      5
5838    1.17    173.88  1.25094  1.16758 0.61594 0.62326 1       2.76    139     4       400     1       50      9
5038    1.16    167.98  1.20849  1.16070 0.51542 0.60483 1       3.18    139     4       400     1       25      8
3238    1.13    141.35  1.01691  1.13314 0.46758 0.48160 1       2.95    139     4       400     1       25      5
2038    1.11    118.49  0.85245  1.11088 0.38826 0.41380 1       2.96    139     4       400     1       25      3
4038    1.10    107.46  0.77309  1.09951 0.49377 0.38716 1       2.12    139     4       400     1       50      6
1438    1.10    104.52  0.75194  1.09700 0.51681 0.37404 1       1.99    139     4       400     1       25      2
238     1.07    73.33   0.52755  1.06721 0.19040 0.26499 1       3.69    139     4       400     1       25      0
2838    1.03    34.62   0.24907  1.03111 0.10290 0.13053 1       3.29    139     4       400     1       50      4
2238    1.02    21.62   0.15554  1.01927 0.05130 0.07578 1       4.12    139     4       400     1       50      3

Tomaremos la mejor, la primera línea.

Recuerde que durante la optimización, todas las redes entrenadas se guardarán en la carpeta MQL5/Files/<nombre del experto>/<fecha de optimización>. En principio, esto se puede omitir, puesto que podemos volver a entrenar una red similar según el valor Randomizer, pero solo si los datos de entrada coinciden por completo. Si la historia de cotizaciones cambia (por ejemplo, tenemos otro bróker), no será posible reproducir la red con estas características exactamente.

Los archivos en la carpeta indicada tienen denominaciones que constan de los nombres y los valores de los parámetros optimizados. Por lo tanto, bastará con buscar en el sistema de archivos:

Depth=4-Reserve=400-HiddenLayerFactor=1-DropOutPercentage=25-Randomizer=6

Digamos que el archivo tiene el nombre:

Depth=4-Reserve=400-HiddenLayerFactor=1-DropOutPercentage=25-Randomizer=6-3838(0.428079).bpn

donde el número entre paréntesis será el error de red, mientras que el número delante de los paréntesis será el número de pasada.

Echemos un vistazo dentro del archivo: a pesar de que el archivo es binario, nuestros metadatos de entrenamiento se guardan como texto al final, concretamente, se indica que el intervalo de entrenamiento ha sido 2021.01.12 00:00-2022.07.28 00:00 (400 barras D1).

Ahora copiaremos un archivo con un nombre más corto, por ejemplo, test3838.bpn, en la carpeta general de los terminales.

Luego introduciremos el nombre test3838.bpn en el parámetro NetBinFileName y en el parámetro Vector size (Depth) - 4 (todos los demás parámetros no son de importancia si el trabajo se realiza exclusivamente en modo de pronóstico).

Después verificaremos el comercio del asesor experto en un periodo aún más largo: dado que el periodo 2022-2023 ha ejercido de prueba forward de validación, capturaremos el año 2020 como periodo desconocido.

Ejemplo de prueba de negociación predictiva fallida fuera de la muestra de entrenamiento

El milagro no ha tenido lugar: el sistema no resulta rentable con los datos "nuevos". Resulta sencillo ver que una imagen similar también es típica para otras configuraciones.

Entonces, tenemos dos noticias: una buena y otra mala.

La mala noticia es que la idea propuesta no funciona; tal vez no funcione en absoluto, o tal vez sea un artefacto derivado de las limitaciones del espacio de factores analizado en nuestro ejemplo demostrativo (después de todo, no hemos ejecutado una super-mega optimización para miles de millones de combinaciones y cientos de símbolos).

La buena noticia es que el kit de herramientas de redes neuronales que proponemos permite evaluar ideas y produce los resultados esperados (desde un punto de vista técnico).

Conclusión

Este artículo introduce clases de redes neuronales con propagación inversa del error en matrices MQL5. Su implementación no implica la dependencia de programas externos, como Python, ni firmware especial (aceleradores gráficos con soporte OpenCL). Además de los modos habituales de entrenamiento y posterior explotación de las redes, las clases ofrecen la visualización del proceso, así como el almacenamiento y la restauración de las redes usando archivos.

Gracias a estas clases, el uso de las redes neuronales se integra con bastante facilidad en cualquier programa, pero debemos recordar que la red es solo una herramienta aplicada a algún material (en nuestro caso, a los datos financieros). Si el material no contiene suficiente información, tiene demasiado ruido o resulta irrelevante, ninguna red neuronal podrá encontrar el Grial en él.

El algoritmo de propagación inversa del error es uno de los métodos básicos de aprendizaje más comunes a partir del cual se pueden construir tecnologías de redes neuronales más complejas: redes recurrentes, redes convolucionales y aprendizaje por refuerzo.