Recetas MQL5 - Programando los canales móviles
1 592
0
Introducción
Es bien sabido que la dirección del precio de mercado o bien puede ser expresada y aparece una tendencia en el gráfico, o bien puede estar ausente, y entonces el gráfico estará plano. Se considera que con tendencia plana funcionan bien los indicadores técnicos incluidos en la familia de los osciladores. Sin embargo, al darse una tendencia, puede existir un cierto diapasón dentro de cuyos límites oscilará el precio.
En esta artículo intentaré mostrar el método dinámico de construcción de los canales equidistantes, que con frecuencia son llamados móviles. Hay que decir que una de las estrategias más populares sobre esta tipo de canales es la de Víktor Barishpolets. Vamos a tocar los aspectos relacionados con las reglas de formación de los canales móviles. Asimismo, trataremos de ampliar estas normas, lo que, en opinión del autor, hará que el canal sea más flexible.
1. Normas de construcción del canal equidistante
Para comenzar, trabajaremos con los esquemas que constituirán la base de la programación del canal euquidistante. Llegados a este punto, yo recomendaría recurrir a la guía del instrumento técnico «Canal equidistante».
Como ya sabemos, el canal se construye a partir de tres puntos, cada uno de los cuales tiene coordenadas de precio y temporales. Para el canal prestaremos atención a las coordenadas temporales de los puntos, dado que su secuencia influye en el tipo de canal. Tomaremos como ejemplo un canal cuya línea principal se construye según dos mínimos locales. El tercer punto será el responsable del máximo local. La ubicación de los puntos puede servir como criterio para el tipado del canal.
Al dibujarse el canal no se usan ni rayos a la izquierda ni rayos a la derecha, si no se indica lo contrario.
El primer tipo se da en el caso de que aparezca primero un mínimo, después un máximo, y luego de nuevo un mínimo. Podemos imaginar esta situación de forma esquemática como en la fig.1.
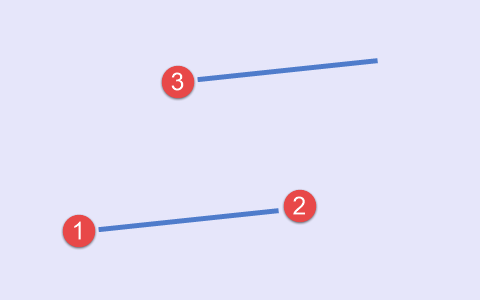
Fig.1 Primer tipo de conjunto de puntos, esquema
En el gráfico de precios, el primer tipo tiene el aspecto siguiente (Fig.2).
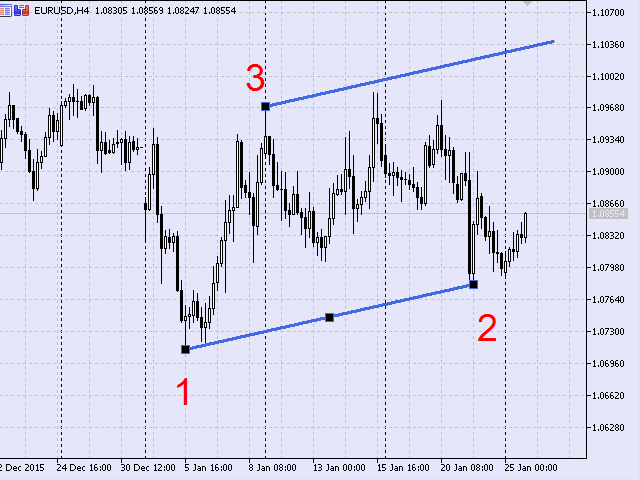
Fig.2 Primer tipo de conjunto de puntos, gráfico de precios
El segundo tipo se da cuando en el gráfico aparecen de forma consecutiva un máximo, un mínimo y de nuevo un mínimo (Fig.3).
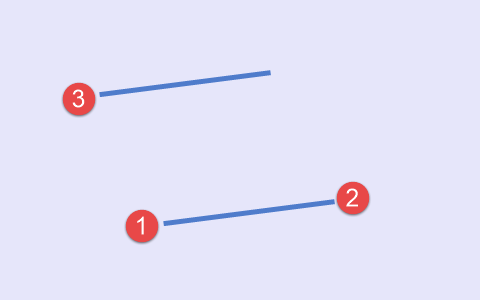
Fig.3 Segundo conjunto de puntos, esquema
El máximo local aparecido al principio se convertirá al final en el tercer punto. La pareja de mínimos que le siga, formará una nueva línea.
El tercer tipo se construye según el esquema «mínimo-mínimo-máximo». En este caso, la línea principal espera a que se forme el máximo local (Fig.4).
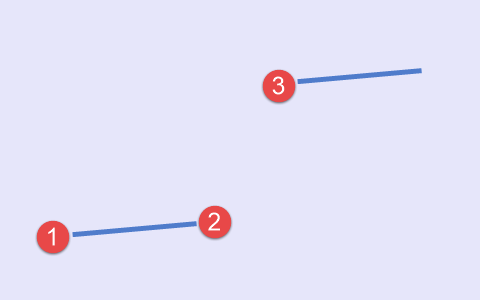
Fig.4 Tercer conjunto de puntos, esquema
Los dos últimos tipos son más bien casos especiales.
La cuarta variante resulta cuando el tiempo de construcción de los puntos tercero y primero coinciden. (Fig.5).
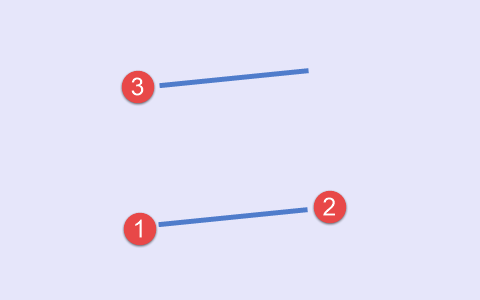
Fig.5 Cuarto conjunto de puntos, esquema
El quinto tipo se da cuando coinciden las coordenadas temporales del segundo y el tercer punto (Fig.6).
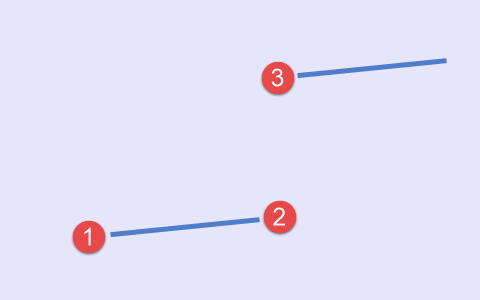
Fig.6 Quinto conjunto de puntos, esquema
Con estos cinco tipos de canales equidistantes vamos a trabajar. En el siguiente apartado intentaremos programar los puntos conforme a los que se construyen las líneas del canal.
2. Tipos auxiliares de datos
Con mayor frecuencia, los puntos que se toman para representar las líneas de tendencia del canal son los fractales. Entonces un punto así es al mismo tiempo una fractal y una base para conducir una línea recta.
Vamos a probar a generalizar y codificar los puntos fractales con la ayuda del instrumental POO.
2.1 Clase del punto fractal
La funcionalidad de esta clase es responsable del punto que se cuenta entre aquellos sobre los que se construye el canal equidistante.
Llamaremos a la clase indicada CFractalPoint y, en la mejor tradición del lenguaje MQL5, la ligaremos a la clase-interfaz CObject mediante una relación de herencia.
//+------------------------------------------------------------------+ //| Clase del punto fractal | //+------------------------------------------------------------------+ class CFractalPoint : public CObject { //--- === Data members === --- private: datetime m_date; // fecha y hora double m_value; // valor ENUM_EXTREMUM_TYPE m_extreme_type; // tipo de extremo int m_idx; // índice (de 0 a 2) //--- === Methods === --- public: //--- constructor/destructor void CFractalPoint(void); void CFractalPoint(datetime _date,double _value, ENUM_EXTREMUM_TYPE _extreme_type,int _idx); void ~CFractalPoint(void){}; //--- métodos-get datetime Date(void) const {return m_date;}; double Value(void) const {return m_value;}; ENUM_EXTREMUM_TYPE FractalType(void) const {return m_extreme_type;}; int Index(void) const {return m_idx;}; //--- métodos-get void Date(const datetime _date) {m_date=_date;}; void Value(const double _value) {m_value=_value;}; void FractalType(const ENUM_EXTREMUM_TYPE extreme_type) {m_extreme_type=extreme_type;}; void Index(const int _bar_idx){m_idx=_bar_idx;}; //--- servicio void Copy(const CFractalPoint &_source_frac); void Print(void); }; //+------------------------------------------------------------------+
La clase tiene cuatro miembros para transmitir los datos:
- m_date — coordenada temporal del punto en el gráfico;
- m_value — coordenada de precio del punto en el gráfico;
- m_extreme_type – tipo de extremo;
- m_idx - índice.
La enumeración ENUM_EXTREMUM_TYPE será la responsable del tipo de extremo:
//+------------------------------------------------------------------+ //| Tipo de extremo | //+------------------------------------------------------------------+ enum ENUM_EXTREMUM_TYPE { EXTREMUM_TYPE_MIN=0, // mínimo EXTREMUM_TYPE_MAX=1, // máximo };
La principal tarea de los métodos CFractalPoint es posibilitar la obtención o actualización de los valores de los miembos privados enumerados más arriba.
Por ejemplo, creamos de forma programática el punto fractal para la vela del 26.01.2016 08:00 en el gráfico EURUSD, H4, indicada en la Fig.7. El fractal se ha formado en el máximo de la vela a un precio de 1,08742.
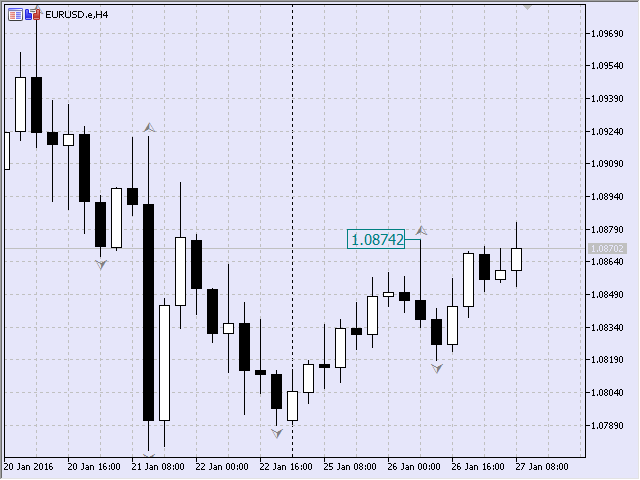
Fig.7 Ejemplo de fractal
Este es el aspecto que puede tener el código para desarrollar la tarea establecida.
//--- datos para el punto fractal datetime pnt_date=D'26.01.2016 08:00'; double pnt_val=1.08742; ENUM_EXTREMUM_TYPE pnt_type=EXTREMUM_TYPE_MAX; int pnt_idx=0; //--- Creación del punto fractal CFractalPoint myFracPoint(pnt_date,pnt_val,pnt_type,pnt_idx); myFracPoint.Print();
En el registro, obtendremos la siguiente impresión:
---=== Datos del punto fractal ===--- Fecha: 2016.01.26 08:00 Precio: 1.08742 Tipo: EXTREMUM_TYPE_MAX Índice: 0
Esta entrada significa que un punto fractal fue encontrado en la barra del 26 enero de 2016 a un precio de 1,08742. Este fractal es un máximo local. El índice cero señala que en un conjunto de puntos análogos, este será el primero.
2.2 Clase del conjunto de puntos fractales
Ahora podemos pasar a la creación de un conjunto de puntos fractales sobre cuya base precisamente construiremos el canal equidistante. Para ello, crearemos la clase CFractalSet, que detecrará y reunirá estos puntos en un conjunto.
Esta clase se incluirá entre los componentes del asesor, y no del indicador, por eso los canales pertenecerán, no a los búferes de indicador, sino a los objetos gráficos del tipo CChartObjectChannel.
La clase CFractalSet es hija de la clase de la Biblioteca estándar CArrayObj. He elegido un tipo de herencia protegida, para hacer la interfaz de la clase de una especialidad concreta.
//+------------------------------------------------------------------+ //| Clase del conjunto de puntos fractales | //+------------------------------------------------------------------+ class CFractalSet : protected CArrayObj { //--- === Data members === --- private: ENUM_SET_TYPE m_set_type; // tipo del conjunto de puntos int m_fractal_num; // número fijo de puntos int m_fractals_ha; // manejador del indicador de fractal CisNewBar m_new_bar; // objeto de la nueva barra CArrayObj m_channels_arr; // objeto de la matriz de índices color m_channel_colors[4]; // colores de los canales bool m_is_init; // bandera de inicialización //--- ajustes del canal int m_prev_frac_num; // fractales anteriores int m_bars_beside; // barras a la izquierda/derecha del fractal int m_bars_between; // número de barras intermedias bool m_to_delete_prev; // ¿Eliminar los canales anteriores? bool m_is_alt; // ¿indicador de fractales alternativo? ENUM_RELEVANT_EXTREMUM m_rel_frac; // punto actual bool m_is_array; // ¿dibujar el rayo? int m_line_wid; // grosor de la línea bool m_to_log; // ¿llevar un registro? //--- === Methods === --- public: //--- constructor/destructor void CFractalSet(void); void CFractalSet(const CFractalSet &_src_frac_set); void ~CFractalSet(void){}; //--- void operator=(const CFractalSet &_src_frac_set); //--- desarrolladores bool Init( int _prev_frac_num, int _bars_beside, int _bars_between=0, bool _to_delete_prev=true, bool _is_alt=false, ENUM_RELEVANT_EXTREMUM _rel_frac=RELEVANT_EXTREMUM_PREV, bool _is_arr=false, int _line_wid=3, bool _to_log=true ); void Deinit(void); void Process(void); //--- servicio CChartObjectChannel *GetChannelByIdx(const int _ch_idx); int ChannelsTotal(void) const {return m_channels_arr.Total();}; private: int AddFrac(const int _buff_len); int CheckSet(const SFracData &_fractals[]); ENUM_SET_TYPE GetTypeOfSet(void) const {return m_set_type;}; void SetTypeOfSet(const ENUM_SET_TYPE _set_type) {m_set_type=_set_type;}; bool PlotChannel(void); bool Crop(const uint _num_to_crop); void BubbleSort(void); }; //+------------------------------------------------------------------+
Enumeramos los miembros para esta clase.
- m_set_type – tipo de conjunto de puntos. Más abajo analizamos la enumeración responsable de la clasificación de los conjuntos;
- m_fractal_num – número fijo de puntos que entran en el conjunto;
- m_fractals_ha – manejador del indicador de fractal;
- m_new_bar – objeto de la nueva barra;
- m_channels_arr – objeto de la matriz de índices;
- m_channel_colors[4] — matriz de colores para la representación de los canales;
- m_is_init — bandera de inicialización.
A continuación va el bloque de miembros responsables de los ajustes del canal. - m_prev_frac_num — número de fractales anteriores usados para construir el primer canal de todos. Si hay 3 puntos, entonces el canal se construye inmediatamente después de la inicialización;
- m_bars_beside — número de barras a la izquierda/derecha del fractal. Si indicamos, por ejemplo, 5, entonces para la búsqueda del fractal se emplearán 11 barras;
- m_bars_between — número de barras intermedias. Es decir, se trata de una especie de mínimo de las barras que deben estar presentes entre puntos fractales colindantes;
- m_to_delete_prev — permiso para eliminar los canales anteriores;
- m_is_alt — bandera para el uso de un indicador de fractales alternativo;
- m_rel_frac — elegir el punto actual. Si no ha habido suficientes barras intermedias, entonces el tipo de este punto indicará qué barra hay que ignorar;
- m_is_array — bandera de dibujado del rayo;
- m_line_wid — grosor de la línea;
- m_to_log — bandera de logging.
La enumeración que procesa los tipos de conjunto de puntos, se presenta de la siguiente forma:
//+------------------------------------------------------------------+ //| Tipo de conjunto de puntos extremos | //+------------------------------------------------------------------+ enum ENUM_SET_TYPE { SET_TYPE_NONE=0, // no establecido SET_TYPE_MINMAX=1, // mín-máx-mín SET_TYPE_MAXMIN=2, // máx-mín-máx };
En este ejemplo, el valor de SET_TYPE_MAXMIN corresponde a esta secuencia de puntos fractales (Fig.8).
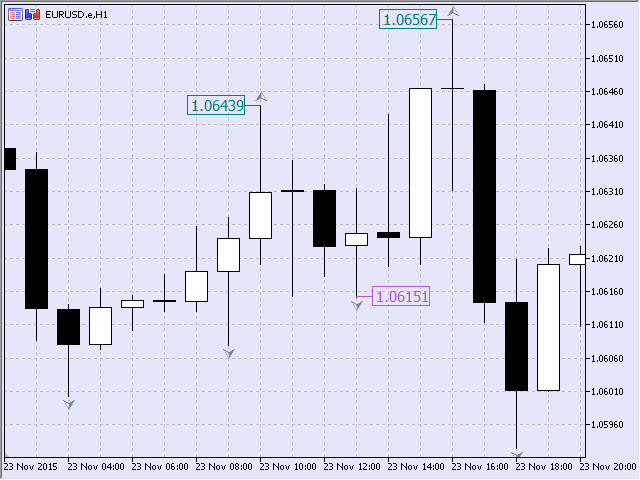
Fig.8 Conjunto del tipo «máx-mín-máx»
Mencionaré de inmediato que la secuencia de los puntos no siempre se logra respetar. A veces resulta que tras un mínimo llega otro más. Como ejemplo, podemos recordar el tercer tipo de conjunto de puntos, descrito en el primer apartado (Fig.4). En cualquier caso, consideraremos que nuestro conjunto está completo si en él se contiene, o bien una pareja de mínimos y un máximo, o bien una pareja de máximos y un mínimo.
La enumeración que procesa los tipos del punto vigente tiene el aspecto que sigue:
//+------------------------------------------------------------------+ //| Tipo de punto vigente | //+------------------------------------------------------------------+ enum ENUM_RELEVANT_EXTREMUM { RELEVANT_EXTREMUM_PREV=0, // anterior RELEVANT_EXTREMUM_LAST=1, // último };
Vamos a pasar a los métodos. Primero vamos a enumerar los manejadores.
- Init() – realiza la inicialización del conjunto. El método es responsable del correcto inicio del funcionamiento del objeto, que representa un conjunto de puntos fractales.
- Deinit() - realiza la desinicialización del conjunto.
- Process() – controla el flujo de precios. En esencia, precisamente este método identifica los puntos y representa el canal.
Métodos de servicio:
- AddFrac() — añade puntos fractales al conjunto.
- CheckSet() – comprueba el estado actual del conjunto.
- PlotChannel() – dibuja el canal equidistante.
- Crop() – recorta el conjunto.
- BubbleSort() — clasifica los puntos en el conjunto según el tiempo de aparición.
2.3 Posibilidades adicionales de la construcción del canal
Recordaré de nuevo que para construir el canal y recurrir a sus propiedades se ha usado la clase de la Biblioteca estándar CChartObjectChannel. Analizaremos ciertos momentos cuya implementación algorítmica puede hacer más flexible el sistema de construcción automática de los canales.
2.3.1 Sincronización de las líneas
Lo más cómodo será la valoración visual del gráfico con los canales en el momento en el que ambas líneas del canal comiencen en la misma barra. Formalmente, a ese enfoque le corresponde el cuarto tipo de canal (Fig.5). Naturalmente, los canales pueden pertenecer también a otros tipos. Por eso en el método CFractalSet::PlotChannel() las coordenadas de tiempo y precio de los puntos fractales se modifican para que el tipo de canal sea el cuarto. Además, en este caso es importante (esto está implementado) que se conserve la inclinación del canal y su anchura.
Veamos el siguiente canal equidistante en el gráfico de precio (Fig.9).
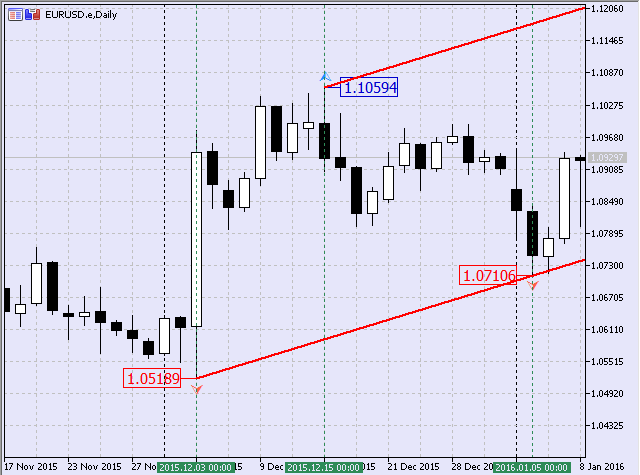
Fig.9 Canal equidistante según puntos de origen
Mencionaré de inmediato que se ha construido de forma manual. Aquí existen los siguientes puntos fractales:
- $1.05189 de 2015.12.03 (mínimo);
- $1.07106 de 2016.01.05 (mínimo);
- $1.10594 de 2016.01.05 (máximo).
Si queremos representar un canal así con la ayuda de la clase CFractalSet, entonces obtendremos la siguiente imagen (fig.10).
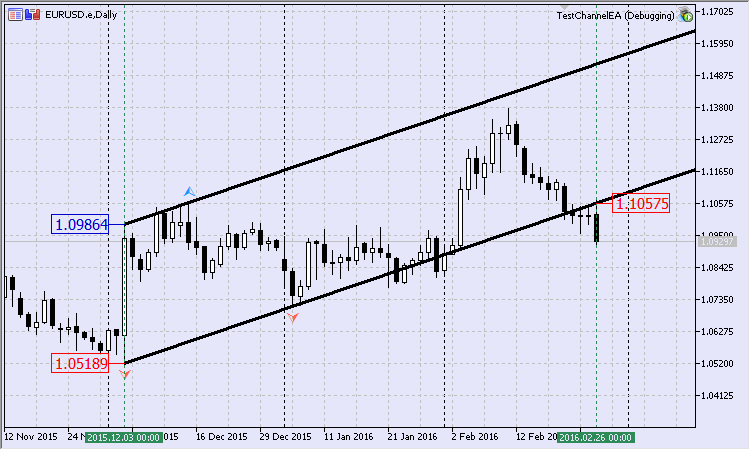
Fig.10 Canal equidistante según puntos calculados
La diferencia, aunque sea poco significativa, es que en la Fig.10 la construcción del canal se da conforme a los puntos calculados. Se calcula el valor de precio y el valor temporal de los puntos segundo y tercero. El último punto deberá coincidir con el primero según su coordenada temporal.
He dividido en 2 partes la tarea de dibujar el canal según los puntos calculados.
La primera parte está relacionada con las coordenadas temporales, se determinan el inicio y el final del canal. En el método indicado hay un bloque de código con el aspecto siguiente:
//--- 1) coordenadas de tiempo //--- inicio del canal int first_date_idx=ArrayMinimum(times); if(first_date_idx<0) { Print("¡Error al obtener la coordenada de tiempo!"); m_channels_arr.Delete(m_channels_arr.Total()-1); return false; } datetime first_point_date=times[first_date_idx]; //--- final del canal datetime dates[]; if(CopyTime(_Symbol,_Period,0,1,dates)!=1) { Print("¡Error al obtener el tiempo de la última barra!"); m_channels_arr.Delete(m_channels_arr.Total()-1); return false; } datetime last_point_date=dates[0];
De esta forma, todos los puntos tendrán los siguientes valores de coordenas de tiempo:
//--- coordenadas de tiempo finales times[0]=times[2]=first_point_date; times[1]=last_point_date;
La segunda parte de la tarea está relacionada con las coordenadas de precio, se determina el nuevo precio o bien para el tercer punto, o bien para el primero.
En primer lugar determinamos cuán rápido cambia el precio de las líneas del canal de una barra a otra y hacia dónde se dirige el propio canal: hacia arriba o hacia abajo.
//--- 2) coordenadas de precio //--- 2.1 inclinación de la línea //--- barras entre el los puntos primero y segundo datetime bars_dates[]; int bars_between=CopyTime(_Symbol,_Period, times[0],times[1],bars_dates ); if(bars_between<2) { Print("¡Error al obtener el número de barras entre los puntos!"); m_channels_arr.Delete(m_channels_arr.Total()-1); return false; } bars_between-=1; //--- diferencial total double price_differential=MathAbs(prices[0]-prices[1]); //--- velocidad del precio (cambio de precio en la primera barra) double price_speed=price_differential/bars_between; //--- dirección del canal bool is_up=(prices[0]<prices[1]);
Ahora se pueden actualizar las coordenadas de precio de los puntos. Aquí es importante saber qué punto se ha formado antes. Además, hay que saber en qué dirección apunta el canal, hacia arriba o hacia abajo:
//--- 2.2 nuevo precio de los puntos primero y tercero if(times[0]!=times[2]) { datetime start,end; start=times[0]; end=times[2]; //--- si el tercer punto está antes del primero bool is_3_point_earlier=false; if(times[2]<times[0]) { start=times[2]; end=times[0]; is_3_point_earlier=true; } //--- barras entre el primer y el tercer punto int bars_between_1_3=CopyTime(_Symbol,_Period, start,end,bars_dates ); if(bars_between_1_3<2) { Print("¡Error al obtener el número de barras entre los puntos!"); m_channels_arr.Delete(m_channels_arr.Total()-1); return false; } bars_between_1_3-=1; //--- si el canal es ascendente if(is_up) { //--- si el tercer punto estaba antes if(is_3_point_earlier) prices[0]-=(bars_between_1_3*price_speed); else prices[2]-=(bars_between_1_3*price_speed); } //--- o si el canal es descendente else { //--- si el tercer punto estaba antes if(is_3_point_earlier) prices[0]+=(bars_between_1_3*price_speed); else prices[2]+=(bars_between_1_3*price_speed); } }En nuestro ejemplo anterior se formó el primer punto, significa que hay que actualizar el precio del tercero.
Y al final actualizamos las coordenadas del segundo punto:
//--- 2.3 nuevo precio del segundo punto if(times[1]<last_point_date) { datetime dates_for_last_bar[]; //--- barras entre el segundo punto y la última barra bars_between=CopyTime(_Symbol,_Period,times[1],last_point_date,dates_for_last_bar); if(bars_between<2) { Print("¡Error al obtener el número de barras entre los puntos!"); m_channels_arr.Delete(m_channels_arr.Total()-1); return false; } bars_between-=1; //--- si el canal es ascendente if(is_up) prices[1]+=(bars_between*price_speed); //--- o si el canal es descendente else prices[1]-=(bars_between*price_speed); }
Entonces obtenemos:
- $1.05189 de 2015.12.03 (mínimo);
- $1.10575 de 2016.02.26 (valor calculado);
- $1.09864 de 2015.12.03 (valor calculado).
El canal puede dibujarse tanto sin utilizar rayos a la derecha, como con ellos. Sin embargo, esta opción se relaciona solo con el canal actual. Todos los objetos anteriores de los canales en el gráfico estarán sin rayo a la derecha.
2.3.2 Registro de los puntos fractales anteriores
A la clase CFractalSet se ha añadido la opción de recurrir a la historia y buscar allí puntos fractales según los parámetros establecidos. Esa posibilidad se usa solo al inicializar el ejemplar de la clase. Recordemos que de la cantidad de "puntos del pasado" (puede haber de 0 a 3) es responsable el miembro m_prev_frac_num.
Veamos un ejemplo (Fig.11). Supongamos que directamente al inicializar el asesor TestChannelEA hay que encontrar varios puntos fractales en el gráfico. Esos pueden ser los fractales designados con las cifras correspondientes.
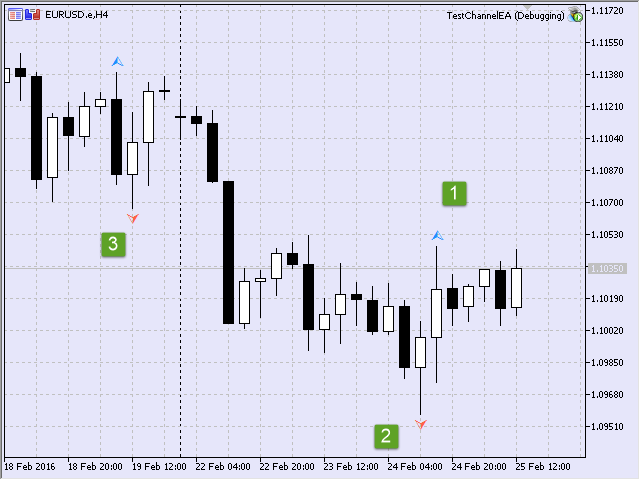
Fig.11 Puntos fractales durante la inicialización
Si tomamos los tres puntos, entonces construiremos el canal (Fig.12).
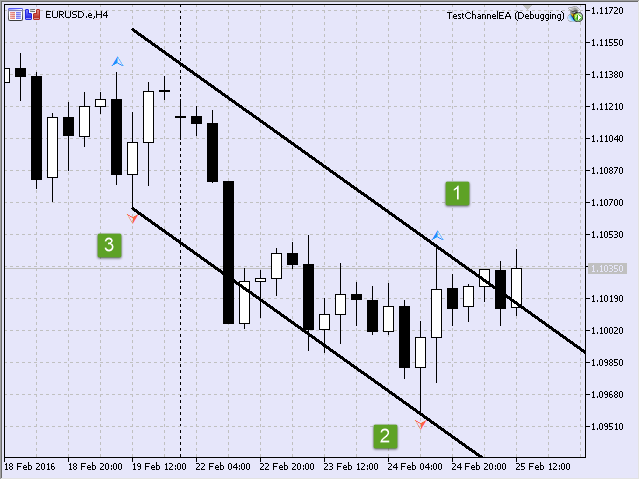
Fig.12 Primer canal construido durante la inicialización
En el registro vemos la entrada:
2016.02.25 15:49:23.248 TestChannelEA (EURUSD.e,H4) Se han añadido los fractales anteriores: 3
No resulta complicado notar que los puntos se añaden al conjunto de derecha a izquierda. Y el canal se construye según los puntos que se deben reunir de izquierda a derecha. El método privado CFractalSet::BubbleSort() permite precisamente ordenar los puntos antes de que el propio canal se dibuje.
El bloque de código responsable del conjunto de puntos al realizarse la inicialización en el método CFractalSet::Init(), se muestra de la siguiente forma:
//--- si se añaden los puntos fractales anteriores if(m_prev_frac_num>0) { //--- 1) Carga de la historia [start] bool synchronized=false; //--- contador del ciclo int attempts=0; //--- 10 intentos para esperar la sincronización while(attempts<10) { if(SeriesInfoInteger(_Symbol,0,SERIES_SYNCHRONIZED)) { synchronized=true; //--- hay sincronización, salimos break; } //--- aumentamos el contador attempts++; //--- esperamos 50 milisegundos hasta la siguiente iteración Sleep(50); } //--- if(!synchronized) { Print("No se ha logrado obtener el número de barras en ",_Symbol); return false; } int curr_bars_num=Bars(_Symbol,_Period); if(curr_bars_num>0) { PrintFormat("Número de barras en la historia del terminal según el símbolo-periodo en este momento: %d", curr_bars_num); } //--- 1) Carga de la historia [end] //--- 2) Datos calculados para el indicador solicitado [start] double Ups[]; int i,copied=CopyBuffer(m_fractals_ha,0,0,curr_bars_num,Ups); if(copied<=0) { Sleep(50); for(i=0;i<100;i++) { if(BarsCalculated(m_fractals_ha)>0) break; Sleep(50); } copied=CopyBuffer(m_fractals_ha,0,0,curr_bars_num,Ups); if(copied<=0) { Print("No se ha logrado copiar los fractales superiores. Error = ",GetLastError(), "i=",i," copied= ",copied); return false; } else { if(m_to_log) Print("Se ha logrado copiar los fractales superiores.", " i = ",i," copied = ",copied); } } else { if(m_to_log) Print("Se ha logrado copiar los fractales superiores. ArraySize = ",ArraySize(Ups)); } //--- 2) Datos calculados para el indicador solicitado [end] //--- 3) Adición de puntos fractales [start] int prev_fracs_num=AddFrac(curr_bars_num-1); if(m_to_log) if(prev_fracs_num>0) PrintFormat("Fractales anteriores añadidos: %d",prev_fracs_num); //--- si se puede representar el canal if(prev_fracs_num==3) if(!this.PlotChannel()) Print("¡No se ha logrado representar el canal!"); //--- 3) Adición de puntos fractales [end] }
Se puede dividir en 3 bloques menores:
- carga de la historia de las cotizaciones;
- cálculo de los datos del indicador de fractal;
- adición de puntos fractales al conjunto.
De esta forma, en el momento de inicialización se puede dibujar el canal. Esto exigirá cierto tiempo, especialmente en los casos en que los datos del gráfico no estén sincronizados con los del servidor.
2.3.3 Registro de las barras entre puntos fractales colindantes
En los gráficos anteriores, los puntos fractales usados (el primero y el segundo, así como el tercero y el cuarto) se encuentran uno junto a otro. Se puede añadir una especie de filtro, que cribará los puntos más cercanos. Puede adoptar ese papel el miembro m_bars_between, el número de barras intermedias entre puntos colindantes. Si establecemos este número como igual a 1, entonces el segundo punto no entrará en el conjunto, y su lugar lo ocupará aquel que sea actualmente el tercero.
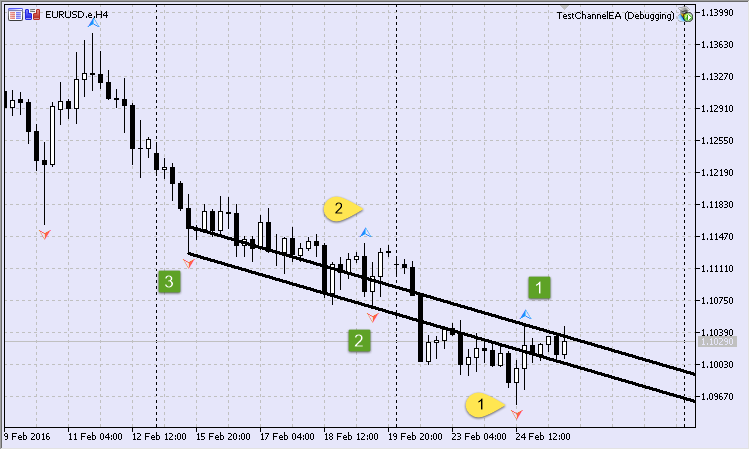
Fig.13 Primer canal, teniendo en cuenta las barras intermedias
Construimos el canal con la condición de que entre los puntos colindantes haya como mínimo 1 barra (Fig.13). Resulta que hay que dejar pasar el punto que sigue al primero, y el punto que sigue al segundo. Se destacan con rótulos amarillos.
Por ejemplo, al realizar el logging, el primer punto que se ignora tendrá la siguiente entrada en el registro:
2016.02.25 16:11:48.037 TestChannelEA (EURUSD.e,H4) El punto anterior será ignorado: 2016.02.24 12:00 2016.02.25 16:11:48.037 TestChannelEA (EURUSD.e,H4) Las barras intermedias son insuficientes. Se ignorará un punto.
Entonces el canal buscado se estrechará y, probablemente, no se convertirá en especialmente funcional desde el punto de vista del tráder.
En lo que respecta al código, la comprobación del número permitido de barras intermedias se realiza en el cuerpo del método privado CFractalSet::CheckSet().
//--- si comprobamos el número de barras entre el último punto y el actual if(m_bars_between>0) { curr_fractal_num=this.Total(); if(curr_fractal_num>0) { CFractalPoint *ptr_prev_frac=this.At(curr_fractal_num-1); if(CheckPointer(ptr_prev_frac)!=POINTER_DYNAMIC) { Print("¡Error al obtener un objeto de punto fractal del conjunto!"); return -1; } datetime time1,time2; time1=ptr_prev_frac.Date(); time2=ptr_temp_frac.Date(); //--- barras entre puntos datetime bars_dates[]; int bars_between=CopyTime(_Symbol,_Period, time1,time2,bars_dates ); if(bars_between<0) { Print("¡Error al obtener los datos de tiempo de apertura de las barras!"); return -1; } bars_between-=2; //--- si es en barras diferentes if(bars_between>=0) //--- si las barras intermedias son insuficientes if(bars_between<m_bars_between) { bool to_delete_frac=false; if(m_to_log) Print("Las barras intermedias son insuficientes. Se ignorará un punto."); // ... } } }
La variable bars_between adopta el número de barras entre dos puntos fractales colindantes. Si el valor es inferior al permitido, el punto es ignorado. Cuál precisamente — el actual o el anterior — lo sabremos en el siguiente apartado.
2.3.4 Elegir el punto fractal vigente
En caso de que las barras intermedias sean insufcientes y uno de los puntos deba ser ignorado, se puede indicar qué punto precisamente se ignorará. En el ejemplo de más arriba, se ha ignorado el punto más antiguo teniendo en cuenta el tiempo, dado que el último punto fractal se consideraba el vigente. Vamos a convertir el punto vigente en anterior y veamos qué es lo que resulta (Fig.14).
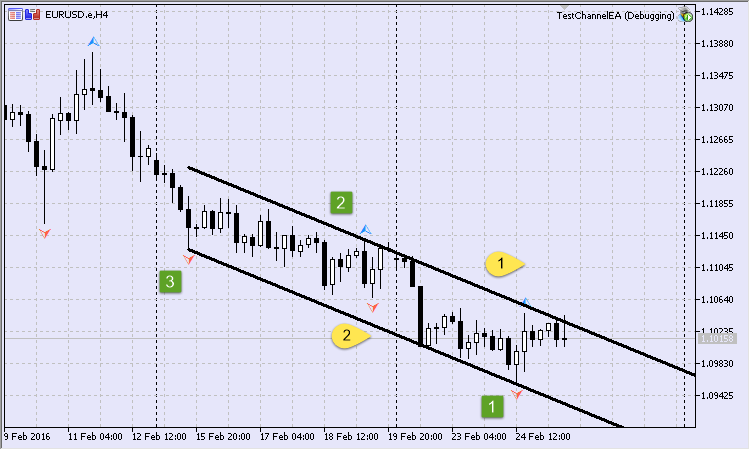
Fig.14 Primer canal, teniendo en cuenta las barras intermedias y el punto vigente anterior
Por ejemplo, para el primer punto ignorado en el registro obtendremos la siguiente entrada:
2016.02.25 16:46:06.212 TestChannelEA (EURUSD.e,H4) El punto actual será ignorado: 2016.02.24 16:00 2016.02.25 16:46:06.212 TestChannelEA (EURUSD.e,H4) Las barras intermedias son insuficientes. Se ignorará un punto.
Es posible que el canal actual parezca más útil, puesto que limita todas las barras colindantes. Pero es difícil decir de antemano qué punto vigente - el anterior o el último - será más productivo al dibujar el canal.
Si nos fijamos en el código (y se trata del mismo código en el cuerpo del método privado CFractalSet::CheckSet()), entonces veremos que son dos los factores que influyen en el comportamiento del método: el tipo elegido de punto vigente y la bandera de inicialización.
//--- si las barras intermedias son insuficientes if(bars_between<m_bars_between) { bool to_delete_frac=false; if(m_to_log) Print("Las barras intermedias son insuficientes. Se ignorará un punto."); //--- si el punto anterior es el vigente if(m_rel_frac==RELEVANT_EXTREMUM_PREV) { datetime curr_frac_date=time2; //--- si ha tenido lugar la inicialización if(m_is_init) { continue; } //--- si no ha habido inicialización else { //--- eliminar el punto actual to_delete_frac=true; curr_frac_date=time1; } if(m_to_log) { PrintFormat("El punto actual será ignorado: %s", TimeToString(curr_frac_date)); } } //--- si el último punto es el vigente else { datetime curr_frac_date=time1; //--- si ha tenido lugar la inicialización if(m_is_init) { //--- eliminar el punto anterior to_delete_frac=true; } //--- si no ha habido inicialización else { curr_frac_date=time2; } if(m_to_log) PrintFormat("El punto anterior será ignorado: %s", TimeToString(curr_frac_date)); if(curr_frac_date==time2) continue; } //--- si se elimina el punto if(to_delete_frac) { if(!this.Delete(curr_fractal_num-1)) { Print("¡Error al eliminar el último punto en el conjunto!"); return -1; } } }
En el siguiente apartado veremos un conjunto de canales equidistantes, variando los parámetros de los cuales se puede obtener una imagen del movimiento del precio.
3. Construcción automática de los canales móviles
Para poner a prueba el dibujado de los canales, se ha creado una versión del asesor con el nombre ChannelsPlotter. El resultado del funcionamiento del asesor se muestra en la Fig.15. Resulta obvio que en base a los fractales normales y en ausencia de una tendencia clara en el mercado, los canales comienzan a "pulular". Por eso se ha añadido la posibilidad de usar un indicador alternativo de fractales, en el que se establece cualquier otro número de barras colindantes con el extremo. El propio indicador X-bars Fractals se ha tomado prestado de la base de códigos fuente.
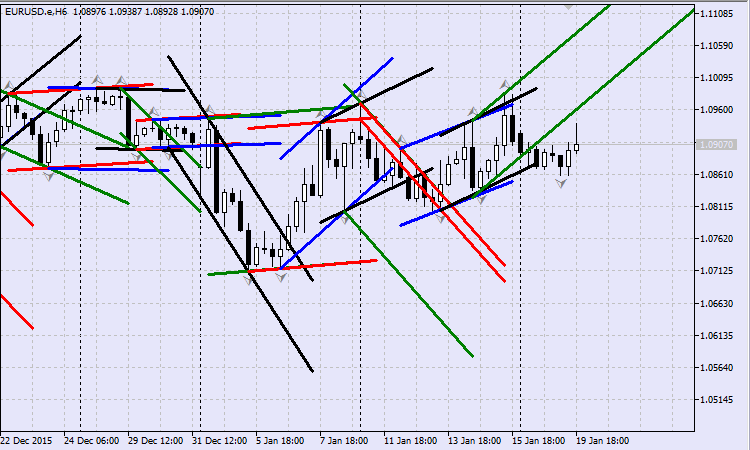
Fig.15 Canales móviles según fractales habituales
Si iniciamos el asesor eligiendo un indicador alternativo de fractales, entonces el aumento en él del número de barras que forman un grupo para determinar el extremo dará un resultado satisfactorio. Y bien, si vamos a buscar un fractal en un grupo de 23 barras, entonces la imagen puede resultar igual que en la Fig.16.
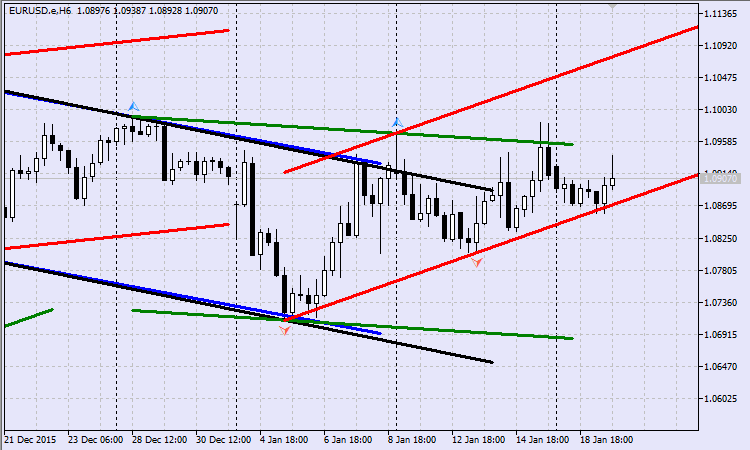
Fig.16 Canales móviles según fractales alternativos
De esta forma, cuanto menos barras colindantes participen en la determinación del fractal, mayor será el ruido "del canal" en el gráfico de precio.
Conclusión
En este artículo he intentado presentar un método de programación del sistema de canales equidistantes. Se han analizado ciertos matices de la construcción de los canales. Como base se ha tomado la idea de Viktor Barishpolets. En el siguiente artículo analizaremos señales comerciales que generan canales móviles.
Ubicación de los archivos:
A mi entender, lo más cómodo sería crear y guardar los archivos en la carpeta del proyecto. Por ejemplo, la ruta podría ser así: <catálogo_de_datos>\MQL5\Projects\ChannelsPlotter. No se olvide de compilar el indicador de fractales alternativo X-bars_Fractals. El archivo fuente del indicador debe encontrarse en la carpeta de indicadores <catálogo_de_datos>\MQL5\Indicators.
Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/1862
Interfaces gráficas II: Control "Menú principal" (Capítulo 4)
ZUP - ZigZag universal con Patrones de Pesavento. Segunda parte
Se ha añadido a MetaTrader 5 el sistema de cobertura de registro de posiciones
El indicador alternativo Ichimoku – Configuración y ejemplos de uso
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso