MQL5 Cookbook - Programming moving channels

Introduction

It is common knowledge that a market price direction may be expressed, thus indicating a trend in the chart, or, in fact, absent, signifying that it is flat. It is considered that technical indicators that belong to the group of oscillators operate efficiently when trading is flat. However, a certain range for price fluctuation may exist also when trends appear.

In this article, I will attempt to enlighten a dynamic way of building equidistant channels, frequently named as moving channels. It should be noted that one of the most popular strategies for such channels is a strategy of Victor Barishpolts. We will touch upon those aspects of his strategy that are connected with the rules of creating moving channels. Also, we will attempt to extend these rules, that, in the author's opinion, would increase the flexibility of the channel system.

1. Fundamentals of equidistant channels

First, we are going to work with schemes used as a framework for programming the equidistant channel. I would recommend using Help to read about the "Equidistant Channel" technical analysis tool.   

It is known that the channel is constructed on three points, and each of them has price and time coordinates. To start with, we will pay attention to the time coordinates, as their sequence affects the channel type. We will use the channel with a main line built on two local minimums as an example. A third point will be in charge of the local maximum. The position of points can be used as criteria for channel typification.

When drawing the channel, neither rays to the left, nor rays to the right are being used, unless stated otherwise.

The first type refers to a case when minimum appears first, followed by maximum, and then minimum again. A schematic view of this situation is presented in Fig.1.

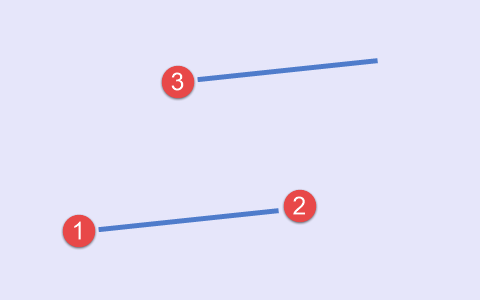
Fig.1 First type of set of points, a scheme

Below is the first type presented on the price chart (Fig.2).

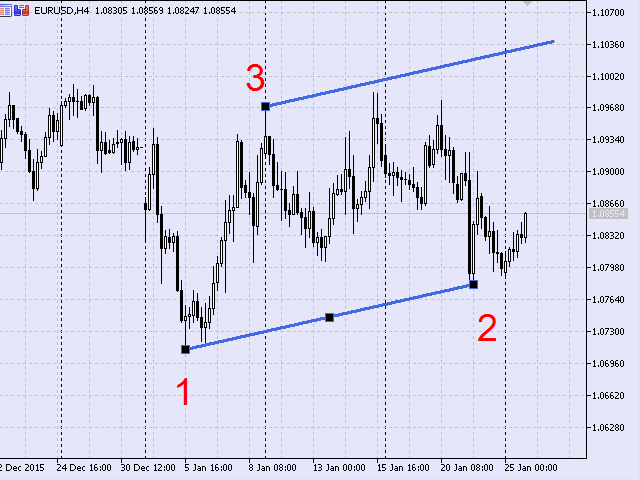
Fig.2 First type of set of points, a price chart

The second type refers to a case when maximum, minimum and minimum appear consequently on the chart (Fig.3).

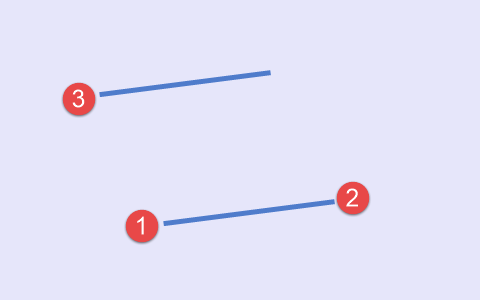
Fig.3 Second type of set of points, a scheme

The local maximum that appears in the beginning will eventually become a third point. It is followed by a pair of minimums forming the main line.

The third type is built based on the "minimum-minimum-maximum" scheme. In this case, the main line waits until the local maximum is formed (Fig.4).

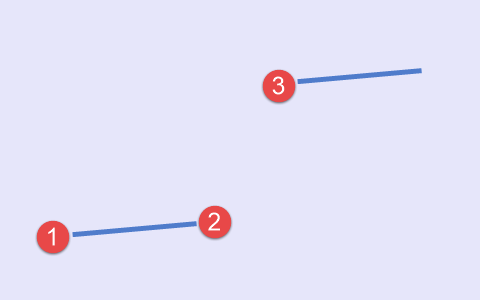
Fig.4 Third type of set of points, a scheme

Two last types are rather particular cases.  

The fourth option applies when third and first points match by the construction time. (Fig.5).

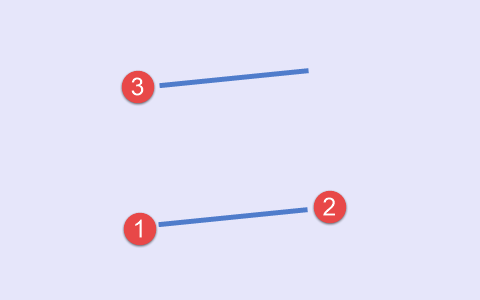
Fig.5 Fourth type of set of points, a scheme

And, finally, the fifth type that occurs when the time coordinates of second and third points match (Fig.6).

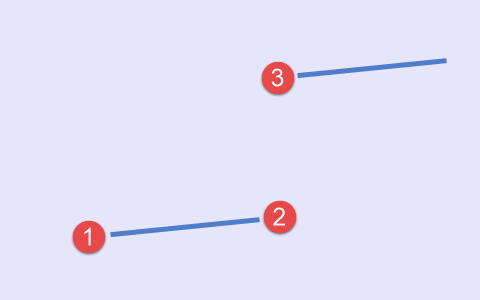
Fig.6 Fifth type of set of points, a scheme

And these are the five types of equidistant channels we are going to work with. In the next section we will try to program the points used for building channel lines.

2. Auxiliary types of data

Points that are used for drawing channel's trend lines are usually fractals. This way, a point is simultaneously a fractal and a base for drawing a straight line.

We will now attempt to summarize and code the fractal points with OOP.

2.1 Class of the fractal point

The feature of this class involves being in charge of the point that is among the points used for building the equidistant channel.

We will name the indicated class as CFractalPoint, and, in the best traditions of the MQL5 language, we will link it to the CObject interface class with a relation of inheritance.

//+------------------------------------------------------------------+
//| Class of the fractal point                                       |
//+------------------------------------------------------------------+
class CFractalPoint : public CObject
  {
   //--- === Data members === --- 
private:
   datetime          m_date;           // date and time
   double            m_value;          // value
   ENUM_EXTREMUM_TYPE m_extreme_type;  // extremum type
   int               m_idx;            // index (from 0 to 2)

   //--- === Methods === --- 
public:
   //--- constructor/destructor
   void              CFractalPoint(void);
   void              CFractalPoint(datetime _date,double _value,
                                   ENUM_EXTREMUM_TYPE _extreme_type,int _idx);
   void             ~CFractalPoint(void){};
   //--- get-methods
   datetime          Date(void) const {return m_date;};
   double            Value(void) const {return m_value;};
   ENUM_EXTREMUM_TYPE FractalType(void) const {return m_extreme_type;};
   int               Index(void) const {return m_idx;};
   //--- set-methods
   void              Date(const datetime _date) {m_date=_date;};
   void              Value(const double _value) {m_value=_value;};
   void              FractalType(const ENUM_EXTREMUM_TYPE extreme_type) {m_extreme_type=extreme_type;};
   void              Index(const int _bar_idx){m_idx=_bar_idx;};
   //--- service
   void              Copy(const CFractalPoint &_source_frac);
   void              Print(void);
  };
//+------------------------------------------------------------------+

The class has 4 members for transferring data:

1. m_date — the point's time coordinate on the chart;
2. m_value — the point's price coordinate on the chart;
3. m_extreme_type –  extremum type;
4. m_idx – index.

The ENUM_EXTREMUM_TYPE enumeration will be in charge of the extremum type:

//+------------------------------------------------------------------+
//| Extremum type                                                    |
//+------------------------------------------------------------------+
enum ENUM_EXTREMUM_TYPE
  {
   EXTREMUM_TYPE_MIN=0, // minimum
   EXTREMUM_TYPE_MAX=1, // maximum
  };

The main goal of the CFractalPoint methods is to ensure that values of the private members listed above are received and refreshed.

For example, let's create a fractal point on the EURUSD, H4 chart for the candlestick dated 26.01.2016 08:00 in Fig.7 programmatically. The fractal was formed on the candlestick maximum at the price 1,08742.

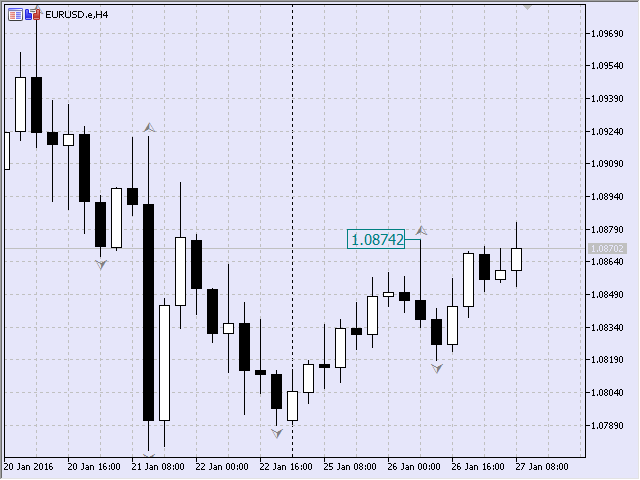
Fig.7 Example of fractal

This is how the code for achieving the objective may look.

//--- fractal point data
   datetime pnt_date=D'26.01.2016 08:00';
   double pnt_val=1.08742;
   ENUM_EXTREMUM_TYPE pnt_type=EXTREMUM_TYPE_MAX;
   int pnt_idx=0;
//--- create fractal point
   CFractalPoint myFracPoint(pnt_date,pnt_val,pnt_type,pnt_idx);
   myFracPoint.Print();

The following appears in the log:

---=== Fractal point data ===---
Date: 2016.01.26 08:00
Price: 1.08742
Type: EXTREMUM_TYPE_MAX
Index: 0

It implies that the fractal point was located on the bar dated 26.01.2016 at the price 1,08742. This fractal is a local maximum. Zero index indicates that it will be the first point in the set of similar points.

2.2 Class of the fractal points' set

Now, we can proceed with creating a set of fractal points that will be used for building the equidistant channel. For this purpose, we will create the CFractalSet class that will identify and gather these points in a set. 

This class will be included in the Expert Advisor, instead of the indicator, therefore, channels will refer to graphic objects of type  CChartObjectChannel, other than indicator buffers.

CFractalSet is a class that derives from the CArrayObj class of the Standard Library. I have selected the protected type of inheritance to make the interface of the class highly specialized.

//+------------------------------------------------------------------+
//| Class of the fractal points' set                                 |
//+------------------------------------------------------------------+
class CFractalSet : protected CArrayObj
  {
   //--- === Data members === --- 
private:
   ENUM_SET_TYPE     m_set_type;           // type of the points' set
   int               m_fractal_num;        // fixed number of points
   int               m_fractals_ha;        // handle of the fractal indicator 
   CisNewBar         m_new_bar;            // object of the new bar
   CArrayObj         m_channels_arr;       // object of the indicator's array
   color             m_channel_colors[4];  // colors of channels
   bool              m_is_init;            // initialization flag
   //--- channel settings of
   int               m_prev_frac_num;      // previous fractals
   int               m_bars_beside;        // bars on the left/right sides of the fractal
   int               m_bars_between;       // number of intermediate bars  
   bool              m_to_delete_prev;     // delete previous channels?
   bool              m_is_alt;             // alternative fractal indicator?
   ENUM_RELEVANT_EXTREMUM m_rel_frac;      // relevant point
   bool              m_is_array;           // draw arrow?
   int               m_line_wid;           // line width
   bool              m_to_log;             // keep the log?

   //--- === Methods === --- 
public:
   //--- constructor/destructor
   void              CFractalSet(void);
   void              CFractalSet(const CFractalSet &_src_frac_set);
   void             ~CFractalSet(void){};
   //---
   void              operator=(const CFractalSet &_src_frac_set);
   //--- handlers
   bool              Init(
                          int _prev_frac_num,
                          int _bars_beside,
                          int _bars_between=0,
                          bool _to_delete_prev=true,
                          bool _is_alt=false,
                          ENUM_RELEVANT_EXTREMUM _rel_frac=RELEVANT_EXTREMUM_PREV,
                          bool _is_arr=false,
                          int _line_wid=3,
                          bool _to_log=true
                          );
   void              Deinit(void);
   void              Process(void);
   //--- service
   CChartObjectChannel *GetChannelByIdx(const int _ch_idx);
   int               ChannelsTotal(void) const {return m_channels_arr.Total();};

private:
   int               AddFrac(const int _buff_len);
   int               CheckSet(const SFracData &_fractals[]);
   ENUM_SET_TYPE     GetTypeOfSet(void) const {return m_set_type;};
   void              SetTypeOfSet(const ENUM_SET_TYPE _set_type) {m_set_type=_set_type;};
   bool              PlotChannel(void);
   bool              Crop(const uint _num_to_crop);
   void              BubbleSort(void);
  };
//+------------------------------------------------------------------+

Here is the list of members of this class. 

1. m_set_type – type of the points' set. Below is the enumeration in charge of the set classification;
   
2. m_fractal_num – fixed number of points included in the set;
3. m_fractals_ha – handle of the fractal indicator;
   
4. m_new_bar – object of a new bar;
5. m_channels_arr – object of the indicator array;
6. m_channel_colors[4] — array of colors to display channels;
7. m_is_init — initialization flag.
   It is followed by the block of members in charge of the channel's settings.
8. m_prev_frac_num — number of previous fractals used to build the very first channel. If there are 3 points, then the channel will be built right after the initialization;  
9. m_bars_beside — number of bars on the left/right sides of the fractal. If, for example, 5 is indicated, then the total of 11 bars will be used for finding a fractal;
10. m_bars_between — number of intermediate bars. In fact, this is a minimum of bars that must be present between the adjacent fractal points;
11. m_to_delete_prev — permission to delete  previous  channels;
12. m_is_alt — flag of using the alternative fractal indicator;
13. m_rel_frac — selection of the relevant point. If intermediate bars are not sufficient, then the type of this point will show which bar we should be skip;
14. m_is_array — flag of drawing the arrow;
15. m_line_wid — line width;
16. m_to_log — logging flag.

The enumeration that processes types of the points' sets is presented below:

//+------------------------------------------------------------------+
//| Type of the extremum points' set                                 |
//+------------------------------------------------------------------+
enum ENUM_SET_TYPE
  {
   SET_TYPE_NONE=0,     // not set
   SET_TYPE_MINMAX=1,   // min-max-min
   SET_TYPE_MAXMIN=2,   // max-min-max                       
  };

The value of SET_TYPE_MAXMIN in this example corresponds to the following sequence of fractal points: maximum, minimum, and maximum (Fig.8).

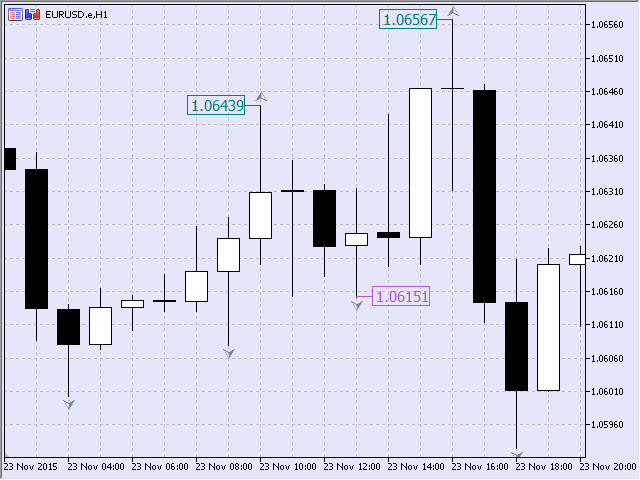
Fig.8 Set of the type "max-min-max"

I hasten to say that the sequence of points cannot be followed all the time. Occasionally, there may be a case when after the first minimum the second minimum will follow. We can refer to the third type of the set of points described in the first section (Fig.4) as an example. In any case, we will consider the set complete if it has either a couple of minimums and a maximum, or a couple of maximums and a minimum.

The enumeration that processes types of the relevant point has the following form:

//+------------------------------------------------------------------+
//| Type of the relevant point                                       |
//+------------------------------------------------------------------+
enum ENUM_RELEVANT_EXTREMUM
  {
   RELEVANT_EXTREMUM_PREV=0, // previous
   RELEVANT_EXTREMUM_LAST=1, // last
  };

Let's proceed to methods. First, we will list the handlers.

1. Init() – initializes the set. The method is responsible for the correct start of operation of the object that presents the set of fractal points.
2. Deinit() - deinitializes the set.
3. Process() – controls the price stream. In fact, this specific method identifies points and displays the channel.

Service methods:

1. AddFrac() — adds fractal points to the set.
2. CheckSet() – checks current state of the set.
3. PlotChannel() – draws the equidistant channel.
4. Crop() – crops the set.
5. BubbleSort() — sorts the points in the set by the time of their appearance.
   

2.3 Additional opportunities of building a channel

Let me remind you again that the CChartObjectChannel class from the Standard Library was used for building the channel and addressing its properties. We will consider certain points whose algorithmic implementation can increase the flexibility of building channels automatically.

2.3.1 Synchronization of lines

It is most convenient to visually evaluate the chart with channels at the moment when both channel lines start from the same bar. Officially, the forth channel type corresponds to this approach (Fig.5). Obviously, channels can belong to other types. For this reason, the price and time coordinates of fractal points are modified in the CFractalSet::PlotChannel() method in order to adjust to the forth channel type. It is also important (is implemented) to save the channel's angle and width.

Consider the following equidistant channel on the price chart (Fig.9).

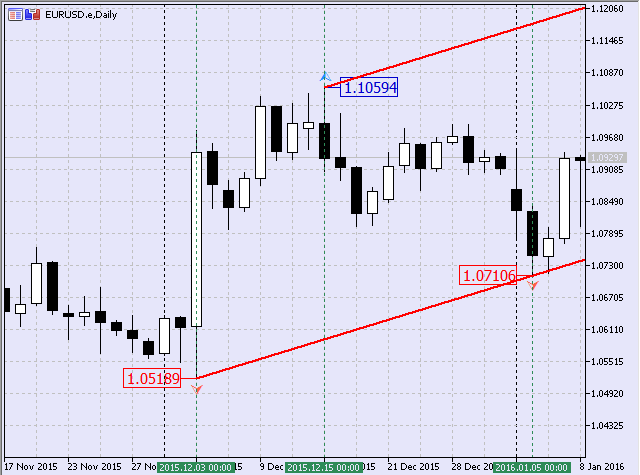
Fig.9 Equidistant channel based on the initial points

I wish to clarify from the beginning that it was built manually. It has the following fractal points:

1. $1.05189 on 2015.12.03 (minimum);
2. $1.07106 on 2016.01.05 (minimum);
3. $1.10594 on 2016.01.05 (maximum).

If we display a similar channel with the CFractalSet class, we will obtain the following image (Fig.10).

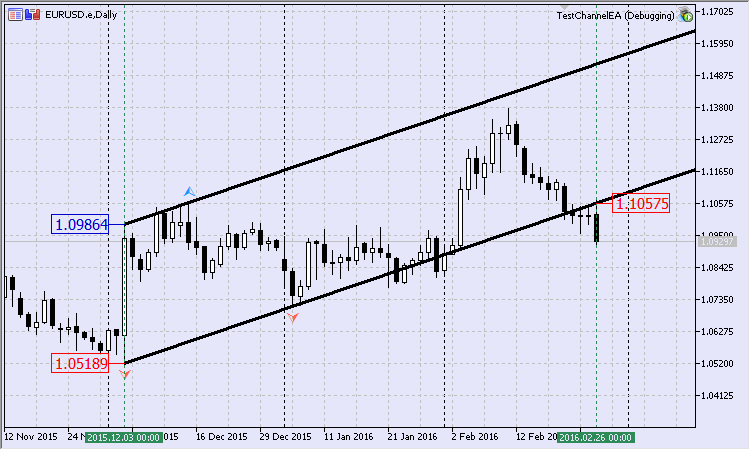
Fig.10 Equidistant channel on calculated points

The insignificant differences lie in the fact that building a channel in Fig. 10 is based on calculated points. Price and time values of the second and third points are being calculated. The last point should match the  time coordinate with the first point.

I will break down the task for drawing a channel on calculated points into 2 parts.

The first part will focus on time coordinates, where the channel's start and the end are defined. The following code block is present in the indicated method:

//--- 1) time coordinates
//--- start of the channel
int first_date_idx=ArrayMinimum(times);
if(first_date_idx<0)
  {
   Print("Error in obtaining the time coordinate!");
   m_channels_arr.Delete(m_channels_arr.Total()-1);
   return false;
  }
datetime first_point_date=times[first_date_idx];
//--- end of the channel
datetime dates[];
if(CopyTime(_Symbol,_Period,0,1,dates)!=1)
  {
   Print("Error in obtaining the time of last bar!");
   m_channels_arr.Delete(m_channels_arr.Total()-1);
   return false;
  }
datetime last_point_date=dates[0];

This way, all points will have such time coordinates:

//--- final time coordinates 
times[0]=times[2]=first_point_date;
times[1]=last_point_date;

The second part of the task refers to price coordinates — a new price is determined for either third or first points.

We will first determine, how quickly the price of the channel's lines changes from bar to bar, and whether the channel is heading up or down.

//--- 2) price coordinates
//--- 2.1 angle of the line
//--- bars between first and second points
datetime bars_dates[];
int bars_between=CopyTime(_Symbol,_Period,
                          times[0],times[1],bars_dates
                          );
if(bars_between<2)
  {
   Print("Error in obtaining the number of bars between points!");
   m_channels_arr.Delete(m_channels_arr.Total()-1);
   return false;
  }
bars_between-=1;
//--- common differential
double price_differential=MathAbs(prices[0]-prices[1]);
//--- price speed (price change on the first bar)
double price_speed=price_differential/bars_between;
//--- direction of the channel
bool is_up=(prices[0]<prices[1]);

The price coordinates of points can be refreshed now. It is important to know, which point was formed earlier. Furthermore, we need to know where the channel is heading — up or down:

//--- 2.2 new price of the first or third points  
if(times[0]!=times[2])
  {
   datetime start,end;
   start=times[0];
   end=times[2];
//--- if the third point is earlier than the first
   bool is_3_point_earlier=false;
   if(times[2]<times[0])
     {
      start=times[2];
      end=times[0];
      is_3_point_earlier=true;
     }
//--- bars between the first and third points
   int bars_between_1_3=CopyTime(_Symbol,_Period,
                                 start,end,bars_dates
                                 );
   if(bars_between_1_3<2)
     {
      Print("Error in obtaining the number of bars between points!");
      m_channels_arr.Delete(m_channels_arr.Total()-1);
      return false;
     }
   bars_between_1_3-=1;

//--- if the channel is ascending
   if(is_up)
     {
      //--- if the 3 point is earlier
      if(is_3_point_earlier)
         prices[0]-=(bars_between_1_3*price_speed);
      else
         prices[2]-=(bars_between_1_3*price_speed);
     }
//--- or if the channel is descending
   else
     {
      //--- if the 3 point is earlier
      if(is_3_point_earlier)
         prices[0]+=(bars_between_1_3*price_speed);
      else
         prices[2]+=(bars_between_1_3*price_speed);
     }
  }

Previously, the first point was formed earlier in our example, which means that the price of the third point should be refreshed.

Finally, we will refresh the coordinates of the second point:

//--- 2.3 new price of the 2 point 
if(times[1]<last_point_date)
  {
   datetime dates_for_last_bar[];
//--- bars between the 2 point and the last bar
   bars_between=CopyTime(_Symbol,_Period,times[1],last_point_date,dates_for_last_bar);
   if(bars_between<2)
     {
      Print("Error in obtaining the number of bars between points!");
      m_channels_arr.Delete(m_channels_arr.Total()-1);
      return false;
     }
   bars_between-=1;
//--- if the channel is ascending
   if(is_up)
      prices[1]+=(bars_between*price_speed);
//--- or if the channel is descending
   else
      prices[1]-=(bars_between*price_speed);
  }

What we obtain:

1. $1.05189 on 2015.12.03 (minimum);
2. $1.10575 on 2016.02.26 (calculated value);
3. $1.09864 on 2015.12.03 (calculated value).

The channel can be drawn with or without using arrows to the right. However, this option relates only to the current channel. All previous channel objects on the chart will be deprived the arrows to the right.

2.3.2 Consideration of previous fractal points

The option of addressing history to search for the fractal points based on given parameters is added to the CFractalSet class. Such opportunity is only used during the initialization of the class sample. Remember that the m_prev_frac_num member is in charge of the "points from the past".

Let us analyze the example (Fig.11). Suppose that right after the initialization of the TestChannelEA Expert Advisor we will need to find several fractal points on the chart. They can be fractals marked with relevant figures.

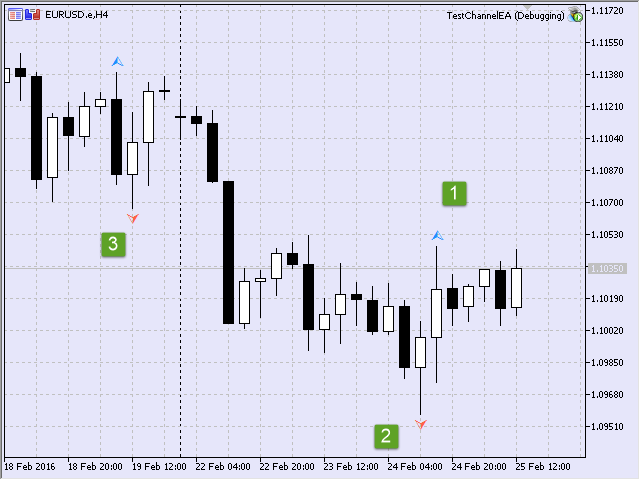
Fig.11 Fractal points during initialization

If we take all three points, then we will be able to build a channel (Fig.12).

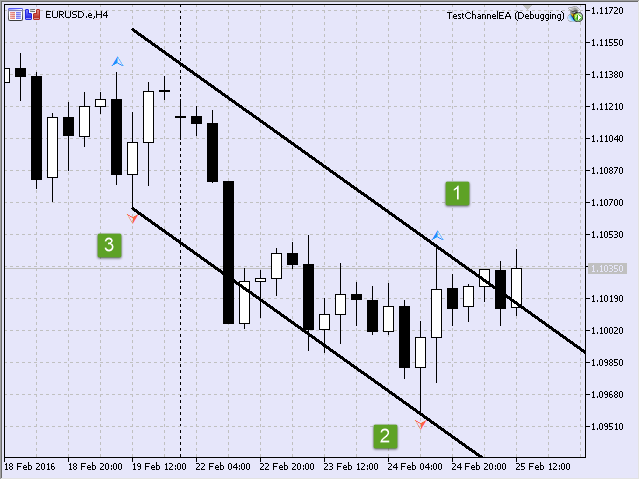
Fig.12 First channel built during initialization

There is a message in the log:

2016.02.25 15:49:23.248 TestChannelEA (EURUSD.e,H4)     Previous fractals added: 3

It's not difficult to notice that points are added to the set from right to left. And the channel is built on points that should be collected from left to right. The private method of sorting  CFractalSet::BubbleSort(), in fact, allows to organize points before drawing the actual channel.

The code black that is in charge of the set of points during initialization in the CFractalSet::Init() method is presented as follows:

//--- if previous fractal points are added
if(m_prev_frac_num>0)
  {
//--- 1) Loading history [start]
   bool synchronized=false;
//--- loop counter
   int attempts=0;
//--- 10 attempts to wait for synchronization
   while(attempts<10)
     {
      if(SeriesInfoInteger(_Symbol,0,SERIES_SYNCHRONIZED))
        {
         synchronized=true;
         //--- synchronization established, exit
         break;
        }
      //--- increase counter
      attempts++;
      //--- wait for 50 milliseconds until the next iteration
      Sleep(50);
     }
//---
   if(!synchronized)
     {
      Print("Failed to obtain the number of bars on ",_Symbol);
      return false;
     }
   int curr_bars_num=Bars(_Symbol,_Period);
   if(curr_bars_num>0)
     {
      PrintFormat("Number of bars in the history of terminal based on the symbol/period at the current moment: %d",
                  curr_bars_num);
     }
//--- 1) Loading history [end]

//--- 2) Calculated data for the requested indicator [start]
   double Ups[];
   int i,copied=CopyBuffer(m_fractals_ha,0,0,curr_bars_num,Ups);
   if(copied<=0)
     {
      Sleep(50);
      for(i=0;i<100;i++)
        {
         if(BarsCalculated(m_fractals_ha)>0)
            break;
         Sleep(50);
        }
      copied=CopyBuffer(m_fractals_ha,0,0,curr_bars_num,Ups);
      if(copied<=0)
        {
         Print("Failed to copy upper fractals. Error = ",GetLastError(),
               "i=",i,"    copied= ",copied);
         return false;
        }
      else
        {
         if(m_to_log)
            Print("Succeeded to copy upper fractals.",
                  " i = ",i,"    copied = ",copied);
        }
     }
   else
     {
      if(m_to_log)
         Print("Succeeded to copy upper fractals. ArraySize = ",ArraySize(Ups));
     }
//--- 2) Calculated data for the requested indicator [end]

//--- 3) Adding fractal points [start]
   int prev_fracs_num=AddFrac(curr_bars_num-1);
   if(m_to_log)
      if(prev_fracs_num>0)
         PrintFormat("Previous fractals added: %d",prev_fracs_num);
//--- if the channel can be displayed
   if(prev_fracs_num==3)
      if(!this.PlotChannel())
         Print("Failed to display channel!");
//--- 3) Adding fractal points [end]
  }

It can be divided into 3 sub-blocks:

1. loading history of quotes;
2. calculation of fractal indicator's data;
3. adding fractal points to the set.

 This way, the channel can be drawn at the moment of initialization. It requires some time, especially in the cases when chart data is not synchronized with server data.

2.3.3 Consideration of bars between adjacent fractal points

Used fractal points (first and second, and third and fourth) are located next to each other on the previous charts. For eliminating the closest points you can add some kind of filter. This function can be carried out by the  m_bars_between member - a number of intermediate bars between adjacent points. If you set the number equal 1, then the second point will not fall in the set, and it will be replaced by the current third point.

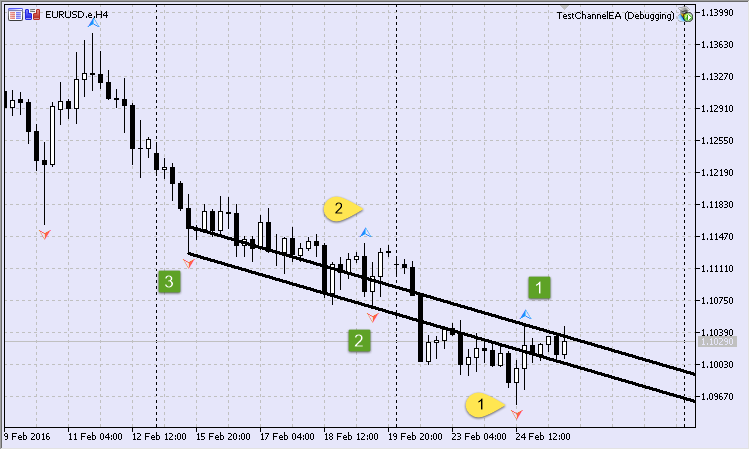
 Fig.13 First channel with consideration of intermediate bars

We will build a channel based on the condition that there will be at least 1 bar (Fig. 13) between the adjacent fractal points (Fig.13). It turns out that points following the first and second points should be skipped. They are highlighted in yellow.

For example, the first missing point will have the following log:

2016.02.25 16:11:48.037 TestChannelEA (EURUSD.e,H4)     The previous point was skipped: 2016.02.24 12:00
2016.02.25 16:11:48.037 TestChannelEA (EURUSD.e,H4)     Intermediate bars are not sufficient. One point will be skipped.

The searched channel will then become narrow and, probably, not particularly functional from the trader's perspective.

As for the code, checking for the permitted number of intermediate bars is executed in the body of the CFractalSet::CheckSet() private method.

//--- when checking the number of bars between the last and current points
if(m_bars_between>0)
  {
   curr_fractal_num=this.Total();
   if(curr_fractal_num>0)
     {
      CFractalPoint *ptr_prev_frac=this.At(curr_fractal_num-1);
      if(CheckPointer(ptr_prev_frac)!=POINTER_DYNAMIC)
        {
         Print("Error in obtaining the fractal point's object from the set!");
         return -1;
        }
      datetime time1,time2;
      time1=ptr_prev_frac.Date();
      time2=ptr_temp_frac.Date();
      //--- bars between points
      datetime bars_dates[];
      int bars_between=CopyTime(_Symbol,_Period,
                                time1,time2,bars_dates
                                );
      if(bars_between<0)
        {
         Print("Error in obtaining data for the bar opening time!");
         return -1;
        }
      bars_between-=2;
      //--- on various bars
      if(bars_between>=0)
         //--- if intermediate bars are not sufficient 
         if(bars_between<m_bars_between)
           {
            bool to_delete_frac=false;
            if(m_to_log)
               Print("Intermediate bars are not sufficient. One point will be skipped.");

            // ...

           }
     }
  }

The bars_between variable receives a number of bars between two adjacent fractal points. If its value is below acceptable, then a point is skipped. We will find out from the next section whether it is a current or previous point.

2.3.4 Selection of the relevant fractal point

When the intermediate bars are not sufficient, and one of the points will have to be ignored, you can specify which point to skip. In the example above, the older point, in terms of the appearance time, was skipped, because the last point was considered to be the relevant fractal point. Let's make the previous point relevant, and see what turns out of it (Fig.14).

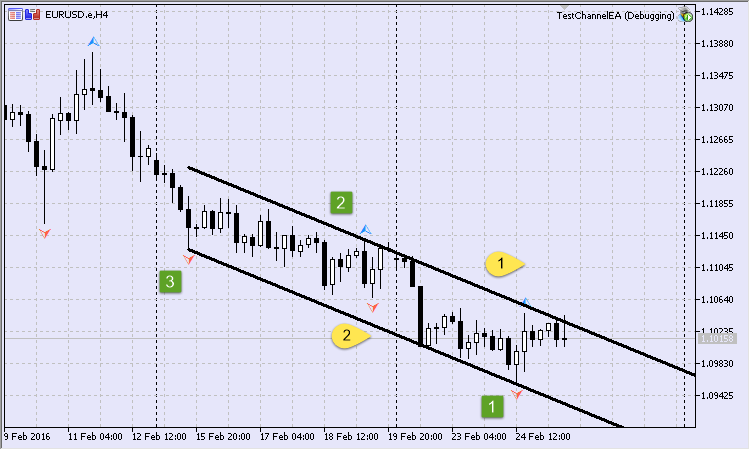
Fig.14 First channel with consideration of intermediate bars and a previous relevant point

For example, we will get the following log for the first skipped point:

2016.02.25 16:46:06.212 TestChannelEA (EURUSD.e,H4)     Current point will be skipped: 2016.02.24 16:00
2016.02.25 16:46:06.212 TestChannelEA (EURUSD.e,H4)     Intermediate bars are not sufficient. One point will be skipped.

Possibly, this channel seems more useful, since it limits all adjacent bars. It is difficult to say in advance, whether previous or last relevant point will become more productive when drawing the channel.

If we look at the code (and it is the same block code in the body of the CFractalSet::CheckSet()) private method, we will see that two factors affect the method behavior: selected type of the actual point and the initialization flag.

//--- if intermediate bars are not sufficient 
if(bars_between<m_bars_between)
  {
   bool to_delete_frac=false;
   if(m_to_log)
      Print("Intermediate bars are not sufficient. One point will be skipped.");
//--- if the previous point is relevant
   if(m_rel_frac==RELEVANT_EXTREMUM_PREV)
     {
      datetime curr_frac_date=time2;
      //--- if there was initialization
      if(m_is_init)
        {
         continue;
        }
      //--- if there was no initialization
      else
        {
         //--- remove current point
         to_delete_frac=true;
         curr_frac_date=time1;
        }
      if(m_to_log)
        {
         PrintFormat("Current point will be missed: %s",
                     TimeToString(curr_frac_date));
        }
     }
//--- if the last point is relevant
   else
     {
      datetime curr_frac_date=time1;
      //--- if there was initialization
      if(m_is_init)
        {
         //--- remove previous point
         to_delete_frac=true;
        }
      //--- if there was no initialization
      else
        {
         curr_frac_date=time2;
        }
      if(m_to_log)
         PrintFormat("Previous point was skipped: %s",
                     TimeToString(curr_frac_date));
      if(curr_frac_date==time2)
         continue;

     }
//--- if the point is deleted
   if(to_delete_frac)
     {
      if(!this.Delete(curr_fractal_num-1))
        {
         Print("Error of deleting the last point in the set!");
         return -1;
        }
     }
  }

In the next section we will look into the set of equidistant channels and obtain the image of a price slide by varying their parameters.

3. Creating moving channels automatically

The version of the Expert Advisor named ChannelsPlotter was created to test the drawing of channels. The results of the Expert Advisor's operation were displayed in Fig.15. Obviously, channels begin to "flicker" on the basis of regular fractals and in the absence of an obvious market trend. Therefore, an option to use the alternative indicator of fractals, where any other number of bars adjacent to the extremum are set, was added. The X-bars Fractals indicator was borrowed from the base of source codes.

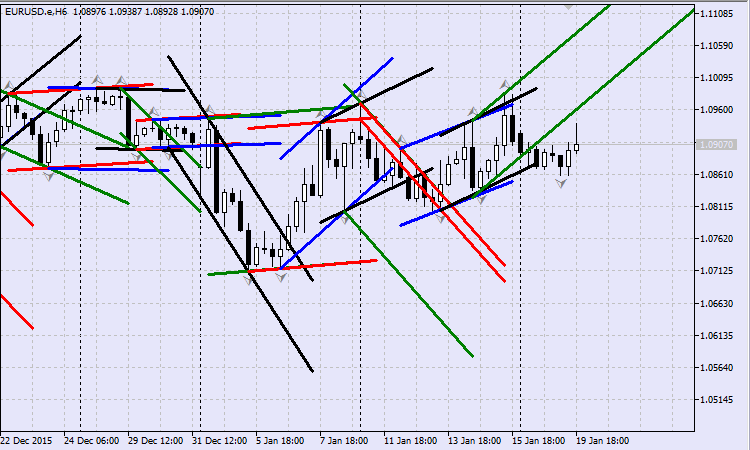
Fig.15 Moving channels based on regular fractals

If you run the Expert Advisor with a selection of the alternative indicator of fractals, then a satisfying result gives an increase of the number of bars in it that form a group for finding the extremum. Thus, if we look for a fractal in a group consisting of 23 bars, then the result may appear as shown in Fig.16.

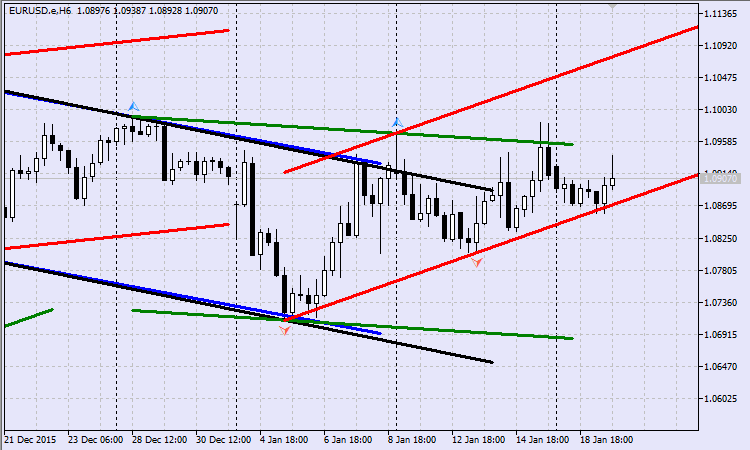
Fig.16 Moving channels based on alternative fractals

This way, the less adjacent bars participate in determining the fractal, the more "channel" noise will appear on the price chart.

Conclusion

In this article, I tried to present a method of programming the system of equidistant channels. Few details of building the channels were considered. The idea of Victor Barishpoltz was used as a framework. In my next article, I will analyze trading signals generated by the moving channels.

File location:

In my opinion, it is most convenient to create and store files in the project's folder. For example, the location can be as follows: <data folder>\MQL5\Projects\ChannelsPlotter. Don't forget to compile the alternative fractal indicator — X-bars_Fractals. The indicator's source code should be located in the indicators' folder — <data folder>\MQL5\Indicators.