MetaTrader 4 / Ejemplos
English Русский 中文 Deutsch 日本語 Português
ZUP - ZigZag universal con Patrones de Pesavento. Segunda parte

ZUP - ZigZag universal con Patrones de Pesavento. Segunda parte

MetaTrader 4 — Ejemplos | 15 marzo 2016, 11:53
1 723 0
Eugeni Neumoin
Eugeni Neumoin

Introducción

El lenguaje de programación MQL4 integrado en el Terminal de cliente MetaTrader 4 permite desarrollar sus propios indicadores. Algunos pueden ser muy sofisticados y otros muy sencillos. Todo depende de la creatividad del desarrollador. El artículo describe el modo de desarrollar un programa sofisticado. Describe, por así decirlo, una plataforma del indicador ZUP. El artículo proporciona también una breve descripción de las herramientas gráficas incluidas en el ZUP. Se actualiza el ZUP constantemente. Vamos a describir las herramientas gráficas para la versión ZUP_v63.

Patrones de Pesavento

En el siguiente gráfico, se unen los puntos de ruptura del ZigZag mediante unas líneas discontinuas. Se coloca un número en medio de cada línea discontinua. Esta líneas discontinuas con números cerca representan una herramienta llamada "patrones de Pesavento". Hay que distinguir la herramienta "patrones de Pesavento" de las figuras de mercado llamadas "patrones de Pesavento". Vamos a explicar a continuación lo que representa la figura de mercado "patrones de Pesavento".


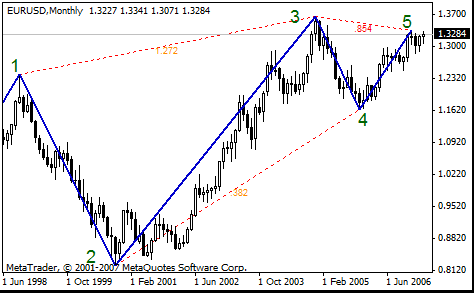
Vamos a calcular el tamaño de los segmentos 23 y 24 en puntos. El tamaño del segmento 23 = (1,3665-0,8225)*10 000=5440. El tamaño del segmento 34 = (1,3665-1,1638)*10 000=2027. Hacemos la divisón: 34/23 = 2027/5440=0,373. Obtenemos un número distinto al nivel de Fibonacci 0,382 por 2,46 %. Se puede ver el valor 0,382 cerca de la línea discontinua que une los puntos 2 y 4.

Se ha constatado que los niveles de Fibonacci empiezan a "funcionar" cuando se aproxima el mercado a un determinado nivel de Fibonacci. A menudo, los mercados se paran o cambian de sentido cerca de un nivel de Fibonacci. El comportamiento del mercado es bastante predecible en una zona determinada. El tamaño de esta zona se expresa en porcentaje y es igual a 2*Delta.

En el siguiente gráfico podemos observar que el nivel de Fibonacci 0,382 está cerca del punto 4. El nivel de Fibonacci está por debajo del mínimo de noviembre en (1,1638-1,1557)*10 000=51 puntos.



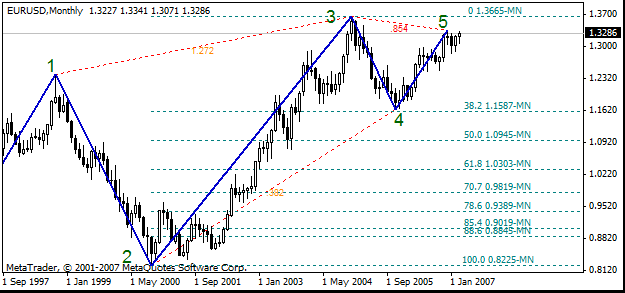
EURUSD no alcanzó el nivel de Fibonacci 0,382 por poco en noviembre 2005 y subió. Es así como "funciona" el nivel de Fibonacci 0,832. En general, el número que se muestra cerca la línea discontinua es igual al tamaño del segmento del ZigZag dividido por el tamaño del segmento anterior. En el ejemplo anterior, la relación entre los segmentos es 34/23. Esta relación se llama el retroceso entre los puntos 2 y 4 del ZigZag.

Entonces, ¿por qué se muestra el número 0,382 cerca de la línea en lugar de 0,373? Se ha observado que sólo "funcionan" unos niveles de Fibonacci muy concretos en el mercado. Esto significa que existe un determinado conjunto de niveles de "funcionamiento" de Fibonacci. Existen distintos conjuntos de Fibonacci proporcionados por distintos autores.


El algoritmo de la herramienta "patrones de Pesavento"

En primer lugar, se calculan los retrocesos entre los picos y los valles del ZigZag. Después se calculan los valores que se van a comparar con el conjunto preestablecido de los niveles de Fibonacci. Si la diferencia entre el número obtenido y el número del conjunto de Fibonacci es inferior a Delta%, se mostrará el número del conjunto de Fibonacci cerca de la línea discontinua. El color del número será igual al color del número predefinido del conjunto de Fibonacci. (Si el conjunto de niveles de Fibonacci coincide con la tabla numérica desarrollada por Larry Pesavento, obtendremos la figura de mercado llamada Patrón de Pesavento). Si la diferencia entre el número obtenido y el número del conjunto de Fibonacci es superior a Delta%, se mostrará el número del conjunto de Fibonacci cerca de la línea discontinua y tendrá un color distinto.

No hace falta calcular los retrocesos cuando la herramienta patrones de Pesavento está disponible. Si el precio se encuentra dentro de un nivel de Fibonacci, el patrón de Pesavento mostrará el valor del nivel con su color predefinido. La herramienta patrones de Pesavento proporcionará uno a partir de las rutinas de cálculo de retrocesos.

Las entradas del indicador para su uso con los patrones de Pesavento.

  • ExtHidden

    0 - no se muestran los patrones de Pesavento. Pero se pueden mostrar otras herramientas.
    1 - muestra todas las líneas entre los picos y valles del ZigZag con un porcentaje de retroceso superior a 0,1 e inferior a 9,36.
    2 - muestra únicamente las líneas con un porcentaje de retroceso igual a un valor del conjunto de niveles de Fibonacci.
    3 - muestra los números del punto 2, además de todas las líneas discontinuas entre los picos y valles del ZigZag.
    4 - muestra los números que no coinciden con los valores del conjunto seleccionado de Fibonacci, además de las líneas conectoras.
    5 - muestra solamente el ZigZag. Todas las demás herramientas están ocultas. (Todo el utillaje está oculto).

Llamaremos a las herramientas del "utillaje" del ZigZag.

  • ExtFiboZigZag - permite mostrar la herramienta "ZigZag Fibonacci"

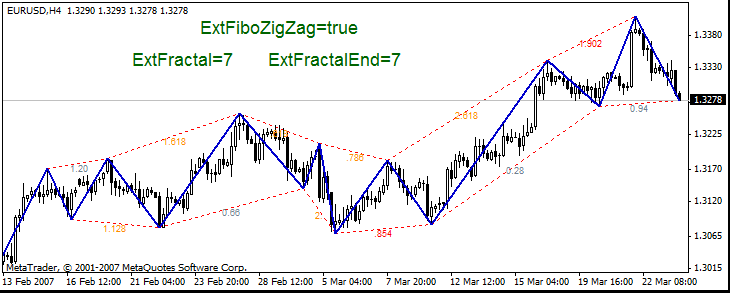
  • ExtFractal - el número de máximos/mínimos del ZigZag a partir de los cuales salen las líneas hacia otros máximos/mínimos del ZigZag
  • ExtFractalEnd - el número de máximos/mínimos del ZigZag a los cuales llegan las líneas. No habrán más líneas conectoras después de este máximo/mínimo.

Se empiezan a contar los máximos/mínimos a partir de la barra cero.

  • ExtFractalEnd - si es 0, las líneas conectoras van hacia arriba/abajo en dirección de la última ruptura del ZigZag, incluyendo la barra cero. El valor mínimo de ExtFractalEnd es 1.
  • ExtDelta - (tolerancia o Delta) desviación de los cálculos. También establece el valor de una posible zona de reversión. Oscila entre estos valores: 0 < ExtDelta < 1.
  • ExtDeltaType - elige el algoritmo para calcular la tolerancia Delta.

    0 - muestra el porcentaje de recuperación "como es", con dos decimales.
    1 - calcula la tolerancia mediante la siguiente fórmula: (retroceso - un número del conjunto seleccionado de los niveles de Fibonacci)
    2 - calcula la tolerancia mediante la siguiente fórmula: (retroceso - un número del conjunto seleccionado de los niveles de Fibonacci)/(un número del conjunto seleccionado de los niveles de Fibonacci)
    3 - muestra el porcentaje de recuperación "como es", con tres decimales.

    Según Larry Pesavento, es suficiente establecer la tolerancia en el orden del 4 % (0,04). Cuando el precio entra en la zona de tolerancia, los números se convierten en el número del conjunto seleccionado de los niveles de Fibonacci y tendrá el mismo color que el número del conjunto seleccionado de Fibonacci.
  • ExtSizeTxt - selecciona el tamaño de la fuente para visualizar los números
  • ExtLine - selecciona el color de las líneas conectoras
  • ExtPesavento - selecciona el color a partir del conjunto seleccionado de los niveles de Fibonacci
  • ExtGartley886 - selecciona el color de los números adicionales
  • ExtNotFibo - selecciona el color de todos los demás números en los patrones de Pesavento
  • ExtPPWithBars

    0 - muestra el valor del retroceso en los patrones de Pesavento
    1 - muestra el valor del retroceso en los patrones de Pesavento e indica entre paréntesis el número de barras entre los picos del ZigZag para el retroceso en cuestión.
    2 - muestra el valor del retroceso en los patrones de Pesavento e indica entre paréntesis el número de barras entre los picos del ZigZag por separado para el primer y el segundo segmento del ZigZag.
    3 - muestra entre paréntesis el tiempo de retroceso después del retroceso del precio. Se calcula el tiempo de retroceso como la relación entre el número de barras del segundo y primer segmento del ZigZag.
    4 - muestra entre paréntesis el tiempo de retroceso calculado como la relación entre el tiempo de formación del segundo y primer segmento.
    5 - muestra entre paréntesis la relación entre las áreas de los rectángulos que contienen dos segmentos adyacentes del ZigZag. Los segmentos del ZigZag son las diagonales de estos rectángulos.
    6 - muestra entre paréntesis el número de puntos y los porcentajes que representan la diferencia entre el precio de ruptura del ZigZag y el número del conjunto seleccionado de los niveles de Fibonacci (o del nivel correspondiente de Fibonacci) Por ejemplo, 2, 618 (7/2,81%). El número 7 entre paréntesis indica que nivel de Fibonacci de 2,618 es superior al máximo de la barra de 7 puntos o 2,81 %. Si es un 7 negativo, nivel de Fibonacci de 2,618 es inferior al máximo de la barra de 7 puntos.

Los patrones de Pesavento tienen la misma función que la herramienta llamada "niveles de Fibonacci".


Conjuntos de niveles de Fibonacci para distintos símbolos

En el ZUP, los conjuntos de niveles de Fibonacci están divididos en un conjunto estándar y en unos conjuntos alternativos. Al conjunto alternativo de números le llamaremos "números de Pesavento".

Mediante el parámetro ExtFiboType, podemos elegir entre el conjunto estándar y un conjunto alternativo de niveles de Fibonacci:

  • ExtFiboType = false - se muestra el conjunto estándar de niveles de Fibonacci
  • ExtFiboType = true - se muestra un conjunto alternativo de niveles de Fibonacci
  • ExtFiboChoice - define el conjunto alternativo de niveles de Fibonacci

Se muestra a continuación una lista completa de los niveles de Fibonacci (números) para distintos símbolos incluidos en ZUP.

  • Pesavento patterns

    Con la versión 58 del indicador ZUP:
    Conjunto estándar de los niveles de Fibonacci: 0,146-0,236-0,382-0,5-0,618-0,764-0,854-1,0-1,236-1, 618
    Números de Pesavento: 0,146-0,236-0,382-0,447-0,5-0,618-0,707-0,786-0,841-0,886-1, 0-1,128-1,272-1,414-1, 5-1,618-1,732-1,902-2,0-2,236-2,414-2,618-3,14-3,618-4,0

    En la versión 59, se puede elegir entre los conjuntos alternativos.
  • Conjunto estándar de niveles de Fibonacci

    0,146 - 0,236 - 0,382 - 0,5 - 0,618 - 0,764 - 0,854 - 1,0 - 1,236 - 1,618 - 4,236
  • Conjuntos alternativos de niveles de Fibonacci

    ExtFiboChoice = 0 - conjunto de números de Larry Pesavento: 0,25 - 0,382 - 0,5 - 0,618 - 0,707 - 0,786 - 0,841 - 1,0 - 1,128 - 1,272 - 1,414 - 1,618 - 2,0 - 2,618 - 4,0
    ExtFiboChoice = 1 - un conjunto de números que se usan para construir los patrones de Gartley: 0,382 - 0,447 - 0,5 - 0, 618 - 0,707 - 0,786 - 0,886 - 1,128 - 1,272 - 1,414 - 1, 618 - 2,0 - 2,236 - 2, 618 - 3,142 - 3,618
    ExtFiboChoice = 2 - un conjunto de números que se usan para construir los patrones de Gartley y otros números útiles. Números que se pueden añadir posteriormente aquí. Por el momento, se incluyen los siguientes números adicionales: 0,146 - 0,236 - 0,854 - 1,732 - 1,902
    ExtFiboChoice = 3 - un conjunto de números que apuntó Bryce Gilmore en su lista general de números de su libro "Geometry of Markets" (Geometría de los mercados) 2 [5;6] como los más importantes: 0,25 - 0,382 - 0,5 - 0,618 - 0,667 - 0,786 - 1,0 - 1,272 - 1,618 - 1,732 - 1,75 - 2,0 - 2,236 - 2,5 - 2,618 - 3,0 - 3,33 - 4,236 - 6,854

    En su libro "Geometry of Markets 2" (Geometría de los mercados 2), Bryce Gilmore ha dividido los números en dos grupos. A continuación se muestran los conjuntos de números del libro de Bryce Gilmore, tal y como lo ha sugerido John Edwards en el foro de ONIX.

    ExtFiboChoice = 4 - conjunto de números geométricos (Geometric) 0,146 - 0,186 - 0,236 - 0,3 - 0,382 - 0,486 - 0, 526 - 0,618 - 0,786 - 1, 0 - 1,272 - 1,618 - 1,902 - 2,058 - 2,618 - 3,33 - 4,236 - 5,388 - 6,854
    ExtFiboChoice = 5 - conjunto de números armónicos (Harmonic) 0,125 - 0,177 - 0,25 - 0,354 - 0,5 - 0,707 - 1,414 - 2,0 - 2,828 - 4,0 - 5,657 - 8,0
    ExtFiboChoice = 6 - conjunto de números aritméticos (Arithmetic) 0,167 - 0,333 - 0,577 - 0,667 - 1,5 - 1,732 - 3, 0 - 6,0
    ExtFiboChoice = 7 - conjunto de números áureos (Golden Mean) 0,236 - 0,30 - 0,486 - 0,618 - 0,786 - 1,272 - 1,618 - 2,058 - 2,618 - 3,33
    ExtFiboChoice = 8 - conjunto de números cuadrados (Square) 0,177 - 0,250 - 0,354 - 0,50 - 0,707 - 1,414 - 2,0 - 2,828 - 4,0 - 5,656
    ExtFiboChoice = 9 - conjunto de números cubo (Cube) 0,111 - 0,192 - 0,333 - 0,577 - 1,732 - 3,0 - 5,2 - 9, 0
    ExtFiboChoice = 10 - conjunto de números rectángulares (Rectangle) (Raíz 5 por Bryce Gilmore) 0,20 - 0,447 - 2,236 - 5,0
    ExtFiboChoice = 11 - conjunto de números adicionales útiles 1,414 * 1,618 = 2,288, 1,414 * 0,618 = 0,874, 2,618 * 1,272 = 3,330, 2,618 * 1,618 = 4,236, 1,618 / 2 = 0,809, 2,618 / 2 = 1,309, 1, 618 * 2 = 3,236, 1,732 * 2 = 3,464, 2,236 * 2 = 4,472
  • Niveles y expansiones de Fibonacci según la descripción de Robert Fisher [6], pero de una manera ligeramente distinta

    Números estándar: 0-0,146-0,236-0,382-0,5-0,618-0,764-0,854-1,0-1,236-1,618-2,618-4, 236-6,854
    Números de Pesavento: 0-0,382-0,5-0,618-0,707-0,786-0,854-0,886-1,0-1,128-1,272-1, 414-1,618-2,0-2,414-2, 618-4,0
  • Expansiones de Fibonacci como en MetaTrader

    Números estándar: 0,236-0,382-0,5-0,618-0,764-0,854-1,0-1,236-1,618-2,0-2,618
    Números de Pesavento: 0,382-0,5-0,618-0,707-0,786-0,886-1,0-1,272-1,414-1,618-2,0-2, 618
  • Abanicos de Fibonacci. Se muestran los abanicos estáticos de Fibonacci con el tridente estático de Andrews. Se muestran los dinámicos en el primer segmento

     Números estándar: 0,236-0,382-0,5-0,618-0,764-0,854
    Números de Pesavento: 0,236-0,382-0,5-0,618-0,786-0,886
  • Abanicos de Fibonacci en puntos aleatorios y a lo largo de la línea mediana del tridente de Andrews

    Números estándar: 0,236-0,236-0,382-0,5-0,618-0,764-0,854-1,0:1,618-2,618
    Números de Pesavento: 0,382-0,5-0,618-0,707-0,786-0,886-1,0-1,272-1,414-1,618-2,618
  • Líneas de reacción (RL)

    Números estándar: 0,236-0,382-0,5-0,618-0,764-1,0-1,618-2,0-2,618-4,0
    Números de Pesavento: 0,382-0,5-0,618-0,707-0,786-0,886-1,0-1,128-1,272-1,414-1,618-2, 0-2,414-2,618-4, 0
  • Líneas de advertencia (UWL y LWL)

    Números estándar: 0,618-1,0-1,618-2,0-2,618
  • Tiempo de Fibonacci

     Números estándar: 0-1-1,236-1,382-1,5-1,618-1,764-1,854-2,0-2,236-2,618-3,0-2,618
    Números de Pesavento: 0-1-1,382-1,5-1,618-1,707-1,786-1,886-2,0-2,272-2,414-2,618-3, 0-3,414-3,618-4, 0
  • Niveles de Versum

    Números estándar - 23,6-38,2-45,5-50,0-54,5-61,8-76,4
    con números de Pesavento - 23,6-38,2-44,7-50,0-61,8-78,6-88,6

Esta lista está sujeta a cambios en el futuro.


Numeración de las rupturas y segmentos del ZigZag

Se basan muchas herramientas en algún segmento o ruptura del Zigzag. Por ejemplo:

  • ExtFiboStaticNum - número del segmento del ZigZag en el cual se construirán los niveles estáticos de Fibonacci.
  • ExtFiboExpansion - expansiones de Fibonacci como en MetaTrader; indican la ubicación de la ruptura del ZigZag donde se ubica el primer punto de la expansión de Fibonacci.

El siguiente gráfico muestra la numeración de las rupturas en color rojo y los segmentos en verde azulado.



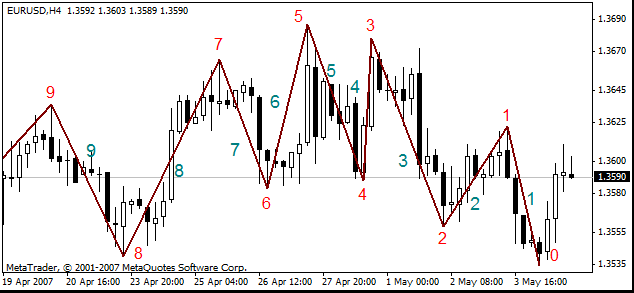
Si se construye algo en el primer segmento o en la ruptura cero (0), la herramienta cambiará de manera dinámica con los cambios del precio. Si las formas no tocan el primer segmento o la ruptura cero, la herramienta no cambiará y en consecuencia será considerada estática. En el ZUP, se construyen todas las herramientas gráficas en los nueve primeros segmentos o los diez primeros picos (0-9). Pero se pueden construir los patrones de Pesavento en todas las rupturas, no sólo en las diez primeras.

Nivels dinámicos y estáticos de Fibonacci. Expansiones de Fibonacci

Las herramientas gráficas incorporadas en el ZUP pueden ser estáticas o dinámicas. Las herramientas gráficas estáticas están ancladas a las rupturas del ZigZag ya existentes, es decir, con las rupturas que ya no van a cambiar. Las herramientas gráficas dinámicas están ancladas al final del primer segmento del ZigZag que siempre cambia de ubicación.

Las herramientas gráficas dinámicas permiten tomar rápidamente una decisión. Si hay un cambio en el mercado, podremos ver la posible tendencia observando la forma de la herramienta gráfica dinámica. Nada más cambia el primer segmento del ZigZag, se reconstruirá automáticamente la herramienta gráfica dinámica.

Los niveles dinámicos de Fibonacci se construyen en el primer segmento que cambia del ZigZag:

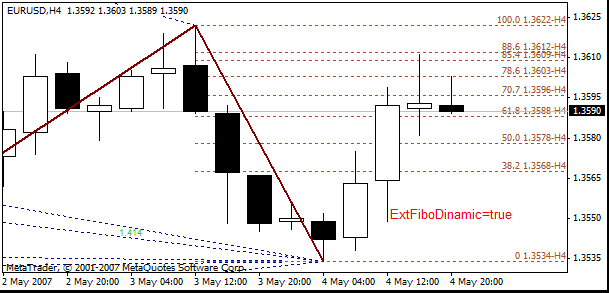
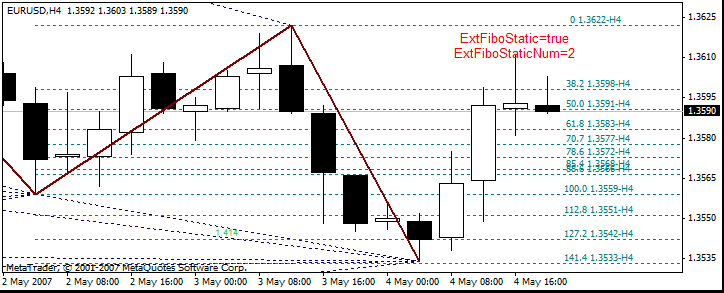
Los niveles estáticos de Fibonacci se construyen en los segmentos 2-9.


Los parámetros que se usan para trabajar con los niveles de Fibonacci son:

  • ExtFiboType = true - niveles de Fibonacci con números de Pesavento, false - niveles de Fibonacci estándar
  • ExtFiboDinamic - permite mostrar los niveles dinámicos de Fibonacci. Se mostrarán los niveles dinámicos de Fibonacci en el primer segmento del ZigZag
  • ExtFiboStatic - permite mostrar los niveles estáticos de Fibonacci
  • ExtFiboStaticNum - número del segmento del ZigZag a partir del cual se empiezan a mostrar los niveles estáticos de Fibonacci
  • ExtFiboS y ExtFiboD - seleccionan el color de los niveles estáticos y dinámicos de Fibonacci

Se muestra aquí el nivel de Fibonacci, por ejemplo 61,8, el precio para los siguientes niveles de Fibonacci y el nombre del período del tiempo en el cual se muestran los niveles de Fibonacci. Es importante conocer el período de tiempo cuando se trabaja en el modo DT. Se muestran los valores dinámicos de Fibonacci muy cerca del borde de la ventana del gráfico. Los valores estáticos de Fibonacci están más separados del borde de la ventana del gráfico.

Cuando se muestran los niveles estáticos y dinámicos de Fibonacci al mismo tiempo, sus valores se superponen parcialmente. Esto puede complicar la visualización de la información. Sin embargo, MetaTrader 4 no permite mostrar los valores estáticos de Fibonacci a cierta distancia del borde de la ventana del gráfico. El nivel dinámico de Fibonacci cambia automáticamente al cambiar el tamaño o la ubicación del primer segmento del ZigZag.

  • ExtFiboCorrectionExpansion conmuta los niveles estáticos y dinámicos de Fibonacci para mostrar las correcciones o expansiones de Fibonacci.

Se mostrarán las expansiones de Fibonacci como las describe Robert Fisher en su libro "The New Fibonacci Trader" (El nuevo trader de Fibonacci) [6]. En este caso, se considera el tamaño del segmento del ZigZag como base. Parece que las expansiones prolongan el segmento. Al igual que en el libro de Robert Fisher, se muestran los números de las expansiones con el prefijo Fe.


  • ExtFiboExpansion - expansiones de Fibonacci como en MetaTrader; establecen la ubicación de la ruptura del ZigZag donde se ubica el primero de lo tres puntos de la expansión de Fibonacci.

    ExtFiboExpansion<2 - no se muestran las expansiones de Fibonacci
    ExtFiboExpansion=2 - expansión dinámica de Fibonacci
    ExtFiboExpansion>2 -

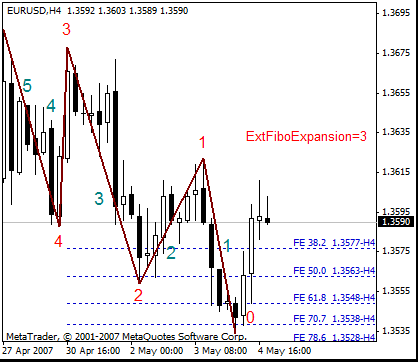
Tridente de Andrews ( http://www.trading-naked.com/alan_andrews_course_1.htm )

El tridente y las estrategias de Andrews que han sido utilizados con esta herramienta fueron descritos por Mikula Patrick (http://www.mikulaforecasting.com/books/aabook.htm). Putnik hizo también una descripción muy detallada de cómo se puede construir el tridente de Andrews en el foro de ONIX: http://onix-trade.net/forum/index.php?showtopic=8249 Además, la construcción del tridente de Andrews fue llevada a cabo en el ZUP por petición de Putnik.

La lista completa de los parámetros para trabajar con el tridente de Andrews:

  • ExtPitchforkDinamic

    > 0 ( = 1) muestra el tridente dinámico de Andrews de los dos últimos extremos del ZigZag
    = 2 - muestra el tridente de Andrews con una línea mediana del 50 %
    = 3 - muestra el 50 % del tridente de Andrews (según la interpretación de Vinsant, un miembro del foro de ONIX)
    = 4 - muestra las líneas de Schiff
  • ExtPitchforkStatic

    > 0 ( = 1 ) muestra el tridente estático de Andrews de los extremos del ZigZag que llevan el número ExtPitchforkStaticNum
    = 2 - muestra el tridente de Andrews con una línea mediana del 50 %
    = 3 - muestra el 50 % del tridente de Andrews (según la interpretación de Vinsant)
    = 4 - muestra las líneas de Schiff
  • 3 <= ExtPitchforkStaticNum <= 9 - número del pico del ZigZag a partir del cual empieza el tridente.
  • ExtLinePitchforkS y ExtLinePitchforkD establecen el color del tridente estático y dinámico.
  • ExtPitchforkStaticColor - establece el color de relleno del tridente estático y habilita el relleno. Se habilita la visualización del relleno seleccionando el color y se inhabilita asignando el valor NONE (ninguno) a este parámetro.
  • ExtFiboFanDinamic - permite mostrar los abanicos dinámicos de Fibonacci.
  • ExtFiboFanStatic - permite mostrar los abanicos estáticos de Fibonacci.
  • ExtFiboFanExp - el número de segmentos de los abanicos de Fibonacci.. True=6, false=4.
  • ExtFiboFanHidden - permite mostrar las etiquetas de los segmentos del abanico de Fibonacci. Sólo procesa los abanicos dinámicos y estáticos de Fibonacci.
  • ExtFiboFanD - establece el color de los abanicos dinámicos de Fibonacci.
  • ExtFiboFanS - establece el color de los abanicos estáticos de Fibonacci.
  • ExtFiboFanMedianaStaticColor y ExtFiboFanMedianaDinamicColor - establecen el color de los abanicos de Fibonacci en la línea mediana de los tridentes estáticos y dinámicos y muestran los correspondientes abanicos de Fibonacci.
  • ExtPitchforkStyle - establece el estilo de salida del tridente:

    0 - línea continua
    1 - línea de trazos
    2 - línea de puntos
    3 - línea de puntos y trazos
    4 - línea de puntos dobles y trazos
    5-10 - establece el grosor de la línea continua
  • ExtFiboTime1 - permite mostrar la zona 1 del tiempo de Fibonacci.
  • ExtFiboTime2 - permite mostrar la zona 2 del tiempo de Fibonacci.
  • ExtFiboTime1C - establece el color de líneas de la zona 1 del tiempo de Fibonacci.
  • ExtFiboTime2C - establece el color de líneas de la zona 2 del tiempo de Fibonacci.
  • ExtPivotZoneStaticColor - establece el color de relleno de la zona de giro estática.
  • ExtPivotZoneDinamicColor - establece el color de relleno de la zona de giro dinámica.
  • ExtPivotZoneFramework - permite mostrar la zona de giro como un cuadro (por defecto) o como un rectángulo relleno.
  • ExtUTL - permite mostrar la línea de control superior del tridente de Andrews.
  • ExtLTL - permite mostrar la línea de control inferior del tridente de Andrews.
  • ExtUWL - permite mostrar las líneas superiores de alertas.
  • ExtLWL - permite mostrar las líneas inferiores de alertas.
  • ExtISLDinamic - permite mostrar las líneas de señales internas del tridente dinámico de Andrews.
  • ExtISLStatic - permite mostrar las líneas de señales internas del tridente estático de Andrews.
  • ExtRLine - permite mostrar las líneas de reacción a lo largo del tridente de Andrews.
  • ExtRLineBase - oculta las líneas que indican la dirección de la reacción .

En la siguiente figura, se muestra un ejemplo de construcción del tridente de Andrews.


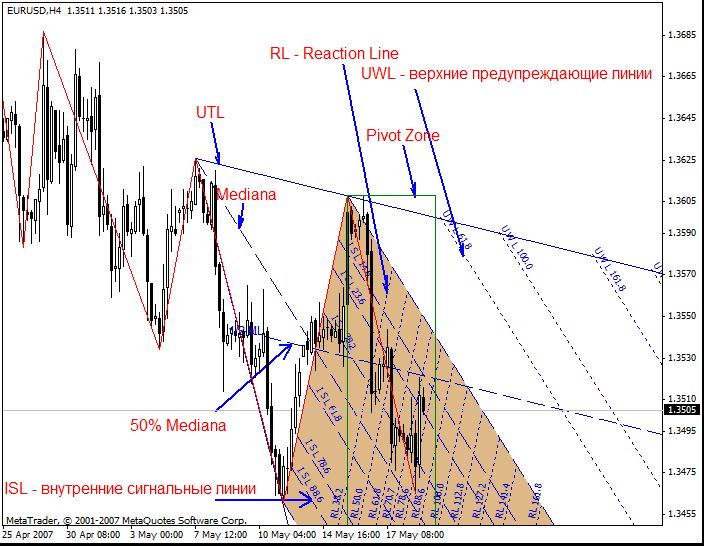
Observación:

Las líneas de reacción se dibujan mediante los canales de Fibonacci. Pueden haber errores en su dibujo en muchos casos. Estos errores son muy pequeños, pero se pueden acumular en un período de tiempo mayor. Es imposible dibujarlas sin errores. No se puede dibujar sin errores con la herramienta estándar de los canales de Fibonacci en MetaTrader 4, debido a la relación particular de los canales de Fibonacci con las velas. En mi primer artículo, ZUP - ZigZag universal con Patrones de Pesavento. Primera parte, ya había mencionado este error. Esta es la razón por la cual hay que utilizar las líneas de reacción con mucho cuidado en esta implementación. Sólo los desarrolladores de MetaTrader 4 pueden corregir este error.

  • ExtPitchforkCandle - permite mostrar el conjunto de tridentes a partir de las velas seleccionadas
  • ExtPitchfork_1_HighLow - cuando se construye el tridente en las velas seleccionadas, determina si el primer punto de construcción del tridente va a ser el máximo o el mínimo de la vela
  • ExtDateTimePitchfork_1, ExtDateTimePitchfork_2, ExtDateTimePitchfork_3 - establece la fecha y la hora de las velas, durante las cuales se construirá el tridente de Andrews para el primer punto, el segundo y el tercero respectivamente.

Cómo mostrar un conjunto de tridentes en las velas seleccionadas

Vamos a seleccionar las velas donde mostraremos el tridente. Colocamos el cursor del ratón encima de estas velas. Después apuntamos la fecha y la hora de las velas por separado en una hoja de papel y abrimos el panel del indicador para modificar sus parámetros. En los parámetros ExtDateTimePitchfork_1, ExtDateTimePitchfork_2, ExtDateTimePitchfork_3, introducimos la fecha y la hora de las velas. Mediante ExtPitchfork_1_HighLow, decidimos si vamos a construir el primer punto del tridente a partir del máximo o del mínimo. Set ExtPitchforkCandle = true. Mediante ExtPitchforkCandle, decidimos si vamos a construir el conjunto de tridentes en los extremos del ZigZag o en los extremos de las velas seleccionadas.

Al seleccionar ExtPitchforkStatic>0, se construirá el conjunto de tridentes estáticos en las velas seleccionadas y se mostrará en la pantalla. Se puede guardar el conjunto de tridentes. Si el tercer punto del tridente se encuentra en la barra cero, se mostrará el tridente dinámico y no se puede guardar.
A continuación se muestra un ejemplo de construcción del tridente de Andrews en las velas seleccionadas. Las velas a las cuales está anclado el tridente son las velas por defecto en el indicador ZUP. Este gráfico se hizo mediante el ZUP_v63. En las versiones anteriores, la construcción de las líneas de reacción RL*** llevaba errores en este gráfico debido a las características de los canales de Fibonacci en MetaTrader 4. Las líneas de reacción se dibujan mediante los canales de Fibonacci.

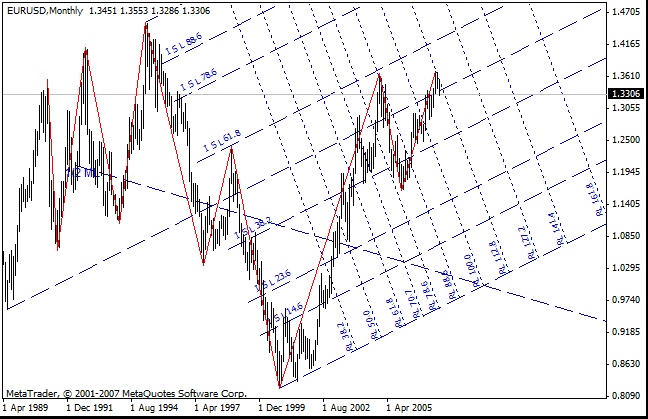
El parámetro ExtSave permite guardar el conjunto de tridentes estáticos, el tiempo de Fibonacci y los niveles estáticos de Fibonacci. Este parámetro no guarda el relleno del canal del tridente estático.

Cómo trabajar con ExtSave:

  1. Hay que construir el conjunto de tridentes de Andrews y todas las líneas auxiliares.
  2. Abrir el panel de configuración del indicador y establecer ExtSave=True.
  3. Cerrar el panel de configuración. Se dibujará el conjunto de tridentes en el gráfico.
  4. Reabrir el panel de configuración del indicador y establecer ExtSave=False.
  5. Cerrar el panel. Se mostrará el conjunto guardado de tridentes en el gráfico. Se mostrará el mismo conjunto de tridentes encima del conjunto anterior, pero al borrar el indicador se borrará el segundo conjunto (el que se muestra encima del primero) y sólo se mantendrá el primer conjunto en el gráfico.

Si no se llevan a cabo los puntos 4 y 5, se guardará el conjunto de tridentes en el gráfico con sus parámetros actuales cada vez que cambian los parámetros del indicador. Si se borra el indicador, se mantendrán unos conjuntos de tridentes en el gráfico, superpuestos unos encima de otros o ligeramente desplazados.

Hay que guardar las herramientas (tridente, abanicos, etc.) en el período de tiempo más corto. Si se guardan las herramientas en un período de tiempo más largo y al cambiar a un período de tiempo más corto, se dibujarán las herramientas guardadas empezando desde la primera vela del período más corto, esta vela puntual está incluida en el período más largo. Esta es otra característica de MetaTrader 4. Al cambiar a otro período de tiempo, las herramientas guardadas se mostrarán con errores.

Si no se guardan las herramientas y sólo se muestran mediante el ZUP, se dibujarán correctamente. En el modo DT del indicador ZUP, se vuelven a calcular las rupturas del ZigZag y se reconstruyen en las velas donde realmente tiene lugar el máximo y el mínimo al cambiar el período de tiempo. De este modo se vuelven a anclar las herramientas a los puntos con más precisión. No se han observado distorsiones en el dibujo.


Canales de micmed

Los canales de micmed representan una nueva herramienta gráfica desarrollada por micmed, un miembro del foro de ONIX. Está basada en el tridente de Andrews, pero los puntos de anclaje del tridente se seleccionan de un modo especial.

A continuación podemos ver algunos fragmentos de los mensajes del foro de ONIX (traducidos al inglés por MetaQuotes Software Corp.):

... tal y como se muestra en las capturas de pantalla, se pueden añadir también al conjunto de tridentes, los llamo "sección áurea". Experimentando con VL (*), he descubierto que estos tridentes retienen los canales correctamente más a menudo...

Esto explica el interés en este dibujo: la sección áurea construida de acuerdo con los requisitos mencionados funciona también como un canal, aunque fue construida antes de que se muestren los límites del canal clásico. Esto está en completa consonancia con los números de Fibonacci...

... en realidad, estos no son tridentes, pero era cómodo construir usándolos. En cuanto a la construcción, he puesto el punto 1 en la línea vertical construida desde el punto B. Estas son algunas observaciones:

  1. Si la diagonal AB es más corta que la diagonal BC, construyo a una distancia del 32,8 % desde el vértice B.
  2. Si la diagonal AB es más larga que la diagonal BC, entonces a una distancia de 61,8 % desde el vértice B.
  3. Hay también 50 % 2-3 triángulos, generalmente en los giros y se siguen.
  4. Si se traspasa el canal, el punto 38,2 cambiará a 61,8 y viceversa (capturas de pantallas).

* - VL - Niveles de Versum (Versum Levels); un nueva herramienta gráfica a describir más adelante.

Parámetros:

  • ExtCM_0_1A_2B - permite mostrar los canales de micmed. Su valor puede ser 1, 2, 3 o 4. El valor por defecto 0, indica que se construirá el tridente normal de Andrews.
  • ExtCM_Fibo - establece la ubicación de la línea mediana del tridente de Andrews para dibujar los canales de micmed. Su valor puede ser 0 o 1.

El parámetro ExtCM_0_1A_2B ancla todos los tridentes de Andrews (ver más arriba) a otros puntos. Para dibujar los canales de micmed hay que construir primero los tridentes de Andrews. Después se seleccionan nuevos puntos de anclaje para los tridentes mediante el parámetro ExtCM_0_1A_2B. El valor del parámetro ExtCM_0_1A_2B depende de la longitud de AB y BC.

El autor describe a continuación cómo se pueden dibujar los canales:

A partir de la versión 55, se construyen los canales micmed en el indicador ZUP mediante la herramienta llamada "tridente de Andrews en tres puntos", se seleccionan los puntos 2 y 3 mediante los picos, al igual que en el tridente habitual, mientras que el punto 1 se selecciona mediante dos parámetros:

  • ExtCM_0_1A_2B (puede ser 0, 1, 2, 3, 4) define la línea vertical, donde se ubica el punto 1

    correspondiente, si es
    0 - no se dibujan los canales de micmed, se dibuja un tridente estándar
    1 - se selecciona el punto 1 en la línea vertical desde el pico A de los niveles de Fibonacci AB
    2 - se selecciona el punto 1 en la línea vertical desde el pico B de los niveles de Fibonacci BC
    3 - se selecciona el punto 1 en la línea vertical desde el pico A de los niveles de Fibonacci BC
    4 - se selecciona el punto 1 en la línea vertical desde el pico B de los niveles de Fibonacci que se calculan con el siguiente algoritmo: si AB>BC, el valor es 0,618; si AB<BC, el valor es 0,382
  • ExtCM_Fibo (puede variar entre 0,0 y 1,0) define el valor para el nivel de Fibonacci del punto 1

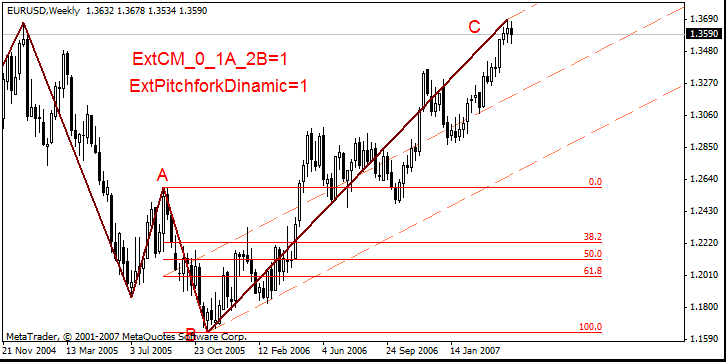
Ejemplos de dibujo:

  • ExtCM_0_1A_2B = 1, ExtCM_Fibo = 0,618



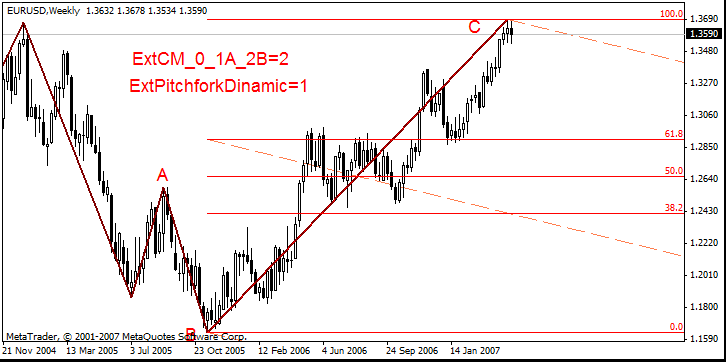
  • ExtCM_0_1A_2B = 2, ExtCM_Fibo = 0,618



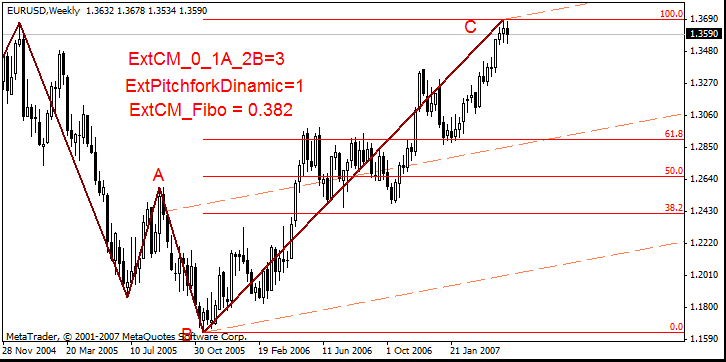
  • ExtCM_0_1A_2B = 3, ExtCM_Fibo = 0,382




Analizando el historial del indicador ZUP_v54 con los parámetros Extindicator=6, minBars=25, en EURUSD diario desde 1989 - se construyeron 103 triángulos, donde

  • si AB>BC, se selecciona el punto 1 en la línea vertical del pico B con el valor 0,618 (31 triángulos)
  • si AB<BC, se selecciona el punto 1 en la línea vertical del pico B con el valor 0,382 (31 triángulos)

Se ha observado también que en los canales atravesados cambia el valor de Fibonacci para el punto 1 de 0,382 a 0,618 y viceversa (cambio de dirección de la tendencia), además del valor 0,5 en las tendencias planas (40 triángulos)

El modo 3 es muy útil cuando los picos se suceden muy rápidamente. De lo contrario, el canal tendrá un angulo muy agudo.

Quiero compartir mi punto de vista sobre una cosa muy importante. En la construcción de un canal en el modo 4 (tal vez en los otros también, pero en este es automático), el precio SIEMPRE(!) alcanza el nivel de intersección de RL 161,8 con la línea mediana del canal y casi siempre en el intervalo de RL 100 - 161,8.

Estos eran fragmentos de los mensajes de micmed. Se hizo esto para entender mejor cómo funciona esta nueva herramienta gráfica "canales de micmed". Se muestran los niveles de Fibonacci en el gráfico para poder observar el algoritmo de construcción de los canales. El ZUP que contiene estas herramientas gráficas no muestra los niveles de Fibonacci.

Niveles de Versum

Esta herramienta gráfica fue desarrollada por Versum, un miembro de los foros KBPauk y ONIX. Es posible también que otros hayan implementado esta herramienta. En el ZUP, esta herramienta se llama "Niveles de Versum".

Parámetros:

  • ExtVLStaticColor - permite mostrar los niveles estáticos de Versum seleccionando el color
  • ExtVLDinamicColor - permite mostrar los niveles dinámicos de Versum seleccionando el color
  • ExtVLStaticNum - establece el número del pico en el cual se van a mostrar los niveles de Versum.

Esta herramienta complementa el tridente de Andrews y se parece al abanico de Fibonacci. Al igual que el tridente de Andrews, funciona en base a la línea mediana. La línea mediana del tridente de Andrews coincide con el 50 % del nivel de VL (Niveles de Versum). Se muestra a continuación un ejemplo de dibujo de VL. Se muestran los niveles de Fibonacci en el gráfico para poder ver cómo se construye esta herramienta. El ZUP que contiene estas herramientas gráficas no muestra los niveles de Fibonacci.



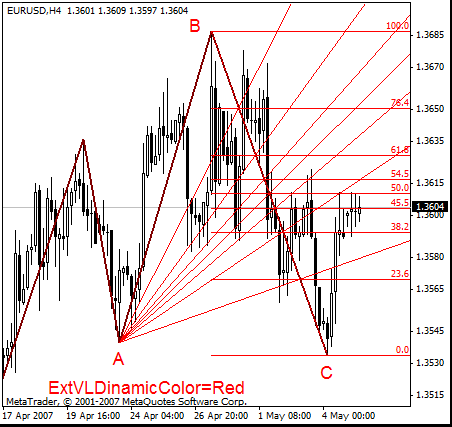
A continuación podemos ver algunos fragmentos de los mensajes de Versum (traducidos al inglés por MetaQuotes Software Corp.):

Esto puede ser considerado un abanico (son líneas que salen del mismo punto) y un abanico de Fibonacci ya que se usa un segmento que cruza estas líneas y que está dividido en varias partes mediante el nivel de Fibonacci (una herramienta que estaba al alcance)... Podemos observar en la figura 1 que el segmento BC está dividido en varios intervalos mediante el nivel de Fibonacci. Se dibujan unas líneas a partir el punto A del pico o valle precedente y los puntos de intersección del nivel de Fibonacci con el segmento BC. Estos son los niveles previstos del precio.

¿Y qué tenemos?

  1. Niveles (es lo más importante) que cambian con el tiempo.
  2. A partir de estas variaciones se desarrollan los patrones de Gartley y otras figuras y modelos, pero son visibles "después"
  3. La evolución prevista de la tendencia.

¿Cómo se usa?

Si el precio iguala o excede el nivel de la línea del 50 % (pasa por el punto que divide el nivel del 50 %), podemos decir (aunque la probabilidad no sea del 100 %) que la tendencia mantiene la misma dirección. Si está por debajo de la línea del 50 %, podemos decir que la tendencia actual pude cambiar...

Observaciones:

  1. No he sido muy estricto con la obtención los resultados, hasta un pip. Creo que esto debería ser considerado como un área.
  2. Tampoco he considerado los niveles de Fibonacci como una solución mágica. Es posible que otras proporciones entre los intervalos del segmento puedan dar mejores resultados.

Abanicos independientes de Fibonacci

En los abanicos de Fibonacci que trabajan junto con el tridente de Andrews, se pueden mostrar los abanicos independientes de Fibonacci. Se muestran estos abanicos de Fibonacci en los nueve primeros segmentos de ZigZag o en sus primeros diez extremos. Se pueden mostrar seleccionando el color mediante el parámetro ExtFiboFanColor. Se ordenan los abanicos mediante el parámetro ExtFiboFanNum.

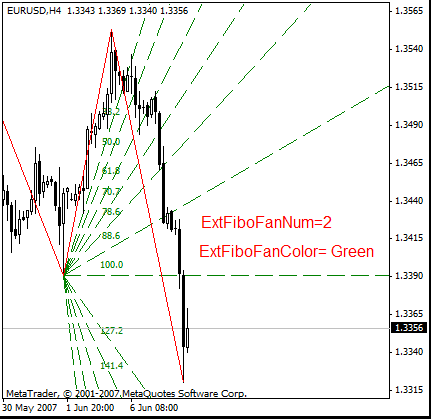
El modo avanzado

Se analiza el mercado con más eficiencia cuando los picos y valles del ZigZag pertenecen a una onda del mismo nivel. Ocurre a menudo que el ZigZag identifica picos y valles como "excesivos" para el nivel de una onda. No se recomienda construir herramientas integradas en el ZUP en estos extremos "excesivos". Este tema requiere un estudio especial y está abierto a todos los interesados...

Se ha creado el modo avanzado especialmente para construir herramientas en los "buenos" extremos. Las siguientes herramientas pueden trabajar en el modo avanzado:

  1. Tridente estático
  2. Niveles estáticos de Fibonacci
  3. Expansiones estáticas de Fibonacci
  4. Abanicos independientes de Fibonacci
  5. Niveles de Versum
  6. Canales de micmed

El conjunto de los tridentes de Andrews es todo lo que hay sobre los tenedores. Se construyen las líneas del conjunto de tenedores a partir de ciertos puntos de los tenedores. Por ejemplo, se dibujan las líneas de control a partir del primer punto del tenedor mediante el segundo y el tercero. En el modo avanzado, todas las líneas están asociadas a sus puntos correspondientes en el tenedor, sea cual sea su ubicación.

Si se establecen los parámetros de las cinco herramientas que pueden funcionar en el modo avanzado igual que antes, no habrá ninguna diferencia.

En el modo avanzado:

  1. Para los tridentes estáticos, en lugar de indicar un sólo número que indica el primer pico, habrá que definir tres picos en los cuales se construirá el tridente. Esto será, por ejemplo, así: ExtPitchforkStaticNum=741.





    El pico 7 se corresponde con el primer punto del tridente, el 4 con el segundo punto y el pico 1 con el tercer punto del tridente. En este caso, se construye la línea mediana del 50 % desde el punto medio del segmento que une los puntos 1 y 2 del tridente (extremos 7 y 4 del ZigZag) y pasa por la línea mediana del segmento que une los puntos 2 y 3 del tridente (extremos 4 y 1 del ZigZag). Las líneas de reacción están ancladas con los puntos 2 y 3 del tridente.

    Si la última cifra del parámetro ExtPitchforkStaticNum es superior a 0, se mostrará un tridente estático. Si es igual a 0, el tridente será dinámico. Pero nada más aparece un nuevo segmento en el ZigZag, el tridente vuelve a ser estático. Si se cambia cualquier parámetro del indicador cuando se cambia del tridente dinámico al estático, se mostrará de nuevo el tridente dinámico.

    Importante: Las cifras (741) deben alternar los picos y valles. No se puede construir un tridente si se especifican consecutivamente dos picos o dos valles. Esto significa que se tiene que alternar números pares e impares.
  2. Para los niveles estáticos de Fibonacci en el modo avanzado, se deben especificar dos extremos del ZigZag en los cuales se construirá el nivel de Fibonacci. Por ejemplo, ExtFiboStaticNum=72.



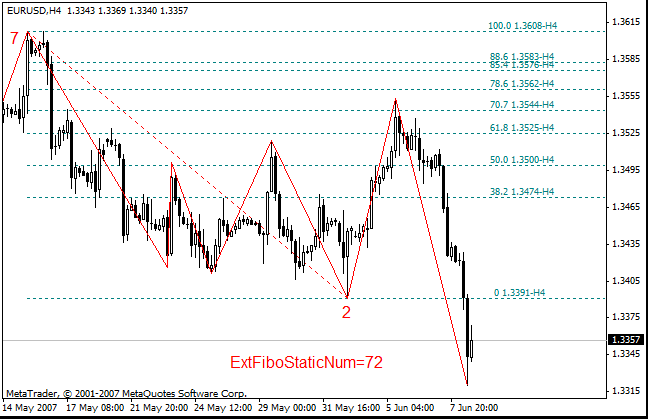
  3. En el modo avanzado, se deben construir las expansiones estáticas de Fibonacci en tres extremos del ZigZag. Ejemplo: ExtFiboExpansion=721.





    En el ejemplo anterior, se construyen las expansiones de Fibonacci como si estuvieran dibujadas en MetaTrader 4. Pero si se muestran los niveles de Fibonacci (herramienta 2) y ExtFiboCorrectionExpansion = true, se mostrarán las expansiones de Fibonacci en lugar de los niveles de Fibonacci. Sin embargo, en este caso se construyen las expansiones en dos puntos y coinciden con lo que está descrito en el libro de Robert Fisher.
  4. En el modo avanzado, se construyen los abanicos de Fibonacci en dos extremos. Ejemplo: ExtFiboFanNum=74



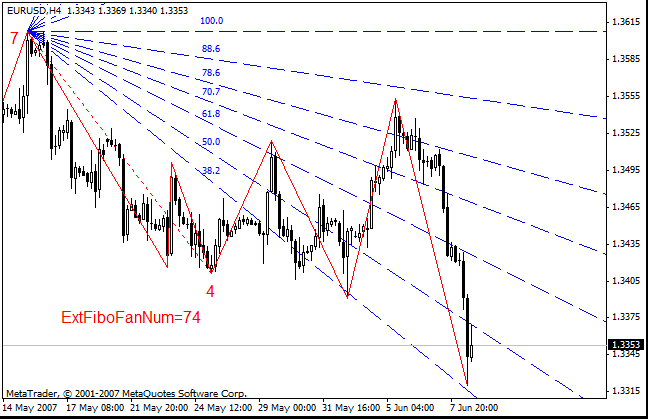
  5. Niveles de Versum:



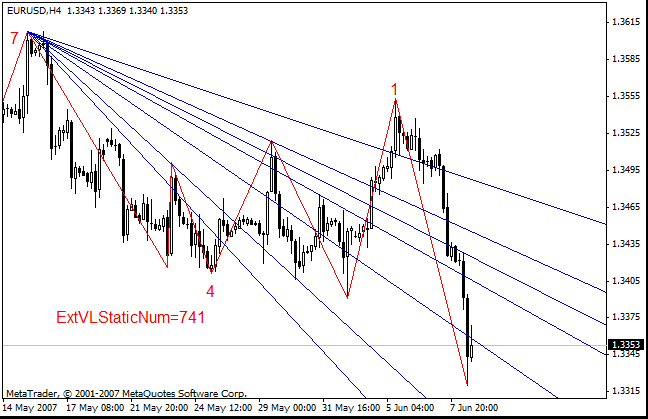
  6. Canales de micmed:




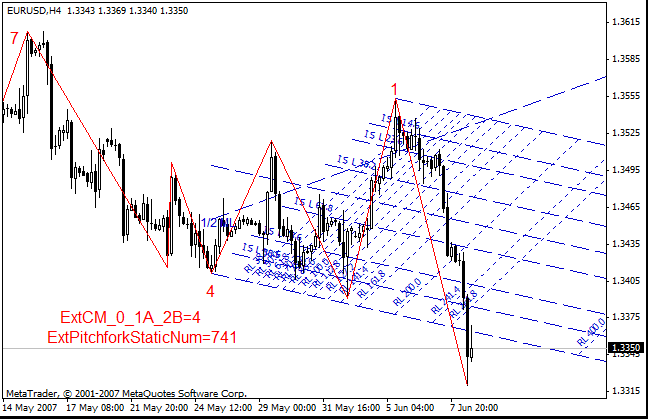
Me gustaría subrayar una vez más lo siguiente:

En el modo avanzado, se tienen que alternar los picos y valles para todas las herramientas. No se puede construir la herramienta con dos picos o valles consecutivos. Con el término "consecutivos" me refiero a dos cifras consecutivas que definen los extremos en un parámetro.

Todas las herramientas en el modo avanzada pueden ser estáticas o dinámicas. Si la última cifra establecida en el parámetro es 0, la herramienta cambiará dinámicamente.

Arcos de Fibonacci

Ya es posible construir los arcos de Fibonacci en el ZUP_v63. Todos los parámetros en el artículo son para la versión ZUP_v63.

Parámetros:

  • ExtArcDinamicNum - establece el número de rupturas del Zigzag en las cuales se construirán los arcos dinámicos de Fibonacci;
  • ExtArcStaticNum - establece el número de rupturas del Zigzag en las cuales se construirán los arcos estáticos de Fibonacci;
  • ExtArcDinamicColor - establece el color de los arcos dinámicos de Fibonacci;
  • ExtArcStaticColor - establece el color de los arcos estáticos de Fibonacci;
  • ExtArcDinamicScale - establece la escala de los arcos dinámicos de Fibonacci: 0: escala automática; >0: escala definida por el usuario;
  • ExtArcStaticScale - establece la escala de los arcos estáticos de Fibonacci: 0: escala automática; >0: escala definida por el usuario.

Los arcos tienen dos puntos de anclaje.

  • Para configurar el parámetro ExtArcStaticNum=21:

    2 - el punto central del arco estático, muestra el número del pico/valle del ZigZag
    1 - el punto 100 % del arco, también muestra el número del pico/valle del ZigZag
  • Para configurar el parámetro ExtArcStaticNum=12

    1 - el punto central
    2 - el punto 100 %

Si, por ejemplo, establecemos ExtArcStaticNum=3, el punto central estará ubicado en la ruptura 3 del ZigZag y el 100 % estará en la ruptura 2.

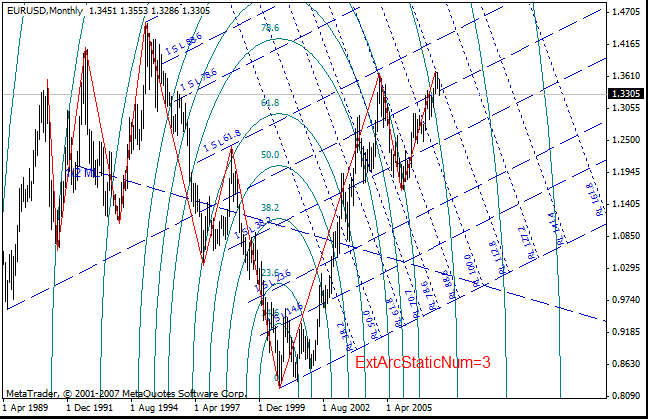
Si establecemos ExtArcStaticNum=83, el punto central estará ubicado en la ruptura 8 del ZigZag y el 100 % estará en la ruptura 3. También se pueden establecer el punto central y el 100 % entre dos picos o dos valles, por ejemplo: ExtArcStaticNum=42.

Se pueden dibujar los arcos estáticos entre cualquiera de las rupturas del ZigZag, desde la ruptura 1 hasta la ruptura 9. Se construyen los arcos dinámicos entre la "ruptura" 0 y cualquiera de las 9 rupturas siguientes.

Si establecemos ExtArcDinamicNum=8, el punto central estará en el punto 0 del ZigZag y el 100 % en la ruptura 8. Si establecemos ExtArcDinamicNum=80, el punto central estará en la ruptura 0 del ZigZag y el 100 % en el punto 0.

Se calibra el arco a lo largo del segmento del ZigZag en el cual se ha construido. El segmento es la línea que conecta el punto central con el punto 100 % al que se anclan los puntos del arco. Se calibra automáticamente mediante los parámetros ExtArcDinamicScale=0 y ExtArcStaticScale=0. Los cálculos son automáticos y se llevan a cabo de la siguiente manera: Se calcula el número de puntos entre el punto central y el punto 100 % del arco y se divide por el número de barras que hay entre estos puntos. El resultado establece el valor de la escala para el dibujo de los arcos. Por lo tanto, se ajusta la escala de los arcos.

Si se introduce un número superior a 0 en los parámetros ExtArcDinamicScale y ExtArcStaticScale, se calibrará (se ajustará la escala) el arco con este número.

Otras características del indicador

Mediante ZigZag ExtIndicator = 1, ExtIndicator = 2 y ExtIndicator = 3 y el parámetro chHL=true, se pueden mostrar los niveles de reconocimiento en el gráfico. Los niveles de reconocimiento permiten visualizar el canal. Si el precio traspasa el lado opuesto del canal, el ZigZag dibujará un nuevo segmento.

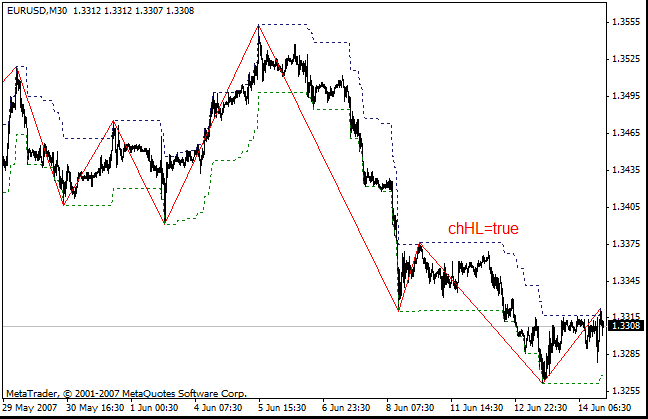
Mediante el parámetro PeakDet = true, se muestran los niveles de los mínimos y máximos anteriores del ZigZag.

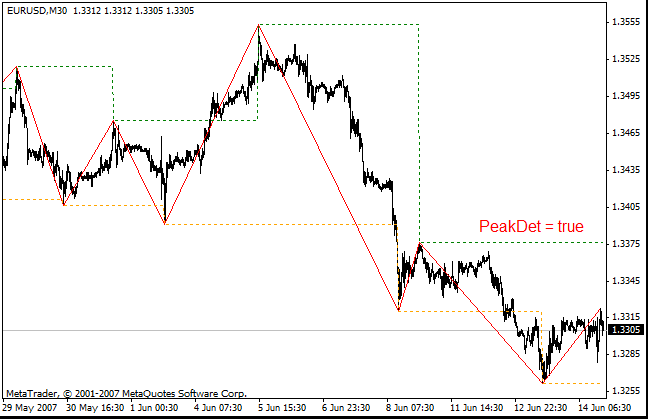
Se toman los parámetros chHL y PeakDet del Zizag original de Alex.

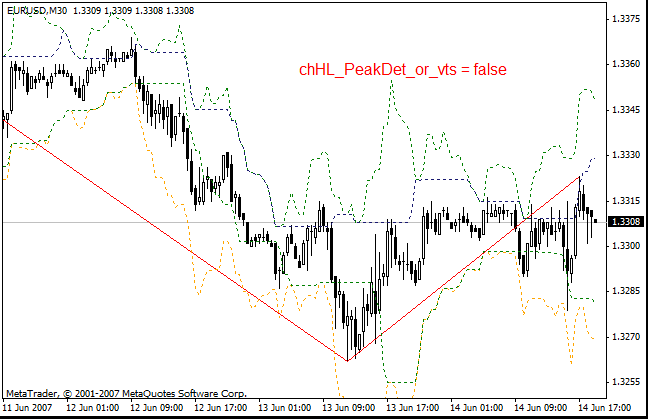
  • chHL_PeakDet_or_vts - si es "true" (por defecto), permite mostrar las líneas de reconocimiento (canal del precio) y los niveles de los máximos anteriores del ZigZag. Si es "false", se mostrará el indicador i-vts. Si ponemos "false", se mostrarán dos copias del indicador v-its con distintas configuraciones en la pantalla.
  • NumberOfBars - el número de barras a calcular (0, todas las barras) para el indicador i-vts.
  • NumberOfVTS - por lo que pude deducir, este es el parámetro de suavizado para i-vts.
  • NumberOfVTS1 - el parámetro de suavizado para la segunda copia de i-vts.

Opciones generales

  • ExtObjectColor - establece el color de la línea que conecta las líneas básicas de los objetos gráficos;
  • ExtObjectStyle - establece el estilo de la línea que conecta las líneas básicas de los objetos gráficos;
  • ExtObjectWidth - establece el grosor de la línea que conecta las líneas básicas de los objetos gráficos.

Estos tres parámetros funcionan con los niveles de Fibonacci, las expansiones de Fibonacci, los arcos de Fibonacci y las zonas de tiempo de Fibonacci (FiboTime). Anteriormente, se conectaban los puntos básicos de estos tres objetos mediante una línea discontinua roja. Estos tres parámetros funcionan simultáneamente con todos los objetos mencionados antes.

  • ExtSendMail - permite enviar por correo electrónico un mensaje sobre el patrón que aparece;
  • ExtAlert - permite enviar mensajes y avisos sonoros cuando aparece un nuevo segmento en el ZigZag;
  • ExtBack - muestra todos los objetos en el fondo;
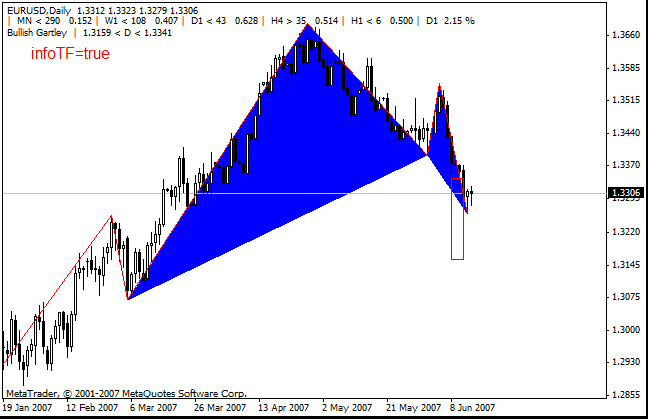
  • infoTF - permite mostrar las información de los 5 períodos de tiempo más largos. Muestra lo siguiente: El nombre del período de tiempo, el tamaño de la vela en puntos, el estado actual del precio en relación con el mínimo. También muestra la altura del primer segmento del ZigZag en porcentaje. Y muestra los nombres de los patrones de Gartley y el tamaño de la posible zona de desarrollo del punto D en los patrones de Gartley.

Conclusión

Este artículo describe la características básicas de las herramientas incorporadas en el indicador ZUP:

  1. los patrones de Pesavento;
  2. un conjunto de herramientas para trabajar con el tridente de Andrews;
  3. los abanicos de Fibonacci;
  4. los niveles de Fibonacci;
  5. los arcos de Fibonacci;
  6. dos versiones de las expansiones de Fibonacci.

Se describen las nuevas herramientas: los niveles de Versum y los canales de micmed. La lista completa con los valores de niveles de Fibonacci usados en distintas herramientas gráficas. También se hace una breve descripción del indicador ZUP.

Sigo tratando de mejorar las características del indicador ZUP. Es posible que en el futuro se mejoren las características de las herramientas ya existentes y se incorporen nuevas herramientas. Además, se añaden nuevos parámetros constantemente. También he podido identificar y corregir varios errores. Se llevan a cabo otros desarrollos del indicador ZUP en el foro de ONIX: http://onix-trade.net/forum/index.php?showforum=54

Es muy difícil completar la descripción ya que se añaden nuevas características al ZUP continuamente. Ya está disponible la versión ZUP_v64. En esta última versión, se han mejorado las características que permiten trabajar con los canales de micmed, es posible ahora trabajar con niveles personalizados de Fibonacci, etc. Se han añadido también dos nuevos ZigZags: ExtIndicator=12 - ZigZag desarrollado por Talex y ExtIndicator=13 - ZigZag desarrollado por Tovaroved.

Se adjuntan al artículo los indicadores ZUP_v63 y ZUP_v64. Se incluye en el indicador ZUP_v64 una breve descripción de las novedades (en una archivo de MS Word).

Referencias bibliográficas

  1. Larry Pesavento. Fibonacci Ratios with Pattern Recognition (Ratios de Fibonacci con reconocimiento de patrones)
  2. Larry Pesavento. Profitable Patterns for Stock Trading (Patrones rentables para el trading bursátil)
  3. Bryce Gilmore. Dynamic Time and Price Analysis of Market Trends (Tiemp odinámico y análisis de precios en tendencias del mercado)
  4. Bryce Gilmore. Geometry of Markets (Geometría de los mercados)
  5. Bryce Gilmore. Geometry of Markets 2 (Geometría de los mercados 2)
  6. Robert Fisher. The New Fibonacci Trader (El nuevo trader de Fibonacci, en su versión rusa).

Traducción del ruso hecha por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/ru/articles/1470

Archivos adjuntos |
Descargar ZIP
ZUP_v63.zip (41.68 KB)
ZUP_v64.zip (46.24 KB)
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.

Otros artículos del autor

Pasar a la discusión en el foro de los operadores
Recetas MQL5 - Programando los canales móviles Recetas MQL5 - Programando los canales móviles
En este artículo se muestra un método de programación del sistema de canales equidistantes. Se analizan ciertos matices en la construcción de este tipo de canales. Asimismo, se realiza una tipificación de los canales, proponiendo un método de canales móviles de tipo universal. Para implementar el código, se ha utilizado el instrumental de la POO.
El indicador alternativo Ichimoku – Configuración y ejemplos de uso El indicador alternativo Ichimoku – Configuración y ejemplos de uso
¿Cómo configurar el indicador Ichimoku correctamente? Un repaso a la descripción de los parámetros de configuración. Este artículo le ayudará a entender los métodos que se usan para configurar loa parámetros del indicador Ichimoku, entre otros. Sin duda le ayudará también a entender mejor cómo configurar el indicador estándar Ichimoku Kinko Hyo.
Interfaces gráficas II: Control "Menú principal" (Capítulo 4) Interfaces gráficas II: Control "Menú principal" (Capítulo 4)
Es el artículo final de la segunda parte de la serie sobre las interfaces gráficas. Aquí vamos a considerar la creación del control “Menú principal”. Se demostrará el proceso de su desarrollo y la configuración de los manejadores de las clases de la librería para una correcta reacción a las acciones del usuario. Además, hablaremos de los modos de conexión de los menús contextuales a los elementos del menú principal. Aparte de eso, trataremos la cuestión del bloqueo de los controles inactivos en el momento actual.
Estrategias de trading basadas en el análisis de los puntos pivote (Pivot Points) Estrategias de trading basadas en el análisis de los puntos pivote (Pivot Points)
El análisis de los puntos pivote (PP) es una de las estrategias más sencillas y eficientes para los mercados con alta volatilidad intradiaria. Fue utilizada en la época anterior a los ordenadores, cuando los traders no disponían de ningún equipo de tratamiento de datos, excepto los ábacos y las calculadoras mecánicas.