Filtrado y extracción de características en el dominio de la frecuencia

Introducción

En el ámbito de los mercados financieros existe una demanda especial de modelos de previsión precisos. Dicho esto, los modelos predictivos sólidos requieren información significativa y pertinente. En el presente artículo exploraremos el uso de varios filtros digitales aplicados en el dominio de la frecuencia como herramientas para la extracción de características. Asimismo, examinaremos algunas de las ventajas e inconvenientes del análisis de series temporales transformadas en el dominio de la frecuencia mediante transformada discreta de Fourier (DFT). En concreto, analizaremos tres tipos de filtros digitales: síncronos, en cuadratura y filtros espejo en cuadratura. Para cada tipo, veremos cuál es su utilidad para analizar series temporales. Por último, presentaremos un código que implementa ejemplos de cada tipo.

Filtrado en el dominio de la frecuencia

En el artículo "Implementación práctica de filtros digitales en MQL5 para principiantes", el autor presentó filtros digitales aplicados al dominio temporal. En el artículo, la fila se multiplica por un conjunto único de pesos de diferentes longitudes según el tipo de filtro y sus parámetros. El número de pesos determinará la ventana deslizante que se convolucionará con los valores correspondientes de la serie de datos al aplicar el filtro a lo largo de los datos. Las medias móviles funcionarán de forma similar.

En este artículo, aplicaremos filtros en el dominio de la frecuencia. Las principales fases de trabajo en la aplicación de filtros son:

1.  En primer lugar, la fila se preprocesa como preparación para la operación de la DFT.
2.  La DFT se aplica a la serie junto con el algoritmo de la Transformada Rápida de Fourier (FFT).
3.  A continuación, modificaremos la forma de onda de la serie de datos de la manera que consideremos necesaria. En otras palabras, aplicaremos un filtro que modifique la forma de onda original de la serie.
4.  Sobre la forma de onda modificada se realizará una operación DFT inversa, convirtiéndola de nuevo al dominio temporal conocido.
5. Al final, anularemos cualquier efecto causado por las operaciones realizadas en el paso inicial de preprocesamiento.

De forma similar a la convolución en el dominio temporal, los términos de la serie DFT se multiplicarán por coeficientes que definen un filtro concreto. Debido al gran número de pasos, puede parecer que el filtrado en el dominio de la frecuencia es mucho más intensivo desde el punto de vista computacional, pero no siempre es así.

Cuando se trata de grandes conjuntos de datos, usar el algoritmo de la transformada rápida de Fourier (FFT) puede resultar mucho más rápido que convolucionar una serie en el dominio temporal, sobre todo cuando se aplican las "mejores prácticas", que veremos más adelante.

Filtrado de formas y funciones

Un filtro se define usando una función cuya salida puede modificarse según la especificación del filtro. Al cambiar la salida de la función, cambiará la forma del filtro. La forma del filtro representa la curva de respuesta del filtro. Esta determinará el comportamiento del filtro en el dominio de la frecuencia. Existen muchas formas de filtros utilizados en el tratamiento de señales en diversos campos de investigación. Al analizar series temporales, resultan preferibles los filtros con esquinas redondeadas.

Los filtros de esquinas redondeadas poseen características únicas que son muy importantes en el análisis de series temporales. En primer lugar, las esquinas redondeadas ofrecerán una respuesta en frecuencia más suave, y esto ayudará a minimizar la distorsión derivada de las transiciones entre componentes de frecuencia. Además, las esquinas redondeadas de la forma del filtro facilitarán su puesta en práctica en el mundo real. Como sus diseños se basan en aproximaciones matemáticas, suelen ofrecer mejores prestaciones. Así se logrará un buen equilibrio entre la capacidad de distinguir entre componentes de frecuencia útiles y no deseados y la minimización de la distorsión.

En este caso, como función de filtro se utilizará la función de filtro gaussiano. Según su forma, el filtro se concentrará en el dominio temporal. Es decir, dura relativamente menos que otras funciones de filtro. Hay muchos factores a considerar a la hora de seleccionar una característica para filtrar. Los requisitos del área de aplicación específica tienen prioridad.

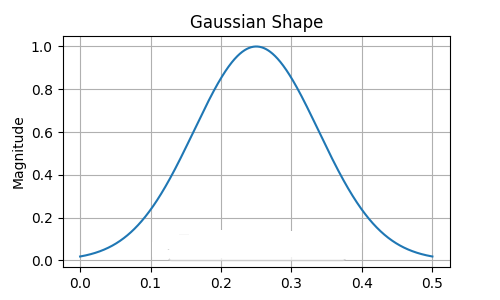
Especificación del filtro

Todos los filtros que encontraremos en este artículo se especifican mediante dos parámetros. El parámetro de frecuencia central y la anchura, a veces denominada escala. Ambos valores deben expresarse en número de ciclos de frecuencia por muestra. La frecuencia central puede adoptar valores entre 0 y 0,5. El parámetro de anchura determinará el rango de frecuencias por encima y por debajo de la frecuencia central en la banda de paso que pasarán a través de la función de filtro sin distorsionar significativamente su forma. La anchura adoptará valores a partir de 0,01.

Filtros síncronos

Empezaremos nuestro estudio de los tipos con los filtros síncronos. La posición de una señal en el tiempo se denomina fase. Los filtros síncronos mantienen la relación de fase entre la señal de entrada y la de salida. Esto significa que cuando la señal de entrada pase a través de un filtro síncrono, la señal de salida filtrada mantendrá la misma relación temporal que la señal de entrada dentro de la gama de frecuencias permitida.

El filtro paso banda es el tipo básico de filtro síncrono, un bloque a partir del cual se pueden construir otros filtros. El filtro deja pasar una determinada gama de frecuencias, atenuando o suprimiendo las que queden fuera de ella, y reduciendo las señales con frecuencias por debajo o por encima del ancho de banda.

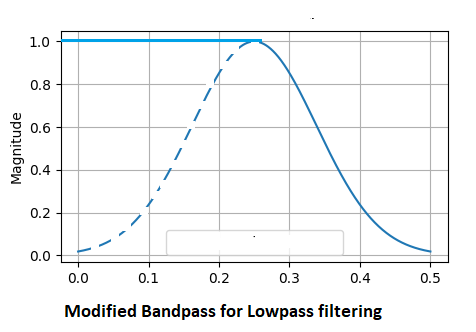
Los filtros paso bajo y paso alto se implementan modificando el filtro paso banda. El filtro paso bajo da prioridad a las frecuencias bajas de la señal. Se utiliza sobre todo para detectar la tendencia general de un proceso. Cuanto más baja sea la frecuencia central, más suave será la señal de salida filtrada. Usando la función de filtro paso banda, multiplicaremos todas las frecuencias inferiores o iguales a la frecuencia central por una constante de 1,0 y atenuaremos en consecuencia el resto de frecuencias superiores. 

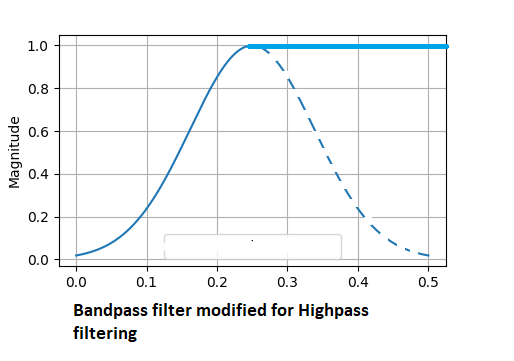
El filtro paso alto elimina todos los cambios lentos de la señal, dejando solo la información sobre los cambios rápidos. En este caso, se reducirán todas las frecuencias por debajo del ancho de banda inferior de la frecuencia central. Solo pasarán las frecuencias de las bandas más altas.

Hay muchas variedades de filtros síncronos, algunos probablemente funcionan mejor que los que hemos mencionado. Todos los filtros analizados aquí compartirán una propiedad básica común: una forma de filtro bastante redonda, que es una cualidad importante.  

Filtros en cuadratura

Estos filtros (también llamados filtros analíticos) están diseñados para procesar señales aplicando un desplazamiento de fase de 90 grados (Pi/2 radianes) con respecto a la señal de entrada. Se usan más a menudo junto con filtros síncronos, rara vez se utilizan solos. En determinadas situaciones, permiten detectar relaciones de fase en las series temporales.

Para entender las ventajas de un filtro en cuadratura, vamos a ver un ejemplo. A continuación le mostramos una serie representada por un componente periódico corto.

El siguiente gráfico muestra la salida de la serie de filtros paso banda mostrada anteriormente. En él podemos ver la sincronía del filtro paso banda. Los movimientos de la señal filtrada coinciden con los movimientos de la serie original.

El siguiente gráfico muestra la señal de salida filtrada de la versión en cuadratura del filtro paso banda. Si se fija bien, verá que los picos de la señal filtrada se corresponden con los pasos por cero de la señal original. Esencialmente, la señal de salida en el filtrado en cuadratura se ecualiza con un desplazamiento aplicado a la señal de salida de paso banda síncrona.

Los picos en la señal de salida en cuadratura indican un cambio significativo en la serie de entrada. Los picos y valles del filtro en cuadratura indican cambios rápidos en la señal de entrada. Y cuando la señal de entrada es estable, la señal de salida será igual o cercana a cero. Esto significa que los filtros en cuadratura son sensibles a los cambios producidos a una determinada velocidad.

Veamos otro ejemplo. La serie siguiente se caracterizará por un fuerte movimiento al alza.

Luego vienen los resultados filtrados síncronos y en cuadratura. Una vez más, obsérvese la posición de los máximos y mínimos en relación con el fuerte movimiento ascendente. Y si bien es difícil detectar el movimiento a partir de la señal de salida síncrona, la serie con filtrado en cuadratura, en cambio, detectará el movimiento explosivo.

Por ello, puede ser conveniente usar estos dos tipos de filtros juntos. El uso combinado de un filtro síncrono y en cuadratura con los mismos parámetros se denomina filtro espejo en cuadratura (filtro QM).

Filtros espejo en cuadratura

Los filtros QM permiten detectar ejemplares localizados de componentes periódicos. Con este filtro, analizaremos la señal de salida síncrona con respecto a la señal de salida en cuadratura. Ambas señales serán cero cuando un determinado evento periódico esté ausente. Las señales de salida de ambas señales pueden combinarse tratando la señal de salida síncrona como la parte real y la señal de salida en cuadratura como la parte imaginaria. Incluye el cálculo de la amplitud y la fase de la señal filtrada.

Antes de pasar a la implementación del código, deberemos tratar uno de los aspectos más importantes de cualquier procedimiento de análisis de series temporales.

Preprocesamiento de series antes de la conversión

El hecho de que las series temporales tengan una longitud finita plantea problemas a la hora de convertirlas al dominio de la frecuencia usando la DFT. La DFT supone que la serie bruta es periódica y, por tanto, se repetirá infinitamente. La aplicación de la DFT a una señal no periódica puede provocar la distorsión de la forma de onda de salida.

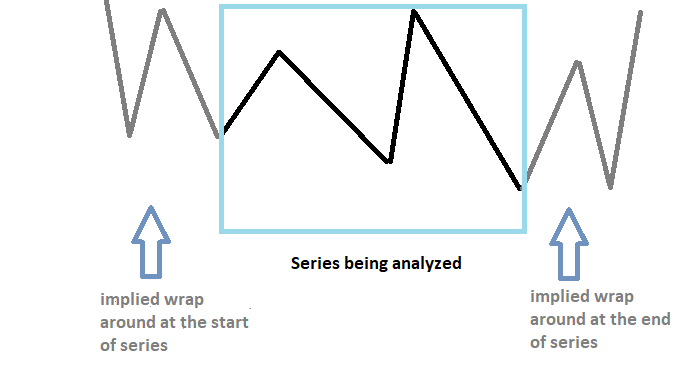
Para reducir este efecto de pérdida, tendremos que estrechar el final de la serie con valores constantes adicionales. El aumento artificial del número de muestras en la serie puede ofrecer una resolución de frecuencia más precisa y reducir la fuga de espectro. Esta operación se denomina complementación. La serie complementada se transformará utilizando la DFT. Los valores adicionales añadidos a la serie ayudarán a reducir la distorsión en el espectro de la serie, pero no son las únicas ventajas.

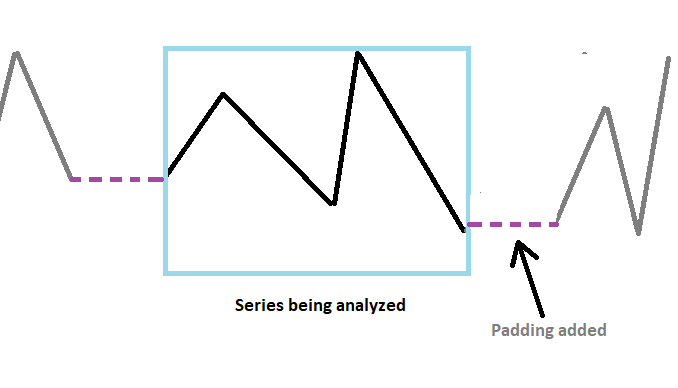
La complementación de la longitud de la serie para que el número total de muestras sea un grado del número 2 mejorará enormemente la eficiencia computacional del algoritmo FFT. A primera vista parece extraño que aumentar deliberadamente la longitud se traduzca en un mejor rendimiento, pero en realidad es así. Por consiguiente, esta operación no deberá descuidarse. Además de usar ceros, la serie podrá aumentarse con la media calculada de la serie.

Las series temporales financieras suelen tener la desagradable característica de no ser estacionarias. Cuando una serie se complementa y contiene un componente de variación lenta, el fuerte contraste entre los valores de ambos extremos de la serie original y los valores utilizados para la complementación puede manifestarse como un componente de frecuencia notable en el dominio de la frecuencia. Esto provoca la llamada contaminación.

Para evitar esta forma de distorsión, deberemos excluir la tendencia de los valores iniciales de la serie. Así, los valores originales de la serie se sustituirán por valores sin tendencia. Cuando necesitemos volver al intervalo de tiempo original de la serie, solo tendremos que restaurar la tendencia. Lo veremos al hablar de la implementación del código en la siguiente sección.

Clase CFilter

La clase CFilter encapsula ejemplos básicos de los tres tipos de filtro discutidos. Presentamos el código en el archivo Filter.mqh, que comienza incluyendo el archivo fasttransforms.mqh de la biblioteca ALGLIB.

//+------------------------------------------------------------------+
//|  CFilter - class implementing select filters in the freq domain  |
//+------------------------------------------------------------------+
class CFilter
  {
   int               m_length;                   //length of original series
   int               m_padded_len;                //modified length of series
   int               m_half_padded_len;           //half of modded series
   double            m_slope, m_intercept;     //slope and intercept of trend in series
   double            m_buffer[];               //general internal buffer
   bool              m_initialized;              //initialization flag
   complex           m_dft[];                 //general complex buffer

public:
                     CFilter(double &series[],uint min_padding=0, bool detrend=true);
                    ~CFilter(void);

   void              Lowpass(double freq,double width,double &out[],bool add_trend);
   void              Highpass(double freq,double width, double &out[]);
   void              Bandpass(double freq,double width, double &out[]);
   void              Qmf(double freq,double width, complex &out[]);
   bool              IsInitialized(void) { return m_initialized; }
  };

La clase CFilter tiene un constructor paramétrico al que el usuario deberá transmitir la serie bruta a filtrar, así como otros dos parámetros que determinarán la magnitud de complementación a aplicar y la necesidad de una operación de eliminación de tendencias en la serie antes de aplicar la transformación DFT. Si min_padding se establece en 0, el valor de complementación real solo estará determinado por el número de muestras. El parámetro min_padding especifica el número mínimo de valores que se añadirán a la serie, excluyendo cualquier valor adicional incluido para complementar la serie al grado dos más cercano.

Dentro del constructor, tras comprobar todos los argumentos, se calculará la longitud final de la fila complementada y se realizará una operación de eliminación de tendencias si es necesario. La serie complementada se escribirá en el array m_buffer. A continuación, se aplicará la DFT con la forma de onda dada en el array de números complejos m_dft. Si se produce un error en el constructor, el parámetro m_initialised se establecerá en false.

//+------------------------------------------------------------------+
//|constructor                                                       |
//+------------------------------------------------------------------+
CFilter::CFilter(double &series[],uint min_padding=0,bool detrend=true)
  {
//---local variables
   m_initialized=false;
   int i;
   int npts = ArraySize(series);
   int pad = (int)MathAbs(min_padding);
//--- check size of series
   if(npts<=0)
     {
      Print("Input array is empty");
      return ;
     }
//---
   m_length = npts ;
   for(m_padded_len=2 ; m_padded_len<INT_MAX ; m_padded_len*=2)
     {
      if(m_padded_len >= npts+pad)
         break ;
     }
//---
   if(m_padded_len<npts+pad)
     {
      Print("Warning, calculated length of modified series is too long");
      return;
     }
//---
   m_half_padded_len = m_padded_len / 2;
//---
   ArrayResize(m_buffer,m_padded_len);
//---
   if(m_padded_len > npts)            // Any padding needed?
     {

      if(detrend)
        {
         m_intercept = series[0] ;
         m_slope = (series[npts-1] - series[0]) / (npts-1) ;
        }
      else
        {
         m_intercept = m_slope = 0.0 ;
         for(i=0 ; i<npts ; i++)
            m_intercept += series[i] ;
         m_intercept /= npts ;
        }

      for(i=0 ; i<npts ; i++)
        {
         m_buffer[i]=series[i] - m_intercept - m_slope * i ;
        }
      for(i=npts ; i<m_padded_len ; i++)
        {
         m_buffer[i]=0.0;
        }
     }

   else
     {
      ArrayCopy(m_buffer,series);
      m_intercept = m_slope = 0.0 ;
     }
//---Compute the Fourier transform of the padded series
   CFastFourierTransform::FFTR1D(m_buffer,int(m_padded_len),m_dft);
//---
   m_initialized = true;

  }

El usuario deberá comprobar si el ejemplar se ha creado correctamente. Para ello, llamaremos a IsInitialized(). Si tiene éxito, la función retornará true.

Tras crear correctamente un ejemplar, el usuario podrá llamar a cualquiera de los métodos disponibles públicamente que aplica el filtro especificado a la señal almacenada en m_dft. La mayoría de ellos tienen requisitos de acceso similares. En primer lugar, se trata de las características del filtro definidas por los parámetros de frecuencia frec y de anchura width. Se corresponden con la frecuencia central y el ancho de banda aplicado. Casi todos los métodos esperarán al menos un array de entrada final en la que almacenar los resultados de la operación de filtrado.

Lowpass() es el único método que admite un cuarto parámetro de entrada que determina si la acción de eliminación de tendencias aplicada originalmente a la señal original debe cancelarse a la salida del filtro.

//+--------------------------------------------------------------------+
//|Filters series in frequency domain and returns output in time domain|
//+--------------------------------------------------------------------+
void CFilter::Lowpass(double freq,double width,double &out[],bool add_trend)
  {
//---
   int i ;
   double f, dist, wt ;
   complex dft_temp[];
   ArrayCopy(dft_temp,m_dft);
//---
   for(i=0 ; i<=m_half_padded_len ; i++)
     {
      f = (double) i / (double) m_padded_len ;  // This frequency
      if(f <= freq)                  // Flat to here
         wt = 1.0 ;
      else
        {
         dist = (f - freq) / width ;
         wt = exp(-dist * dist) ;
        }
      dft_temp[i].real*=wt;
      dft_temp[i].imag*=wt;
     }
//---
   double temp[];
//---
   CFastFourierTransform::FFTR1DInv(dft_temp,m_padded_len,temp);
//---
   ArrayResize(out, m_length);
//---
   for(int i = 0; i<m_length; i++)
      out[i]=(add_trend)?temp[i] + m_intercept + m_slope*i:temp[i];

  }

 La implementación de los filtros síncronos consta de dos pasos: en primer lugar, la forma de onda colocada en m_dft se multiplicará por una función de filtro modificada. En esta aplicación, se tratará de una función gaussiana. A continuación, se realizará la operación DFT inversa, que devolverá la serie al dominio temporal.  

Para calcular los parámetros de salida del filtro QM, multiplicaremos los términos DFT de la señal por la versión en cuadratura de la función de filtro. Una función de filtro en cuadratura es una función de filtro síncrono a la que se aplica un desplazamiento de fase de 90 grados. Para obtener dicho desfase, la función de filtro síncrono se multiplica por i, haciéndola puramente imaginaria. El resultado será una función cuyas salidas resultarán simétricas con respecto a la frecuencia de Nyquist. Los términos de salida a ambos lados de la frecuencia 0,5 serán iguales en términos absolutos pero con signo opuesto.

Basándose en este hecho, el método Qmf() multiplicará los términos DFT de la forma de onda por la suma de las funciones de filtro síncrono y en cuadratura. Para ello, haremos real la función de filtro en cuadratura (recordando que la función de filtro en cuadratura es imaginaria); para ello, la multiplicaremos por i. Al sumar las funciones de filtro, las salidas más allá de la frecuencia de Nyquist se anularán entre sí. En el código, los términos DFT filtrados superiores a 0,5 se fijarán en 0. Solo deberán calcularse las salidas filtradas que sean inferiores o iguales a la frecuencia de Nyquist. Una vez filtrada la señal, se realizará una operación DFT inversa compleja para volver al dominio temporal.

//+------------------------------------------------------------------+
//| Implements Quadrature Mirror Filter, output is complex           |
//+------------------------------------------------------------------+
void CFilter::Qmf(double freq,double width,complex &out[])
  {
//---
   int i ;
   double f, dist, wt ;
   complex dft_temp[];
   ArrayCopy(dft_temp,m_dft);
//---
   for(i=1 ; i<m_half_padded_len ; i++)
     {
      f = (double) i / (double) m_padded_len ;    // This frequency
      dist = (f - freq) / width ;
      wt = exp(-dist * dist) ;
      dft_temp[i].real *= wt ;
      dft_temp[i].imag *= wt ;
      dft_temp[m_padded_len-i].real = dft_temp[m_padded_len-i].imag = 0.0 ;  // Causes QMF outputs
     }

//---
   dft_temp[0].real = 0.0 ;
   dist = (0.5 - freq) / width ;
   dft_temp[m_half_padded_len].real = 0.5 * dft_temp[m_half_padded_len].imag * exp(-dist * dist) ;
//---
   dft_temp[0].imag = dft_temp[m_half_padded_len].imag = 0.0 ;     // By definition of real transform
//---
   CFastFourierTransform::FFTC1DInv(dft_temp,m_padded_len);
   ArrayResize(out,m_length);
//---
   for(i=0 ; i<m_length ; i++)
     {
      out[i].real = dft_temp[i].real/double(m_half_padded_len) ;
      out[i].imag = dft_temp[i].imag/double(m_half_padded_len) ;
     }
  }
//+------------------------------------------------------------------+

Programa AFD.mq5

Veamos el uso de la función CFilter en el ejemplo de la aplicación AFD.mq5. La aplicación se implementará como asesor. El asesor permitirá a los usuarios generar secuencias aleatorias de una longitud determinada. Los usuarios podrán establecer la longitud de las series generadas, así como ajustar el valor inicial de los números aleatorios. La serie se indicará en azul en el gráfico superior. En el segundo gráfico se puede observar el resultado de la aplicación del filtro seleccionado a la serie generada. Todos los parámetros del filtro podrán configurarse desde la interfaz gráfica del programa. Este será el aspecto de la aplicación.

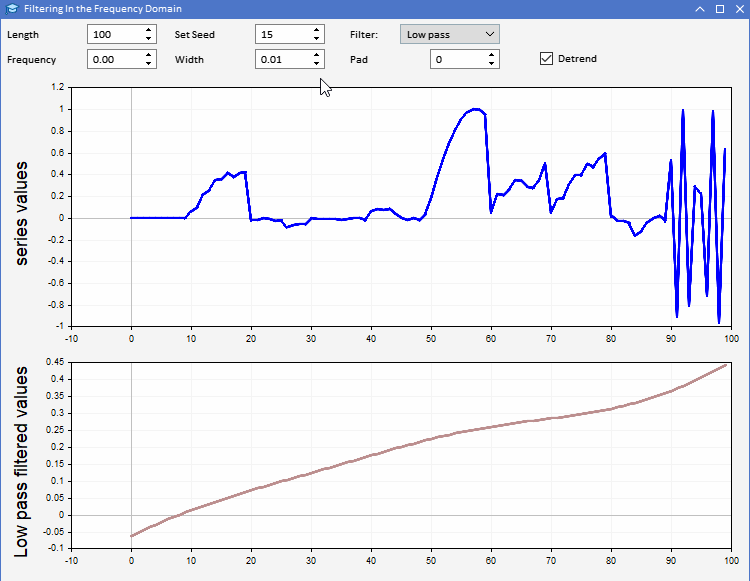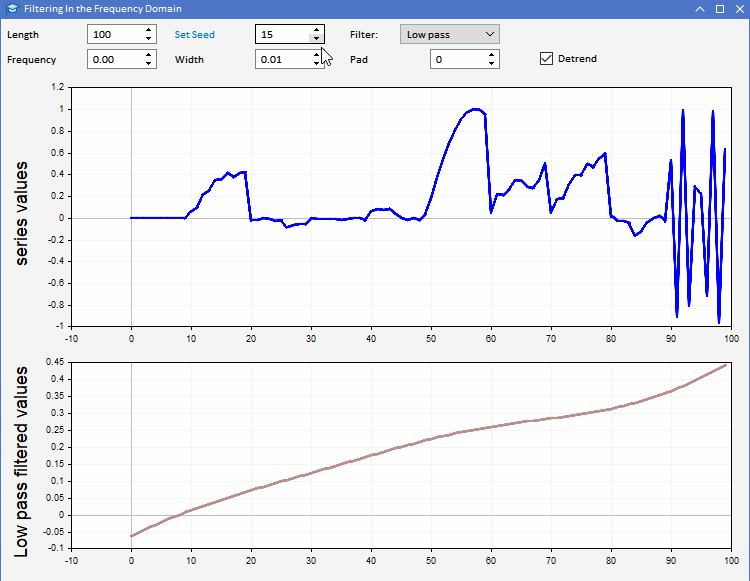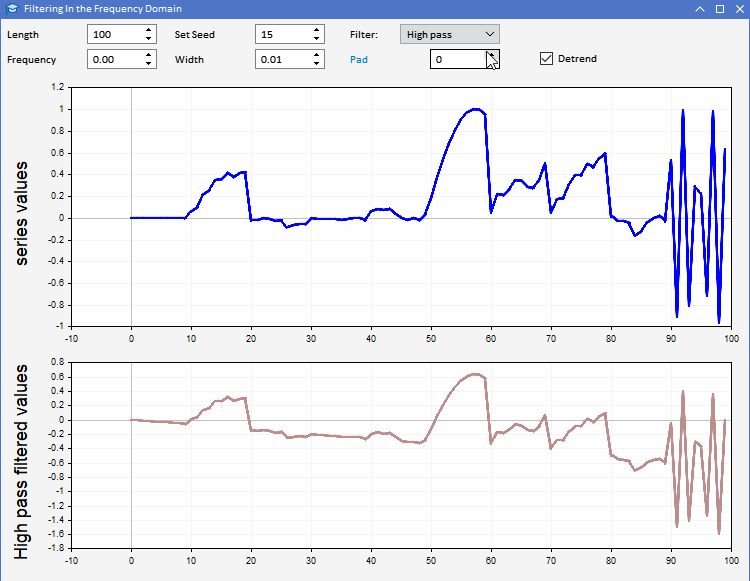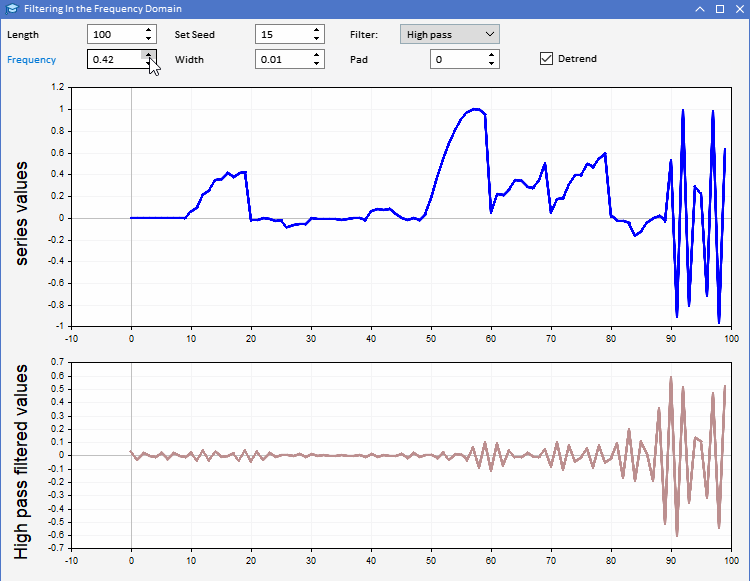
Gracias a la aplicación AFD, podremos comprender mejor los distintos tipos de información que producen los filtros. Existen dos formas de utilizar la señal del filtro síncrono. La salida del filtro paso bajo puede utilizarse para obtener información sobre el valor medio de la serie de entrada en cualquier momento. La salida del filtro paso alto identifica los máximos y mínimos aleatorios observados en la serie original. Estos resultados indicarán el estado de las series de entrada en cada momento.

Las salidas del filtro paso banda son menos evidentes en cuanto a su importancia. Probablemente nadie pueda entender el significado de la salida del filtro simplemente observando, aunque es posible que estos datos puedan resultar útiles para un modelo de previsión. Quizá encontrar la salida de un determinado ancho de banda en un pico o mínimo indique algo en la serie original.

Veamos el ancho de banda de salida de una serie aleatoria a diferentes frecuencias.

Los resultados muestran otro tipo de información. Los picos de las señales de salida del ancho de banda representan la magnitud de las variaciones periódicas en un intervalo de tiempo específico. Más concretamente, muestran la amplitud del cambio, lo cual indica la presencia de un cambio periódico. Los picos más bajos indican menos cambios.

La amplitud se ajusta muestreando la salida del filtro QM. Los cálculos de amplitud y fase con uso de los valores del filtro QM se muestran en el siguiente fragmento de código de AFD.mq5.

 case ENUM_QMF_AMPLITUDE:
        {
         y_name = "Amplitude";
         complex comp[];
         filter.Qmf(freq,scale,comp);
         ArrayResize(m_output1,ArraySize(comp));
         for(int i=0; i<ArraySize(m_output); i++)
            m_output1[i]=MathSqrt(comp[i].real*comp[i].real + comp[i].imag*comp[i].imag);
        }
      break;
      case ENUM_QMF_PHASE:
        {
         y_name = "Phase";
         complex comp[];
         filter.Qmf(freq,scale,comp);
         ArrayResize(m_output1,ArraySize(comp));
         for(int i=0; i<ArraySize(m_output); i++)
            m_output1[i]=(comp[i].real>=1.e-40 || comp[i].imag>=1.e-40)?atan2(comp[i].imag, comp[i].real):0.0;
        }
      break;

La diferencia en el ancho de banda de salida a distintas frecuencias demuestra que disponemos de información variada. De esta forma, podemos crear características únicas para utilizarlas en un algoritmo de aprendizaje automático. Para crear los conjuntos de datos adecuados, el profesional deberá comprender claramente los parámetros que definen un filtro concreto.

Parámetro de anchura

Como ya hemos dicho, los parámetros de todos los filtros aplicados se expresan en número de ciclos de frecuencia por unidad de tiempo. Uno de los inconvenientes de los análisis en el dominio de la frecuencia es la dificultad de relacionar los componentes de frecuencia con su extensión en el dominio temporal. Usando el ejemplo de la serie aleatoria que comentamos en el apartado anterior, las señales de salida de ancho de banda se han discretizado a las frecuencias 0,15, 0,3 y 0,45 con la misma anchura de 0,03. Debemos entender lo que significan estos valores, sobre todo en lo que respecta al dominio temporal de la serie.

Una frecuencia de 0,15 tendrá un periodo de 1/0,15 = 6,67 muestras por ciclo. La anchura determinará la resolución en el dominio de la frecuencia. Si tenemos que aislar una banda estrecha de frecuencias, utilizaremos una anchura pequeña, normalmente 0,01 es el mínimo, aunque puede ser menor. Volvamos a nuestro ejemplo. La anchura se ha fijado en 0,03, por lo que el ancho de banda se extiende de 0,15-0,03 a 0,15+0,03, es decir, de 0,12 a 0,18. Las frecuencias dentro de esta gama se pasarán por alto, mientras que las frecuencias por encima y por debajo se filtrarán casi por completo.

La anchura también indica la resolución en el dominio temporal. La relación entre la resolución en el dominio de la frecuencia y la resolución en el dominio temporal es inversa. Una mayor resolución en un área conllevará una pérdida de resolución en otra. Para estimar la extensión del dominio temporal en relación con la anchura, aplicaremos la fórmula 0,8/anchura.

Con ella, podremos estimar el número de muestras en el dominio temporal que se verán afectadas por el ancho de banda de frecuencia, en relación con la posición actual. En otras palabras, estimaremos el número de muestras anteriores y posteriores a la posición actual que afectarán al resultado observado. Volviendo al ejemplo, una anchura de 0,03 implica una magnitud de tiempo de 0,8/0,03 = 27 muestras. Esto significa que el valor de cada una de las salidas estará determinado o influido por las 27 observaciones anteriores y las 27 siguientes.

En general, la anchura del filtro deberá ser proporcional a la frecuencia central del ancho de banda que queremos estudiar. Esto se debe al periodo de la frecuencia. Las frecuencias más bajas tienen periodos más largos y las más altas, periodos más cortos. Por ello, para frecuencias más bajas, podemos permitirnos sacrificar la resolución en el dominio temporal y elegir una anchura estrecha. Pero las frecuencias más altas se beneficiarán de los parámetros de mayor anchura, lo que se reflejará menos en el dominio temporal.

Por último, el parámetro de anchura también afectará a los valores transmitidos al modelo de predicción. Volvamos al ejemplo anterior, cuyo intervalo de tiempo implícito, según nuestros cálculos, es de unas 27 observaciones. Supongamos que necesitamos predecir el próximo valor de la serie en el intervalo temporal 201. Así, proporcionaremos el valor de salida filtrado calculado a partir de 200 valores conocidos, es decir, 27 ranuras desde el final de la fila. No podemos usar deliberadamente ninguna salida filtrada más allá de este punto, ya que sabemos que estará sujeta a los efectos causados por la DFT, según las restricciones de los parámetros del filtro.

En el último ejemplo, hemos filtrado la salida a distintas frecuencias pero de la misma anchura. En la práctica, resultaría más útil muestrear los datos de salida filtrados a frecuencias y anchuras elegidas estratégicamente para obtener toda la información útil posible.

Conclusión

Hemos visto tres tipos de filtros:

• Los filtros síncronos ayudan a descomponer una serie ruidosa en distintos componentes, resaltando la información importante y eliminando los elementos superfluos que cusan distracciones. Transmitiendo la información pertinente a los algoritmos de aprendizaje, resulta posible construir mejores modelos de predicción.

• Los filtros en cuadratura pueden usarse para identificar zonas de cambio rápido de nivel en una serie. Aunque puede resultar fácil advertir movimientos importantes en una serie, puede ser difícil trasladar esos fenómenos a un algoritmo de aprendizaje. Precisamente ahí reside el valor de los filtros en cuadratura.

• La combinación de filtros síncronos y en cuadratura puede detectar la presencia de una característica periódica. Estas herramientas pueden ser eficaces para identificar y estudiar características que parecen aparecer aleatoriamente en las series temporales.

El filtrado en el dominio de la frecuencia mejora la eficiencia computacional que ofrece el algoritmo FFT. Comparado con el método de convolución en el dominio temporal, este es otro nivel. Pero no todo resulta coser y cantar. La transformación de series en el dominio de la frecuencia está plagada de trampas que pueden llevar a conclusiones completamente falsas debido a las distorsiones introducidas por una manipulación descuidada de los datos. Por ello, debemos tener mucho cuidado con su uso.

Adjuntamos el código de todas las herramientas y programas analizados. El archivo AFD.mq5 usa la maravillosa biblioteca Easy and Fast (EAF) GUI. Está disponible en la biblioteca de códigos de mql5.com. Nota: al utilizar la biblioteca EAF junto con ALGLIB, asegúrese siempre de incluir EAF en último lugar en su aplicación, ya que existen algunos conflictos de nombres entre estas bibliotecas que provocan errores de compilación.  

Nombre del archivo	Descripción
Mql5\Include\Filter.mqh	Contiene la definición de la clase CFilter, que implementa filtros digitales básicos en el dominio de la frecuencia.
Mql5\Include\RandomStationarySeries.mqh	Contiene funciones para generar series aleatorias de diversas características. Se usa en la aplicación AFD.ex5.
Mql5\Experts\AFD.mq5	Este es el código fuente de la aplicación AFD, usa la librería Easy and Fast GUI publicada en el Code Base en mql5.com.
Mql5\Experts\AFD.ex5	Aplicación AFD compilada e implementada como asesor.