MetaTrader 5 / Ticaret
English Русский 中文 Español Deutsch 日本語 Português 한국어 Français Italiano
preview
Veri Bilimi ve Makine Öğrenimi (Bölüm 06): Gradyan İniş

Veri Bilimi ve Makine Öğrenimi (Bölüm 06): Gradyan İniş

MetaTrader 5 — Ticaret | 13 Nisan 2023, 16:03
725 0
Omega J Msigwa
Omega J Msigwa

Erken optimizasyon, programlamadaki tüm kötülüklerin anasıdır.

- Donald Knuth 

Giriş

Wikipedia'ya göre, gradyan iniş (en dik iniş olarak da adlandırılır), türevlenebilir bir fonksiyonun yerel minimumunu bulmak için birinci dereceden yinelemeli bir optimizasyon algoritmasıdır. Buradaki fikir, mevcut noktadaki fonksiyonun gradyanının (veya yaklaşık gradyanının) tersi yönünde tekrarlanan adımlar atmaktır, çünkü bu en dik iniş yönüdür. Tersine, gradyan yönünde adım atmak, o fonksiyonun yerel maksimumuyla sonuçlanacaktır; bu süreç ise gradyan çıkış olarak adlandırılır.


Temel olarak, gradyan iniş, bir fonksiyonun minimumunu bulmak için kullanılan bir optimizasyon algoritmasıdır:

Gradyan İniş makalesi görüntüsü

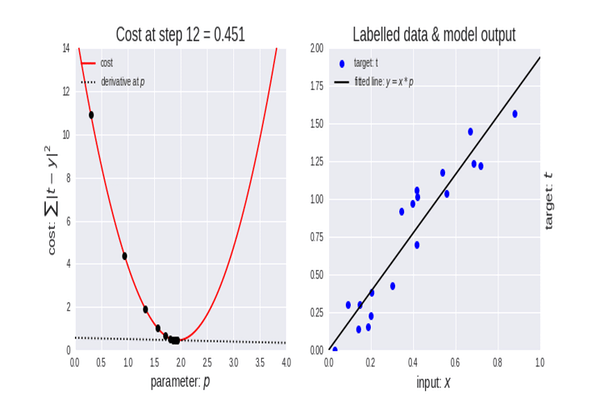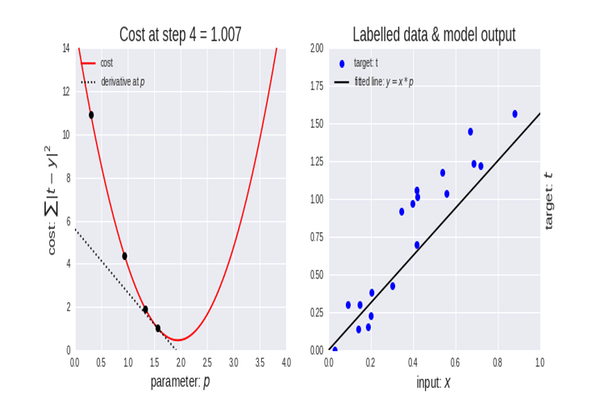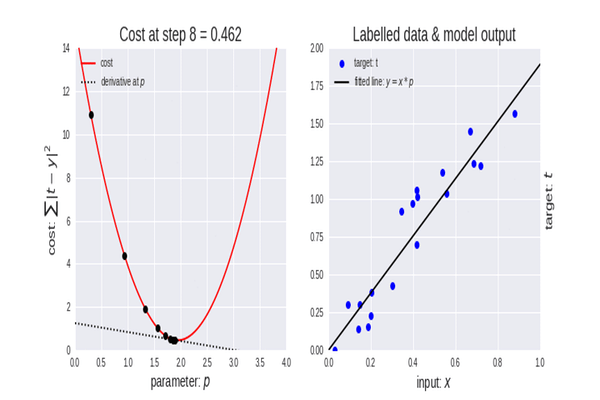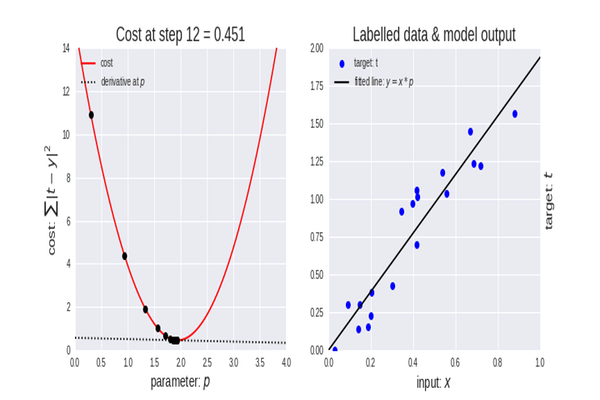
Gradyan iniş, veri kümemiz için en iyi modelin parametrelerini bulmamıza yardımcı olduğu için makine öğreniminde çok önemli bir algoritmadır. Öncelikle maliyet fonksiyonu terimini açıklayalım.


Maliyet Fonksiyonu

Aynı zamanda kayıp fonksiyonu olarak da adlandırılır, belki bu isim size daha tanıdık gelebilir. Bu fonksiyon, modelimizin x ve y değerleri arasındaki ilişkiyi ne kadar iyi veya kötü öngördüğünü hesaplamak için kullanılan bir metriktir.

Bir modelin öngörü kalitesini belirlemek için kullanılabilecek birçok farklı metrik vardır. Ancak, diğerlerinden farklı olarak, maliyet fonksiyonu tüm veri kümesindeki ortalama kaybı bulur. Maliyet fonksiyonu ne kadar büyük olursa, modelimizin de veri kümemizdeki ilişkileri öngörmesi o kadar kötü olacaktır.

Gradyan inişin amacı, maliyet fonksiyonunu en aza indirmektir, çünkü en küçük maliyet/kayıp fonksiyonuna sahip model en iyi modeldir. Daha iyi anlamanız için aşağıdaki örneğe bakalım.

Maliyet fonksiyonumuzun şu denklem olduğunu varsayalım: 

Python dilini kullanarak bu fonksiyonun grafiğini çizersek, şu şekilde görünecektir:

Pyplot

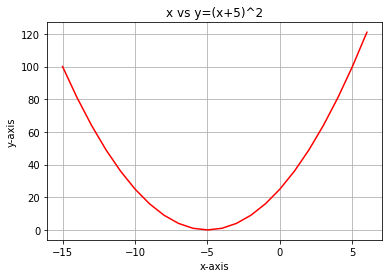
Maliyet fonksiyonumuzla yapmamız gereken ilk adım, zincir kuralını kullanarak türevini almaktır:

y=(x+5)2 denklemi bir bileşke fonksiyondur (bir fonksiyonun içerisinde başka bir fonksiyon vardır). Dış fonksiyon (x+5)2, iç fonksiyon da (x+5)’tir. Türev almak için zincir kuralını uygulayalım:

Zincir kuralı

Bunu anlamakta zorlandıysanız, aşağıya matematik işlemlerini elle yaptığım bir video ekledim, onu izleyebilirsiniz. Elde ettiğimiz bu fonksiyon gradyandır. Denklemin gradyanını bulma süreci en önemli adımdır. Keşke matematik öğretmenlerim bana bir fonksiyonun türevini almanın amacının fonksiyonun gradyanını elde etmek olduğunu söyleseydi.

Bu ilk ve en önemli adımdır. Şimdi ikinci adıma geçelim:

2. adım:

Gradyanın negatif yönünde hareket ediyoruz. Burada şu soru ortaya çıkıyor, ne kadar hareket etmeliyiz? İşte öğrenme oranı burada devreye giriyor.


Öğrenme Oranı

Tanım olarak, öğrenme oranı, kayıp fonksiyonunun minimumuna doğru hareket ederken her yinelemedeki adım boyutudur. Dağdan inen bir insanı düşünelim, bu kişinin adımları öğrenme oranıdır. Adımları ne kadar küçük olursa, dağın dibine ulaşması o kadar uzun sürecektir ve bunun tersi de geçerlidir.

Algoritma öğrenme oranı küçük değerlerde tutulmalıdır, ancak tabi ki 0,0001 gibi çok küçük değerler seçilmemelidir. Çünkü bu kadar küçük bir değer kullanırsak, algoritmanın minimum değerlere ulaşması daha uzun sürebileceğinden programın yürütme süresini artırmış oluruz. Tersine, öğrenme oranı için büyük değerler seçersek, bu kez de algoritmanın çok büyük adımlar atmasına ve sonunda hedeflenen minimum değeri kaçırmasına neden olabiliriz.

Varsayılan öğrenme oranı 0,01'dir.

Algoritmanın nasıl çalıştığını görmek için yinelemeleri gerçekleştirelim.

Birinci yineleme: Algoritma için başlangıç noktası olarak rastgele bir nokta seçiyoruz. x'in ilk değeri olarak 0'ı seçtim. x'in değerlerini güncellemek için formül şu şekildedir:

Gradyan inişte yeni değerler

 Her yinelemede, fonksiyonun minimum değerine doğru ineceğiz ve işte bu nedenle algoritmanın adı gradyan iniştir. Şimdi daha net, değil mi?

Şimdi daha net, değil mi?

Bunun nasıl çalıştığını ayrıntılı olarak görelim. Neler olup bittiğine dair sağlam bir fikir edinmek amacıyla değerleri iki yinelemede manuel olarak hesaplayalım.

1. yineleme:

Formül: x 1 = x 0 - öğrenme oranı * (2*(x 0 +5))

x 1 = 0 - 0,01 * (2*(0+5))

x 1 = -0,01 * 10

x 1 = -0,1 

Daha sonra eski değerlerin üzerine yeni değerleri yerleştirerek değerleri güncelliyoruz ve fonksiyonun minimum değerine ulaşana kadar bu işlemi tekrarlıyoruz.

x 0 = x 1

2. yineleme:

x 1 = -0,1 - 0,01 * 2*(-0,1+5)

x 1 = -0,198

Sonrasında yine: x 0 = x 1

Bu işlemi birkaç kez tekrarlarsak, ilk 10 yinelemenin çıktısı şu şekilde olacaktır:

RS      0       17:15:16.793    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction CUSTOM
QQ      0       17:15:16.793    gradient-descent test (EURUSD,M1)       1 x0 = 0.0000000000 x1 = -0.1000000000 CostFunction = 10.0000000000
ES      0       17:15:16.793    gradient-descent test (EURUSD,M1)       2 x0 = -0.1000000000 x1 = -0.1980000000 CostFunction = 9.8000000000
PR      0       17:15:16.793    gradient-descent test (EURUSD,M1)       3 x0 = -0.1980000000 x1 = -0.2940400000 CostFunction = 9.6040000000
LE      0       17:15:16.793    gradient-descent test (EURUSD,M1)       4 x0 = -0.2940400000 x1 = -0.3881592000 CostFunction = 9.4119200000
JD      0       17:15:16.793    gradient-descent test (EURUSD,M1)       5 x0 = -0.3881592000 x1 = -0.4803960160 CostFunction = 9.2236816000
IG      0       17:15:16.793    gradient-descent test (EURUSD,M1)       6 x0 = -0.4803960160 x1 = -0.5707880957 CostFunction = 9.0392079680
IG      0       17:15:16.793    gradient-descent test (EURUSD,M1)       7 x0 = -0.5707880957 x1 = -0.6593723338 CostFunction = 8.8584238086
JF      0       17:15:16.793    gradient-descent test (EURUSD,M1)       8 x0 = -0.6593723338 x1 = -0.7461848871 CostFunction = 8.6812553325
NI      0       17:15:16.793    gradient-descent test (EURUSD,M1)       9 x0 = -0.7461848871 x1 = -0.8312611893 CostFunction = 8.5076302258
CK      0       17:15:16.793    gradient-descent test (EURUSD,M1)       10 x0 = -0.8312611893 x1 = -0.9146359656 CostFunction = 8.3374776213

Fonksiyonun minimumuna çok yaklaştığımızda algoritmanın şu on değerini de görelim:

GK      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1052 x0 = -4.9999999970 x1 = -4.9999999971 CostFunction = 0.0000000060
IH      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1053 x0 = -4.9999999971 x1 = -4.9999999971 CostFunction = 0.0000000059
NH      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1054 x0 = -4.9999999971 x1 = -4.9999999972 CostFunction = 0.0000000058
QI      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1055 x0 = -4.9999999972 x1 = -4.9999999972 CostFunction = 0.0000000057
II      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1056 x0 = -4.9999999972 x1 = -4.9999999973 CostFunction = 0.0000000055
RN      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1057 x0 = -4.9999999973 x1 = -4.9999999973 CostFunction = 0.0000000054
KN      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1058 x0 = -4.9999999973 x1 = -4.9999999974 CostFunction = 0.0000000053
JO      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1059 x0 = -4.9999999974 x1 = -4.9999999974 CostFunction = 0.0000000052
JO      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1060 x0 = -4.9999999974 x1 = -4.9999999975 CostFunction = 0.0000000051
QL      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1061 x0 = -4.9999999975 x1 = -4.9999999975 CostFunction = 0.0000000050
QL      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1062 x0 = -4.9999999975 x1 = -4.9999999976 CostFunction = 0.0000000049
HP      0       17:15:16.800    gradient-descent test (EURUSD,M1)       Local miminum found =-4.999999997546217

1062 (bin altmış iki) yinelemeden sonra, algoritma bu fonksiyonun yerel minimumuna ulaşmayı başardı.

Bu algoritmada dikkat edilmesi gereken bir şey

Maliyet fonksiyonunun değerlerine baktığınızda, başlangıçtaki değerlerinde büyük değişiklikler olduğunu, ancak son değerlerinde çok küçük değişiklikler meydana geldiğini fark edeceksiniz.

Gradyan iniş, başlangıçta fonksiyonun minimumundan henüz uzaktayken büyük adımlar atmaktadır, ancak fonksiyonun minimumuna yaklaştıkça daha küçük adımlar atmaktadır. Dağın dibine yaklaştıkça biz de aynı şeyi yapıyoruz. Buradan, gradyan inişin oldukça akıllı olduğunu anlayabiliriz!

Sonunda yerel minimumu elde ediyoruz: 

HP      0       17:15:16.800    gradient-descent test (EURUSD,M1)       Local miminum found =-4.999999997546217

Doğru değerdir çünkü bu fonksiyonun minimum değeri -5,0'dır!

Önemli bir soru

Gradyan iniş ne zaman duracağını nasıl biliyor? Algoritma sonsuza kadar veya bilgisayarın hesaplama gücü tükenene kadar yinelemeye devam edebilir.

Maliyet fonksiyonu sıfır olduğunda, gradyan iniş sonlanır.

Şimdi tüm bu süreci MQL5'te kodlayalım:

       while (true)
        {
           iterations++;
           
           x1 = x0 - m_learning_rate * CustomCostFunction(x0);
           
           printf("%d x0 = %.10f x1 = %.10f CostFunction = %.10f",iterations,x0,x1,CustomCostFunction(x0)); 
           
           if (NormalizeDouble(CustomCostFunction(x0),8) == 0) { Print("Local minimum found =",x0);  break;  }
              
           x0 = x1;
        }   

Yukarıdaki kod bloğu, bize istediğimiz sonuçları elde edebilecek koddur, ancak CGradientDescent sınıfında yalnız değildir. CustomCostFunction fonksiyonu, türevi alınan denklemimizin tutulduğu ve hesaplandığı yerdir:

double CGradientDescent::CustomCostFunction(double x)
 {
   return(2 * ( x + 5 ));
 }


Amaç Nedir?

Bu makale serisinde daha önce tartıştığımız önceki kütüphanelerde oluşturulan varsayılan lineer modeli kullanabiliyorken, tüm bu hesaplamaların amacının ne olduğunu kendinize sorabilirsiniz. Ancak varsayılan değerler kullanılarak oluşturulan model mutlaka en iyi model değildir. Bu nedenle, bilgisayarın az hata içeren model için en iyi parametreleri (en iyi model) öğrenmesini sağlamalıyız.

Yapay sinir ağları oluşturmaya birkaç makale daha yaklaştık. Sinir ağlarının geri yayılım ve diğer tekniklerle nasıl öğrendiğinin (kendilerine kalıpları nasıl öğrettiğini) anlaşılabilmesi açısından, gradyan iniş, tüm bunları mümkün kılan en popüler algoritmadır. Bu temel süreci net bir şekilde anlamadan, gerisini anlamak imkansız olacaktır, çünkü her şey daha da karmaşık hale gelmektedir.


Bir Regresyon Modeli için Gradyan İniş

Maaş veri kümesini kullanarak, gradyan inişle en iyi modeli oluşturalım.

Veri kümesine genel bakış

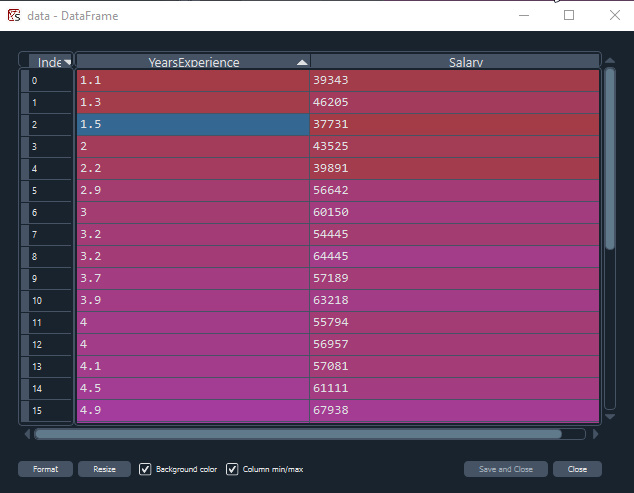
Python'da verileri görselleştirelim:

import pandas as pd 
import numpy as np
import matplotlib.pyplot as plt


data  = pd.read_csv(r"C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\Salary_Data.csv")

print(data.head(10))

x = data["YearsExperience"]
y = data["Salary"]

plt.figure(figsize=(16,9))
plt.title("Experience vs Salary")
plt.scatter(x,y,c="green")
plt.xlabel(xlabel="Years of Experience")
plt.ylabel(ylabel="Salary")
plt.show()

Grafiğimiz şu şekilde olacaktır:

Tecrübe yılı vs maaş

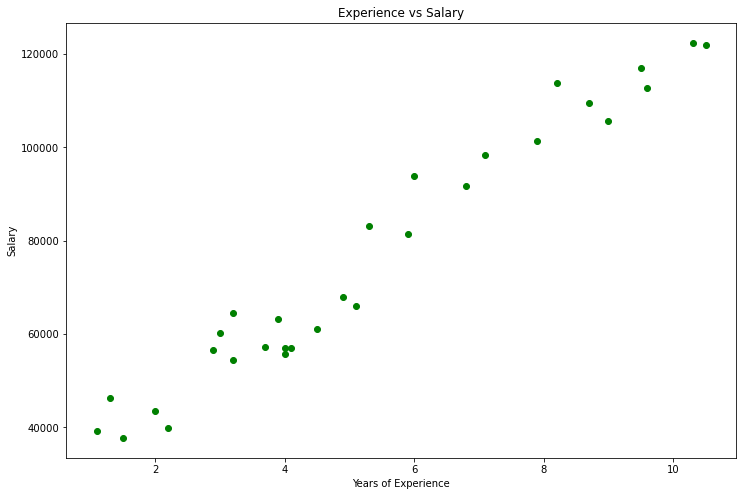
Veri kümemize baktığımızda, bu veri kümesinin regresyon problemleri için olduğunu fark etmememiz mümkün değildir. Ancak, öngörüde bulunmamıza veya elde etmeye çalıştığımız her neyse, bize yardımcı olacak milyonlarca modelimiz olabilir.

Çok sayıda model

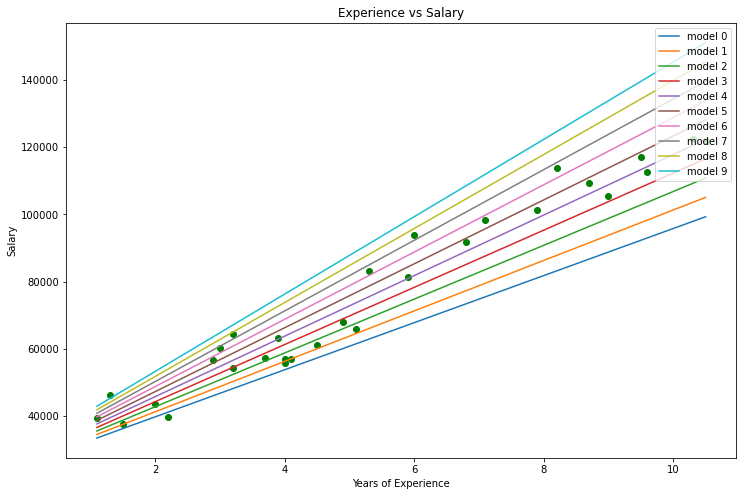
Bir kişinin tecrübesini ve maaşını öngörmek için kullanılacak en iyi model nedir? İşte bunu bulacağız. Ama önce, regresyon modelimiz için maliyet fonksiyonunu türetelim.

Teori

Lineer regresyon'a geri gidelim.

Her lineer modelin kendisiyle ilişkili hatalara sahip olduğu gerçeğini biliyoruz. Ayrıca bu grafikte bir milyon çizgi oluşturabileceğimizi ve en uygun çizginin her zaman en az hata içeren çizgi olacağını da biliyoruz.

Maliyet fonksiyonu, gerçek ve öngörülen değerler arasındaki hatayı temsil eder. Maliyet fonksiyonunun formülünü şu şekilde yazabiliriz:

Maliyet = y'nin gerçek değeri - y'nin öngörülen değeri

Hataların büyüklüğü önemli olduğu için karesini alıyoruz:

Ancak tüm veri kümemizde hatalar arıyoruz, bu yüzden toplama yapmamız gerekiyor: 

Son olarak, hataların toplamını veri kümesindeki eleman sayısı olan m'ye bölüyoruz:

Lineer regresyon maliyet fonksiyonu

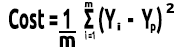
İşte elle yapılan tüm matematiksel hesaplamaların videosu:

Artık maliyet fonksiyonuna sahip olduğumuza göre, gradyan inişi kodlayalım ve şu iki değer için en iyi parametreleri bulalım: B 0 olarak gösterilen x (eğim) katsayısı ve B 1 olarak gösterilen y kesimi. 

   
   double cost_B0=0, cost_B1=0;
   
   if (costFunction == MSE)
    {
      int iterations=0;
      for (int i=0; i<m_iterations; i++, iterations++)
        {
        
           cost_B0 = Mse(b0,b1,Intercept);
           cost_B1 = Mse(b0,b1,Slope);
           
           b0 = b0 - m_learning_rate * cost_B0; 
           b1 = b1 - m_learning_rate * cost_B1;
           
           printf("%d b0 = %.8f cost_B0 = %.8f B1 = %.8f cost_B1 = %.8f",iterations,b0,cost_B0,b1,cost_B1);
           
           DBL_MAX_MIN(b0); DBL_MAX_MIN(cost_B0); DBL_MAX_MIN(cost_B1);
           
           if (NormalizeDouble(cost_B0,8) == 0 && NormalizeDouble(cost_B1,8) == 0)  break; 
           
        }
      printf("%d Iterations Local Minima are\nB0(Intercept) = %.5f  ||  B1(Coefficient) = %.5f",iterations,b0,b1);    
    }

Gradyan iniş kodunda birkaç şeye dikkat edilmelidir:

  • İşlem daha önce yaptığımızla aynı şekildedir, ancak bu sefer B o ve B 1 değerlerini aynı anda iki kez bulup güncelliyoruz.
  • Sınırlı sayıda yineleme vardır. Birisi bir keresinde sonsuz döngü yapmanın en iyi yolunun while döngüsü kullanmak olduğunu söylemişti, ama bu kez while döngüsünü kullanmıyoruz. Bunun yerine, en iyi modelin katsayılarını bulacak algoritma çalıştırmalarının sayısını sınırlayacağız.
  • DBL_MAX_MIN, bilgisayarın matematiksel sınırlarına ulaşıp ulaşmadığımızı kontrol etmek ve bize bildirmekle sorumlu hata ayıklama amaçlı bir fonksiyondur.

Öğrenme oranı = 0,01 ve yineleme sayısı = 10000 olduğunda algoritmanın çıktısı şu şekildedir: 

PD      0       17:29:17.999    gradient-descent test (EURUSD,M1)       [20]  91738.0000  98273.0000 101302.0000 113812.0000 109431.0000 105582.0000 116969.0000 112635.0000 122391.0000 121872.0000
JS      0       17:29:17.999    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction MSE
RF      0       17:29:17.999    gradient-descent test (EURUSD,M1)       0 b0 = 1520.06000000 cost_B0 = -152006.00000000 B1 = 9547.97400000 cost_B1 = -954797.40000000
OP      0       17:29:17.999    gradient-descent test (EURUSD,M1)       1 b0 = 1995.08742960 cost_B0 = -47502.74296000 B1 = 12056.69235267 cost_B1 = -250871.83526667
LP      0       17:29:17.999    gradient-descent test (EURUSD,M1)       2 b0 = 2194.02117366 cost_B0 = -19893.37440646 B1 = 12707.81767044 cost_B1 = -65112.53177770
QN      0       17:29:17.999    gradient-descent test (EURUSD,M1)       3 b0 = 2319.78332575 cost_B0 = -12576.21520809 B1 = 12868.77569178 cost_B1 = -16095.80213357
LO      0       17:29:17.999    gradient-descent test (EURUSD,M1)       4 b0 = 2425.92576238 cost_B0 = -10614.24366387 B1 = 12900.42596039 cost_B1 = -3165.02686058
GH      0       17:29:17.999    gradient-descent test (EURUSD,M1)       5 b0 = 2526.58198175 cost_B0 = -10065.62193621 B1 = 12897.99808257 cost_B1 = 242.78778134
CJ      0       17:29:17.999    gradient-descent test (EURUSD,M1)       6 b0 = 2625.48307920 cost_B0 = -9890.10974571 B1 = 12886.62268517 cost_B1 = 1137.53974060
DD      0       17:29:17.999    gradient-descent test (EURUSD,M1)       7 b0 = 2723.61498028 cost_B0 = -9813.19010723 B1 = 12872.93147573 cost_B1 = 1369.12094310
HF      0       17:29:17.999    gradient-descent test (EURUSD,M1)       8 b0 = 2821.23916252 cost_B0 = -9762.41822398 B1 = 12858.67435081 cost_B1 = 1425.71249248

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< Last Iterations >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

EI      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6672 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
NG      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6673 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
GD      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6674 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
PR      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6675 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
IS      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6676 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
RQ      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6677 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
KN      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6678 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
DL      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6679 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
RM      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6680 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
IK      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6681 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
PH      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6682 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
GF      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6683 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
MG      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6684 b0 = 25792.20019866 cost_B0 = -0.00000000 B1 = 9449.96232146 cost_B1 = 0.00000000
LE      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6684 Iterations Local Minima are
OJ      0       17:29:48.247    gradient-descent test (EURUSD,M1)       B0(Intercept) = 25792.20020  ||  B1(Coefficient) = 9449.96232

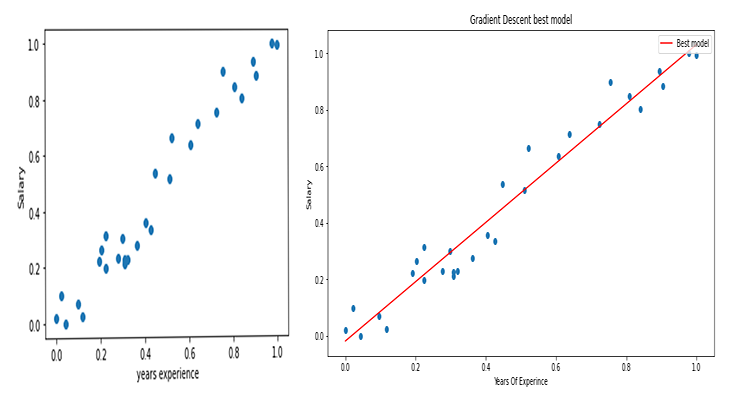
Matplotlib kullanarak grafiği çizersek: 

Gradyan inişle en iyi model

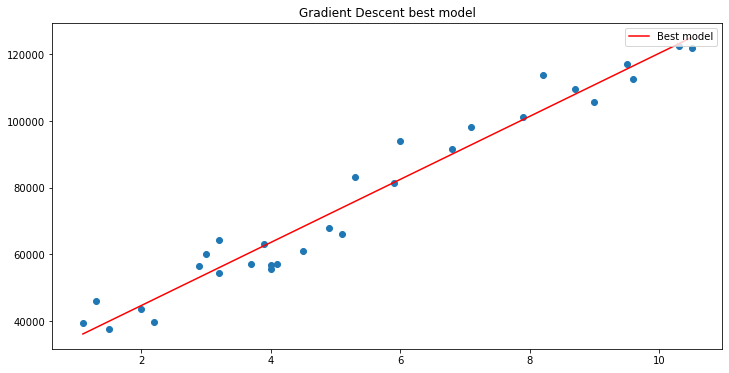
Ta-da! Gradyan iniş, denediğimiz 10000 model arasından en iyi modeli başarıyla elde etmeyi başardı. Harika, ancak atladığımız çok önemli bir adım vardır, ki bu da modelimizin garip davranmasına ve istemediğimiz sonuçlar almamıza neden olabilir.


Lineer Regresyon Girdi Değişkeni Verilerini Normalleştirme

Farklı veri kümeleri için en iyi modellerin, farklı sayıda yinelemelerden sonra bulunabileceğini biliyoruz. Bazılarının en iyi modellere ulaşması 100 yineleme gerektirebilirken, bazılarının maliyet fonksiyonunun sıfıra ulaşması 10000, hatta bir milyona kadar yineleme gerektirebilir. Öğrenme oranı olarak yanlış değerler kullanırsak yerel minimumları kaçırabileceğimizden bahsetmiyorum bile. Ve eğer bu hedefi kaçırırsak, sonunda bilgisayarın matematiksel sınırlarına ulaşmış olacağız, bunu bir örnekle görelim.

Öğrenme oranı=0,1 - Yineleme=1000


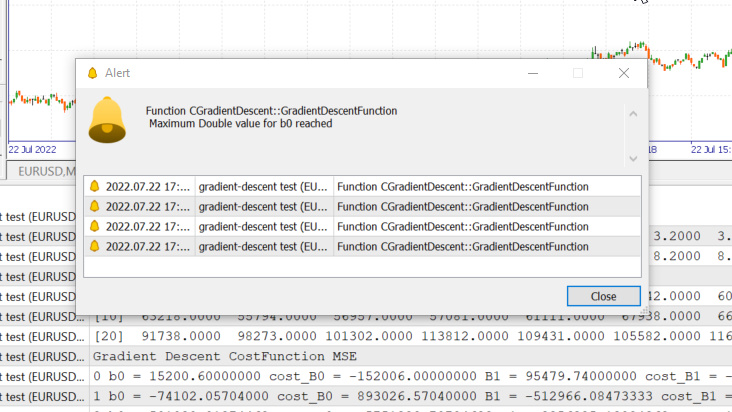
Sistemin izin verdiği maksimum double türü değere ulaştık. Günlük:

GM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction MSE
OP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       0 b0 = 15200.60000000 cost_B0 = -152006.00000000 B1 = 95479.74000000 cost_B1 = -954797.40000000
GR      0       17:28:14.819    gradient-descent test (EURUSD,M1)       1 b0 = -74102.05704000 cost_B0 = 893026.57040000 B1 = -512966.08473333 cost_B1 = 6084458.24733333
NM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       2 b0 = 501030.91374462 cost_B0 = -5751329.70784622 B1 = 3356325.13824362 cost_B1 = -38692912.22976952
LH      0       17:28:14.819    gradient-descent test (EURUSD,M1)       3 b0 = -3150629.51591119 cost_B0 = 36516604.29655810 B1 = -21257352.71857720 cost_B1 = 246136778.56820822
KD      0       17:28:14.819    gradient-descent test (EURUSD,M1)       4 b0 = 20084177.14287909 cost_B0 = -232348066.58790281 B1 = 135309993.40314889 cost_B1 = -1565673461.21726084
OQ      0       17:28:14.819    gradient-descent test (EURUSD,M1)       5 b0 = -127706877.34210962 cost_B0 = 1477910544.84988713 B1 = -860620298.24803317 cost_B1 = 9959302916.51181984
FM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       6 b0 = 812402202.33122230 cost_B0 = -9401090796.73331833 B1 = 5474519904.86084747 cost_B1 = -63351402031.08880615
JJ      0       17:28:14.819    gradient-descent test (EURUSD,M1)       7 b0 = -5167652856.43381691 cost_B0 = 59800550587.65039062 B1 = -34823489070.42410278 cost_B1 = 402980089752.84948730
MP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       8 b0 = 32871653967.62362671 cost_B0 = -380393068240.57440186 B1 = 221513298448.70788574 cost_B1 = -2563367875191.31982422
MM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       9 b0 = -209097460110.12799072 cost_B0 = 2419691140777.51611328 B1 = -1409052343513.33935547 cost_B1 = 16305656419620.47265625
HD      0       17:28:14.819    gradient-descent test (EURUSD,M1)       10 b0 = 1330075004152.67309570 cost_B0 = -15391724642628.00976562 B1 = 8963022367351.18359375 cost_B1 = -103720747108645.23437500
DP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       11 b0 = -8460645083849.12207031 cost_B0 = 97907200880017.93750000 B1 = -57014041694401.67187500 cost_B1 = 659770640617528.50000000

Bu, öğrenme oranını yanlış seçersek, en iyi modeli bulma olasılığımızın çok düşük, hatta sıfır olabileceği ve az önce uyarıda gördüğümüz gibi, sonunda bilgisayarın matematiksel sınırlarına ulaşma olasılığımızın yüksek olabileceği anlamına gelir.

Bu veri kümesinde öğrenme oranı için 0,01'i kullanırsak, eğitim süreci çok daha yavaş olsa da sorun yaşamayacağız. Ama bu veri kümesi için bu öğrenme oranını kullandığımızda, sonunda bilgisayarın matematiksel sınırlarına ulaşacağız. Artık her veri kümesinin kendi öğrenme oranına sahip olduğunu biliyorsunuz. Ancak bazen çok değişkenli karmaşık veri kümeleri nedeniyle öğrenme oranını optimize etmemiz mümkün olmayabilir.

Çözüm, tüm veri kümesini aynı ölçekte olacak şekilde normalleştirmektir. Bu, değerler aynı eksende görüntüleneceğinden okunabilirliği artıracak ve normalleştirilmiş değerler genellikle 0 ile 1 aralığında olacağından eğitim süresini iyileştirecektir. Ayrıca, artık öğrenme oranı konusunda endişelenmemize de gerek kalmayacaktır, çünkü sadece bir adet öğrenme oranı parametremiz olacağından, onu karşılaşabileceğimiz herhangi bir veri kümesi için kullanabileceğiz. Örneğin bizim durumumuzda öğrenme oranı 0,01'dir. Normalleştirme hakkında daha fazlasını buradan okuyabilirsiniz.

Sonuncu fakat bir o kadar önemli bir husus:

Ayrıca, maaş değerlerinin 39343 ile 121782 arasında, tecrübe yılı değerlerinin ise 1,1 ile 10,5 arasında değiştiğini de biliyoruz. Verileri bu şekilde tutarsak, maaş değerleri o kadar büyük olacaktır ki, modelin maaşın diğer tüm değerlerden daha önemli olduğunu düşünmesine neden olabilecektir ve dolayısıyla maaş, tecrübe yılına kıyasla çok büyük bir etkiye sahip olacaktır. Tüm bağımsız değişkenlerin diğerleriyle aynı etkiye sahip olmasına ihtiyacımız vardır. Şimdi değerleri normalleştirmenin ne kadar önemli olduğunu görüyorsunuz.


Min-Maks Skaler Normalleştirme

Bu yaklaşımda, veriler 0 ile 1 arasında olacak şekilde normalleştirilir. Formül aşağıdaki gibidir:

Min-maks skaler normalleştirme formülü

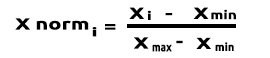
Bu formülü MQL5'te kod satırlarına dönüştürürsek, şu şekilde olacaktır:

void CGradientDescent::MinMaxScaler(double &Array[])
 {
   double mean = Mean(Array);
   double max,min;
   double Norm[];
   
   ArrayResize(Norm,ArraySize(Array));
   
   max = Array[ArrayMaximum(Array)];   min = Array[ArrayMinimum(Array)];
   
    for (int i=0; i<ArraySize(Array); i++)
         Norm[i] = (Array[i] - min) / (max - min); 
   
   printf("Scaled data Mean = %.5f Std = %.5f",Mean(Norm),std(Norm));
   
   ArrayFree(Array);
   ArrayCopy(Array,Norm);
 }

std() fonksiyonu, veriler normalleştirildikten sonra standart sapmayı bulabilmemiz için gereklidir. İşte kodu:

double CGradientDescent::std(double &data[])
 {
   double mean =  Mean(data);
   double sum = 0;
   
    for (int i=0; i<ArraySize(data); i++)
       sum += MathPow(data[i] - mean,2);
    
    return(MathSqrt(sum/ArraySize(data)));  
 }

Şimdi tüm bunları çağıralım ve çıktıyı yazdıralım:

void OnStart()
  {
//---
      string filename = "Salary_Data.csv";

      double XMatrix[];
      double YMatrix[];
      
      
      grad = new CGradientDescent(1, 0.01,1000);
      
      grad.ReadCsvCol(filename,1,XMatrix);
      grad.ReadCsvCol(filename,2,YMatrix);
       
      grad.MinMaxScaler(XMatrix);
      grad.MinMaxScaler(YMatrix);
      
      ArrayPrint("Normalized X",XMatrix);
      ArrayPrint("Normalized Y",YMatrix);
      
      
      grad.GradientDescentFunction(XMatrix,YMatrix,MSE);
      
      delete (grad);
  }

Çıktı:

OK      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Scaled data Mean = 0.44823 Std = 0.29683
MG      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Scaled data Mean = 0.45207 Std = 0.31838
MP      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Normalized X
JG      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [ 0] 0.0000 0.0213 0.0426 0.0957 0.1170 0.1915 0.2021 0.2234 0.2234 0.2766 0.2979 0.3085 0.3085 0.3191 0.3617
ER      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [15] 0.4043 0.4255 0.4468 0.5106 0.5213 0.6064 0.6383 0.7234 0.7553 0.8085 0.8404 0.8936 0.9043 0.9787 1.0000
NQ      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Normalized Y
IF      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [ 0] 0.0190 0.1001 0.0000 0.0684 0.0255 0.2234 0.2648 0.1974 0.3155 0.2298 0.3011 0.2134 0.2271 0.2286 0.2762
IS      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [15] 0.3568 0.3343 0.5358 0.5154 0.6639 0.6379 0.7151 0.7509 0.8987 0.8469 0.8015 0.9360 0.8848 1.0000 0.9939

Grafikler şimdi şu şekilde görünecektir:

Normalleştirilmiş grafikler

Lojistik Regresyon İçin Gradyan İniş

Gradyan inişin lineer tarafını gördük, şimdi lojistik tarafına bakalım.

Burada az önce lineer regresyon kısmında yaptığımız işlemlerin aynısını yapıyoruz, çünkü tamamen aynı süreçler söz konusudur, yalnızca lojistik regresyonun türevini alma işlemi lineer modelden daha karmaşık hale gelmektedir. Öncelikle maliyet fonksiyonuna bakalım.

Serinin lojistik regresyonla ilgili ikinci makalesinde bahsettiğimiz gibi, bir lojistik regresyon modelinin maliyet fonksiyonu ikili çapraz entropidir (kayıp fonksiyonu):

İkili çapraz entropi (kayıp fonksiyonu)

Şimdi önce zor kısmı yapalım, gradyanını elde etmek için bu fonksiyonun türevini alalım.

Türevler: 

Maliyet fonksiyonunun türevleri

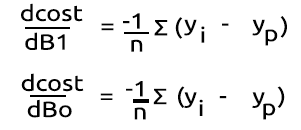
Formülleri, ikili çapraz entropi anlamına gelen BCE (Binary Cross Entropy) fonksiyonu içerisinde MQL5 koduna çevirelim.

double CGradientDescent::Bce(double Bo,double B1,Beta wrt)
 {
   double sum_sqr=0;
   double m = ArraySize(Y);
   double x[];
   
   MatrixColumn(m_XMatrix,x,2);
   
    if (wrt == Slope)
      for (int i=0; i<ArraySize(Y); i++)
        { 
          double Yp = Sigmoid(Bo+B1*x[i]);
          
          sum_sqr += (Y[i] - Yp) * x[i];
        }
        
    if (wrt == Intercept)
      for (int i=0; i<ArraySize(Y); i++)
         {
            double Yp = Sigmoid(Bo+B1*x[i]);
            sum_sqr += (Y[i] - Yp);
         } 
    return((-1/m)*sum_sqr);
 }

Sınıflandırma modeliyle uğraştığımız için veri kümemiz lojistik regresyonda kullandığımız Titanik veri kümesi olacaktır. Bağımsız değişkenimiz Pclass (yolcu sınıfı), bağımlı değişkenimiz ise Survived (hayatta kaldı) olacaktır.

Titanik veri kümesi - yolcu sınıfı vs hayatta kaldı

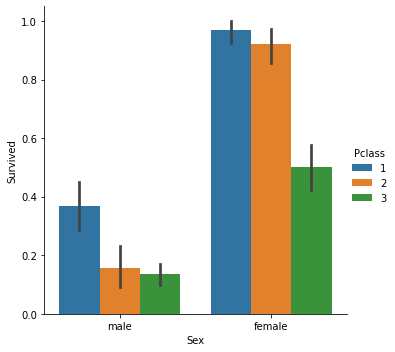
Sınıflandırılmış dağılım grafiği:

Yolcu sınıfı vs hayatta kaldı dağılım grafiği

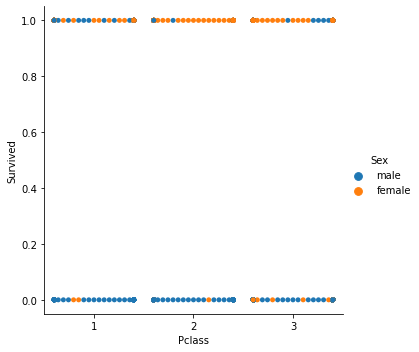
Şimdi gradyan iniş sınıfını çağıralım ama bu sefer maliyet fonksiyonumuz olarak BCE ile.

      filename = "titanic.csv";
      
      ZeroMemory(XMatrix);
      ZeroMemory(YMatrix);
      
      grad.ReadCsvCol(filename,3,XMatrix);
      grad.ReadCsvCol(filename,2,YMatrix);
      
      grad.GradientDescentFunction(XMatrix,YMatrix,BCE);
      
      delete (grad);
      

Sonuca bakalım:

CP      0       07:19:08.906    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction BCE
KD      0       07:19:08.906    gradient-descent test (EURUSD,M1)       0 b0 = -0.01161616 cost_B0 = 0.11616162 B1 = -0.04057239 cost_B1 = 0.40572391
FD      0       07:19:08.906    gradient-descent test (EURUSD,M1)       1 b0 = -0.02060337 cost_B0 = 0.08987211 B1 = -0.07436893 cost_B1 = 0.33796541
KE      0       07:19:08.906    gradient-descent test (EURUSD,M1)       2 b0 = -0.02743120 cost_B0 = 0.06827832 B1 = -0.10259883 cost_B1 = 0.28229898
QE      0       07:19:08.906    gradient-descent test (EURUSD,M1)       3 b0 = -0.03248925 cost_B0 = 0.05058047 B1 = -0.12626640 cost_B1 = 0.23667566
EE      0       07:19:08.907    gradient-descent test (EURUSD,M1)       4 b0 = -0.03609603 cost_B0 = 0.03606775 B1 = -0.14619252 cost_B1 = 0.19926123
CF      0       07:19:08.907    gradient-descent test (EURUSD,M1)       5 b0 = -0.03851035 cost_B0 = 0.02414322 B1 = -0.16304363 cost_B1 = 0.16851108
MF      0       07:19:08.907    gradient-descent test (EURUSD,M1)       6 b0 = -0.03994229 cost_B0 = 0.01431946 B1 = -0.17735996 cost_B1 = 0.14316329
JG      0       07:19:08.907    gradient-descent test (EURUSD,M1)       7 b0 = -0.04056266 cost_B0 = 0.00620364 B1 = -0.18958010 cost_B1 = 0.12220146
HE      0       07:19:08.907    gradient-descent test (EURUSD,M1)       8 b0 = -0.04051073 cost_B0 = -0.00051932 B1 = -0.20006123 cost_B1 = 0.10481129
ME      0       07:19:08.907    gradient-descent test (EURUSD,M1)       9 b0 = -0.03990051 cost_B0 = -0.00610216 B1 = -0.20909530 cost_B1 = 0.09034065
JQ      0       07:19:08.907    gradient-descent test (EURUSD,M1)       10 b0 = -0.03882570 cost_B0 = -0.01074812 B1 = -0.21692190 cost_B1 = 0.07826600
        <<<<<<  Last  10 iterations >>>>>>

FN      0       07:19:09.725    gradient-descent test (EURUSD,M1)       6935 b0 = 1.44678930 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
PN      0       07:19:09.725    gradient-descent test (EURUSD,M1)       6936 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
NM      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6937 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
KL      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6938 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
PK      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6939 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
RK      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6940 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
MJ      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6941 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
HI      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6942 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
CH      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6943 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
MH      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6944 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
QG      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6945 b0 = 1.44678931 cost_B0 = -0.00000000 B1 = -0.85010666 cost_B1 = 0.00000000
NG      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6945 Iterations Local Minima are
MJ      0       07:19:09.727    gradient-descent test (EURUSD,M1)       B0(Intercept) = 1.44679  ||  B1(Coefficient) = -0.85011

Lojistik regresyon için sınıflandırılmış verileri lineer regresyonda yaptığımız gibi normalleştirmez veya ölçeklendirmeyiz.

Böylece en önemli makine öğrenimi modellerinden ikisi için gradyan inişe sahip olduk. Umarım anlaşılması kolay ve yardımcı olmuştur. Bu makalede kullanılan Python kodu ve veri kümesi bu GitHub deposunda bulunmaktadır.


Sonuç

Bir bağımsız ve bir bağımlı değişken için gradyan inişi gördük. Birden çok bağımsız değişken için, denklemlerin vektör/matris biçiminin kullanılması gerekir. MQL5’te kısa süre önce yayınlanan matrisler için kütüphaneye sahip olduğumuza göre, bu sefer okuyucuların her şeyi kendi başlarına denemelerinin daha kolay olacağını düşünüyorum. Matrislerle ilgili herhangi bir yardıma ihtiyacınız olduğunda benimle iletişime geçmekten çekinmeyin, size yardımcı olmaktan mutluluk duyarım.

Saygılarımla.

Hesaplamalar hakkında daha fazla bilgi edinin:


MetaQuotes Ltd tarafından İngilizceden çevrilmiştir.
Orijinal makale: https://www.mql5.com/en/articles/11200

Ekli dosyalar |
ZIP indir
Gradient_Descent.zip (41.03 KB)
Uyarı: Bu materyallerin tüm hakları MetaQuotes Ltd.'a aittir. Bu materyallerin tamamen veya kısmen kopyalanması veya yeniden yazdırılması yasaktır.

Bu yazarın diğer makaleleri

Tartışmaya git
Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 16): İnternetteki verilere erişme (II) Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 16): İnternetteki verilere erişme (II)
İnternetten Uzman Danışmana verilerin nasıl alınacağı o kadar net değildir. MetaTrader 5'in sunduğu tüm olanakları anlamadan bunu yapabilmek zordur.
CCI göstergesi: Yeni hesaplama yöntemleri CCI göstergesi: Yeni hesaplama yöntemleri
Bu makalede, CCI göstergesini yeni hesaplama yöntemleriyle iyileştirmeye çalışacağız.
Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 17): İnternetteki verilere erişme (III) Sıfırdan bir ticaret Uzman Danışmanı geliştirme (Bölüm 17): İnternetteki verilere erişme (III)
Bu makalede, internetten nasıl veri elde edileceğini ve Uzman Danışmanda nasıl kullanılacağını ele almaya devam ediyoruz. Bu kez alternatif bir sistem geliştireceğiz.
Williams %R göstergesine dayalı bir ticaret sistemi nasıl geliştirilir? Williams %R göstergesine dayalı bir ticaret sistemi nasıl geliştirilir?
MetaTrader 5’te kullanılmak üzere MQL5 dili aracılığıyla en popüler teknik göstergelere dayalı ticaret sistemleri geliştirdiğimiz serimizin yeni makalesindeyiz. Bu makalemizde, Williams %R göstergesiyle basit bir ticaret sisteminin nasıl geliştirileceğini öğreneceğiz.