MetaTrader 5 / Trading
English Русский 中文 Español Deutsch 日本語 Português 한국어 Français Türkçe
preview
Scienza dei dati e apprendimento automatico (Parte 06): Discesa del Gradiente

Scienza dei dati e apprendimento automatico (Parte 06): Discesa del Gradiente

MetaTrader 5 — Trading | 13 febbraio 2023, 16:50
956 0
Omega J Msigwa
Omega J Msigwa

L'ottimizzazione prematura è la radice di tutti i mali nella programmazione

-Donald Knut 

Introduzione

Secondo Wikipedia la discesa del gradiente (spesso chiamata anche discesa più ripida) è un algoritmo di ottimizzazione iterativo di primo ordine per trovare un minimo locale di una funzione differenziabile. L'idea è di fare passi ripetuti nella direzione opposta al gradiente (o gradiente approssimativo) della funzione al punto attuale, perché questa è la direzione della discesa più ripida. Al contrario, un passo nella direzione del gradiente porterà a un massimo locale di quella funzione; la procedura è quindi nota come salita del gradiente.


Fondamentalmente, la discesa del gradiente è un algoritmo di ottimizzazione utilizzato per trovare il minimo di una funzione:

discesa gradiente articolo gif

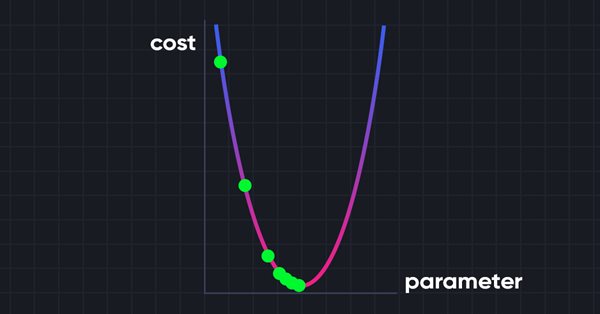
La discesa del gradiente è un algoritmo molto importante nell'apprendimento automatico in quanto ci aiuta a trovare i parametri per il miglior modello per il nostro set di dati. Vorrei prima spiegare il termine Funzione di Costo.


Funzione di costo

Alcune persone la chiamano funzione di perdita, è una metrica per calcolare quanto è buono o cattivo il nostro modello nel prevedere la relazione tra i valori di x e y.

Ci sono molte metriche che possono essere utilizzate per determinare come il modello sta prevedendo, ma a differenza di tutte queste, la funzione di costo trova la perdita media sull'intero set di dati, maggiore è la funzione di costo, meno il nostro modello riesce a trovare le relazioni nel nostro insieme di dati.

La Discesa del Gradiente mira a minimizzare la funzione di costo perché il modello con la funzione di costo più bassa è il modello migliore. Per farti capire cosa ho appena spiegato, vediamo l’esempio seguente.

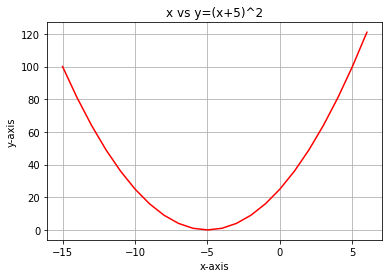
Supponiamo che la nostra funzione di costo sia l'equazione 

Se tracciamo un grafico di questa funzione con Python, ecco come apparirà:

pyplot

Il primo passo che dobbiamo fare per la nostra funzione di costo è differenziare la funzione di costo, usando la Regola della Catena:

L'equazione y= (x+5)^2 è una funzione composta (c'è una funzione all'interno di un'altra). La funzione esterna è (x+5)^2 la funzione interna è (x+5). Per differenziare questo, applichiamo la Regola della Catena, vedi l'immagine:

regola della catena

C'è un video allegato alla fine, di me che faccio i conti a mano, se trovi tutto ciò difficile da capire. Ok, quindi ora questa funzione che abbiamo appena ottenuto è il Gradiente. Il processo per trovare il gradiente di un'equazione è il passaggio più importante di tutti e vorrei che i miei insegnanti di matematica mi avessero detto in passato che lo scopo di differenziare la funzione è quello di ottenere il gradiente di una funzione.

Questo è il primo e più importante passo, di seguito c’è il secondo passaggio.

   Fase 02.

Ci muoviamo nella direzione negativa del gradiente, qui sorge la domanda, quanto dovremmo muoverci? È qui che entra in gioco il tasso di apprendimento.


Tasso di apprendimento

Per definizione, questa è la dimensione del passo ad ogni iterazione mentre ci si sposta verso un minimo di una funzione di perdita, prendi l’esempio di una persona che scende dalla montagna, i suoi passi sono il tasso di apprendimento, più piccoli sono i passi maggiore tempo ci vorrà per raggiungere il fondo della montagna e viceversa.

Mantieni il tasso di apprendimento dell'algoritmo su valori piccoli ma non molto piccoli come 0,0001, perché in questo modo stai aumentando il tempo di esecuzione del programma poiché potrebbe essere necessario più tempo prima che l'algoritmo raggiunga i valori minimi. Al contrario, l'utilizzo di numeri grandi per il tasso di apprendimento farà sì che l'algoritmo salti i valori minimi che alla fine potrebbero causarti la perdita del valore minimo designato.

Il tasso di apprendimento predefinito è 0,01.

Eseguiamo l'iterazione per vedere come funziona l'algoritmo.

Prima iterazione: Scegliamo un punto casuale qualsiasi come punto di partenza per il nostro algoritmo, ho scelto 0 come primo valore di x ora, per aggiornare i valori di x questa è la formula

nuovi valori Discesa del Gradiente

 Ad ogni iterazione, scenderemo verso il valore minimo della funzione e da qui il nome Discesa del Gradiente. Ha senso ora?

ha un senso ora

Vediamo come funziona in dettaglio. Ora calcoliamo manualmente i valori su 2 iterazioni in modo da ottenere una solida comprensione di ciò che sta accadendo:

1a iterazione:

formula: x1 = x0 - tasso di apprendimento * ( 2*(x+5) )

x1 = 0 - 0.01 * 0.01 * 2*(0+5)

x1 = -0.01 * 10

x1 = -0.1 (finalmente) 

Ora finalmente aggiorniamo i valori assegnando il nuovo valore al vecchio valore e ripetiamo la procedura per altrettante iterazioni fino a raggiungere il minimo di una funzione:

x0 = x1

2a iterazione:

x1 = -0.1 - 0.01 * 2*(-0.1+5)

x1 = -0,198

Allora: x0 = x1

Se ripetiamo questa procedura più volte l'output per le prime 10 iterazioni sarà:

RS      0       17:15:16.793    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction CUSTOM
QQ      0       17:15:16.793    gradient-descent test (EURUSD,M1)       1 x0 = 0.0000000000 x1 = -0.1000000000 CostFunction = 10.0000000000
ES      0       17:15:16.793    gradient-descent test (EURUSD,M1)       2 x0 = -0.1000000000 x1 = -0.1980000000 CostFunction = 9.8000000000
PR      0       17:15:16.793    gradient-descent test (EURUSD,M1)       3 x0 = -0.1980000000 x1 = -0.2940400000 CostFunction = 9.6040000000
LE      0       17:15:16.793    gradient-descent test (EURUSD,M1)       4 x0 = -0.2940400000 x1 = -0.3881592000 CostFunction = 9.4119200000
JD      0       17:15:16.793    gradient-descent test (EURUSD,M1)       5 x0 = -0.3881592000 x1 = -0.4803960160 CostFunction = 9.2236816000
IG      0       17:15:16.793    gradient-descent test (EURUSD,M1)       6 x0 = -0.4803960160 x1 = -0.5707880957 CostFunction = 9.0392079680
IG      0       17:15:16.793    gradient-descent test (EURUSD,M1)       7 x0 = -0.5707880957 x1 = -0.6593723338 CostFunction = 8.8584238086
JF      0       17:15:16.793    gradient-descent test (EURUSD,M1)       8 x0 = -0.6593723338 x1 = -0.7461848871 CostFunction = 8.6812553325
NI      0       17:15:16.793    gradient-descent test (EURUSD,M1)       9 x0 = -0.7461848871 x1 = -0.8312611893 CostFunction = 8.5076302258
CK      0       17:15:16.793    gradient-descent test (EURUSD,M1)       10 x0 = -0.8312611893 x1 = -0.9146359656 CostFunction = 8.3374776213

Vediamo anche gli altri dieci valori dell'algoritmo quando è molto vicino al minimo della funzione:

GK      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1052 x0 = -4.9999999970 x1 = -4.9999999971 CostFunction = 0.0000000060
IH      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1053 x0 = -4.9999999971 x1 = -4.9999999971 CostFunction = 0.0000000059
NH      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1054 x0 = -4.9999999971 x1 = -4.9999999972 CostFunction = 0.0000000058
QI      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1055 x0 = -4.9999999972 x1 = -4.9999999972 CostFunction = 0.0000000057
II      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1056 x0 = -4.9999999972 x1 = -4.9999999973 CostFunction = 0.0000000055
RN      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1057 x0 = -4.9999999973 x1 = -4.9999999973 CostFunction = 0.0000000054
KN      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1058 x0 = -4.9999999973 x1 = -4.9999999974 CostFunction = 0.0000000053
JO      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1059 x0 = -4.9999999974 x1 = -4.9999999974 CostFunction = 0.0000000052
JO      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1060 x0 = -4.9999999974 x1 = -4.9999999975 CostFunction = 0.0000000051
QL      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1061 x0 = -4.9999999975 x1 = -4.9999999975 CostFunction = 0.0000000050
QL      0       17:15:16.800    gradient-descent test (EURUSD,M1)       1062 x0 = -4.9999999975 x1 = -4.9999999976 CostFunction = 0.0000000049
HP      0       17:15:16.800    gradient-descent test (EURUSD,M1)       Local miminum found =-4.999999997546217

Dopo 1062 (millesessantadue) iterazioni l'algoritmo è riuscito a raggiungere il minimo locale di questa funzione.

Una cosa da notare da questo algoritmo

Osservando i valori della Funzione di Costo noterai un enorme cambiamento nei valori all'inizio, ma piccolissimi cambiamenti apprezzabili agli ultimi valori della funzione di costo.

La discesa del gradiente fa passi più grandi quando non è neanche lontanamente vicino al minimo di una funzione ma, fa piccoli passi quando è vicino al minimo della funzione, la stessa cosa che farai quando sarai vicino al fondo della montagna, quindi ora sai che la discesa del gradiente è piuttosto intelligente!

Alla fine il minimo locale è 

HP      0       17:15:16.800    gradient-descent test (EURUSD,M1)       Local miminum found =-4.999999997546217

Qual è il valore esatto perché il minimo di questa funzione è -5.0!

La vera domanda

Come fa il Gradiente a sapere quando fermarsi? Vedi, possiamo lasciare che l'algoritmo continui a iterare fino all'infinito o almeno fino alla fine della capacità di calcolo di un computer.

Quando la funzione di costo è Zero è quando sappiamo che la discesa del gradiente ha svolto il suo lavoro.

Ora codifichiamo l'intera operazione in MQL5:

       while (true)
        {
           iterations++;
           
           x1 = x0 - m_learning_rate * CustomCostFunction(x0);
           
           printf("%d x0 = %.10f x1 = %.10f CostFunction = %.10f",iterations,x0,x1,CustomCostFunction(x0)); 
           
           if (NormalizeDouble(CustomCostFunction(x0),8) == 0) { Print("Local minimum found =",x0);  break;  }
              
           x0 = x1;
        }   

Il blocco di codice sopra è quello che è stato in grado di darci i risultati che volevamo ma non è solo nella classe CGradientDescent. La funzione CustomCostFunction è dove la nostra equazione differenziata è stata conservata e calcolata, eccola qui:

double CGradientDescent::CustomCostFunction(double x)
 {
   return(2 * ( x + 5 ));
 }


Qual è lo scopo?

Ci si potrebbe chiedere qual è lo scopo di tutti questi calcoli quando è possibile utilizzare semplicemente il modello lineare predefinito creato con le librerie precedenti di cui abbiamo discusso in questa serie di articoli. Notizia flash, il modello creato utilizzando i valori predefiniti non è necessariamente il modello migliore, quindi è necessario consentire al computer di apprendere i parametri migliori per il modello con pochi errori (modello migliore).

Siamo alcuni articoli più vicini alla costruzione di Reti Neurali Artificiali e affinché tutti siano in grado di capire come le reti neurali apprendono (insegnano a se stesse i modelli) nel processo di Retropropagazione dell'errore e altre tecniche, la discesa del gradiente è l'algoritmo più popolare che ha reso tutto questo possibile. Senza una solida comprensione di esso potresti non capire mai il processo perché le cose si complicheranno.


Discesa del Gradiente per un Modello di Regressione

Usando il set di dati Salary costruiamo il modello migliore usando la discesa del gradiente.

panoramica del set di dati

Visualizzazione dei dati in Python:

import pandas as pd 
import numpy as np
import matplotlib.pyplot as plt


data  = pd.read_csv(r"C:\Users\Omega Joctan\AppData\Roaming\MetaQuotes\Terminal\892B47EBC091D6EF95E3961284A76097\MQL5\Files\Salary_Data.csv")

print(data.head(10))

x = data["YearsExperience"]
y = data["Salary"]

plt.figure(figsize=(16,9))
plt.title("Experience vs Salary")
plt.scatter(x,y,c="green")
plt.xlabel(xlabel="Years of Experience")
plt.ylabel(ylabel="Salary")
plt.show()

Questo sarà il nostro grafico:

Anni di esperienza Vs Stipendio

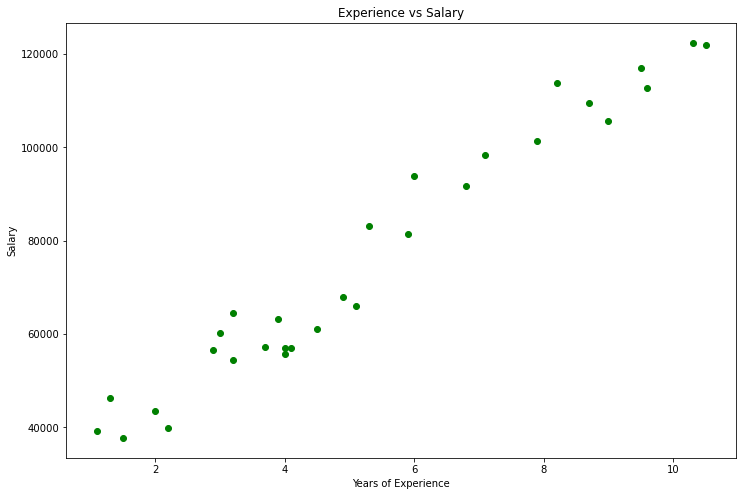
Guardando il nostro set di dati non puoi fare a meno di notare che questo set di dati riguarda un problema di regressione, ma possiamo avere un milione di modelli che ci aiuti a fare la previsione o qualunque cosa stiamo cercando di ottenere.

modalità multipla

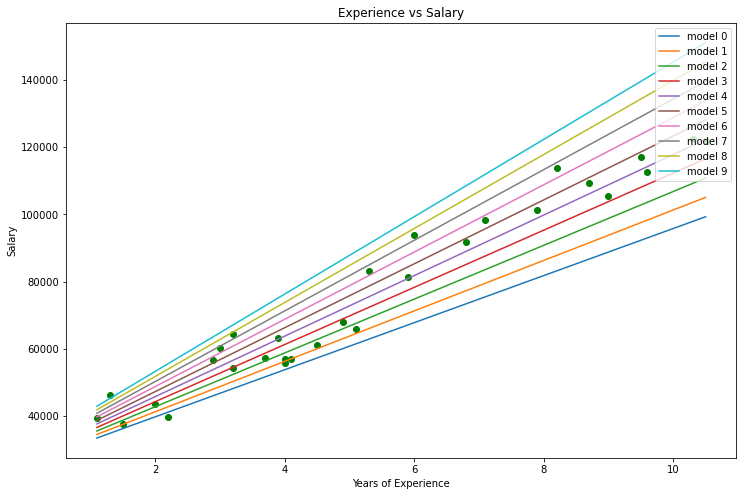
Qual è il miglior modello da utilizzare per fare previsioni sull'esperienza di una persona e quale sarà il suo salario, ecco cosa scopriremo. Ma prima deriviamo la funzione di costo per il nostro modello di regressione.

Teoria

Lascia che ti riporti indietro alla Regressione Lineare.

Sappiamo per certo che ogni modello lineare ha errori associati ad esso. Sappiamo anche che possiamo creare un milione di linee in questo grafico e la linea più adatta è sempre la linea con il minor numero di errori.

La funzione di costo rappresenta l'errore tra i nostri valori attuali e i valori previsti, possiamo scrivere la formula affinché la funzione di costo sia uguale a:

Costo = Y attuale - Y previsto

Dal momento che stiamo vedendo l’entità degli errori, eleviamo al quadrato, la nostra formula ora diventa:

Ma stiamo cercando errori nel nostro intero set di dati, dobbiamo fare la somma: 

Infine, dividiamo la somma degli errori per m che è il numero di elementi nel set di dati:

regressione lineare funzione di costo

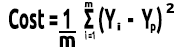
Qui il video di tutte le procedure matematiche fatte a mano.

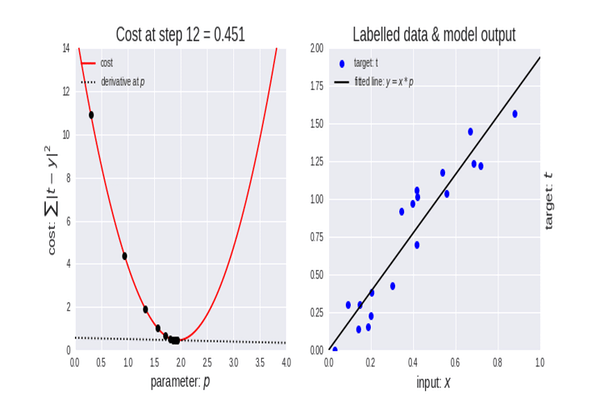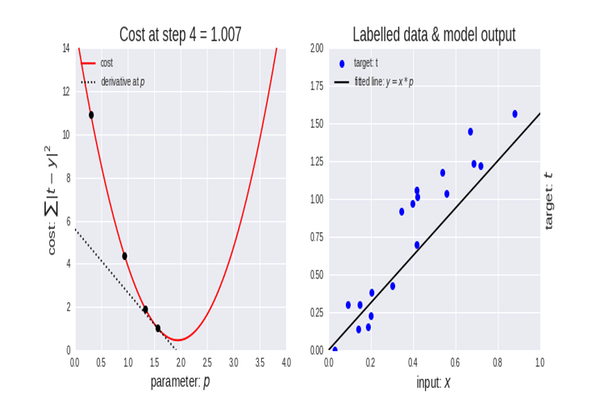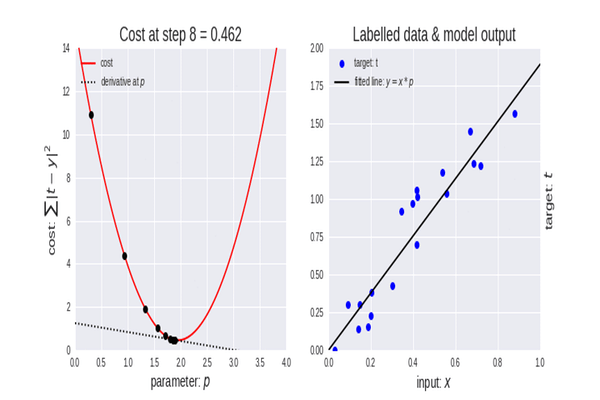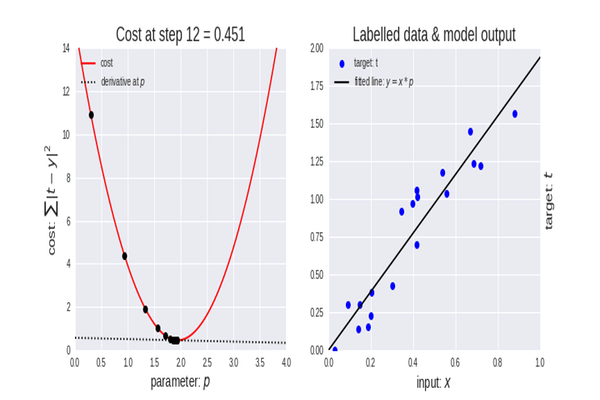
Ora che abbiamo la funzione di costo, codifichiamo la discesa del gradiente e troviamo i parametri migliori per entrambi. Coefficiente di X(Slope) indicato come B0 e l’Intercetta Y indicata come B1 

   
   double cost_B0=0, cost_B1=0;
   
   if (costFunction == MSE)
    {
      int iterations=0;
      for (int i=0; i<m_iterations; i++, iterations++)
        {
        
           cost_B0 = Mse(b0,b1,Intercept);
           cost_B1 = Mse(b0,b1,Slope);
           
           b0 = b0 - m_learning_rate * cost_B0; 
           b1 = b1 - m_learning_rate * cost_B1;
           
           printf("%d b0 = %.8f cost_B0 = %.8f B1 = %.8f cost_B1 = %.8f",iterations,b0,cost_B0,b1,cost_B1);
           
           DBL_MAX_MIN(b0); DBL_MAX_MIN(cost_B0); DBL_MAX_MIN(cost_B1);
           
           if (NormalizeDouble(cost_B0,8) == 0 && NormalizeDouble(cost_B1,8) == 0)  break; 
           
        }
      printf("%d Iterations Local Minima are\nB0(Intercept) = %.5f  ||  B1(Coefficient) = %.5f",iterations,b0,b1);    
    }

Nota alcune cose dal codice della Discesa del Gradiente:

  • Il processo è sempre lo stesso di quello che abbiamo eseguito prima, ma questa volta troviamo e aggiorniamo i valori due volte contemporaneamente B0 e B1.
  • C'è un numero limitato di iterazioni, qualcuno una volta ha detto che il modo migliore per creare un ciclo infinito è usare un ciclo while, questa volta non usiamo il ciclo while ma invece vogliamo limitare il numero di volte in cui l'algoritmo funzionerà per trovare i coefficienti per il modello migliore.
  • DBL_MAX_MIN è una funzione a scopo di debug che ha il compito di controllare e notificarci se abbiamo raggiunto i limiti matematici di un computer.

Questo è l'output delle operazioni dell'algoritmo. Tasso di Apprendimento = 0,01 Iterazioni = 10000

PD      0       17:29:17.999    gradient-descent test (EURUSD,M1)       [20]  91738.0000  98273.0000 101302.0000 113812.0000 109431.0000 105582.0000 116969.0000 112635.0000 122391.0000 121872.0000
JS      0       17:29:17.999    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction MSE
RF      0       17:29:17.999    gradient-descent test (EURUSD,M1)       0 b0 = 1520.06000000 cost_B0 = -152006.00000000 B1 = 9547.97400000 cost_B1 = -954797.40000000
OP      0       17:29:17.999    gradient-descent test (EURUSD,M1)       1 b0 = 1995.08742960 cost_B0 = -47502.74296000 B1 = 12056.69235267 cost_B1 = -250871.83526667
LP      0       17:29:17.999    gradient-descent test (EURUSD,M1)       2 b0 = 2194.02117366 cost_B0 = -19893.37440646 B1 = 12707.81767044 cost_B1 = -65112.53177770
QN      0       17:29:17.999    gradient-descent test (EURUSD,M1)       3 b0 = 2319.78332575 cost_B0 = -12576.21520809 B1 = 12868.77569178 cost_B1 = -16095.80213357
LO      0       17:29:17.999    gradient-descent test (EURUSD,M1)       4 b0 = 2425.92576238 cost_B0 = -10614.24366387 B1 = 12900.42596039 cost_B1 = -3165.02686058
GH      0       17:29:17.999    gradient-descent test (EURUSD,M1)       5 b0 = 2526.58198175 cost_B0 = -10065.62193621 B1 = 12897.99808257 cost_B1 = 242.78778134
CJ      0       17:29:17.999    gradient-descent test (EURUSD,M1)       6 b0 = 2625.48307920 cost_B0 = -9890.10974571 B1 = 12886.62268517 cost_B1 = 1137.53974060
DD      0       17:29:17.999    gradient-descent test (EURUSD,M1)       7 b0 = 2723.61498028 cost_B0 = -9813.19010723 B1 = 12872.93147573 cost_B1 = 1369.12094310
HF      0       17:29:17.999    gradient-descent test (EURUSD,M1)       8 b0 = 2821.23916252 cost_B0 = -9762.41822398 B1 = 12858.67435081 cost_B1 = 1425.71249248

<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< Last Iterations >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>

EI      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6672 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
NG      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6673 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
GD      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6674 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
PR      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6675 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
IS      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6676 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
RQ      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6677 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
KN      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6678 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
DL      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6679 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
RM      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6680 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
IK      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6681 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
PH      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6682 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
GF      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6683 b0 = 25792.20019866 cost_B0 = -0.00000001 B1 = 9449.96232146 cost_B1 = 0.00000000
MG      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6684 b0 = 25792.20019866 cost_B0 = -0.00000000 B1 = 9449.96232146 cost_B1 = 0.00000000
LE      0       17:29:48.247    gradient-descent test (EURUSD,M1)       6684 Iterations Local Minima are
OJ      0       17:29:48.247    gradient-descent test (EURUSD,M1)       B0(Intercept) = 25792.20020  ||  B1(Coefficient) = 9449.96232

Se tracciamo il grafico usando matplotlib 

modello migliore discesa del gradiente

B A M, la Discesa del Gradiente è stato in grado di ottenere con successo il miglior modello su 10000 modelli che abbiamo provato, grande, ma c'è un passaggio cruciale che ci stiamo perdendo che potrebbe causare un comportamento strano del nostro modello e farci ottenere i risultati che non vogliamo.


Normalizzazione dei Dati delle Variabili di Input della Regressione Lineare

Sappiamo che per diversi set di dati i migliori modelli possono essere trovati dopo diverse iterazioni, alcuni potrebbero richiedere 100 iterazioni per raggiungere i migliori modelli e altri potrebbero richiedere 10000 o fino a un milione di iterazioni affinché la funzione di costo diventi zero, per non parlare del fatto che se otteniamo i valori sbagliati del tasso di apprendimento potremmo finire per perdere i minimi locali e se manchiamo quell'obiettivo finiremo per colpire i limiti matematici di un computer, vediamolo in pratica.

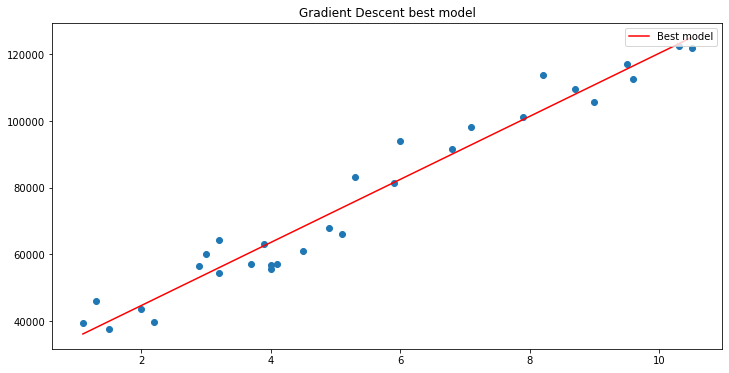
Tasso di apprendimento = 0,1 Iterazioni 1000


Abbiamo appena raggiunto il valore massimo double consentito dal sistema. Ecco i nostri log.

GM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction MSE
OP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       0 b0 = 15200.60000000 cost_B0 = -152006.00000000 B1 = 95479.74000000 cost_B1 = -954797.40000000
GR      0       17:28:14.819    gradient-descent test (EURUSD,M1)       1 b0 = -74102.05704000 cost_B0 = 893026.57040000 B1 = -512966.08473333 cost_B1 = 6084458.24733333
NM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       2 b0 = 501030.91374462 cost_B0 = -5751329.70784622 B1 = 3356325.13824362 cost_B1 = -38692912.22976952
LH      0       17:28:14.819    gradient-descent test (EURUSD,M1)       3 b0 = -3150629.51591119 cost_B0 = 36516604.29655810 B1 = -21257352.71857720 cost_B1 = 246136778.56820822
KD      0       17:28:14.819    gradient-descent test (EURUSD,M1)       4 b0 = 20084177.14287909 cost_B0 = -232348066.58790281 B1 = 135309993.40314889 cost_B1 = -1565673461.21726084
OQ      0       17:28:14.819    gradient-descent test (EURUSD,M1)       5 b0 = -127706877.34210962 cost_B0 = 1477910544.84988713 B1 = -860620298.24803317 cost_B1 = 9959302916.51181984
FM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       6 b0 = 812402202.33122230 cost_B0 = -9401090796.73331833 B1 = 5474519904.86084747 cost_B1 = -63351402031.08880615
JJ      0       17:28:14.819    gradient-descent test (EURUSD,M1)       7 b0 = -5167652856.43381691 cost_B0 = 59800550587.65039062 B1 = -34823489070.42410278 cost_B1 = 402980089752.84948730
MP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       8 b0 = 32871653967.62362671 cost_B0 = -380393068240.57440186 B1 = 221513298448.70788574 cost_B1 = -2563367875191.31982422
MM      0       17:28:14.819    gradient-descent test (EURUSD,M1)       9 b0 = -209097460110.12799072 cost_B0 = 2419691140777.51611328 B1 = -1409052343513.33935547 cost_B1 = 16305656419620.47265625
HD      0       17:28:14.819    gradient-descent test (EURUSD,M1)       10 b0 = 1330075004152.67309570 cost_B0 = -15391724642628.00976562 B1 = 8963022367351.18359375 cost_B1 = -103720747108645.23437500
DP      0       17:28:14.819    gradient-descent test (EURUSD,M1)       11 b0 = -8460645083849.12207031 cost_B0 = 97907200880017.93750000 B1 = -57014041694401.67187500 cost_B1 = 659770640617528.50000000

Questo significa che se otteniamo il tasso di apprendimento sbagliato potremmo avere poche o nessuna possibilità di trovare il modello migliore e le probabilità di finire per raggiungere il limite matematico di un computer sono alte, come hai appena visto dall'avvertimento.

Ma se provo 0,01 come tasso di apprendimento in questo set di dati, finiremo per non avere problemi anche se il processo di addestramento diventerà molto più lento, ma quando utilizzo questo tasso di apprendimento per questo set di dati finirò per raggiungere i limiti matematici, quindi ora sai che ogni set di dati ha il suo tasso di apprendimento ma potremmo non avere la possibilità di ottimizzare per il tasso di apprendimento perché a volte abbiamo complessi set di dati con più variabili e anche questo è un modo inefficace per eseguire l'intero processo.

La soluzione a tutto ciò è normalizzare l'intero set di dati così che possa essere sulla stessa scala, questo migliora la leggibilità quando tracciamo i valori sullo stesso asse, inoltre migliora il tempo di addestramento perché i valori normalizzati sono generalmente nell'intervallo da 0 a 1, inoltre non dobbiamo più preoccuparci del tasso di apprendimento perché una volta che abbiamo un solo parametro del tasso di apprendimento, potremmo usarlo per qualsiasi set di dati che affrontiamo, ad esempio il tasso di apprendimento di 0,01. Ulteriori informazioni sulla normalizzazione qui.

Ultimo, ma non meno importante

Inoltre sappiamo che i valori dei nostri dati sul salario vanno in media da 39.343 a 121.782 mentre gli Anni di Esperienzavanno da 1,1 a 10,5 se manteniamo i dati in questo modo, i valori per il salario sono enormi e potrebbero far pensare al modello che sono più importanti di qualsiasi valore quindi avranno un impatto enorme rispetto agli anni di esperienza, abbiamo bisogno che tutte le variabili indipendenti abbiano lo stesso impatto di qualsiasi altra variabile, ora vedi quanto sia importante normalizzare i valori.


(Normalizzazione) Min-Max Scalare

In questo approccio normalizziamo i dati in modo che siano compresi nell'intervallo 0 e 1. La formula è quella riportata di seguito:

normalizzazione min-max-scalare

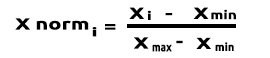
La conversione di questa formula in righe di codice in MQL5 diventerà:

void CGradientDescent::MinMaxScaler(double &Array[])
 {
   double mean = Mean(Array);
   double max,min;
   double Norm[];
   
   ArrayResize(Norm,ArraySize(Array));
   
   max = Array[ArrayMaximum(Array)];   min = Array[ArrayMinimum(Array)];
   
    for (int i=0; i<ArraySize(Array); i++)
         Norm[i] = (Array[i] - min) / (max - min); 
   
   printf("Scaled data Mean = %.5f Std = %.5f",Mean(Norm),std(Norm));
   
   ArrayFree(Array);
   ArrayCopy(Array,Norm);
 }

La funzione std() è solo per farci conoscere la deviazione standard dopo che i dati sono stati normalizzati. Ecco il suo codice:

double CGradientDescent::std(double &data[])
 {
   double mean =  Mean(data);
   double sum = 0;
   
    for (int i=0; i<ArraySize(data); i++)
       sum += MathPow(data[i] - mean,2);
    
    return(MathSqrt(sum/ArraySize(data)));  
 }

Ora chiamiamo tutto questo e stampiamo l'output per vedere cosa succede:

void OnStart()
  {
//---
      string filename = "Salary_Data.csv";

      double XMatrix[];
      double YMatrix[];
      
      
      grad = new CGradientDescent(1, 0.01,1000);
      
      grad.ReadCsvCol(filename,1,XMatrix);
      grad.ReadCsvCol(filename,2,YMatrix);
       
      grad.MinMaxScaler(XMatrix);
      grad.MinMaxScaler(YMatrix);
      
      ArrayPrint("Normalized X",XMatrix);
      ArrayPrint("Normalized Y",YMatrix);
      
      
      grad.GradientDescentFunction(XMatrix,YMatrix,MSE);
      
      delete (grad);
  }

Produzione

OK      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Scaled data Mean = 0.44823 Std = 0.29683
MG      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Scaled data Mean = 0.45207 Std = 0.31838
MP      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Normalized X
JG      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [ 0] 0.0000 0.0213 0.0426 0.0957 0.1170 0.1915 0.2021 0.2234 0.2234 0.2766 0.2979 0.3085 0.3085 0.3191 0.3617
ER      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [15] 0.4043 0.4255 0.4468 0.5106 0.5213 0.6064 0.6383 0.7234 0.7553 0.8085 0.8404 0.8936 0.9043 0.9787 1.0000
NQ      0       18:50:53.387    gradient-descent test (EURUSD,M1)       Normalized Y
IF      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [ 0] 0.0190 0.1001 0.0000 0.0684 0.0255 0.2234 0.2648 0.1974 0.3155 0.2298 0.3011 0.2134 0.2271 0.2286 0.2762
IS      0       18:50:53.387    gradient-descent test (EURUSD,M1)       [15] 0.3568 0.3343 0.5358 0.5154 0.6639 0.6379 0.7151 0.7509 0.8987 0.8469 0.8015 0.9360 0.8848 1.0000 0.9939

I grafici ora saranno simili a questi:

Normalizza il grafico dei prezzi

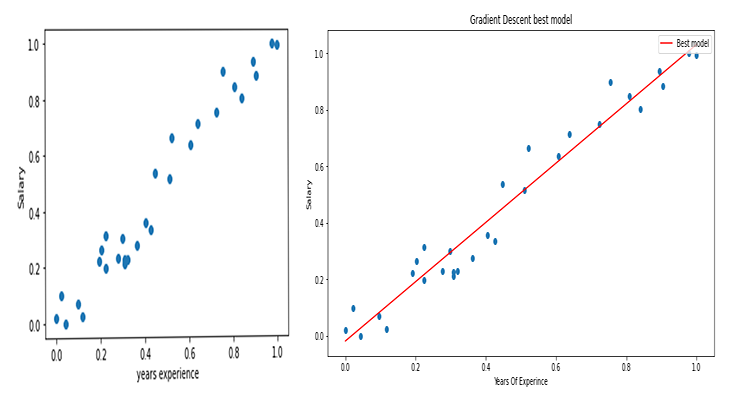
Gradiente discendente per la regressione logistica

Abbiamo visto com’è il lato lineare della discesa del gradiente, ora vediamo il lato logistico.

Qui facciamo gli stessi processi che abbiamo appena fatto sulla parte della regressione lineare perché i processi coinvolti sono esattamente gli stessi solo il processo di differenziazione della regressione logistica diventa più complesso di quello di un modello lineare, vediamo prima la funzione di costo.

Come discusso nel secondo articolo della serie sulla Regressione Logistica, la funzione di costo di un modello di regressione logistica è la Binary Cross Entropy anche detta Log Loss, indicata di seguito.

Entropia incrociata binaria o perdita logaritmica

Ora facciamo prima la parte difficile, differenziare questa funzione per ottenere il suo gradiente.

Dopo aver trovato le derivate 

derivate della funzione di costo

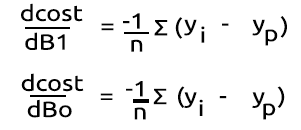
Trasformiamo le formule in codice MQL5 all'interno della funzione BCE che sta per Binary Cross Entropy.

double CGradientDescent::Bce(double Bo,double B1,Beta wrt)
 {
   double sum_sqr=0;
   double m = ArraySize(Y);
   double x[];
   
   MatrixColumn(m_XMatrix,x,2);
   
    if (wrt == Slope)
      for (int i=0; i<ArraySize(Y); i++)
        { 
          double Yp = Sigmoid(Bo+B1*x[i]);
          
          sum_sqr += (Y[i] - Yp) * x[i];
        }
        
    if (wrt == Intercept)
      for (int i=0; i<ArraySize(Y); i++)
         {
            double Yp = Sigmoid(Bo+B1*x[i]);
            sum_sqr += (Y[i] - Yp);
         } 
    return((-1/m)*sum_sqr);
 }

Poiché abbiamo a che fare con il modello di classificazione, il nostro set di dati preferito è il set di dati del Titanic che abbiamo utilizzato nella regressione logistica. La nostra variabile indipendente è Pclass (classe Passeggero)la nostra variabile dipendente invece è Survived.

classe vs sopravvivenza titanic set di dati

grafico di dispersione delle classi

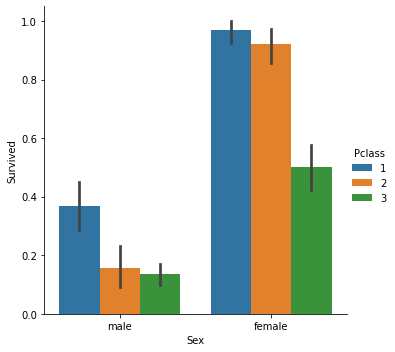
sopravvissuto vs grafico di dispersione delle classi

Ora chiameremo la classe Gradient Descent ma questa volta con BCE (Binary Cross Entropy) come nostra funzione di costo.

      filename = "titanic.csv";
      
      ZeroMemory(XMatrix);
      ZeroMemory(YMatrix);
      
      grad.ReadCsvCol(filename,3,XMatrix);
      grad.ReadCsvCol(filename,2,YMatrix);
      
      grad.GradientDescentFunction(XMatrix,YMatrix,BCE);
      
      delete (grad);
      

Vediamo il risultato:

CP      0       07:19:08.906    gradient-descent test (EURUSD,M1)       Gradient Descent CostFunction BCE
KD      0       07:19:08.906    gradient-descent test (EURUSD,M1)       0 b0 = -0.01161616 cost_B0 = 0.11616162 B1 = -0.04057239 cost_B1 = 0.40572391
FD      0       07:19:08.906    gradient-descent test (EURUSD,M1)       1 b0 = -0.02060337 cost_B0 = 0.08987211 B1 = -0.07436893 cost_B1 = 0.33796541
KE      0       07:19:08.906    gradient-descent test (EURUSD,M1)       2 b0 = -0.02743120 cost_B0 = 0.06827832 B1 = -0.10259883 cost_B1 = 0.28229898
QE      0       07:19:08.906    gradient-descent test (EURUSD,M1)       3 b0 = -0.03248925 cost_B0 = 0.05058047 B1 = -0.12626640 cost_B1 = 0.23667566
EE      0       07:19:08.907    gradient-descent test (EURUSD,M1)       4 b0 = -0.03609603 cost_B0 = 0.03606775 B1 = -0.14619252 cost_B1 = 0.19926123
CF      0       07:19:08.907    gradient-descent test (EURUSD,M1)       5 b0 = -0.03851035 cost_B0 = 0.02414322 B1 = -0.16304363 cost_B1 = 0.16851108
MF      0       07:19:08.907    gradient-descent test (EURUSD,M1)       6 b0 = -0.03994229 cost_B0 = 0.01431946 B1 = -0.17735996 cost_B1 = 0.14316329
JG      0       07:19:08.907    gradient-descent test (EURUSD,M1)       7 b0 = -0.04056266 cost_B0 = 0.00620364 B1 = -0.18958010 cost_B1 = 0.12220146
HE      0       07:19:08.907    gradient-descent test (EURUSD,M1)       8 b0 = -0.04051073 cost_B0 = -0.00051932 B1 = -0.20006123 cost_B1 = 0.10481129
ME      0       07:19:08.907    gradient-descent test (EURUSD,M1)       9 b0 = -0.03990051 cost_B0 = -0.00610216 B1 = -0.20909530 cost_B1 = 0.09034065
JQ      0       07:19:08.907    gradient-descent test (EURUSD,M1)       10 b0 = -0.03882570 cost_B0 = -0.01074812 B1 = -0.21692190 cost_B1 = 0.07826600
        <<<<<<  Last  10 iterations >>>>>>

FN      0       07:19:09.725    gradient-descent test (EURUSD,M1)       6935 b0 = 1.44678930 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
PN      0       07:19:09.725    gradient-descent test (EURUSD,M1)       6936 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
NM      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6937 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
KL      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6938 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
PK      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6939 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
RK      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6940 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
MJ      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6941 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
HI      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6942 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
CH      0       07:19:09.726    gradient-descent test (EURUSD,M1)       6943 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
MH      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6944 b0 = 1.44678931 cost_B0 = -0.00000001 B1 = -0.85010666 cost_B1 = 0.00000000
QG      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6945 b0 = 1.44678931 cost_B0 = -0.00000000 B1 = -0.85010666 cost_B1 = 0.00000000
NG      0       07:19:09.727    gradient-descent test (EURUSD,M1)       6945 Iterations Local Minima are
MJ      0       07:19:09.727    gradient-descent test (EURUSD,M1)       B0(Intercept) = 1.44679  ||  B1(Coefficient) = -0.85011

Non normalizziamo o ridimensioniamo i dati classificati per la regressione logistica come abbiamo fatto nella regressione lineare.

Ecco la discesa del gradiente per i due e più importanti modelli di apprendimento automatico, spero che sia stato facile da capire e utile il codice Python utilizzato in questo articolo e il set di dati è allegato a questo GitHub repo.


Conclusioni

Abbiamo visto la discesa del gradiente per una variabile indipendente e una variabile dipendente, per più variabili indipendenti è necessario utilizzare la forma vettori/matrici delle equazioni, penso che questa volta possa diventare facile per chiunque provare a scoprire da soli ora che abbiamo la Libreria per matrici rilasciata recentemente da MQL5, per qualsiasi aiuto sulle matrici sentiti libero di contattarmi, sarò più che felice di aiutarti.

Cordiali saluti.

Ulteriori informazioni sul calcolo:


Tradotto dall’inglese da MetaQuotes Ltd.
Articolo originale: https://www.mql5.com/en/articles/11200

File allegati |
Scarica ZIP
Gradient_Descent.zip (41.03 KB)
Avvertimento: Tutti i diritti su questi materiali sono riservati a MetaQuotes Ltd. La copia o la ristampa di questi materiali in tutto o in parte sono proibite.

Altri articoli di questo autore

Vai alla discussione
Sviluppare un Expert Advisor per il trading da zero (Parte 16): Accesso ai dati sul web (II) Sviluppare un Expert Advisor per il trading da zero (Parte 16): Accesso ai dati sul web (II)
Conoscere come inserire dati dal Web in un Expert Advisor non è così scontato. Non è così facile farlo, senza comprendere tutte le possibilità offerte da MetaTrader 5.
Indicatore CCI. Aggiornamento e nuove funzionalità Indicatore CCI. Aggiornamento e nuove funzionalità
In questo articolo prenderò in considerazione la possibilità di aggiornare l'indicatore CCI. Inoltre, presenterò una modifica dell'indicatore.
Sviluppare un Expert Advisor per il trading da zero (Parte 17): Accesso ai dati sul web (III) Sviluppare un Expert Advisor per il trading da zero (Parte 17): Accesso ai dati sul web (III)
In questo articolo continuiamo a considerare come ottenere dati dal web e utilizzarli in un Expert Advisor. Questa volta procederemo allo sviluppo di un sistema alternativo.
Scopri come progettare un sistema di trading tramite Williams PR Scopri come progettare un sistema di trading tramite Williams PR
Un nuovo articolo della nostra serie sull'imparare a progettare un sistema di trading con gli indicatori tecnici più popolari tramite MQL5 per poterli utilizzare in MetaTrader 5. In questo articolo impareremo come progettare un sistema di trading tramite l'indicatore Williams %R.