Building Volatility models in MQL5 (Part I): The Initial Implementation

Introduction

In this article, we present an MQL5 library for modeling and forecasting volatility. The primary goal is to provide a flexible tool for specifying different types of volatility processes. These tools are accompanied by a set of analytic utilities used to quantify the quality of the constructed models. We will demonstrate the construction of various volatility processes from the ARCH and GARCH families in MQL5.

An overview of the code

The library presented here is inspired by Python’s arch package, a specialized toolkit for financial econometrics focusing on Autoregressive Conditional Heteroskedasticity (ARCH) and Generalized ARCH (GARCH) models. While the primary function of the arch package is to implement various volatility models, it also provides diverse options for modeling the mean equation—such as constant mean, zero mean, or autoregressive (AR) models. Furthermore, users can specify different distributions for standardized residuals, including Normal, Student's t, and Skewed Student's t-distributions. Our objective is to natively reproduce this functionality within MQL5.

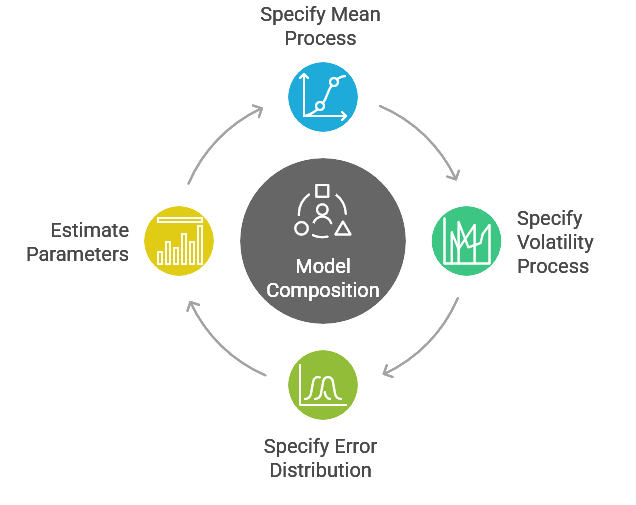
The architecture of this native implementation is modular, decoupling the mean process from the volatility process and the error distribution. Consequently, a model is a composition of these three distinct components. The mean process serves as the primary component to which the others are attached; notably, the joint estimation of all parameters is managed exclusively through this central component. Each element is implemented as a base class, with subclasses representing specific variations.

All classes within the library follow a standardized structure. Each features a parametric constructor in addition to a default constructor. Additionally, every class includes an initialize() method, which must be invoked when an instance is created via the default constructor. For convenience, the initialize() method is called implicitly when using a parametric constructor. The following sections provide a discussion of the implementation for the mean processes, volatility processes, and error distributions.

Configuring a model

The code for modeling the conditional mean is located in mean.mqh. Within this file, the HARX class is defined as the base type for all mean model implementations. As previously mentioned, mean models also serve as the primary interface for a full volatility model. This class provides the functionality required for fitting models to data and generating forecasts.

//+------------------------------------------------------------------+
//| Heterogeneous Autoregression (HAR)                               |
//+------------------------------------------------------------------+
class HARX: public CArchModel
  {
protected:
   bool _initialize(ArchParameters &vol_dist_params);

public:
   HARX(void):m_extra_simulation_params(0)
   HARX(ArchParameters& model_specification)
   ~HARX(void)

      bool    initialize(ArchParameters& vol_dist_params)
      matrix  get_x(void) { return m_model_spec.x; }
      matrix  get_regressors(void) { return m_regressors; }
      vector  get_y(void) { return m_model_spec.y; }

   virtual vector resids(vector &params, vector &y, matrix &regressors);
   virtual ulong  num_params(void);

   bool set_volatility_process(CVolatilityProcess* &vp);
   bool set_distribution(CDistribution* &dist);

   virtual matrix simulate(vector &params, ulong nobs, ulong burn, 
                           vector &initial_vals,matrix &x, 
                           vector &initial_vals_vol);

   ArchForecast forecast(ulong horizon = 1, long start = -1, 
                         ENUM_FORECAST_METHOD method=FORECAST_ANALYTIC, 
                         ulong simulations=1000, uint seed=0);

   ArchForecast forecast(matrix& x[],ulong horizon = 1, long start = -1, 
                         ENUM_FORECAST_METHOD method=FORECAST_ANALYTIC, 
                         ulong simulations=1000, uint seed=0);

   virtual ArchForecast forecast(vector& params, matrix& x[],ulong horizon = 1, 
                                 long start = -1, 
                                 ENUM_FORECAST_METHOD method=FORECAST_ANALYTIC, 
                                 ulong simulations=1000, uint seed=0);

   ArchModelFixedResult fix(vector& params,long first_obs = 0, long last_obs = -1);

   ArchModelResult fit(double scaling = 1.0, uint maxits = 0,
                       ENUM_COVAR_TYPE cov_type = COVAR_ROBUST, 
                       long first = 0, long last = -1, double tol = 1e-9, 
                       bool guardsmoothness=false, 
                       double gradient_test_step = 0.0);

   ArchModelResult fit(vector& startingvalues,vector& backcast,
                       double scaling = 1.0, uint maxits = 0,
                       ENUM_COVAR_TYPE cov_type = COVAR_ROBUST, 
                       long first = 0, long last = -1, double tol = 1e-9, 
                       bool guardsmoothness=false, 
                       double gradient_test_step = 0.0);

  };

Variations of mean models are implemented as subclasses of the HARX class. The parametric constructors for all mean models, as well as their initialize() methods, share a single input parameter: a custom struct named ArchParameters.

struct ArchParameters
  {
  // --- Data & Core Configuration
   vector            observations;          
   matrix            exog_data;             
   vector            mean_lags;             
   
   ENUM_MEAN_MODEL   mean_model_type;       
   ENUM_VOLATILITY_MODEL    vol_model_type;        
   ENUM_DISTRIBUTION_MODEL   dist_type;             
   
   ulong             holdout_size;          
   bool              is_rescale_enabled;    
   double            scaling_factor;        
   
   // --- Mean Model Parameters
   bool              include_constant;      
   bool              use_har_rotation;      
   
   // --- Volatility Process Parameters (GARCH/ARCH)
   int               vol_rng_seed;         
   ulong             garch_p;               
   ulong             garch_o;               
   ulong             garch_q;              
   double            vol_power;            
   
   long              sample_start_idx;      
   long              sample_end_idx;       
   ulong             min_bootstrap_sims;   
   
   // --- Distribution Parameters
   vector            dist_init_params;      
   int               dist_rng_seed;  
};

This struct encapsulates all the variables necessary to instantiate a full volatility model. Its properties are listed below.

Property	Data Type	Description
observations	vector	This vector should contain the time series to be modeled.
exog_data	matrix	This is an optional matrix for any exogenous variables to be included in the model. Each column represents a variable, and the number of rows must match the length of the dependent variable, which is defined in the y property of the struct.
mean_lags	vector	Here, users can specify arbitrary lags for either an AR or HAR process. For an AR model, the lags are simply references to previous values relative to the current value. These lags can be contiguous or non-contiguous. For an HAR process, the lag values represent period lengths or lookbacks over which averages are calculated.
mean_model_type	ENUM_MEAN_MODEL enumeration	This enumeration explicitly specifies the mean process used to model the expected value of the dependent variable. Currently, six mean models have been implemented: constant mean, zero mean, and both AR and HAR processes, each with or without exogenous variables.
vol_model_type	ENUM_VOLATILITY_MODEL enumeration	This property defines the volatility process used to model the conditional variance of the dependent variable, y. Seven options are available, ranging from constant variance to various ARCH and GARCH families of volatility processes. The default option is the constant variance process.
dist_type	ENUM_DISTRIBUTION_MODEL enumeration	This property is an enumeration stipulating the error distribution for the full model. Currently, there are four distributions to choose from: the Normal distribution, Student's T distribution, the Skewed Student's T distribution, and the Generalized Error Distribution (GED). The default is the Normal distribution.
holdout_size	unsigned long	This property specifies the number of observations to be held out when fitting the model to the data.
is_rescale_enabled	bool	This boolean flag indicates whether the scale of the data should be checked. When set to true, the model will assess the data's scale; if rescaling is necessary, a warning will be output to the MetaTrader 5 terminal advising the user to scale the data, along with the recommended scaling factor.
include_constant	bool	This boolean property specifies whether a constant should be included in the mean model.
use_har_rotation	bool	This property is relevant only when a HAR mean model is specified with lags. When set to true, it stipulates that averaging should be performed over non-overlapping periods. For example, suppose the lags {1,5,22} are specified: if this property is false, the model uses averages over the previous 1, 5, and 22 values of the dependent variable. Conversely, if true, the averages are calculated using disjoint windows—specifically, the first lag (1), the period from 2 to 5, and the period from 6 to 22.
vol_rng_seed	integer	This is an optional seed value for the random number generator used by the volatility process.
garch_p	unsigned long	The p parameter for ARCH/GARCH processes.
garch_o	unsigned long	The o parameter for GARCH type processes.
garch_q	unsigned long	The q parameter for GARCH type processes.
vol_power	double	The power parameter of a GARCH type volatility process.
min_bootstrap_sims	unsigned long	This is the minimum number of bootstraps used when forecasting with the bootstrap method.
dist_init_params	vector	This vector contains the initial parameters for the error distribution.
dist_rng_seed	integer	This is an optional seed for the random number generator used by the specified distribution.

An ArchParameters variable must be declared and configured before being passed to either the parametric constructor of a mean model or its initialize() method.

The initialize() method is responsible for validating all parameters to ensure they correspond correctly to the selected mean process, volatility process, and error distribution. Any minor conflicts identified at this stage are quietly corrected.

bool              _initialize(ArchParameters &vol_dist_params)
     {
      if(m_model_spec.mean_model_type!=WRONG_VALUE && vol_dist_params.mean_model_type!=WRONG_VALUE && vol_dist_params.mean_model_type!=m_model_spec.mean_model_type)
        {
         m_initialized = false;
         Print(__FUNCTION__" Incorrect initialization of mean model. \nMake sure input parameters correspond with the correct class ");
         return false;
        }

      if(m_model_spec.mean_model_type!=WRONG_VALUE && vol_dist_params.mean_model_type==WRONG_VALUE)
         vol_dist_params.mean_model_type = m_model_spec.mean_model_type;

      m_model_spec = vol_dist_params;

      switch(m_model_spec.mean_model_type)
        {
         case MEAN_CONSTANT:
            m_model_spec.mean_lags = vector::Zeros(0);
            m_name = "Constant Mean";
            m_model_spec.include_constant = true;
            m_model_spec.use_har_rotation = false;
            break;
         case MEAN_AR:
            m_model_spec.use_har_rotation = false;
            m_model_spec.exog_data = matrix::Zeros(0,0);
            m_name = "AR";
            break;
         case MEAN_ARX:
            m_model_spec.use_har_rotation = false;
            m_name ="AR-X";
            break;
         case MEAN_HAR:
            m_model_spec.exog_data = matrix::Zeros(0,0);
            m_name = "HAR";
            break;
         case MEAN_HARX:
            m_name = "HAR-X";
            break;
         case MEAN_ZERO:
            m_model_spec.exog_data=matrix::Zeros(0,0);
            m_model_spec.mean_lags = vector::Zeros(0);
            m_model_spec.include_constant = false;
            m_model_spec.use_har_rotation = false;
            m_name = "Zero Mean";
            break;
         default:
            m_name = "HAR-X";
            break;
        }

      m_fit_indices = vector::Zeros(2);
      m_fit_indices[1] = (m_model_spec.observations.Size())?double(m_model_spec.observations.Size()):-1.;
      if(m_model_spec.mean_lags.Size())
        {
         switch(m_model_spec.mean_model_type)
           {
            case MEAN_AR:
            case MEAN_ARX:
               m_lags = matrix::Zeros(2,m_model_spec.mean_lags.Size());
               m_lags.Row(m_model_spec.mean_lags,0);
               m_lags.Row(m_model_spec.mean_lags,1);
               break;
            case MEAN_HAR:
            case MEAN_HARX:
               m_lags = matrix::Zeros(1,m_model_spec.mean_lags.Size());
               m_lags.Row(m_model_spec.mean_lags,0);
               break;
           }
        }
      else
         m_lags = matrix::Zeros(0,0);
      m_constant = m_model_spec.include_constant;
      m_rescale = m_model_spec.is_rescale_enabled;
      m_rotated = m_model_spec.use_har_rotation;
      m_holdback = m_model_spec.holdout_size;
      m_initialized = _init_model();
      if(!m_initialized)
         return false;

      m_num_params = num_params();

      if(CheckPointer(m_vp)==POINTER_DYNAMIC)
         delete m_vp;
      m_vp = NULL;

      switch(vol_dist_params.vol_model_type)
        {
         case VOL_CONST:
            m_vp = new CConstantVariance(m_model_spec.vol_rng_seed,m_model_spec.min_bootstrap_sims);
            break;
         case VOL_ARCH:
            m_vp = new CArchProcess(m_model_spec.garch_p,m_model_spec.vol_rng_seed,m_model_spec.min_bootstrap_sims);
            break;
             case VOL_GARCH:
            m_vp = new CGarchProcess(m_model_spec.garch_p,m_model_spec.garch_q,m_model_spec.vol_rng_seed,m_model_spec.min_bootstrap_sims);
            break;
         default:
            m_vp = new CConstantVariance(m_model_spec.vol_rng_seed,m_model_spec.min_bootstrap_sims);
            break;
        }

      if(CheckPointer(m_distribution)==POINTER_DYNAMIC)
         delete m_distribution;
      m_distribution = NULL;

      switch(vol_dist_params.dist_type)
        {
         case DIST_NORMAL:
            m_distribution = new CNormal();
            break;
         default:
            m_distribution = new CNormal();
            break;
        }

      m_initialized = (
                         m_distribution!=NULL  &&
                         m_vp!=NULL            &&
                         m_vp.is_initialized() &&
                         m_distribution.initialize(m_model_spec.dist_init_params,
                               m_model_spec.dist_rng_seed)
                      );

      return m_initialized;
     }

The method will only fail if there are issues with the sample data or if the specified parameters conflict with the supplied sample series; in such cases, the method returns false . If the model specification is valid, the method proceeds to initialize the remaining components of the full model. If any errors occur during this secondary phase, the initialize() method will flag them and return false . Once the initialize() method executes successfully, the fitting process can commence.

Joint estimation of the model's parameters is performed by calling one of the fit() methods.

Fitting a model to data

The fitting procedure is handled with the help of Alglib's Nonlinearly constrained optimization with preconditioned augmented Lagrangian algorithm, implemented as the CMinNLC class. The function being minimized is the log-likelihood function defined as member of the HARX class. 

vector objective(vector& parameters, vector& sigma2, 
                 vector &backcast, matrix& varbounds, 
                 bool individual=false)
     {
      return _loglikelihood(parameters,sigma2,backcast,varbounds,individual);
     }

The inputs for the fit() methods are listed and explained in the table below.

Parameter Name	Data Type	Description
startingvalues	vector	This is a vector of starting values for the model parameters used in the optimization process. Users may specify their own values; otherwise, the parameter accepts an empty vector, in which case suitable starting values will be calculated automatically.
backcast	vector	This vector is used to estimate the parameters of a conditional volatility process. Because the equation for conditional variance is recursive, initial values are required to compute the first observation when pre-sample data is unavailable. This parameter also accepts an empty vector, in which case suitable backcast values are determined internally.
scaling	double	This is the scaling factor used to transform the sample series. The optimizer performs more effectively if it has knowledge of how the data was transformed, if at all. The default value is 1.
cov_type	ENUM_COV_TYPE enumeration	This is an enumeration specifying the method used to estimate the parameter covariance matrix.
maxits	unsigned long	This value stipulates the maximum number of iterations allowed for the optimizer.
first,last	integers	These values are indices specifying the start and end of the range within the sample series to be used for model parameter estimation.
tol	double	This parameter specifies the tolerance level or threshold used to determine when the optimization process has converged.
guardsmoothness	bool	This value configures the optimizer by activating or deactivating non-smoothness monitoring. When enabled, the optimizer accounts for functions that may not be perfectly differentiable; further details regarding this mechanism can be found in the ALGLIB documentation.
gradient_test_step	double	When enabled (set to a non-zero value), this option instructs the optimizer to verify the analytic gradient or Jacobian function provided. While this ensures mathematical consistency and can prevent errors in the optimization logic, it significantly impacts the speed of the process. Refer to the ALGLIB documentation to determine the appropriate configuration value for a specific use case.

The fit() method returns an ArchModelResult struct, which encapsulates the outcome of the optimization process, including the estimated coefficients, statistical significance, and model diagnostics.

struct ArchModelFixedResult
  {
   double            loglikelihood;
   vector            params;
   vector            conditional_volatility;
   ulong             nobs;
   vector            resid;
 };

//+------------------------------------------------------------------+
//| arch model result                                                |
//+------------------------------------------------------------------+
struct ArchModelResult: public ArchModelFixedResult
  {
   long              fit_indices[2];
   matrix            param_cov;
   double            r2;
   ENUM_COVAR_TYPE   cov_type;

Below are the properties and methods contained within the ArchModelResult struct.

Property Name	Data Type	Description
params	vector	These are the results of the optimization process, representing the volatility model's parameters. The values are organized in a specific, sequential order: Mean Model Parameters: These appear first (e.g., constant, AR/HAR coefficients, exogenous variables). Volatility Parameters: These follow second (e.g., omega, alpha, and beta in a GARCH process). Distribution Parameters: These are listed last (e.g., degrees of freedom or skewness parameters).
conditional_volatility	vector	This vector holds the in-sample conditional volatility, representing the model's volatility forecasts over the estimation period.
nobs	integer	This property indicates the total number of observations from the sample series actually utilized to fit the model parameters.
resids	vector	This vector contains the residuals of the full model, representing the difference between the observed values and the values predicted by the mean equation. These can be used for gauging the quality of the model fit.
loglikelihood	double	This is the value of the log-likelihood function at the point of convergence. It represents the minimum value achieved by the objective function during the optimization process.
fit_indices	vector	This vector contains two elements that explicitly define the index range (start and end) of the sample series used during the model estimation.
param_cov	matrix	This matrix holds the estimated covariance matrix of the model parameters. It is a square matrix where the dimensions correspond to the total number of estimated parameters.
r2	double	This gives a measure of the proportion of variance in the dependent variable that is explained by the mean model.
cov_type	enumeration	This property indicates the specific method or estimator used to compute the parameter covariance matrix.

The methods of the ArchModelResult struct provide more statistical depth, that goes beyond simple point estimates to determine if the model is truly adequate. Below are the statistical methods and the metrics they provide:

tvalues(void)	Returns a vector of the t-statistic for each parameter. It is calculated as the ratio of the estimated coefficient to its standard error.

vector tvalues(void)
     {
      return params/std_err();
     }

pvalues(void)	Returns the p-values associated with the t-statistics. This helps you determine the probability that the observed parameter value occurred by chance, typically, a value less than 0.05 indicates statistical significance.

vector pvalues(void)
     {
      vector pvals = tvalues();
      for(ulong i = 0; i<pvals.Size(); ++i)
         pvals[i] = CAlglib::NormalCDF(-1.0*MathAbs(pvals[i]))*2.0;

      return pvals;
     }

rsquaredadj(void)	Returns the Adjusted R-Squared for the mean model. Unlike the standard R-squared, this penalizes the inclusion of unnecessary variables, indicating how much variance is explained by the model relative to its complexity.

double rsquared_adj(void)
     {
      return 1.0 - ((1.0-r2)*double(nobs-1)/double(nobs-num_params()));
     }

stderror(void)	Returns the standard errors of the parameters. These represent the precision of the estimates; smaller errors indicate more reliable parameter estimates.

vector std_err(void)
     {
      return sqrt(param_cov.Diag());
     }

If the optimization process fails to converge, the ArchModelResult properties will typically contain default values and the params vector will be empty. It is therefore best practice to check if the params vector before proceeding with any analysis or forecasting.

Forecasting

Once a model is successfully fitted, forecasting is handled by an overloaded forecast method. This flexibility allows for the generation of predictions based on different data inputs. The following parameters are used across the various overloads of the forecast method to generate future volatility and mean estimates. 

Parameter Name	Data Type	Description
horizon	unsigned long	An integer defining the forecast horizon. It determines how many steps into the future the model will predict both the conditional mean and the conditional volatility. The default value is 1.
start	integer	This parameter identifies the point in your data series that serves as the origin for the forecast. It determines which observation the future predictions will immediately follow. By default, this is set to the last available index in the data.
method	ENUM_FORECAST_METHOD enumeration	This parameter determines the mathematical approach used to project future volatility. While the mean model usually follows a standard path, the volatility process can be projected in multiple ways depending on the complexity of the model. Options are Analytic, Simulation, or Bootstrap. It defaults to Analytic. The Analytic method uses closed-form mathematical formulas to calculate the expected variance. However, it has a significant limitation regarding the power parameter. If the model assumes that variance is the squared residuals, the analytic method works for any horizon. Otherwise, if the model uses a power other than 2, the analytic method cannot be used for horizons greater than one. This is because the expectation of the non-linear transformation does not have a simple recursive solution. The Simulation (Monte Carlo) method uses the assumed distribution  to simulate numerous potential paths and averages them. Whereas, Bootstrap resamples directly from the historical residuals to generate future paths without assuming a specific distribution.
simulations	integer	An integer specifying the number of paths (or draws) to generate. This is used exclusively when the method is set to Simulation or Bootstrap.
seed	integer	An optional integer value used to initialize the pseudo-random number generator (RNG). It ensures that the random paths generated during Simulation or Bootstrap forecasting are reproducible.
params	vector	An optional vector of coefficients. If provided, the forecast will be calculated using these specific values instead of the results from the internal fit() method.
x	array of matrices	This parameter is relevant when the mean model incorporates exogenous variables. Since these variables are external to the volatility process itself, the model cannot "predict" their future values; they must be pre-specified to generate a complete forecast. If the model was fitted with k exogenous variables, this input is required to compute the forecast. Pay close attention to the dimensions of each matrix provided for this variable. The required shape depends on the horizon parameter, the number of exogenous variables, and the value of start relative to the size of the sample series used to build the model. The size of the array (the total number of matrices) must equal the number of exogenous variables. For each matrix, the number of rows must be at least equal to the difference between the total sample size and the starting index (forecast origin). Finally, the number of columns must match the horizon parameter.

When invoking the forecast() method, it returns an ArchForecast struct. This container encapsulates the projected paths for both the mean and the volatility. The struct is organized into three primary matrices.

//+------------------------------------------------------------------+
//|  arch forecast result                                            |
//+------------------------------------------------------------------+
struct ArchForecast
  {
   matrix            mean;
   matrix            variance;
   matrix            residual_variance;

The mean matrix holds the forecasted values for the conditional mean (the expected price or return). The variance property is a matrix with the forecast values for the conditional volatility. And finally the residual_variance matrix represents the forecasts of the conditional variance of the residuals.

Model validation

After fitting a model, the Lagrange Multiplier (LM) test (sometimes called called Engle’s ARCH Test), is the standard diagnostic tool used to confirm if any ARCH effects (heteroskedasticity) remain in the residuals. If the model is adequate, the residuals should be white noise, meaning the test should fail to find significant autocorrelation in the squared residuals. The archlmtest() function evaluates this by regressing the squared residuals on their own lags.

//+------------------------------------------------------------------+
//| The Lagrange multiplier test                                     |
//+------------------------------------------------------------------+
WaldTestStatistic archlmtest(vector& residuals,vector& conditional_volatility,ulong lags,bool standardized = false)
  {
   WaldTestStatistic out;
   vector resids = residuals;
   if(standardized)
      resids = resids/conditional_volatility;
   if(resids.HasNan())
     {
      vector nresids = vector::Zeros(resids.Size() - resids.HasNan());
      for(ulong i = 0, k = 0; i<resids.Size(); ++i)
         if(MathClassify(resids[i]) == FP_NAN)
            continue;
         else
            nresids[k++] = resids[i];
      resids = nresids;
     }
   int nobs = (int)resids.Size();
   vector resid2 = MathPow(resids,2.0);
   if(!lags)
      lags = ulong(ceil(12.0*pow(nobs/100.0,1.0/4.0)));
   lags = MathMax(MathMin(resids.Size()/2 - 1,lags),1);
   if(resid2.Size()<3)
     {
      Print(__FUNCTION__, " Test requires at least 3 non-nan observations ");
      return out;
     }
   matrix matres = matrix::Zeros(resid2.Size(),1);
   matres.Col(resid2,0);
   matrix lag[];
   if(!lagmat(matres,lag,lags,TRIM_BOTH,ORIGINAL_SEP))
     {
      Print(__FUNCTION__, " lagmat failed ");
      return out;
     }
   matrix lagout;
   if(!addtrend(lag[0],lagout,TREND_CONST_ONLY,true,HAS_CONST_SKIP))
     {
      Print(__FUNCTION__, " addtrend failed ");
      return out;
     }
   lag[0] = lagout;
   OLS ols;
   if(!ols.Fit(lag[1].Col(0),lag[0]))
     {
      Print(__FUNCTION__, " OLS fitting failed ");
      return out;
     }

   out.stat = nobs*ols.Rsqe();
   if(standardized)
     {
      out.null = "Standardized residuals are homoskedastic";
      out.alternative = "Standardized residuals are conditionally heteroskedastic";
     }
   else
     {
      out.null = "Residuals are homoskedastic";
      out.alternative = "Residuals are conditionally heteroskedastic";
     }

   out.df = lags;
   return out;
  }

It requires the following inputs. 

Parameter Name	Data Type	Description
residuals	vector	The vector of residuals obtained from the ArchModelResult. These are the raw errors from the fitted model.
conditional_volatility	vector	This is the in sample conditional volatility for a fitted model.
lags	unsigned long	An integer specifying the number of lags to include in the test regression.
standardized	bool	This boolean flag specifies whether to standardize the residuals using the conditional_volatility.

Calling the archlmtest() function returns a WaldTestStatistic struct.

//+------------------------------------------------------------------+
//|Test statistic holder for Wald-type tests                         |
//+------------------------------------------------------------------+
struct WaldTestStatistic
 {
  ulong df;
  double stat;
  string null;
  string alternative;
  
  WaldTestStatistic(void)
   {
    stat = EMPTY_VALUE;
    df = 0; 
    null = alternative = NULL;
   }
  WaldTestStatistic(double _stat, ulong _df, string _null, string _alt)
   {
    stat = _stat;
    df = _df;
    null = _null;
    alternative = _alt;
   }
  WaldTestStatistic(WaldTestStatistic &other)
   {
    stat = other.stat;
    df = other.df;
    null = other.null;
    alternative = other.alternative;
   }
  void operator=(WaldTestStatistic &other)
   {
    stat = other.stat;
    df = other.df;
    null = other.null;
    alternative = other.alternative;
   }
  double pvalue(void)
   {
    int ecode = 0;
    double val = 1.- MathCumulativeDistributionChiSquare(stat,double(df),ecode);
    
    if(ecode)
     Print(__FUNCTION__," Chisquare cdf error ", ecode);
    return val;
   }
  vector critical_values(void)
   {
    vector out = {0.9,0.95,0.99};
    int ecode = 0;
    for(ulong i = 0; i<out.Size(); ++i)
         out[i] = MathQuantileChiSquare(out[i],double(df),ecode);
    if(ecode)
     Print(__FUNCTION__," Chisquare cdf error ", ecode);
    return out;
   }
 };

This structure contains the formal statistical results needed to determine if the model has successfully removed the volatility clusters from the data.

Property Name	Data Type	Description
df	unsigned long	Degrees of freedom for the test, which corresponds to the number of lags specified in the function call.
stat	double	The calculated test statistic. This value follows a Chi-squared distribution under the null hypothesis.
pvalue(void)	double	The pvalue() method returns the probability of observing a test statistic as extreme as the one calculated, assuming no ARCH effects remain.
crtical(void)	vector	The critical() method returns a vector of the critical values at three confidence levels: 90%,95% and 99%.

To gauge the adequacy of the model, we primarily look at the p-value. If the p-value is larger than 0.05, it is a pass. Meaning we cannot reject the null hypothesis. This indicates that the residuals are homoskedastic (constant variance), meaning the ARCH/GARCH model has done its job. On the other hand, if the p-value is less than or equal to 0.05, we reject the null hypothesis. This suggests ARCH effects remain in the residuals, and the model is likely inadequate. We may need to increase the lag order or try a different model type. The stat increases as the correlation in the squared residuals increases. A very large stat will result in a very small p-value, signaling that the model has missed significant volatility patterns.

An example incorporating exogenous variables

This section demonstrates how to specify a model incorporating exogenous variables. The "X" in ARX and HARX refers to these external, independent variables within a regression equation. In this framework, the time series being modeled serves as the dependent variable, while the exogenous predictors are supplied as a matrix where each column represents a single variable.

To illustrate the flexibility of exogenous variables, we examine an interesting relationship between ARX and Heterogeneous Autoregressive (HAR) models. By using averaged historical data as exogenous inputs in an ARX model, we can replicate the behavior of an HAR model. This comparison highlights both the practical application of exogenous variables and the underlying structure of HAR models. The HAR model, was specifically designed to model realized volatility in financial markets, though it can be adapted for other variables. It is called "Heterogeneous" because it breaks down the influence of the past into different time horizons (short, medium, and long) based on the assumption that different types of market participants react to volatility over different time scales.

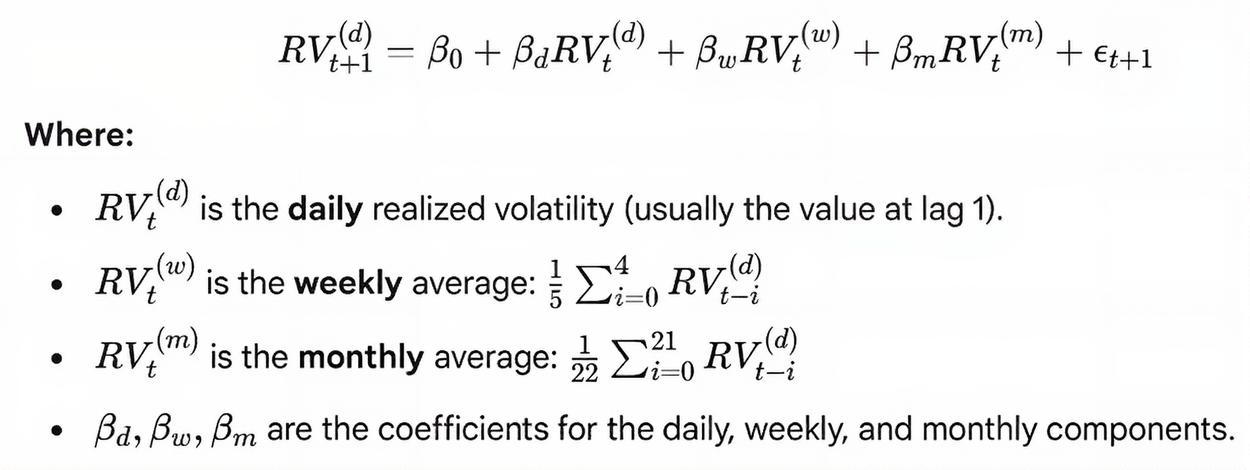
The most common version of the HAR model uses realized volatility measurements over three period lengths: short, medium and long. Where each period defines the number of time points used to calculate the average realized volatility. The HAR model captures long-term memory in volatility through the overlapping average terms. 

The ARX model combines a standard Autoregressive (AR) process with  exogenous (X) inputs. It assumes the current value depends on its own past values and current or past values of external variables. The general formula for an ARX(p,q) model is as follows.

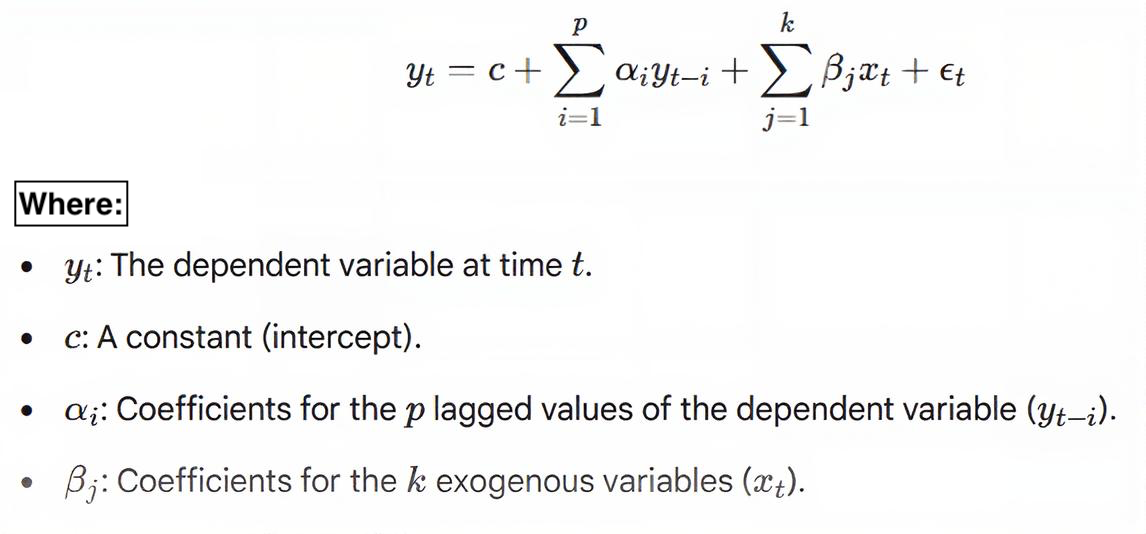
The script HAR_as_ARX_Demo.ex5, demonstrates how an ARX model can be used to mimic a HAR model. The script implements the following steps:

• Builds a standard HAR model using a selectable number of averaged terms.
• Specifies an ARX model using those same averaged terms as its exogenous input matrix.
• Compares the parameters of both models to demonstrate their equivalence.

//+------------------------------------------------------------------+
//|                                              HAR_as_ARX_Demo.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Arch\Univariate\mean.mqh>

//--- input parameters
input string   Symbol_="AUDUSD";
input ENUM_TIMEFRAMES   TimeFrame=PERIOD_D1;
input datetime StartDate=D'2025.01.01';
input ulong HistoryLen = 504;
input double ScaleFactor=100.;
input bool MeanConstant = true;
input string MeanLags ="1,5,22";

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---download data
   vector prices;
   if(!prices.CopyRates(Symbol_,TimeFrame,COPY_RATES_CLOSE,StartDate,HistoryLen))
    {
     Print(" failed to get close prices for ", Symbol_,". Error ", GetLastError());
     return;
    }
//---
   prices = log(prices);
//---
   vector returns = np::diff(prices);
//---
   string lag_info[];
//---
   vector lags=vector::Zeros(0);
//---
   int nlags = StringSplit(MeanLags,StringGetCharacter(",",0),lag_info);
//---
   double atod;
   if(nlags>0)
    {
     for(uint i = 0; i<uint(nlags); ++i)
      {
       if(StringLen(lag_info[i])>0)
        {
         atod = StringToDouble(lag_info[i]);
         if(atod>0 && ulong(atod)<returns.Size()-1)
           if(lags.Resize(lags.Size()+1,3))
              lags[lags.Size()-1] = atod;
        }
      }
    }
//---
  if(lags.Size())
    np::sort(lags);
//---build the HAR model
  ArchParameters har_spec;
  har_spec.observations=returns*ScaleFactor;
  har_spec.include_constant = MeanConstant;
  har_spec.mean_lags = lags;
  har_spec.vol_model_type = VOL_CONST;
//---
  HAR harmodel;
//---
  if(!harmodel.initialize(har_spec))
    return;
//---
  ArchModelResult har = harmodel.fit(ScaleFactor);
//---
  if(!har.params.Size())
   {
    Print("Convergence failed ", GetLastError());
    return;
   }
//---
  Print(" Har model parameters\n", har.params);
//---Now we build an equivalent ARX model
  matrix exogvars = matrix::Zeros(returns.Size(),lags.Size());
//---calculate averages  
  double sum;
  ulong lag,count;
  for(ulong i = 0; i<exogvars.Cols(); ++i)
   {
    lag = (ulong)lags[i];
    count = lag;
    for(ulong k = lag; k<exogvars.Rows(); ++k)
     {
       sum = 0.0;
       for(ulong j = 0; j<count; ++j)
         sum+=returns[k-j-1];
       exogvars[k,i] = sum/double(count);
     }
   }
//---
  ArchParameters arx_spec;
  arx_spec.observations = ScaleFactor*np::sliceVector(returns,long(lags[lags.Size()-1]));
  arx_spec.exog_data = ScaleFactor*np::sliceMatrixRows(exogvars,long(lags[lags.Size()-1]));
  arx_spec.include_constant = MeanConstant;
  arx_spec.vol_model_type=VOL_CONST; 
//---
  ARX arxmodel;
  if(!arxmodel.initialize(arx_spec))
   return;
//---
  ArchModelResult arx = arxmodel.fit(ScaleFactor);
  if(!arx.params.Size())
   {
    Print(" convergence failed ", GetLastError());
    return;
   }
//---
  Print("ARX model parameters\n", arx.params);
 } 
//+------------------------------------------------------------------+

The script was run with the default parameters.

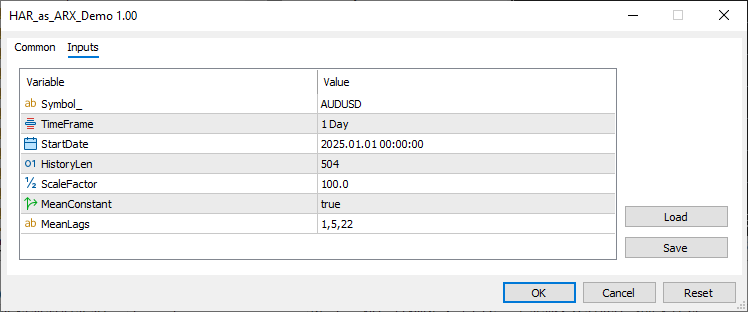
Yielding the following output showing the fitted model parameters.

NR      0       22:12:43.671    HAR_as_ARX_Demo (XAUUSD,D1)      Har model parameters
CE      0       22:12:43.672    HAR_as_ARX_Demo (XAUUSD,D1)     [-0.02336784243846212,-0.04576660950059414,0.02963893847811298,-0.1589020837643845,0.3352700836173772]
RE      0       22:12:43.691    HAR_as_ARX_Demo (XAUUSD,D1)     ARX model parameters
HN      0       22:12:43.691    HAR_as_ARX_Demo (XAUUSD,D1)     [-0.02336784243846212,-0.04576660950059416,0.02963893847811294,-0.1589020837643847,0.3352700836173772]

The demonstration confirms that both approaches yield identical model parameters as shown by the output of the script.

Conclusion

In this article, we have laid the groundwork for native volatility modeling in MQL5. By standardizing the interface through the ArchParameters and ArchModelResult structures, we have created a workflow that enables model specification, optimization, and validation. This framework allows for the straightforward initialization of a model, fitting it to a dataset, and performing rigorous diagnostic checks—such as the ARCH-LM test—to ensure that residuals are free of heteroskedasticity.

While the current version of the library implements several foundational volatility processes, it is presently limited to the assumption that error distributions follow a Standard Normal profile. In an upcoming installment, we will implement more advanced volatility processes and expand the library to support a wider range of error distributions. All code related to the article is provided below. 

File	Description
MQL5/include/Arch	This folder contains all the header files for the volatility modeling library.
MQL5/include/Regression	This folder contains some regression utilities used in the volatility modeling code.
MQL5/include/np.mqh	This header file contains various utilities for manipulating vectors and matrices.
MQL5/scripts/HAR_as_ARX_Demo.mq5	This is a script that demonstrates the specification of a HAR model as a AR model with exogenous variables.