MetaTrader 5 / Examples
preview
Bivariate Copulae in MQL5: (Part 3): Implementation and Tuning of Mixed Copula Models in MQL5

Bivariate Copulae in MQL5: (Part 3): Implementation and Tuning of Mixed Copula Models in MQL5

MetaTrader 5 — Examples |
234 0
Francis Dube
Francis Dube

Introduction

The first two articles in our exploration of copula functions covered the two most common classes: Elliptical and Archimedean copulas. Through that analysis, it was established that different copulas capture distinct types of data dependence. However, because financial data is inherently complex, a single copula family may not adequately capture the full spectrum of dependence structures within a dataset. In that regard, mixed copulas may be able to address this limitation by combining the strengths of individual copula families to model a broader range of dependencies. In this article, we describe the implementation of mixed copula models using the families introduced in our previous installments.


What is a Mixed Copula?

Simply put, a mixed copula is a multivariate function constructed from multiple copula families. Formally, a mixed copula function is a linear combination of distinct copulas used to capture the complex structures that define how data is related.

The mathematical definition of a mixed copula is expressed below.

Mixed Copula formula

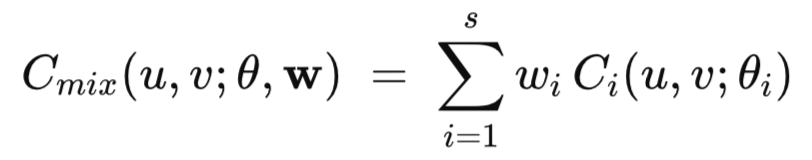
In this formula, w_i​ represents the weights assigned to each individual copula, where the sum of all weights must equal one. The variable s denotes the total number of single copulas included in the mixture. The parameters of the mixed copula encompass the individual parameters (θi​) of each constituent copula. This structure affords mixed copulae the flexibility to model a broad range of dependence structures that a single copula could not capture. The objective is to construct a model from enough candidate copulas to fully describe the dependence structures of a dataset.

While determining the optimal number and specific families of copulas for a given dataset is beyond the scope of this article, we will demonstrate the implementation of a mixed copula composed of three distinct families. This approach follows the methodology established by Fernando Sabino da Silva, Flavio Ziegelmann, and João Caldeira in their paper, "Mixed Copula Pairs Trading Strategy on the S&P 500". The authors propose a pairs trading strategy utilizing Clayton-Frank-Gumbel and Clayton-Student-t-Gumbel mixtures. These combinations are designed to capture both asymmetric tail dependence and potential regime-switching behavior within the data. The effectiveness of these mixtures stems from the unique strengths of each individual component, as outlined in the table below. 

Copula  Characteristic  Relevance 
Clayton Lower tail dependence Captures joint extreme downward movements.
Gumbel Upper tail dependence Captures joint extreme upward movements.
Frank Symmetry with no tail dependence Captures the normal dependency in the center of the distribution without assuming extremes will happen together.
Student-t  Symmetric with tail dependence Captures fat tails in both directions. The assumption in this case, is that if an extreme event happens (up or down), the symbols will likely move together. 

The mixture weights prioritize the constituent copula that best describes dependence in the data. For instance, the Frank copula is most effective when data exhibits low to moderate correlation without extreme tail behavior. Conversely, the Student-t component is designed to capture extreme moves that are not necessarily asymmetric. The Clayton-Frank-Gumbel mixture is purely Archimedean, making it highly effective at distinguishing between lower-tail, upper-tail, and independent-middle behaviors. This combination offers the dual advantages of computational efficiency and high interpretability. In contrast, the Clayton-Student-t-Gumbel mixture acts as a hybrid; the Student-t copula introduces a layer of flexibility that the Frank copula lacks by capturing tail dependence in both directions simultaneously. This is particularly relevant for lower-timeframe data where volatility clusters are prominent.

While the previously mentioned paper outlines the concept we aim to reproduce, it lacks specific implementation details for mixed copulas. To bridge this gap, we reference a second academic source: "Selection of Mixed Copula Models via Penalized Likelihood" by Zongwu Cai and Xian Wang, published in the Journal of the American Statistical Association (ASA).


Estimating the parameters of a Mixed Copula

The ASA article introduces a data-driven framework for selecting and estimating mixed copula models by employing a penalized likelihood approach combined with a shrinkage operator. The authors address the challenge of capturing complex dependence structures in financial data by allowing multiple copula families to be combined and refined simultaneously.

Their technique filters out redundant or insignificant copula components by applying a Smoothly Clipped Absolute Deviation (SCAD) penalty to the likelihood maximization procedure. This approach is designed to perform model selection and parameter estimation concurrently. Using an approach that penalizes the weights, the method shrinks the coefficients of less relevant copulae to zero. The process begins with the initial selection of candidate copulae for the mixture, followed by a cross-validation procedure to determine the optimal SCAD tuning parameters.

SCAD

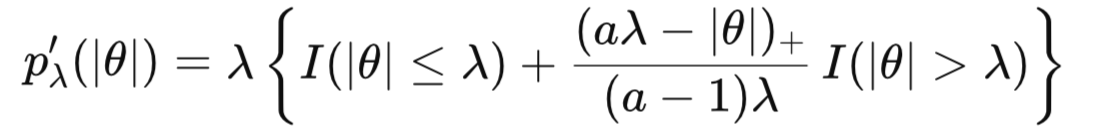
SCAD is a regularization method introduced to perform variable selection and parameter estimation simultaneously. It was designed to overcome the limitations of Lasso (L1​) and Ridge (L2​) regularization. Specifically, the bias Lasso introduces by over-shrinking large coefficients. Generally, an ideal penalty function should possess three properties, refered to as Oracle properties. 

  • The first is the property of sparsity, it must have the ability to set small, irrelevant coefficients to zero.
  • The second oracle property, is that is must be unbiased. This means that it must not excessively shrink large, significant coefficients.
  • The last oracle property is that of continuity. The function must remain stable and not fluctuate erratically with small changes in the data.

SCAD is widely utilized because it is one of the few functions that achieves all three. The SCAD penalty is defined by its derivative rather than a single simple formula. Its behavior shifts based on the magnitude of the parameter it is applied to, which, in this context are the weights. The method works in three steps.

  1. For small coefficients, the penalty function has the same effect as Lasso regularization, to force coefficients toward zero.


    SCAD small coefficients

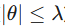
  2. In the case of medium sized coefficients, the penalty function's "Lasso effect", decreases with a quadratic transition.


    SCAD medium coefficients

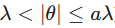
  3. The penalty function converts large coefficients to constants. Once a coefficient is sufficiently large, SCAD stops suppressing it, eliminating the estimation bias found in Lasso regularization.

    SCAD large coefficients

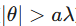
In the formulaic depictions above, λ is the tuning parameter for the sparsity threshold, while a controls how quickly the penalty levels off and θ is the parameter being penalized. The primary drawback of the SCAD penalty is that it makes the objective function non-convex. Unlike the bowl shape of Ridge or Lasso, the SCAD objective function may have multiple local minima, requiring sophisticated optimization routines.

To find the optimal tuning parameters, a cross-validation procedure is used. The data is split into training and test sets, and a grid search is performed over candidate λ and a values. For each pair, the mixed copula model is fitted to the training data, and its penalized likelihood is calculated on the test data. The objective is to maximize the likelihood of the constituent copula parameters minus the SCAD penalty applied to the copula weights.

Once the optimal SCAD parameters are determined, the final model parameters are estimated using the full dataset. Because estimating multiple copulae simultaneously is computationally complex, the process uses the Expectation-Maximization (EM) algorithm.

  1. The process begins with a two-step estimation to find starting values. Weights are typically distributed equally, and initial copula parameters are set to valid values according to their respective constraints.
  2. The following step is the Expectation step. This phase refines the weights. It calculates how much each data point belongs to a specific copula component.
  3. The last step of the EM algorithm is the Maximization step. This phase updates the individual copula parameters to maximize the likelihood, weighted by the values calculated in the previous step.

These steps iterate until convergence, ensuring the mixed copula reflects the observed dependencies. The next section discusses the code that implements the procedures just described. 


MQL5 Implementation of Mixed Copula Models

The implementation discussed here is adapted from a Hudson and Thames repository originally written in Python. The core logic for the native MQL5 implementation of mixed copulae is contained in the mixed.mqh header file. In this file, the abstract class CMixedCopula serves as the foundation for all mixed copula implementations. This class defines several protected properties for managing the mixture.

The class defines the m_copulas array representing the individual constituent copula families. The mixing proportions assigned to each component copula are stored in the vector m_weights. The specific parameters for each individual copula component are all stored in one vector, m_cop_parameters. By using an abstract base class, the architecture remains modular. This allows for the construction of different copula combinations while maintaining a uniform interface.

//+------------------------------------------------------------------+
//|base class for mixed copula                                       |
//+------------------------------------------------------------------+
class CMixedCopula:public CObject
  {
protected:
   uint              m_num_cops;
   CBivariateCopula* m_copulas[];
   vector            m_weights;
   vector            m_cop_params;
   ENUM_COPULA_MIX   m_mixture;
public:
                     CMixedCopula(void):m_weights(vector::Zeros(0)),
                     m_cop_params(vector::Zeros(0)),
                     m_num_cops(0),
                     m_mixture(WRONG_VALUE)
     {
     }
                    ~CMixedCopula(void)
     {
      for(uint i = 0; i<m_copulas.Size(); ++i)
         if(CheckPointer(m_copulas[i]) == POINTER_DYNAMIC)
            delete m_copulas[i];
     }

The CMixedCopula class also provides methods for statistical analysis, sampling, and model management. With regard to evaluating the statistical properties of mixed copula models, the class defines the Copula_PDF() method that evaluates the joint density of the copula. 

double            Copula_PDF(double u, double v, double _eps = 1.e-5)
     {
      u = fmin(fmax(_eps,u),1. - _eps);
      v = fmin(fmax(_eps,v),1. - _eps);
      vector pdf_ = vector::Zeros(m_weights.Size());
      for(uint i = 0; i<m_copulas.Size(); ++i)
         pdf_[i] = m_copulas[i]?m_weights[i]*m_copulas[i].Copula_PDF(u,v,false):0.0;
      return pdf_.Sum();
     }

vector            Copula_PDF(vector& u, vector& v, double _eps = 1.e-5)
     {
      vector pdf_ = vector::Zeros(u.Size());
      for(uint i = 0; i<m_copulas.Size(); ++i)
        {
         if(!m_copulas[i])
            continue;
         m_copulas[i].Set_eps(_eps);
         pdf_ += m_weights[i]*m_copulas[i].Copula_PDF(u,v);
        }
      return pdf_;
     }

The Copula_CDF() method computes the joint cumulative distribution of the copula, and the Conditional_Probability() method determines the conditional cumulative probability.

double            Copula_CDF(double u, double v, double _eps = 1.e-5)
     {
      u = fmin(fmax(_eps,u),1. - _eps);
      v = fmin(fmax(_eps,v),1. - _eps);
      vector cdf_ = vector::Zeros(m_weights.Size());
      for(uint i = 0; i<m_copulas.Size(); ++i)
         cdf_[i] = m_copulas[i]?m_weights[i]*m_copulas[i].Copula_CDF(u,v,false):0.0;
      return cdf_.Sum();
     }

vector            Copula_CDF(vector& u, vector& v, double _eps = 1.e-5)
     {
      vector cdf_ = vector::Zeros(u.Size());
      for(uint i = 0; i<m_copulas.Size(); ++i)
        {
         if(!m_copulas[i])
            continue;
         m_copulas[i].Set_eps(_eps);
         cdf_+=m_weights[i]*m_copulas[i].Copula_CDF(u,v);
        }
      return cdf_;
     }
double            Conditional_Probability(double u, double v, double _eps = 1.e-5)
     {
      u = fmin(fmax(_eps,u),1. - _eps);
      v = fmin(fmax(_eps,v),1. - _eps);
      vector result_ = vector::Zeros(m_weights.Size());
      for(uint i = 0; i<m_copulas.Size(); ++i)
         result_[i] = m_copulas[i]?m_weights[i]*m_copulas[i].Conditional_Probability(u,v,false):0.0;
      return result_.Sum();
     }

vector            Conditional_Probability(vector& u, vector& v, double _eps = 1.e-5)
     {
      vector result_ = vector::Zeros(u.Size());
      for(uint i = 0; i<m_copulas.Size(); ++i)
        {
         if(!m_copulas[i])
            continue;
         m_copulas[i].Set_eps(_eps);
         result_+=m_weights[i]*m_copulas[i].Conditional_Probability(u,v);
        }
      return result_;
     }

The Sample() method is used to generate synthetic data points from a fitted mixed copula model. 

matrix            Sample(ulong num)
     {
      vector r = np::arange(m_weights.Size());
      vector cop_identities = np::choice(r,m_weights,num);
      matrix sample_pairs = matrix::Zeros(num,2);
      matrix temp;
      for(ulong i = 0; i<cop_identities.Size(); ++i)
        {
         temp = m_copulas[uint(cop_identities[i])].Sample(1);
         sample_pairs.Row(temp.Row(0),i);
        }
      return sample_pairs;
     }

Whilst the Save() and Load() methods facilitate model persistence, allowing the state of a trained model to be stored and retrieved without retraining. 

virtual bool      Save(const int file_handle)
     {
      if(file_handle!=INVALID_HANDLE)
        {
         if(FileWriteLong(file_handle,-1)==sizeof(long))
           {
            if(FileWriteInteger(file_handle,int(m_copulas.Size()),INT_VALUE)!=INT_VALUE)
               return(false);
            if(FileWriteInteger(file_handle,int(m_mixture),INT_VALUE)!=INT_VALUE)
               return(false);
            if(FileWriteLong(file_handle,long(m_weights.Size()))!=sizeof(long))
               return(false);
            if(m_weights.Size())
              {
               for(ulong i = 0; i<m_weights.Size(); ++i)
                  if(FileWriteDouble(file_handle,m_weights[i])!=sizeof(double))
                     return(false);
              }
           }
        }
      else
         return false;

      for(ulong i = 0; i<m_copulas.Size(); ++i)
        {
         if(CheckPointer(m_copulas[i])!=POINTER_INVALID)
           {
            if(!m_copulas[i].Save(file_handle))
               return false;
           }
        }
      return true;
     }
   virtual bool      Load(const int file_handle)
     {
      if(file_handle!=INVALID_HANDLE)
        {
         long ff = FileReadLong(file_handle);
         if(ff == -1)
           {
            int size = FileReadInteger(file_handle,INT_VALUE);
            ENUM_COPULA_MIX mixture = ENUM_COPULA_MIX(FileReadInteger(file_handle,INT_VALUE));
            if(ArraySize(m_copulas)!=size || mixture!=m_mixture)
              {
               Print(__FUNCTION__, " You are attempting to load a model incompatible with this class ");
               return false;
              }
            ulong size_weights = (ulong)FileReadLong(file_handle);
            if(size_weights)
              {
               m_weights = vector::Zeros(size_weights);
               switch(m_mixture)
                 {
                  case CFG_MIX:
                     m_cop_params = vector::Zeros(size_weights);
                     break;
                  case CTG_MIX:
                     m_cop_params = vector::Zeros(size_weights+1);
                     break;
                 }
               for(ulong i = 0; i<size_weights; ++i)
                  m_weights[i] = FileReadDouble(file_handle);
              }
           }
         else
            return false;
        }
      else
         return false;
      //---
      for(ulong i = 0,k = 0; i<m_copulas.Size(); ++i)
        {
         m_copulas[i] = bivariate_copula(file_handle);
         if(m_copulas[i]==NULL)
           {
            Print(__FUNCTION__, " failed to load a bivariate copula from file ", GetLastError());
            return false;
           }
         if(m_weights.Size())
           {
            switch(ENUM_COPULA_TYPE(m_copulas[i].Type()))
              {
               case CLAYTON_COPULA:
               case GUMBEL_COPULA:
               case JOE_COPULA:
               case N13_COPULA:
               case N14_COPULA:
               case FRANK_COPULA:
                  m_cop_params[k++] = m_copulas[i].Get_theta();
                  break;
               case STUDENT_COPULA:
                  m_cop_params[k++] = m_copulas[i].Get_nu();
                  m_cop_params[k++] = m_copulas[i].Get_rho();
                  break;
              }
           }
        }
      return true;
     }

Lastly, the class defines two virtual methods that are meant to be overridden. The Fit() method should implement the logic that estimates the parameters of the copula given a sample of pseudo-observations, by minimizing the likelihood function specified as the Penalized_Log_Likelihood() method, incorporating the SCAD penalty.

virtual double    Fit(matrix& qdata, ulong maxiter = 25, double gamma_scad = 0.0, double a_scad = 0.0,double weight_margin=1.e-2)
     {
      return EMPTY_VALUE;
     }

virtual double    Penalized_Log_Likelihood(matrix &data,double g_scad, double a_scad)
     {
      return EMPTY_VALUE;
     }

Also defined in mixed.mqh is the ENUM_COPULA_MIX enumeration, which serves to provide a list of the mixed copula types that have been implemented , for easy selection.

//+------------------------------------------------------------------+
//| mixed copula type                                                |
//+------------------------------------------------------------------+
enum ENUM_COPULA_MIX
  {
   CFG_MIX=0,//Clayton-Frank-Gumbel
   CFJ_MIX,//Clayton-Frank-Joe
   CTG_MIX,//Clayton-Student-Gumbel
   JFG_MIX//Joe-Frank-Gumbel
  };

The CFGMixCop class represents the Clayton-Frank-Gumbel mixed copula. It features a parametric constructor for cases where the user prefers to define model parameters explicitly rather than fitting them from data.

public:
                     CFGMixCop(void)
     {
      m_mixture = CFG_MIX;
      m_num_cops = 3;
      ArrayResize(m_copulas,int(m_num_cops));
      for(uint i = 0; i<m_num_cops; ++i)
         m_copulas[i] = NULL;
     }

                     CFGMixCop(vector &params, vector& weights)
     {
      m_mixture = CFG_MIX;
      m_num_cops = 3;
      ArrayResize(m_copulas,int(m_num_cops));
      if(params.Size()<3 || weights.Size()<3)
         Print(__FUNCTION__, " invalid parameters ");
      else
        {
         m_weights = weights;
         m_cop_params = params;
         for(ulong i = 0; i<3; ++i)
           {
            if(!i)
               m_copulas[i] = new CClayton();
            else
               if(i==1)
                  m_copulas[i] = new CFrank();
               else
                  m_copulas[i] = new CGumbel();
            m_copulas[i].Set_theta(m_cop_params[i]);
           }
        }
     }

When using the parametric constructor, parameters must be provided in vector containers. Both the copula parameters and their corresponding weights must follow a specific sequence:

  1. Clayton parameter
  2. Frank parameter
  3. Gumbel parameter

Similarly, calling any getter methods will return values in this consistent order, ensuring predictable data handling across the model. The Fit() method handles the estimation of the model from data. 

virtual double            Fit(matrix& qdata, ulong maxiter = 50, double gamma_scad = 0.0,double a_scad = 0.0, double weight_margin = 1.e-2) override
     {
      if(CheckPointer(m_copulas[0])==POINTER_INVALID)
         m_copulas[0] = new CClayton();
      if(CheckPointer(m_copulas[1])==POINTER_INVALID)
         m_copulas[1] = new CFrank();
      if(CheckPointer(m_copulas[2])==POINTER_INVALID)
         m_copulas[2] = new CGumbel();

      matrix wc = _fit_quantile_em(qdata,maxiter,gamma_scad,a_scad);
      if(!wc.Rows())
         return EMPTY_VALUE;
      wc.Row(adjust_weights(wc.Row(0),weight_margin),0);
      m_weights = wc.Row(0);
      m_cop_params = wc.Row(1);

      m_copulas[0].Set_theta(m_cop_params[0]);
      m_copulas[1].Set_theta(m_cop_params[1]);
      m_copulas[2].Set_theta(m_cop_params[2]);

      vector u1 = qdata.Col(0);
      vector u2 = qdata.Col(1);

      return _ml_qfunction(u1,u2,wc.Row(1),wc.Row(0),gamma_scad,a_scad,false);
     }
  • The data input variable is a matrix (minimum 2 columns) of pseudo-observations (raw values transformed to the [0,1] interval).
  • The maxiter function input is an integer defining the maximum iterations for the EM algorithm.
  • The inputs gamma_scad and a_scad are of type double representing the SCAD hyperparameters.
  • The weight_margin input is a threshold value, such that, weights falling below this limit are truncated to zero to enforce sparsity.

On successful execution, Fit() returns the non-penalized log-likelihood; otherwise, it returns EMPTY_VALUE. The core estimation logic is encapsulated within the protected _fit_quantile_em() method, which orchestrates the iterative process. 

matrix            _fit_quantile_em(matrix &qd, ulong max_iter,double gamma_scad, double a_scad)
     {
      vector init_weights = {0.33, 0.33, 1. - 0.33 - 0.33};
      vector init_cop_params = {3,4,5};
      vector weights = _expectation_step(qd,gamma_scad,a_scad,init_cop_params,init_weights);
      if(!weights.Size())
         return matrix::Zeros(0,0);
      vector cop_params = _maximization_step(qd,gamma_scad,a_scad,init_cop_params,weights);
      if(!cop_params.Size())
         return matrix::Zeros(0,0);
      vector oldparams,newparams;
      oldparams = newparams = vector::Zeros(6);

      np::vectorCopy(oldparams,init_weights,0,3);
      np::vectorCopy(oldparams,init_cop_params,3);

      np::vectorCopy(newparams,weights,0,3);
      np::vectorCopy(newparams,cop_params,3);

      double ll_diff = MathAbs(oldparams-newparams).Sum();
      ulong i = 1;
      while(i<max_iter && ll_diff>(5.*1.e-2))
        {
         np::vectorCopy(oldparams,weights,0,3);
         np::vectorCopy(oldparams,cop_params,3);

         weights = _expectation_step(qd,gamma_scad,a_scad,cop_params,weights);
         if(!weights.Size())
           {
            Print(__FUNCTION__, " invalid weights ", i);
            return matrix::Zeros(0,0);
           }

         cop_params = _maximization_step(qd,gamma_scad,a_scad,cop_params,weights);
         if(!cop_params.Size())
           {
            Print(__FUNCTION__, " failed convergence at iteration ", i);
            return matrix::Zeros(0,0);
           }

         np::vectorCopy(newparams,weights,0,3);
         np::vectorCopy(newparams,cop_params,3);

         ll_diff = MathAbs(oldparams-newparams).Sum();
         i+=1;
        }

      matrix out = matrix::Zeros(3,3);
      out.Row(weights,0);
      out.Row(cop_params,1);
      return out;
     }
The protected _expectation_step() method implements the expectation stage of the EM algorithm. This method operates in two distinct modes depending on the values of the SCAD parameters provided. If both SCAD parameters are valid (sparsity parameter >0.0 and bias parameter >2.0), the penalized likelihood is engaged, allowing the model to perform automatic variable selection by driving insignificant weights toward zero. Conversely, if either SCAD parameter is invalid, the SCAD penalty is disengaged, and the method defaults to a standard Maximum Likelihood Estimation (MLE). 
vector            _expectation_step(matrix &qd,double gamma_scad, double a_scad,vector& cop_params,vector &weights)
     {
      //---
      ulong num = qd.Rows();
      vector u1 = qd.Col(0);
      vector u2 = qd.Col(1);
      //---
      double dif = 1;
      double tol_weight = 1.e-2;
      long iteration = 0;
      //---
      for(ulong i = 0; i<3; ++i)
         m_copulas[i].Set_theta(cop_params[i]);
      //---
      vector nweights;
      //---
      if(gamma_scad>0.0 && a_scad>2.0)
        {
         while(dif>tol_weight && iteration<10)
           {
            nweights = vector::Zeros(3);
            nweights.Fill(double("nan"));
            iteration+=1;
            for(ulong i = 0; i<3; ++i)
              {
               vector sum_ml_1st = vector::Zeros(u1.Size());
               double sum,sum_ml,numerator,denominator;
               sum = sum_ml = numerator = denominator = 1.e-12;
               for(ulong t = 0; t<num; ++t)
                 {
                  sum = 1.e-12;
                  for(ulong j = 0; j<3; ++j)
                     sum+=weights[j]*m_copulas[j].Copula_PDF(u1[t],u2[t],true,true);
                  sum_ml_1st[t] = weights[i]*m_copulas[i].Copula_PDF(u1[t],u2[t],true,true)/sum;
                 }
               sum_ml = sum_ml_1st.Sum();
               numerator = weights[i]*scad_derivative(weights[i],gamma_scad,a_scad)-sum_ml/double(num);
               for(ulong j = 0; j<3; ++j)
                  denominator+=weights[j]*scad_derivative(weights[j],gamma_scad,a_scad);
               denominator-=1.;
               nweights[i] = fabs(numerator/denominator);
              }
            dif = MathAbs(weights-nweights).Sum();
            weights = nweights;
           }
        }
      else
        {
         matrix wd = matrix::Zeros(weights.Size(),num);
         vector td, temp;
         while(dif>tol_weight && iteration<10)
           {
            nweights = vector::Zeros(weights.Size());
            iteration+=1;

            for(ulong i = 0; i<wd.Rows(); ++i)
               if(!wd.Row(weights[i]*m_copulas[i].Copula_PDF(u1,u2,true,true),i))
                 {
                  Print(__FUNCTION__, " row insertion error ", GetLastError());
                  return vector::Zeros(0);
                 }
            td = wd.Sum(0);
            td.Clip(1.e-12,DBL_MAX);
            for(ulong i = 0; i<weights.Size(); ++i)
              {
               temp = (wd.Row(i)/td);
               nweights[i] = fabs(temp.Sum()/double(num));
              }
            dif = MathAbs(weights-nweights).Sum();
            weights = nweights;
           }
        }
      //---
      return weights;
     }

The maximization step is defined as the _maximization_step() method. 

vector            _maximization_step(matrix&qd, double gamma_scad, double a_scad, vector& cop_params, vector& weights)
     {
      vector u1 = qd.Col(0);
      vector u2 = qd.Col(1);

      double eps = 1.e-3;

      double _x_[3];
      for(uint i = 0; i<_x_.Size(); _x_[i] = cop_params[i], ++i);

      double bndl[3] = {-1.,-50.,1.};
      double bndu[3] = {100.,50.,100.};

      CObject             obj;
      CNDimensional_Func1 ffunc;
      CNDimensional_Rep   frep;

      ffunc.set_params(this,u1,u2,weights,gamma_scad,a_scad,bool(gamma_scad>0.0&&a_scad>2.0),-1);

      CMinBLEICStateShell state;

      CMinBLEICReportShell rep;

      double epsg=eps;

      double epsf=0;

      double epsx=0;

      double epso=eps;

      double epsi=eps;

      double diffstep=1.0e-6;

      CAlglib::MinBLEICCreateF(_x_,diffstep,state);

      CAlglib::MinBLEICSetBC(state,bndl,bndu);

      CAlglib::MinBLEICSetInnerCond(state,epsg,epsf,epsx);

      CAlglib::MinBLEICSetOuterCond(state,epso,epsi);

      CAlglib::MinBLEICOptimize(state,ffunc,frep,false,obj);

      CAlglib::MinBLEICResults(state,_x_,rep);

      vector out = vector::Zeros(0);

      int termination_reason = rep.GetTerminationType();

      if(termination_reason<0)
        {
         Print(__FUNCTION__, " termination reason ", termination_reason);
         return out;
        }

      out.Assign(_x_);

      return out;
     }

This step leverages ALGLIB’s  Boundary, Linear Equality-Inequality Constraints (BLEIC) minimization algorithm. The minimizer targets the _ml_qfunc() method, which defines the penalized log-likelihood. This is exposed via the public objective() method, allowing the ALGLIB optimizer instance to access the function during its execution.

double                   objective(vector& x,vector& u1, vector& u2,vector& weights, double gamma_scad, double a_scad, bool if_penalty = true, double multiplier= 1.)
     {
      return  _ml_qfunction(u1,u2,x,weights,gamma_scad,a_scad,if_penalty,multiplier);
     }

The Fit() method triggers the minimization procedure. The nature of the objective function being minimized depends on the SCAD parameters passed to the method. If either parameter is invalid ( gamma_scad <= 0.0 or a_scad <= 2.0 ), the objective function defaults to the standard maximum likelihood estimate (MLE) without the penalty. Otherwise, the objective function is the penalized MLE.

The CTGMixCop class, which implements the Clayton-Student-t-Gumbel mixed copula, follows a design nearly identical to that of the CFGMixCop class. The primary distinction is the substitution of the Frank copula with the Student-t copula.

public:
                     CTGMixCop(void)
     {
      m_mixture = CTG_MIX;
      m_num_cops = 3;
      ArrayResize(m_copulas,int(m_num_cops));
      for(uint i = 0; i<m_num_cops; ++i)
         m_copulas[i] = NULL;
     }
                     CTGMixCop(vector& params, vector& weights)
     {
      m_mixture = CTG_MIX;
      m_num_cops = 3;
      ArrayResize(m_copulas,int(m_num_cops));
      if(params.Size()<4 || weights.Size()<3)
         Print(__FUNCTION__, " invalid parameters ");
      else
        {
         m_weights = weights;
         m_cop_params = params;
         for(ulong i = 0; i<3; ++i)
           {
            if(i == 0 || i == 2)
              {
               if(!i)
                 {
                  m_copulas[i] = new CClayton();
                  m_copulas[i].Set_theta(m_cop_params[0]);
                 }
               else
                 {
                  m_copulas[i] = new CGumbel();
                  m_copulas[i].Set_theta(m_cop_params[3]);
                 }
              }
            else
              {
               m_copulas[i] = new CStudent();
               matrix corr = {{1.,m_cop_params[1]},{m_cop_params[1],1.}};
               m_copulas[i].Set_covariance(corr);
               m_copulas[i].Set_nu(m_cop_params[2]);
              }
           }
        }
     }

Also defined in the mixed.mqh header file is a specialized routine for tuning the SCAD hyperparameters. The tune_scad_parameters() function implements a grid search to optimize the regularization parameters. 

//+------------------------------------------------------------------+
//|Implements the 5-fold cross-validation tuning process of the SCAD |
//|parameters                                                        |
//+------------------------------------------------------------------+
bool tune_scad_parameters(matrix &data, double gama_start, double gama_stop, ulong gamma_count, double a_start, double a_stop,ulong a_count, ENUM_COPULA_MIX mix, bool shuffle, int seed, bool show_details, double& out_gamma, double& out_a)
  {
   np::Folds folds[];
   if(!np::kfold(data.Rows(),folds,5,shuffle,seed))
      return false;

   CMixedCopula* mixedcop = NULL;

   switch(mix)
     {
      case CFG_MIX:
         mixedcop = new CFGMixCop();
         break;
      case CTG_MIX:
         mixedcop = new CTGMixCop();
         break;
      case CFJ_MIX:
         mixedcop = new CFJMixCop();
         break;
      case JFG_MIX:
         mixedcop = new JFGMixCop();
         break;
     }

   if(CheckPointer(mixedcop) == POINTER_INVALID)
     {
      Print(__FUNCTION__, " failed to initialize ", EnumToString(mix), " copula ");
      return false;
     }

   matrix traindata,testdata;
   double ll, best_score;
   vector scores = vector::Zeros(folds.Size());
   vector gamma_grid = np::linspace(gama_start,gama_stop,gamma_count);
   vector a_grid = np::linspace(a_start,a_stop,a_count);
   best_score = -DBL_MAX;
   bool use_mle = false;
   double mle = 0;
   double p_mle = 0;
   for(ulong i = 0; i<gamma_grid.Size(); ++i)
     {
      for(ulong j = 0; j<a_grid.Size(); ++j)
        {
         for(uint k = 0; k<folds.Size() && !IsStopped(); ++k)
           {
            traindata = np::selectMatrixRows(data,folds[k].train_indices);
            testdata = np::selectMatrixRows(data,folds[k].test_indices);
            ll = mixedcop.Fit(traindata,25,gamma_grid[i],a_grid[j]);

            if(ll == EMPTY_VALUE)
              {
               Print(__FUNCTION__, " error fitting data ", "| sparcity ", gamma_grid[i], " bias ", a_grid[j]);
               continue;
              }

            scores[k] = mixedcop.Penalized_Log_Likelihood(testdata,gamma_grid[i],a_grid[j]);

           }
         ll = scores.Sum();
         if(show_details)
            Print(__FUNCTION__, "| sparcity: ", gamma_grid[i], "| bias: ", a_grid[j], "| likelihood  ", ll, " \nweights ", mixedcop.Weights(), "| params ", mixedcop.Params());
         if(ll>best_score)
           {
            best_score = ll;
            out_a = a_grid[j];
            out_gamma = gamma_grid[i];
           }
        }
     }

   delete mixedcop;
   return true;
  }

It accepts the following inputs.

  • The data input is a matrix of pseudo-observations where each column represents a series.
  • The function then specifies six input variables: the first three are prefixed with gamma and the last three with a. These define the bounds and granularity of the grid search for the optimal SCAD hyperparameter pair. Arguments with the count suffix specify the number of candidate values to evaluate within the ranges defined by the arguments with start and stop suffixes, respectively.
  • The function then specifies six input variables: the first three are prefixed with gamma and the last three with a. These define the bounds and granularity of the grid search for the optimal SCAD hyperparameter pair. Arguments with the count suffix specify the number of candidate values to evaluate within the ranges defined by the arguments with start and stop suffixes, respectively.
  • The mix input is an enumeration that specifies which mixed copula model to evaluate during the search.
  • The shuffle input is a boolean argument that determines whether the data should be randomized before splitting, and the seed input is a seed value for the pseudo-random number generator to ensure reproducible results.
  • The show_details boolean flag specifies whether to output execution details for each iteration to the terminal's journal.
  • The reference inputs out_a and out_gamma are the output parameters that store the optimal SCAD parameters discovered by the procedure.

The SCAD penalty function and its derivative are defined in utils.mqh. These implement the shrinkage mechanism, allowing the model to distinguish between significant and negligible copula weights.

//+------------------------------------------------------------------+
//|SCAD (smoothly clipped absolute deviation) penalty function.      |
//+------------------------------------------------------------------+
double scad_penalty(double x, double gamma, double a)
  {
   bool is_linear = (fabs(x)<=gamma);
   bool is_quadratic = (gamma<fabs(x)) & (fabs(x)<=a*gamma);
   bool is_constant = ((a*gamma)<fabs(x));

   double linear_part = gamma * fabs(x) * double(is_linear);
   double quadratic_part = (2.*a*gamma*fabs(x) - pow(x,2.)- pow(gamma,2.))/(2.*(a-1.))*double(is_quadratic);
   double constant_part = (pow(gamma,2.)*(a+1.))/2.*(double(is_constant));

//Print(__FUNCTION__, " linear part ", linear_part,"\n quadratic part ", quadratic_part, "\n constant part ", constant_part);

   return linear_part+quadratic_part+constant_part;
  }
//+------------------------------------------------------------------+
//|The derivative of SCAD penalty function w.r.t x.                  |
//+------------------------------------------------------------------+
double scad_derivative(double x, double gamma, double a)
  {
   double p1 = gamma*double(x<=gamma);
   double p2 = gamma *(a*gamma-x)*double((a*gamma-x)>0.)/((a - 1.)*gamma)*double(x>gamma);
   return p1+p2;
  }

In the next section, we delve into the process of selecting suitable hyperparameters for the SCAD penalty. Practitioners should be aware of certain nuances beyond simply executing the cross-validation procedure.


Tuning SCAD Hyperparameters

In the context of the SCAD penalty, the tuning parameters λ (sparsity) and a (bias reduction) govern the threshold for sparsity and the rate of bias reduction, respectively. While optimal values are ultimately data-driven, there are well-established ranges used in academic literature and practice. The bias reduction parameter controls how quickly the penalty levels off. When tuning the bias parameter, only values greater than two should be considered; the parameter must be strictly greater than two for the function to maintain thresholding properties that differ from hard thresholding.

The sparsity parameter, on the other hand, is sensitive to the scale of the training data and the sample size. It defines the cutoff point below which coefficients are pushed to zero. The range of values considered when tuning this parameter typically spans from 0 to 1. The lower bound should be small enough to allow the model to approach the unpenalized Maximum Likelihood Estimate (MLE)—for example, 0.001. Conversely, the upper bound should be large enough to potentially zero out all coefficients (the weights applied to the component copulae in the mixture). Generally, a larger sample size necessitates a smaller sparsity parameter.

When the sparsity parameter is high, the model becomes sparse, causing many mixture weights to become zero. When the bias reduction parameter is high, the penalty remains in effect longer, making the transition from penalized to unbiased much slower. The closer the bias reduction parameter is to 2, the more rapidly the penalty drops off.

To put these concepts to the test, the script Scad_CV.mq5 demonstrates the tune_scad_parameters() function in action.

//+------------------------------------------------------------------+
//|                                                      Scad_CV.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Copulas\Bivariate\mixed.mqh>
#include<ECDF\linear_cdf.mqh>

input string   FirstSymbol="XAUUSD";
input string   SecondSymbol="XAUEUR";
input datetime TrainingDataStart=D'2025.01.01';
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input ENUM_COPULA_MIX CopulaType = CTG_MIX;
input ulong    HistorySize=1200;
input bool     Show_details = true;
input bool     Shuffle_Data = false;
input int      Random_Seed = 0;
input double   g_from = 0.001;
input double   g_to = 1.0;
input ulong    g_count = 5;
input double   a_from = 2.0;
input double   a_to = 10.0;
input ulong    a_count_ = 5; 
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
  //---
   vector p_1,p_2,p_3,p_n;
   matrix pdata,pobs;
   if(!p_1.CopyRates(FirstSymbol,TimeFrame,COPY_RATES_CLOSE,TrainingDataStart,HistorySize) ||
      !p_2.CopyRates(SecondSymbol,TimeFrame,COPY_RATES_CLOSE,TrainingDataStart,HistorySize) ||
      p_1.Size()!=p_2.Size() ||
      !pdata.Resize(p_1.Size(),2) ||
      !pdata.Col(p_1,0) ||
      !pdata.Col(p_2,1))
     {
      Print(" failed to collect and initialize rates matrix ", GetLastError());
      return;
     }
//---
   CLinearCDF qt();
   if(!qt.fit(pdata))
      return;
//---
   pobs = qt.to_quantile(pdata);
   
    double gamma_scad,a_scad;
   if(!tune_scad_parameters(pobs,g_from,g_to,g_count,a_from,a_to,a_count_,CopulaType,Shuffle_Data,Random_Seed,Show_details,gamma_scad,a_scad))
    {
     Print(" failed ");
     return;
    }
   
   Print(EnumToString(CopulaType)," sparcity -> ", gamma_scad, " || bias -> ", a_scad);
  }
//+------------------------------------------------------------------+

The default user-adjustable inputs of the Scad_CV.ex5 script specify a fairly narrow grid of sparsity and bias trial values. This configuration ensures the script executes efficiently on sample sizes of just over one thousand observations. Note that the trial grid includes a bias parameter value of 2.0; because this is an invalid value for the bias parameter, it disables the SCAD penalty altogether. This allows us to determine whether minimizing the non-penalized likelihood yields superior results. Running the script with the Clayton-Frank-Gumbel mixture selected produces the following output.

PE      0       07:19:59.780    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.001| bias: 2.0| likelihood  584.3449797418596 
NH      0       07:19:59.780    Scad_CV (XAUUSD,D1)     weights [0,0.2503264642029614,0.7496735357960386]| params [0.07777184570809823,4.98716120261952,2.938523462235503]
JG      0       07:20:04.549    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.001| bias: 4.0| likelihood  584.3388831186738 
GI      0       07:20:04.549    Scad_CV (XAUUSD,D1)     weights [0,0.2503330189828707,0.7496669810161294]| params [0.07783293123073377,4.987168638354295,2.938531600897639]
NJ      0       07:20:09.278    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.001| bias: 6.0| likelihood  584.5057912775926 
LF      0       07:20:09.278    Scad_CV (XAUUSD,D1)     weights [0,0.2475903622229043,0.7524096377760957]| params [0.08186119438950079,4.982135308682525,2.934272675707406]
OL      0       07:20:13.997    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.001| bias: 8.0| likelihood  584.5035349829863 
ED      0       07:20:13.997    Scad_CV (XAUUSD,D1)     weights [0,0.2475907179493826,0.7524092820496174]| params [0.08234560301866138,4.982135272704732,2.934273169230999]
JL      0       07:20:18.700    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.001| bias: 10.0| likelihood  584.5011307062207 
ER      0       07:20:18.700    Scad_CV (XAUUSD,D1)     weights [0,0.2475914144776672,0.7524085855213327]| params [0.08233571375095404,4.98213630991471,2.934274176680373]
FQ      0       07:20:23.187    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.25075| bias: 2.0| likelihood  584.3449797418596 
PL      0       07:20:23.187    Scad_CV (XAUUSD,D1)     weights [0,0.2503264642029614,0.7496735357960386]| params [0.07777184570809823,4.98716120261952,2.938523462235503]
ES      0       07:20:27.501    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.25075| bias: 4.0| likelihood  283.7391184805832 
RM      0       07:20:27.501    Scad_CV (XAUUSD,D1)     weights [0,0.9999999999989904,0]| params [0.1511818127315188,7.344139133115162,20.25573962738841]
ID      0       07:20:31.999    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.25075| bias: 6.0| likelihood  5659.479627674678 
JO      0       07:20:31.999    Scad_CV (XAUUSD,D1)     weights [0,0.5844120297582153,0.4155879702407769]| params [0.1376209847408496,5.640552910020598,3.811839085505817]
JF      0       07:20:38.263    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.25075| bias: 8.0| likelihood  334.8224130043968 
KJ      0       07:20:38.263    Scad_CV (XAUUSD,D1)     weights [0,0.02895916433928,0.97104083565972]| params [0.1037932306526668,4.669895137807593,2.641209026360089]
OK      0       07:20:42.346    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.25075| bias: 10.0| likelihood  6420.623549439398 
ND      0       07:20:42.346    Scad_CV (XAUUSD,D1)     weights [0,0.04002009450317316,0.9599799054958269]| params [0.1193049328638911,4.63258676700795,2.654870180909923]
DH      0       07:20:46.831    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.5005| bias: 2.0| likelihood  584.3449797418596 
KF      0       07:20:46.831    Scad_CV (XAUUSD,D1)     weights [0,0.2503264642029614,0.7496735357960386]| params [0.07777184570809823,4.98716120261952,2.938523462235503]
FN      0       07:20:49.490    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.5005| bias: 4.0| likelihood  34.55576102335817 
KR      0       07:20:49.490    Scad_CV (XAUUSD,D1)     weights [0,0,0.9999999999989903]| params [0.1197956723049384,4.584548412565545,2.619284560176268]
NN      0       07:20:52.885    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.5005| bias: 6.0| likelihood  15.363216317653269 
HR      0       07:20:52.885    Scad_CV (XAUUSD,D1)     weights [0,0.01784571505390212,0.9821542849450979]| params [0.1043980264613316,4.628446940510745,2.628580283819081]
QS      0       07:20:56.830    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.5005| bias: 8.0| likelihood  6102.473148256049 
RP      0       07:20:56.830    Scad_CV (XAUUSD,D1)     weights [0,0.02673340177232474,0.9732665982266753]| params [0.1037622447823746,4.698345592025231,2.638332966096248]
IS      0       07:21:00.708    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.5005| bias: 10.0| likelihood  3.301592693093255 
RM      0       07:21:00.708    Scad_CV (XAUUSD,D1)     weights [0,0.0300952343044497,0.9699047656945503]| params [0.1029115313643473,4.61667495323261,2.643127744938425]
KE      0       07:21:05.196    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.75025| bias: 2.0| likelihood  584.3449797418596 
QH      0       07:21:05.196    Scad_CV (XAUUSD,D1)     weights [0,0.2503264642029614,0.7496735357960386]| params [0.07777184570809823,4.98716120261952,2.938523462235503]
JI      0       07:21:08.606    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.75025| bias: 4.0| likelihood  -297.39396856892415 
GH      0       07:21:08.606    Scad_CV (XAUUSD,D1)     weights [0,0.01107956745287137,0.9889204325461286]| params [2.9984906563128,4.76765198814707,2.620207254516393]
KH      0       07:21:12.649    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.75025| bias: 6.0| likelihood  -303.8281831341336 
CE      0       07:21:12.649    Scad_CV (XAUUSD,D1)     weights [0,0.01742743973978789,0.9825725602592119]| params [2.9984906563128,4.637005162809593,2.628040342667032]
FO      0       07:21:18.050    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.75025| bias: 8.0| likelihood  5512.03076596105 
DG      0       07:21:18.050    Scad_CV (XAUUSD,D1)     weights [0,0.02364115960349121,0.9763588403955088]| params [2.9984906563128,4.667363798628771,2.635026851516195]
PM      0       07:21:23.276    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.75025| bias: 10.0| likelihood  5953.875750743017 
OR      0       07:21:23.276    Scad_CV (XAUUSD,D1)     weights [0,0.03021524144755516,0.9697847585514447]| params [2.9984906563128,4.626181869637053,2.643168795782705]
KQ      0       07:21:27.767    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 1.0| bias: 2.0| likelihood  584.3449797418596 
ML      0       07:21:27.767    Scad_CV (XAUUSD,D1)     weights [0,0.2503264642029614,0.7496735357960386]| params [0.07777184570809823,4.98716120261952,2.938523462235503]
FQ      0       07:21:31.781    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 1.0| bias: 4.0| likelihood  -727.4266957539727 
GN      0       07:21:31.781    Scad_CV (XAUUSD,D1)     weights [0.4409776856415021,0,0.5590223143574978]| params [0.2842084359703793,8.160381312758863,3.894704689012704]
JG      0       07:21:35.806    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 1.0| bias: 6.0| likelihood  -727.4266957539727 
IH      0       07:21:35.806    Scad_CV (XAUUSD,D1)     weights [0.4409776856415021,0,0.5590223143574978]| params [0.2842084359703793,8.160381312758863,3.894704689012704]
JE      0       07:21:39.839    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 1.0| bias: 8.0| likelihood  -727.4266957539727 
GJ      0       07:21:39.839    Scad_CV (XAUUSD,D1)     weights [0.4409776856415021,0,0.5590223143574978]| params [0.2842084359703793,8.160381312758863,3.894704689012704]
MH      0       07:21:43.911    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 1.0| bias: 10.0| likelihood  -727.4266957539727 
QD      0       07:21:43.911    Scad_CV (XAUUSD,D1)     weights [0.4409776856415021,0,0.5590223143574978]| params [0.2842084359703793,8.160381312758863,3.894704689012704]
DK      0       07:21:43.911    Scad_CV (XAUUSD,D1)     CFG_MIX sparcity -> 0.25075 || bias -> 10.0

The results indicate that the optimal SCAD parameters for the Clayton-Frank-Gumbel mixture are a sparsity of 0.25075 and a bias of 10. The next set of results, for the Clayton-Student-Gumbel mixture are particularly insightful.

JF      0       07:23:09.254    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.001| bias: 2.0| likelihood  599.6351926572415 
HK      0       07:23:09.254    Scad_CV (XAUUSD,D1)     weights [0,0.03267640297340715,0.9673235970255923]| params [0.026704520400007,0.5822697866462155,7,2.635263431033769]
NH      0       07:23:31.432    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.001| bias: 4.0| likelihood  599.6274718728072 
FI      0       07:23:31.433    Scad_CV (XAUUSD,D1)     weights [0,0.03267798343975953,0.96732201655924]| params [0.02669592147577486,0.5822648258079013,7,2.6352494228926]
FK      0       07:23:53.828    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.001| bias: 6.0| likelihood  599.6244749857701 
GD      0       07:23:53.828    Scad_CV (XAUUSD,D1)     weights [0,0.03267834828227598,0.9673216517167235]| params [0.02669671670147136,0.5822637634505266,7,2.635245690184943]
CN      0       07:24:16.075    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.001| bias: 8.0| likelihood  599.6215815910193 
ES      0       07:24:16.075    Scad_CV (XAUUSD,D1)     weights [0,0.03267864853568959,0.9673213514633099]| params [0.02669727070086427,0.5822626295795441,7,2.635242405736884]
ER      0       07:24:38.223    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.001| bias: 10.0| likelihood  599.61866242213 
MQ      0       07:24:38.223    Scad_CV (XAUUSD,D1)     weights [0,0.03267912346489563,0.9673208765341038]| params [0.02669711773038876,0.5822617798491028,7,2.635240094669517]
ES      0       07:24:59.495    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.25075| bias: 2.0| likelihood  599.6351926572415 
KM      0       07:24:59.495    Scad_CV (XAUUSD,D1)     weights [0,0.03267640297340715,0.9673235970255923]| params [0.026704520400007,0.5822697866462155,7,2.635263431033769]
EE      0       07:25:12.505    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.25075| bias: 4.0| likelihood  468.644205273507 
GK      0       07:25:12.505    Scad_CV (XAUUSD,D1)     weights [0,0.01620981928802398,0.983790180710976]| params [2.862242105331717,0.9975906244136006,7,2.566020598217]
PH      0       07:26:18.429    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.25075| bias: 6.0| likelihood  359.9685977593964 
JD      0       07:26:18.429    Scad_CV (XAUUSD,D1)     weights [0,0,0.999999999999]| params [0.02596060043458071,0.5877560061777306,7,2.60814677938215]
GJ      0       07:26:35.438    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.25075| bias: 8.0| likelihood  341.04401153470667 
EE      0       07:26:35.438    Scad_CV (XAUUSD,D1)     weights [0,0.0101303301858873,0.9898696698131126]| params [0.03276229272869093,0.5873194208156135,7,2.6159294869276]
PL      0       07:26:50.782    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.25075| bias: 10.0| likelihood  331.81315199928497 
OE      0       07:26:50.782    Scad_CV (XAUUSD,D1)     weights [0,0.01344107163199763,0.9865589283670023]| params [0.01828802392046799,0.5853696555031691,7,2.618615230362836]
DL      0       07:27:12.118    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.5005| bias: 2.0| likelihood  599.6351926572415 
OP      0       07:27:12.118    Scad_CV (XAUUSD,D1)     weights [0,0.03267640297340715,0.9673235970255923]| params [0.026704520400007,0.5822697866462155,7,2.635263431033769]
NR      0       07:28:58.374    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.5005| bias: 4.0| likelihood  39.715438762939925 
NM      0       07:28:58.374    Scad_CV (XAUUSD,D1)     weights [0,0,0.999999999999]| params [2.885268158668136,0.5815643981885116,7,2.60814677938215]
MR      0       07:29:14.021    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.5005| bias: 6.0| likelihood  15.766736485645538 
PM      0       07:29:14.021    Scad_CV (XAUUSD,D1)     weights [0,0,0.999999999999]| params [2.886114952573396,0.5885681475003665,7,2.60814677938215]
FR      0       07:31:20.013    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.5005| bias: 8.0| likelihood  12.582743928163211 
KN      0       07:31:20.013    Scad_CV (XAUUSD,D1)     weights [0,0,0.999999999999]| params [2.886068065102342,0.588279448169273,7,2.60814677938215]
GR      0       07:33:38.602    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.5005| bias: 10.0| likelihood  9.373323825700936 
HM      0       07:33:38.602    Scad_CV (XAUUSD,D1)     weights [0,0,0.999999999999]| params [2.885905528406098,0.5876282323959312,7,2.60814677938215]
LR      0       07:33:59.933    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.75025| bias: 2.0| likelihood  599.6351926572415 
NO      0       07:33:59.933    Scad_CV (XAUUSD,D1)     weights [0,0.03267640297340715,0.9673235970255923]| params [0.026704520400007,0.5822697866462155,7,2.635263431033769]
PF      0       07:34:12.979    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.75025| bias: 4.0| likelihood  -342.3070420888405 
GK      0       07:34:12.979    Scad_CV (XAUUSD,D1)     weights [0,0,0.999999999999]| params [2.999235107389794,0.5744384247930826,7,2.608146780258969]
MG      0       07:34:25.802    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.75025| bias: 6.0| likelihood  -313.5880991228416 
NK      0       07:34:25.802    Scad_CV (XAUUSD,D1)     weights [0,0,0.999999999999]| params [2.999235107389794,0.5712426547670767,7,2.608146780258969]
JG      0       07:34:38.627    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.75025| bias: 8.0| likelihood  -315.3277234364691 
GK      0       07:34:38.627    Scad_CV (XAUUSD,D1)     weights [0,0,0.999999999999]| params [2.999235107389794,0.5700039115725434,7,2.608146780258969]
PG      0       07:34:51.411    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 0.75025| bias: 10.0| likelihood  -316.34493893784384 
OJ      0       07:34:51.411    Scad_CV (XAUUSD,D1)     weights [0,0,0.999999999999]| params [2.999235107389794,0.5700489107543522,7,2.608146780258969]
RF      0       07:35:12.660    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 1.0| bias: 2.0| likelihood  599.6351926572415 
DJ      0       07:35:12.660    Scad_CV (XAUUSD,D1)     weights [0,0.03267640297340715,0.9673235970255923]| params [0.026704520400007,0.5822697866462155,7,2.635263431033769]
CH      0       07:35:14.020    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 1.0| bias: 4.0| likelihood  689.1665208571073 
DH      0       07:35:14.020    Scad_CV (XAUUSD,D1)     weights [0,0,0]| params [3,0.5,4,2.608146566441139]
DR      0       07:35:15.389    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 1.0| bias: 6.0| likelihood  689.1665208571073 
EN      0       07:35:15.389    Scad_CV (XAUUSD,D1)     weights [0,0,0]| params [3,0.5,4,2.608146566441139]
KL      0       07:35:16.734    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 1.0| bias: 8.0| likelihood  689.1665208571073 
PD      0       07:35:16.734    Scad_CV (XAUUSD,D1)     weights [0,0,0]| params [3,0.5,4,2.608146566441139]
CE      0       07:35:18.094    Scad_CV (XAUUSD,D1)     tune_scad_parameters| sparcity: 1.0| bias: 10.0| likelihood  689.1665208571073 
MJ      0       07:35:18.094    Scad_CV (XAUUSD,D1)     weights [0,0,0]| params [3,0.5,4,2.608146566441139]
DS      0       07:35:18.094    Scad_CV (XAUUSD,D1)     CTG_MIX sparcity -> 1.0 || bias -> 4.0

In this case, the optimal SCAD parameters are shown as 1.0 and 4.0. A sparsity of 1.0 is quite high and has driven all weights to zero—a nonsensical result for a mixture model. Such an outcome often signals that the specific mixture model may be ill-suited for the data or that the penalty is too aggressive.

When this occurs, it is prudent to first attempt fitting the model using the MLE approach without the SCAD penalty. If the MLE approach yields sensible weights, the issue is confirmed to be an excessively large sparsity parameter. In such cases, one should either utilize the MLE method or lower the upper bound of the sparsity parameters trialed during the cross-validation procedure.

Consequently, we ignore the trials that produced weights of all zeros. Upon doing so, we find that the non-penalized MLE approach achieves the highest likelihood. At this stage, we have identified the optimal SCAD parameters for the Clayton-Frank-Gumbel mixture (0.25075, 10) and the Clayton-Student-Gumbel mixture (0.001, 2.0). This information can now be used to build and compare mixed copula models using the full training dataset.


Model Selection and Comparison

The purpose of the script MixedCopulaSelection.mq5 is to identify the mixed copula that best fits a specified data sample.

//+------------------------------------------------------------------+
//|                                         MixedCopulaSelection.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Copulas\Bivariate\mixed.mqh>
#include<ECDF\linear_cdf.mqh>
#include<Files\FileBin.mqh>
//--- input parameters
input string   FirstSymbol="XAUUSD";
input string   SecondSymbol="XAUEUR";
input datetime TrainingDataStart=D'2025.01.01';
input ENUM_TIMEFRAMES TimeFrame = PERIOD_D1;
input ulong    HistorySize=1200;
input double   CTG_Scad_Gamma = 0.0;
input double   CTG_Scad_A = 2.0;
input double   CFG_Scad_Gamma = 0.25075;
input double   CFG_Scad_A = 10.0;
input uint     Max_Iterations = 25;
input bool     SaveModel = true;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   vector p_1,p_2,p_3,p_n;
   matrix pdata,pobs;
   if(!p_1.CopyRates(FirstSymbol,TimeFrame,COPY_RATES_CLOSE,TrainingDataStart,HistorySize) ||
      !p_2.CopyRates(SecondSymbol,TimeFrame,COPY_RATES_CLOSE,TrainingDataStart,HistorySize) ||
      p_1.Size()!=p_2.Size() ||
      !pdata.Resize(p_1.Size(),2) ||
      !pdata.Col(p_1,0) ||
      !pdata.Col(p_2,1))
     {
      Print(" failed to collect and initialize rates matrix ", GetLastError());
      return;
     }
//---
   CLinearCDF qt();
   if(!qt.fit(pdata))
      return;
//---
   pobs = qt.to_quantile(pdata);
//---
   if(SaveModel)
     {
      CFileBin file;
      string filename = FirstSymbol+"_"+SecondSymbol+".ecdf";
      file.Open(filename,FILE_WRITE|FILE_COMMON);
      if(!qt.save(file.Handle()))
         Print(" Failed to save ", filename);
      else
         Print("Ecdf model save to ", filename);
      file.Close();
     }

//---
   vector lowest = vector::Zeros(4);
   lowest.Fill(DBL_MAX);
//---
   Print("[[ Clayton - Student - Gumbel ]]");
//---
   CTGMixCop ctg;
   double fit;
//---
   fit = ctg.Fit(pobs,Max_Iterations,CTG_Scad_Gamma,CTG_Scad_A);
//---
   Print(" CTG loglikelihood ", fit);
   Print(" CTG weights ", ctg.Weights());
   Print(" CTG Params ", ctg.Params());
//---
   lowest[2] = aic(fit,int(pobs.Rows()));
   Print(" CTG sic ", sic(fit,int(pobs.Rows())));
   Print(" CTG aic ", lowest[2]);
   Print(" CTG hqic ", hqic(fit,int(pobs.Rows())));
//---
   Print("[[ Clayton - Frank - Gumbel ]]");
//---
   CFGMixCop cfg;
//---
   fit = cfg.Fit(pobs,Max_Iterations,CFG_Scad_Gamma,CFG_Scad_A);
//---
   Print(" CFG loglikelihood ", fit);
   Print(" CFG weights ", cfg.Weights());
   Print(" CFG Params ", cfg.Params());
//---
   lowest[0] = aic(fit,int(pobs.Rows()));
   Print(" CFG sic ", sic(fit,int(pobs.Rows())));
   Print(" CFG aic ", lowest[0]);
   Print(" CFG hqic ", hqic(fit,int(pobs.Rows())));
//---
   if(SaveModel)
     {
      CFileBin file;
      string filename,extension;
      ulong shift = lowest.ArgMin();
      CMixedCopula* mcop  = NULL;
      ENUM_COPULA_MIX mixtype = (ENUM_COPULA_MIX)shift;

      switch(mixtype)
        {
         case CFG_MIX:
            mcop = GetPointer(cfg);
            extension = ".cfgcopula";
            break;
         case CTG_MIX:
            mcop = GetPointer(ctg);
            extension = ".ctgcopula";
            break;
        }

      filename = FirstSymbol+"_"+SecondSymbol+extension;
      file.Open(filename,FILE_WRITE|FILE_COMMON);
      if(!mcop.Save(file.Handle()))
         Print("Failed to save ", filename);
      else
         Print("MixedCopula saved to ", filename, " in common folder.");
      file.Close();
      mcop = NULL;
     }
//---
  }
//+------------------------------------------------------------------+

This involves a comparative procedure where the Clayton-Frank-Gumbel and Clayton-Student-Gumbel mixed copula models are fitted to the same training dataset using either a penalized or non-penalized likelihood approach, depending on the assigned SCAD parameters. The script determines which mixture provides the highest statistical fit by comparing their respective information criteria. The superior model is then serialized and saved to a file. Upon successful execution, the terminal generates an output log confirming the log-likelihood values and the filename of the saved model. Below is the output from the script, using the SCAD parameters learnt from the cross-validation procedure.

JQ      0       11:26:22.119    MixedCopulaSelection (XAUUSD,D1)        Ecdf model save to XAUUSD_XAUEUR.ecdf
CO      0       11:26:22.119    MixedCopulaSelection (XAUUSD,D1)        [[ Clayton - Student - Gumbel ]]
IJ      0       11:26:30.566    MixedCopulaSelection (XAUUSD,D1)         CTG loglikelihood 821.3707128783087
NR      0       11:26:30.566    MixedCopulaSelection (XAUUSD,D1)         CTG weights [0,0.03552603447650678,0.9644739655224931]
NL      0       11:26:30.566    MixedCopulaSelection (XAUUSD,D1)         CTG Params [-0.006169340694795771,0.4543309925241095,7,3.054494819573707]
ER      0       11:26:30.566    MixedCopulaSelection (XAUUSD,D1)         CTG sic -1635.6513489208414
QI      0       11:26:30.566    MixedCopulaSelection (XAUUSD,D1)         CTG aic -1640.7414257566174
HJ      0       11:26:30.566    MixedCopulaSelection (XAUUSD,D1)         CTG hqic -1638.824033401239
QL      0       11:26:30.566    MixedCopulaSelection (XAUUSD,D1)        [[ Clayton - Frank - Gumbel ]]
QJ      0       11:26:32.184    MixedCopulaSelection (XAUUSD,D1)         CFG loglikelihood 821.5620161629782
JD      0       11:26:32.184    MixedCopulaSelection (XAUUSD,D1)         CFG weights [0,0.03875313891414744,0.9612468610848526]
HO      0       11:26:32.184    MixedCopulaSelection (XAUUSD,D1)         CFG Params [0.002088006991783055,4.242903358363938,3.061932796342449]
MR      0       11:26:32.184    MixedCopulaSelection (XAUUSD,D1)         CFG sic -1636.0339554901805
RI      0       11:26:32.184    MixedCopulaSelection (XAUUSD,D1)         CFG aic -1641.1240323259565
RK      0       11:26:32.184    MixedCopulaSelection (XAUUSD,D1)         CFG hqic -1639.206639970578
PL      0       11:26:32.185    MixedCopulaSelection (XAUUSD,D1)        MixedCopula saved to XAUUSD_XAUEUR.cfgcopula in common folder.

The best-fit mixed copula model is found to be the Clayton-Frank-Gumbel mixture. A comparison of these results against fitted single copula models demonstrates that the best-fit mixed copula provides an inferior fit to the best-fit single copula model. 

QS      0       18:48:06.788    CopulaSelection (XAUUSD,D1)     CLAYTON_COPULA
RD      0       18:48:06.788    CopulaSelection (XAUUSD,D1)      sic 1009.0424155712477
HL      0       18:48:06.788    CopulaSelection (XAUUSD,D1)      aic 1003.9523387354716
DK      0       18:48:06.788    CopulaSelection (XAUUSD,D1)      hqic 1005.8697310908501
KL      0       18:48:06.795    CopulaSelection (XAUUSD,D1)     FRANK_COPULA
OH      0       18:48:06.795    CopulaSelection (XAUUSD,D1)      sic -1282.6359542297741
RP      0       18:48:06.795    CopulaSelection (XAUUSD,D1)      aic -1287.7260310655502
RD      0       18:48:06.795    CopulaSelection (XAUUSD,D1)      hqic -1285.8086387101716
NS      0       18:48:06.802    CopulaSelection (XAUUSD,D1)     GUMBEL_COPULA
PK      0       18:48:06.802    CopulaSelection (XAUUSD,D1)      sic -1620.5768024034212
FE      0       18:48:06.802    CopulaSelection (XAUUSD,D1)      aic -1625.6668792391972
PS      0       18:48:06.802    CopulaSelection (XAUUSD,D1)      hqic -1623.7494868838187
GK      0       18:48:11.931    CopulaSelection (XAUUSD,D1)     JOE_COPULA
NM      0       18:48:11.931    CopulaSelection (XAUUSD,D1)      sic -1917.6641571237963
DG      0       18:48:11.931    CopulaSelection (XAUUSD,D1)      aic -1922.7542339595723
NQ      0       18:48:11.932    CopulaSelection (XAUUSD,D1)      hqic -1920.8368416041938
LE      0       18:48:12.337    CopulaSelection (XAUUSD,D1)     N13_COPULA
CL      0       18:48:12.337    CopulaSelection (XAUUSD,D1)      sic -560.6680141126138
MJ      0       18:48:12.337    CopulaSelection (XAUUSD,D1)      aic -565.75809094839
EL      0       18:48:12.337    CopulaSelection (XAUUSD,D1)      hqic -563.8406985930114
JG      0       18:48:12.345    CopulaSelection (XAUUSD,D1)     N14_COPULA
MR      0       18:48:12.345    CopulaSelection (XAUUSD,D1)      sic -757.9453503106477
MH      0       18:48:12.345    CopulaSelection (XAUUSD,D1)      aic -763.0354271464238
HN      0       18:48:12.345    CopulaSelection (XAUUSD,D1)      hqic -761.1180347910453
QL      0       18:48:12.353    CopulaSelection (XAUUSD,D1)     GAUSSIAN_COPULA
ID      0       18:48:12.353    CopulaSelection (XAUUSD,D1)      sic -1189.1571905959859
ML      0       18:48:12.353    CopulaSelection (XAUUSD,D1)      aic -1194.2472674317619
IH      0       18:48:12.353    CopulaSelection (XAUUSD,D1)      hqic -1192.3298750763834
OR      0       18:48:12.830    CopulaSelection (XAUUSD,D1)     STUDENT_COPULA
PG      0       18:48:12.830    CopulaSelection (XAUUSD,D1)      sic -1233.3072453920256
OQ      0       18:48:12.830    CopulaSelection (XAUUSD,D1)      aic -1238.3973222278016
OD      0       18:48:12.830    CopulaSelection (XAUUSD,D1)      hqic -1236.479929872423

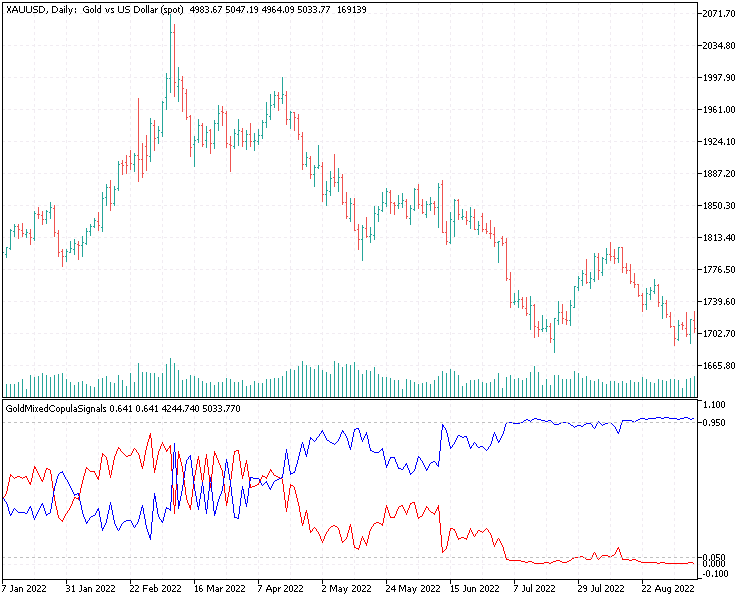
Regardless, we can still use the mixed copula model in place of the single copula model in the SimpleCopulaStrategy.ex5 expert advisor presented in part two of the Bivariate Copulae article series. The indicator GoldMixedCopulaSignals.mq5 has been modified to utilize the mixed copula model, and SimpleMixedCopulaStrategy.mq5 serves as the mixed-copula-based EA. 

GoldMixedCopulaSignals indicator


Conclusion

In this article, we have successfully demonstrated the implementation of mixed copula models in MQL5. By moving beyond single-component copulae, we have established a framework that has the capability to better model the nuanced dependencies often found in financial time series. While the mixed copula approach requires greater computational overhead and careful hyperparameter tuning, the potential for creating superior copula models may be worth it.

The integration of ALGLIB for non-convex optimization and the modular class structure of CMixedCopula provides a foundation for exploration of higher-dimensional mixtures. Ultimately, the success of applying copula models in strategy development hinges on the representative quality of the training data and the periodic recalibration of the models to ensure they remain aligned with evolving market dynamics. All code referenced in the article is attached below with descriptions of the files listed in the table. 

File  Description 
MQL5/include/Copulas/ This folder contains the header files of all copula models implemented so far, including those described in this article.
MQL5/include/ECDF/ This folder holds the header files implementing the empirical cumulative distribution function. 
MQL5/include/np.mqh A header file of miscellaneous vector and matrix utilities. 
MQL5/scripts/Scad_CV.mq5 This script demonstrates a cross-validation procedure used to tune the SCAD hyperparameters.
MQL5/scripts/MixedCopulaSelection.mq5 The script fits mixed copula models to a sample dataset and compares them in order to select the best fit copula. 
MQL5/indicator s/ GoldMixedCopulaSignals.mq5 An indicator that uses a mixed copula model. 
MQL5/experts/ SimpleMixedCopulaStrategy.mq5 An EA based on signals generated from a mixed copula model. 
Attached files |
Download ZIP
BivariateCopulaeppt3p.zip (64.96 KB)

Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.

Other articles by this author

Go to discussion
Larry Williams Market Secrets (Part 11): Detecting Smash Day Reversals with a Custom Indicator Larry Williams Market Secrets (Part 11): Detecting Smash Day Reversals with a Custom Indicator
We convert Larry Williams’ Smash Day reversal rules into a practical MQL5 indicator that flags confirmed setups with arrows. Step by step, the text shows buffer binding, plot properties, historical mapping, and real‑time updates inside OnCalculate. Adjustable lookback parameters and clean chart rendering help you detect valid reversals quickly while keeping final trade decisions discretionary and context‑driven.
Price Action Analysis Toolkit Development (Part 60): Objective Swing-Based Trendlines for Structural Analysis Price Action Analysis Toolkit Development (Part 60): Objective Swing-Based Trendlines for Structural Analysis
We present a rule-based approach to trendlines that avoids indicator pivots and uses ordered swings derived from raw prices. The article walks through swing detection, size qualification via ATR or fixed thresholds, and validation of ascending and descending structures, then implements these rules in MQL5 with non-repainting drawing and selective output. You get a clear, repeatable way to track structural support and resistance that holds up across market conditions.
From Basic to Intermediate: Struct (III) From Basic to Intermediate: Struct (III)
In this article, we will explore what structured code is. Many people confuse structured code with organized code, but there is a difference between these two concepts. This is exactly what will be discussed in this article. Despite the apparent complexity you may feel when first encountering this type of code writing, I have tried to approach the topic as simply as possible. However, this article is just the first step toward something greater.
MQL5 Trading Tools (Part 16): Improved Super-Sampling Anti-Aliasing (SSAA) and High-Resolution Rendering MQL5 Trading Tools (Part 16): Improved Super-Sampling Anti-Aliasing (SSAA) and High-Resolution Rendering
We add supersampling‑driven anti‑aliasing and high‑resolution rendering to the MQL5 canvas dashboard, then downsample to the target size. The article implements rounded rectangle fills and borders, rounded triangle arrows, and a custom scrollbar with theming for the stats and text panels. These tools help you build smoother, more legible UI components in MetaTrader 5.