Bivariate Copulae in MQL5 (Part 2): Implementing Archimedean copulae in MQL5

MetaTrader 5 — Examples | 10 November 2025, 10:02

1 826

Francis Dube

Introduction

In the previous article we presented the MQL5 implementations of bivariate elliptical copulae, specifically the Gaussian copula and Student's t-copula. When it comes to the application of these copulae, there are at least two drawbacks: their algebraic expression is complicated, and their level of symmetry can be problematic. These problems have provided the impetus for the search for copulae with convenient algebraic expressions that can also model asymmetric dependency in datasets. One of the most popular families of copulae which satisfy both requirements is the class of Archimedean copulae. Therefore, in this article, we discuss common bivariate Archimedean copulae and their implementation in MQL5. We will see the expansion of the bivariate copulas library by adding implementations of Frank, Joe, Gumbel, Clayton, N13 and N14 copulae.

Introducing Archimedean copulae

A bivariate Archimedean copula is a specific type of copula C(u,v) used in statistics to model the dependence structure between two random variables with uniform marginal distributions. Its defining property is its generative form, which can be expressed using a single, continuous, strictly decreasing, and convex function called the generator function ϕ.

The generator ϕ must satisfy ϕ(1)=0. This structure gives Archimedean copulae a high degree of symmetry (C(u,v)=C(v,u)) and allows for a wide range of dependence structures to be modeled simply by choosing different generator functions. Archimedean copulae are fundamentally more flexible than common copulae, but that flexibility is usually reduced for practical use. Theoretically, there are an infinite number of choices for the generator function. Every slight change in the function creates a new, unique copula. In practice, one usually chooses a parametric family governed by a unique generator function, defined by a single scalar input variable. This makes estimation and modeling much easier. Therefore, most common Archimedean families are characterized by a single parameter embedded within the generator function, which governs the strength of the dependence.

The generator function defines an Archimedean copula and captures the entire dependence structure between the random variables. In simple terms, its role is to translate the marginal probabilities into a dependence structure that can be easily combined using simple addition. The function transforms the marginal variable. Because the generator is strictly decreasing, low probabilities get mapped to large numbers, and high probabilities get mapped to 0. This is an inversion of the probability scale. The specific shape and parameters of the generator function entirely determine the resulting copula family and, therefore, the exact way the two variables depend on each other. We begin our exploration of Archimedean copulae with the bivariate Frank copula in the next section.

Bivariate Frank copula

The bivariate Frank copula is a symmetric Archimedean copula that can model both positive and negative dependencies without exhibiting tail dependence. It is defined by the generator function:

Frank Generator Function

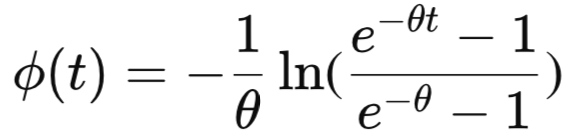
where θ (theta) determines the strength and direction of association. θ values of zero are undefined for the Frank copula's generator. Positive values of θ indicate positive dependence, while negative values correspond to negative dependence; as θ tends to 0, the copula approaches the independence copula. The Frank copula is radially symmetric, meaning it treats both tails equally, and does not exhibit upper or lower tail dependence. This makes it well-suited for modeling moderate dependence structures that are symmetric around the center of the distribution, such as in applications involving continuous variables where extreme co-movements are unlikely.

The class CFrank defined in frank.mqh, inherits from CBivariateCopula to represent a Frank copula.

//+------------------------------------------------------------------+
//|                                                        frank.mqh |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "base.mqh"
//+------------------------------------------------------------------+
//| Frank Copula.                                                    |
//+------------------------------------------------------------------+
class CFrank:public CBivariateCopula
  {
private:
   class CInt_Function_1_Func : public CIntegrator1_Func
     {
   private:
      double         m_th;
   public:
      //---
                     CInt_Function_1_Func(void) {}
                    ~CInt_Function_1_Func(void) {}
      void              set_theta(double theta)
        {
         m_th = theta;
        }
      virtual void      Int_Func(double x,double xminusa,double bminusx,double &y,CObject &obj)
        {
         y = x/m_th/(exp(x)-1.0);
        }
     };
   class CBrent1:public CBrentQ
     {
   private:
      double            debyel(double theta)
        {
         CInt_Function_1_Func fint;
         fint.set_theta(theta);
         CObject obj;
         CAutoGKStateShell s;
         double integral;
         CAutoGKReportShell rep;
         //---
         CAlglib::AutoGKSmooth(0.0,theta,s);
         //---
         CAlglib::AutoGKIntegrate(s,fint,obj);
         //---
         CAlglib::AutoGKResults(s,integral,rep);

         CAutoGKReport report = rep.GetInnerObj();

         if(report.m_terminationtype<0.0)
            Print(__FUNCTION__, " integration error ",report.m_terminationtype);

         return integral;
        }
   public:
                     CBrent1(void)
        {
        }
                    ~CBrent1(void)
        {
        }
      virtual double objective(double u, double v,double y)
        {
         return (1.0 - 4.0/u+4.0*debyel(u)/u) - y;
        }
     };

   virtual double    theta_hat(const double tau) override
     {
      CBrent1 fun;
      return fun.minimize(0,tau,-100.0,100.0,2.e-12,4.0*2.e-16,100);
     }
   vector            generate_pair(double v1, double v2)
     {
      vector out(2);
      out[0] = v1;
      out[1] = -1.0/m_theta*log(1.0+(v2*(1.0-exp(-m_theta)))/(v2*(exp(-m_theta*v1)-1.0)-exp(-m_theta*v1)));
      return out;
     }
protected:
   virtual double    pdf(double u,double v) override
     {
      double et,eut,evt,pd;
      et = exp(m_theta);
      eut = exp(u*m_theta);
      evt = exp(v*m_theta);
      pd = et*eut*evt*(et - 1.0)*m_theta/pow(et+eut*evt-et*eut-et*evt,2.0);
      return pd;
     }
   virtual double    cdf(double u, double v) override
     {
      return (-1.0 / m_theta * log(1.0 + (exp(-1.0 * m_theta * u) - 1.0) * (exp(-1.0 * m_theta * v) - 1.0)/ (exp(-1 * m_theta) - 1.0)));
     }
   virtual double    condi_cdf(double u, double v) override
     {
      double enut = exp(-u*m_theta);
      double envt = exp(-v*m_theta);
      double ent = exp(-m_theta);
      double denominator = ((ent - 1.0) + (enut - 1.0) * (envt - 1.0));
      if(denominator)
         return (envt * (enut - 1.0)/ (denominator));
      else
         return EMPTY_VALUE;
     }
   virtual vector    pdf(vector &u,vector &v) override
     {
      vector eut,evt,pd;
      double et = exp(m_theta);
      eut = exp(u*m_theta);
      evt = exp(v*m_theta);
      pd = et*eut*evt*(et - 1.0)*m_theta/pow(et+eut*evt-et*eut-et*evt,2.0);
      return pd;
     }
   virtual vector    cdf(vector &u, vector &v) override
     {
      return (-1.0 / m_theta * log(1.0 + (exp(-1.0 * m_theta * u) - 1.0) * (exp(-1.0 * m_theta * v) - 1.0)/ (exp(-1 * m_theta) - 1.0)));
     }
   virtual vector    condi_cdf(vector &u, vector &v) override
     {
      vector enut = exp(-1.0*u*m_theta);
      vector envt = exp(-1.0*v*m_theta);
      double ent = exp(-m_theta);

      return (envt * (enut - 1.0)/ ((ent - 1.0) + (enut - 1.0) * (envt - 1.0)));
     }
public:
                     CFrank(void)
     {
      m_threshold = 1.e-10;
      m_copula_type = FRANK_COPULA;
      m_invalid_theta = 0.0;
     }
                    ~CFrank(void)
     {
     }
   virtual matrix    Sample(ulong num_samples) override
     {
      double unf_v[],unf_c[];

      vector v,c,u;

      if(!MathRandomUniform(0.0,1.0,int(num_samples),unf_v) ||
         !MathRandomUniform(0.0,1.0,int(num_samples),unf_c) ||
         !v.Assign(unf_v) || !c.Assign(unf_c))
        {
         Print(__FUNCTION__, " failed to get uniform random numbers ", GetLastError());
         return matrix::Zeros(0,0);
        }

      matrix out(num_samples,2);

      for(ulong irow = 0; irow<num_samples; irow++)
         out.Row(generate_pair(v[irow],c[irow]),irow);

      return out;

     }

  };
//+------------------------------------------------------------------+

The θ parameter is determined from data samples by estimating the rank correlation τ (Kendall's Tau) using the following relationship:

Theta and Kendall’s Tau relationship

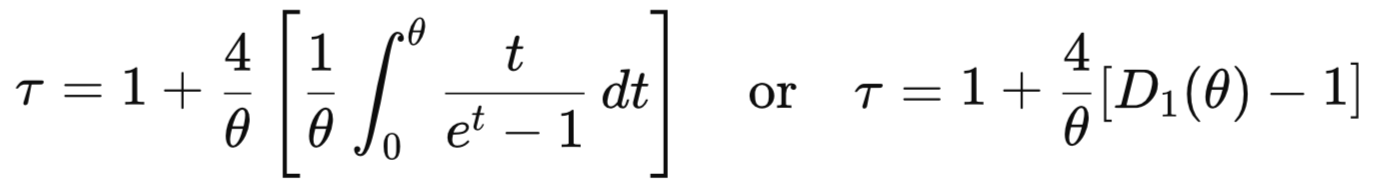
where D1(θ) is the Debye function of order 1. Below is a scatter plot of a synthetic dataset sampled from a Frank copula with theta parameter 5.

Frank Copula sample

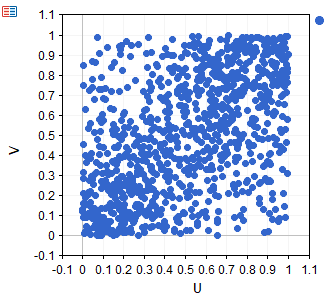
Bivariate Clayton copula

Next up, is the bivariate Clayton copula, characterized by its ability to model strong lower-tail dependence and asymmetry between the tails of a joint distribution. It is defined by the generator function:

Clayton Generator Function

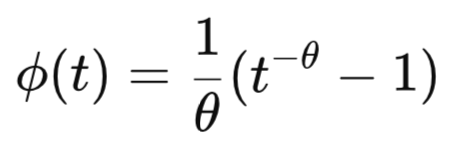
The larger the value of θ, the stronger the association in the lower tail. The Clayton copula exhibits lower-tail dependence with coefficient:

It has no upper-tail dependence (λU=0), making it particularly suitable for modeling situations where extreme low values tend to occur together. It captures only positive dependence (θ>0) and approaches the independence copula as θ values approach 0. Note that the Clayton copula is undefined for θ=0. Its asymmetric nature allows it to effectively represent relationships where joint downturns are more likely than joint upturns. The header file clayton.mqh contains the definition of the CClayton class.

//+------------------------------------------------------------------+
//|                                                      clayton.mqh |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "base.mqh"
//+------------------------------------------------------------------+
//| Clayton copula.                                                  |
//+------------------------------------------------------------------+
class CClayton:public CBivariateCopula
  {
private:
   virtual double    theta_hat(const double tau) override
     {
      return 2.0*tau/(1.0-tau);
     }
   vector            generate_pair(double v1, double v2)
     {
      vector out(2);
      double w = 0.0;

      out[0] = v1;
      out[1] = pow(pow(v1,-m_theta)*(pow(v2,(-m_theta / (1 + m_theta))) - 1.0)+1.0,-1.0/m_theta);
      return out;
     }
protected:
   virtual double    pdf(double u,double v) override
     {
      double u_part,v_part,pd;
      u_part = pow(u,(-1 - m_theta));
      v_part = pow(v,(-1 - m_theta));
      pd = ((1.0 + m_theta) * u_part * v_part*pow(-1.0 + u_part * u + v_part * v, (-2.0 - 1.0 / m_theta)));
      return pd;
     }
   virtual double    cdf(double u, double v) override
     {
      double expo = pow(MathMax(pow(u,-m_theta)+pow(v,-m_theta)-1.0,0.0),-1.0/m_theta);

      return expo;
     }
   virtual double    condi_cdf(double u, double v) override
     {
      double unt = pow(u,-m_theta);
      double vnt = pow(v,-m_theta);
      double tpow = 1.0/m_theta + 1.0;
      double denominator = pow(unt+vnt-1.0,tpow);
      if(denominator)
         return vnt/v/pow(unt+vnt-1.0,tpow);
      else
         return EMPTY_VALUE;
     }
   virtual double    inv_condi_cdf(double y, double V) override
     {
      if(m_theta < 0.0)
         return V;
      else
        {
         double a = pow(y,m_theta/(-1.0 - m_theta));
         double b = pow(V, m_theta);

         if(b==0)
            return 1.0;
         return pow((a + b - 1.0)/b, -1.0/m_theta);
        }
     }
   virtual vector    inv_condi_cdf(vector& y, vector& V) override
     {
      if(m_theta < 0.0)
         return V;
      else
        {
         vector a = pow(y,m_theta/(-1.0 - m_theta));
         vector b = pow(V, m_theta);

         if(b.CompareEqual(vector::Zeros(b.Size()))==0)
            return vector::Ones(V.Size());
         return pow((a + b - 1.0)/b, -1.0/m_theta);
        }
     }
   virtual vector    pdf(vector &u,vector &v) override
     {
      vector u_part,v_part,pd;
      u_part = pow(u,(-1 - m_theta));
      v_part = pow(v,(-1 - m_theta));
      pd = ((1.0 + m_theta) * u_part * v_part*pow(-1.0 + u_part * u + v_part * v, (-2.0 - 1.0 / m_theta)));
      return pd;
     }
   virtual vector    cdf(vector &u, vector &v) override
     {
      vector out(u.Size());
      for(ulong i = 0; i<u.Size(); ++i)
         out[i] = cdf(u[i],v[i]);
      return out;
     }
   virtual vector    condi_cdf(vector &u, vector &v) override
     {
      vector unt = pow(u,-m_theta);
      vector vnt = pow(v,-m_theta);
      double tpow = 1.0/m_theta + 1.0;
      return vnt/v/pow(unt+vnt-1.0,tpow);
     }
public:
                     CClayton(void)
     {
      m_threshold = 1.e-10;
      m_bounds[0] = -1.0;
      m_bounds[1] = DBL_MAX;
      m_invalid_theta = 0.0;
      m_copula_type = CLAYTON_COPULA;
     }
                    ~CClayton(void)
     {
     }
   virtual matrix    Sample(ulong num_samples) override
     {
      double unf_v[],unf_c[];

      vector v,c,u;

      if(!MathRandomUniform(0.0,1.0,int(num_samples),unf_v) ||
         !MathRandomUniform(0.0,1.0,int(num_samples),unf_c) ||
         !v.Assign(unf_v) || !c.Assign(unf_c))
        {
         Print(__FUNCTION__, " failed to get uniform random numbers ", GetLastError());
         return matrix::Zeros(0,0);
        }

      matrix out(num_samples,2);

      for(ulong irow = 0; irow<num_samples; irow++)
         out.Row(generate_pair(v[irow],c[irow]),irow);

      return out;

     }

  };
//+------------------------------------------------------------------+

Here we can see a scatter plot of a dataset sampled from a synthetic clayton bivariate distribution.

Bivariate Clayton sample dataset

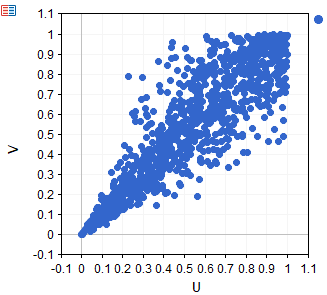
Bivariate Gumbel copula

The bivariate Gumbel copula is an Archimedean copula that effectively models upper-tail dependence while remaining asymmetric between the upper and lower tails. It is defined by the generator function:

Where larger values of theta indicate stronger dependence where larger values of θ indicate stronger dependence. The Gumbel copula exhibits upper-tail dependence with coefficient:

And no lower-tail dependence, making it particularly useful for capturing the tendency of extreme high values in one variable to coincide with extreme high values in another. It can only represent positive dependence and converges to the independence copula when θ equals one. The Gumbel copula is implemented as the CGumbel class defined in gumbel.mqh.

//+------------------------------------------------------------------+
//|                                                       gumbel.mqh |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "base.mqh"
//+------------------------------------------------------------------+
//| Gumbel Copula.                                                   |
//+------------------------------------------------------------------+
class CGumbel:public CBivariateCopula
  {
private:
   class CBrent1:public CBrentQ
     {
   public:
                     CBrent1(void)
        {
        }
                    ~CBrent1(void)
        {
        }
      virtual double objective(double u, double v,double y)
        {
         return (u*(1.0 - log(u)/v)) - y;
        }
     };
   virtual double    theta_hat(const double tau) override
     {
      return 1.0/(1.0-tau);
     }
   vector            generate_pair(double v1, double v2)
     {
      vector out(2);
      double w = 0.0;
      if(v2>m_threshold)
        {
         CBrent1 fun;
         w = fun.minimize(m_theta,v2,m_threshold,1.0,2.e-12,4.0*2.e-16,100);
        }
      else
         w = 1.e10;
      out[0] = exp(pow(v1,1.0/m_theta)*log(w));
      out[1] = exp(pow((1.0-v1),1.0/m_theta)*log(w));
      return out;
     }
protected:
   virtual double    pdf(double u,double v) override
     {
      double u_part,v_part,expo,pd;
      u_part = pow(-1.0*log(u),m_theta);
      v_part = pow(-1.0*log(v),m_theta);
      expo = pow(u_part+v_part,1.0/m_theta);
      pd = 1.0/(u*v) * (exp(-1.0*expo)* u_part/(-1.0*log(u)) * v_part/(-1.0*log(v))*(m_theta+expo-1.0)*pow(u_part+v_part,(1.0/m_theta-2.0)));
      return pd;
     }
   virtual double    cdf(double u, double v) override
     {
      double expo = pow(pow(-1.0*log(u),m_theta) + pow(-1.0*log(v),m_theta),(1. / m_theta));

      return exp(-1.0*expo);
     }
   virtual double    condi_cdf(double u, double v) override
     {
      double expo = pow(pow(-1.0*log(u),m_theta)+pow(-1.0*log(v),m_theta),((1 - m_theta) / m_theta));
      return (cdf(u,v) * expo * pow(-1.0*log(v),m_theta-1.0)/v);
     }
   virtual vector    pdf(vector &u,vector &v) override
     {
      vector u_part,v_part,expo,pd;
      u_part = pow(-1.0*log(u),m_theta);
      v_part = pow(-1.0*log(v),m_theta);
      expo = pow(u_part+v_part,1.0/m_theta);
      pd = 1.0/(u*v) * (exp(-1.0*expo)* u_part/(-1.0*log(u)) * v_part/(-1.0*log(v))*(m_theta+expo-1.0)*pow(u_part+v_part,(1.0/m_theta-2.0)));
      return pd;
     }
   virtual vector    cdf(vector &u, vector &v) override
     {

      vector expo = pow(pow(-1.0*log(u),m_theta) + pow(-1.0*log(v),m_theta),(1. / m_theta));
      return exp(-1.0*expo);
     }
   virtual vector    condi_cdf(vector &u, vector &v) override
     {

      vector expo = pow(pow(-1.0*log(u),m_theta)+pow(-1.0*log(v),m_theta),((1 - m_theta) / m_theta));
      return (cdf(u,v) * expo * pow(-1.0*log(v),m_theta-1.0)/v);
     }
public:
                     CGumbel(void)
     {
      m_threshold = 1.e-10;
      m_bounds[0] = 1.0;
      m_bounds[1] = DBL_MAX;
      m_copula_type = GUMBEL_COPULA;
     }
                    ~CGumbel(void)
     {
     }
   virtual matrix    Sample(ulong num_samples) override
     {
      double unf_v[],unf_c[];

      vector v,c,u;

      if(!MathRandomUniform(0.0,1.0,int(num_samples),unf_v) ||
         !MathRandomUniform(0.0,1.0,int(num_samples),unf_c) ||
         !v.Assign(unf_v) || !c.Assign(unf_c))
        {
         Print(__FUNCTION__, " failed to get uniform random numbers ", GetLastError());
         return matrix::Zeros(0,0);
        }

      matrix out(num_samples,2);

      for(ulong irow = 0; irow<num_samples; irow++)
         out.Row(generate_pair(v[irow],c[irow]),irow);

      return out;

     }

  };
//+------------------------------------------------------------------+

Below is a scatter plot that depicts data sampled from a Gumbel copula with theta parameter 5.

Bivariate Gumbel sample dataset

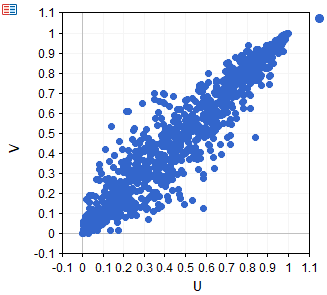
Bivariate Joe copula

The bivariate Joe copula is an Archimedean copula known for modeling strong upper-tail dependence while exhibiting asymmetry between the upper and lower tails. It captures situations where extreme high values in one variable are likely to coincide with extreme high values in the other, but not necessarily for low values. The copula is defined by the generator function:

Joe Generator Function

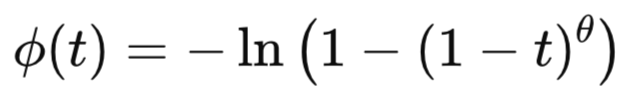
Larger values of θ indicate stronger association. The Joe copula always exhibits positive dependence and belongs to the family of non-elliptical copulas, making it flexible in modeling non-linear relationships. Importantly, it has upper-tail dependence coefficient:

And no lower-tail dependence. The code implementing the joe copula is listed in joe.mqh.

//+------------------------------------------------------------------+
//|                                                          joe.mqh |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "base.mqh"
//+------------------------------------------------------------------+
//| Joe Copula.                                                      |
//+------------------------------------------------------------------+
class CJoe:public CBivariateCopula
  {
private:
   class CInt_Function_1_Func : public CIntegrator1_Func
     {
   private:
      double         m_th;
   public:
      //---
                     CInt_Function_1_Func(void) {}
                    ~CInt_Function_1_Func(void) {}
      void              set_theta(double theta)
        {
         m_th = theta;
        }
      virtual void      Int_Func(double x,double xminusa,double bminusx,double &y,CObject &obj)
        {
         y = (1.0 - pow(1.0 - x,m_th)) * pow(1.0 - x,1.0 - m_th) * log(1.0 - pow(1.0 - x,m_th)) / m_th;
        }
     };
   class CBrent1:public CBrentQ
     {
   public:
                     CBrent1(void)
        {
        }
                    ~CBrent1(void)
        {
        }
      virtual double objective(double u, double v,double y)
        {
         return (u-1.0/v*(log(1.0-pow(1.0-u,v))*(1.0-pow(1.0-u,v))/pow(1.0-u,(v-1.0)))) - y;
        }
     };
   class CBrent2:public CBrentQ
     {
   public:
                     CBrent2(void)
        {
        }
                    ~CBrent2(void)
        {
        }
      virtual double objective(double u, double v,double y)
        {
         CInt_Function_1_Func fint;
         fint.set_theta(u);
         CObject obj;
         CAutoGKStateShell s;
         double integral;
         CAutoGKReportShell rep;
         //---
         CAlglib::AutoGKSmooth(0.0,1.0,s);
         //---
         CAlglib::AutoGKIntegrate(s,fint,obj);
         //---
         CAlglib::AutoGKResults(s,integral,rep);

         CAutoGKReport report = rep.GetInnerObj();

         if(report.m_terminationtype<0.0)
            Print(__FUNCTION__, " integration error ",report.m_terminationtype);

         return (1.0+4.0*integral)-y;
        }
     };
   virtual double    theta_hat(const double tau) override
     {
      CBrent2 fun;
      return fun.minimize(0,tau,1.0,100.0,2.e-12,4.0*2.e-16,100);
     }
   vector            generate_pair(double v1, double v2)
     {
      vector out(2);
      double w = 0;
      if(v2>m_threshold)
        {
         CBrent1 fun;
         w = fun.minimize(m_theta,v2,m_threshold,1.0-m_threshold,2.e-12,4.0*2.e-16,100);
        }
      else
         w = m_threshold;
      out[0] = 1.0 - pow(1.0 - pow(1.0 - pow(1.0 - w, m_theta), v1),(1.0 / m_theta));
      out[1] = 1.0 - pow(1.0 - pow(1.0 - pow(1.0 - w, m_theta), (1.0-v1)),(1.0 / m_theta));
      return out;
     }
protected:
   virtual double    pdf(double u,double v) override
     {
      double up,vp,pd;
      up = pow(1.0-u,m_theta);
      vp = pow(1.0-v,m_theta);
      pd = (up/(1.0-u)*vp/(1.0-v)*pow(up+vp-up*vp,1.0/m_theta-2.0)*(m_theta-(up-1.0)*(vp-1.0)));
      return pd;
     }
   virtual double    cdf(double u, double v) override
     {
      double up = pow(1.0-u,m_theta);
      double vp = pow(1.0-v,m_theta);
      return 1.0 - pow(up+vp-up*vp,1.0/m_theta);
     }
   virtual double    condi_cdf(double u, double v) override
     {
      double up = pow(1.0-u,m_theta);
      double vp = pow(1.0-v,m_theta);
      return (-(-1.0+up)*pow(up+vp-up*vp,-1.0+1.0/m_theta)*vp/(1.0-v));
     }
   virtual vector    pdf(vector &u,vector &v) override
     {
      vector up,vp,pd;
      up = pow(1.0-u,m_theta);
      vp = pow(1.0-v,m_theta);
      pd = (up/(1.0-u)*vp/(1.0-v)*pow(up+vp-up*vp,1.0/m_theta-2.0)*(m_theta-(up-1.0)*(vp-1.0)));
      return pd;
     }
   virtual vector    cdf(vector &u, vector &v) override
     {
      vector up = pow(1.0-u,m_theta);
      vector vp = pow(1.0-v,m_theta);
      return 1.0 - pow(up+vp-up*vp,1.0/m_theta);
     }
   virtual vector    condi_cdf(vector &u, vector &v) override
     {

      vector up = pow(1.0-u,m_theta);
      vector vp = pow(1.0-v,m_theta);
      return (-1.0*(-1.0+up)*pow(up+vp-up*vp,-1.0+1.0/m_theta)*vp/(1.0-v));
     }
public:
                     CJoe(void)
     {
      m_threshold = 1.e-10;
      m_copula_type = JOE_COPULA;
      m_bounds[0] = 1.0;
      m_bounds[1] = DBL_MAX;
     }
                    ~CJoe(void)
     {
     }
   virtual matrix    Sample(ulong num_samples) override
     {
      double unf_v[],unf_c[];

      vector v,c,u;

      if(!MathRandomUniform(0.0,1.0,int(num_samples),unf_v) ||
         !MathRandomUniform(0.0,1.0,int(num_samples),unf_c) ||
         !v.Assign(unf_v) || !c.Assign(unf_c))
        {
         Print(__FUNCTION__, " failed to get uniform random numbers ", GetLastError());
         return matrix::Zeros(0,0);
        }

      matrix out(num_samples,2);

      for(ulong irow = 0; irow<num_samples; irow++)
         out.Row(generate_pair(v[irow],c[irow]),irow);

      return out;

     }

  };
//+------------------------------------------------------------------+

Here we can see the dependency depicted by a synthetic dataset sampled from a Joe copula with theta parameter 5.

Bivariate Joe sample dataset

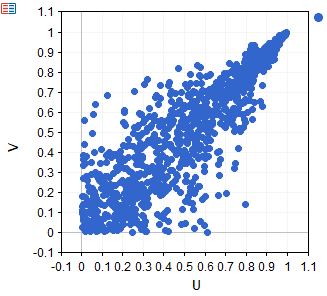
Bivariate N13 copula

The N13 copula is an Archimedean, one-parameter family that models positive dependence only and, unlike some other Archimedean families, does not exhibit asymptotic tail dependence. As the family’s parameter θ increases, the overall concordance strengthens, and at the lower parameter boundary (θ=0) it approaches independence. Because it lacks nonzero tail coefficients, the N13 is useful when greater mid-range or upper-middle dependence than the Gaussian or Frank families is needed, as opposed to the clustering of simultaneous extremes. The N13 copula is defined by the generator function:

n13 Generator Function

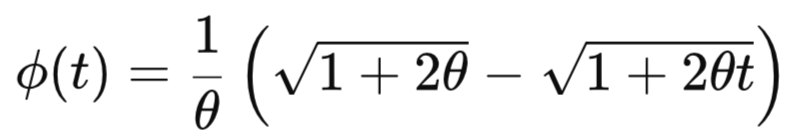
It is implemented in MQL5 as the CN13 class, defined in n13.mqh.

//+------------------------------------------------------------------+
//|                                                          n13.mqh |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "base.mqh"
//+------------------------------------------------------------------+
//| N13 Copula (Nelsen 13)                                           |
//+------------------------------------------------------------------+
class CN13:public CBivariateCopula
  {
private:
   class CInt_Function_1_Func : public CIntegrator1_Func
     {
   private:
      double         m_th;
   public:
      //---
                     CInt_Function_1_Func(void) {}
                    ~CInt_Function_1_Func(void) {}
      void              set_theta(double theta)
        {
         m_th = theta;
        }
      virtual void      Int_Func(double x,double xminusa,double bminusx,double &y,CObject &obj)
        {
         y = -((x - x * pow((1 - log(x)),1 - m_th) - x * log(x)) / m_th);
        }
     };
   class CBrent1:public CBrentQ
     {
   public:
                     CBrent1(void)
        {
        }
                    ~CBrent1(void)
        {
        }
      virtual double objective(double u, double v,double y)
        {
         return (u+1.0/v*(u-u*pow(1.0-1.0*log(u),1.0-v)-u*log(u))) - y;;
        }
     };
   class CBrent2:public CBrentQ
     {
   public:
                     CBrent2(void)
        {
        }
                    ~CBrent2(void)
        {
        }
      virtual double objective(double u, double v,double y)
        {
         CInt_Function_1_Func fint;
         fint.set_theta(u);
         CObject obj;
         CAutoGKStateShell s;
         double integral;
         CAutoGKReportShell rep;
         //---
         CAlglib::AutoGKSmooth(0.0,1.0,s);
         //---
         CAlglib::AutoGKIntegrate(s,fint,obj);
         //---
         CAlglib::AutoGKResults(s,integral,rep);

         CAutoGKReport report = rep.GetInnerObj();

         if(report.m_terminationtype<0.0)
            Print(__FUNCTION__, " integration error ",report.m_terminationtype);

         return (1.0 + 4.0*integral) - y;
        }
     };
   virtual double    theta_hat(const double tau) override
     {
      CBrent2 fun;
      return fun.minimize(0,tau,1.e-7,100.0,2.e-12,4.0*2.e-16,100);
     }
   vector            generate_pair(double v1, double v2)
     {
      vector out(2);
      double w = 0.0;
      if(v2>m_threshold)
        {
         CBrent1 fun;
         w = fun.minimize(m_theta,v2,m_threshold,1.0-m_threshold,2.e-12,4.0*2.e-16,100);
        }
      else
         w = m_threshold;
      out[0] = exp(1. - pow(v1 * (pow((1.0 - log(w)),m_theta) - 1.) + 1.,(1. / m_theta)));
      out[1] = exp(1. - pow((1.0-v1) * (pow((1.0 - log(w)),m_theta) - 1.) + 1.,(1. / m_theta)));
      return out;
     }
protected:
   virtual double    pdf(double u,double v) override
     {
      double Cuv,u_part,v_part,numerator,denominator;
      Cuv = cdf(u,v);
      u_part = pow(1.0 - log(u),m_theta);
      v_part = pow(1.0 - log(v),m_theta);
      numerator = Cuv * u_part *v_part * (-1.0+m_theta + pow(-1.0+u_part +v_part,1.0/m_theta))*pow(-1.0+u_part+v_part,1.0/m_theta);
      denominator = u*v*(1.0-1.0*log(u))*(1.0 - log(v))*pow(-1.0+u_part+v_part,2.0);
      return (numerator+1.e-8)/(denominator+1.e-8);
     }
   virtual double    cdf(double u, double v) override
     {
      double u_part = pow(1.0-1.0*log(u),m_theta);
      double v_part = pow(1.0-1.0*log(v),m_theta);
      double cdf = exp(1.0 - pow(-1.0+u_part+v_part,1.0/m_theta));
      return cdf;
     }
   virtual double    condi_cdf(double u, double v) override
     {
      if(!m_theta)
         return EMPTY_VALUE;

      double u_part = pow(1.0 - log(u),m_theta);
      double v_part = pow(1.0 - log(v),m_theta);
      double cuv = cdf(u,v);

      double numerator = cuv *pow(-1.0+u_part+v_part,1.0/m_theta)*v_part;
      double denominator = v*(-1.0+u_part+v_part)*(1.0-1.0*log(v));

      return (numerator+1.e-8)/(denominator+1.e-8);
     }
   virtual vector    pdf(vector &u,vector &v) override
     {
      vector Cuv,u_part,v_part,numerator,denominator;
      Cuv = cdf(u,v);
      u_part = pow(1.0 - log(u),m_theta);
      v_part = pow(1.0 - log(v),m_theta);
      numerator = Cuv * u_part *v_part * (-1.0+m_theta + pow(-1.0+u_part +v_part,1.0/m_theta))*pow(-1.0+u_part+v_part,1.0/m_theta);
      denominator = u*v*(1.0-1.0*log(u))*(1.0 - log(v))*pow(-1.0+u_part+v_part,2.0);
      return (numerator+1.e-8)/(denominator+1.e-8);
     }
   virtual vector    cdf(vector &u, vector &v) override
     {
      vector u_part = pow(1.0-1.0*log(u),m_theta);
      vector v_part = pow(1.0-1.0*log(v),m_theta);
      vector cdf = exp(1.0 - pow(-1.0+u_part+v_part,1.0/m_theta));
      return cdf;
     }
   virtual vector    condi_cdf(vector &u, vector &v) override
     {

      vector u_part = pow(1.0 - log(u),m_theta);
      vector v_part = pow(1.0 - log(v),m_theta);
      vector cuv = cdf(u,v);

      vector numerator = cuv *pow(-1.0+u_part+v_part,1.0/m_theta)*v_part;
      vector denominator = v*(-1.0+u_part+v_part)*(1.0-1.0*log(v));

      return (numerator+1.e-8)/(denominator+1.e-8);
     }
public:
                     CN13(void)
     {
      m_threshold = 1.e-10;
      m_bounds[0] = 0.0;
      m_bounds[1] = DBL_MAX;
      m_copula_type = N13_COPULA;
     }
                    ~CN13(void)
     {
     }
   virtual matrix    Sample(ulong num_samples) override
     {
      double unf_v[],unf_c[];

      vector v,c,u;

      if(!MathRandomUniform(0.0,1.0,int(num_samples),unf_v) ||
         !MathRandomUniform(0.0,1.0,int(num_samples),unf_c) ||
         !v.Assign(unf_v) || !c.Assign(unf_c))
        {
         Print(__FUNCTION__, " failed to get uniform random numbers ", GetLastError());
         return matrix::Zeros(0,0);
        }

      matrix out(num_samples,2);

      for(ulong irow = 0; irow<num_samples; irow++)
         out.Row(generate_pair(v[irow],c[irow]),irow);

      return out;

     }

  };
//+------------------------------------------------------------------+

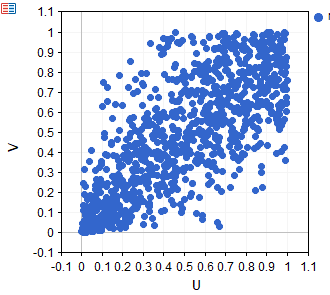
Next is a visualization of a dataset sampled from an N13 copula.

Bivariate N13 sample dataset

Bivariate N14 copula

The N14 copula is another Archimedean one-parameter family that also models only positive dependence, but does permit tail dependence in both corners. It produces upper-tail dependence and typically weaker lower-tail dependence as the parameter θ moves away from independence. The N14 copula can capture the tendency of joint extreme high values and, to a lesser extent, joint extreme low values. Dependence strengthens with the parameter, and the copula tends toward independence at the lower bound. Empirical studies of financial pairs often find N14 fits real data well because of these asymmetric tail features. The N14 copula has the following generator function:

n14 Generator Function

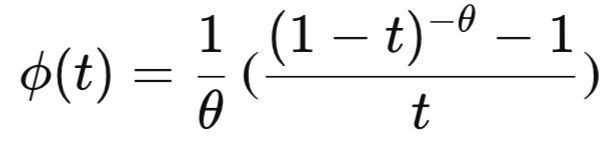
The class CN14, defined in n14.mqh is the MQL5 representation of the N14 copula.

//+------------------------------------------------------------------+
//|                                                          n14.mqh |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#include "base.mqh"
//+------------------------------------------------------------------+
//| N14 Copula (Nelsen 14)                                           |
//+------------------------------------------------------------------+
class CN14:public CBivariateCopula
  {
private:
   class CBrent:public CBrentQ
     {
   public:
                     CBrent(void)
        {
        }
                    ~CBrent(void)
        {
        }
      virtual double objective(double u, double v,double y) override
        {
         return ((-1.0*u) * (-2.0 + pow(u,1.0/v))) - y;
        }
     };
   virtual double    theta_hat(const double tau) override
     {
      return (1.0 + tau)/(2.0 - 2.0*tau);
     }
   vector            generate_pair(double v1, double v2)
     {
      vector out(2);
      double w = 0.0;
      if(v2>m_threshold)
        {
         CBrent brent;
         w = brent.minimize(m_theta,v2,m_threshold,1.0-m_threshold,2.e-12,4.0*2.e-16,100);
        }
      else
         w = m_threshold;
      out[0] = pow(1.0 + pow(v1 * pow(pow(w,-1.0/m_theta)-1.0,m_theta),1.0/m_theta),-1.0*m_theta);
      out[1] = pow(1.0 + pow((1.0-v1) * pow(pow(w,-1.0/m_theta)-1.0,m_theta),1.0/m_theta),-1.0*m_theta);
      return out;
     }
protected:
   virtual double    pdf(double u,double v) override
     {
      double u_ker,v_ker,u_part,v_part,cdf_ker,numerator,denominator;
      u_ker = -1.0+pow(u,1.0/m_theta);
      v_ker = -1.0+pow(v,1.0/m_theta);
      u_part = pow(-1.0 + pow(u,-1.0/m_theta),m_theta);
      v_part = pow(-1.0 + pow(v,-1.0/m_theta),m_theta);
      cdf_ker = 1.0 + pow(u_part+v_part,1.0/m_theta);
      numerator = (u_part * v_part *(cdf_ker - 1.0)*(-1.0 + m_theta + 2.0*m_theta*(cdf_ker-1.0)));
      denominator = pow(u_part + v_part,2.0) * pow(cdf_ker,(2.0 + m_theta))* u * v * u_ker * v_ker * m_theta;

      return (numerator+1.e-8)/(denominator+1.e-8);
     }
   virtual double    cdf(double u, double v) override
     {
      double u_part = pow(-1.0+pow(u,-1.0/m_theta),m_theta);
      double v_part = pow(-1.0+pow(v,-1.0/m_theta),m_theta);
      double cdf = pow(1.0 + pow(u_part+v_part,1.0/m_theta),-1*m_theta);
      return cdf;
     }
   virtual double    condi_cdf(double u, double v) override
     {
      double v_ker = -1.0 + pow(v, -1.0 / m_theta);
      double u_part = pow(-1.0 + pow(u, -1.0 / m_theta),m_theta);
      double v_part = pow(-1.0 + pow(v, -1.0 / m_theta),m_theta);
      double cdf_ker = 1.0 + pow(u_part + v_part, (1.0/ m_theta));

      double numerator = v_part * (cdf_ker - 1.0);
      double denominator = pow(v, (1.0 + 1.0 / m_theta)) * v_ker * (u_part + v_part) * pow(cdf_ker,1.0 + m_theta);

      return (numerator+1.e-8)/(denominator+1.e-8);
     }
   virtual vector    pdf(vector&u,vector&v) override
     {
      vector u_ker,v_ker,u_part,v_part,cdf_ker,numerator,denominator;
      u_ker = -1.0+pow(u,1.0/m_theta);
      v_ker = -1.0+pow(v,1.0/m_theta);
      u_part = pow(-1.0 + pow(u,-1.0/m_theta),m_theta);
      v_part = pow(-1.0 + pow(v,-1.0/m_theta),m_theta);
      cdf_ker = 1.0 + pow(u_part+v_part,1.0/m_theta);
      numerator = (u_part * v_part *(cdf_ker - 1.0)*(-1.0 + m_theta + 2.0*m_theta*(cdf_ker-1.0)));
      denominator = pow(u_part + v_part,2.0) * pow(cdf_ker,(2.0 + m_theta))* u * v * u_ker * v_ker * m_theta;

      return (numerator+1.e-8)/(denominator+1.e-8);
     }
   virtual vector    cdf(vector&u, vector&v) override
     {
      vector u_part = pow(-1.0+pow(u,-1.0/m_theta),m_theta);
      vector v_part = pow(-1.0+pow(v,-1.0/m_theta),m_theta);
      vector cdf = pow(1.0 + pow(u_part+v_part,1.0/m_theta),-1*m_theta);
      return cdf;
     }
   virtual vector    condi_cdf(vector&u, vector&v) override
     {
      vector v_ker = -1.0 + pow(v, -1.0 / m_theta);
      vector u_part = pow(-1.0 + pow(u, -1.0 / m_theta),m_theta);
      vector v_part = pow(-1.0 + pow(v, -1.0 / m_theta),m_theta);
      vector cdf_ker = 1.0 + pow(u_part + v_part, (1.0/ m_theta));

      vector numerator = v_part * (cdf_ker - 1.0);
      vector denominator = pow(v, (1.0 + 1.0 / m_theta)) * v_ker * (u_part + v_part) * pow(cdf_ker,1.0 + m_theta);

      return (numerator+1.e-8)/(denominator+1.e-8);
     }
public:
                     CN14(void)
     {
      m_threshold = 1.e-10;
      m_bounds[0] = 1.0;
      m_bounds[1] = DBL_MAX;
      m_copula_type = N14_COPULA;
     }
                    ~CN14(void)
     {
     }
   virtual matrix    Sample(ulong num_samples) override
     {
      double unf_v[],unf_c[];

      vector v,c,u;

      if(!MathRandomUniform(0.0,1.0,int(num_samples),unf_v) ||
         !MathRandomUniform(0.0,1.0,int(num_samples),unf_c) ||
         !v.Assign(unf_v) || !c.Assign(unf_c))
        {
         Print(__FUNCTION__, " failed to get uniform random numbers ", GetLastError());
         return matrix::Zeros(0,0);
        }

      matrix out(num_samples,2);

      for(ulong irow = 0; irow<num_samples; irow++)
         out.Row(generate_pair(v[irow],c[irow]),irow);

      return out;

     }
  };
//+------------------------------------------------------------------+

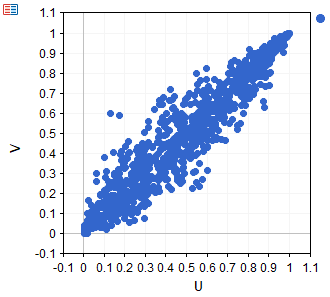
The scatter plot below shows a dataset sampled from an N14 copula.

Bivariate N14 sample dataset

Counting the copulae we have implemented so far, we now have a fair number that can capture various types of dependencies in bivariate datasets. In the next section, we discuss what can be inferred from the dependence models captured by copulae. This will help us better understand how to apply them.

Interpretation of copula operations

It has been established that a copula captures the dependence amongst variables. The parameters of the copula describe the strength of this dependence, which is easy enough to understand. Due to copulae being rooted in probability theory, we can also deduce certain characteristics of the individual variables based on this characterization of dependence defined by the model. This is done by evaluating the CDF, PDF, and conditional CDF of a copula. Such inference is done on variables that represent the quantiles or percentiles of the raw variable. Quantiles and percentiles are measures of position in statistics used to divide a sorted dataset into equal-sized portions. They help illustrate the distribution and relative standing of a particular data point.

Given quantiles, u and v, the copula CDF C(u,v) represents the joint probability: P(U≤u,V≤v). This quantifies the probability that one variable lies below its u-quantile and the other below its v-quantile, accounting for their mutual dependence. For instance, evaluating a copula at u=0.8, v=0.9 tells us the probability that one variable falls within the lowest 80% of its distribution while the other is in the bottom 90%. In code, this is done via the Copula_CDF() method of a copula object.

Complementing the CDF is the probability density function of a copula, c(u,v), evaluated via the Copula_PDF() method. While the CDF gives the accumulated probability mass up to a point, the PDF indicates how densely that probability mass is concentrated at the point itself. A high PDF value signifies that the particular combination of outcomes (u,v) is highly likely. More specifically, the copula PDF is by the following formula.

Copula PDF

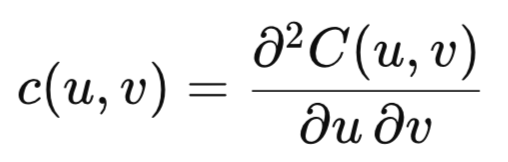
A high PDF value implies a high local dependence between variables relative to the independence case. Low or near-zero values signify unlikely joint outcomes.

Conditional probability can be calculated by finding the partial derivative of the copula's CDF with respect to one variable, often denoted as C(v∣u) or C(u∣v). This captures the conditional behavior of one quantile given that the other is fixed at a certain level. When applied in the context of risk management, one might ask, "Given that Asset A’s return is at the 10th percentile (u=0.10), what is the likelihood that Asset B’s return is at or below its 5th percentile (V≤0.05)?". This is implemented via the Conditional_Probability() method. The first input to the method corresponds to the variable held fixed, and the second gives the conditional quantile. Finally, the Inv_Conditional_Probability() method provides the inverse of the conditional CDF. Given a conditional probability y and a conditional quantile v, it solves for u such that C(v∣u)=y. In the next section, we see how to apply copula inference to the formulation of pairs trading strategies.

Copula based pairs trading strategies

Traditional pairs trading methods, such as the distance method and cointegration, may sometimes falter due to their inability to account for the non-linear or asymmetric relationship between asset prices by assuming the trading spread follows a normal distribution and a linear relationship. The copula-based method could, in theory, offer a solution to this by allowing for flexible modeling that captures non-normality and tail dependence. This framework generates trading signals by using the copula to calculate conditional probabilities that define a mispricing event. An asset is deemed undervalued when the conditional probability of a low return is very high given its pair's return. Conversely, it is overvalued when this probability is very low. Trade entries are therefore not based on linear thresholds but on a quantile-based confidence level derived from the joint distribution, specifically:

Copula Signals

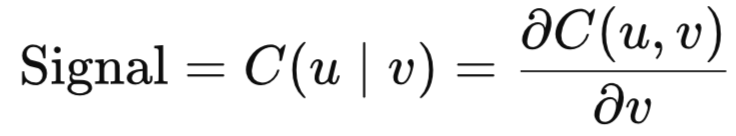
Despite the proposed hypothetical suitability of copulae in modeling the dependence of asset prices, readers should be aware of their limitations. Firstly, a copula works best when applied to stationary multivariate datasets. If the data is non-stationary, the estimated parameters of the marginal distributions and the copula function will capture relationships that are only valid for the specific time period they were estimated from, leading to unreliable inference and poor forecasting for future time periods where the properties may have shifted. Non-stationary time series often exhibit high correlation or dependence purely due to common trends. If the marginal distributions are not stationary, a copula model might capture a dependence structure that is simply an artifact of these changing marginal properties, rather than a genuine, time-invariant link between the variables.

When dealing with non-stationary time series, the transformation to a uniform distribution (via the Probability Integral Transform) may not result in data that is independent and identically distributed (i.i.d.) in the uniform space, which is typically the input requirement for the copula estimation. Stationarity helps ensure a clearer separation between the marginal behavior and the dependence structure, which is the primary advantage of employing a copula approach. If the margins are non-stationary, the estimated copula might be implicitly capturing the non-stationary dynamics of the marginals, confusing the two components. Despite these limitations, academic literature is littered with examples of pairs trading strategies based on copula models.

It is important to note that the requirement for stationarity is for standard or static copula models. For datasets that are inherently non-stationary, there are specialized methods that can be applied. The data can be pre-processed to render the resulting series stationary, and the copula is then applied to this filtered dataset. More advanced models, like time-varying or non-stationary copulae, allow the dependence parameter to change over time, often driven by a time variable or other covariates. These models are explicitly designed to handle non-stationary data. Such copulae will be the subject of another article. For now, we investigate the efficacy of standard or static copulae in modeling the dependence of a pair of raw asset prices. To effectively apply this type of strategy, we first have to define a method for identifying suitable symbols to trade.

Selecting the pairs to trade

Various methods can be applied when selecting symbols for copula-based pairs trading, including those used in traditional pairs trading strategies. These include the cointegration and distance methods. Cointegration is generally considered the most rigorous method. The goal is to find two non-stationary price series whose linear combination is stationary. Tests like the Engle-Granger Two-Step or the Johansen Test are used on the price series. A stationary spread implies a stable, long-term equilibrium relationship that the prices will generally follow. The distance method (Sum of Squared Distances - SSD) is a simpler, non-parametric approach.

Sum of Squared Distances

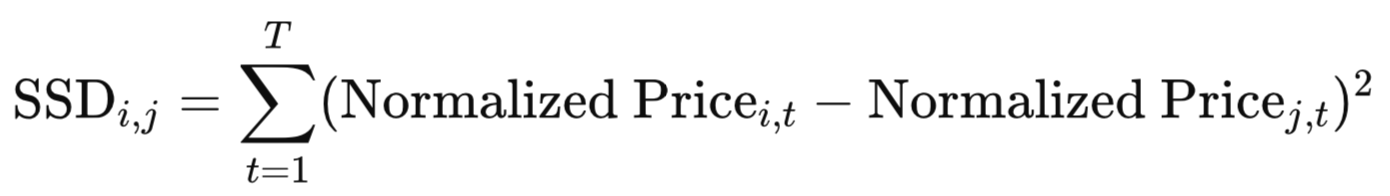
This approach selects pairs that minimize the historical SSD between their normalized price series or cumulative returns. The pairs with the lowest SSD are selected as they have historically moved most closely together.

In this text, we will employ measures of concordance for the selection of a suitable pair of symbols. Measures of concordance are non-parametric tools used to quantify the strength and nature of the dependence between the assets' price series, which is the core principle of the strategy. The most common non-parametric measures of concordance are:

Kendall's Tau: This measure is based on the difference between the probability of observing concordant pairs and discordant pairs. It is a robust measure of the strength of dependence.
Spearman's Rho: This is essentially the Pearson correlation coefficient calculated on the ranked data instead of the raw data. It measures the strength of the monotonic relationship, which is the tendency of corresponding variables to move in the same or opposite direction.

High concordance points to strong co-movement. Pairs with the highest values for Kendall's tau or Spearman's rho are selected. A high value (close to 1) indicates a strong tendency for the symbols' prices to move together, suggesting a long-term relationship that a pairs trade can exploit. The MetaTrader 5 script, Concordance.ex5, takes a list of symbols and calculates the pair with the highest measure of concordance.

//+------------------------------------------------------------------+
//|                                                  Concordance.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<dependence.mqh>
input string   input_symbols = "AUDUSD,NZDUSD,XAUUSD,XAGUSD,EURUSD,XAUEUR";
input datetime input_start_date = D'2025.01.01 00:00';
input ulong    input_count_bars = 260;
input ENUM_TIMEFRAMES input_time_frame = PERIOD_D1;
input ENUM_DEPENDENCE_MEASURE dependence_measure = KENDAL_TAU;
input bool Use_Returns = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   string test_symbols[];
   int num_symbols = StringSplit(input_symbols,StringGetCharacter(",",0),test_symbols);
   if(StringFind(input_symbols,",",StringLen(input_symbols)-1) == StringLen(input_symbols)-1)
     {
      --num_symbols;
      ArrayRemove(test_symbols,uint(num_symbols),1);
     }

   if(num_symbols<2)
     {
      Print(" 2 or more symbols expected ");
      return;
     }

   matrix prices = matrix::Zeros(input_count_bars,ulong(num_symbols));
   vector dwnload;
   for(ulong i = 0; i<prices.Cols(); ++i)
     {
      int try = 10;
      ResetLastError();
      while((!dwnload.CopyRates(test_symbols[i],input_time_frame,COPY_RATES_CLOSE,input_start_date,input_count_bars) ||
         !prices.Col(dwnload,i)) && try)
       {
         Sleep(10000);
         --try;
       }
      /*if(StringFind(test_symbols[i],"XAUEUR")>=0)
        {
         prices.Col(dwnload*prices.Col(i-1),i);
        }*/
      if(GetLastError())
       {
        Print("Could not download data");
        return;
       }
     }
     
   if(Use_Returns)
     {
      prices = log(prices);
      prices = np::diff(prices,1,false);
     }

   matrix dep_mat = dependence(prices,dependence_measure);
   Print(dep_mat);
   Print(EnumToString(dependence_measure), "\n","Using ", Use_Returns?"Returns":"Raw prices");
   if(test_symbols.Size()>2)
     {
      matrix mm = dep_mat.TriL(-1);
      int index = int(mm.ArgMax());
      Print("Pair with highest dependence: ", test_symbols[int(index/int(dep_mat.Cols()))], " and ", test_symbols[int(MathMod(index,dep_mat.Cols()))]);
     }
  }
//+------------------------------------------------------------------+

Below is output from a run using a universe of the following symbols: AUDUSD, NZDUSD, XAUUSD, XAGUSD, EURUSD, and XAUEUR.

Concordance script output

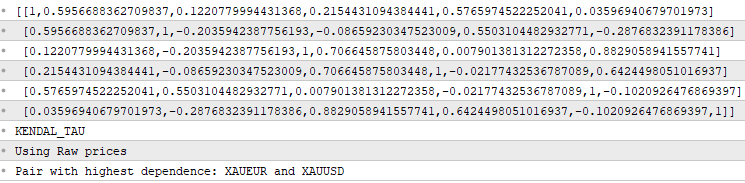
Beyond statistical measurements, it is usually desirable for a selected pair's dependence to be underpinned by economic fundamentals. Looking at the results from the test run of the Concordance.ex5 script, XAUEUR and XAUUSD had the highest measure of co-movement. The dependence of this pair can be easily explained by the fact that they are both derived from the same underlying asset. We therefore have a suitable pair of symbols to trade; the next step is to select a copula model that best fits the dependency characteristics of the symbols.

Selecting a copula model

The primary methods employed in selecting an appropriate copula involve Model-Selection Criteria and Goodness-of-Fit Tests. Model-Selection criteria or information criteria balance the goodness-of-fit of a model with its complexity (number of parameters). A lower value for these criteria generally indicates a better model. The most common ones are the Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC) and the Hannan-Quinn Information Criterion (HQIC). This method follows a three-step procedure. It begins by first estimating parameters of several candidate copula models and calculating each model's log-likelihood estimate. The next step is to compute the information criteria for each candidate model, using any of AIC, BIC, or HQIC. The last step compares the information criteria values of all candidate models and picking out the model that has the lowest value.

Alternatively, selection of an appropriate copula can be done by applying Goodness-of-Fit (GoF) tests. These tests statistically determine whether the dependence structure captured by a specific copula model is consistent with the observed data. They are formal hypothesis tests. Where the null hypothesis is: The data is generated by the assumed copula family. Examples of test statistics that can be used include:

Cramér-von Mises statistic: Measures the squared difference between the empirical and parametric copula.
Kolmogorov-Smirnov statistic: Measures the maximum absolute difference between the empirical and parametric copula.

A parametric bootstrap procedure is frequently used to simulate the null distribution and calculate the p-value. A high p-value suggests that the null hypothesis cannot be rejected, meaning the copula is a plausible model for the data. Native MQL5 implementations of the Kolmogorov-Smirnov and Cramér-von Mises test statistics for copulae are unavailable, so we have to rely on the model-selection criteria method.

//+------------------------------------------------------------------+
//|                                              CopulaSelection.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Copulas\Bivariate\bivariate_copula.mqh>
#include <ECDF\linear_cdf.mqh>
//--- input parameters
input string   FirstSymbol="XAUUSD";
input string   SecondSymbol="XAUEUR";
input datetime TrainingDataStart=D'2025.01.01';
input ulong    HistorySize=260;
input bool     SaveModel = false;
input string   EcdfModel = "model.ecdf";
input string   CopulaModel = "model.copula";
//---
//string   NormalizingSymbol="EURUSD";
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   vector p_1,p_2,p_3,p_n;
   matrix pdata,pobs;
   if(!p_1.CopyRates(FirstSymbol,PERIOD_CURRENT,COPY_RATES_CLOSE,TrainingDataStart,HistorySize) ||
      !p_2.CopyRates(SecondSymbol,PERIOD_CURRENT,COPY_RATES_CLOSE,TrainingDataStart,HistorySize) ||
      p_1.Size()!=p_2.Size() ||
      !pdata.Resize(p_1.Size(),2) ||
      !pdata.Col(p_1,0) ||
      !pdata.Col(p_2,1))
     {
      Print(" failed to collect and initialize rates matrix ", GetLastError());
      return;
     }
//---
   CLinearCDF qt();
   if(!qt.fit(pdata))
      return;
//---
   pobs = qt.to_quantile(pdata);
//---
   if(SaveModel)
     {
      CFileBin file;
      file.Open(EcdfModel,FILE_WRITE|FILE_BIN|FILE_COMMON);
      if(!qt.save(file.Handle()))
         Print(" Failed to save ", EcdfModel);
      file.Close();
     }
//---
   vector lowest = vector::Zeros(8);
   CBivariateCopula *bcop[8];
//---
   bcop[0] = new CClayton();
   bcop[1] = new CFrank();
   bcop[2] = new CGumbel();
   bcop[3] = new CJoe();
   bcop[4] = new CN13();
   bcop[5] = new CN14();
   bcop[6] = new CGaussian();
   bcop[7] = new CStudent();
//---
   for(uint i = 0; i<bcop.Size(); ++i)
     {
      bool fitted = bcop[i].Fit(pobs.Col(0),pobs.Col(1));
      //---
      if(fitted)
        {
         double ll = bcop[i].Log_likelihood(pobs.Col(0),pobs.Col(1));
         lowest[i] = aic(ll,int(pobs.Rows()));
         Print(EnumToString((ENUM_COPULA_TYPE)bcop[i].Type()));
         Print(" sic ", sic(ll,int(pobs.Rows())));
         Print(" aic ", lowest[i]);
         Print(" hqic ", hqic(ll,int(pobs.Rows())));
        }
     }
//---
   if(SaveModel)
     {
      ulong shift = lowest.ArgMin();
      CFileBin file;
      file.Open(CopulaModel,FILE_WRITE|FILE_BIN|FILE_COMMON);
      if(!bcop[shift].Save(file.Handle()))
         Print("Failed to save ", CopulaModel);
      file.Close();
     }
//---
   for(uint i = 0; i<bcop.Size(); delete bcop[i], ++i);
  }
//+------------------------------------------------------------------+

The script CopulaSelection.ex5 allows users to specify a pair of symbols, a starting date, and the number of bars, that define samples to be used to build candidate copula models. The script will calculate the log-likelihood for each candidate copula model and then compute its information criteria. The script allows for the selected copula model to be saved along with the corresponding empirical cumulative distribution function model. The results are output to MetaTrader 5's journal tab for the user's edification. Here is the output from a run that applied the script to the XAUUSD and XAUEUR symbols.

CopulaSelection script output

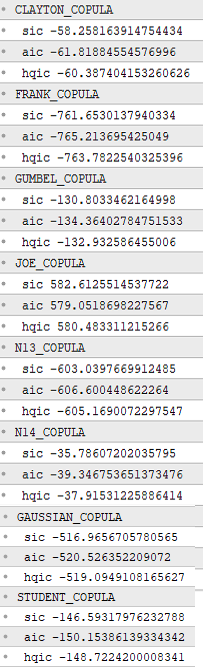
The output from the script clearly indicates that the Frank copula has the lowest information criteria, thereby suggesting it is the best-fit model for the sample dataset. The saved models will be used in an indicator and expert advisor that implements a copula-based pairs strategy.

An example of a copula-based pairs trading strategy

The strategy we will implement is a modified version of the one described in the Journal of Derivatives & Hedge Funds by Liew, R.Q. and Wu, Y., following the approach detailed on Hudson and Thames. It relies on a copula model trained on a sample of price data to capture the dependency between the pairs. The idea is to use conditional probabilities, calculated from the quantiles of current prices, to generate trading signals. The entry logic is as follows.

If C(u_1 | u_2) <= 0.05 and C(u_2 | u_1) >= 0.95, then Symbol 1 is considered undervalued and Symbol 2 is over-valued, generating a simultaneous buy signal for Symbol 1 and sell signal for Symbol 2.
If C(u_1 | u_2) >= 0.95 and C(u_2 | u_1) <= 0.05, then Symbol 2 is considered undervalued and Symbol 1 is over-valued, triggering a simultaneous sell signal for Symbol 1 and buy signal for Symbol 2.

The variables u_1 and u_2 represent the quantiles for Symbol 1 and Symbol 2, respectively. The positions are closed in one of two ways.

The first exit option closes both trades if either conditional probability crosses above an upper exit threshold or crosses below a lower exit threshold.
The second exit option closes both positions only if one of the conditional probabilities crosses over an upper exit threshold and the other simultaneously crosses under a lower exit threshold.

The strategy is implemented out of pure curiosity. Theoretically, it should be obvious that once prices fall or climb beyond the maximum or minimum levels observed in the training data, the model will quickly break down and become irrelevant. The goal in implementing this strategy is to assess whether the copula is able to signal exploitable trading opportunities. To do this effectively, the strategy will be tested over the same period used to train the copula model (in-sample testing). To that end, an indicator was created, called GoldCopulaSignals.ex5. The indicator loads the empirical CDF and copula models saved by the CopulaSelection.ex5 script and displays the conditional probabilities calculated from the quantiles of the XAUEUR and XAUUSD symbols.

//+------------------------------------------------------------------+
//|                                            GoldCopulaSignals.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property indicator_separate_window
#property indicator_buffers 4
#property indicator_plots   4
#property indicator_maximum 1.1
#property indicator_minimum -0.1
#property indicator_level1  0.05
#property indicator_level2  0.5
#property indicator_level3  0.95
#include<Copulas\Bivariate\bivariate_copula.mqh>
#include<ECDF\linear_cdf.mqh>
//--- plot S1
#property indicator_label1  "S1"
#property indicator_type1   DRAW_LINE
#property indicator_color1  clrRed
#property indicator_style1  STYLE_SOLID
#property indicator_width1  1
//--- plot S2
#property indicator_label2  "S2"
#property indicator_type2   DRAW_LINE
#property indicator_color2  clrBlue
#property indicator_style2  STYLE_SOLID
#property indicator_width2  1
//---
#property indicator_label3  "EURGold"
#property indicator_type3   DRAW_NONE

//---
#property indicator_label4  "USDGold"
#property indicator_type4  DRAW_NONE

//--- input parameters
input ENUM_COPULA_TYPE Copulatype = FRANK_COPULA;
input string   CopulaModelName = "model.copula";
input string   ECDFModelName = "model.ecdf";
//---
string   FirstSymbol="XAUUSD";
string   SecondSymbol="XAUEUR";
//--- indicator buffers
double         S1Buffer[];
double         S2Buffer[];
double         S3Buffer[];
double         S4Buffer[];
matrix         mat_;
CLinearCDF* qt;
CBivariateCopula *bcop;
CFileBin savedcop,savedcdf;
//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {

//---
   qt = new CLinearCDF();
//---
   switch(Copulatype)
     {
      case CLAYTON_COPULA:
         bcop = new CClayton();
         break;
      case FRANK_COPULA:
         bcop = new CFrank();
         break;
      case GUMBEL_COPULA:
         bcop = new CGumbel();
         break;
      case JOE_COPULA:
         bcop = new CJoe();
         break;
      case N13_COPULA:
         bcop = new CN13();
         break;
      case N14_COPULA:
         bcop = new CN14();
         break;
      case GAUSSIAN_COPULA:
         bcop = new CGaussian();
         break;
      case STUDENT_COPULA:
         bcop = new CStudent();
         break;
     }
//---
   savedcop.Open(CopulaModelName,FILE_READ|FILE_BIN|FILE_COMMON);
   if(!bcop.Load(savedcop.Handle()))
     {
      Print("Failed to load copula model ", CopulaModelName, " ", GetLastError());
      return INIT_FAILED;
     }
//---
   if((ENUM_COPULA_TYPE)bcop.Type() != Copulatype)
     {
      Print("Invalid copula model. Instantiated copula is ", EnumToString((ENUM_COPULA_TYPE)bcop.Type()),"\n but specified copula in input settings is ", EnumToString(Copulatype));
      return INIT_FAILED;
     }
//---
   savedcop.Close();
//---
   savedcdf.Open(ECDFModelName,FILE_READ|FILE_BIN|FILE_COMMON);
   if(!qt.load(savedcdf.Handle()))
     {
      Print("Failed to load the ECDF model ", ECDFModelName, " ", GetLastError());
      return INIT_FAILED;
     }
//---
   savedcdf.Close();
//---
   mat_.Resize(1,2);
//--- indicator buffers mapping
   SetIndexBuffer(0,S1Buffer,INDICATOR_DATA);
   SetIndexBuffer(1,S2Buffer,INDICATOR_DATA);
   SetIndexBuffer(2,S3Buffer,INDICATOR_DATA);
   SetIndexBuffer(3,S4Buffer,INDICATOR_DATA);
//---
   ArraySetAsSeries(S1Buffer,true);
   ArraySetAsSeries(S2Buffer,true);
   ArraySetAsSeries(S3Buffer,true);
   ArraySetAsSeries(S4Buffer,true);
//---
   PlotIndexSetString(0,PLOT_LABEL,FirstSymbol);
   PlotIndexSetString(1,PLOT_LABEL,SecondSymbol);
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| On deinitialization                                              |
//+------------------------------------------------------------------+
void  OnDeinit(const int  reason)
  {
//---
   if(CheckPointer(qt) == POINTER_DYNAMIC)
      delete qt;
//---
   if(CheckPointer(bcop) == POINTER_DYNAMIC)
      delete bcop;
  }
//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int32_t rates_total,
                const int32_t prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int32_t &spread[])
  {
//---
   int32_t limit;
   if(prev_calculated<=0)
      limit= rates_total-2;
   else
      limit=rates_total-prev_calculated;
//---
   for(int32_t i =limit; i >=0 ; --i)
     {
      mat_[0,0] = iClose(FirstSymbol,PERIOD_CURRENT,i);
      mat_[0,1] = iClose(SecondSymbol,PERIOD_CURRENT,i);
      S3Buffer[i] = mat_[0,1];
      S4Buffer[i] = mat_[0,0];
      mat_ = qt.to_quantile(mat_);
      S1Buffer[i] = bcop.Conditional_Probability(mat_[0][0],mat_[0][1]);
      S2Buffer[i] = bcop.Conditional_Probability(mat_[0][1],mat_[0][0]);
     }
//--- return value of prev_calculated for next call
   return(rates_total);
  }
//+------------------------------------------------------------------+

The screenshot below shows what the indicator looks like (subwindow).

GoldCopulaSignals indicator

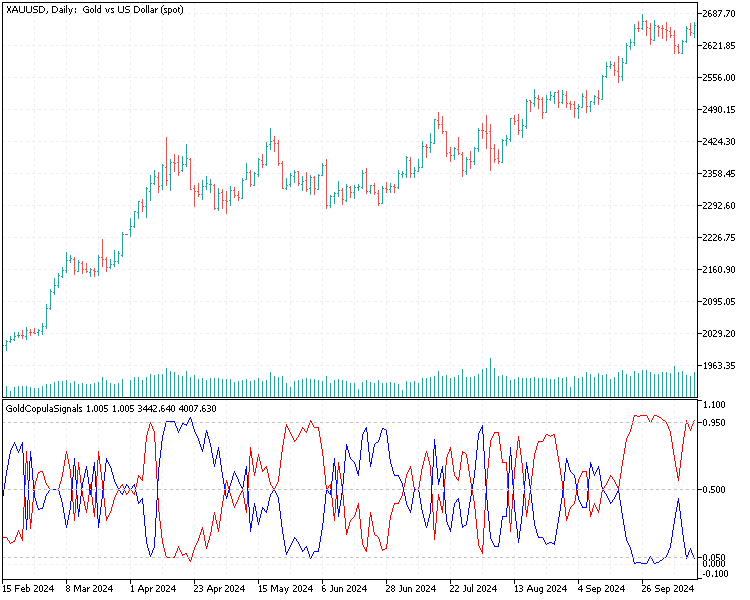
The blue line represents the conditional probabilities of the XAUEUR symbol, while the red line represents the probabilities of the XAUUSD. The strategy itself is implemented as the expert advisor, SimpleCopulaPairsStrategy.ex5.

//+------------------------------------------------------------------+
//|                                    SimpleCopulaPairsStrategy.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <Trade\Trade.mqh>
#include <Trade\SymbolInfo.mqh>
#include <Trade\AccountInfo.mqh>
#include <TimeOptions.mqh>
#include<Copulas\Bivariate\base.mqh>
#resource "\\Indicators\\GoldCopulaSignals.ex5"
//---
#define USDGOLD "XAUUSD"
#define EURGOLD "XAUEUR"
//--- input parameters
enum ENUM_EXIT_RULE
  {
   AND_EXIT=0,//"And exit"
   OR_EXIT//Or exit
  };
//--- input parameters
input ENUM_COPULA_TYPE Copulatype = FRANK_COPULA;
input string   CopulaModelName = "model.copula";
input string   ECDFModelName = "model.ecdf";
input double   OpenThresholdProbability_First = 0.05;
input double   OpenThresholdProbability_Second = 0.95;
input double   UpperExitThresholdProbability = 0.5;
input double   LowerExitThresholdProbability = 0.5;
input ENUM_EXIT_RULE ExitRule = OR_EXIT;
input ulong    SlippagePoints = 10;
input double   TradingLots = 0.01;
input ulong    MagicNumber = 18973984;
double   StopLossPoints = 0.0;
double   TakeProfitPoints = 0.0;
int  OpenShift = 1;
int  CloseShift = 1;
//---
ENUM_DAY_TIME_MINUTES TradeSessionOpen = 6;
ENUM_DAY_TIME_MINUTES TradeSessionClose = 1435;
//--- indicator buffers
CSymbolInfo usd,eur;
//--
double usd_sigs[2],eur_sigs[2];
int indicator_handle;
//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//---
   if(!usd.Name(USDGOLD) || !eur.Name(EURGOLD))
     {
      Print("Symbol info config error, ");
      return INIT_FAILED;
     }
//---
   indicator_handle = INVALID_HANDLE;
   int try
         = 10;
   while(indicator_handle == INVALID_HANDLE && try
            >0)
        {
         indicator_handle = iCustom(NULL,PERIOD_CURRENT,"::Indicators\\GoldCopulaSignals.ex5",Copulatype,CopulaModelName,ECDFModelName);
         --try;
        }
//---
   if(indicator_handle == INVALID_HANDLE)
     {
      Print(" failed to initialize the indicator ", GetLastError());
      return INIT_FAILED;
     }
//---
   return(INIT_SUCCEEDED);
  }
//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//---
  }
//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//---
   datetime sessionopen = iTime(NULL,PERIOD_D1,0) + int(TradeSessionOpen*60);
   datetime sessionclose = iTime(NULL,PERIOD_D1,0) + int(TradeSessionClose*60);
//---
   if(TimeCurrent()<sessionopen || TimeCurrent()>=sessionclose)
      return;
//---
   if(SumMarketOrders(MagicNumber))
     {
      long exit = GetExitSignal(CloseShift);
      if(exit)
        {
         if(CloseAll(MagicNumber,NULL,WRONG_VALUE,SlippagePoints)!=2)
            Print("Failed to close all opened orders ");
        }
     }
   else
     {
      long entry = GetEntrySignal(OpenShift);
      if(entry>0)
        {
         if(!OpenOrder(usd,ORDER_TYPE_BUY,StopLossPoints,TakeProfitPoints,TradingLots,SlippagePoints,MagicNumber))
            Print(" Failed long entry for ", usd.Name());
         if(!OpenOrder(eur,ORDER_TYPE_SELL,StopLossPoints,TakeProfitPoints,TradingLots,SlippagePoints,MagicNumber))
            Print(" Failed short entry for ", eur.Name());
        }
      else
         if(entry<0)
           {
            if(!OpenOrder(eur,ORDER_TYPE_BUY,StopLossPoints,TakeProfitPoints,TradingLots,SlippagePoints,MagicNumber))
               Print(" Failed long entry for ", eur.Name());
            if(!OpenOrder(usd,ORDER_TYPE_SELL,StopLossPoints,TakeProfitPoints,TradingLots,SlippagePoints,MagicNumber))
               Print(" Failed short entry for ", usd.Name());
           }
     }
  }
//+------------------------------------------------------------------+
//| get the entry signal                                             |
//+------------------------------------------------------------------+
long GetEntrySignal(int shift = 1)
  {
   static datetime last;
   if(shift>0)
     {
      if(iTime(NULL,PERIOD_CURRENT,0)<=last)
         return 0;
      else
         last = iTime(NULL,PERIOD_CURRENT,0);
     }
   else
     {
      datetime last = (datetime)MathMax(eur.Time(),usd.Time());
      if(TimeCurrent()<=last)
         return 0;
      //---
      eur.RefreshRates();
      usd.RefreshRates();
     }
//---
   if(CopyBuffer(indicator_handle,0,shift,2,usd_sigs)<2 ||
      CopyBuffer(indicator_handle,1,shift,2,eur_sigs)<2)
     {
      Print(__FUNCTION__, " error copying from indicator buffers ");
      return 0;
     }
   double current_prob_first,current_prob_second;
//---
   current_prob_first = usd_sigs[1];
   current_prob_second = eur_sigs[1];
//---
   if(current_prob_first<=OpenThresholdProbability_First && current_prob_second>=OpenThresholdProbability_Second)
     {
      //Print(__FUNCTION__, " go long ");
      return 1;
     }
   else
      if(current_prob_first>=OpenThresholdProbability_Second && current_prob_second<=OpenThresholdProbability_First)
        {
         //Print(__FUNCTION__, " go short ");
         return -1;
        }
//---
   return 0;
  }
//+------------------------------------------------------------------+
//| get the exit signal                                              |
//+------------------------------------------------------------------+
long GetExitSignal(int shift = 1)
  {
   datetime last = (datetime)MathMax(eur.Time(),usd.Time());

   if(shift>0)
     {
      if(iTime(NULL,PERIOD_CURRENT,0)<=last)
         return 0;
     }
   else
     {
      if(TimeCurrent()<=last)
         return 0;
     }
//---
   eur.RefreshRates();
   usd.RefreshRates();

//---
   if(CopyBuffer(indicator_handle,0,shift,2,usd_sigs)<2 ||
      CopyBuffer(indicator_handle,1,shift,2,eur_sigs)<2)
     {
      Print(__FUNCTION__, " error copying from indicator buffers ");
      return 0;
     }
//---
   double prev_prob_first,prev_prob_second;
   double current_prob_first,current_prob_second;
//---
   prev_prob_first = usd_sigs[0];
   prev_prob_second = eur_sigs[0];
//---
   current_prob_first = usd_sigs[1];
   current_prob_second = eur_sigs[1];
//---
   bool u1_up,u2_dwn,u2_up,u1_dwn;
   u1_up = (prev_prob_first<= LowerExitThresholdProbability && current_prob_first>=UpperExitThresholdProbability);
   u1_dwn = (prev_prob_first>=UpperExitThresholdProbability && current_prob_first<=LowerExitThresholdProbability);
   u2_up = (prev_prob_second<=LowerExitThresholdProbability && current_prob_second>=UpperExitThresholdProbability);
   u2_dwn = (prev_prob_second>=UpperExitThresholdProbability && current_prob_second<=LowerExitThresholdProbability);

   if(ExitRule == AND_EXIT)
     {
      if(u1_up && u2_dwn)
         return -1;
      else
         if(u2_up && u1_dwn)
            return 1;
     }
   else
     {
      if(u1_up || u2_dwn)
         return -1;
      else
         if(u2_up || u1_dwn)
            return 1;
     }
   return 0;
  }
//+------------------------------------------------------------------+
//|Enumerate all market orders                                       |
//+------------------------------------------------------------------+
uint SumMarketOrders(ulong magic_number=ULONG_MAX,const string sym=NULL,const ENUM_POSITION_TYPE ordertype=WRONG_VALUE)
  {
   CPositionInfo posinfo;
//---
   uint count=0;
//---
   for(int i = PositionsTotal()-1; i>-1;--i)
     {
      if(!posinfo.SelectByIndex(i))
         continue;
      if(magic_number<ULONG_MAX && posinfo.Magic()!=long(magic_number))
         continue;
      if(sym!=NULL && posinfo.Symbol()!=sym)
         continue;
      if(ordertype!=WRONG_VALUE && posinfo.PositionType()!=ordertype)
         continue;
      count++;
     }
//---
   return count;
  }
//+------------------------------------------------------------------+
//|Enumerate all market orders                                       |
//+------------------------------------------------------------------+
ENUM_POSITION_TYPE LastOrderType(ulong magic_number=ULONG_MAX)
  {
   CPositionInfo posinfo;
//---
   ENUM_POSITION_TYPE direction_type = WRONG_VALUE;
   string symb = NULL;
//---
   for(int i = PositionsTotal()-1; i>-1;--i)
     {
      if(!posinfo.SelectByIndex(i))
         continue;
      if(magic_number<ULONG_MAX && posinfo.Magic()!=long(magic_number))
         continue;
      symb = posinfo.Symbol();
      direction_type = posinfo.PositionType();
      //---
      switch(direction_type)
        {
         case POSITION_TYPE_BUY:
           {
            if(symb == EURGOLD)
               return POSITION_TYPE_SELL;
            else
               if(symb == USDGOLD)
                  return POSITION_TYPE_BUY;
           }
         case POSITION_TYPE_SELL:
           {
            if(symb == EURGOLD)
               return POSITION_TYPE_BUY;
            else
               if(symb == USDGOLD)
                  return POSITION_TYPE_SELL;
           }
         default:
            return WRONG_VALUE;
        }
     }
//---
   return WRONG_VALUE;
  }
//+------------------------------------------------------------------+
//| Profit                                                           |
//+------------------------------------------------------------------+
double Profit(ulong magic_number=ULONG_MAX)
  {
   CPositionInfo posinfo;
//---
   double profit = 0.0;
//---
   for(int i = PositionsTotal()-1; i>-1;--i)
     {
      if(!posinfo.SelectByIndex(i))
         continue;
      if(magic_number<ULONG_MAX && posinfo.Magic()!=long(magic_number))
         continue;
      profit += (posinfo.Profit() + posinfo.Commission() + posinfo.Swap());
     }
//---
   return profit;
  }
//+------------------------------------------------------------------+
//|Open trade                                                        |
//+------------------------------------------------------------------+
bool OpenOrder(CSymbolInfo &syminfo, ENUM_ORDER_TYPE type,double stoplosspoints=0.0, double takeprofitpoints = 0.0,double lotsize=0.1,ulong slippage=10,ulong magic=12345678,string tradecomment=NULL)
  {
   CTrade trade;
//---
   CAccountInfo accinfo;
//---
   trade.SetExpertMagicNumber(magic); // magic
   trade.SetMarginMode();
   trade.SetDeviationInPoints(slippage);
//---
   if(!trade.SetTypeFillingBySymbol(syminfo.Name()))
     {
      Print(__FUNCTION__," Unknown Type filling mode for ", syminfo.Name());
      return false;
     }
//---
   bool ans=false;
   syminfo.RefreshRates();
   string sy = syminfo.Name();
//---
   double price = (type == ORDER_TYPE_BUY)?syminfo.Ask():syminfo.Bid();
//---
   price = NormalizeDouble(MathAbs(price),syminfo.Digits());
//---
   bool result = false;
//---
   switch(type)
     {
      case ORDER_TYPE_BUY:
         if(accinfo.FreeMarginCheck(sy,type,lotsize,price)<0.0)
           {
            Print("Insufficient funds to open long order ("+sy+"). Free Margin = ", accinfo.FreeMargin());
            return false;
           }
         result = trade.Buy(lotsize,sy,price,(stoplosspoints)?NormalizeDouble(price - MathAbs(stoplosspoints*syminfo.Point()),syminfo.Digits()):0.0,(takeprofitpoints)?NormalizeDouble(price + MathAbs(takeprofitpoints*syminfo.Point()),syminfo.Digits()):0.0,tradecomment);
         break;
      case ORDER_TYPE_SELL:
         if(accinfo.FreeMarginCheck(sy,type,lotsize,price)<0.0)
           {
            Print("Insufficient funds to open short order ("+sy+"). Free Margin = ", accinfo.FreeMargin());
            return false;
           }
         result = trade.Sell(lotsize,sy,price,(stoplosspoints)?NormalizeDouble(price + MathAbs(stoplosspoints*syminfo.Point()),syminfo.Digits()):0.0,(takeprofitpoints)?NormalizeDouble(price - MathAbs(takeprofitpoints*syminfo.Point()),syminfo.Digits()):0.0,tradecomment);
         break;
     }
//---
   if(!result)
      Print(__FUNCTION__, " ", trade.CheckResultRetcodeDescription());
//---
   return result;
  }
//+------------------------------------------------------------------+
//| Close market order                                               |
//+------------------------------------------------------------------+
bool CloseOrder(ulong ticket,ulong magic,ulong slp=10)
  {
//---
   CTrade trade;
//---
   trade.SetExpertMagicNumber(magic);
//---
   bool  result = trade.PositionClose(ticket,slp);
//---
   if(!result)
      Print(trade.CheckResultRetcodeDescription());
//---
   return result;
  }
//+------------------------------------------------------------------+
//|  Close all orders                                                |
//+------------------------------------------------------------------+
uint CloseAll(ulong magic_number=ULONG_MAX,const string sym=NULL,const ENUM_POSITION_TYPE ordertype=WRONG_VALUE,const ulong mslip=10)
  {
   CPositionInfo posinfo;
//---
   uint countclosed=0;
//---
   for(int i = PositionsTotal()-1; i>-1;--i)
     {
      if(!posinfo.SelectByIndex(i))
         continue;
      if(magic_number<ULONG_MAX && posinfo.Magic()!=long(magic_number))
         continue;
      if(sym!=NULL && posinfo.Symbol()!=sym)
         continue;
      if(ordertype!=WRONG_VALUE && posinfo.PositionType()!=ordertype)
         continue;
      if(CloseOrder(posinfo.Ticket(),mslip))
         countclosed++;
     }
//---
   return countclosed;
  }
//+------------------------------------------------------------------+

The entry and exit thresholds are user-adjustable, allowing for evaluation or optimization of these parameters. The EA also allows users to specify their own copula and empirical CDF models for testing. It is important for readers to realize that results shown here may vary with those obtained when replicating this test due to slight differences in symbol rates.

Here are the results.

EA report

Equity Graph

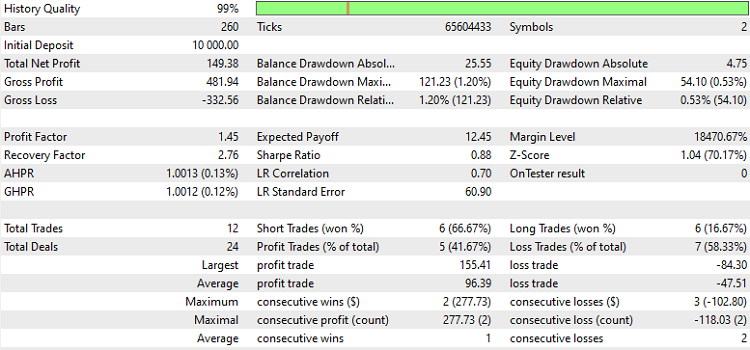
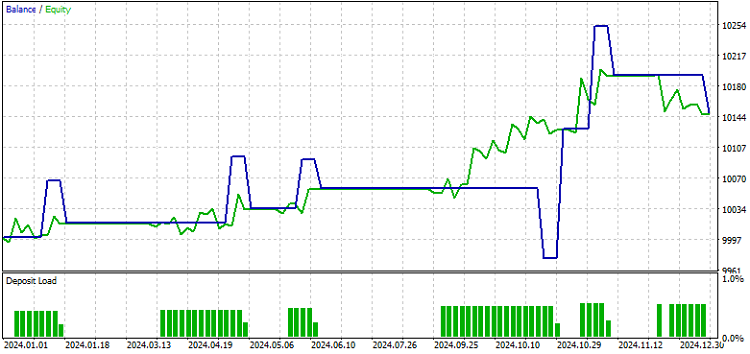
As can be seen, the results are rather favorable, suggesting that there could be merit to this type of strategy. Still, readers must remember that these results are effectively from an in-sample test. We know that the model will break down and the indicator will start providing invalid signals when prices exceed the training range. This is seen from the screenshot below, which shows how the indicator behaves when prices drift towards new highs.

GoldCopulsSignals indicator as model breaks down

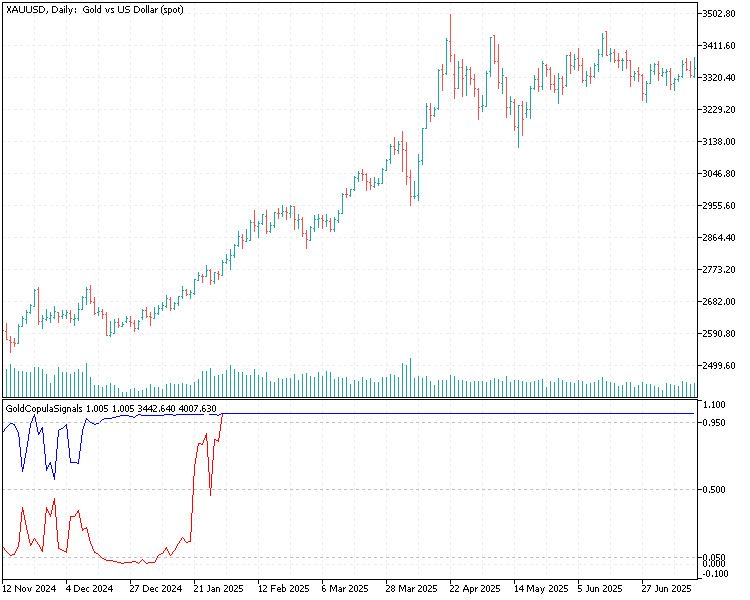
Despite this, the results are encouraging and provide impetus for further study.

Conclusion

The article presented the implementation of common bivariate Archimedean copulae in pure MQL5, namely the Frank, Joe, Gumbel, Clayton, N13, and N14 copulae. We discussed the type of dependency each one is capable of capturing. Later in the article, we saw how copulae can be applied to the formulation of pairs trading strategies. We even implemented a simple one and observed the results. Upcoming articles will explore copulae further. All code referenced in the article is available below.

Files or Folders	Description
MQL5/include/Copulas	This folder holds all the header files that implement all copula models.
MQL5/include/Brent	This folder contains a header file used by the copula implementations.
MQL5/include/ECDF	The folder contains the header files related to the implementation of the empirical cumulative distribution function
MQL5/include/dependence.mqh	This header file contains implementations of concordance measures.
MQL5/include/info_criteria.mqh	This file defines functions for calculating the AIC,HQIC and BIC.
MQL5/include/np.mqh	This header file defines various vector and matrix function utilities.
MQL5/scripts/Concordance.mq5	This script is used to find a pair of symbols with the highest measure of co-movement from a set of candidates.
MQL5/scripts/CopulaSelection.mq5	This script calculates the model selection criteria for all copulae that have been implemented.
MQL5/indicators/GoldCopulaSignals.mq5	This is an indicator used to generate entry and exit signals for the expert advisor described in the text.
MQL5/experts/SimpleCopulaPairsStrategy.mq5	This is expert advisor that implements a copula-based pairs trading strategy.

Attached files |

Download ZIP

BivariateCopulae_Pt2.zip (53.39 KB)

Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.