Algoritmi di ottimizzazione della popolazione: Ottimizzazione del Foraggiamento Batterico (Bacterial Foraging Optimization - BFO)

Contenuto

1. Introduzione
2. Descrizione dell'algoritmo
3. Risultati del test

1. Introduzione

L'algoritmo di Ottimizzazione del Foraggiamento Batterico (BFO) è un'affascinante tecnica di ottimizzazione che può essere utilizzata per trovare soluzioni approssimate a problemi di massimizzazione/minimizzazione di funzioni numeriche estremamente complesse o impossibili. L'algoritmo è ampiamente riconosciuto come un algoritmo di ottimizzazione globale per l'ottimizzazione e il controllo distribuito. BFO si ispira al comportamento sociale di foraggiamento dell'Escherichia coli. Il BFO ha già attirato l'attenzione dei ricercatori per la sua efficacia nella risoluzione di problemi di ottimizzazione del mondo reale che sorgono in diverse aree applicative. La biologia alla base della strategia di foraggiamento di E. coli viene emulata in modo originale e utilizzata come semplice algoritmo di ottimizzazione.

I batteri, come l'E. coli o la salmonella, sono tra gli organismi di maggior successo del pianeta. Questi agili batteri sono dotati di appendici semirigide chiamate flagelli, con le quali si spingono con un movimento rotatorio. Quando tutti i flagelli ruotano in senso antiorario, si crea un effetto elica e il batterio si muove in direzione più o meno rettilinea. In questo caso, il batterio compie un movimento chiamato nuoto. Tutti i flagelli ruotano nella stessa direzione.

I flagelli aiutano il batterio E. coli a rotolare o a nuotare, che sono le due operazioni principali svolte dal batterio durante il foraggiamento. Quando ruotano i flagelli in senso orario, ogni flagello spinge contro la cellula. Quando i flagelli ruotano in direzioni diverse, il batterio si muove. In un ambiente favorevole il batterio si muove con un minor numero di rotolamenti, mentre in un ambiente dannoso si muove frequentemente per trovare il gradiente di nutrienti. Il movimento antiorario dei flagelli aiuta i batteri a nuotare a una velocità molto elevata.

Nell'algoritmo sopra descritto, il comportamento dei batteri è determinato da un meccanismo chiamato chemiotassi batterica, che è una reazione motoria di questi microrganismi ad uno stimolo chimico nell'ambiente. Questo meccanismo consente al batterio di spostarsi verso gli attrattori (spesso sostanze nutritive) e di allontanarsi dai repellenti (sostanze potenzialmente dannose per il batterio). I recettori che rilevano gli attrattori e i repellenti sono situati ai poli del batterio.

A causa delle piccole dimensioni del batterio, non è in grado di cogliere la differenza di concentrazione di sostanze utili e nocive tra i poli. I batteri determinano i gradienti di queste sostanze misurando le variazioni delle loro concentrazioni durante il movimento. La velocità di questo movimento può raggiungere diverse decine di lunghezze di batterio al secondo. Ad esempio, l'Escherichia coli si muove di solito a una velocità pari a 10-20 volte la sua lunghezza al secondo.

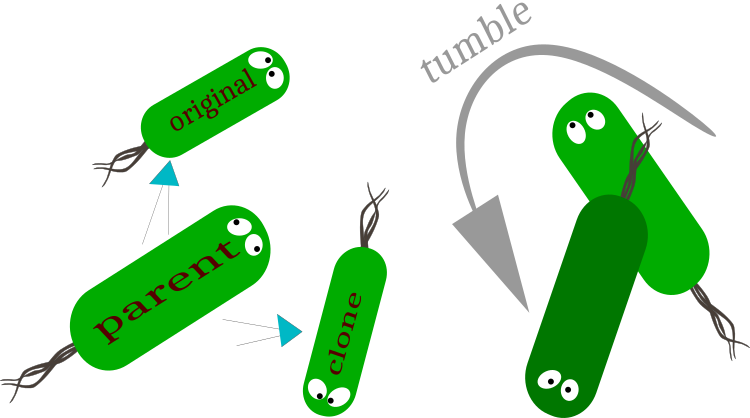
Fig. 1. Riproduzione: divisione in batteri originali (conservazione del vettore di movimento) e clonati (modifica del vettore di movimento).
Rotolamento - un cambiamento nel vettore del movimento del batterio

Se la direzione di movimento scelta dal batterio corrisponde ad un aumento della concentrazione dell'attrattivo (e a una diminuzione della concentrazione del repellente), il tempo che intercorre fino al rotolamento successivo aumenta. A causa delle piccole dimensioni del batterio, il suo movimento è fortemente influenzato dal moto Browniano. Di conseguenza, il batterio si muove in media solo in direzione di sostanze benefiche e lontano da quelle dannose.

Il meccanismo di movimento batterico considerato non è l'unico. Alcuni batteri hanno un solo flagello. Le varianti del movimento del batterio in questo caso forniscono diverse modalità di rotazione e di arresto. Tuttavia, in tutti i casi, se il batterio si muove nella giusta direzione, la durata di tale movimento aumenta. In generale, quindi, la chemiotassi batterica può essere definita come una complessa combinazione di nuoto e rotolamento, che consente ai batteri di rimanere in luoghi ad alta concentrazione di sostanze nutritive e di evitare concentrazioni inaccettabili di sostanze nocive.

Nel contesto di un problema di ottimizzazione del motore di ricerca, la chemiotassi batterica può anche essere interpretata come un meccanismo per ottimizzare l'uso delle risorse alimentari note da parte di un batterio e per cercare nuove aree potenzialmente più preziose.Una popolazione di batteri di sufficiente abbondanza può formare strutture spazio-temporali complesse - l'effetto della formazione di strutture nelle popolazioni batteriche. Questo effetto può essere causato sia dalla chemiotassi sia da molte altre ragioni.

Per alcuni batteri, la formazione di tali strutture è spiegata dalle proprietà regolatrici dei loro prodotti metabolici. Un effetto simile è possibile sulla base dei fenomeni di magnetotassi (sensibilità a un campo magnetico), bioconvezione, geotassi negativa (movimento preferenziale dei microrganismi contro la direzione della gravità) e altri fenomeni. Di norma, i batteri percorrono una distanza maggiore in un ambiente amichevole. Quando ricevono cibo a sufficienza, crescono in lunghezza e, alla giusta temperatura, si rompono al centro, trasformandosi in una copia esatta di se stessi.

Questo fenomeno ha ispirato Passino a introdurre l'evento di riproduzione nel BFO. A causa di improvvisi cambiamenti nell'ambiente o di un attacco, il processo chemiotattico può essere interrotto e il gruppo di batteri può spostarsi in un altro posto. Questo rappresenta un evento di eliminazione e dispersione in una popolazione batterica reale, quando tutti i batteri della regione muoiono oppure quando un gruppo di batteri si disperde in una nuova parte dell'ambiente. Inoltre, le procedure considerate di chemiotassi e riproduzione sono generalmente insufficienti per trovare il massimo globale della funzione obiettivo multiestremale, poiché queste procedure non consentono ai batteri di lasciare i massimi locali di questa funzione che hanno trovato. La procedura di eliminazione e dispersione è stata concepita per superare questa mancanza. Secondo la selezione naturale (sopravvivenza del più adatto), i batteri con scarsa idoneità saranno distrutti e i batteri con idoneità più elevata si riprodurranno.

2. Descrizione dell'algoritmo

La versione canonica di BFO comprende le seguenti fasi principali:

1. Inizializzare una colonia di batteri.
2. Chemiotassi.
3. Sciamatura.
4. Riproduzione.
5. Liquidazione e rimozione.

      
1. Inizializzazione del parametro.
I batteri possono formare complessi schemi spazio-temporali stabili in alcuni nutrienti semisolidi e possono sopravvivere in un ambiente se inizialmente vengono collocati insieme al centro. Inoltre, in determinate condizioni, secernono segnali attrattivi intercellulari in modo da raggrupparsi e proteggersi a vicenda.
2. Chemiotassi.
Le caratteristiche del movimento dei batteri alla ricerca di cibo possono essere determinate in due modi cioè nuotando e ruzzolando insieme, conosciuta come chemiotassi. Si dice che un batterio "nuota" se si muove nella direzione giusta, e "ruzzola" se si muove nella direzione del deterioramento dell'ambiente.

3. Sciamatura.
Affinché i batteri raggiungano il luogo più ricco di cibo, è auspicabile che il batterio ottimale, fino a un certo punto del periodo di ricerca, cerchi di attirare altri batteri in modo che convergano insieme più rapidamente verso il luogo desiderato. A tal fine, alla funzione di costo originale viene aggiunta una funzione di penalizzazione basata sulla distanza relativa di ciascun batterio, dal batterio più adatto alla durata della ricerca. Infine, quando tutti i batteri si uniscono al punto di decisione, questa funzione di penalizzazione diventa zero. L'effetto della sciamatura è che i batteri si riuniscono in gruppi e si muovono in schemi concentrici con un'alta densità di batteri.

4. Riproduzione.
L'insieme iniziale dei batteri, dopo aver superato diversi stadi chemiotattici, raggiungono la fase della riproduzione. In questo caso, il miglior set di batteri viene diviso in due gruppi. La metà più sana viene sostituita dall'altra metà dei batteri, che vengono distrutti a causa della loro minore capacità di trovare cibo. Questo rende la popolazione di batteri costante nel corso dell'evoluzione.

5. Eliminazione e dispersione.
Durante l'evoluzione, può verificarsi un evento improvviso e imprevisto che può cambiare drasticamente il regolare processo di evoluzione e causare l'eliminazione di molti batteri e/o la loro dispersione in un nuovo ambiente. Ironia della sorte, invece di interrompere la normale crescita chemiotattica di un gruppo di batteri, questo evento sconosciuto può portare un nuovo gruppo di batteri più vicino al luogo in cui si trova il cibo. Da un punto di vista generale, l'eliminazione e la dispersione fanno parte del comportamento di una popolazione su lunghe distanze. Se applicato all'ottimizzazione, questo aiuta a ridurre la stagnazione spesso riscontrata in questi algoritmi di ricerca parallela.

La mia implementazione di BFO è leggermente differente dalla versione canonica. Quando prenderò in considerazione sezioni specifiche del codice, mi soffermerò sulle differenze e sulle motivazioni che hanno reso necessarie queste modifiche. In generale, i cambiamenti nell'implementazione non possono essere considerati significativi, quindi non assegnerò il contrassegno "m" (versione modificata) al nome dell'algoritmo. Mi limito a constatare che le modifiche apportate hanno migliorato i risultati.

Poi consideriamo l'algoritmo e il codice che ho implementato.

Fasi dell'algoritmo:

1. Inizializzazione delle colonie batteriche.
2. Misurare la salute dei batteri (fitness).
3. Replicazione?
3.1. Sì Eseguire la replica.
3.2. No. p.4.
4. Vecchio (limite di vita raggiunto)?
4.1. Sì Eseguire un rotolamento (cambiare il vettore di movimento).
4.2. No. p.5.
5. Ci stiamo muovendo nella giusta direzione?
5.1. Sì Continuare a muoversi con lo stesso vettore.
5.2. No. Eseguire un rotolamento (cambiare il vettore di movimento).
6. Misurare la salute (fitness) dei batteri.
7. Continuare da p. 3 fino a quando non viene soddisfatto il criterio di arresto.

Lo schema logico dell'algoritmo è illustrato nella Fig. 1.

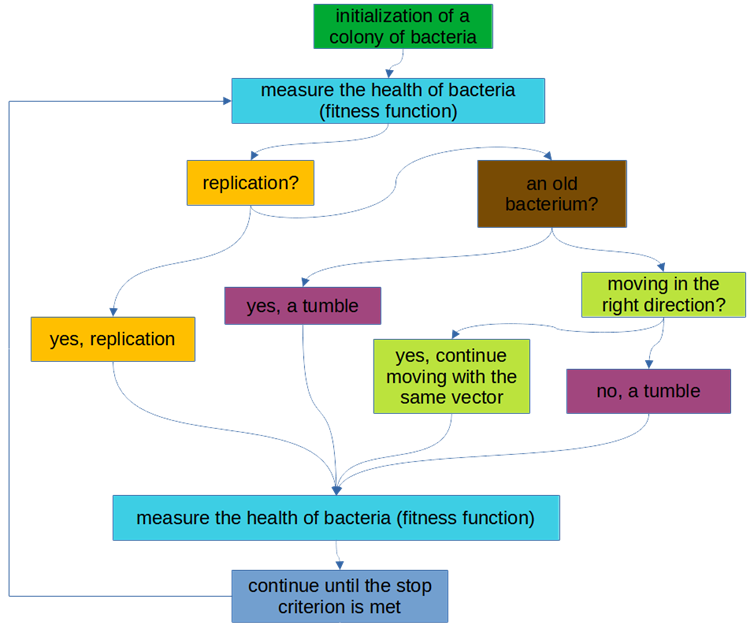
Fig. 2. Diagramma a blocchi dell'algoritmo BFO

Diamo un'occhiata al codice.

Il modo migliore per descrivere un batterio è una struttura contenente array di coordinate e vettori di movimento. Valori di salute e contatore di vita attuali e precedenti del batterio. In sostanza, il contatore della vita è necessario per limitare la quantità di movimento sequenziale in una direzione, a differenza della versione originale, in cui, una volta raggiunto il limite di vita, il batterio viene distrutto e ne viene creato uno nuovo in un punto casuale dello spazio di ricerca. Tuttavia, poiché abbiamo già affrontato questo argomento in articoli precedenti, la creazione di un nuovo agente in un luogo casuale non ha alcun significato pratico e peggiora solo le capacità di ricerca. In questo caso, è meglio creare un nuovo agente nella posizione della soluzione migliore, oppure continuare a muoversi dalla posizione attuale, ma cambiando il vettore di direzione. La seconda opzione ha dato risultati migliori.

La versione canonica utilizza un vettore di movimento costante. Con un numero elevato di vite, questo porterebbe al movimento dei batteri lungo una linea retta nello spazio di ricerca. Se questa linea non passasse per nessun estremo migliore, allora questo processo di movimento rettilineo si verificherebbe all'infinito, ma in questo caso il contatore svolge il ruolo di forzare il rotolamento, che permette al batterio di evitare il movimento rettilineo per tutta la sua vita. Nelle funzioni con aree che non presentano un gradiente, alla fine si arriverà comunque a un punto in cui si potrà iniziare a migliorare la propria fitness.

//——————————————————————————————————————————————————————————————————————————————
struct S_Bacteria
{
  double c  [];   //coordinates
  double v  [];   //vector
  double f;       //current health
  double fLast;   //previous health
  double lifeCNT; //life counter
};
//——————————————————————————————————————————————————————————————————————————————

Dichiariamo la classe dell'algoritmo BFO come C_AO_BFO. La classe contiene la dichiarazione della colonia batterica, i confini dello spazio di ricerca, il valore della soluzione migliore e l'array di coordinate della soluzione migliore. Inoltre, dichiarare i valori costanti dei parametri dell'algoritmo.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BFO
{
  //----------------------------------------------------------------------------
  public: S_Bacteria b     []; //bacteria
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP);   //life counter

  public: void Swimming   ();
  public: void Evaluation ();

  //----------------------------------------------------------------------------
  private: double NewVector (int paramInd);
  private: S_Bacteria bT []; //bacteria
  private: double v      [];
  private: int    ind    [];
  private: double val    [];
  private: int    populationSize; //population size
  private: int    parameters;     //number of optimized parameters
  private: double lambda;         //lambda
  private: double reproduction;   //probability of reproduction
  private: int    lifeCounter;    //life counter
  private: bool   evaluation;

  private: void   Sorting ();
  private: double SeInDiSp             (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI            (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Il metodo pubblico Init () serve per inizializzare le variabili costanti, distribuire le dimensioni degli array e reimpostare i flag e il valore della soluzione migliore.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP)    //life counter
{
  fB = -DBL_MAX;
  evaluation = false;

  parameters      = paramsP;
  populationSize  = populationSizeP;
  lambda          = lambdaP;
  reproduction    = reproductionP;
  lifeCounter     = lifeCounterP;

  ArrayResize (rangeMax,  parameters);
  ArrayResize (rangeMin,  parameters);
  ArrayResize (rangeStep, parameters);
  ArrayResize (v,         parameters);

  ArrayResize (ind,       populationSize);
  ArrayResize (val,       populationSize);

  ArrayResize (b,  populationSize);
  ArrayResize (bT, populationSize);

  for (int i = 0; i < populationSize; i++)
  {
    ArrayResize (b [i].c,  parameters);
    ArrayResize (b [i].v,  parameters);
    b [i].f  = -DBL_MAX;
    b [i].fLast = -DBL_MAX;

    ArrayResize (bT [i].c,  parameters);
    ArrayResize (bT [i].v,  parameters);
  }

  ArrayResize (cB, parameters);
}
//——————————————————————————————————————————————————————————————————————————————

Il primo metodo pubblico che deve essere richiamato a ogni iterazione - Swimming (), o nuoto batterico - include tutta la logica principale dell'algoritmo.

void C_AO_BFO::Swimming ()
{}

Esaminiamo il metodo nel dettaglio. Alla prima iterazione, quando il flag di valutazione è impostato su 'false', spargiamo i batteri sull'intero spazio di ricerca in modo casuale con una distribuzione uniforme. In questa fase, la salute attuale (fitness) e quella precedente sono sconosciute. Assegniamo il valore DBL_MAX alle variabili corrispondenti. Controllare che le coordinate ottenute casualmente non superino i limiti e applicare la fase di modifica dei parametri ottimizzati. A questa iterazione, è necessario impostare un vettore di spostamento individuale per ogni batterio, utilizzando il metodo privato NewVector () (lo considereremo più avanti). Tutti i batteri nuotano uniformemente in avanti e in linea retta con lo stesso vettore individuale finché non si verificano le condizioni per il suo cambiamento.

//----------------------------------------------------------------------------
if (!evaluation)
{
  fB = -DBL_MAX;

  for (int s = 0; s < populationSize; s++)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);

      v [k] = rangeMax [k] - rangeMin [k];

      b [s].v [k] = NewVector (k);

      b [s].f  = -DBL_MAX;
      b [s].fLast = -DBL_MAX;

      b [s].lifeCNT = 0;
    }
  }

  evaluation = true;
}

Nella seconda iterazione e in quelle successive, le operazioni di nuoto, rotazione, replicazione e distruzione dei batteri vengono eseguite quando si raggiunge il limite di vite. La prima nella logica è l'operazione di riproduzione (con la probabilità specificata nei parametri). Implica che la colonia batterica sia ordinata all'iterazione precedente in ordine decrescente di valore di salute.

La riproduzione nell'algoritmo svolge una funzione importante: accelerare la convergenza dell'algoritmo migliorando il "pool genetico" della colonia batterica. L'operazione consiste in una divisione immaginaria dei batteri in due parti, e solo la prima, migliore metà della colonia può dividersi. La prima metà della colonia viene dimezzata, la versione originale del genitore viene collocata nella seconda metà della colonia. Il batterio genitore continuerà a muoversi con lo stesso vettore rispetto al suo clone. Il clone rimane al suo posto nella colonia e gli viene assegnato un nuovo vettore di movimento. Il genitore e il suo clone continueranno a muoversi dal punto dello spazio in cui è avvenuta la divisione.

r = RNDfromCI (0.0, 1.0);

//==========================================================================
if (r < reproduction)
{
  int st = populationSize / 2;
  for (int s = 0; s < st; s++)
  {
    //bacterium original--------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [st + s].v [k] = b [s].v [k];
      b [st + s].c [k] = b [s].c [k] + b [s].v [k];
      b [st + s].c [k] = SeInDiSp (b [st + s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [st + s].fLast = b [s].f;
      b [st + s].lifeCNT++;
    }

    //bacterium clone-------------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT = 0;
    }
  }
}

Se la probabilità di replicazione non è implementata, viene eseguito un controllo per il raggiungimento del limite delle vite batteriche. Nella versione canonica dell'algoritmo, il batterio "vecchio" deve essere distrutto e al suo posto ne deve essere creato uno nuovo in un punto casuale dello spazio di ricerca all'interno dell'elenco dei batteri. Nel caso generale, le operazioni di riproduzione e chemiotassi non sono sufficienti a trovare il massimo globale della funzione fitness multiestremale, poiché
queste procedure non permettono ai batteri di uscire dai minimi locali che hanno trovato. La procedura di liquidazione è stata concepita per ovviare a questa lacuna. Tuttavia, come ha dimostrato la pratica degli esperimenti con questo e altri algoritmi, in questo caso è più efficiente modificare semplicemente il vettore di movimento. Il contatore di vita viene azzerato. Il contatore è un elemento che attiva il cambio di direzione del movimento dopo un determinato numero di passi (vite). Il numero totale di batteri, come risultato della replicazione e dell'eliminazione, rimane costante.

if (b [s].lifeCNT >= lifeCounter)
{
  for (int k = 0; k < parameters; k++)
  {
    b [s].v [k] = NewVector (k);
    b [s].c [k] = b [s].c [k] + b [s].v [k];
    b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    b [s].fLast = b [s].f;
    b [s].lifeCNT = 0;
  }
}

Se il limite di vita non è stato esaurito, allora controlleremo se il batterio si sta muovendo per migliorare il gradiente della funzione di fitness. In altre parole, controlliamo due valori di salute: quello dell'iterazione corrente e quello precedente. Se lo stato di salute è migliorato, il vettore di movimento viene conservato, altrimenti il batterio deve ruzzolare (cambiare il vettore di movimento).

Nella versione canonica, viene eseguito un rigoroso controllo della salute attuale e precedente "maggiore di", mentre nella mia versione viene applicato "maggiore o uguale a", che consente al batterio di continuare a muoversi anche su una sezione completamente "orizzontale" della superficie in esame, dove non esiste un gradiente della funzione di fitness, altrimenti il batterio ruzzolerebbe all'infinito in un punto (non c'è cambiamento di salute, il che significa che non c'è direzione di nuoto). In questa fase, dobbiamo anche verificare che le nuove coordinate ricevute non vadano oltre i confini dello spazio di ricerca.

else
{
  if (b [s].f >= b [s].fLast)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
  else
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
}

NewVector () - è un metodo privato per cambiare il vettore di movimento (ruzzolare). Il metodo viene applicato per ogni coordinata. L'idea qui è semplice: la differenza tra i confini di ricerca per la coordinata v corrispondente viene moltiplicata per un numero casuale r compreso nell'intervallo [-1,0;1,0] e moltiplicato per il fattore di scala lambda (uno dei parametri dell'algoritmo). Il batterio utilizza il vettore di movimento senza modifiche fino all'esaurimento del limite di vite (un nuovo batterio viene creato nello stesso posto, ma con un nuovo vettore di movimento), durante la replicazione (il clone ha un nuovo vettore) e durante il deterioramento della salute (nel tentativo di trovare un nuovo ambiente più favorevole).  

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BFO::NewVector (int paramInd)
{
  double r = RNDfromCI (-1.0, 1.0);
  return lambda * v [paramInd] * r;
}
//——————————————————————————————————————————————————————————————————————————————

Il secondo metodo pubblico Evaluation(), che deve essere eseguito a ogni iterazione, richiama il metodo di ordinamento, controlla gli aggiornamenti della soluzione globale e confronta la salute del miglior batterio nella colonia ordinata con la migliore soluzione trovata.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Evaluation ()
{
  Sorting ();

  if (b [0].f > fB)
  {
    fB = b [0].f;
    ArrayCopy (cB, b [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Risultati del test

Risultati del banco di prova BFO:

2023.01.21 12:52:46.501 Test_AO_BFO (.US500Cash,M1) C_AO_BFO:50;0.01;0.8;100
2023.01.21 12:52:46.501 Test_AO_BFO (.US500Cash,M1) =============================
2023.01.21 12:52:48.451 Test_AO_BFO (.US500Cash,M1) 5 Rastrigin's; Func cicli 10000 risultato: 72.94540549092933
2023.01.21 12:52:48.451 Test_AO_BFO (.US500Cash,M1) Punteggio: 0.90383
2023.01.21 12:52:51.778 Test_AO_BFO (.US500Cash,M1) 25 Rastrigin's; Func cicli 10000 risultato: 54.75744312933767
2023.01.21 12:52:51.778 Test_AO_BFO (.US500Cash,M1) Punteggio: 0.67848
2023.01.21 12:53:21.197 Test_AO_BFO (.US500Cash,M1) 500 Rastrigin's; Func cicli 10000 risultato: 40.668487609790404
2023.01.21 12:53:21.197 Test_AO_BFO (.US500Cash,M1) Punteggio: 0.50391
2023.01.21 12:53:21.197 Test_AO_BFO (.US500Cash,M1) =============================
2023.01.21 12:53:23.211 Test_AO_BFO (.US500Cash,M1) 5 Forest; Func cicli 10000 risultato: 0.8569098398505888
2023.01.21 12:53:23.211 Test_AO_BFO (.US500Cash,M1) Punteggio: 0.48471
2023.01.21 12:53:26.878 Test_AO_BFO (.US500Cash,M1) 25 Forest; Func cicli 10000 risultato: 0.37618151461180294
2023.01.21 12:53:26.878 Test_AO_BFO (.US500Cash,M1) Punteggio: 0.21279
2023.01.21 12:54:22.339 Test_AO_BFO (.US500Cash,M1) 500 Forest; Func cicli 10000 risultato: 0.08748190028975696
2023.01.21 12:54:22.339 Test_AO_BFO (.US500Cash,M1) Punteggio: 0.04948
2023.01.21 12:54:22.339 Test_AO_BFO (.US500Cash,M1) =============================
2023.01.21 12:54:28.849 Test_AO_BFO (.US500Cash,M1) 5 Megacity; Func cicli 10000 risultato: 4.8
2023.01.21 12:54:28.849 Test_AO_BFO (.US500Cash,M1) Punteggio: 0.40000
2023.01.21 12:54:40.089 Test_AO_BFO (.US500Cash,M1) 25 Megacity; Func cicli 10000 risultato: 2.216
2023.01.21 12:54:40.089 Test_AO_BFO (.US500Cash,M1) Punteggio: 0.18467
2023.01.21 12:55:24.640 Test_AO_BFO (.US500Cash,M1) 500 Megacity; Func cicli 10000 risultato: 0.4232
2023.01.21 12:55:24.640 Test_AO_BFO (.US500Cash,M1) Punteggio: 0.03527

È troppo presto per trarre conclusioni univoche. È necessario analizzare prima i risultati in relazione agli altri partecipanti al test.

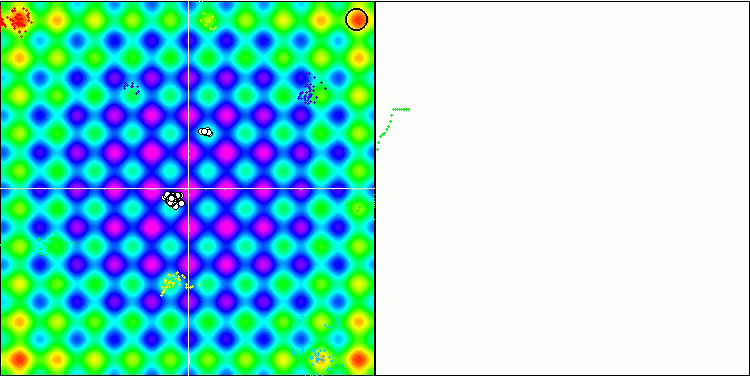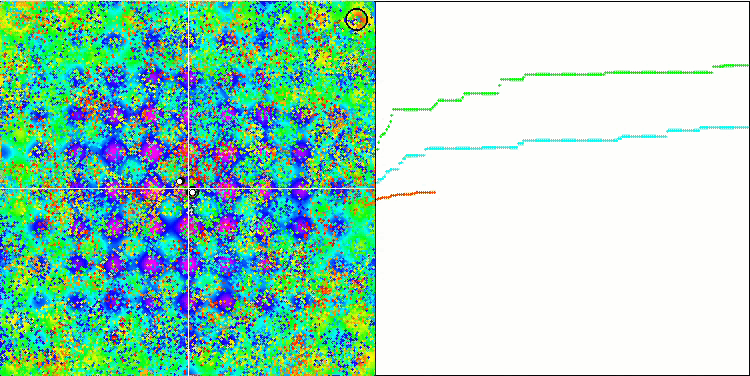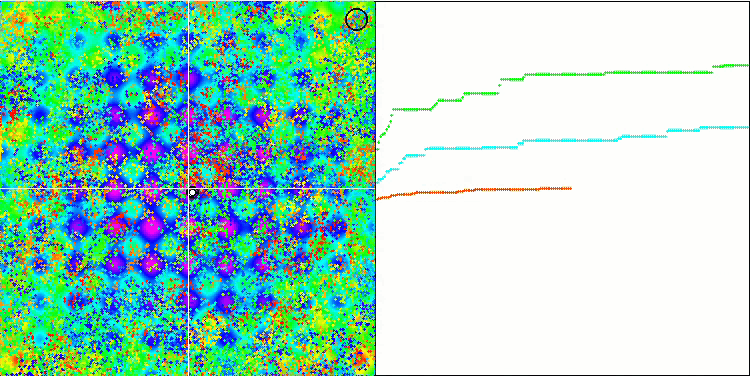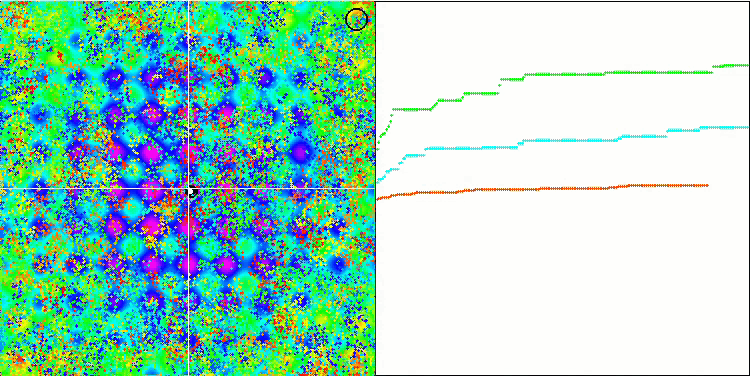
  BFO sulla funzione di test Rastrigin.

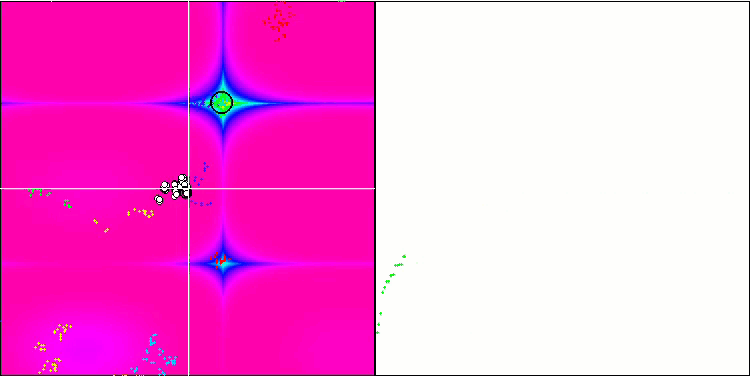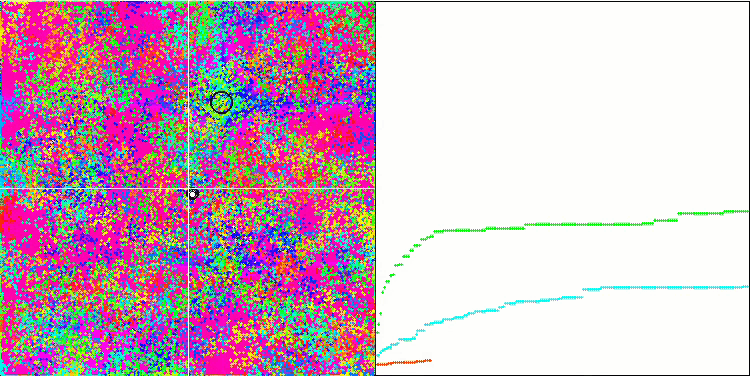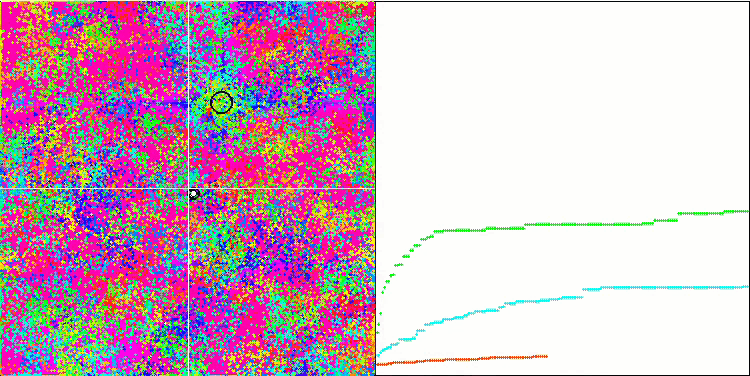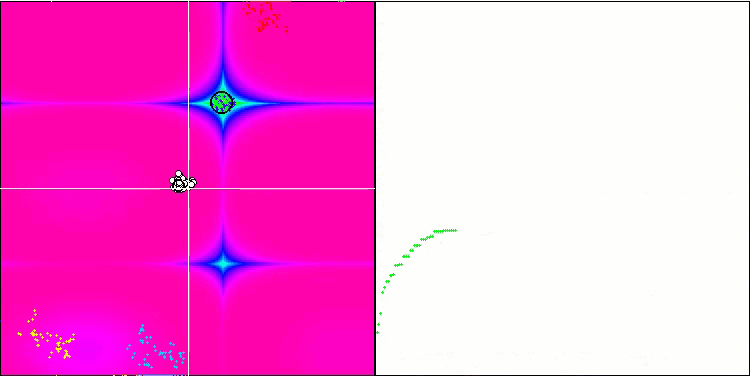
BFO sulla funzione di test Forest.

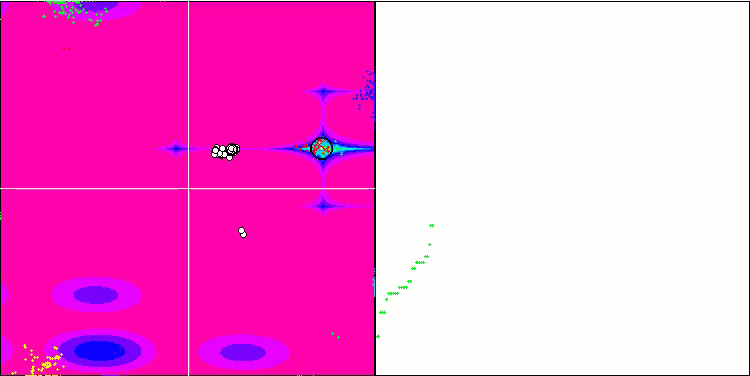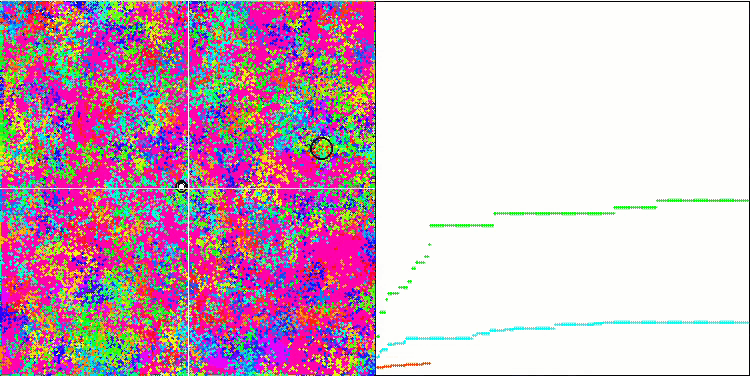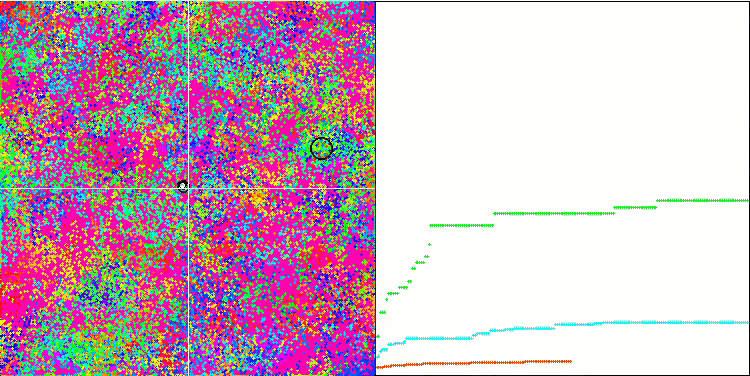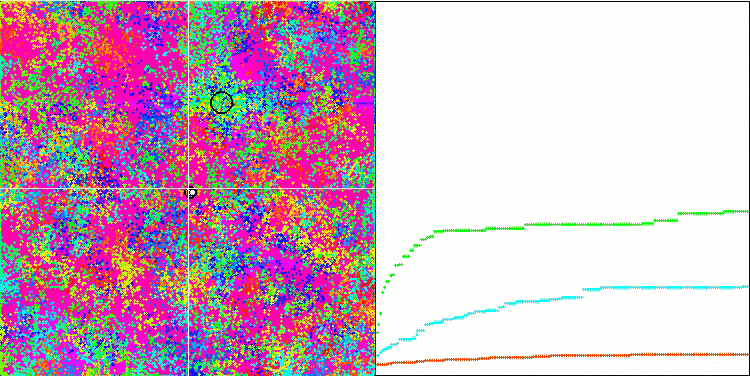
BFO sulla funzione di test Megacity.

Prestiamo attenzione alla visualizzazione del test. L'animazione ha confermato la correttezza della decisione di sostituire il segno "maggiore di" con "maggiore o uguale a" nel nostro algoritmo. Questo ha permesso ai batteri di continuare a muoversi nelle sezioni orizzontali delle funzioni di prova. Ciò è particolarmente evidente nelle funzioni Forest e Megacity. I batteri cercano di andare avanti anche dove non c'è alcun gradiente di funzione. È inoltre necessario notare la capacità di una colonia batterica di dividersi in più colonie separate, visivamente suddivise in estremi locali distinti, che può essere considerata inequivocabilmente una caratteristica positiva, sebbene l'algoritmo non contenga alcun metodo logico per la formazione di colonie secondarie. In generale, si nota un movimento uniforme dei batteri nello spazio di ricerca senza tentativi di salti bruschi in nessuna delle direzioni, il che si spiega con un movimento incrementale uniforme - la chemiotassi.

AO	Descrizione	Rastrigin			Finale Rastrigin	Forest			Finale Forest	Megacity (discreta)			Finale Megacity	Risultato finale
		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)		10 parametri (5 F)	50 parametri (25 F)	1000 parametri (500 F)
IWO	Ottimizzazione delle piante infestanti	1.00000	1.00000	0.33519	2.33519	0.79937	0.46349	0.41071	1.67357	0.75912	0.44903	0.94088	2.14903	100.000
ACOm	Ottimizzazione della colonia di formiche M	0.36118	0.26810	0.17991	0.80919	1.00000	1.00000	1.00000	3.00000	1.00000	1.00000	0.10959	2.10959	95.996
COAm	Algoritmo di ottimizzazione a cucù M	0.96423	0.69756	0.28892	1.95071	0.64504	0.34034	0.21362	1.19900	0.67153	0.34273	0.45422	1.46848	74.204
FAm	Algoritmo della lucciola M	0.62430	0.50653	0.18102	1.31185	0.55408	0.42299	0.64360	1.62067	0.21167	0.28416	1.00000	1.49583	71.024
BA	Algoritmo del pipistrello	0.42290	0.95047	1.00000	2.37337	0.17768	0.17477	0.33595	0.68840	0.15329	0.07158	0.46287	0.68774	59.650
ABC	Colonia di api artificiali	0.81573	0.48767	0.22588	1.52928	0.58850	0.21455	0.17249	0.97554	0.47444	0.26681	0.35941	1.10066	57.237
BFO	ottimizzazione del foraggiamento batterico	0.70129	0.46155	0.11627	1.27911	0.41251	0.26623	0.26695	0.94569	0.42336	0.34491	0.50973	1.27800	55.516
FSS	Ricerca del banco di pesci	0.48850	0.37769	0.11006	0.97625	0.07806	0.05013	0.08423	0.21242	0.00000	0.01084	0.18998	0.20082	20.109
PSO	Ottimizzazione dello sciame di particelle	0.21339	0.12224	0.05966	0.39529	0.15345	0.10486	0.28099	0.53930	0.08028	0.02385	0.00000	0.10413	14.232
RND	Casuale	0.17559	0.14524	0.07011	0.39094	0.08623	0.04810	0.06094	0.19527	0.00000	0.00000	0.08904	0.08904	8.142
GWO	Ottimizzazione del lupo grigio	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.00000	0.18977	0.04119	0.01802	0.24898	1.000

È il momento di analizzare i risultati del test. BFO si trova a metà della tabella di valutazione con un punteggio complessivo di poco superiore a 55 nell'attuale elenco degli algoritmi partecipanti. I risultati non sono impressionanti, ma non sono neanche male. In particolare, sono stati ottenuti buoni risultati sulla funzione Rastrigin con 10 variabili. Nel caso di 50 e 1000 variabili, i risultati sono sensibilmente peggiori. Inoltre, l'algoritmo non ha ottenuto buoni risultati con la funzione Forest. Il comportamento relativamente buono della funzione Megacity discreta è sorprendente, poiché l'algoritmo non prevede meccanismi per lavorare su tali funzioni. Inoltre, la scalabilità è buona rispetto ad altri algoritmi (test con 1000 parametri Megacity).

Il BFO è un campo scientifico con un'ampia gamma di possibilità. Ci sono diversi aspetti del foraggiamento batterico e di quello animale in generale che possono essere modellati per migliorare le prestazioni di ottimizzazione. Per l'algoritmo BFO, l'adattamento automatico dei parametri di controllo può essere di particolare importanza, dato che i parametri sono numerosi, e può fornire prestazioni migliori, il che è un motivo per ulteriori esperimenti.

Il BFO presenta una serie di vantaggi, tra cui la bassa sensibilità ai valori iniziali delle coordinate durante l'inizializzazione e la scelta dei parametri, la buona affidabilità, la semplicità della logica, la facilità di implementazione, la possibilità di parallelizzazione e la ricerca globale. Pertanto, l'algoritmo BFO viene utilizzato per risolvere un'ampia gamma di problemi di ottimizzazione. Tuttavia, il BFO presenta anche una serie di svantaggi, tra cui la lentezza della convergenza, l'impossibilità di superare l’optima locale in alcuni casi e una lunghezza di passo fissa. Il BFO è metaeuristico, cioè è semplicemente un quadro concettuale che può essere utilizzato per sviluppare modifiche agli algoritmi. La versione di BFO che ho presentato qui è solo una delle tante possibilità e deve essere vista come un punto di partenza per la sperimentazione, piuttosto che come ultima parola sull'argomento.

Di seguito è riportato l'istogramma dei risultati del test dell'algoritmo.

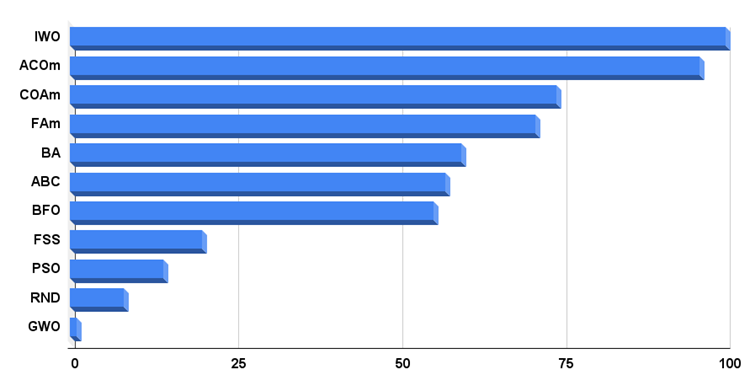
Fig. 3. Istogramma dei risultati finali degli algoritmi di test

Conclusioni sulle proprietà dell'algoritmo di Ottimizzazione del Foraggiamento Batterico (BFO):

Pro:
1. Alta velocità
2. Logica semplice.
3. Convergenza in tutte le iterazioni, anche se lentamente.

Contro:
1. Convergenza lenta.
2. Nessun metodo per uscire dagli estremi locali.