Algorithmes d'optimisation de la population : Optimisation de la Recherche Bactérienne (Bacterial Foraging Optimization, BFO)

Sommaire

1. Introduction
2. Description de l'algorithme
3. Résultats des tests

1. Introduction

L'algorithme Bacterial Foraging Optimization (BFO) est une technique d'optimisation fascinante qui peut être utilisée pour trouver des solutions approximatives à des problèmes de maximisation/minimisation de fonctions numériques extrêmement complexes ou impossibles à résoudre. L'algorithme est largement reconnu comme un algorithme d'optimisation globale pour l'optimisation et le contrôle distribués. BFO s'inspire du comportement social de recherche de nourriture d'Escherichia coli. Le BFO a déjà attiré l'attention des chercheurs en raison de son efficacité à résoudre les problèmes d'optimisation du monde réel qui se posent dans plusieurs domaines d'application. La biologie qui sous-tend la stratégie de recherche de nourriture d'E. coli est émulée de manière originale et utilisée comme un simple algorithme d'optimisation.

Les bactéries, telles que E. coli ou les salmonelles, comptent parmi les organismes les plus performants de la planète. Ces bactéries agiles possèdent des appendices semi-rigides appelés flagelles, avec lesquels elles se propulsent par un mouvement de torsion. Lorsque tous les flagelles tournent dans le sens inverse des aiguilles d'une montre, un effet d'hélice est créé et la bactérie se déplace dans une direction plus ou moins rectiligne. Dans ce cas, la bactérie effectue un mouvement appelé nage. Tous les flagelles tournent dans le même sens.

Les flagelles permettent à la bactérie E. coli de culbuter ou de nager, qui sont les deux principales opérations effectuées par la bactérie lors de la recherche de nourriture. En tournant les flagelles dans le sens des aiguilles d'une montre, chaque flagelle pousse contre la cellule. Lorsque les flagelles tournent dans des directions différentes, la bactérie bascule. La bactérie se déplace avec moins de culbutes dans un environnement favorable, alors que dans un environnement nocif, elle culbute fréquemment pour trouver le gradient de nutriments. Le mouvement des flagelles dans le sens inverse des aiguilles d'une montre permet à la bactérie de nager à une vitesse très élevée.

Dans l'algorithme ci-dessus, le comportement des bactéries est déterminé par un mécanisme appelé chimiotaxie bactérienne, qui est une réaction motrice de ces micro-organismes à un stimulus chimique dans l'environnement. Ce mécanisme permet à la bactérie de se déplacer vers les attracteurs (le plus souvent des nutriments) et de s'éloigner des répulsifs (substances potentiellement nocives pour la bactérie). Les récepteurs qui détectent les attractifs et les répulsifs sont situés aux pôles de la bactérie.

En raison de sa petite taille, la bactérie n'est pas en mesure de capter la différence de concentration des substances utiles et nocives entre les pôles. Les bactéries déterminent les gradients de ces substances en mesurant les variations de leurs concentrations au cours de leurs déplacements. La vitesse de ce mouvement peut atteindre plusieurs dizaines de longueurs de bactéries par seconde. Par exemple, Escherichia coli se déplace généralement à une vitesse de 10 à 20 fois sa longueur par seconde.

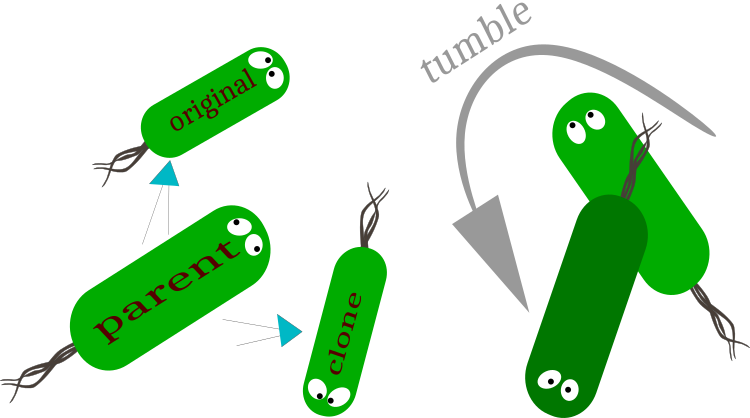
Fig. 1 : Réplication : division en bactéries originales (conservation du vecteur de mouvement) et clonées (modification du vecteur de mouvement).
Tumble - un changement dans le vecteur de mouvement de la bactérie

Si la direction de mouvement choisie par la bactérie correspond à une augmentation de la concentration de l'attractif (une diminution de la concentration du répulsif), alors le temps jusqu'à la prochaine culbute augmente. En raison de la petite taille de la bactérie, son mouvement est fortement influencé par le mouvement brownien. Par conséquent, la bactérie ne se déplace en moyenne que vers les substances bénéfiques et à l'écart des substances nocives.

Le mécanisme de mouvement bactérien envisagé n'est pas le seul. Certaines bactéries ont un seul flagelle. Les variantes du mouvement de la bactérie dans ce cas fournissent différents modes de rotation et d'arrêt. Mais dans tous les cas, si la bactérie se déplace dans la bonne direction, la durée de ce mouvement augmente. Ainsi, en général, la chimiotaxie bactérienne peut être définie comme une combinaison complexe de natation et de culbute, qui permet aux bactéries de rester dans des endroits à forte concentration de nutriments et d'éviter des concentrations inacceptables de substances nocives.

Dans le contexte d'un problème d'optimisation de moteur de recherche, la chimiotaxie bactérienne peut également être interprétée comme un mécanisme d'optimisation de l'utilisation des ressources alimentaires connues par une bactérie et de recherche de nouvelles zones potentiellement plus précieuses. Une population de bactéries suffisamment abondante peut former des structures spatio-temporelles complexes - l'effet de la formation de structures dans les populations bactériennes. Cet effet peut être dû à la fois à la chimiotaxie et à de nombreuses autres raisons.

Pour certaines bactéries, la formation de telles structures s'explique par les propriétés régulatrices de leurs produits métaboliques. Un effet similaire est possible sur la base des phénomènes de magnéto-taxie (sensibilité à un champ magnétique), de bio-convection, de géo-taxie négative (mouvement préférentiel des micro-organismes contre la direction de la gravité) et d'autres phénomènes. En règle générale, les bactéries parcourent une plus grande distance dans un environnement favorable. Lorsqu'ils reçoivent suffisamment de nourriture, ils s'allongent et, à la bonne température, se brisent en leur milieu, se transformant en une réplique exacte d'eux-mêmes.

Ce phénomène a incité Passino à introduire l'événement de reproduction dans le BFO. En raison de changements soudains dans l'environnement ou d'une attaque, le processus chimiotactique peut être perturbé et le groupe de bactéries peut se déplacer vers un autre endroit. Cela représente un événement d'élimination et de dispersion dans une population bactérienne réelle, lorsque toutes les bactéries de la région meurent ou qu'un groupe de bactéries se disperse dans une nouvelle partie de l'environnement. Les procédures de chimiotaxie et de reproduction envisagées sont également généralement insuffisantes pour trouver le maximum global de la fonction objectif multi-extrêmes, puisque ces procédures ne permettent pas aux bactéries de quitter les maxima locaux de cette fonction qu'elles ont trouvés. La procédure d'élimination et de dispersion est conçue pour remédier à cette lacune. Selon la sélection naturelle (survie du plus apte), les bactéries de faible aptitude seront détruites et les bactéries d'aptitude supérieure se reproduiront.

2. Description de l'algorithme

La version canonique de BFO comprend les principales étapes suivantes :

1. Initialisation d’une colonie de bactéries
2. Chimiotaxie
3. Essaimage
4. Reproduction
5. Elimination et dispersion

      
1. Initialisation du paramètre
Les bactéries peuvent former des motifs spatio-temporels complexes et stables dans certains nutriments semi-solides, et elles peuvent survivre dans un environnement si elles sont initialement placées ensemble au centre. Dans certaines conditions, elles sécrètent également des signaux d'attraction intercellulaires afin de se regrouper et de se protéger les uns les autres.
2. Chimiotaxie
Les caractéristiques du mouvement des bactéries à la recherche de nourriture peuvent être déterminées de deux manières, à savoir la nage et la culbute ensemble, ce qui est connu sous le nom de chimiotaxie. On dit qu'une bactérie "nage" si elle va dans la bonne direction, et qu'elle "dégringole" si elle va dans le sens de la détérioration de l'environnement.

3. Essaimage
Pour que les bactéries atteignent l'endroit le plus riche en nourriture, il est souhaitable que la bactérie optimale, jusqu'à un certain moment de la période de recherche, essaie d'attirer d'autres bactéries afin qu'elles convergent ensemble plus rapidement vers l'endroit désiré. Pour ce faire, une fonction de pénalité est ajoutée à la fonction de coût originale en fonction de la distance relative de chaque bactérie par rapport à la bactérie la plus adaptée à cette durée de recherche. Enfin, lorsque toutes les bactéries rejoignent le point de décision, cette fonction de pénalité devient nulle. L'effet de l'essaimage est que les bactéries se rassemblent en groupes et se déplacent en motifs concentriques avec une forte densité de bactéries.

4. Reproduction
Le groupe initial de bactéries, après avoir franchi plusieurs étapes de chimiotactisme, atteint le stade de la reproduction. Ici, le meilleur ensemble de bactéries est divisé en 2 groupes. La moitié la plus saine est remplacée par l'autre moitié des bactéries, qui sont détruites en raison de leur moindre capacité à trouver de la nourriture. La population de bactéries est donc constante au cours de l'évolution.

5. Élimination et dispersion
Au cours de l'évolution, un événement soudain et imprévu peut se produire et modifier radicalement le processus d'évolution et entraîner l'élimination de nombreuses bactéries et/ou leur dispersion dans un nouvel environnement. Paradoxalement, au lieu de perturber la croissance chimiotactique normale d'un groupe de bactéries, cet événement inconnu pourrait placer un nouveau groupe de bactéries plus près de l'endroit où se trouve la nourriture. D'un point de vue général, l'élimination et la dispersion font partie du comportement d'une population sur de longues distances. Appliqué à l'optimisation, cela permet de réduire la stagnation souvent observée dans les algorithmes de recherche parallèle.

Mon implémentation de BFO est légèrement différente de la version canonique. Lorsque j'examinerai des sections spécifiques du code, je m'attarderai sur les différences ainsi que sur la justification de la nécessité de ces changements. En général, les changements dans la mise en œuvre ne peuvent pas être considérés comme significatifs, c'est pourquoi je n'attribuerai pas le marqueur "m" (version modifiée) au nom de l'algorithme. Je me contenterai de noter que les changements mis en œuvre ont permis d'améliorer les résultats.

Considérons ensuite l'algorithme et le code que j'ai mis en œuvre.

Étapes de l'algorithme :

1. Initialisation de la colonie de bactéries
2. Mesure de la santé des bactéries (fitness)
3. Réplication ?
3.1. Oui. Effectuer la réplication.
3.2. Non. Continuer avec 4.
4. Vieille (limite de vie atteinte) ?
4.1. Oui. Effectuer une culbute (changer le vecteur de mouvement).
4.2. Non. Continuer avec 5.
5. Dans la bonne direction ?
5.1. Oui. Continuer à se déplacer avec le même vecteur.
5.2. Non. Effectuer une culbute (changer le vecteur de mouvement).
6. Mesurer la santé des bactéries (fitness)
7. Continuer à partir 3 jusqu'à ce que le critère d'arrêt soit atteint.

Le schéma logique de l'algorithme est présenté dans la figure 1.

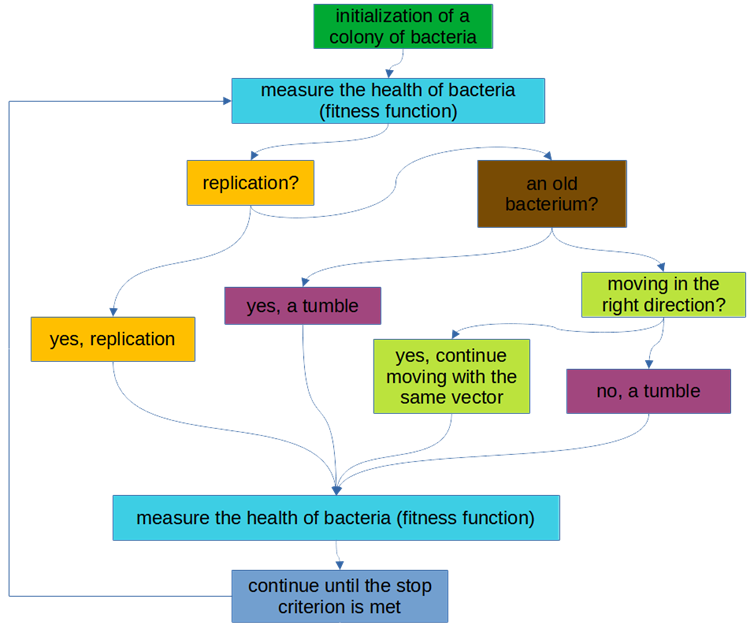
Figure 2 : Schéma logique de l'algorithme BFO

Jetons un coup d'œil au code.

La meilleure façon de décrire une bactérie est une structure contenant des tableaux de coordonnées et des vecteurs de mouvement, les valeurs de santé actuelles et précédentes de la bactérie et son compteur de vie. En substance, le compteur de vie est nécessaire pour limiter la quantité de mouvements séquentiels dans une direction, contrairement à la version originale, dans laquelle, lorsque la limite de vie est atteinte, la bactérie est détruite et une nouvelle est créée à un endroit aléatoire de l'espace de recherche. Mais comme nous avons déjà abordé ce sujet dans des articles précédents, la création d'un nouvel agent à un endroit aléatoire n'a aucune signification pratique et ne fait qu'affaiblir les capacités de recherche. Dans ce cas, il est préférable de créer un nouvel agent à l'emplacement de la meilleure solution ou de continuer à se déplacer à partir de l'emplacement actuel, mais en changeant le vecteur de direction. La deuxième option a donné de meilleurs résultats.

La version canonique utilise un vecteur de mouvement constant. Avec un grand nombre de vies, cela conduirait au déplacement des bactéries le long d'une ligne droite dans l'espace de recherche. Si cette ligne ne passait par aucun extremum meilleur, alors ce processus de mouvement rectiligne se produirait à l'infini. Mais ici le compteur joue le rôle d'un culbuto forcé, ce qui permet à la bactérie d'éviter le mouvement rectiligne tout au long de sa vie. Sur les fonctions dont les zones n'ont pas de gradient, elle aboutira toujours à un endroit où elle pourra commencer à améliorer sa condition physique.

//——————————————————————————————————————————————————————————————————————————————
struct S_Bacteria
{
  double c  [];   //coordinates
  double v  [];   //vector
  double f;       //current health
  double fLast;   //previous health
  double lifeCNT; //life counter
};
//——————————————————————————————————————————————————————————————————————————————

Déclarons la classe C_AO_BFO de l'algorithme BFO. La classe contient la déclaration de la colonie de bactéries, les limites de l'espace de recherche, la valeur de la meilleure solution et le tableau des coordonnées de la meilleure solution. Déclarons également des valeurs constantes pour les paramètres de l'algorithme.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BFO
{
  //----------------------------------------------------------------------------
  public: S_Bacteria b     []; //bacteria
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP);   //life counter

  public: void Swimming   ();
  public: void Evaluation ();

  //----------------------------------------------------------------------------
  private: double NewVector (int paramInd);
  private: S_Bacteria bT []; //bacteria
  private: double v      [];
  private: int    ind    [];
  private: double val    [];
  private: int    populationSize; //population size
  private: int    parameters;     //number of optimized parameters
  private: double lambda;         //lambda
  private: double reproduction;   //probability of reproduction
  private: int    lifeCounter;    //life counter
  private: bool   evaluation;

  private: void   Sorting ();
  private: double SeInDiSp             (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI            (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

La méthode publique Init() est destinée à initialiser les variables constantes, à répartir la taille des tableaux et à réinitialiser les flags et la valeur de la meilleure solution.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP)    //life counter
{
  fB = -DBL_MAX;
  evaluation = false;

  parameters      = paramsP;
  populationSize  = populationSizeP;
  lambda          = lambdaP;
  reproduction    = reproductionP;
  lifeCounter     = lifeCounterP;

  ArrayResize (rangeMax,  parameters);
  ArrayResize (rangeMin,  parameters);
  ArrayResize (rangeStep, parameters);
  ArrayResize (v,         parameters);

  ArrayResize (ind,       populationSize);
  ArrayResize (val,       populationSize);

  ArrayResize (b,  populationSize);
  ArrayResize (bT, populationSize);

  for (int i = 0; i < populationSize; i++)
  {
    ArrayResize (b [i].c,  parameters);
    ArrayResize (b [i].v,  parameters);
    b [i].f  = -DBL_MAX;
    b [i].fLast = -DBL_MAX;

    ArrayResize (bT [i].c,  parameters);
    ArrayResize (bT [i].v,  parameters);
  }

  ArrayResize (cB, parameters);
}
//——————————————————————————————————————————————————————————————————————————————

La première méthode publique qui doit être appelée à chaque itération - Swimming(), ou nage de la bactérie, comprend toute la logique principale de l'algorithme.

void C_AO_BFO::Swimming ()
{}

Examinons la méthode en détail. À la première itération, lorsque le flag d'évaluation est "false", nous dispersons les bactéries sur l'ensemble de l'espace de recherche de manière aléatoire avec une distribution uniforme. À ce stade, l'état de santé actuel et l'état de santé précédent sont inconnus. Attribuons la valeur DBL_MAX aux variables correspondantes. Vérifions que les coordonnées obtenues de manière aléatoire ne dépassent pas les limites et appliquons l'étape de modification des paramètres optimisés. A cette itération, il est nécessaire de définir un vecteur de déplacement individuel pour chaque bactérie en utilisant la méthode privée NewVector() (je l'examinerai plus loin). Toutes les bactéries nagent uniformément vers l'avant et en ligne droite avec le même vecteur individuel jusqu'à ce que les conditions de son changement soient réunies.

//----------------------------------------------------------------------------
if (!evaluation)
{
  fB = -DBL_MAX;

  for (int s = 0; s < populationSize; s++)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);

      v [k] = rangeMax [k] - rangeMin [k];

      b [s].v [k] = NewVector (k);

      b [s].f  = -DBL_MAX;
      b [s].fLast = -DBL_MAX;

      b [s].lifeCNT = 0;
    }
  }

  evaluation = true;
}

Lors de la deuxième itération et des itérations suivantes, les opérations de nage, de culbute, de réplication et de destruction des bactéries sont effectuées lorsque la limite de vies est atteinte. Le premier élément de la logique est l'opération de reproduction (avec la probabilité spécifiée dans les paramètres). Cela signifie que la colonie bactérienne est triée à l'itération précédente dans l'ordre décroissant de sa valeur de santé.

La reproduction dans l'algorithme remplit une fonction importante : elle accélère la convergence de l'algorithme en améliorant le "patrimoine génétique" de la colonie bactérienne. L'opération consiste en une division imaginaire des bactéries en 2 parties, et seule la première moitié de la colonie, la meilleure, est autorisée à se diviser. La première moitié de la colonie est divisée en deux, la version parentale originale est placée dans la seconde moitié de la colonie. La bactérie mère continuera à se déplacer avec le même vecteur que son clone. Le clone reste à sa place dans la colonie et un nouveau vecteur de mouvement lui est attribué. Le parent et son clone continueront à se déplacer à partir du point de l'espace où la division s'est produite.

r = RNDfromCI (0.0, 1.0);

//==========================================================================
if (r < reproduction)
{
  int st = populationSize / 2;
  for (int s = 0; s < st; s++)
  {
    //bacterium original--------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [st + s].v [k] = b [s].v [k];
      b [st + s].c [k] = b [s].c [k] + b [s].v [k];
      b [st + s].c [k] = SeInDiSp (b [st + s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [st + s].fLast = b [s].f;
      b [st + s].lifeCNT++;
    }

    //bacterium clone-------------------------------------------------------
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT = 0;
    }
  }
}

Si la probabilité de réplication n'est pas mise en œuvre, une vérification de l'atteinte de la limite de vie des bactéries est effectuée. Dans la version canonique de l'algorithme, l'"ancienne" bactérie doit être détruite et une nouvelle doit être créée à sa place à un endroit aléatoire de l'espace de recherche dans la liste des bactéries. Dans le cas général, les opérations de reproduction et de chimiotaxie ne suffisent pas à trouver le maximum global de la fonction de fitness multi-extrêmes, puisque
ces procédures ne permettent pas aux bactéries de quitter les minima locaux qu'elles ont trouvés. La procédure de liquidation est conçue pour remédier à cette lacune. Mais comme l'ont montré les expériences menées avec cet algorithme entre autres, il est plus efficace dans ce cas de modifier simplement le vecteur de mouvement. Le compteur de vies est remis à zéro. Le compteur est un déclencheur de changement de direction du mouvement après un nombre donné de pas (vies). Le nombre total de bactéries résultant de la réplication et de l'élimination reste constant.

if (b [s].lifeCNT >= lifeCounter)
{
  for (int k = 0; k < parameters; k++)
  {
    b [s].v [k] = NewVector (k);
    b [s].c [k] = b [s].c [k] + b [s].v [k];
    b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    b [s].fLast = b [s].f;
    b [s].lifeCNT = 0;
  }
}

Si la limite de vie n'est pas épuisée, nous vérifions si la bactérie évolue vers une amélioration du gradient de la fonction d'aptitude. En d'autres termes, nous vérifions deux valeurs de santé - à l'itération actuelle et à l'itération précédente. Si la santé s'est améliorée, le vecteur de mouvement est conservé, sinon la bactérie doit effectuer une culbute (changer le vecteur de mouvement).

Dans la version canonique, une vérification stricte de l'état de santé actuel et antérieur est effectuée. Dans ma version, l'expression "supérieur ou égal à" est appliquée, ce qui permet à la bactérie de continuer à se déplacer même sur une section complètement "horizontale" de la surface étudiée, où il n'y a pas de gradient de la fonction d'aptitude, sinon la bactérie culbuterait sans fin au même endroit (il n'y a pas de changement d'état de santé, ce qui signifie qu'il n'y a pas de direction de nage). À ce stade, nous devons également vérifier que les nouvelles coordonnées reçues ne sortent pas des limites de l'espace de recherche.

else
{
  if (b [s].f >= b [s].fLast)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
  else
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].v [k] = NewVector (k);
      b [s].c [k] = b [s].c [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      b [s].fLast = b [s].f;
      b [s].lifeCNT++;
    }
  }
}

NewVector() - est une méthode privée pour changer le vecteur de mouvement (tumble). La méthode est appliquée pour chaque coordonnée. L'idée est simple : la différence entre les limites de recherche pour la coordonnée v correspondante est multipliée par un nombre aléatoire r dans l'intervalle [-1,0 ; 1,0] et multipliée par le facteur d'échelle lambda (l'un des paramètres de l'algorithme). La bactérie utilise le vecteur de déplacement sans changement jusqu'à ce que la limite de vies soit épuisée (une nouvelle bactérie est créée au même endroit, mais avec un nouveau vecteur de déplacement), pendant la réplication (le clone a un nouveau vecteur) et pendant la détérioration de la santé (une tentative de trouver un nouvel environnement plus favorable).  

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BFO::NewVector (int paramInd)
{
  double r = RNDfromCI (-1.0, 1.0);
  return lambda * v [paramInd] * r;
}
//——————————————————————————————————————————————————————————————————————————————

La deuxième méthode publique Evaluation(), qui doit être exécutée à chaque itération, appelle la méthode de tri, vérifie les mises à jour de la solution globale et compare la santé de la meilleure bactérie de la colonie triée avec la meilleure solution trouvée.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO::Evaluation ()
{
  Sorting ();

  if (b [0].f > fB)
  {
    fB = b [0].f;
    ArrayCopy (cB, b [0].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Résultats des tests

Résultats du banc d'essai BFO :

2023.01.21 12:52:46.501    Test_AO_BFO (.US500Cash, M1)    C_AO_BFO:50;0.01;0.8;100
2023.01.21 12:52:46.501    Test_AO_BFO (.US500Cash, M1) =============================
2023.01.21 12:52:48.451    Test_AO_BFO (.US500Cash, M1)    5 Rastrigin's ; Func runs 10000 result : 72.94540549092933
2023.01.21 12:52:48.451    Test_AO_BFO (.US500Cash, M1)    Score : 0.90383
2023.01.21 12:52:51.778    Test_AO_BFO (.US500Cash, M1)    25 Rastrigin's ; Func runs 10000 result : 54.75744312933767
2023.01.21 12:52:51.778    Test_AO_BFO (.US500Cash, M1)    Score : 0.67848
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash, M1)    500 Rastrigin's ; Func runs 10000 result : 40.668487609790404
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash, M1)    Score : 0.50391
2023.01.21 12:53:21.197    Test_AO_BFO (.US500Cash, M1) =============================
2023.01.21 12:53:23.211    Test_AO_BFO (.US500Cash, M1)    5 Forest's ; Func runs 10000 result : 0.8569098398505888
2023.01.21 12:53:23.211    Test_AO_BFO (.US500Cash, M1)    Score : 0.48471
2023.01.21 12:53:26.878    Test_AO_BFO (.US500Cash, M1)    25 Forest's ; Func runs 10000 result : 0.37618151461180294
2023.01.21 12:53:26.878    Test_AO_BFO (.US500Cash, M1)    Score : 0.21279
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash, M1)    500 Forest's ; Func runs 10000 result : 0.08748190028975696
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash, M1)    Score : 0.04948
2023.01.21 12:54:22.339    Test_AO_BFO (.US500Cash, M1) =============================
2023.01.21 12:54:28.849    Test_AO_BFO (.US500Cash, M1)    5 Megacity's ; Func runs 10000 result : 4.8
2023.01.21 12:54:28.849    Test_AO_BFO (.US500Cash, M1)    Score : 0.40000
2023.01.21 12:54:40.089    Test_AO_BFO (.US500Cash, M1)    25 Megacity's ; Func runs 10000 result : 2.216
2023.01.21 12:54:40.089    Test_AO_BFO (.US500Cash, M1)    Score : 0.18467
2023.01.21 12:55:24.640    Test_AO_BFO (.US500Cash, M1)    500 Megacity's ; Func runs 10000 result : 0.4232
2023.01.21 12:55:24.640    Test_AO_BFO (.US500Cash, M1)    Score : 0.03527

Il est trop tôt pour tirer des conclusions sans ambiguïté. Il est nécessaire d'analyser d'abord les résultats par rapport aux autres participants au test.

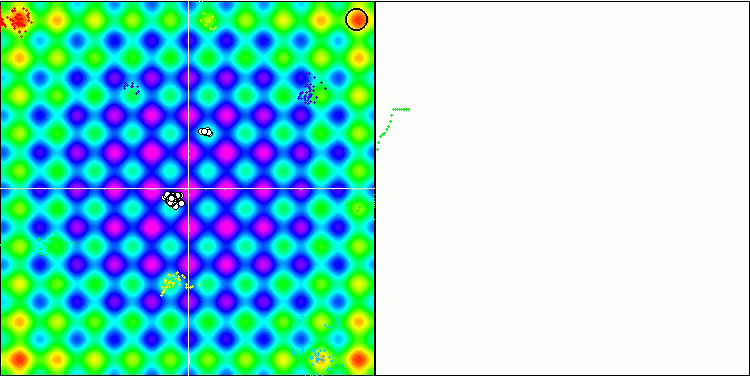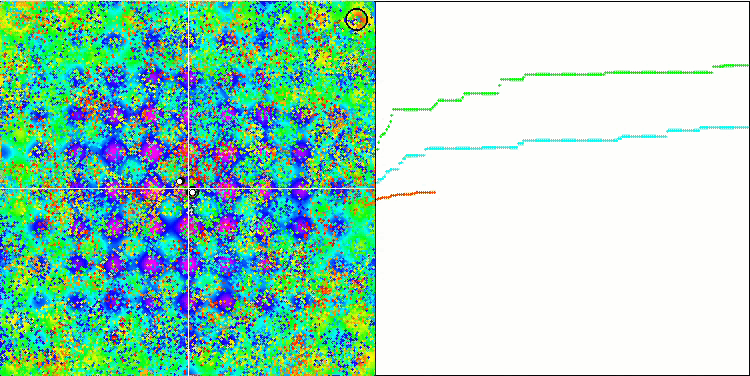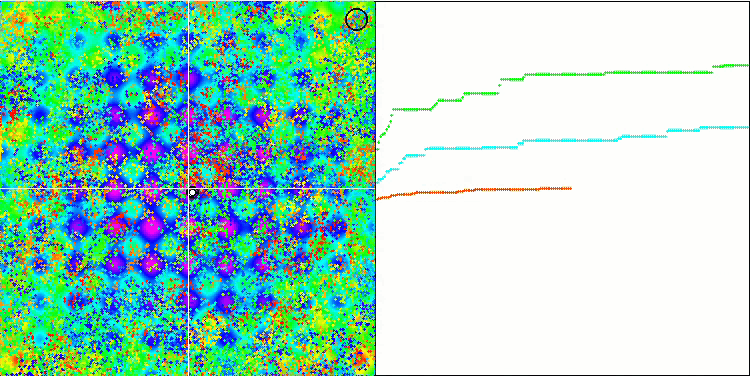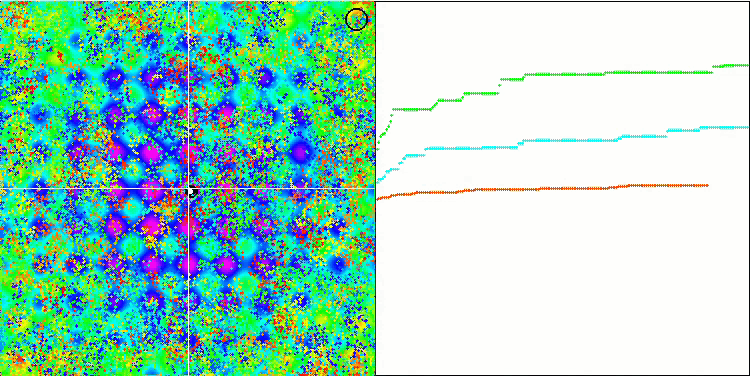
  BFO sur la fonction du test de Rastrigin.

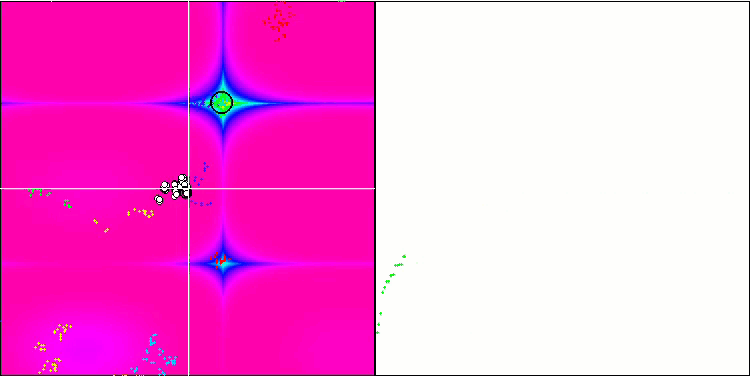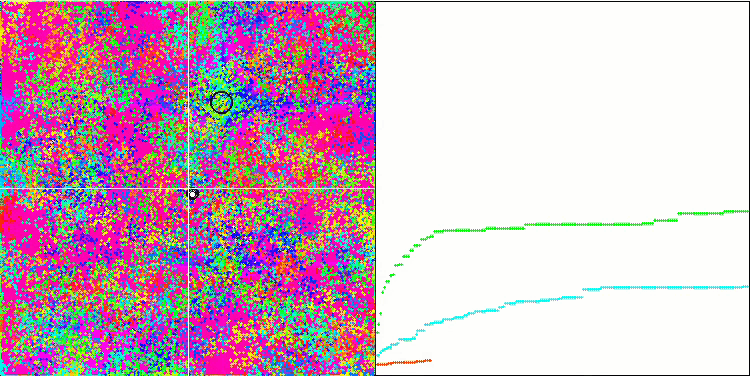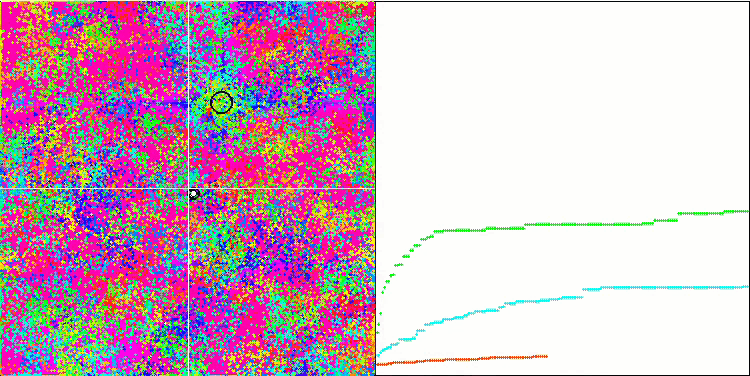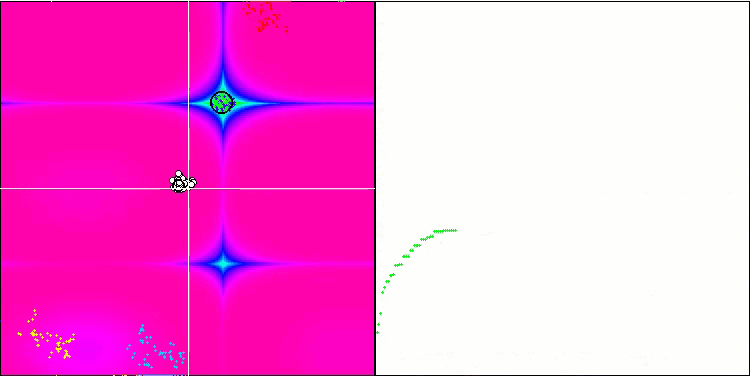
BFO sur la fonction de test Forest.

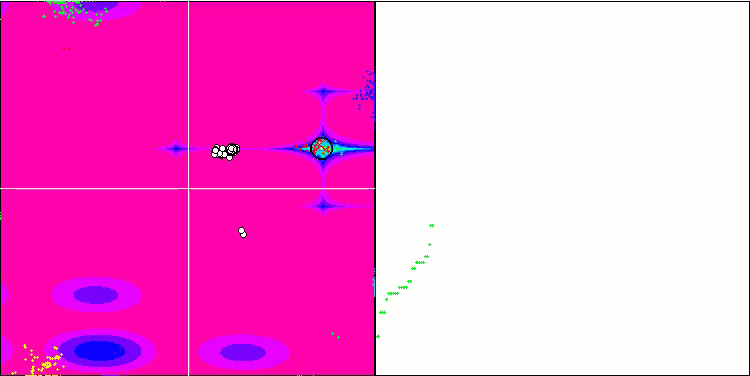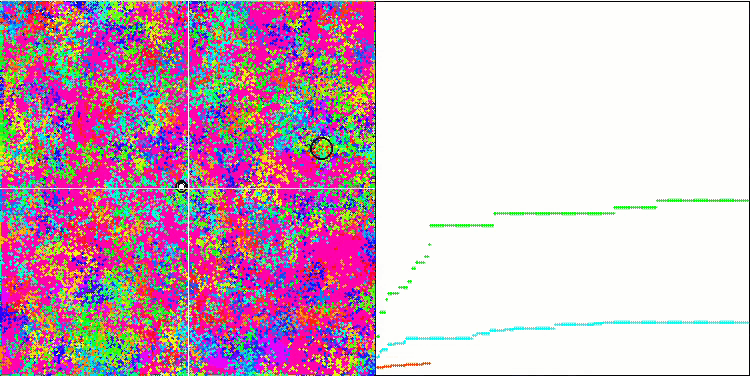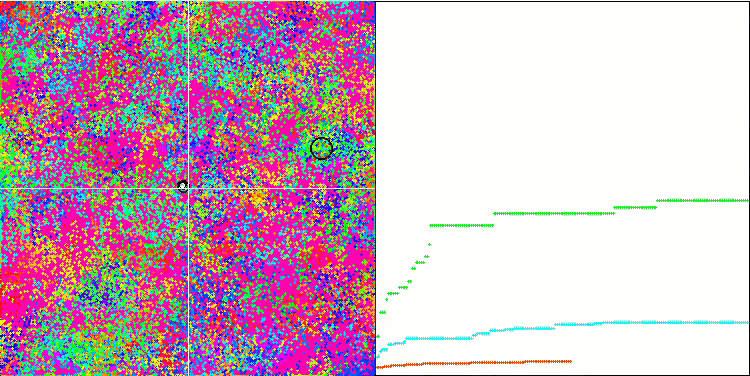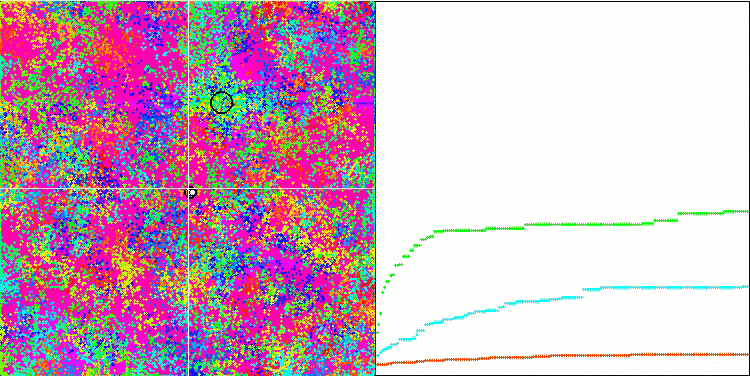
BFO sur la fonction de test Megacity.

Intéressons-nous à la visualisation du test. L'animation a confirmé la justesse de la décision de remplacer le signe "supérieur à" par "supérieur ou égal à" dans notre algorithme. Cela a permis aux bactéries de continuer à se déplacer dans les sections horizontales des fonctions d'essai. Ceci est particulièrement visible pour les fonctions "Forest" et "Megacity". Les bactéries essaient de se déplacer même là où il n'y a pas de gradient de fonction. Il est également nécessaire de noter la capacité d'une colonie bactérienne à se diviser en plusieurs colonies distinctes visuellement divisées en extrêmes locaux distincts, ce qui peut être considéré sans ambiguïté comme une caractéristique positive, bien que l'algorithme ne contienne aucune méthode logique pour la formation de sous-colonies. En général, un mouvement uniforme des bactéries dans l'espace de recherche est perceptible sans tentative de saut brusque dans l'une ou l'autre des directions, ce qui s'explique par un mouvement incrémentiel uniforme - la chimiotaxie.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrète)			Megacity final	Résultat final
		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)
IWO	Optimisation des mauvaises herbes envahissantes	1,00000	1,00000	0,33519	2,33519	0,79937	0,46349	0,41071	1,67357	0,75912	0,44903	0,94088	2,14903	100,000
ACOm	optimisation des colonies de fourmis M	0,36118	0,26810	0,17991	0,80919	1,00000	1,00000	1,00000	3,00000	1,00000	1,00000	0,10959	2,10959	95,996
COAm	algorithme d'optimisation coucou M	0,96423	0,69756	0,28892	1,95071	0,64504	0,34034	0,21362	1,19900	0,67153	0,34273	0,45422	1,46848	74,204
FAm	algorithme firefly M	0,62430	0,50653	0,18102	1,31185	0,55408	0,42299	0,64360	1,62067	0,21167	0,28416	1,00000	1,49583	71,024
BA	algorithme des chauves-souris	0,42290	0,95047	1,00000	2,37337	0,17768	0,17477	0,33595	0,68840	0,15329	0,07158	0,46287	0,68774	59,650
ABC	colonie d'abeilles artificielles	0,81573	0,48767	0,22588	1,52928	0,58850	0,21455	0,17249	0,97554	0,47444	0,26681	0,35941	1,10066	57,237
BFO	optimisation du butinage bactérien	0.70129	0.46155	0.11627	1.27911	0.41251	0.26623	0.26695	0.94569	0.42336	0.34491	0.50973	1.27800	55.516
FSS	recherche d'un banc de poissons	0,48850	0,37769	0,11006	0,97625	0,07806	0,05013	0,08423	0,21242	0,00000	0,01084	0,18998	0,20082	20,109
PSO	optimisation par essaims de particules	0,21339	0,12224	0,05966	0,39529	0,15345	0,10486	0,28099	0,53930	0,08028	0,02385	0,00000	0,10413	14,232
RND	aléatoire	0,17559	0,14524	0,07011	0,39094	0,08623	0,04810	0,06094	0,19527	0,00000	0,00000	0,08904	0,08904	8,142
GWO	optimiseur du loup gris	0,00000	0,00000	0,00000	0,00000	0,00000	0,00000	0,00000	0,00000	0,18977	0,04119	0,01802	0,24898	1,000

Il est temps d'analyser les résultats des tests. BFO se situe au milieu du tableau d'évaluation avec un score global d'un peu plus de 55 dans la liste actuelle des algorithmes participants. Les résultats ne sont pas impressionnants, mais pas mauvais non plus. En particulier, de bons résultats ont été obtenus sur la fonction de Rastrigin avec 10 variables. Dans le cas de 50 et 1000 variables, les résultats sont nettement moins bons. L'algorithme n'a pas non plus obtenu de bons résultats avec la fonction Forest. Le comportement relativement bon de la fonction de Megacity discrète est surprenant, étant donné que l'algorithme ne comporte aucun mécanisme permettant de travailler sur de telles fonctions. Il y a également une bonne évolutivité par rapport à d'autres algorithmes (test avec 1000 paramètres Megacity).

Le BFO est un domaine scientifique qui offre un large éventail de possibilités. Un certain nombre d'aspects du butinage bactérien et du butinage animal en général peuvent être modélisés afin d'améliorer les performances d'optimisation. Pour l'algorithme BFO, l'adaptation automatique des paramètres de contrôle peut revêtir une importance particulière, étant donné qu'il y a beaucoup de paramètres, et qu'elle peut améliorer les performances, ce qui justifie des expériences supplémentaires.

BFO présente un certain nombre d'avantages, notamment une faible sensibilité aux valeurs initiales des coordonnées lors de l'initialisation et du choix des paramètres, une bonne fiabilité, la simplicité de la logique, la facilité de mise en œuvre, la possibilité de parallélisme et de recherche globale. L'algorithme BFO est donc utilisé pour résoudre un large éventail de problèmes d'optimisation. Mais le BFO présente également un certain nombre d'inconvénients, notamment une convergence lente, l'impossibilité de dépasser les optima locaux dans certains cas et une longueur de pas fixe. BFO est une métaheuristique, ce qui signifie qu'il s'agit simplement d'un cadre conceptuel qui peut être utilisé pour développer des modifications d'algorithmes. La version de BFO que j'ai présentée ici n'est qu'une possibilité parmi d'autres et doit être considérée comme un point de départ pour l'expérimentation, plutôt que comme le dernier mot sur le sujet.

L'histogramme des résultats du test de l'algorithme est présenté ci-dessous.

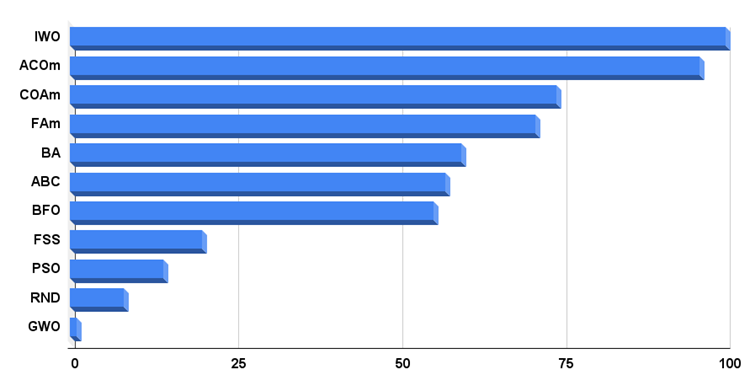
Fig. 3 : Histogramme des résultats finaux des algorithmes de test

Conclusions sur les propriétés de l'algorithme Bacterial Foraging Optimization (BFO) :

Avantages :
1. Grande vitesse
2. Logique simple
3. Convergence sur l'ensemble des itérations, bien que lente

Inconvénients :
1. Lenteur de la convergence
2. Pas de méthodes pour sortir des extrema locaux