Entwicklung von Trendhandelsstrategien mit maschinellem Lernen

Einführung

Mehrere Arten von Handelsstrategien haben ihre Wirksamkeit im Handel bewiesen. Eine solche Strategie – die Strategie Rückkehr zum Mittelwert – wurde in einem früheren Artikel behandelt. In diesem Artikel möchte ich dem Leser einige Ideen vorstellen, wie maschinelles Lernen zur Entwicklung trendbasierter oder trendfolgender Strategien genutzt werden kann.

In diesem Artikel wird ein ähnlicher Ansatz auf der Grundlage von Datenclustern zur Ermittlung von Marktregimen verwendet. Die tatsächlichen Handelsetikettierer werden sich jedoch erheblich unterscheiden. Daher empfehle ich, zunächst den ersten Artikel zu lesen und dann als logische Fortsetzung mit dem vorliegenden fortzufahren. So können Sie den Unterschied zwischen der ersten und der zweiten Art von Strategien sowie die Unterschiede bei der Kennzeichnung von Trainingsbeispielen erkennen. Na dann, auf geht's!

Ansätze zur Kennzeichnung von Daten für Trendfolgestrategien

Der Hauptunterschied zwischen Trendfolgestrategien und Mean-Reversion-Strategien besteht darin, dass bei Trendfolgestrategien die genaue Identifizierung des aktuellen Trends entscheidend ist. Für Strategien mit der Rückkehr zum Mittelwert reicht es aus, dass die Kurse um einen bestimmten Durchschnittswert oszillieren und diesen häufig überschreiten. Man kann sagen, dass diese Strategien diametral entgegengesetzt sind. Wenn die Rückkehr zum Mittelwert eine hohe Wahrscheinlichkeit für eine Umkehrung der Preisbewegungsrichtung impliziert, dann impliziert Trendfolge eine Fortsetzung des aktuellen Trends.

Währungspaare werden oft als schwankend (flach) oder tendenziell eingestuft. Natürlich ist dies eine eher bedingte Klassifizierung, da sowohl Trends als auch Konsolidierungszonen in beiden Typen vorhanden sein können. Hier wird eher danach unterschieden, wie häufig sie sich in dem einen oder anderen Zustand aufhalten. In diesem Artikel werden wir nicht im Detail untersuchen, welche Instrumente wirklich im Trend liegen. Wir werden den Ansatz einfach am Währungspaar EURUSD testen, das als Trendpaar gilt, im Gegensatz zum EURGBP, der im vorherigen Artikel als Trendpaar untersucht wurde.

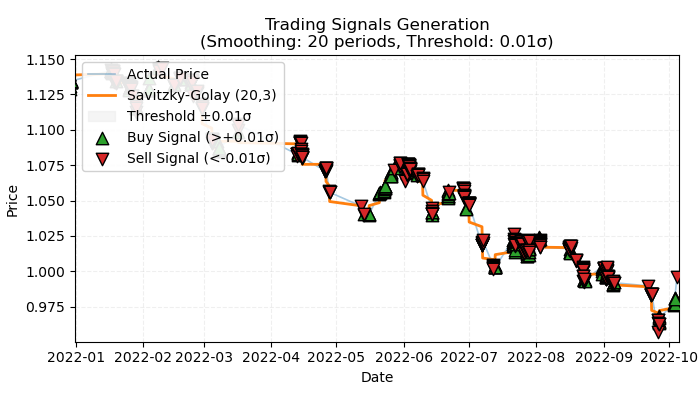
Abbildung 1. Visuelle Darstellung von markierten trendbasierten Handelsgeschäften

Abbildung 1 veranschaulicht das Grundprinzip, das für die Kennzeichnung von trendbasierten Handelsgeschäften verwendet werden soll. Um die kurzfristigen Schwankungen durch das Rauschen zu glätten, habe ich wieder den Savitzky-Golay-Filter verwendet, der im vorherigen Artikel ausführlich besprochen wurde. Anstatt jedoch wie beim letzten Mal die Kursabweichungen vom Filter zu berechnen, interessieren wir uns jetzt für die Richtung des Filters als Indikator für den Trend. Wenn die Richtung positiv ist, wird ein Kaufgeschäft gekennzeichnet, andernfalls ein Verkaufgeschäft. Wenn die Richtung nicht definiert ist, werden solche Handelsgeschäfte vom Trainingsprozess ausgeschlossen. Die Kennzeichnungsfunktion enthält einen eingebetteten Trendstärkefilter oder Schwellenwert, der unbedeutende Trends auf der Grundlage der Volatilität herausfiltert und weiter unten erläutert wird.

Eine grundlegende Methode zur Kennzeichnung von trendbasierten Handelsgeschäften

Um den Mechanismus vollständig zu verstehen, sollten wir die Funktion der Handelskennzeichnung von innen heraus betrachten.

@njit
def calculate_labels_trend(normalized_trend, threshold):
    labels = np.empty(len(normalized_trend), dtype=np.float64)
    for i in range(len(normalized_trend)):
        if normalized_trend[i] > threshold:
            labels[i] = 0.0  # Buy (Up trend)
        elif normalized_trend[i] < -threshold:
            labels[i] = 1.0  # Sell (Down trend)
        else:
            labels[i] = 2.0  # No signal
    return labels

def get_labels_trend(dataset, rolling=200, polyorder=3, threshold=0.5, vol_window=50) -> pd.DataFrame:
    smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=polyorder)
    trend = np.gradient(smoothed_prices)
    vol = dataset['close'].rolling(vol_window).std().values
    normalized_trend = np.where(vol != 0, trend / vol, np.nan)  # Set NaN where vol is 0
    labels = calculate_labels_trend(normalized_trend, threshold)
    dataset = dataset.iloc[:len(labels)].copy()
    dataset['labels'] = labels
    dataset = dataset.dropna()  # Remove rows with NaN
    return dataset

Die Funktion get_labels_trend verarbeitet die Rohdaten – einen Datensatz, der eine „close“-Spalte (Schlusskurse) enthält – und liefert einen Datenrahmen mit einer zusätzlichen Spalte mit beschrifteten Signalen.

Die wichtigsten Schritte der Kennzeichnung:

• Preisglättung. Zur Glättung der Schlusskurse wird ein Savitzky-Golay-Filter eingesetzt. Zu den Parametern gehören die Länge des Glättungsfensters und die Polynomordnung. Ziel ist es, das Rauschen zu eliminieren und den zugrunde liegenden Trend hervorzuheben.

smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=polyorder)

• Trendberechnung. Die Steigung der geglätteten Preise wird berechnet. Die Steigung gibt die Geschwindigkeit und Richtung der Preisänderung an. Ein positiver Gradient bedeutet einen Aufwärtstrend, ein negativer einen Abwärtstrend. 

trend = np.gradient(smoothed_prices)

• Berechnung der Volatilität. Die Volatilität wird als Standardabweichung der Schlusskurse über ein rollierendes Zeitfenster berechnet. Dies hilft bei der Bewertung der Preisvariabilität zur Normalisierung des Trends.

vol = dataset['close'].rolling(vol_window).std().values

• Trend-Normalisierung. Der Trend wird durch die Volatilität geteilt, um den Marktschwankungen Rechnung zu tragen. 

normalized_trend = np.where(vol != 0, trend / vol, np.nan)

• Erzeugung von Kennzeichnungen. Die Kennzeichnungen für Kauf- und Verkaufssignale werden auf der Grundlage des normalisierten Trends und eines Schwellenwerts erstellt.

labels = calculate_labels_trend(normalized_trend, threshold)

• Anwendung der Schwellenwerte. Dieser Wert filtert geringfügige Gradientenabweichungen heraus. Er wird empirisch gewählt und liegt in der Regel im Bereich von 0,01 bis 0,5. Trends innerhalb der Filtergrenzen werden als unbedeutend ignoriert.

Wir werden diesen Ansatz der Kennzeichnung als Grundlage nehmen und weitere Kennzeichnungsprogramme schreiben, um mehr Möglichkeiten zum Experimentieren zu haben.

Kennzeichnung mit strikter Beschränkung auf rentable Abschlüsse

Der grundlegende Ansatz beinhaltet naturgemäß einige Verlustgeschäfte, da diese am Ende eines Trends kurz vor einer Umkehrung auftreten können. Dies entspricht den Signalen echter Handelssysteme, die falsch sein können. Ausschlaggebend ist das prozentuale Verhältnis von gewinnbringenden zu verlustbringenden Handelsgeschäften, wobei die mit Gewinn bevorzugt werden sollten. Wir können diesen Fehler jedoch beseitigen, indem wir nur gewinnbringende Handelsgeschäfte kennzeichnen und die Verlustgeschäfte ignorieren. Dies trägt zur Glättung der Equity-Kurve bei Trainings- und möglicherweise auch bei Testdaten bei. Der Code für eine solche Kennzeichnung ist unten dargestellt.

@njit
def calculate_labels_trend_with_profit(close, normalized_trend, threshold, markup, min_l, max_l):
    labels = np.empty(len(normalized_trend) - max_l, dtype=np.float64)
    for i in range(len(normalized_trend) - max_l):
        if normalized_trend[i] > threshold:
            # Проверяем условие для Buy
            rand = random.randint(min_l, max_l)
            future_pr = close[i + rand]
            if future_pr >= close[i] + markup:
                labels[i] = 0.0  # Buy (Profit reached)
            else:
                labels[i] = 2.0  # No profit
        elif normalized_trend[i] < -threshold:
            # Проверяем условие для Sell
            rand = random.randint(min_l, max_l)
            future_pr = close[i + rand]
            if future_pr <= close[i] - markup:
                labels[i] = 1.0  # Sell (Profit reached)
            else:
                labels[i] = 2.0  # No profit
        else:
            labels[i] = 2.0  # No signal
    return labels

def get_labels_trend_with_profit(dataset, rolling=200, polyorder=3, threshold=0.5, 
                    vol_window=50, markup=0.00005, min_l=1, max_l=15) -> pd.DataFrame:
    # Smoothing and trend calculation
    smoothed_prices = savgol_filter(dataset['close'].values, window_length=rolling, polyorder=polyorder)
    trend = np.gradient(smoothed_prices)
    
    # Normalizing the trend by volatility
    vol = dataset['close'].rolling(vol_window).std().values
    normalized_trend = np.where(vol != 0, trend / vol, np.nan)
    
    # Removing NaN and synchronizing data
    valid_mask = ~np.isnan(normalized_trend)
    normalized_trend_clean = normalized_trend[valid_mask]
    close_clean = dataset['close'].values[valid_mask]
    dataset_clean = dataset[valid_mask].copy()
    
    # Generating labels
    labels = calculate_labels_trend_with_profit(close_clean, normalized_trend_clean, threshold, markup, min_l, max_l)
    
    # Trimming the dataset and adding labels
    dataset_clean = dataset_clean.iloc[:len(labels)].copy()
    dataset_clean['labels'] = labels
    
    # Filtering the results
    dataset_clean = dataset_clean.dropna()    
    return dataset_clean

Hauptunterschiede zum Basisansatz:

• Der Parameter min_l wurde hinzugefügt, der die Mindestanzahl von Future-Balken für die Messung der Preisänderung festlegt.
• Der Parameter max_l wurde hinzugefügt, der die maximale Anzahl von Future-Balken für die Messung von Preisänderungen festlegt.
• Ein zukünftiger Balken wird zufällig innerhalb des durch diese Parameter festgelegten Bereichs ausgewählt. Prüfungen mit fester Länge können durchgeführt werden, indem beide Parameter auf denselben Wert gesetzt werden.
• Wenn ein eröffneter Handel bei + n Bars Forward einen Gewinn gebracht hat, dann wird ein solcher Handel dem Trainingsdatensatz hinzugefügt, andernfalls wird er als 2.0 (kein Handel) gekennzeichnet.
• Markup-Parameter wurden hinzugefügt, die ungefähr auf den durchschnittlichen Spread + Kommission + Slippage für das Handelsinstrument gesetzt werden sollten, eventuell mit einer Marge, eingestellt werden. Dieser Wert wirkt sich auf die Anzahl der als profitabel eingestuften Handelsgeschäfte aus – je höher er ist, desto weniger Handelsgeschäfte werden als profitabel eingestuft, weil sie diesen Schwellenwert nicht erreichen.

Kennzeichnung mit Filterauswahlmöglichkeit und strikter Begrenzung der profitablen Handelsgeschäfte

Wie im vorherigen Artikel wollen wir eine Auswahl an Filtern haben, nicht nur Savitzky-Golay. Dies ermöglicht mehr Variationen bei der Etikettierung und eine bessere Anpassung des Handelssystems an die Eigenschaften der verschiedenen Instrumente. Ich schlage vor, den einfachen gleitenden Durchschnitt, den exponentiellen gleitenden Durchschnitt und Spline als zusätzliche Filter hinzuzufügen. Nur als Beispiele, denn Sie können Ihre eigenen durch Analogie hinzufügen.

@njit
def calculate_labels_trend_different_filters(close, normalized_trend, threshold, markup, min_l, max_l):
    labels = np.empty(len(normalized_trend) - max_l, dtype=np.float64)
    for i in range(len(normalized_trend) - max_l):
        if normalized_trend[i] > threshold:
            # Проверяем условие для Buy
            rand = random.randint(min_l, max_l)
            future_pr = close[i + rand]
            if future_pr >= close[i] + markup:
                labels[i] = 0.0  # Buy (Profit reached)
            else:
                labels[i] = 2.0  # No profit
        elif normalized_trend[i] < -threshold:
            # Проверяем условие для Sell
            rand = random.randint(min_l, max_l)
            future_pr = close[i + rand]
            if future_pr <= close[i] - markup:
                labels[i] = 1.0  # Sell (Profit reached)
            else:
                labels[i] = 2.0  # No profit
        else:
            labels[i] = 2.0  # No signal
    return labels

def get_labels_trend_with_profit_different_filters(dataset, method='savgol', rolling=200, polyorder=3, threshold=0.5, 
                    vol_window=50, markup=0.5, min_l=1, max_l=15) -> pd.DataFrame:
    # Smoothing and trend calculation
    close_prices = dataset['close'].values
    if method == 'savgol':
        smoothed_prices = savgol_filter(close_prices, window_length=rolling, polyorder=polyorder)
    elif method == 'spline':
        x = np.arange(len(close_prices))
        spline = UnivariateSpline(x, close_prices, k=polyorder, s=rolling)
        smoothed_prices = spline(x)
    elif method == 'sma':
        smoothed_series = pd.Series(close_prices).rolling(window=rolling).mean()
        smoothed_prices = smoothed_series.values
    elif method == 'ema':
        smoothed_series = pd.Series(close_prices).ewm(span=rolling, adjust=False).mean()
        smoothed_prices = smoothed_series.values
    else:
        raise ValueError(f"Unknown smoothing method: {method}")
    
    trend = np.gradient(smoothed_prices)
    
    # Normalizing the trend by volatility
    vol = dataset['close'].rolling(vol_window).std().values
    normalized_trend = np.where(vol != 0, trend / vol, np.nan)
    
    # Removing NaN and synchronizing data
    valid_mask = ~np.isnan(normalized_trend)
    normalized_trend_clean = normalized_trend[valid_mask]
    close_clean = dataset['close'].values[valid_mask]
    dataset_clean = dataset[valid_mask].copy()
    
    # Generating labels
    labels = calculate_labels_trend_different_filters(close_clean, normalized_trend_clean, threshold, markup, min_l, max_l)
    
    # Trimming the dataset and adding labels
    dataset_clean = dataset_clean.iloc[:len(labels)].copy()
    dataset_clean['labels'] = labels
    
    # Filtering the results
    dataset_clean = dataset_clean.dropna()    
    return dataset_clean

Die wichtigste Änderung im Vergleich zum vorherigen Beschriftungsalgorithmus ist die Hinzufügung des Methodenparameters, der die folgenden Werte annehmen kann:

• savgol — Savitsky-Golei-Filter
• spline — Spline-Interpolation
• sma — Glättung mit einfachem gleitenden Mittelwert
• ema — Glättung mit exponentiellem gleitendem Mittelwert.

Kennzeichnung auf der Grundlage von Filtern mit unterschiedlichen Zeiträumen und strikter Begrenzung der profitablen Handelsgeschäfte

Machen wir unsere Wahrnehmung der Realität kompliziert und folglich auch die Methode der Handelskennzeichnung. Es gibt keine Einschränkung, nur eine einzige ausgewählte Glättungsperiode zu verwenden. Mehrere Filter desselben Typs mit unterschiedlichen Zeiträumen können gleichzeitig verwendet werden, um Handelsgeschäfte zu kennzeichnen, wenn mindestens eine Bedingung erfüllt ist. Ein Beispiel für einen solchen Probenehmer wird im Folgenden vorgestellt:

@njit
def calculate_labels_trend_multi(close, normalized_trends, threshold, markup, min_l, max_l):
    num_periods = normalized_trends.shape[0]  # Number of periods
    labels = np.empty(len(close) - max_l, dtype=np.float64)
    for i in range(len(close) - max_l):
        # Select a random number of bars forward once for all periods
        rand = np.random.randint(min_l, max_l + 1)
        buy_signals = 0
        sell_signals = 0
        # Check conditions for each period
        for j in range(num_periods):
            if normalized_trends[j, i] > threshold:
                if close[i + rand] >= close[i] + markup:
                    buy_signals += 1
            elif normalized_trends[j, i] < -threshold:
                if close[i + rand] <= close[i] - markup:
                    sell_signals += 1
        # Combine signals
        if buy_signals > 0 and sell_signals == 0:
            labels[i] = 0.0  # Buy
        elif sell_signals > 0 and buy_signals == 0:
            labels[i] = 1.0  # Sell
        else:
            labels[i] = 2.0  # No signal or conflict
    return labels

def get_labels_trend_with_profit_multi(dataset, method='savgol', rolling_periods=[10, 20, 30], polyorder=3, threshold=0.5, 
                                       vol_window=50, markup=0.5, min_l=1, max_l=15) -> pd.DataFrame:
    """
    Generates labels for trading signals (Buy/Sell) based on the normalized trend,
    calculated for multiple smoothing periods.

    Args:
        dataset (pd.DataFrame): DataFrame with data, containing the 'close' column.
        method (str): Smoothing method ('savgol', 'spline', 'sma', 'ema').
        rolling_periods (list): List of smoothing window sizes. Default is [200].
        polyorder (int): Polynomial order for 'savgol' and 'spline' methods.
        threshold (float): Threshold for the normalized trend.
        vol_window (int): Window for volatility calculation.
        markup (float): Minimum profit to confirm the signal.
        min_l (int): Minimum number of bars forward.
        max_l (int): Maximum number of bars forward.

    Returns:
        pd.DataFrame: DataFrame with added 'labels' column:
                      - 0.0: Buy
                      - 1.0: Sell
                      - 2.0: No signal
    """
    close_prices = dataset['close'].values
    normalized_trends = []

    # Calculate normalized trend for each period
    for rolling in rolling_periods:
        if method == 'savgol':
            smoothed_prices = savgol_filter(close_prices, window_length=rolling, polyorder=polyorder)
        elif method == 'spline':
            x = np.arange(len(close_prices))
            spline = UnivariateSpline(x, close_prices, k=polyorder, s=rolling)
            smoothed_prices = spline(x)
        elif method == 'sma':
            smoothed_series = pd.Series(close_prices).rolling(window=rolling).mean()
            smoothed_prices = smoothed_series.values
        elif method == 'ema':
            smoothed_series = pd.Series(close_prices).ewm(span=rolling, adjust=False).mean()
            smoothed_prices = smoothed_series.values
        else:
            raise ValueError(f"Unknown smoothing method: {method}")
        
        trend = np.gradient(smoothed_prices)
        vol = pd.Series(close_prices).rolling(vol_window).std().values
        normalized_trend = np.where(vol != 0, trend / vol, np.nan)
        normalized_trends.append(normalized_trend)

    # Transform list into 2D array
    normalized_trends_array = np.vstack(normalized_trends)

    # Remove rows with NaN
    valid_mask = ~np.isnan(normalized_trends_array).any(axis=0)
    normalized_trends_clean = normalized_trends_array[:, valid_mask]
    close_clean = close_prices[valid_mask]
    dataset_clean = dataset[valid_mask].copy()

    # Generate labels
    labels = calculate_labels_trend_multi(close_clean, normalized_trends_clean, threshold, markup, min_l, max_l)

    # Trim data and add labels
    dataset_clean = dataset_clean.iloc[:len(labels)].copy()
    dataset_clean['labels'] = labels

    # Remove remaining NaN
    dataset_clean = dataset_clean.dropna()
    return dataset_clean

Wichtige Punkte (begrifflich hervorgehoben):

• Die Kennzeichnungsfunktion akzeptiert jetzt eine Liste beliebiger Länge, die Werte für die Glättungsperiode enthält.
• Die Filter werden für alle angegebenen Zeiträume in einer Schleife berechnet.
• Trendgradienten über alle Filter hinweg nehmen an der Kennzeichnungsfunktion teil.
• Ein Handel wird gekennzeichnet, wenn mindestens eine Kauf- oder Verkaufsbedingung erfüllt ist, vorausgesetzt, es liegen keine entgegengesetzten Signale vor.

Das Modul labeling_lib.py wurde um vier neue Probenehmer erweitert:

def get_labels_trend(dataset, rolling=200, polyorder=3, threshold=0.5, vol_window=50) -> pd.DataFrame:
def get_labels_trend_with_profit(dataset, rolling=200, polyorder=3, threshold=0.5, 
def get_labels_trend_with_profit_different_filters(dataset, method='savgol', rolling=200, polyorder=3, threshold=0.5, 
def get_labels_trend_with_profit_multi(dataset, method='savgol', rolling_periods=[10, 20, 30], polyorder=3, threshold=0.5, 

 Lassen wir es bei diesen Varianten bewenden. Sie sind völlig ausreichend, um die Kernidee der Trendkennzeichnung zu testen.

Modellschulung und Testverfahren

Die Kernlogik für die Datenaufbereitung und -schulung wurde aus dem vorigen Artikel übernommen, sodass ihre Einzelheiten hier nicht näher beschrieben werden. Es gibt jedoch einige Änderungen: Der gesamte Ausbildungszyklus ist nun in eine separate Verarbeitungsfunktion ausgelagert, die neue Möglichkeiten für die Verwaltung des Prozesses bietet.

Zuvor wurden die mit 2,0 gekennzeichneten Handelsgeschäfte einfach aus dem Trainingsdatensatz entfernt und nahmen nicht am Lernen teil. Dies könnte zu Informationsverlusten aufgrund von Lücken in der Etikettenfolge führen. Aber wie können diese Informationen in das Handelssystem integriert werden, wenn ein binärer Klassifikator verwendet wird und 2,0 Labels (keine Aktion) eine 3.

Erinnern wir uns, dass zwei Klassifikatoren am Training beteiligt sind: Der erste lernt, Kauf-/Verkaufsmarken vorherzusagen, und der zweite lernt, das aktuelle Marktregime vorherzusagen (wann gehandelt werden sollte und wann nicht). Das bedeutet, dass wir Beispiele mit 2.0-Etiketten in das zweite Modell migrieren können, wodurch Informationen erhalten bleiben, anstatt sie zu verwerfen.

def processing(iterations = 1, 
               rolling = [10],
               threshold=0.01,
               polyorder=5,
               vol_window=100,  
               use_meta_dilution = True):
    models = []
    for i in range(iterations):
        data = clustering(dataset, n_clusters=hyper_params['n_clusters'])
        sorted_clusters = data['clusters'].unique()
        sorted_clusters.sort()
        for clust in sorted_clusters:
            clustered_data = data[data['clusters'] == clust].copy()
            if len(clustered_data) < 500:
                print('too few samples: {}'.format(len(clustered_data)))
                continue

            clustered_data = get_labels_trend_with_profit_multi(
                                                    clustered_data,
                                                    method='savgol',
                                                    rolling_periods=rolling,
                                                    polyorder=polyorder,
                                                    threshold=threshold,
                                                    vol_window=vol_window,
                                                    min_l=1,
                                                    max_l=15,   
                                                    markup=hyper_params['markup'])
            
            
            print(f'Iteration: {i}, Cluster: {clust}')
            clustered_data = clustered_data.drop(['close', 'clusters'], axis=1)
            meta_data = data.copy()
            meta_data['clusters'] = meta_data['clusters'].apply(lambda x: 1 if x == clust else 0)
            if use_meta_dilution:
                for dt in clustered_data.index:
                    if clustered_data.loc[dt, 'labels'] == 2.0:
                        if dt in meta_data.index:  # Check if datetime exists in meta_data
                            meta_data.loc[dt, 'clusters'] = 0
            clustered_data = clustered_data.drop(clustered_data[clustered_data.labels == 2.0].index)

            # Синхронизация meta_data с bad_data
            models.append(fit_final_models(clustered_data, meta_data.drop(['close'], axis=1)))
        models.sort(key=lambda x: x[0])
    return models

Im Code wird gezeigt, dass Beispiele, die im Datensatz für das erste Modell mit 2,0 gekennzeichnet sind, im Datensatz für das zweite Modell anhand der entsprechenden Daten/Zeilen ausgewählt werden und in der Spalte Cluster Nullen gesetzt werden. Das zweite Modell wird nun nicht nur das Marktregime vorhersagen, sondern auch unerwünschte Einstiegspunkte für den Handel gemäß dem Trade Sampler. Mit anderen Worten: Das zweite Modell wird nun sowohl die erforderliche Marktordnung als auch unerwünschte Markteintrittspunkte vorhersagen.

Ich schlage vor, den letzten Sampler sofort zu verwenden, da er die besten Funktionen enthält und flexible Einstellungen bietet.

Führen wir 10 Trainingszyklen mit den folgenden Einstellungen durch:

hyper_params = {
    'symbol': 'EURUSD_H1',
    'export_path': '/Users/dmitrievsky/Library/Containers/com.isaacmarovitz.Whisky/Bottles/54CFA88F-36A3-47F7-915A-D09B24E89192/drive_c/Program Files/MetaTrader 5/MQL5/Include/Mean reversion/',
    'model_number': 0,
    'markup': 0.00010,
    'stop_loss':  0.00500,
    'take_profit': 0.00200,
    'periods': [i for i in range(5, 300, 30)],
    'periods_meta': [100],
    'backward': datetime(2000, 1, 1),
    'forward': datetime(2024, 1, 1),
    'full forward': datetime(2026, 1, 1),
    'n_clusters': 10,
    'rolling': [10],
}

Die Trainingsfunktion selbst wird wie folgt aufgerufen:

dataset = get_features(get_prices())
models = processing(iterations = 10, 
               threshold=0.001,
               polyorder=3,
               vol_window=100,  
               use_meta_dilution = True)

Während des Trainings werden die R^2-Werte für jeden Durchgang (Cluster) angezeigt:

Iteration: 0, Cluster: 0
R2: 0.9837358133371028
Iteration: 0, Cluster: 1
R2: 0.9002342482016827
Iteration: 0, Cluster: 2
R2: 0.9755114279213657
Iteration: 0, Cluster: 3
R2: 0.9833351908595832
Iteration: 0, Cluster: 4
R2: 0.9537875370012954
Iteration: 0, Cluster: 5
R2: 0.9863566422346429
too few samples: 471
Iteration: 0, Cluster: 7
R2: 0.9852545217737659
Iteration: 0, Cluster: 8
R2: 0.9934196831544163

Testen wir das beste Modell aus der gesamten Liste:

test_model(models[-1][1:],
           hyper_params['stop_loss'], 
           hyper_params['take_profit'], 
           hyper_params['forward'], 
           plt=True)

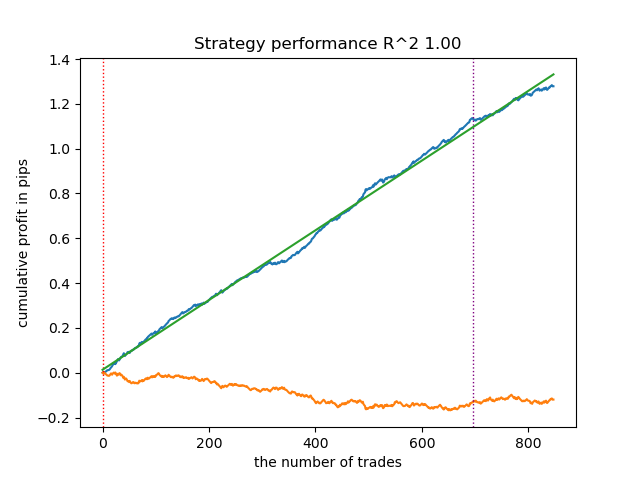
Abbildung 2. Modellprüfung mit Trainings- und neuen Daten

Jetzt können wir die Funktion aufrufen, um die Modelle in das MetaTrader 5 Terminal zu exportieren.

export_model_to_ONNX(model = models[-1],
                     symbol = hyper_params['symbol'],
                     periods = hyper_params['periods'],
                     periods_meta = hyper_params['periods_meta'],
                     model_number = hyper_params['model_number'],
                     export_path = hyper_params['export_path'])

Abschließende Modellprüfung und allgemeine Bemerkungen zum Algorithmus

Mein Ansatz ist universell, d. h. der Export von Modellen in das Terminal erfolgt auf genau dieselbe Weise wie im vorherigen Artikel beschrieben.

Betrachten wir den gesamten Trainings- und Testzeitraum und den Testzeitraum separat. Die Abbildungen zeigen, dass die Aktienkurve bei den Trainingsdaten glatter verläuft als bei den Testdaten ab 2024. Da das Training von 2020 bis 2024 durchgeführt wurde, wird der Test ab 2019 gezeigt, um zu verdeutlichen, dass auch der Zeitraum vor dem Training nicht vollkommen glatt ist.

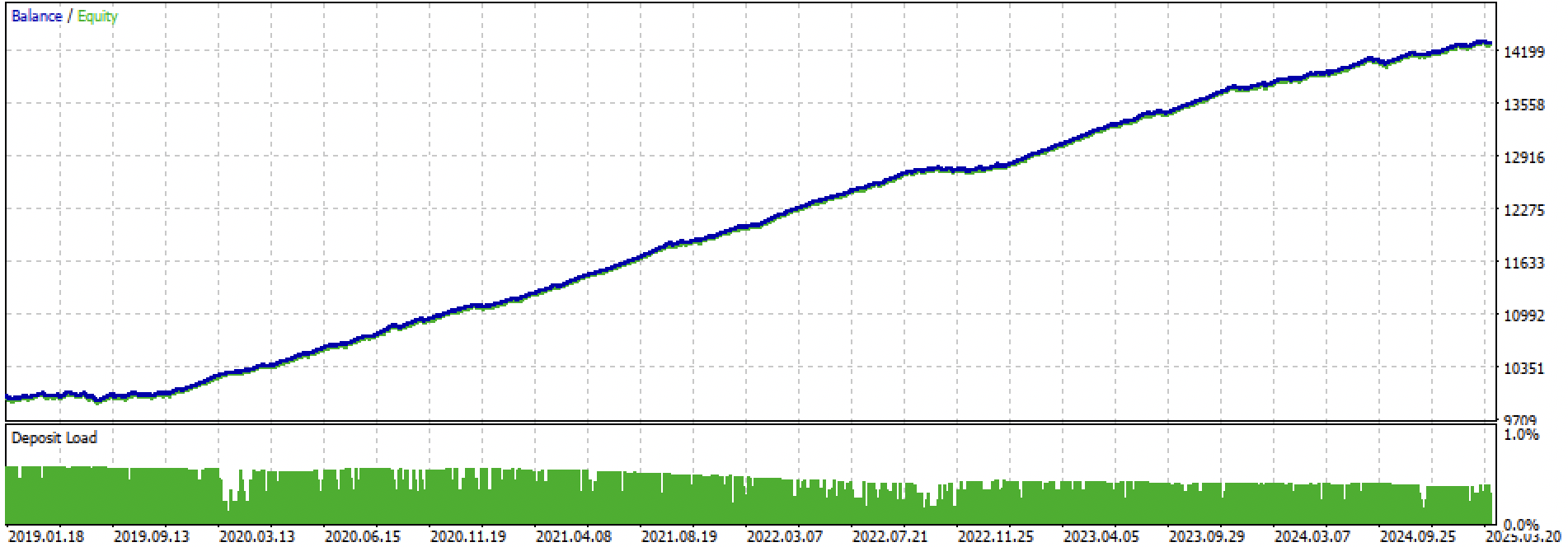
Abbildung 3. Tests von 2019 bis 2025.

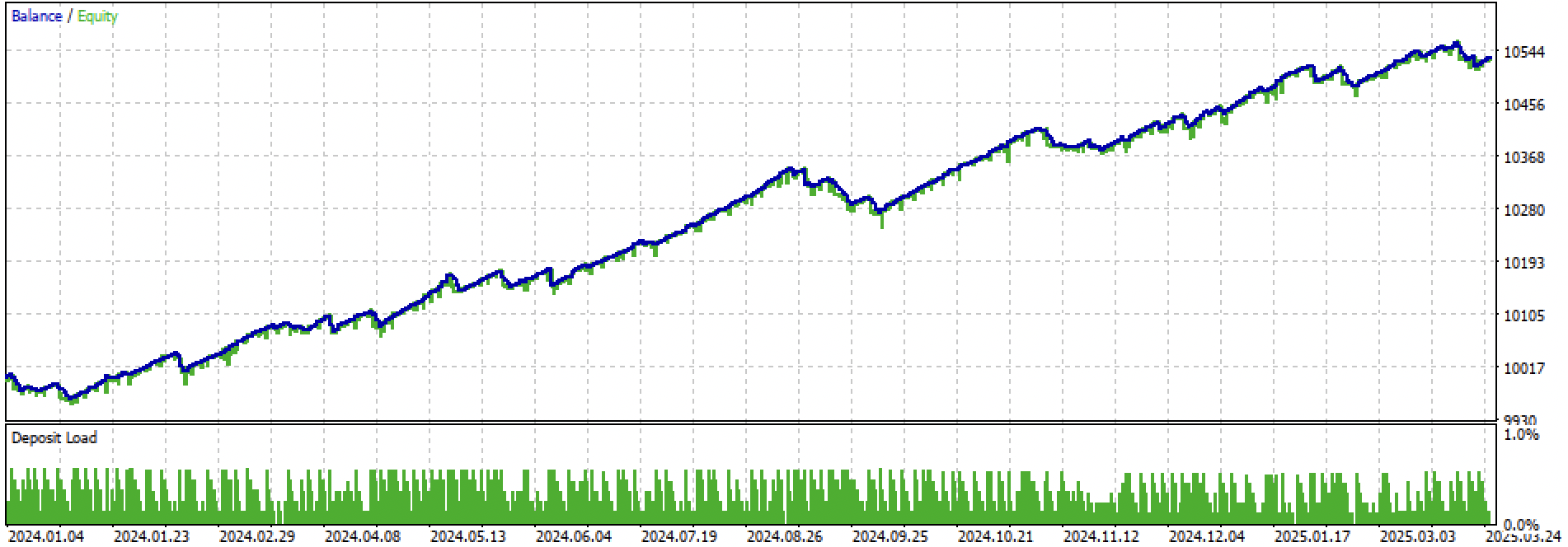
Abbildung 4: Tests für den Zeitraum von Anfang 2024 bis zum 27. März 2025

Auf der Grundlage der durchgeführten Experimente komme ich zu dem Schluss, dass Trendfolgestrategien in Bezug auf ihre Leistung bei neuen Daten empfindlicher sind oder dass dieser Ansatz für die Erstellung solcher Strategien für das EURUSD-Paar nicht gut geeignet ist. Dennoch lassen sich durch das Experimentieren mit der Abstimmung der Hyperparameter recht gute Modelle erzielen. Die Nachteile werden teilweise dadurch kompensiert, dass solche Modelle bei einem sehr kurzen Stop-Loss, z.B. bei 20 vierstelligen Punkten, gute Ergebnisse zeigen können. Dies ermöglicht eine Risikokontrolle und die rechtzeitige Deaktivierung von Modellen, wenn diese ausfallen.

Außerdem konnte ich keinen signifikanten Satz von Hyperparametern identifizieren. Ich habe den Eindruck, dass der Algorithmus grundsätzlich nicht in der Lage ist, stabile Muster zu finden, oder dass solche Muster einfach nicht vorhanden sind.

Um eine Überanpassung zu vermeiden, kann die Modellkomplexität mit der Funktion fit_final_models() reduziert werden:

def fit_final_models(clustered, meta) -> list:
    # features for model\meta models. We learn main model only on filtered labels 
    X, X_meta = clustered[clustered.columns[:-1]], meta[meta.columns[:-1]]
    X = X.loc[:, ~X.columns.str.contains('meta_feature')]
    X_meta = X_meta.loc[:, X_meta.columns.str.contains('meta_feature')]
    
    # labels for model\meta models
    y = clustered['labels']
    y_meta = meta['clusters']
    
    y = y.astype('int16')
    y_meta = y_meta.astype('int16')

    # train\test split
    train_X, test_X, train_y, test_y = train_test_split(
        X, y, train_size=0.7, test_size=0.3, shuffle=True)
    
    train_X_m, test_X_m, train_y_m, test_y_m = train_test_split(
        X_meta, y_meta, train_size=0.7, test_size=0.3, shuffle=True)


    # learn main model with train and validation subsets
    model = CatBoostClassifier(iterations=100,
                               custom_loss=['Accuracy'],
                               eval_metric='Accuracy',
                               verbose=False,
                               use_best_model=True,
                               task_type='CPU',
                               thread_count=-1)
    model.fit(train_X, train_y, eval_set=(test_X, test_y),
              early_stopping_rounds=15, plot=False)
    
    # learn meta model with train and validation subsets
    meta_model = CatBoostClassifier(iterations=100,
                                    custom_loss=['F1'],
                                    eval_metric='F1',
                                    verbose=False,
                                    use_best_model=True,
                                    task_type='CPU',
                                    thread_count=-1)
    meta_model.fit(train_X_m, train_y_m, eval_set=(test_X_m, test_y_m),
              early_stopping_rounds=15, plot=False)

    
    R2 = test_model([model, meta_model], hyper_params['stop_loss'], hyper_params['take_profit'], hyper_params['full forward'])
    if math.isnan(R2):
        R2 = -1.0
        print('R2 is fixed to -1.0')
    print('R2: ' + str(R2))

    return [R2, model, meta_model]

Die Anzahl der Iterationen steuert die Anzahl der Splits im Modell und die Anzahl der ausgewählten Merkmale. Ursprünglich waren es 1000 Iterationen; wir reduzieren sie auf 100. Frühzeitiges Abbrechen beendet das Training vorzeitig, wenn sich der Klassifikationsfehler bei den Validierungsdaten in 15 aufeinanderfolgenden Iterationen nicht verbessert.

Dies führte zu einer geräuschvolleren und gleichmäßigeren, aber weniger „schönen“ Kapitalkurve.

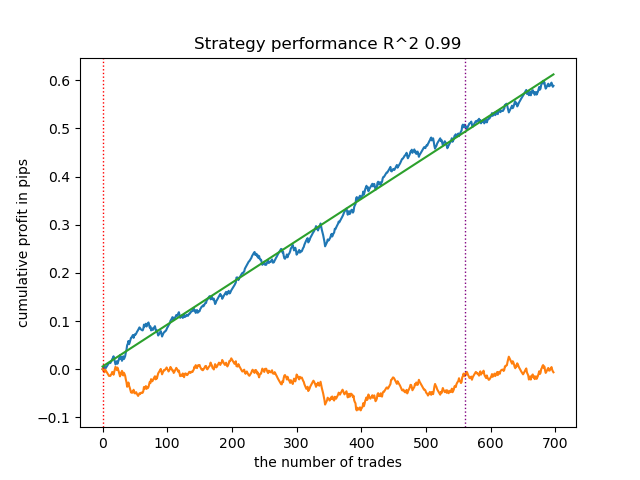
Abbildung 5: Kapitalkurve nach Reduzierung der Modellkomplexität.

Schlussfolgerung

Die Entwicklung von Trendfolgestrategien auf der Grundlage von Clustering und binärer Klassifizierung ist eine größere Herausforderung. Es sind neue Erkenntnisse darüber erforderlich, wie dies erreicht werden kann. Ein spezifisches Problem scheinen die Preise von Finanzanlagen zu sein, die sich außerhalb des Wertebereichs bewegen, für den das Modell trainiert wurde. Anders als bei der Ausbildung an Messgeräten, bei der die Preise bei neuen Daten häufiger denen entsprechen, die bei der Ausbildung festgestellt wurden. Bei der Anwendung von Merkmalen, die auf Preisunterschieden beruhen, zeigt das Modell erneut eine schlechte Generalisierungsfähigkeit.

Mit diesem Artikel wollte ich meine Experimente mit dem Marktregime-Clustering-Ansatz zusammenfassen, und vor Ihnen liegen neue, noch interessantere Ideen.

Beigefügte Materialien:

Dateiname	Beschreibung
labeling_lib.py	Aktualisierte Bibliothek von Samplern
trend_following.py	Skript für das Modelltraining
cat model_EURUSD_H1_0.onnx	Hauptmodell, einschließlich Ordner
catmodel_m_EURUSD_H1_0.onnx	Metamodell, Include-Ordner
EURUSD_H1_ONNX_include_0.mqh	Header Datei
trend_following.mq5	Trading Expert Advisor Quellcode
trend_following.ex5	Kompilierter Bot