Vom Neuling zum Experten: Autogeometrisches Analysesystem

Inhalt:

1. Einführung
2. Hintergrund
3. Übersicht
4. Umsetzung
5. Ergebnisse und Tests
6. Schlussfolgerung

Einführung

Die heutige Diskussion zielt darauf ab, die Herausforderung der Analyse von Kerzenmuster mit geometrischen Ansätzen anzugehen. In unserem kürzlich erschienenen Artikel „Vom Neuling zum Experten: Programmieren von Kerzen“ haben wir uns auf die Identifizierung einfacher Kerzenmuster konzentriert, die in der Regel aus nur wenigen Kerzen bestehen. Bei der Arbeit mit größeren Sequenzen von Kerzen wird die Mustererkennung jedoch komplexer, da die Konsistenz bei langen Serien tendenziell abnimmt.

Eine klare Erkenntnis ist jedoch, dass wir in den Daten immer noch die wichtigen Hochs und Tiefs erkennen können. Die Verknüpfung dieser Punkte kann uns helfen, Trends besser zu erkennen.

Als wir zum ersten Mal mit dem Devisenhandel in Berührung kamen, wurde in vielen Lehrbüchern die Idee von Dreiecksformationen und anderen geometrischen Mustern in der Marktpreisentwicklung vorgestellt. Und in der Tat ist die Geometrie auf den Märkten präsent - sie kann eine vereinfachte und visuelle Zusammenfassung dessen bieten, was der Markt tut.

Die meisten Händler sind daran gewöhnt, diese Formen manuell zu erkennen, indem sie Trendlinien zeichnen oder geometrische Objekte auf Charts platzieren. Heute wollen wir einen Schritt weiter gehen, indem wir MQL5 einsetzen, um diesen Prozess zu automatisieren, sodass manuelle Eingriffe überflüssig werden und eine schnellere und einheitlichere Analyse möglich ist.

Hintergrund

Der Vorteil der objektorientierten Programmierung (OOP) liegt in ihrer leistungsfähigen Fähigkeit, reale Berechnungsprobleme effizient zu modellieren und zu lösen. MQL5, eine von C++ abgeleitete Sprache, erbt diese Stärke und ist ein wertvolles Hilfsmittel für die Entwicklung von Handelsalgorithmen. In Anbetracht des vorliegenden Problems sind wir aufgrund der strukturellen und modularen Vorteile, die OOP bietet, bereits mit einem erheblichen Vorteil ausgestattet.

In diesem Abschnitt werden wir kurz die wichtigsten Begriffe zu unserem Thema definieren, bevor wir die traditionellen Methoden zur Identifizierung geometrischer Formen im Handel untersuchen. Obwohl es in der technischen Analyse viele Formen gibt, werden wir uns auf zwei gängige Beispiele konzentrieren: Rechtecke und Dreiecke.

Was ist Geometrie?

Die Geometrie ist ein Teilgebiet der Mathematik, das sich mit den Eigenschaften und Beziehungen des Raums beschäftigt. Dazu gehört das Studium von Entfernungen, Formen, Größen, Winkeln und der relativen Position von Figuren. Die Geometrie bietet einen robusten Rahmen für die Interpretation der physischen Welt, indem sie uns ermöglicht, räumliche Beziehungen zu modellieren und zu analysieren.

Warum ist Geometrie im Zusammenhang mit dem Handel wichtig?

Die Geometrie bietet einen visuellen und strukturellen Rahmen für das Verständnis und die Interpretation von Marktverhalten. Händler verlassen sich oft auf Muster und Formen, die sich aus der Preisentwicklung ergeben, und diese Muster sind von Natur aus geometrisch. Es hilft bei der Erkennung von Mustern, und hier ist eine Liste von häufigen Mustern, die den meisten Händlern bekannt sind:

• Dreieck (aufsteigend, absteigend, symmetrisch)
• Rechtecke (Konsolidierungsgebiete)
• Kanäle (parallele Trendlinien)
• Kopf und Schultern, Double Tops/Bottoms - alle hängen von geometrischer Symmetrie ab

Diese Muster helfen den Händlern:

• Potenzielle Ausbrüche oder Umkehrungen erkennen
• Trendstärke ablesen
• Einstiegs-/Ausstiegspunkte festlegen

In dieser Tabelle habe ich die wichtigsten Überlegungen zur Anwendung der geometrischen Analyse auf Marktpreisdaten zusammengestellt.

Aspekt	Die Rolle der Geometrie
Visuelle Klarheit	Hilft bei der Vereinfachung komplexer Marktdaten in erkennbare Formen
Entscheidungshilfe	Die Formen leiten den Einstieg, den Ausstieg und den Handelsaufbau
Objektivität	Reduziert Rätselraten durch präzise räumliche Logik
Automatisierung	Ermöglicht algorithmische Erkennung von Mustern und Schlüsselebenen
Marktpsychologie	Die Formen spiegeln oft das kollektive Verhalten von Händlern wider (z. B. zeigen Dreiecke eine Kompression).

Werfen wir einen Blick darauf, wie Dreiecks- und Rechteckgeometrien traditionell im Handel eingesetzt werden. Ich werde einen allgemeinen Überblick darüber geben, was die verschiedenen Dreiecksmuster typischerweise über die Preisentwicklung aussagen, aber ich werde nicht näher auf spezifische Handelsstrategien eingehen. Ich habe nämlich festgestellt, dass viele der allgemein anerkannten Regeln unter realen Marktbedingungen oft nicht mehr gültig sind. Auch wenn diese Muster bis zu einem gewissen Grad funktionieren, ist es ratsam, das Kursverhalten vor der Bildung der geometrischen Strukturen genau zu beobachten.

Obwohl zum Beispiel von einem aufsteigenden Dreieck im Allgemeinen erwartet wird, dass es zu einem Ausbruch nach oben führt, habe ich zahlreiche Fälle gesehen, in denen das Gegenteil der Fall war. Diese Formen stellen oft Entscheidungspunkte auf dem Markt dar, keine Garantien. Auch wenn das Muster eine bestimmte Richtung vorgibt, ist es wichtig, dass Sie Ihre Interpretation mit dem tatsächlichen Preiskontext abgleichen, der dem Muster vorausgeht. Sich allein auf Lehrbucherwartungen ohne Marktkontext zu verlassen, kann zu irreführenden Schlussfolgerungen führen.

Dreieck

Ein Dreieck ist eine geometrische Grundform, die durch drei Seiten und drei Ecken (Scheitelpunkte) definiert ist. Beim Devisenhandel weisen Dreiecksmuster auf mögliche Trendfortsetzungen oder -umkehrungen hin. Die wichtigsten Arten von Dreiecksmustern sind:

1. Symmetrical Triangle:

Zeigt eine Konsolidierungsphase mit abnehmender Volatilität an; sie geht häufig einem Ausbruch in eine der beiden Richtungen voraus.

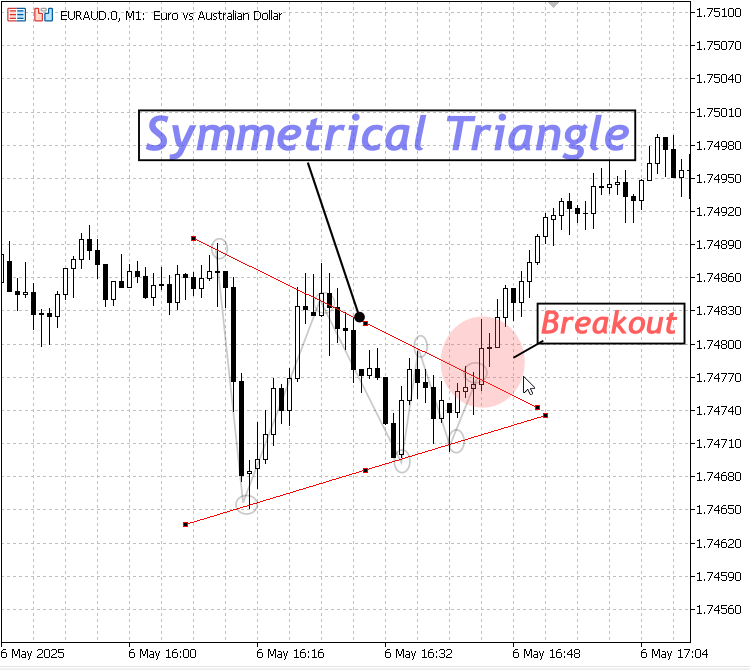
Symmetrisches Dreieck

2. Ascending Triangle:

Gekennzeichnet durch ein flaches oder leicht geneigtes Widerstandsniveau und eine steigende Unterstützung; typischerweise ein zinsbullisches Muster, das einen potenziellen Ausbruch nach oben signalisiert.

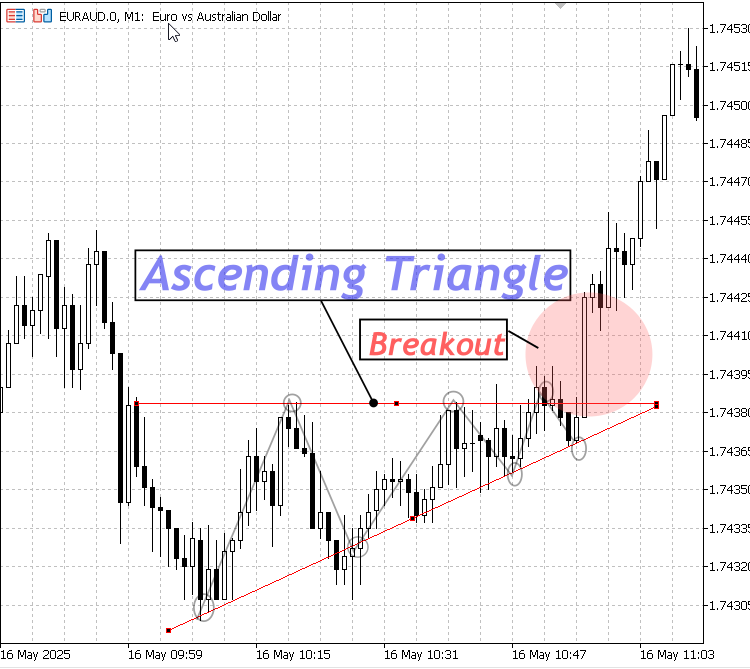
Aufsteigendes Dreieck

3. Descending Triangle:

Weist eine flache oder leicht geneigte Unterstützungslinie und einen abnehmenden Widerstand auf; in der Regel fallend, was auf einen Ausbruch nach unten hindeutet.

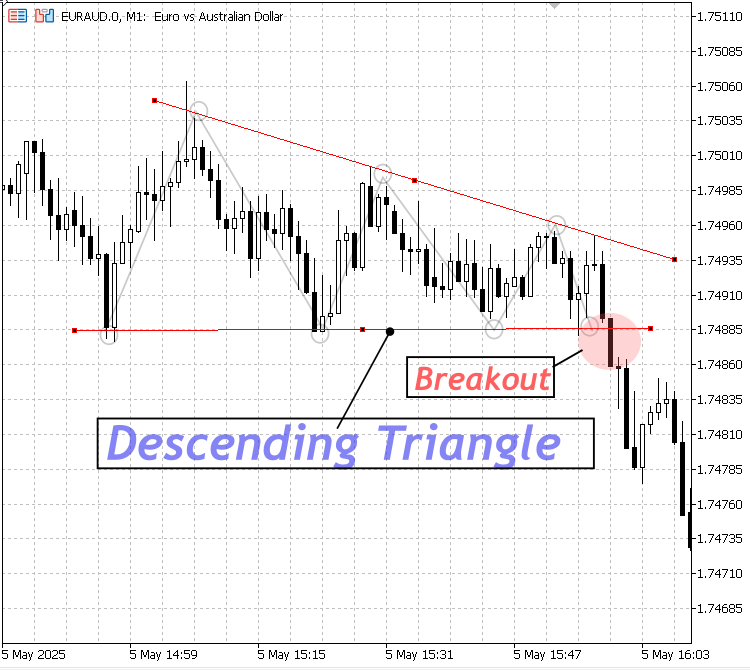
Absteigendes Dreieck

Rectangle

Ein Rechteck ist eine vierseitige geometrische Form, deren gegenüberliegende Seiten gleich und parallel sind. Er hat an jeder Ecke einen rechten Winkel (jeweils 90 Grad). In der Forex- und technischen Analyse ist ein Rechteck (auch Trading Range oder Konsolidierungszone genannt) ein Chartmuster, bei dem sich der Kurs innerhalb horizontaler Unterstützungs- und Widerstandsniveaus seitwärts bewegt. Er deutet auf eine Phase der Unentschlossenheit hin, bevor der Markt möglicherweise den vorherigen Trend fortsetzt oder umkehrt. Es ist unter den Marktanalyse-Tools auf dem Meta Trader 5 Terminal verfügbar.

Hier sind die wichtigsten Merkmale:

• Der Kurs pendelt zwischen einer klaren oberen Widerstandslinie und einer unteren Unterstützungslinie.
• Das Muster sieht auf dem Chart wie ein Rechteck oder ein Kasten aus.
• Ausbrüche über den Widerstand oder unter die Unterstützung signalisieren oft den Beginn eines neuen Trends.

Dieses Konzept lässt sich auch mit dem integrierten Tool für parallele Linien veranschaulichen, die horizontal ausgerichtet sind und Unterstützungs- und Widerstandsniveaus darstellen. Da es aus zwei parallelen Linien besteht, hebt er die Preisspanne während der Konsolidierung wirksam hervor. Das Rechteck ist jedoch nach wie vor die bevorzugte Wahl zur Kennzeichnung von Konsolidierungszonen, da es den spezifischen Zeitraum, in dem sich der Kurs seitwärts bewegt hat, visuell „einrahmt“. Es ist wichtig, daran zu denken, dass die Konsolidierung eine vorübergehende Phase ist - irgendwann wird der Markt aus dieser Spanne ausbrechen und seinen Trend fortsetzen oder die Richtung umkehren.

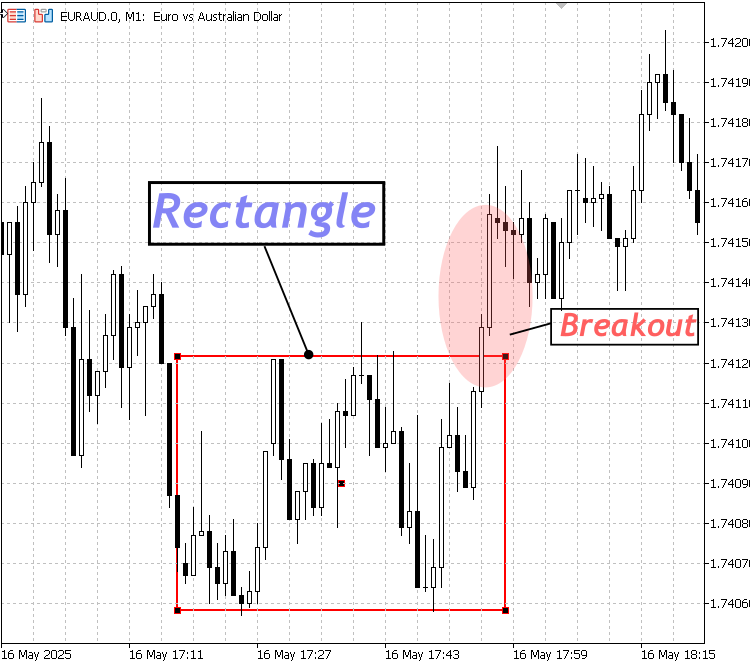
Rechteckige Struktur

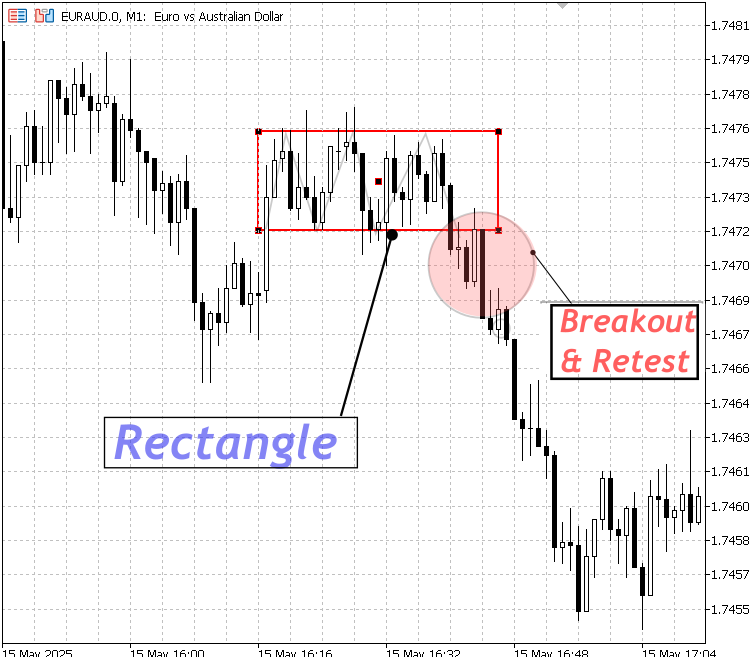
Ausbruch unter eine Rechteckstruktur

Übersicht

Nachdem wir nun die theoretische Grundlage für unsere Diskussion gelegt haben, folgt nun ein Überblick über die praktische Umsetzung. Wir werden modulare Programmiertechniken verwenden, um Komponenten für ein System zur Erkennung geometrischer Strukturen zu erstellen. Insbesondere werden wir separate Klassen zur Erkennung von Dreiecks- und Rechteckformationen in der Marktstruktur entwickeln. Dies sind nur die ersten Beispiele - der Ansatz ist erweiterbar, sodass wir bei Bedarf auch andere Formen unterstützen können. Dies ist einer der Hauptvorteile der objektorientierten und modularen Programmierfunktionen von MQL5, die es uns ermöglichen, komplexe reale Probleme mit sauberem, wartbarem Code zu lösen.

Die Header-Dateien, die wir in diesem Abschnitt erstellen, können leicht in den Haupt-Expert Advisor oder Indikator integriert werden. Außerdem können sie über mehrere Projekte hinweg wiederverwendet werden, was die Konsistenz und die Entwicklungseffizienz fördert.

In meinem Ansatz benötigt jede geometrische Form einen Satz von Referenzpunkten in den Preisdaten. Normalerweise brauchen wir zwei Hochs und zwei Tiefs. Diese Punkte werden mit Linien verbunden, um Formen zu bilden. So bilden beispielsweise zwei Punkte eine Linie, und ein Dreieck kann durch zwei Linien gebildet werden, die in einem Punkt in der Zukunft zusammenlaufen. Ein Rechteck ist hingegen zu erkennen, wenn sowohl die Widerstands- als auch die Unterstützungsebene zweimal berührt werden. Sobald diese Bedingungen erfüllt sind, kann die geometrische Form durch Verbinden der entsprechenden Referenzpunkte gezeichnet werden.

Um Ihnen das Verständnis zu erleichtern, habe ich unten einige Illustrationen beigefügt, die zeigen, wie diese Formen mit Hilfe von Computerlogik auf dem Chart konstruiert werden können. In der Regel benötigen wir mindestens vier Schlüsselpunkte, um jede Form zu umreißen. In den Bildern beginnen wir mit der Identifizierung der Punkte a, b, c und d - diese dienen als grundlegende Ankerpunkte für unsere Formstruktur. Von diesen Punkten aus kann die Form im Voraus projiziert werden. Die gestrichelten roten Linien stellen theoretische Erwartungen dar und zeigen, wie der Markt auf die erwarteten Grenzen der Form reagieren könnte. Die Art und Weise, wie der Kurs mit diesen Linien interagiert, kann wichtige Hinweise auf die künftige Kursentwicklung geben, z. B. auf mögliche Ausbrüche oder Abpraller.

Theoretische Erkennung eines Dreiecks

In der obigen Dreiecksabbildung sind die Umkehrpunkte a zu d als Bezugspunkte angegeben, aus denen ein Dreieck konstruiert werden kann, wobei sich die konvergierenden Linien im Punkt X treffen. Die Punkte e und f stellen theoretische zukünftige Berührungen dar - sie sind spekulativ und können sich nicht genau so entwickeln wie dargestellt. Sie sollen uns dabei helfen, das Muster zu konzipieren, damit wir die Idee in Code umsetzen können. Dasselbe Konzept gilt für das unten abgebildete Rechteck, bei dem die Struktur nach einer ähnlichen Logik erkannt wird; der entscheidende Unterschied ist jedoch, dass die Seiten parallel sind.

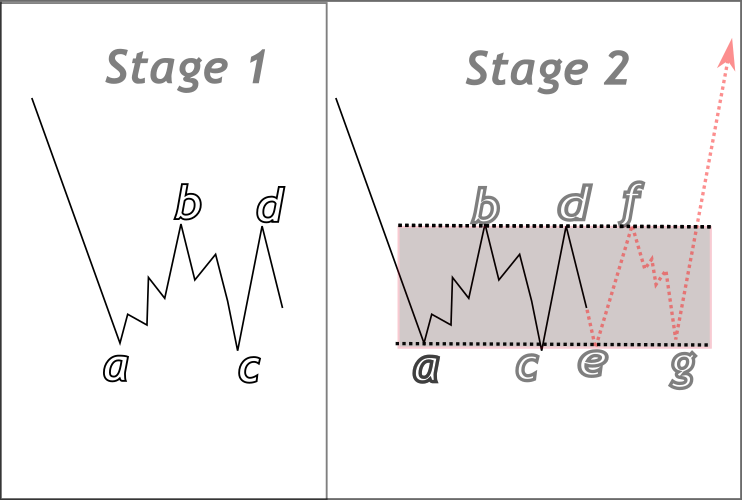
Erkennen von Rechteckstrukturen

Umsetzung

In diesem Stadium beginnt die eigentliche Entwicklung. Wir beginnen mit der Erstellung einer Header-Datei namens GeometricPatternDetector.mqh, die alle für die Erkennung geometrischer Muster erforderlichen Klassen enthält. Sobald der Header fertig ist, werden wir einen Expert Advisor (EA) entwickeln, der zeigt, wie die Klassen effektiv genutzt werden können. Gehen wir nun die folgenden Schritte durch, um zu verstehen, wie alles zusammenhängt.

Einschließlich des erforderlichen Headers

Ganz oben in GeometricPatternDetector.mqh ziehen wir drei wichtige MQL5-Bibliotheken hinzu, um unserem Detektor alle notwendigen Werkzeuge zu geben. Zunächst wird Arrays\ArrayObj.mqh eingebunden, damit wir CArrayObj - eine dynamische, objektorientierte Array-Klasse - verwenden können, um unsere Umkehrpunkte (SwingPoint) und Musterergebnisse (PatternResult) zu speichern, ohne uns mit rohen Zeigern oder manueller Speicherverwaltung herumschlagen zu müssen.

Indicators\Indicators.mqh bringt die in MetaTrader eingebauten Indikatorfunktionen wie iATR, CopyHigh, CopyLow und CopyTime ein, die es uns ermöglichen, historische Kursdaten abzurufen und die Average True Range problemlos zu berechnen. Math\Stat\Math.mqh schließlich stellt mathematische Konstanten wie M_PI und Hilfsfunktionen wie MathArctan bereit, die wir zur Berechnung von Steigungen, Winkeln und Ebenheitstoleranzen in unseren Algorithmen zur Mustererkennung verwenden. Zusammen bilden diese Bestandteile die Grundlage für robusten, lesbaren und wartbaren Code.

#include <Arrays\ArrayObj.mqh>       // For CArrayObj: dynamic arrays of objects 
#include <Indicators\Indicators.mqh> // For iATR, CopyHigh, CopyLow, CopyTime
#include <Math\Stat\Math.mqh>        // For M_PI, MathArctan, and other math utilities

Container-Klassen

Die Kopfzeile GeometricPatternDetector.mqh beginnt mit der Definition zweier einfacher Containerklassen: SwingPoint und PatternResult. Beide erben von MQL5's base CObject. Die Klasse SwingPoint enthält den Zeitstempel, den Preis und ein boolesches Flag, das angibt, ob der Pivot ein Hoch oder ein Tief ist. Auf diese Weise können wir die einzelnen Market Pivots in einem einzigen Objekt-Array sammeln und verwalten.

Die Klasse PatternResult kapselt alle Informationen, die zur Beschreibung eines erkannten Musters erforderlich sind, d. h. das Symbol, den Zeitrahmen, den Mustertyp, drei definierende „Scheitelpunkte“ und den Punkt, an dem ein Label platziert werden soll. Indem diese Datenelemente in Objekte verpackt werden, bleibt der Detektorcode sauber und konsistent, da er auf CArrayObj zur Speicherung zurückgreift und nicht auf manuelle parallele Arrays von Primitiven.

// SwingPoint: holds one market pivot
class SwingPoint : public CObject {
public:
   datetime time;
   double   price;
   bool     isHigh;
   SwingPoint(datetime t=0,double p=0.0,bool h=false)
     : time(t), price(p), isHigh(h) {}
};

// PatternResult: holds the details of one detected pattern
class PatternResult : public CObject {
public:
   string            symbol;
   ENUM_TIMEFRAMES   timeframe;
   ENUM_PATTERN_TYPE type;
   datetime          detectionTime;
   datetime          labelTime;
   double            labelPrice;
   datetime          vertex1Time;
   double            vertex1Price;
   datetime          vertex2Time;
   double            vertex2Price;
   datetime          vertex3Time;
   double            vertex3Price;
   PatternResult(const string _s,const ENUM_TIMEFRAMES _tf,const ENUM_PATTERN_TYPE _t,
                 datetime lt,double lp,
                 datetime v1t,double v1p,
                 datetime v2t,double v2p,
                 datetime v3t,double v3p)
     : symbol(_s), timeframe(_tf), type(_t), detectionTime(TimeCurrent()),
       labelTime(lt), labelPrice(lp),
       vertex1Time(v1t), vertex1Price(v1p),
       vertex2Time(v2t), vertex2Price(v2p),
       vertex3Time(v3t), vertex3Price(v3p) {}
};

Struktur der Detektorklasse

Den Kern des Headers bildet die Klasse CGeometricPatternDetector. Sein privater Abschnitt deklariert Mitgliedsvariablen für die Speicherung der Pivot-Objekte, Konfigurationsparameter (wie Swing-Lookback, ATR-Multiplikator und minimale Berührungspunkte) und den Status, der benötigt wird, um doppelte Zeichnungen zu verhindern (Namen und Hashes des letzten Dreiecks und Rechtecks, zusammen mit ihren Erkennungszeiten).

Vier Hilfsmethoden - IsNewBar, UpdateSwingPoints, CalculateATR und GetSwingHash - werden privat deklariert. Diese Dienstprogramme übernehmen die Identifizierung neuer Bars, die Extraktion von Swing-Pivots aus den jüngsten Daten von Hoch und Tief, die Berechnung eines Marktsensitivitätsmaßes über ATR und die Generierung eines eindeutigen String-Schlüssels für jeden Satz von vier Pivots. Zusammen unterstützen sie die beiden wichtigsten öffentlichen Erkennungsroutinen, DetectTriangle und DetectRectangle, sowie eine Update-Methode, die alles miteinander verbindet, und die Methoden GetLastPattern und ClearPatterns zum Abrufen von Ergebnissen und Aufräumen von Ressourcen.

class CGeometricPatternDetector {
private:
   CArrayObj   m_swings;
   int         m_swingLookback;
   double      m_atrMultiplier;
   int         m_minTouchPoints;

   string      m_lastTriangle;
   string      m_lastSwingHash;
   datetime    m_lastTriangleTime;

   string      m_lastRectangle;
   string      m_lastRectangleHash;
   datetime    m_lastRectangleTime;

   bool    IsNewBar(const string sym,const ENUM_TIMEFRAMES tf);
   void    UpdateSwingPoints(const string sym,const ENUM_TIMEFRAMES tf);
   double  CalculateATR(const string sym,const ENUM_TIMEFRAMES tf,const int period=14);
   string  GetSwingHash(SwingPoint *p1,SwingPoint *p2,SwingPoint *p3,SwingPoint *p4);

public:
   CGeometricPatternDetector(int swingLookback=3,double atrMultiplier=1.5,int minTouchPoints=2);
   ~CGeometricPatternDetector();

   void Update(const string sym,const ENUM_TIMEFRAMES tf);
   void DetectTriangle(const string sym,const ENUM_TIMEFRAMES tf);
   void DetectRectangle(const string sym,const ENUM_TIMEFRAMES tf);
   ENUM_PATTERN_TYPE GetLastPattern();
   void ClearPatterns();

   CArrayObj m_currentPatterns;
};

Extraktion von Umkehrpunkten

Die Methode zur Extraktion der Umkehrpunkte (swing points), UpdateSwingPoints, wird bei jedem neuen Balken aufgerufen. Er kopiert ein Fenster mit Hochs, Tiefs und Zeitstempeln aus dem Chart und bestimmt dann den zentralen Balken in diesem Fenster als Swing-High, wenn sein Preis über beiden Nachbarn liegt, oder als Swing-Low, wenn sein Preis unter beiden Nachbarn liegt. Jeder bestätigte Drehpunkt wird in ein Objekt SwingPoint verpackt und an das Array m_swings angehängt.

Wenn das Array über eine bestimmte Kapazität hinaus wächst, werden die ältesten Einträge verworfen. Diese gleitende Liste von Pivots bildet die Grundlage sowohl für die Dreiecks- als auch für die Rechteckerkennung und stellt sicher, dass nur die jüngsten und wichtigsten Marktbewegungen berücksichtigt werden.

void CGeometricPatternDetector::UpdateSwingPoints(const string sym,const ENUM_TIMEFRAMES tf)
{
   int bars = m_swingLookback*2 + 1;
   double highs[], lows[];
   datetime times[];
   ArraySetAsSeries(highs,true);
   ArraySetAsSeries(lows,true);
   ArraySetAsSeries(times,true);

   if(CopyHigh(sym,tf,0,bars,highs)<bars ||
      CopyLow(sym,tf,0,bars,lows)<bars   ||
      CopyTime(sym,tf,0,bars,times)<bars)
   {
      Print("Error: Failed to copy price/time data");
      return;
   }

   int mid = m_swingLookback;
   datetime t = times[mid];
   double h = highs[mid], l = lows[mid];

   bool isH = true;
   for(int i=1; i<=m_swingLookback; i++)
      if(h<=highs[mid-i] || h<=highs[mid+i]) { isH=false; break; }
   if(isH) {
      m_swings.Add(new SwingPoint(t,h,true));
      Print("Swing High detected at ",TimeToString(t)," Price: ",h);
   }

   bool isL = true;
   for(int i=1; i<=m_swingLookback; i++)
      if(l>=lows[mid-i] || l>=lows[mid+i]) { isL=false; break; }
   if(isL) {
      m_swings.Add(new SwingPoint(t,l,false));
      Print("Swing Low detected at ",TimeToString(t)," Price: ",l);
   }

   while(m_swings.Total()>50) {
      delete (SwingPoint*)m_swings.At(0);
      m_swings.Delete(0);
   }
}

CalculateATR verwendet den in MQL5 integrierten ATR-Indikator ein, um eine marktsensitive Größeneinheit bereitzustellen, während GetSwingHash vier Pivot-Zeiten und Preise zu einem String-Schlüssel verkettet. Der ATR-Wert skaliert die Toleranzen sowohl für die „Flachheit“ bei Dreiecken als auch für die Ausrichtung bei Rechtecken. Die Hash-Zeichenkette stellt sicher, dass jeder eindeutige Pivot-Satz nur einmal in der Sperrfrist gezogen wird.

double CGeometricPatternDetector::CalculateATR(const string sym,const ENUM_TIMEFRAMES tf,const int period)
{
   int h = iATR(sym,tf,period);
   if(h==INVALID_HANDLE) { Print("ATR handle error"); return 0; }
   double buf[]; ArraySetAsSeries(buf,true);
   if(CopyBuffer(h,0,0,1,buf)!=1) { Print("ATR copy error"); return 0; }
   return buf[0];
}

string CGeometricPatternDetector::GetSwingHash(SwingPoint *p1,SwingPoint *p2,SwingPoint *p3,SwingPoint *p4)
{
   return TimeToString(p1.time)+"*"+DoubleToString(p1.price,8)+"*"
        + TimeToString(p2.time)+"*"+DoubleToString(p2.price,8)+"*"
        + TimeToString(p3.time)+"*"+DoubleToString(p3.price,8)+"*"
        + TimeToString(p4.time)+"_"+DoubleToString(p4.price,8);
}

Logik der Dreieckserkennung

Die Routine zum Erkennen der Dreiecke sucht strikt nach vier aufeinanderfolgenden Umkehrpunkten in der Reihenfolge Tief zu Hoch zu Tief zu Hoch. Nachdem eine Mindestspanne für jeden Schenkel festgelegt wurde, werden die Steigungen der unteren und oberen Seite berechnet, indem die Preisunterschiede durch die Zeitunterschiede geteilt werden. Eine ATR-basierte Toleranz bestimmt, ob die Ober- oder Unterseite des Dreiecks ausreichend flach ist, um als absteigend oder aufsteigend eingestuft zu werden; ist keine der beiden Seiten flach genug, wird das Muster als symmetrisch eingestuft.

Die beiden Seitenlinien werden dann analytisch geschnitten, um den Scheitelpunkt des Dreiecks in der Zukunft zu finden. Ein einzelnes OBJ_TRIANGLE-Objekt wird unter Verwendung der beiden Umkehrpunkte und des berechneten Scheitelpunkts gezeichnet, und ein Objekt PatternResult wird erstellt und gespeichert. Um Flimmern zu verhindern, vergleicht der Detektor einen Hash der vier Drehpunkte mit dem zuletzt gezeichneten Muster und sperrt Neuzeichnungen derselben Form für eine bestimmte Anzahl von Balken.

void CGeometricPatternDetector::DetectTriangle(const string sym,const ENUM_TIMEFRAMES tf)
{
   int tot = m_swings.Total();
   if(tot < 4) return;
   ulong barSec = PeriodSeconds(tf);
   ulong minSpan = (ulong)m_swingLookback * barSec;

   for(int i=0; i<=tot-4; i++)
   {
      SwingPoint *p1 = (SwingPoint*)m_swings.At(i);
      SwingPoint *p2 = (SwingPoint*)m_swings.At(i+1);
      SwingPoint *p3 = (SwingPoint*)m_swings.At(i+2);
      SwingPoint *p4 = (SwingPoint*)m_swings.At(i+3);

      if(!( !p1.isHigh && p2.isHigh && !p3.isHigh && p4.isHigh )) continue;
      if((ulong)(p2.time-p1.time)<minSpan ||
         (ulong)(p3.time-p2.time)<minSpan ||
         (ulong)(p4.time-p3.time)<minSpan) continue;

      double m_low  = (p3.price - p1.price) / double(p3.time - p1.time);
      double m_high = (p4.price - p2.price) / double(p4.time - p2.time);
      double tolFlat = CalculateATR(sym,tf,14) * m_atrMultiplier;

      bool lowerFlat = MathAbs(p3.price-p1.price) < tolFlat;
      bool upperFlat = MathAbs(p4.price-p2.price) < tolFlat;

      ENUM_PATTERN_TYPE type;
      if(lowerFlat && m_high < 0)             type = PATTERN_TRIANGLE_DESCENDING;
      else if(upperFlat && m_low > 0)         type = PATTERN_TRIANGLE_ASCENDING;
      else                                    type = PATTERN_TRIANGLE_SYMMETRICAL;

      double denom = m_low - m_high;
      if(MathAbs(denom)<1e-12) continue;
      double num = (p2.price - p1.price) + (m_low*p1.time - m_high*p2.time);
      double tx  = num/denom;
      double px  = p1.price + m_low*(tx-p1.time);

      datetime latest = MathMax(p1.time,p2.time);
      if(tx<=latest || tx>TimeCurrent()+barSec*50) continue;

      if(StringLen(m_lastTriangle)>0)
         ObjectDelete(0,m_lastTriangle);

      string base = "GPD_"+sym+"_"+EnumToString(tf)+"_"+TimeToString(TimeCurrent(),TIME_SECONDS);
      long cid    = ChartID();
      m_lastTriangle = base+"_T";

      ObjectCreate(cid,m_lastTriangle,OBJ_TRIANGLE,0,
                   p1.time,p1.price,
                   p2.time,p2.price,
                   tx,      px);
      ObjectSetInteger(cid,m_lastTriangle,OBJPROP_COLOR,clrOrange);
      ObjectSetInteger(cid,m_lastTriangle,OBJPROP_WIDTH,2);
      ObjectSetInteger(cid,m_lastTriangle,OBJPROP_FILL,false);

      m_lastSwingHash    = GetSwingHash(p1,p2,p3,p4);
      m_lastTriangleTime = TimeCurrent();
      m_currentPatterns.Add(new PatternResult(
         sym,tf,type,
         latest,(p2.price+p4.price)/2.0,
         p1.time,p1.price,
         p2.time,p2.price,
         (datetime)tx,px
      ));

      ChartRedraw(cid);
      break;
   }
}

Die Logik der Erkennung eines Rechtecks

Die Erkennung von Rechtecken folgt einer ähnlichen Pivot-Sequenz, unterliegt aber strengeren Einschränkungen. Zunächst werden vier Umkehrpunkte in demselben Muster von Tief-Hoch zu Tief-Hoch identifiziert, wobei sich jeder Umkehrpunkt (Tief zu Hoch und der zweite Tief zu Hoch) über mindestens fünf Balken erstrecken und eine ATR-skalierte Größenschwelle überschreiten muss. Die Unterseite des Rechtecks wird am Durchschnitt der beiden Tiefststände ausgerichtet, sofern diese innerhalb der ATR-Toleranz liegen. Wenn die beiden Höchstwerte ebenfalls innerhalb dieser Toleranz liegen, wird die Oberseite auf ihren Mittelwert gesetzt; andernfalls wird eine Mindesthöhe von einer ATR-Einheit verwendet, damit das Rechteck sichtbar bleibt.

Das Rechteck wird mit OBJ_RECTANGLE gezeichnet und erstreckt sich vom frühesten Pivot-Zeitpunkt bis genau zwanzig Balken später, um ein unbegrenztes Wachstum zu verhindern. Ein eindeutiger Hash eines Umkehrpunkts stellt sicher, dass jedes einzelne Rechteck nur einmal pro Sperrfrist gezeichnet wird, und seine Details werden in einem PatternResult aufgezeichnet.

void CGeometricPatternDetector::DetectRectangle(const string sym,const ENUM_TIMEFRAMES tf)
{
   int tot = m_swings.Total();
   if(tot < 4) return;

   ulong barSec    = PeriodSeconds(tf);
   ulong minSpan5  = 5 * barSec;                        
   double tolATR   = CalculateATR(sym,tf,14) * m_atrMultiplier;

   for(int i=0; i<=tot-4; i++)
   {
      SwingPoint *a = (SwingPoint*)m_swings.At(i);
      SwingPoint *b = (SwingPoint*)m_swings.At(i+1);
      SwingPoint *c = (SwingPoint*)m_swings.At(i+2);
      SwingPoint *d = (SwingPoint*)m_swings.At(i+3);

      if(!( !a.isHigh && b.isHigh && !c.isHigh && d.isHigh )) continue;
      if((ulong)(b.time - a.time) < minSpan5 ||
         (ulong)(d.time - c.time) < minSpan5) continue;
      if(MathAbs(b.price - a.price) < tolATR ||
         MathAbs(d.price - c.price) < tolATR) continue;
      if(MathAbs(a.price - c.price) > tolATR) continue;

      bool highAligned = MathAbs(b.price - d.price) < tolATR;
      double lowP  = (a.price + c.price) / 2.0;
      double highP = highAligned ? (b.price + d.price)/2.0 : lowP + tolATR;

      datetime leftT  = MathMin(a.time, c.time);
      datetime rightT = leftT + (datetime)(20 * barSec);

      string rh = TimeToString(leftT,TIME_SECONDS) + "_" +
                  DoubleToString(lowP,8) + "_" +
                  DoubleToString(highP,8);
      datetime lockT = m_lastRectangleTime + (datetime)(40 * barSec);
      if(rh == m_lastRectangleHash && TimeCurrent() < lockT) return;

      if(StringLen(m_lastRectangle) > 0)
         ObjectDelete(0,m_lastRectangle);

      string base = "GPD_"+sym+"_"+EnumToString(tf)+"_"+TimeToString(TimeCurrent(),TIME_SECONDS);
      long cid    = ChartID();
      m_lastRectangle = base+"_Rect";

      ObjectCreate(cid,m_lastRectangle,OBJ_RECTANGLE,0,
                   leftT,   highP,
                   rightT,  lowP);
      ObjectSetInteger(cid,m_lastRectangle,OBJPROP_COLOR, clrBlue);
      ObjectSetInteger(cid,m_lastRectangle,OBJPROP_WIDTH, 2);
      ObjectSetInteger(cid,m_lastRectangle,OBJPROP_FILL,  false);

      m_currentPatterns.Add(new PatternResult(
         sym,tf,PATTERN_RECTANGLE,
         leftT,(highP+lowP)/2.0,
         leftT,highP,
         leftT,lowP,
         rightT,lowP
      ));
      m_lastRectangleHash = rh;
      m_lastRectangleTime = TimeCurrent();

      ChartRedraw(cid);
      break;
   }
}

Verwendung der Kopfzeile in einem Expert Advisor

Die Integration dieser Kopfzeile in einen Expert Advisor ist einfach. Wir binden es einfach ein, instanziieren einen CGeometricPatternDetector mit unseren bevorzugten Parametern und rufen seine Methode Update(Symbol(), _Period) in OnTick auf. Nach jeder Aktualisierung zeigt GetLastPattern an, ob ein neues Dreieck oder Rechteck erkannt wurde, und Sie können detector.m_currentPatterns untersuchen, um vollständige Details abzurufen, Warnungen auszugeben oder Chartbeschriftungen zu platzieren.

Der EA muss die zugrundeliegende Geometrie oder Pivot-Logik nicht kennen; er steuert einfach den Detektor und reagiert auf die Ergebnisse auf höchster Ebene. Diese Trennung - Deklaration im Header, detaillierte Implementierung in derselben Datei und einfache Verwendung im EA - zeigt, wie objektorientiertes Design in MQL5 die Komplexität kapselt und wiederverwendbaren, wartbaren Code erzeugt. Gehen wir im Folgenden die einzelnen Schritte durch.

Einbinder des Headers und globaler Status

Ganz oben in GeometryAnalyzerEA.mq5 fügen wir unseren Detektor-Header ein, damit der Expert Advisor auf die Klasse CGeometricPatternDetector und ihre unterstützenden Typen zugreifen kann. Unmittelbar danach instanziieren wir ein einzelnes Detektorobjekt mit ausgewählten Parametern - drei Balken Rückblick für Pivots, ein ATR-Multiplikator von 1,5 für die Toleranz und zwei Mindestberührungspunkte für Muster. Wir deklarieren auch drei globale Variablen: lastAlerted speichert den Typ des letzten Musters, das wir alarmiert haben, damit wir es nicht auf demselben Balken wiederholen, lastBarTime verfolgt, wann ein neuer Balken eintrifft, und lastLabelName enthält den Namen des Textlabels, das wir platziert haben, damit es gelöscht werden kann, wenn ein neues Muster erscheint.

#include <GeometricPatternDetector.mqh>

//–– detector instance & state
CGeometricPatternDetector  detector(3, 1.5, 2);
ENUM_PATTERN_TYPE          lastAlerted    = PATTERN_NONE;
datetime                   lastBarTime    = 0;
string                     lastLabelName  = "";

Initialisierung und Bereinigung

Die Funktion OnInit wird einmal beim Start des EA ausgeführt. Hier drucken wir einfach eine Nachricht, um die Initialisierung zu bestätigen, obwohl Sie bei Bedarf auch einen Timer starten oder Ressourcen zuweisen könnten. Umgekehrt wird OnDeinit ausgeführt, wenn der EA entfernt oder das Chart geschlossen wird. In dieser Routine löschen wir alle gezeichneten Muster mittels detector.ClearPatterns() und löschen alle verbleibenden Textbeschriftungen nach Namen. Schließlich protokollieren wir den Grund für die Deinitialisierung, sodass es einfacher ist, zu diagnostizieren, warum der EA angehalten hat.

int OnInit()
{
   Print("GeometryAnalyzerEA initialized");
   return(INIT_SUCCEEDED);
}

void OnDeinit(const int reason)
{
   detector.ClearPatterns();
   if(StringLen(lastLabelName) > 0)
      ObjectDelete(0, lastLabelName);
   Print("GeometryAnalyzerEA deinitialized, reason=", reason);
}

Erkennen eines neuen Balkens

Innerhalb von OnTick wird zunächst festgestellt, ob der eingehende Tick zu einem neu gebildeten Balken gehört. Wir holen die Öffnungszeit des aktuellen Balkens ab und vergleichen sie mit unserer gespeicherten lastBarTime. Wenn der Balken neu ist, setzen wir lastAlerted zurück, damit die Muster erneut ausgelöst werden, und löschen die vorherige Textbeschriftung, um das Chart sauber zu halten. Wenn der Balken nicht neu ist, kehren wir einfach zurück und tun nichts weiter, sodass die Mustererkennung nur einmal pro Balken ausgeführt wird.

void OnTick()
{
   datetime curBar = iTime(Symbol(), _Period, 0);
   bool isNewBar  = (curBar != lastBarTime);
   if(isNewBar)
   {
      lastBarTime = curBar;
      lastAlerted = PATTERN_NONE;
      if(StringLen(lastLabelName) > 0)
      {
         ObjectDelete(0, lastLabelName);
         lastLabelName = "";
      }
   }
   if(!isNewBar)
      return;
   // …
}

Betrieb des Detektors

Sobald wir einen neuen Balken bestätigt haben, rufen wir die Update-Methode des Detektors auf und geben dabei das aktuelle Symbol und den Zeitrahmen an. Dieser einzige Aufruf aktualisiert die Umkehrpunkte und führt sowohl die Erkennungsroutinen der Dreiecke und der Rechtecke „unter der Haube“ aus. Nach der Rückkehr von Update wird GetLastPattern() abgefragt, um festzustellen, ob für diesen Balken ein gültiges Muster gefunden wurde. Wenn kein neues Muster auftaucht, oder wenn es mit dem Muster übereinstimmt, das wir bereits alarmiert haben, beenden wir die Suche vorzeitig.

detector.Update(Symbol(), _Period);

ENUM_PATTERN_TYPE pattern = detector.GetLastPattern();
if(pattern == PATTERN_NONE || pattern == lastAlerted)
   return;
lastAlerted = pattern;

Behandlung eines erkannten Musters

Wenn ein neues Muster auftaucht, wird das letzte PatternResult aus dem Pattern-Array des Detektors abgerufen. Anschließend übersetzen wir die Enumeration der Muster in sprechende Namen und formatieren seine Eckpunkte für die Protokollierung. Rechtecke werden besonders behandelt, weil sie nur drei Eckpunkte liefern; wir approximieren den vierten, um einen vollständigen Satz von Koordinaten zu erhalten. Wir geben sowohl eine Warnmeldung als auch eine Druckanweisung aus, die den Musternamen, die Zeit, den Preis und die Eckkoordinaten anzeigt.

int count = detector.m_currentPatterns.Total();
PatternResult *pr = (PatternResult*)detector.m_currentPatterns.At(count - 1);

string name = (pattern == PATTERN_RECTANGLE) ? "Rectangle" :
              (pattern == PATTERN_TRIANGLE_ASCENDING)   ? "Ascending Triangle" :
              (pattern == PATTERN_TRIANGLE_DESCENDING)  ? "Descending Triangle" :
                                                         "Symmetrical Triangle";

Alert("GeometryAnalyzerEA: Detected ", name, " on ", Symbol(), " ", EnumToString(_Period));
Print("GeometryAnalyzerEA: ", name,
      " @", TimeToString(pr.labelTime, TIME_SECONDS),
      " Price=", pr.labelPrice);

Zeichnen der Kennzeichnungen

Zum Schluss platzieren wir eine Textbeschriftung auf dem Chart zum angegebenen Zeitpunkt und Preis des Musters. Ein eindeutiger Objektname wird durch die Kombination des Musternamens mit dem Etikett time erzeugt. Mithilfe von Chartobjektfunktionen zeichnen wir OBJ_TEXT und legen seine Eigenschaften fest - Textinhalt, Farbe, Schriftgröße und Hintergrund - damit er im Chart deutlich sichtbar ist. Wir zeichnen den Namen des letzten Etiketts auf, damit er beim nächsten neuen Balken entfernt werden kann, bevor ein neues Etikett gezeichnet wird. Ein Aufruf zum erneuten Zeichnen des Charts sorgt für eine sofortige Darstellung.

   lastLabelName = name + "_" + TimeToString(pr.labelTime, TIME_SECONDS);
   long chartId = ChartID();
   if(ObjectCreate(chartId, lastLabelName, OBJ_TEXT, 0, pr.labelTime, pr.labelPrice))
   {
      ObjectSetString(chartId, lastLabelName, OBJPROP_TEXT,     name);
      ObjectSetInteger(chartId, lastLabelName, OBJPROP_COLOR,    clrOrangeRed);
      ObjectSetInteger(chartId, lastLabelName, OBJPROP_FONTSIZE, 12);
      ObjectSetInteger(chartId, lastLabelName, OBJPROP_BACK,     true);
   }
   ChartRedraw(chartId);
}

Tests und Ergebnisse

Um die Leistung des EA schnell zu bewerten, haben wir den Strategietester verwendet, um sein Verhalten anhand historischer Daten zu überprüfen. Die Ergebnisse waren vielversprechend: Muster wurden korrekt erkannt und Formen wie erwartet gezeichnet. Außerdem hatte ich die Gelegenheit, den EA in einem Live-Chart zu beobachten, wo er bemerkenswert gut funktionierte. Die Auslösung von Mustersignalen erfolgte problemlos neben der Formwiedergabe in Echtzeit und bestätigte die Robustheit der Integration. Werfen Sie einen Blick auf die nachstehende Präsentation.

Strategie-Tester Visualisierung: GeometricAnalyzerEA

Nachfolgend finden Sie ein Protokoll, das die Erkennung eines aufsteigenden Dreiecks während des Tests zeigt.

2025.05.20 13:40:54.241 2025.01.14 18:45:00   Alert: GeometryAnalyzerEA: Detected Ascending Triangle on AUDJPY.0 PERIOD_M1
2025.05.20 13:40:54.241 2025.01.14 18:45:00   GeometryAnalyzerEA: Ascending Triangle @14:03:00 Price=97.45599999999999 → Vertices: (1736863200@97.381), (1736863380@97.448), (1736873819@97.912)
2025.05.20 13:40:54.242 2025.01.14 18:46:00   Swing High detected at 2025.01.14 18:43 Price: 97.789

Schlussfolgerung

Zusammenfassend lässt sich sagen, dass wir mit MQL5 erfolgreich ein automatisiertes System entwickelt haben, das in der Lage ist, Dreiecks- und Rechteck-Marktstrukturen zu erkennen. Diese geometrischen Muster, die in der technischen Analyse seit langem anerkannt sind, bieten aussagekräftige Einblicke in das Marktverhalten - insbesondere bei der Identifizierung potenzieller Fortsetzungs- oder Umkehrzonen. Indem wir uns auf klar definierte Formen wie aufsteigende Dreiecke und Rechtecke konzentrieren, zeigen wir, wie die Geometrie Kursbewegungen in visuelle, algorithmische Strukturen übersetzen kann, die sowohl handlungsfähig als auch zuverlässig sind.

Der von uns umgesetzte Ansatz bildet eine solide Grundlage für den Aufbau komplexerer Analysesysteme. Die Klasse GeometricPatternDetector ist modular und wiederverwendbar - sie kann in andere Projekte integriert und für eine verbesserte Erkennungsgenauigkeit und Flexibilität erweitert werden.

Obwohl unser System die Formen auf dem Chart akkurat zeichnet, gibt es Raum für die Verfeinerung der Strukturerkennungslogik, um Randfälle zu behandeln und die Präzision der Mustererkennung zu verbessern. Dieses Projekt zeigt, wie algorithmische Ansätze die Erkennung komplexer Marktmuster vereinfachen und einen ansonsten sehr aufwändigen manuellen Prozess rationalisieren können.

Diese Reise war eine Reise des ständigen Lernens. Dabei haben wir gesehen, wie die klassenbasierte Entwicklung in MQL5 nicht nur die Modularität verbessert, sondern auch die Wiederverwendung von Code und die Abstraktion von Schnittstellen fördert. Dies ermöglicht es anderen Entwicklern - oder sogar Endnutzern - mit einer sauberen High-Level-Schnittstelle zu arbeiten, ohne die Low-Level-Erkennungslogik verstehen zu müssen.

Für diejenigen von uns, die solche Systeme entwickeln, ist die Beherrschung der internen Implementierung von entscheidender Bedeutung. Dank des gekapselten Designs können aber auch andere von der Funktionalität profitieren, ohne sich mit dem zugrunde liegenden Code auseinandersetzen zu müssen. Mit dieser Struktur können wir das System nun selbstbewusst entwickeln und erweitern, um jedes beliebige Marktmuster zu erkennen, indem wir einfach geeignete Klassen entwerfen.

Die nächste logische Weiterentwicklung wäre die Integration einer Logik für die Auftragsausführung, die auf bestätigten Mustern basiert, wie z. B. die Ausführung von Kaufaufträgen beim Ausbruch aus einem aufsteigenden Dreieck, die Platzierung von Stop-Loss-Punkten an den letzten Swing-Punkten und die Festlegung dynamischer Take-Profits anhand der Höhe des Musters. Zu den fortschrittlicheren Verbesserungen gehören die Bestätigung von Mustern mit Volumen- oder Oszillatorindikatoren, die Anwendung von Multi-Timeframe-Analysen zur Validierung und die Implementierung eines Rankingsystems zur Priorisierung hochwertiger Setups.

Anhänge:

Datei	Beschreibung
GeometricPatternDetector.mqh	Diese Header-Datei enthält die vollständige, klassenbasierte Implementierung der Logik der geometrischen Mustererkennung. Es definiert Datenstrukturen für Umkehrpunkte und Musterergebnisse, verwaltet die Erkennung der Umkehrpunkte, berechnet die Marktsensitivität mit Hilfe der ATR und enthält Routinen zur Identifizierung von Dreiecken und Rechtecken. Die Datei ist für die modulare Integration in Expert Advisors konzipiert.
GeometryAnalyzerEA.mq5	Dieser Expert Advisor demonstriert die praktische Anwendung des Pattern Detection Headers. Es initialisiert und aktualisiert die Klasse „CGeometricPatternDetector“ bei jedem neuen Balken, holt die Musterergebnisse ab und kommentiert die erkannten Muster visuell auf dem Chart. Es dient als einfaches, praxisnahes Beispiel für die Integration der objektorientierten Mustererkennung in eine Handelsstrategie.