Diskussion zum Artikel "Ökonometrische Instrumente zur Prognose der Volatilität: das GARCH-Modell"
Sehr gute Arbeit!
Ich habe sie in einem Augenblick gelesen.
Ich danke Ihnen!
Guter Artikel. Es wäre interessant, Ihre Meinung zu Stepanovs Artikel zu erfahren, in dem er eine Hypothese über die nicht-stochastische Natur von Volatilitätsschwankungen aufstellt.
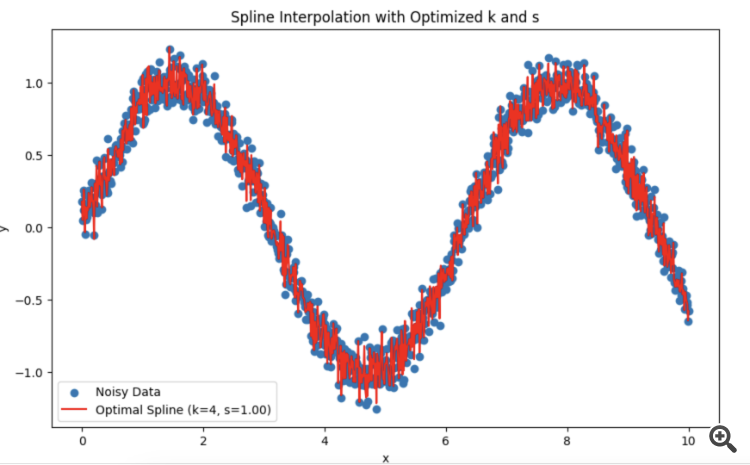
Sie haben mich direkt mit meinem TS konfrontiert. Ich versuche es mit Splines anstelle von HP.
Ich habe mich gefragt, wie ich die Periode und den Grad der Glättung am besten wählen soll.
Es stellt sich heraus, dass es besser ist, sich auf den Test auf Normalverteilung der Residuen zu verlassen?
Du hast mich genau in meinem TC getroffen. Ich versuche es mit Splines anstelle von HP.
Ich habe mich gefragt, was besser ist, um die Periode und den Grad der Glättung zu wählen.
Es stellt sich heraus, dass es besser ist, sich auf den Test auf Normalverteilung der Residuen zu verlassen?
Guter Artikel. Es wäre interessant, Ihre Meinung zu Stepanovs Artikel zu erfahren, in dem er eine Hypothese über die nicht-stochastische Natur von Volatilitätsschwankungen aufstellt.
Der Artikel ist komplex und widersprüchlich. Einerseits verwendet der Autor eine probabilistische Terminologie und statistische Instrumente, charakterisiert Preissteigerungen und Volatilität als Zufallsvariablen, konstruiert Verteilungen verschiedener Volatilitätsmaße usw., andererseits hält er nichts von stochastischen Volatilitätsmodellen.
Imho, ja, wenn man Modelle für Inkremente über konstante Zeitintervalle erstellt, muss man am Ende alles auf Gaußsches Rauschen reduzieren. Das ist wahrscheinlich der ganze Sinn der Ökonometrie - alle Faktoren, die im Modell nicht berücksichtigt werden, sollten sich wie glattes Rauschen verhalten.
Interessant, ich habe das noch nicht gemacht. In dem Artikel hat der Autor die Parameter sozusagen empirisch ausgewählt. Es ist jedoch möglich, eine Optimierung über die Likelihood-Funktion durchzuführen.
Ein Thema für die Forschung :)
Interessant, ich habe das noch nicht gemacht. In dem Artikel hat der Autor die Parameter sozusagen empirisch ausgewählt. Aber es ist möglich, eine Optimierung durch die Likelihood-Funktion durchzuführen.
Ein Thema für die Forschung :)
Ich habe LLM DeepSeek mit Gottes Hilfeentwickelt. Sie können Ihre eigenen Daten ersetzen.
Zur Erläuterung:
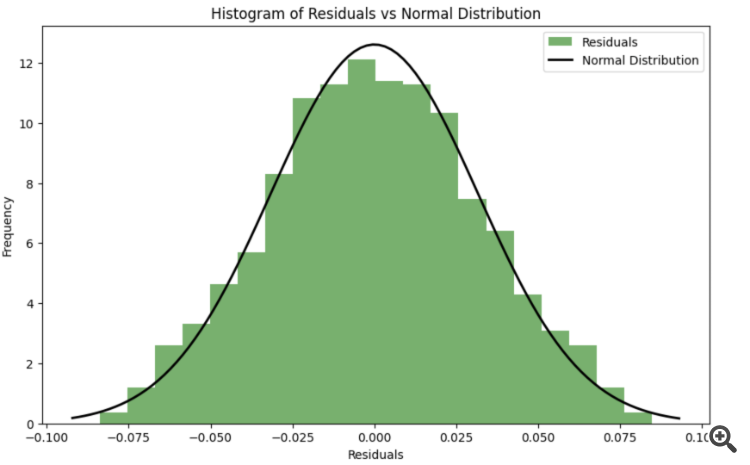
Um die Residuen während des Optimierungsprozesses so nahe wie möglich an eine Normalverteilung heranzuführen, kann ein Übereinstimmungskriterium (z.B. Shapiro-Wilk-Kriterium oder Kolmogorov-Smirnov-Kriterium) verwendet werden, um die Normalität der Residuen zu beurteilen. Die Parameter k k und s skönnen dann so optimiert werden, dass die Abweichung der Residuen von der Normalverteilung minimiert wird.
-
Fehlerfunktion unter Berücksichtigung der Normalität der Residuen: Es wird eine neue Funktion spline_error_with_normality eingeführt, die die Residuen berechnet und das Shapiro-Wilk-Kriterium zur Bewertung ihrer Normalität verwendet. Der negative p-Wert wird minimiert, um die Normalität der Residuen zu maximieren.
-
Optimierung: Sie wird zur Optimierung der Parameter k k und s s auf der Grundlage einer neuen Fehlerfunktion verwendet .
Mit diesem Ansatz können die Spline-Parameter so angepasst werden, dass die Residuen die Normalverteilung maximieren, was die Qualität des Modells und die Interpretierbarkeit der Ergebnisse verbessern kann.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel Ökonometrische Instrumente zur Prognose der Volatilität: das GARCH-Modell :
Der Artikel beschreibt die Eigenschaften des nichtlinearen Modells der bedingten Heteroskedastizität (GARCH). Der Indikator iGARCH wurde auf seiner Grundlage für die Vorhersage der Volatilität einen Schritt weiter entwickelt. Die numerische Analysebibliothek ALGLIB wird zur Schätzung der Modellparameter verwendet.
Die Volatilität ist ein wichtiger Indikator für die Bewertung der Variabilität der Preise von Finanzanlagen. Bei der Analyse von Börsenkursen wird seit langem festgestellt, dass große Preisänderungen sehr oft zu noch größeren Veränderungen führen, insbesondere in Finanzkrisen. Auf kleine Veränderungen folgen in der Regel auch kleine Preisänderungen. Auf ruhige Zeiten folgen also Zeiten relativer Instabilität.
Das erste Modell, mit dem versucht wurde, dieses Phänomen zu erklären, war ARCH, entwickelt von Engle: „Autoregressive conditional heteroscedasticity (heterogeneity)“ (Autoregressive bedingte Heteroskedastizität (Heterogenität)). Neben dem Clustering-Effekt (Gruppierung der Renditen in Bündel von großen und kleinen Werten) erklärt das Modell auch das Auftreten von starken Ausläufer und positiver Kurtosis, die für alle Verteilungen von Preissteigerungen charakteristisch sind. Der Erfolg des bedingten Gauß-Modells ARCH führte zur Entstehung einer Reihe von Verallgemeinerungen dieses Modells. Ihr Ziel war es, Erklärungen für eine Reihe anderer Phänomene zu liefern, die bei der Analyse von Finanzzeitreihen beobachtet werden. Historisch gesehen ist eine der ersten Verallgemeinerungen von ARCH das Modell GARCH (verallgemeinertes ARCH) Modell.
Der Hauptvorteil von GARCH im Vergleich zu ARCH liegt in der Tatsache, dass es sparsamer ist und bei der Anpassung von Stichprobendaten keine langfristige Struktur erfordert. In diesem Artikel möchte ich das Modell GARCH beschreiben und vor allem ein fertiges Tool für die Volatilitätsprognose auf der Grundlage dieses Modells anbieten, da die Prognose eines der Hauptziele bei der Analyse von Finanzdaten ist.
Autor: Evgeniy Chernish