
모집단 최적화 알고리즘: 하모니 검색(HS)
콘텐츠:
1. 소개
음악의 구성 요소는 리듬, 멜로디, 하모니 등 여러 구성 요소로 이루어져 있습니다. 리듬과 멜로디가 음악 작품의 전체를 구성하는 하나의 요소라면 하모니는 이들에 의해 만들어지는 것입니다. 하모니가 없는 연극이나 노래는 동화책의 무채색 그림과 같습니다. 그림은 그려져 있지만 색도 없고 밝기도 없고 표현력도 없는 것입니다. 적절하게 선택된 하모니는 귀를 즐겁게 하고 소리를 고상하게 만들어 피아노, 기타 또는 다른 악기의 멋진 소리를 충분히 즐길 수 있도록 합니다. 멜로디는 부를 수 있지만 하모니는 연주만 될 수 있습니다. 음악적 하모니는 화음의 집합으로, 화음이 없으면 어떤 노래나 음악도 온전하고 완전한 소리를 낼 수 없습니다.
하모니는 두 소리를 차례로 또는 동시에 연결할 때 정확하게 나타납니다. 더 넓은 의미의 동의어는 '조합'이 될 수 있습니다. 한 소리가 다른 소리와 연결되면 조합을 얻게 됩니다. 그리고 이 안에서 계층 구조가 이미 나름의 방식으로 정렬을 시도하게 됩니다. 음악 학교, 대학 및 음악원에는 학생들이 음악 이론에 존재하는 모든 화음을 공부하고 실제로 적용하고 화음 문제를 해결하는 방법을 배우는 특별한 학문인 하모니가 있습니다.
즉흥 연주를 하는 동안 뮤지션은 악기의 음정을 조율하여 기분 좋은 하모니(최상의 상태)를 만들기 위해 노력합니다. 자연에서 하모니는 서로 다른 주파수를 가진 여러 음파 간의 특별한 관계에 의해 결정됩니다. 즉흥 하모니의 품질은 미적 평가에 의해 결정됩니다. 미적 감상을 향상시키고 최상의 하모니를 찾기 위해 음악가들은 연습에 연습을 거듭합니다. 이러한 즉흥적인 작업과 최적화에는 비슷한 점이 있습니다.
하모니 검색(HS) 방법은 지난 10년간 수많은 복잡한 문제를 해결하는 데 사용되어 온 새로운 메타 휴리스틱 최적화 알고리즘입니다. 하모니 검색 알고리즘(HS)은 2001년 Z. W.에 의해 처음 제안되었습니다. Geem. HS 방식은 음악적 즉흥성과 음악적 조화를 추구하는 기본 원칙에서 영감을 받았습니다. 소리의 완벽한 조화 조합은 다차원 최적화 문제에서 글로벌 극한값과 일치하는 반면, 음악적 즉흥 연주 과정은 극한값을 찾는 것과 일치합니다.
즉흥연주를 하는 동안 각 연주자는 악기가 낼 수 있는 능력의 범위 내에서 음악의 모든 부분에서 소리를 재현하므로, 오케스트라의 모든 연주자의 소리가 하나의 하모니의 벡터를 이룹니다. "좋은" 하모니를 형성하는 소리의 조합은 각 뮤지션이 기억해 두었다가 음악의 다음 소절에서 더 좋은 하모니를 형성하는 데 사용할 수 있습니다.
일반적으로 즉흥 연주 중에 음악가는 다음 세 가지 사항 중 하나를 달성합니다. 사용 가능한 사운드 범위에서 완전히 무작위적인 사운드 형성, 하모니 메모리에서 임의의 사운드 재생, 동일한 메모리에서 인접한 하모니 벡터 재생. HS 알고리즘의 주요 특징은 연속 및 이산 최적화 문제를 모두 해결하는 데 사용할 수 있다는 점이며
HS의 가장 큰 특징은 알고리즘의 단순성과 검색의 효율성입니다. 이 때문에 이 알고리즘은 연구자들의 상당한 관심을 끌고 있으며 이론적, 실용적 측면에서 빠르게 발전하고 있습니다. HS는 검색 프로세스에서 탐색과 개척 단계 사이에 높은 안정성을 제공하는 메타 휴리스틱 기법으로 인간의 창의성에서 영감을 얻었으며 주어진 문제에 대한 완벽한 해결책을 찾는 방법은 음악가가 기분 좋은 화음을 찾는 것과 유사합니다. 피트니스 함수의 값을 구하는 데 사용되는 방법은 각 악기의 음정을 사용하여 참조를 구하는 방법과 유사합니다.
2. 알고리즘
HS 로직 작업은 완벽한 하모니를 만들어내는 음악가의 작업과 유사합니다. 뮤지션은 완벽한 하모니를 찾을 때까지 다양한 음색을 바꿔가며 연주합니다. 그 후 발견된 하모니 모음은 메모리에 저장됩니다. 최적화 문제에서 하모니는 다양한 변화를 겪습니다. 변화의 결과가 좋으면 메모리에 하모니를 추가하고 바람직하지 않은 요소를 제거하여 메모리를 새로 고칩니다... 이 모든 것이 꽤 혼란스럽게 들릴 수 있습니다. 그렇다면 하모니란 무엇일까요? 톤이란 무엇인가요? 우리만의 용어를 사용하여 알고리즘을 이해해 보겠습니다.
음악이란 무엇인가요? 물론 저는 음악가는 아니고(안타깝게도) 프로그래머입니다. 그러나 알고리즘의 감지를 위해서는 "음"의 개념을 적용하는 것으로 충분합니다. 음악은 음(화음)으로 구성되어 있습니다. 그림 1은 음악을 만드는 '메커니즘'을 개략적으로 보여줍니다. 음은 음악이나 음악 교육에 대한 조예가 없어도 쉽게 선택할 수 있는 음악 작품에 해당합니다. 맞힐 의향이 있는 분은 아래에 댓글을 남겨 주세요.
HS 알고리즘을 최적화하는 방법은 음이 있는 녹색 바를 곡 자체의 파란색 바 위로 이동하는 것입니다. 녹색 막대의 범위는 옥타브로, 개별 음으로 구성되어 있습니다. 제품(파란색 막대)은 최적화 솔루션 중 하나에 해당합니다. 녹색바의 음은 문제의 해당 최적화 매개변수입니다. 뮤지션의 메모리는 곡의 여러 버전(파란색 바의 여러 변형)을 저장하는데 이것이 바로 알고리즘 모집단입니다.
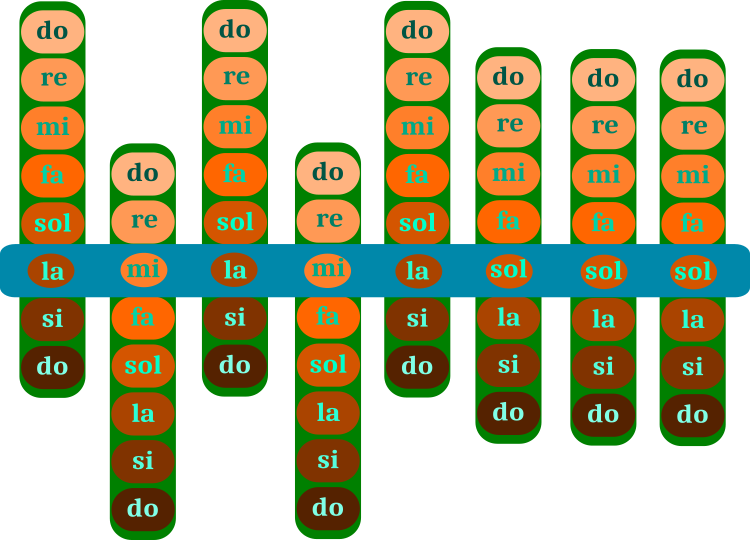
그림 1. 음악 작품에서 음 선택(하모니를 검색). 파란색 바는 조각입니다. 녹색 바는 음 세트입니다.
그림 1의 예는 매개변수에 8단계가 있는 이산형 문제의 해법에 해당합니다. 이 예제는 알고리즘의 작동을 쉽게 이해할 수 있도록 제공되었습니다. 그러나 임의의 작업에서는 최적화된 매개변수의 모든 단계가 있을 수 있으며 중간음인 반음도 있습니다. 문제 해결을 위한 올바른 매개 변수는 작품의 올바른 음에 해당합니다.
따라서 음악을 만드는 과정은 악기의 재생 가능한 주파수 범위에 있는 악기의 무작위의 사운드 세트에서 시작됩니다. 변형 악보의 개별 섹션을 결합하려면 한 곡의 변형 음을 여러 개 만들어야 합니다. 다음 단계는 이러한 변형의 음을 변경하는 것입니다. 이 작업은 세 가지 방법으로 수행할 수 있습니다:
1. 악기 음역대에 있는 곡의 음 중 하나를 무작위로 변경합니다.
2. 다른 버전의 작품에서 해당 일련번호를 메모할 수 있습니다.
3. 다른 버전의 곡에서 음을 가져와서 키의 높낮이를 약간 변경할 수 있습니다.
이렇게 음악 작품의 새로운 변형 세트를 얻은 후, 사운드 하모니 측면에서 각 변형을 평가하고 새 버전이 이전 버전보다 나은 경우 변형을 메모리의 원래 위치에 저장합니다. 이 알고리즘의 고유한 특징은 모집단(이 경우 제품 세트)을 정렬할 필요가 없다는 것입니다. 새로운 최고의 옵션은 같은 위치에서 기존의 최악의 옵션을 대체합니다. 이 과정은 적자생존을 통해 진화를 모방하는 유전 알고리즘의 작동과 비슷합니다. 또한 염색체의 유전자 조합에서도 이와 같은 유사성이 관찰됩니다.
앞서 설명한 내용을 바탕으로 우리는 HS 알고리즘의 의사 코드를 미리 작성할 수 있습니다:
1. 무작위 하모니 생성.
2. 하모니의 품질 측정(피트니스 함수 계산).
3. 무작위로 선택된 화음의 코드 선택에는 Eh의 확률을 사용합니다.
3.1 화음이 Ep의 확률로 어떤 화음에서 선택된 경우 공식에 따라 화음을 변경합니다.
3.1.1 선택한 화음은 변경하지 않고 그대로 둡니다.
3.2 방정식에 따른 새로운 화음.
4. 하모니의 품질 측정(피트니스 함수 계산).
5. 정지 기준이 충족될 때까지 3페이지부터 반복합니다.
이제 알고리즘의 입력 매개변수에 대해 설명해 보겠습니다. 몇 가지 간단하고 직관적입니다.
input int Population_P = 50; //모집단 사이즈
input double Eh_P = 0.9; //임의 선택 빈도
input double Ep_P = 0.1; //단계별 조정 빈도
input double Range_P = 0.2; //범위
- Population_P - 음악가의 메모리에 있는 곡의 변형 개수(모집단 크기);
- Eh_P - 메모리에서 악보의 변형이 선택되는 빈도는 우리가 다른 변형을 참조해 음을 빌리는 빈도에 영향을 줍니다. 값이 높을수록 알고리즘의 조합 속성이 높다는 의미입니다;
- Ep_P - 다른 버전의 곡에서 음을 선택한 경우 음을 약간 높거나 낮게 변경해야 하는 빈도입니다;
- 범위_P - 다른 버전에서 가져온 것이 아니면 편집된 버전의 악보에 있는 음의 범위입니다. 예를 들어 0.2는 악기의 음의 범위의 20%를 의미합니다.
HS 알고리즘은 하모니(음악적 구성)로 작동하며 이는 S_Harmony 구조로 설명될 수 있습니다. 하모니는 음(코드)으로 구성되며 최적화할 c[] 매개변수를 나타내는 배열입니다. 곡의 가장 좋은 화음은 cB [] 배열에 저장됩니다. 성공적인 작곡이 전송되는 것은 이 배열에 있으며 우리는 이러한 작곡 (하모니)으로 음을 차용하는 조합 순열을 수행 할 것입니다. 하모니의 품질은 h 변수에 저장되며 최상의 하모니는 hB 변수에 저장됩니다.
//—————————————————————————————————————————————————————————————————————————————— struct S_Harmony //musical composition { double c []; //chords double cB []; //best chords double h; //harmony quality double hB; //best harmony quality }; //——————————————————————————————————————————————————————————————————————————————
하모니 구조의 배열은 C_AO_HS 클래스에서 사용됩니다. 알고리즘이 매우 간결하고 계산 요구 사항이 낮기 때문에 메서드와 멤버 클래스의 선언은 간결합니다. 여기서는 다른 많은 최적화 알고리즘에서 사용되는 정렬을 볼 수 없습니다. 우리에게는 최적화할 매개변수의 최대, 최소, 단계를 설정하는 배열(코드의 범위와 단계 역할을 함)과 알고리즘의 외부 매개변수를 전달하기 위한 상수 변수가 필요합니다. HS의 주요 로직이 포함된 메서드에 대한 설명으로 넘어가겠습니다.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_HS { //---------------------------------------------------------------------------- public: S_Harmony h []; //harmonies matrix public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: double cB []; //best chords public: double hB; //best harmony quality public: void Init (const int chordsNumberP, //chords number const int harmoniesNumberP, //harmonies number const double EhP, //random selection frequency const double EpP, //frequency of step-by-step adjustment const double rangeP, //range const int maxIterationsP); //max Iterations public: void Moving (int iter); public: void Revision (); //---------------------------------------------------------------------------- private: int chordsNumber; //chords number private: int harmoniesNumber; //harmonies number private: double Eh; //random selection frequency private: double Ep; //frequency of step-by-step adjustment private: double range; //range private: int maxIterations; private: double frequency []; //frequency range private: bool revision; private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers); }; //——————————————————————————————————————————————————————————————————————————————
Init () 공용 메서드는 알고리즘을 초기화합니다. 여기서 배열의 크기를 설정합니다. 최고인 하모니의 품질 지표를 가능한 최소의 '더블' 값으로 초기화합니다. 하모니 구조 배열의 해당 변수에 대해서도 동일한 작업을 수행합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_HS::Init (const int chordsNumberP, //chords number const int harmoniesNumberP, //harmonies number const double EhP, //random selection frequency const double EpP, //frequency of step-by-step adjustment const double rangeP, //range const int maxIterationsP) //max Iterations { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator hB = -DBL_MAX; revision = false; chordsNumber = chordsNumberP; harmoniesNumber = harmoniesNumberP; Eh = EhP; Ep = EpP; range = rangeP; maxIterations = maxIterationsP; ArrayResize (rangeMax, chordsNumber); ArrayResize (rangeMin, chordsNumber); ArrayResize (rangeStep, chordsNumber); ArrayResize (frequency, chordsNumber); ArrayResize (h, harmoniesNumberP); for (int i = 0; i < harmoniesNumberP; i++) { ArrayResize (h [i].c, chordsNumber); ArrayResize (h [i].cB, chordsNumber); h [i].h = -DBL_MAX; h [i].hB = -DBL_MAX; } ArrayResize (cB, chordsNumber); } //——————————————————————————————————————————————————————————————————————————————
각 반복마다 실행해야 하는 첫 번째 공용 메서드 Moving()에는 현재 반복인 'iter' 입력이 있습니다. 첫 번째 반복에서 '리비전' 플래그가 '거짓'이면 악기 범위에서 임의의 값으로 하모니를 초기화해야 하는데 이는 음악가가 코드를 무작위로 연주하는 것과 같습니다. 반복 작업을 줄이기 위해 해당 코드의 사운드 주파수 범위(최적화된 매개변수)를 frequency[] 배열에 저장해 보겠습니다.
//---------------------------------------------------------------------------- if (!revision) { hB = -DBL_MAX; for (int har = 0; har < harmoniesNumber; har++) { for (int c = 0; c < chordsNumber; c++) { h [har].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); h [har].c [c] = SeInDiSp (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); h [har].h = -DBL_MAX; h [har].hB = -DBL_MAX; frequency [c] = rangeMax [c] - rangeMin [c]; } } revision = true; }
두 번째 이후 반복에서는 즉흥 연주, 즉 코드와 그 조합을 순차적으로 변경하는 작업이 이루어집니다. 메모리에는 여러 가지 하모니가 있으며 우리는 이를 변경하고 결합할 것입니다. 새로운 화음에 대해 우리는 순차적으로 화음을 정렬합니다. 각 화음에 대해 화음의 메모리에서 무작위로 선택될 확률이 있습니다. 즉, 화음은 무작위로 선택됩니다(모든 화음에 대해 동일하게). 화음이 하모니의 메모리에서 가져온 것이라면 그 변화의 확률도 방정식으로 확인됩니다:
h [har].c [c] = h [har].c [c] + r * B * frequency [c];
설명:
r - -1에서 1 사이의 난수
frequency - 기기의 주파수 범위
B - 공식에 의해 계산된 계수:
B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;
설명:
maxIterations - 최대 반복 횟수
iter - 현재 반복
maxB - 최대 계수 제한
minB - 최소 계수 제한
그림 2는 알고리즘의 튜닝 파라미터와 현재 반복에 대한 계수 B의 의존성을 보여줍니다.
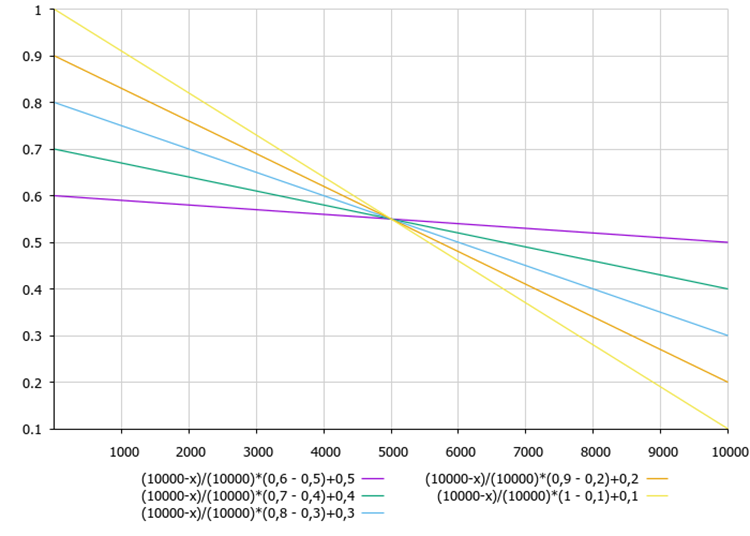
그림 2. maxB와 minB 알고리즘 및 현재 반복의 튜닝 매개변수에 대한 계수 B의 의존성
B 계수 계산 방정식은 반복할 때마다 B 계수가 감소한다는 것을 보여줍니다. 따라서 발견된 극한값은 최적화가 끝날 때까지 정제됩니다.
화음 메모리에서 화음을 선택하지 않은 경우 현재 이미 존재하는 화음이 변경됩니다. 코드 변경의 이전 변경과의 차이는 음파 값의 고정 범위입니다.
코드 변경 프로세스가 완료된 후 결과 코드가 악기의 허용 값을 초과했는지 확인해 보겠습니다.
//---------------------------------------------------------------------------- else { double r = 0.0; int harAdress = 0; double minB = 0.0; double maxB = 0.3; double B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB; for (int har = 0; har < harmoniesNumber; har++) { for (int c = 0; c < chordsNumber; c++) { r = RNDfromCI (0.0, 1.0); if (r <= Eh) { r = RNDfromCI (0.0, harmoniesNumber - 1); harAdress = (int)MathRound (r); if (harAdress < 0) harAdress = 0; if (harAdress > harmoniesNumber - 1) harAdress = harmoniesNumber - 1; h [har].c [c] = h [harAdress].cB [c]; r = RNDfromCI (0.0, 1.0); if (r < Ep) { r = RNDfromCI (-1.0, 1.0); h [har].c [c] = h [har].c [c] + r * B * frequency [c]; } } else { r = RNDfromCI (-1.0, 1.0); h [har].c [c] = h [har].cB [c] + r * range * frequency [c]; } h [har].c [c] = SeInDiSp (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } }
Revision()은 적합도 함수가 계산된 후 각각의 반복에서 호출되는 두 번째 공용 메서드이며 그 목적은 찾은 글로벌 솔루션을 업데이트하는 것이며 하모니가 최상의 버전인 h > hB보다 나은 경우 이 하모니의 최상의 버전을 업데이트합니다.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_HS::Revision () { for (int har = 0; har < harmoniesNumber; har++) { if (h [har].h > hB) { hB = h [har].h; ArrayCopy (cB, h [har].c, 0, 0, WHOLE_ARRAY); } if (h [har].h > h [har].hB) { h [har].hB = h [har].h; ArrayCopy (h [har].cB, h [har].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
코드를 주의 깊게 살펴본 결과 하모니 검색 알고리즘에 근본적으로 새로운 아이디어는 없다는 것을 알 수 있었습니다. 하모니 검색 알고리즘은 글로벌 균일 재조합, 균일 돌연변이, 가우스 돌연변이, 매 세대 최악의 개체 교체 등 이전에 사용되었던 진화 알고리즘의 아이디어를 차용합니다. 일부에서는 메모리에서 최악의 하모니를 새로운 하모니로 교체해야 한다고 지적하기도 합니다. 우리의 알고리즘에서는 하모니가 최상의 솔루션을 대체할 수 있을 뿐입니다. 저의 연구에 따르면 이러한 구현이 더 생산적인 알고리즘의 구현이기 때문에 이것은 클래식 버전과 약간 다릅니다.
하모니 검색 알고리즘이 기여한 것은 두 가지가 있습니다. 이 알고리즘에서 이러한 아이디어의 조합은 참신하고 하모니 검색 알고리즘의 음악적 동기는 새롭습니다. 하모니 검색에 관한 출판물 중 음악적 모티브나 하모니 검색 알고리즘의 확장에 대해 논의하는 경우는 거의 없습니다. 대부분의 출판물은 하모니 검색 알고리즘과 다른 진화 알고리즘의 하이브리드화, 하모니 검색 매개변수 조정 또는 특정 문제에 하모니 검색 알고리즘을 적용하는 것에 관한 내용입니다. HS 알고리즘에 더 많은 음악적 조건 확장을 적용할 수 있다면 이 알고리즘을 별도의 진화 알고리즘으로 구분하는 데 도움이 될 것입니다. 이러한 연구를 위해서는 음악 이론 연구, 음악 작곡 및 편곡 과정에 대한 연구, 음악 교육 이론 연구 및 이러한 이론을 하모니 검색 알고리즘에 창의적으로 적용하는 것이 필요합니다.
3. 테스트 결과
HS 테스트 스탠드 결과는 다음과 같습니다:
2023.02.08 17:30:05.710 Test_AO_HS (EURUSD,M1) C_AO_HS:50;0.9;0.1;0.2
2023.02.08 17:30:05.711 Test_AO_HS (EURUSD,M1) =============================
2023.02.08 17:30:07.919 Test_AO_HS (EURUSD,M1) 5 Rastrigin's; Func 10000 실행 결과: 80.62868417575105
2023.02.08 17:30:07.919 Test_AO_HS (EURUSD,M1) 점수: 0.99903
2023.02.08 17:30:11.563 Test_AO_HS (EURUSD,M1) 25 Rastrigin's; Func 10000 실행 결과: 75.85009280972398
2023.02.08 17:30:11.563 Test_AO_HS (EURUSD,M1) 점수: 0.93983
2023.02.08 17:30:45.823 Test_AO_HS (EURUSD,M1) 500 Rastrigin's; Func 10000 실행 결과: 50.26867628386793
2023.02.08 17:30:45.823 Test_AO_HS (EURUSD,M1) 점수: 0.62286
2023.02.08 17:30:45.823 Test_AO_HS (EURUSD,M1) =============================
2023.02.08 17:30:47.878 Test_AO_HS (EURUSD,M1) 5 Forest's; Func 10000 실행 결과: 1.7224980742302596
2023.02.08 17:30:47.878 Test_AO_HS (EURUSD,M1) 점수: 0.97433
2023.02.08 17:30:51.546 Test_AO_HS (EURUSD,M1) 25 Forest's; Func 10000 실행 결과: 1.0610723369605124
2023.02.08 17:30:51.546 Test_AO_HS (EURUSD,M1) 점수: 0.60020
2023.02.08 17:31:31.229 Test_AO_HS (EURUSD,M1) 500 Forest's; Func 10000 실행 결과: 0.13820341163584177
2023.02.08 17:31:31.229 Test_AO_HS (EURUSD,M1) 점수: 0.07817
2023.02.08 17:31:31.229 Test_AO_HS (EURUSD,M1) =============================
2023.02.08 17:31:34.315 Test_AO_HS (EURUSD,M1) 5 Megacity's; Func 10000 실행 결과: 7.959999999999999
2023.02.08 17:31:34.315 Test_AO_HS (EURUSD,M1) 점수: 0.66333
2023.02.08 17:31:42.862 Test_AO_HS (EURUSD,M1) 25 Megacity's; Func 10000 실행 결과: 5.112
2023.02.08 17:31:42.862 Test_AO_HS (EURUSD,M1) 점수: 0.42600
2023.02.08 17:32:25.172 Test_AO_HS (EURUSD,M1) 500 Megacity's; Func 10000 실행 결과: 0.6492
2023.02.08 17:32:25.172 Test_AO_HS (EURUSD,M1) 점수: 0.05410
테스트 함수의 수치가 높습니다. 전체 테스트 점수에서 뛰어난 결과를 얻을 수 있을 것이라는 희망을 줍니다. 시각화에서 HS의 특징은 일부 이전 알고리즘의 경우처럼 좌표 그룹 형태의 구조적 형성이 보이지 않는다는 것입니다. 시각적으로 검색 공간에서 에이전트의 움직임에는 패턴이 없습니다. 이는 RND 최적화 알고리즘의 동작과 유사하지만 수렴 그래프는 매우 자신감 있게 동작하며 최적화 문제의 해에 점진적으로 접근합니다. 로컬 극한값에서 멈추는 것은 이 알고리즘의 일반적인 경우가 아닙니다.
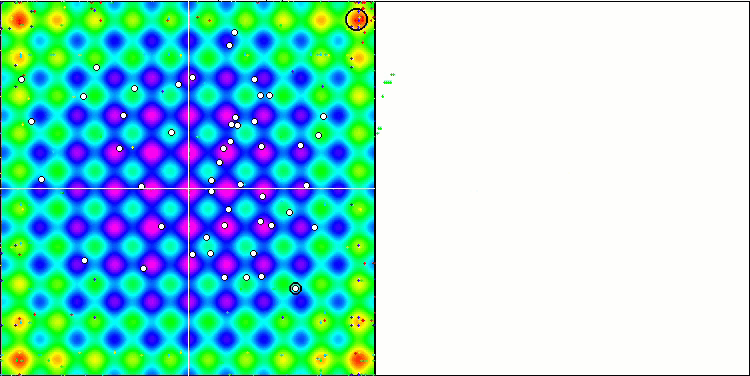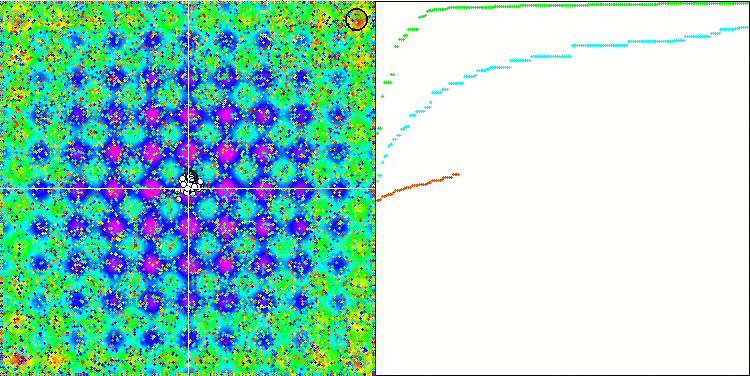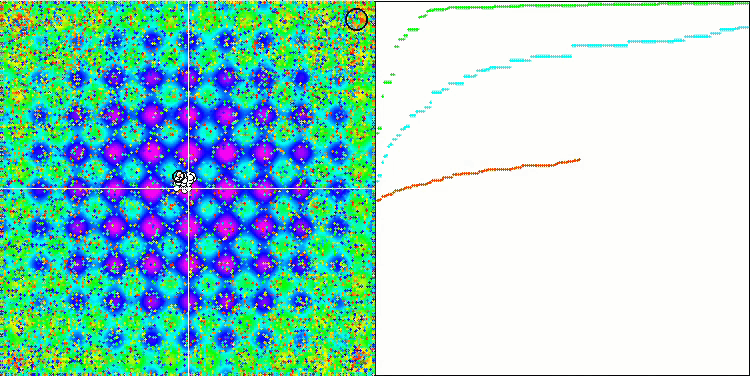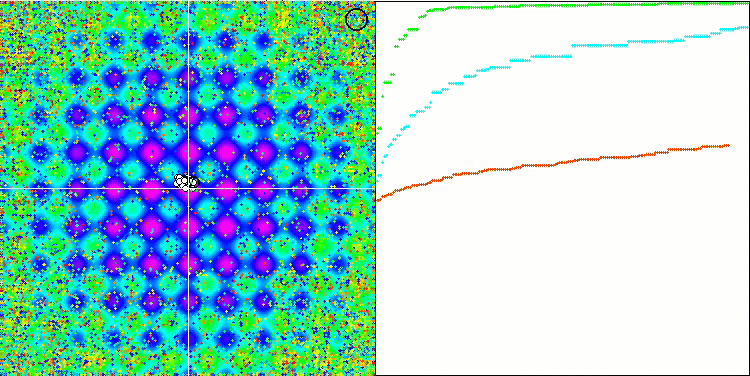
라스트리진 테스트 함수에서 HS
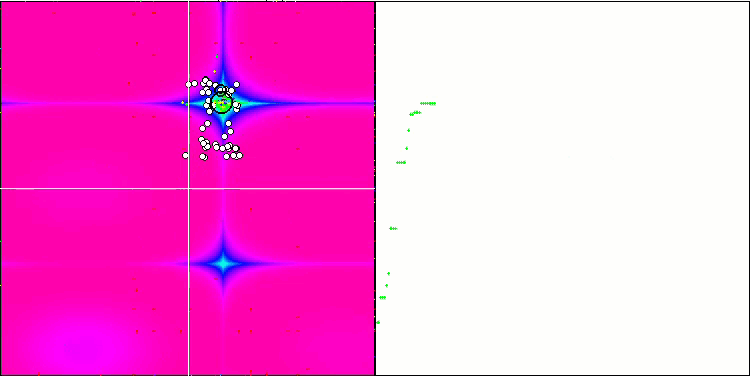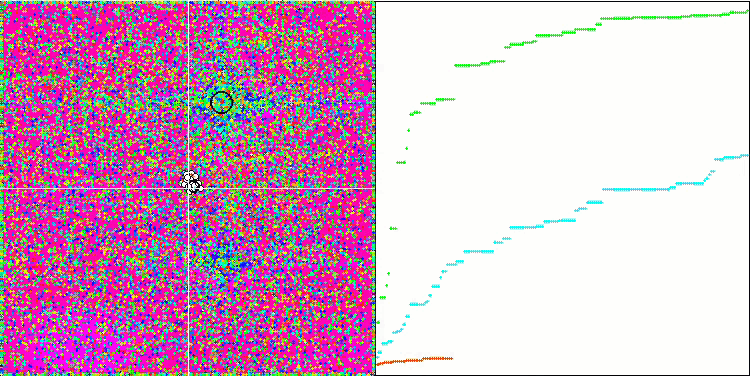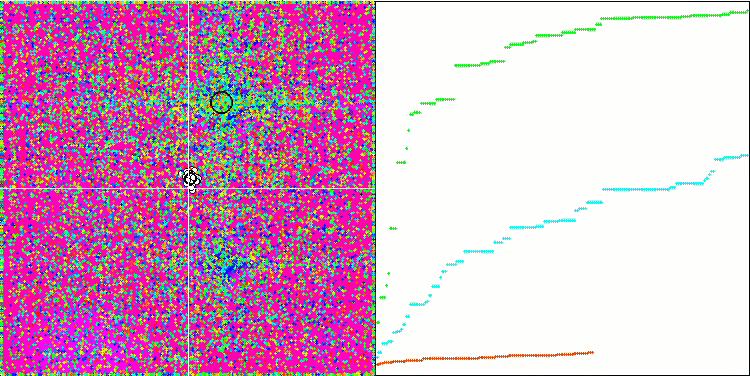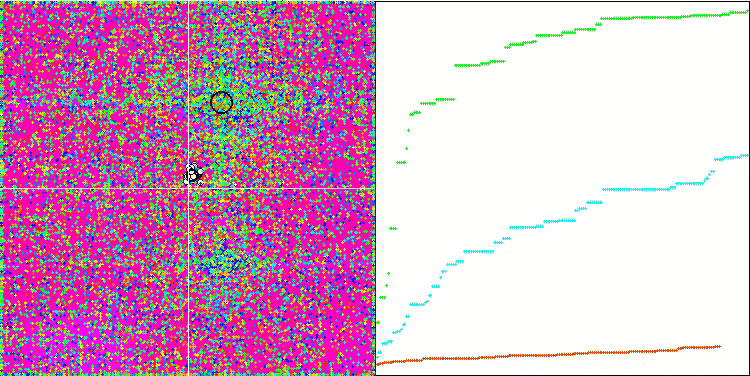
숲 테스트 함수에서 HS
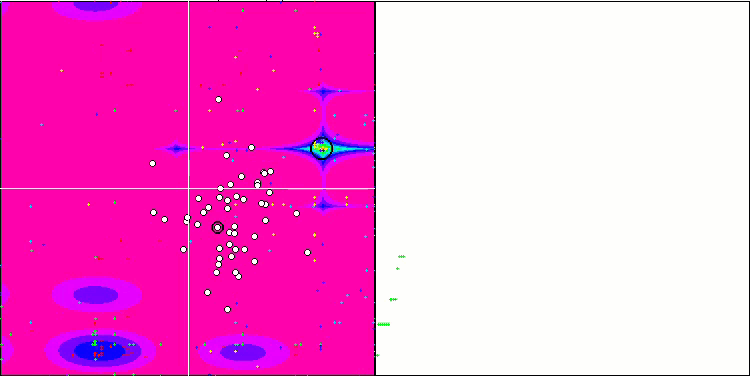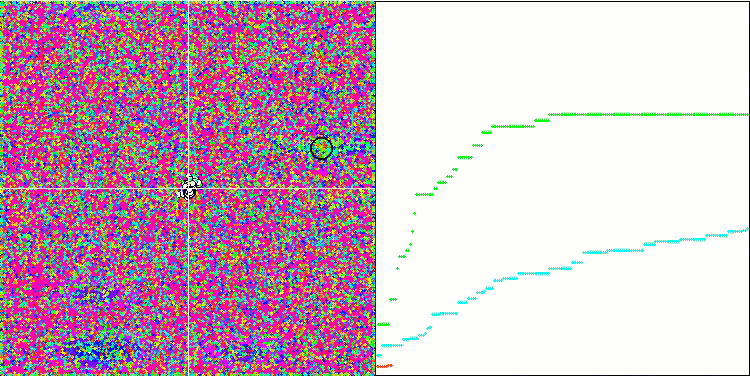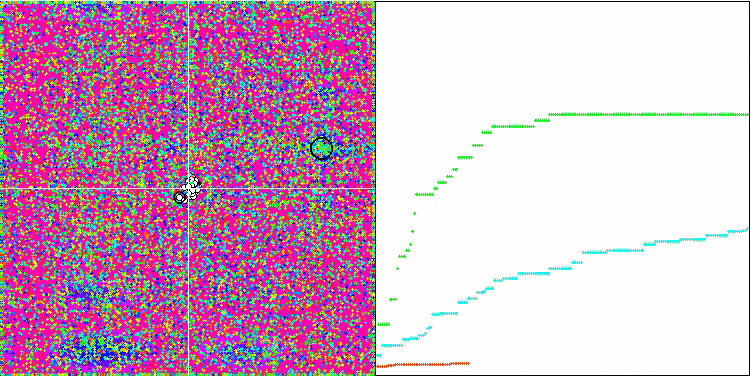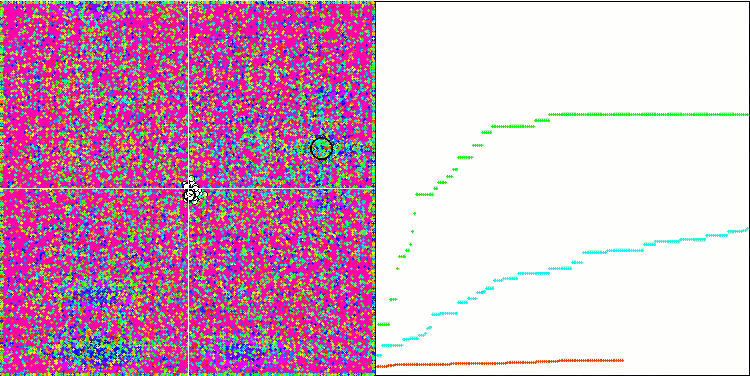
메가시티 테스트 함수에서 HS
이제 표의 결과를 분석하고 기사 제목에 있던 질문에 답할 차례입니다. 저는 이전 글에서 불연속 함수에서 평점 테이블의 리더를 우회하는 알고리즘을 볼 수 있을지 의문을 표한 적이 있습니다. 시각적으로 무작위처럼 보이는 이 알고리즘은 이산 함수(3개 테스트에서 최고)뿐만 아니라 다른 테스트 함수에서도 리더가 되어 결국 9개 테스트 중 6개에서 최고가 될 수 있었습니다.
| AO | 설명 | 라스트진 | 라스트진 최종 | 숲 | 숲 최종 | 메가시티(이산) | 메가시티 최종 | 최종 결과 | ||||||
| 10 params (5 F) | 50 params (25 F) | 1000 params(500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params(500 F) | 10 params (5 F) | 50 params (25 F) | 1000 params(500 F) | ||||||
| HS | 하모니 검색 | 1.00000 | 1.00000 | 0.57048 | 2.57048 | 1.00000 | 0.98931 | 0.57917 | 2.56848 | 1.00000 | 1.00000 | 1.00000 | 3.00000 | 100.00000 |
| ACOm | 개미 식민지 최적화 M | 0.34724 | 0.18876 | 0.20182 | 0.73782 | 0.85966 | 1.00000 | 1.00000 | 2.85966 | 1.00000 | 0.88484 | 0.13497 | 2.01981 | 68.094 |
| IWO | 침입성 잡초 최적화 | 0.96140 | 0.70405 | 0.35295 | 2.01840 | 0.68718 | 0.46349 | 0.41071 | 1.56138 | 0.75912 | 0.39732 | 0.80145 | 1.95789 | 67.087 |
| COAm | 뻐꾸기 최적화 알고리즘 M | 0.92701 | 0.49111 | 0.30792 | 1.72604 | 0.55451 | 0.34034 | 0.21362 | 1.10847 | 0.67153 | 0.30326 | 0.41127 | 1.38606 | 50.422 |
| FAm | 반딧불이 알고리즘 M | 0.60020 | 0.35662 | 0.20290 | 1.15972 | 0.47632 | 0.42299 | 0.64360 | 1.54291 | 0.21167 | 0.25143 | 0.84884 | 1.31194 | 47.816 |
| BA | 박쥐 알고리즘 | 0.40658 | 0.66918 | 1.00000 | 2.07576 | 0.15275 | 0.17477 | 0.33595 | 0.66347 | 0.15329 | 0.06334 | 0.41821 | 0.63484 | 39.711 |
| ABC | 인공 꿀벌 군집 | 0.78424 | 0.34335 | 0.24656 | 1.37415 | 0.50591 | 0.21455 | 0.17249 | 0.89295 | 0.47444 | 0.23609 | 0.33526 | 1.04579 | 38.937 |
| BFO | 박테리아 먹이 채집 최적화 | 0.67422 | 0.32496 | 0.13988 | 1.13906 | 0.35462 | 0.26623 | 0.26695 | 0.88780 | 0.42336 | 0.30519 | 0.45578 | 1.18433 | 37.651 |
| GSA | 중력 검색 알고리즘 | 0.70396 | 0.47456 | 0.00000 | 1.17852 | 0.26854 | 0.36416 | 0.42921 | 1.06191 | 0.51095 | 0.32436 | 0.00000 | 0.83531 | 35.937 |
| FSS | 물고기 떼 검색 | 0.46965 | 0.26591 | 0.13383 | 0.86939 | 0.06711 | 0.05013 | 0.08423 | 0.20147 | 0.00000 | 0.00959 | 0.19942 | 0.20901 | 13.215 |
| PSO | 파티클 스웜 최적화 | 0.20515 | 0.08606 | 0.08448 | 0.37569 | 0.13192 | 0.10486 | 0.28099 | 0.51777 | 0.08028 | 0.21100 | 0.04711 | 0.33839 | 10.208 |
| RND | 랜덤 | 0.16881 | 0.10226 | 0.09495 | 0.36602 | 0.07413 | 0.04810 | 0.06094 | 0.18317 | 0.00000 | 0.00000 | 0.11850 | 0.11850 | 5.469 |
| GWO | 회색 늑대 최적화 | 0.00000 | 0.00000 | 0.02672 | 0.02672 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.18977 | 0.03645 | 0.06156 | 0.28778 | 1.000 |
요약해 보겠습니다. 이 글을 쓰는 시점에서 HS 알고리즘은 테스트 결과 히스토그램에서 다른 최적화 알고리즘에 비해 큰 차이로 선두 자리를 차지하고 있습니다. 이는 다양한 복잡성의 문제를 해결하는 프로세스를 최적화하는 분야에서 이 알고리즘의 강점과 힘, 그리고 잠재력을 나타냅니다.
제 생각에 매우 복잡한 테스트 함수를 포함한 다양한 유형의 테스트 함수에서 인상적인 결과를 보여줄 수 있는 중요한 요소는 다른 최적화 알고리즘에 존재하는 일부 메서드(기술)을 상속하는 것입니다: HS에는 솔루션 풀 정렬이 없으며 각 솔루션은 로컬 결정만 업데이트합니다 - 이는 뻐꾸기 검색 최적화 알고리즘의 전형적인 면으로 결정 분기 개발을 위한 새로운 경로는 알이 둥지에 있는 것보다 더 나은 경우에만 발생합니다. 또한 HS 메서드는 솔루션 요소의 조합이라는 유전 알고리즘에서 사용되는 메서드와 유사합니다.
매우 높은 성능을 자랑하는 강력한 HS 최적화 알고리즘은 부드러운 스케일링 함수와 복잡한 이산 조합 문제 등 변수가 많은 다양한 복잡한 문제를 해결하는 데 안전하게 추천할만 하며 이미 엔지니어링(구조물의 토폴로지 최적화 및 부품의 최적 형태), 전자 및 물류의 여러 분야에서 성공적으로 적용되었습니다.
HS 알고리즘은 간편하게 구현할 수 있기 때문에 우리에게는 다양한 최적화 전략을 추가하고 조합할 수 있는 연구 여지가 있습니다. 이는 알고리즘의 기능이 완전히 실현되기에는 아직 멀었다는 것을 의미합니다.
알고리즘 테스트 결과의 히스토그램은 아래에 나와 있습니다.
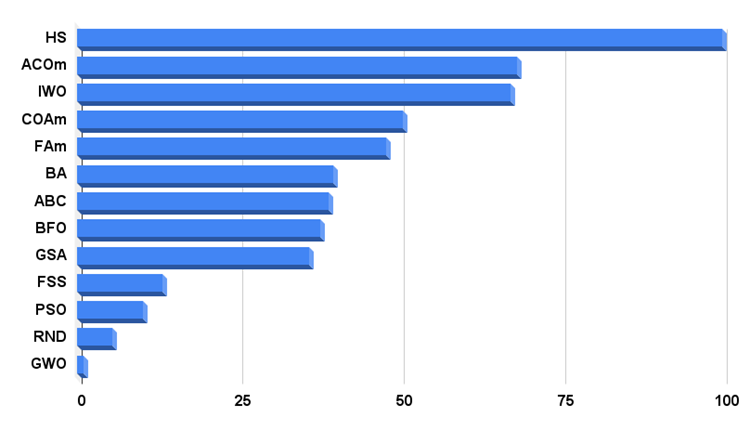
그림 3. 알고리즘 테스트 결과 히스토그램
HS 검색 알고리즘의 장단점:
1. 간편한 구현.
2. 모든 유형의 함수에서 예외 없이 뛰어난 융합성을 발휘.
3. 인상적인 확장성.
4. 매우 빠름.
5. 적은 수의 외부 매개변수.
단점:
없음.
각각의 기사에는 이전의 모든 기사에서 다룬 알고리즘 코드의 최신 버전이 업데이트된 아카이브에 포함되어 있습니다. 이 기사는 저자의 축적된 경험을 바탕으로 작성되었으며 저의 개인적인 의견이 반영되어 있습니다. 결론과 판단은 실험을 기반으로 합니다.
MetaQuotes 소프트웨어 사를 통해 러시아어가 번역됨.
원본 기고글: https://www.mql5.com/ru/articles/12163
경고: 이 자료들에 대한 모든 권한은 MetaQuotes(MetaQuotes Ltd.)에 있습니다. 이 자료들의 전부 또는 일부에 대한 복제 및 재출력은 금지됩니다.
이 글은 사이트 사용자가 작성했으며 개인의 견해를 반영합니다. Metaquotes Ltd는 제시된 정보의 정확성 또는 설명 된 솔루션, 전략 또는 권장 사항의 사용으로 인한 결과에 대해 책임을 지지 않습니다.