Popülasyon optimizasyon algoritmaları: Armoni arama (Harmony Search, HS)

İçindekiler:

1. Giriş
2. Algoritma
3. Test sonuçları

1. Giriş

Müzikal kompozisyon birkaç bileşenden oluşur - ritim, melodi ve armoni. Ritim ve melodi bir müzik eserinin tek bir bütününü oluştururken, armoni bu bütünün süslenmesidir. Armonisi olmayan bir oyun ya da şarkı, çocuk kitaplarındaki renksiz bir resim gibidir - çizilmiştir ama renk, parlaklık, ifade yoktur. Doğru seçilmiş bir armoni kulakları okşar, sesi yüceltir ve piyanonun, gitarın ya da başka bir müzik aletinin harika seslerinden tam anlamıyla keyif almamızı sağlar. Bir melodi söylenebilirken, bir armoni sadece çalınabilir. Müzikal armoni, onsuz herhangi bir şarkının veya müzik eserinin tam teşekküllü ve tam sesli olmayacağı bir dizi akordur.

Armoni tam olarak iki sesi birbirine bağladığımız anda ortaya çıkar - birbiri ardına veya eşzamanlı akışta. Daha geniş kapsamlı bir eşanlamlısı "kombinasyon" olabilir. Bir ses diğerine bağlandıktan sonra, hiyerarşinin zaten kendi yolunda sıralanmaya çalıştığı bir kombinasyon elde ederiz. Müzik okullarında, üniversitelerde ve konservatuarlarda özel bir disiplin vardır - öğrencilerin müzik teorisinde var olan tüm akorları inceledikleri, bunları pratikte uygulamayı öğrendikleri ve hatta onla ilişkili problemleri çözdükleri armoni.

Müzikal bir doğaçlama sırasında, müzisyenler hoş bir armoni (en iyi durum) elde etmek için enstrümanlarının perdesini ayarlamaya çalışırlar. Doğada armoni, farklı frekanslara sahip çeşitli ses dalgaları arasındaki özel bir ilişki ile belirlenir. Doğaçlama armoninin kalitesi estetik değerlendirme ile belirlenir. Estetik beğeniyi geliştirmek ve en iyi armoniyi bulmak için müzisyenler pratik üstüne pratik yaparlar. Doğaçlama ve optimizasyon arasında bir benzerlik vardır.

Armoni arama (HS) yöntemi, son on yılda çok sayıda karmaşık problemi çözmek için kullanılmış yeni bir metasezgisel optimizasyon algoritmasıdır. Armoni arama (HS) algoritması ilk olarak 2001 yılında Z. W. Geem tarafından önerilmiştir. HS yöntemi, müzikal doğaçlamanın kurucu ilkelerinden ve müzikal armoni arayışından esinlenmiştir. Seslerin mükemmel armonisinin kombinasyonları, çok boyutlu optimizasyon problemindeki global ekstremum ile eşleştirilirken, müzikal doğaçlama süreci de ekstremum arayışı ile eşleştirilir.

Doğaçlama sırasında, her müzisyen bir müzik eserinin herhangi bir ölçüsünde (enstrümanının yetenekleri dahilinde) bir ses üretir, böylece orkestradaki tüm müzisyenlerin bu ölçüdeki sesleri bir armoni vektörü oluşturur. "İyi" armoniler oluşturan ses kombinasyonları müzisyenlerin her biri tarafından ezberlenir ve müzik eserinin sonraki ölçülerinde daha da iyi armoniler oluşturmak için kullanılabilir.

Kural olarak, doğaçlama sırasında bir müzisyen şu üç gereklilikten birini yerine getirir: mevcut ses yelpazesinden tamamen rastgele bir ses oluşturmak; armoni hafızasından herhangi bir ses çalmak; aynı hafızadan bitişik bir armoni vektörü çalmak. HS algoritmasının temel özelliği, hem sürekli hem de ayrık optimizasyon problemlerini çözmek için kullanılabilmesidir.

HS'nin ayırt edici özellikleri algoritmanın basitliği ve aramanın verimliliğidir. Bu nedenle, algoritma araştırmacıların büyük ilgisini çekmekte ve hem teorik hem de pratik açıdan hızla gelişmektedir. HS, arama sürecindeki keşif ve sömürü aşamaları arasında yüksek kararlılık sağlayan bir metasezgisel tekniktir. HS, insan yaratıcılığından ilham alır ve belirli bir probleme mükemmel bir çözüm bulma yöntemi, hoş bir armoni bulmaya çalışan bir müzisyenin kullandığına benzer. Uygunluk fonksiyonunun değerini elde etmek için kullanılan yöntem, her bir müzik aletinin perdesini kullanarak bir referans elde etme yöntemine benzer.

2. Algoritma

HS mantığının çalışması, bir müzisyenin mükemmel armoniyi yaratma çalışmasına benzer. Müzisyen mükemmel armoniyi bulana kadar çeşitli tonları değiştirmeye çalışır. Devamında, bulunan armoni koleksiyonu hafızada saklanır. Bir optimizasyon probleminde, armoniler çeşitli değişimlere uğrar; değişimin sonuçları olumlu ise, hafızaya armoni eklenerek ve istenmeyen unsurlar çıkarılarak hafıza yenilenir... Tüm bunlar kulağa oldukça kafa karıştırıcı gelebilir. Armoni nedir? Tonlar nedir? Algoritmayı kendi terimlerimizi kullanarak anlamaya çalışalım.

Bir müzik eseri nedir? Tabii ki ben bir müzisyen değilim (ne yazık ki), bir programcıyım. Ancak algoritma tespiti için "nota" kavramını uygulamak yeterli olacaktır. Bir müzik eseri notalardan (akorlardan) oluşur. Şekil 1, bir müzik eserinin oluşturulmasına yönelik "mekanizmayı" şematik olarak göstermektedir. Notaların seçimi, müzik kulağı veya müzik eğitimi olmadan bile kolayca belirlenebilen bir müzik eserine karşılık gelir. Tahmin etmek isteyenler aşağıya yorum bırakabilirler.

HS algoritmasının optimizasyonu, notaların bulunduğu yeşil çubukların eserin mavi çubuğu boyunca hareket ettirilmesinden oluşur. Yeşil çubuğun aralığı, tek tek notalardan oluşan bir oktavdır. Eser (mavi çubuk) optimizasyon çözümlerinden birine karşılık gelmektedir. Yeşil çubuk üzerindeki notalar, problemin ilgili optimizasyon parametreleridir. Müzisyenin hafızası eserin çeşitli versiyonlarını (mavi çubukların çeşitli varyantları) depolar, bu algoritma popülasyonudur.

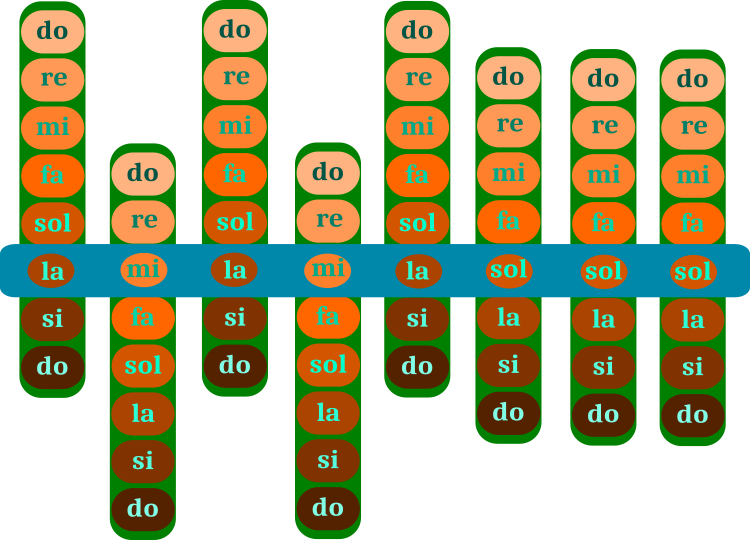
Şekil 1. Bir müzik eserindeki notaların seçimi (armoni arayışı). Mavi çubuk bir eserdir. Yeşil çubuklar nota kümeleridir

Şekil 1'deki örnek, parametrede sekiz adımın bulunduğu ayrık bir problemin çözümüne karşılık gelmektedir. Örnek, algoritmanın işleyişini anlamayı kolaylaştırmak için verilmiştir. Bununla birlikte, rastgele bir görevde, optimize edilen parametrelerin herhangi bir adımı olabilir ve ayrıca ara notalar - yarı tonlar da vardır. Problemi çözmek için doğru parametreler eserdeki doğru notalara karşılık gelir.

Dolayısıyla, bir müzik eseri yaratma süreci, bir müzik enstrümanının yeniden üretilebilir frekans aralığında yer alan rastgele bir dizi sesle başlar. Eserin çeşitli varyasyonlarının oluşturulması, varyasyonların bireysel nota bölümlerinin birleştirilebilmesi için gereklidir. Bir sonraki adım, bu varyasyonlardaki notaları değiştirmektir. Bunu üç olası yolla yapabiliriz:

1. Müzik aletinin çalma aralığında olan eserdeki notalardan birini rastgele değiştirebiliriz.
2. Eserin diğer versiyonlarından ilgili seri numarası ile bir nota alabiliriz.
3. Eserin başka bir versiyonundan bir nota alabilir ve onu biraz değiştirerek daha yüksek veya daha alçak bir nota haline getirebiliriz.

Böylece bir müzik eserinin yeni bir dizi varyantını elde ettikten sonra, varyantların her birini ses armonisi açısından değerlendirir ve yeni versiyonun önceki versiyonundan daha iyi olması koşuluyla varyantları bellekteki orijinal konumlarında saklarız. Algoritmanın benzersiz özelliği, popülasyonu, yani bizim durumumuzda ürün kümesini sıralamaya gerek olmamasıdır. Her yeni en iyi seçenek, aynı yerdeki eski en kötü seçeneğin yerini alacaktır. Bu süreç, en uygun bireylerin hayatta kaldığı evrimi taklit eden genetik algoritmaların çalışmasına benzer. Ayrıca, bir kromozomdaki genlerin kombinasyonu ile de benzerlikler göstermektedir.

Yukarıdakilere dayanarak, HS algoritmasının yalancı kodunu oluşturabiliriz:

1. Rastgele armoniler üret.
2. Armonilerin kalitesini ölç (uygunluk fonksiyonunu hesapla).
3. Rastgele seçilen bir armoninin akor seçimini Eh olasılığı ile yap.
  3.1 Akorun Ep olasılığı ile bazı armonilerden seçilmesi durumunda akoru denkleme göre değiştir.
    3.1.1 Seçilen akoru değiştirmeden bırak.
  3.2 Denkleme göre yeni akor.
4. Armonilerin kalitesini ölç (uygunluk fonksiyonunu hesapla).
5. Durma kriteri karşılanana kadar 3. adımdan itibaren tekrarla.

Şimdi, algoritmanın az sayıda ve sezgisel olan girdi parametrelerini tanımlamaya geçelim.

input int    Population_P = 50;    //Population size
input double Eh_P         = 0.9;   //random selection frequency
input double Ep_P         = 0.1;   //frequency of step-by-step adjustment
input double Range_P      = 0.2;   //range

• Population_P - müzisyenin belleğindeki bir eserin varyantlarının sayısı (popülasyon büyüklüğü);
• Eh_P - bir eserin bir varyantının hafızadan ne sıklıkla seçildiği, bir notayı almak için diğer varyantlara ne sıklıkla başvuracağımızı etkiler. Daha yüksek bir değer, algoritmanın daha yüksek kombinatoryal özellikleri anlamına gelir;
• Ep_P - eğer nota eserin başka bir versiyonundan seçilmişse, notayı ton olarak ne sıklıkla biraz değiştirmemiz, daha yüksek veya daha alçak yapmamız gerektiği;
• Range_P - başka bir versiyondan alınmamışsa, eserin düzenlenmiş versiyonundaki notanın aralığı. Örneğin, 0.2 müzik aleti nota aralığının %20'si anlamına gelir.
• 
  

HS algoritması, S_Harmony yapısı ile tanımlanabilen armoniler (müzikal kompozisyonlar) ile çalışır. Armoni notalardan (akorlardan) oluşur, bu optimize edilecek c[] parametrelerini temsil eden bir dizidir. Eserin en iyi akorları cB[] dizisinde saklanacaktır. Başarılı kompozisyon bu diziye gönderilecek ve bu kompozisyonlarla (armonilerle) onlardan notalar alarak kombinatoryal permütasyonlar gerçekleştireceğiz. Armoninin kalitesi h değişkeninde saklanır ve en iyi armoni de hB değişkeninde saklanır.

//——————————————————————————————————————————————————————————————————————————————
struct S_Harmony //musical composition
{
  double c  []; //chords
  double cB []; //best chords
  double h;     //harmony quality
  double hB;    //best harmony quality
};
//——————————————————————————————————————————————————————————————————————————————

Armoni yapıları dizisi C_AO_HS sınıfında kullanılır. Algoritma son derece özlü olduğundan ve düşük hesaplama gereksinimlerine sahip olduğundan, metot ve üye sınıfındaki bildirimler kompakttır. Burada, diğer birçok optimizasyon algoritmasında kullanılan sıralamayı görmeyeceğiz. Optimize edilen parametrelerin maksimum, minimum ve adımını ayarlamak için dizilere (akorların aralığı ve adımı rolünü oynarlar) ve algoritmanın dış parametrelerini bunlara aktarmak için sabit değişkenlere ihtiyacımız olacaktır. HS'nin ana mantığını içeren metotların açıklamasına geçelim.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_HS
{
  //----------------------------------------------------------------------------
  public: S_Harmony h      []; //harmonies matrix
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best chords
  public: double hB;           //best harmony quality

  public: void Init (const int    chordsNumberP,      //chords number
                     const int    harmoniesNumberP,   //harmonies number
                     const double EhP,                //random selection frequency
                     const double EpP,                //frequency of step-by-step adjustment
                     const double rangeP,             //range
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    chordsNumber;      //chords number
  private: int    harmoniesNumber;   //harmonies number
  private: double Eh;                //random selection frequency
  private: double Ep;                //frequency of step-by-step adjustment
  private: double range;             //range
  private: int    maxIterations;
  private: double frequency [];      //frequency range
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Init() public metodu algoritmayı başlatır. Burada dizilerin boyutunu ayarlıyoruz. Bulunan en iyi armoninin kalite göstergesini mümkün olan en düşük “double” değeriyle başlatıyoruz. Aynı şeyi armoni yapıları dizisinin ilgili değişkenleri için de yapacağız.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Init (const int    chordsNumberP,      //chords number
                    const int    harmoniesNumberP,   //harmonies number
                    const double EhP,                //random selection frequency
                    const double EpP,                //frequency of step-by-step adjustment
                    const double rangeP,             //range
                    const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  chordsNumber    = chordsNumberP;
  harmoniesNumber = harmoniesNumberP;
  Eh              = EhP;
  Ep              = EpP;
  range           = rangeP;
  maxIterations   = maxIterationsP;

  ArrayResize (rangeMax,  chordsNumber);
  ArrayResize (rangeMin,  chordsNumber);
  ArrayResize (rangeStep, chordsNumber);
  ArrayResize (frequency, chordsNumber);

  ArrayResize (h, harmoniesNumberP);

  for (int i = 0; i < harmoniesNumberP; i++)
  {
    ArrayResize (h [i].c,  chordsNumber);
    ArrayResize (h [i].cB, chordsNumber);
    h [i].h  = -DBL_MAX;
    h [i].hB = -DBL_MAX;
  }

  ArrayResize (cB, chordsNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Her yinelemede çalıştırılması gereken ilk public metot Moving(), “iter” girdisine sahiptir - mevcut yineleme. İlk yinelemede, “revision” bayrağı “false” olduğunda, armonileri müzik aletleri aralığında rastgele değerlerle başlatmak gerekir, bu da bir müzisyen tarafından rastgele akor çalmaya eşdeğerdir. Tekrarlayan işlemleri azaltmak için, ilgili akorların ses frekans aralığını (optimize edilen parametreler) frequency[] dizisinde saklayalım.

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      h [har].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      h [har].c [c] = SeInDiSp  (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      h [har].h     = -DBL_MAX;
      h [har].hB    = -DBL_MAX;

      frequency [c] = rangeMax [c] - rangeMin [c];
    }
  }

  revision = true;
}

İkinci ve sonraki yinelemelerde doğaçlama, yani akorların ve kombinasyonlarının sıralı değişimi gerçekleşir. Hafızada değiştireceğimiz ve birleştireceğimiz birkaç armoni vardır. Her yeni armoni için akorları sırayla sıralayacağız. Her bir akor için, armoninin hafızasından rastgele seçilme olasılığı vardır, yani armoni rastgele seçilecektir (tüm armoniler için eşit olasılıkla). Akor, armonilerin hafızasından alınırsa, değişim olasılığı da denklem tarafından kontrol edilir:

h [har].c [c] = h [har].c [c] + r*B*frequency [c];

Tanımlamalar:

r: -1 ile 1 arasında rastgele sayı
frequency: enstrümanın frekans aralığı
B: formül ile hesaplanan katsayı:

B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

Burada:

maxIterations: maksimum yineleme sayısı
iter: mevcut yineleme
maxB: maksimum katsayı limiti
minB: minimum katsayı limiti

Şekil 2, B katsayısının algoritmanın ayar parametrelerine ve mevcut yinelemeye olan bağımlılığını göstermektedir.

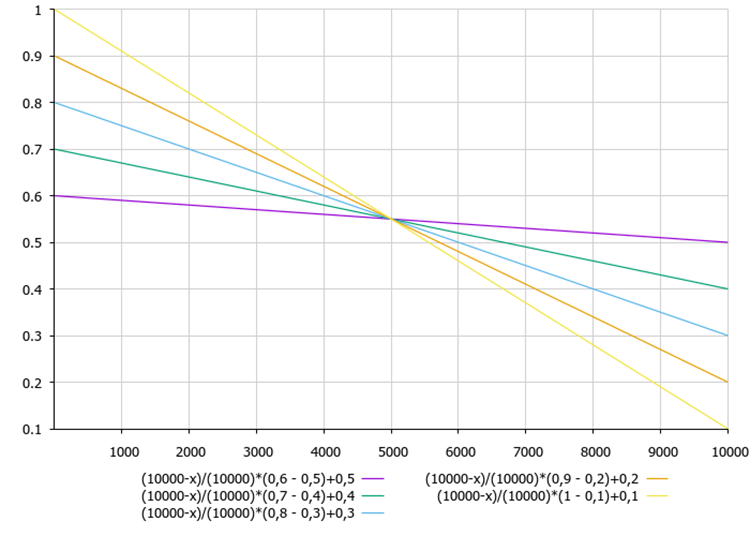
Şekil 2. B katsayısının maxB, minB algoritma ayar parametrelerine ve mevcut yinelemeye bağımlılığı

B katsayısı hesaplama denklemi, B katsayısının her yinelemede azaldığını göstermektedir. Böylece, bulunan ekstremumlar optimizasyonun sonunda rafine edilir.
Armoni belleğinden bir akor seçilmemişse, o anda mevcut olan akor değiştirilecektir. Bir akor değişiminin bir önceki değişimden farkı, ses dalgası değerlerinin sabit aralığıdır.

Akor değiştirme işlemi tamamlandıktan sonra, ortaya çıkan akorun müzik aletinin izin verilen değerlerinin ötesine geçip geçmediğini kontrol edelim.

//----------------------------------------------------------------------------
else
{
  double r         = 0.0;
  int    harAdress = 0;
  double minB      = 0.0;
  double maxB      = 0.3;
  double B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      r = RNDfromCI (0.0, 1.0);

      if (r <= Eh)
      {
        r = RNDfromCI (0.0, harmoniesNumber - 1);
        harAdress = (int)MathRound (r);
        if (harAdress < 0) harAdress = 0;
        if (harAdress > harmoniesNumber - 1) harAdress = harmoniesNumber - 1;

        h [har].c [c] = h [harAdress].cB [c];

        r = RNDfromCI (0.0, 1.0);

        if (r < Ep)
        {
          r = RNDfromCI (-1.0, 1.0);
          h [har].c [c] = h [har].c [c] + r * B * frequency [c];
        }
      }
      else
      {
        r = RNDfromCI (-1.0, 1.0);
        h [har].c [c] = h [har].cB [c] + r * range * frequency [c];
      }

      h [har].c [c] = SeInDiSp (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Revision(), uygunluk fonksiyonu hesaplandıktan sonra her yinelemede çağrılan ikinci public metottur. Amacı, bulunan global çözümü güncellemektir. Armoninin en iyi versiyonundan daha iyi olması (h>hB) durumunda, bu armoninin en iyi versiyonunu güncelleriz.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Revision ()
{
  for (int har = 0; har < harmoniesNumber; har++)
  {
    if (h [har].h > hB)
    {
      hB = h [har].h;
      ArrayCopy (cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
    if (h [har].h > h [har].hB)
    {
      h [har].hB = h [har].h;
      ArrayCopy (h [har].cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Kodu dikkatle incelediğimizde, armoni arama algoritmasında temelde yeni bir fikir olmadığını görüyoruz. Armoni arama algoritması, global tekdüze rekombinasyon, tekdüze mutasyon, Gauss mutasyonu ve her nesilde en kötü bireyin değiştirilmesi dahil olmak üzere daha önce kullanılan evrimsel algoritma fikirlerinden faydalanmaktadır. Bazı kaynaklar hafızalardaki en kötü armoninin yenisiyle değiştirilmesi gerektiğine işaret eder. Algoritmamızda, armoni yalnızca en iyi çözümünü değiştirebilir. Bu klasik versiyondan biraz farklıdır, çünkü çalışmalarım algoritmanın bu şekilde uygulanmasının daha verimli olacağını gösteriyor.

Armoni arama algoritmasının katkısı iki alanda yatmaktadır: bu fikirlerin bu algoritmada birleştirilmesi yenidir; armoni arama algoritmasının müzikal motivasyonu yenidir. Armoni arama üzerine çok az yayın müzikal motifleri veya armoni arama algoritmasının uzantılarını tartışmaktadır. Yayınların çoğu, armoni arama algoritmasının diğer evrimsel algoritmalarla hibridizasyonuna, armoni arama parametrelerinin ayarlanmasına veya armoni arama algoritmasının belirli problemlere uygulanmasına ayrılmıştır. HS algoritmasına müzikal olarak daha fazla koşullandırılmış uzantılar uygulanabilirse, bu onu ayrı bir evrimsel algoritma olarak ayırt etmeye yardımcı olacaktır. Bu tür bir araştırma, müzik teorisinin incelenmesini, müzikal kompozisyon ve düzenleme sürecinin incelenmesini, müzik eğitim teorilerinin incelenmesini ve bu teorilerin armoni arama algoritmasında yaratıcı bir şekilde uygulanmasını gerektirecektir.

3. Test sonuçları

Test ortamı sonuçları aşağıdaki gibidir:

2023.02.08 17:30:05.710    Test_AO_HS (EURUSD,M1)    C_AO_HS:50;0.9;0.1;0.2
2023.02.08 17:30:05.711    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 80.62868417575105
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    Score: 0.99903
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 75.85009280972398
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    Score: 0.93983
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 50.26867628386793
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    Score: 0.62286
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    5 Forest's; Func runs 10000 result: 1.7224980742302596
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    Score: 0.97433
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    25 Forest's; Func runs 10000 result: 1.0610723369605124
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    Score: 0.60020
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.13820341163584177
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    Score: 0.07817
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 7.959999999999999
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    Score: 0.66333
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 5.112
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    Score: 0.42600
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.6492
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    Score: 0.05410

Test fonksiyonlarının yüksek değerleri dikkat çekicidir ve genel test skorundaki sonuçların çok başarılı olacağına dair umut vermektedir. Görselleştirmede HS'nin karakteristik bir özelliği, önceki algoritmaların bazılarında olduğu gibi koordinat grupları şeklinde herhangi bir yapısal oluşum görmememizdir. Görsel olarak, temsilcilerin arama alanındaki hareketlerinde herhangi bir model yoktur. Bu, RND optimizasyon algoritmasının davranışına benzerdir, ancak yakınsama grafikleri optimizasyon probleminin çözümüne aşamalı olarak yaklaşarak çok güvenli bir şekilde davranmaktadır. Yerel ekstremumlarda takılıp kalmak bu algoritma için tipik değildir.

  Rastrigin test fonksiyonu üzerinde HS

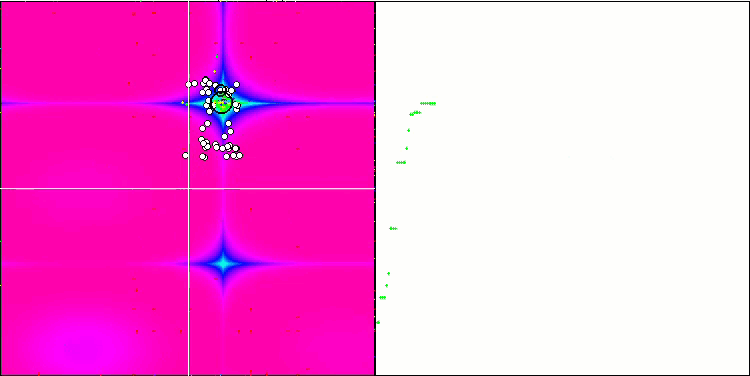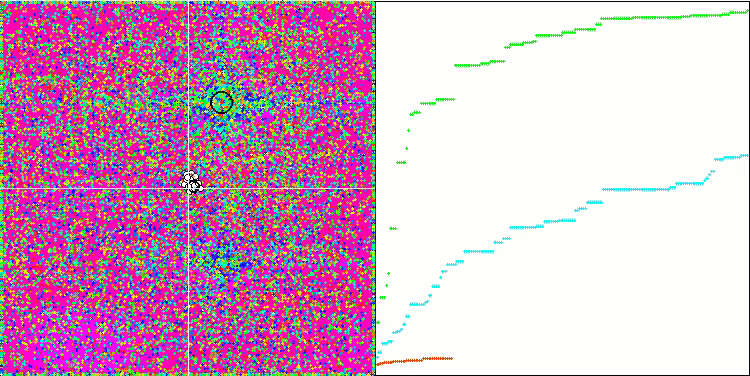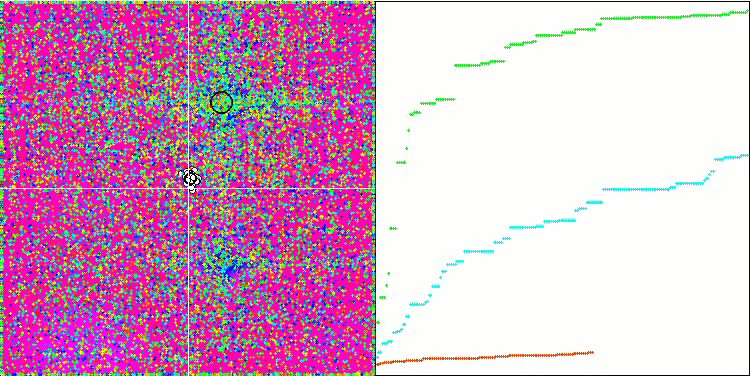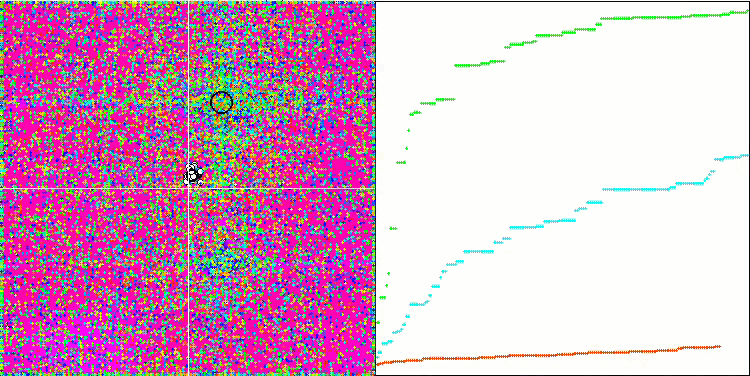
  Forest test fonksiyonu üzerinde HS

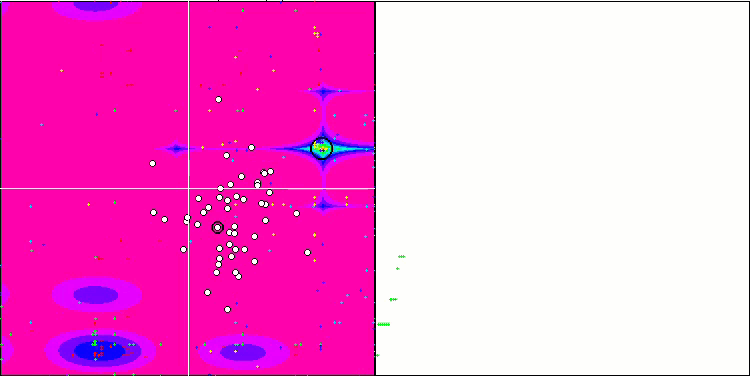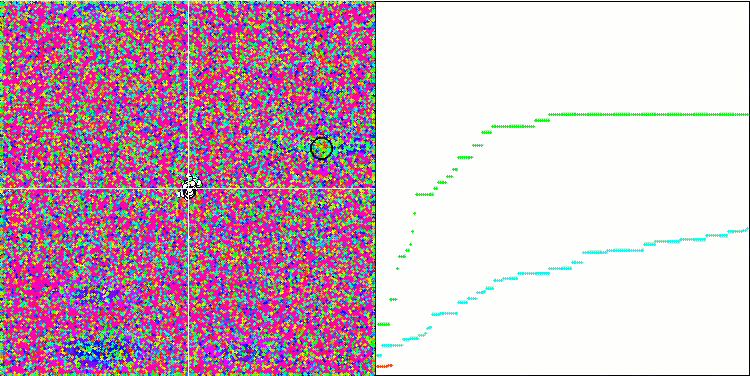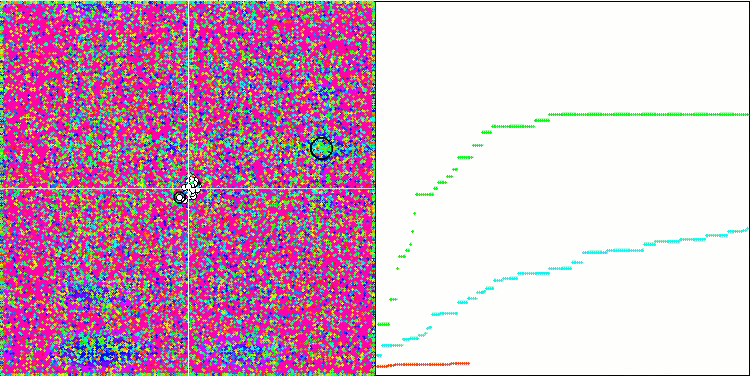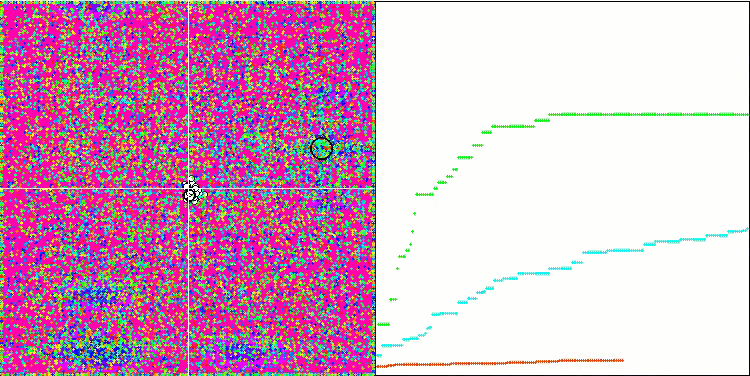
  Megacity test fonksiyonu üzerinde HS

Şimdi tablodaki sonuçları analiz etme ve makale başlığında belirtilen soruyu yanıtlama zamanı. Önceki makalelerde, ayrık bir fonksiyonda derecelendirme tablosundaki lideri geçecek bir algoritma görüp göremeyeceğimize dair şüphelerimi dile getirmiştim. Görsel olarak rastgele bir algoritma gibi görünen bu algoritma, sadece ayrık bir fonksiyonda değil (üç testte en iyi), aynı zamanda diğer test fonksiyonlarında da lider olmayı başardı ve sonunda 9 testten 6'sında en iyi oldu.

AO	Açıklama	Rastrigin			Rastrigin için nihai sonuç	Forest			Forest için nihai sonuç	Megacity (ayrık)			Megacity için nihai sonuç	Nihai sonuç
		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)		10 parametre (5 F)	50 parametre (25 F)	1000 parametre (500 F)
HS	Armoni araması	1.00000	1.00000	0.57048	2.57048	1.00000	0.98931	0.57917	2.56848	1.00000	1.00000	1.00000	3.00000	100.00000
ACOm	Karınca kolonisi optimizasyonu (m)	0.34724	0.18876	0.20182	0.73782	0.85966	1.00000	1.00000	2.85966	1.00000	0.88484	0.13497	2.01981	68.094
IWO	İstilacı yabancı ot optimizasyonu	0.96140	0.70405	0.35295	2.01840	0.68718	0.46349	0.41071	1.56138	0.75912	0.39732	0.80145	1.95789	67.087
COAm	Guguk kuşu optimizasyon algoritması (m)	0.92701	0.49111	0.30792	1.72604	0.55451	0.34034	0.21362	1.10847	0.67153	0.30326	0.41127	1.38606	50.422
FAm	Ateş böceği algoritması (m)	0.60020	0.35662	0.20290	1.15972	0.47632	0.42299	0.64360	1.54291	0.21167	0.25143	0.84884	1.31194	47.816
BA	Yarasa algoritması	0.40658	0.66918	1.00000	2.07576	0.15275	0.17477	0.33595	0.66347	0.15329	0.06334	0.41821	0.63484	39.711
ABC	Yapay arı kolonisi	0.78424	0.34335	0.24656	1.37415	0.50591	0.21455	0.17249	0.89295	0.47444	0.23609	0.33526	1.04579	38.937
BFO	Bakteri yiyecek arama optimizasyonu	0.67422	0.32496	0.13988	1.13906	0.35462	0.26623	0.26695	0.88780	0.42336	0.30519	0.45578	1.18433	37.651
GSA	Yerçekimsel arama algoritması	0.70396	0.47456	0.00000	1.17852	0.26854	0.36416	0.42921	1.06191	0.51095	0.32436	0.00000	0.83531	35.937
FSS	Balık sürüsü arama	0.46965	0.26591	0.13383	0.86939	0.06711	0.05013	0.08423	0.20147	0.00000	0.00959	0.19942	0.20901	13.215
PSO	Parçacık sürüsü optimizasyonu	0.20515	0.08606	0.08448	0.37569	0.13192	0.10486	0.28099	0.51777	0.08028	0.21100	0.04711	0.33839	10.208
RND	Rastgele	0.16881	0.10226	0.09495	0.36602	0.07413	0.04810	0.06094	0.18317	0.00000	0.00000	0.11850	0.11850	5.469
GWO	Gri kurt optimizasyonu	0.00000	0.00000	0.02672	0.02672	0.00000	0.00000	0.00000	0.00000	0.18977	0.03645	0.06156	0.28778	1.000

Özetleyelim. Bu makalenin yazıldığı sırada HS algoritması, test sonuçları histogramında diğer optimizasyon algoritmalarına göre büyük bir farkla lider konumdadır; bu da algoritmanın gücünü ve değişen karmaşıklıktaki problemleri çözme süreçlerini optimize etme alanındaki potansiyelini göstermektedir.

Bence, çok karmaşık olanlar da dahil olmak üzere çeşitli test fonksiyonları üzerinde etkileyici sonuçlar elde edilmesini sağlayan çok önemli bir faktör, diğer optimizasyon algoritmalarında bulunan bazı yöntemlerin (tekniklerin) miras alınmasıdır: HS'nin bir çözüm havuzu sıralaması yoktur, her çözüm yalnızca yerel kararını günceller - bu, bir karar dalının gelişimi için yeni bir yolun yalnızca yumurtanın yuvadakinden daha iyi olması durumunda ortaya çıktığı guguk kuşu arama optimizasyon algoritmasının tipik bir örneğidir. Ayrıca, HS yöntemleri genetik algoritmalarda kullanılan yöntemlere benzerdir - çözüm elemanlarının kombinatoriği.

Olağanüstü yüksek performansa sahip olan güçlü HS optimizasyon algoritması, hem düzgün ölçekleme fonksiyonları hem de karmaşık ayrık kombinatoryal problemler için çok değişkenli çok çeşitli karmaşık problemlerin çözümü için güvenle tavsiye edilebilir. HS algoritması mühendislik (yapıların topolojisinin optimizasyonu ve parçaların optimum şekli), elektronik ve lojistik gibi birçok alanda başarıyla uygulanmıştır.

HS algoritmasının uygulama kolaylığı, çeşitli optimizasyon stratejilerini eklememize ve birleştirmemize olanak tanıyan araştırma için alan sağlar. Bu, algoritmanın yeteneklerinin tam olarak gerçekleşmiş olmaktan uzak olduğunu göstermektedir.

Algoritma test sonuçlarının histogramı aşağıda verilmiştir.

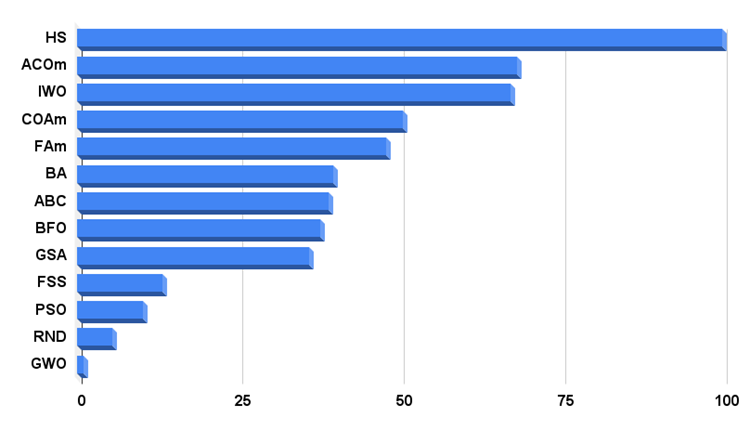
Şekil 3. Algoritmaların test sonuçlarının histogramı

HS armoni arama algoritmasının artıları ve eksileri:

Avantajları:
1. Kolay uygulama.
2. İstisnasız tüm fonksiyon türlerinde mükemmel yakınsama.
3. Etkileyici ölçeklenebilirlik.
4. Çok hızlı.
5. Az sayıda harici parametre.

Dezavantajları:
Bulunamadı.

Her makale, önceki tüm makalelerdeki algoritma kodlarının güncellenmiş sürümlerini içeren bir arşive sahiptir. Makale, yazarın birikmiş deneyimlerine dayanmaktadır ve kişisel görüşünü temsil etmektedir. Sonuçlar ve yargılar deneylere dayanmaktadır.