Kategorientheorie in MQL5 (Teil 3)
Einführung
Im Anschluss an den vorangegangenen Artikel, in dem wir die Definition einer Kategorie behandelt haben, indem wir uns auf ihre Axiome konzentriert und Ontologieprotokolle eingeführt haben. Wir werden diese Serie zur Kategorientheorie fortsetzen, indem wir Limites & Kolimites, in ihren jeweiligen Arten von Produkte & Koprodukte untersuchen, und schließen mit ihren jeweiligen Ansichten über Universelle Eigenschaften ab. Bevor wir uns jedoch damit befassen, wie diese Konzepte in MQL5 entwickelt werden können, ist es vielleicht ermutigend, auf der Grundlage dessen, was bis zu diesem Artikel behandelt wurde, einige Ideen zu teilen, wie die Kategorientheorie in einem Handelssystem angewendet und genutzt werden kann. Das hier vorgestellte System ist sehr rudimentär und soll lediglich das Potenzial des Themas für einen Händler aufzeigen. Dies wird zunächst im Prolog behandelt.
Prolog
In diesem Artikel werden wir uns mit Produkten befassen, die in der Kategorientheorie eine Möglichkeit darstellen, die Elementpaare von Domänen aufzuzählen, ohne dabei Informationen über die vorherigen Bestandteile zu verlieren. Indem wir dies in einer Signaldatei des MQL5-Assistenten verwenden, erstellen wir einen Expert Advisor. Unser Produkt wird also zwischen 2 Bereichen liegen, nämlich den Indikatorwerten von De-Marker und den Indikatorwerten von Williams Percent Range. Jede dieser Domänen hat dann Morphismen mit den Domänen der „Kauf-Bedingung“ und der „Verkaufs-Bedingung“. Das Nettoergebnis aus der Summierung der Ausgaben der beiden Bereiche, die gleichbedeutend mit den Kauf- und Verkaufsfunktionen einer typischen Signaldatei sind, bestimmt, ob der Experte kauft oder verkauft. Hier ist die Auflistung unserer Signaldatei.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class CSignalCT : public CExpertSignal { protected: CiDeMarker m_dmk; // object-oscillator (first corner) CiWPR m_wpr; // object-indicator (second corner) //--- adjusted parameters int m_periods; // the "period of calculation" parameter of the oscillator & indicator ENUM_APPLIED_PRICE m_applied; // the "prices series" parameter of the oscillator & indicator double m_longdmk; // long dmk weight double m_shortdmk; // short dmk weight double m_longwpr; // long wpr weight double m_shortwpr; // short wpr weight public: //--- methods of setting adjustable parameters void Periods(int value) { m_periods=value; } void Applied(ENUM_APPLIED_PRICE value) { m_applied=value; } void LongDMK(double value) { m_longdmk=value; } void ShortDMK(double value) { m_shortdmk=value; } void LongWPR(double value) { m_longwpr=value; } void ShortWPR(double value) { m_shortwpr=value; } //--- method of verification of settings virtual bool ValidationSettings(void); //--- method of creating the indicator and timeseries virtual bool InitIndicators(CIndicators *indicators); //--- methods of checking if the market models are formed virtual int LongCondition(void); virtual int ShortCondition(void); CSignalCT(void); ~CSignalCT(void); protected: virtual void LongMorphism(void); virtual void ShortMorphism(void); virtual double Product(ENUM_POSITION_TYPE Position); NCT:: CDomain<double> long_product,short_product; //--- method of initialization of the oscillator bool InitDMK(CIndicators *indicators); bool InitWPR(CIndicators *indicators); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ CSignalCT::CSignalCT(void) { //--- initialization of protected data m_used_series=USE_SERIES_HIGH+USE_SERIES_LOW+USE_SERIES_CLOSE+USE_SERIES_TIME; } //+------------------------------------------------------------------+ //| Destructor | //+------------------------------------------------------------------+ CSignalCT::~CSignalCT(void) { } //+------------------------------------------------------------------+ //| "Voting" that price will grow. | //+------------------------------------------------------------------+ int CSignalCT::LongCondition(void) { int result=0; //Using Domains Indicator biases (long or short) //e.g. an DMK reading of 75 => long-25, short-75 //or price at upper WPR => long-0, short-100 LongMorphism(); result=int(round(Product(POSITION_TYPE_BUY))); return(result); } //+------------------------------------------------------------------+ //| "Voting" that price will fall. | //+------------------------------------------------------------------+ int CSignalCT::ShortCondition(void) { int result=0; ShortMorphism(); result=int(round(Product(POSITION_TYPE_SELL))); return(result); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalCT::LongMorphism(void) { int _index=StartIndex(); m_wpr.Refresh(-1); m_dmk.Refresh(-1); m_close.Refresh(-1); double _wpr=-1.0*(m_dmk.GetData(0,_index)/100.0); double _dmk=(1.0-m_dmk.GetData(0,_index)); NCT::CElement<double> _e; _e.Cardinality(2); _e.Set(0,_dmk);_e.Set(1,_wpr); long_product.Cardinality(1); long_product.Set(0,_e,true); } //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ void CSignalCT::ShortMorphism(void) { int _index=StartIndex(); m_wpr.Refresh(-1); m_dmk.Refresh(-1); m_close.Refresh(-1); double _wpr=-1.0+((m_dmk.GetData(0,_index))/100.0); double _dmk=(m_dmk.GetData(0,_index)); NCT::CElement<double> _e; _e.Cardinality(2); _e.Set(0,_dmk);_e.Set(1,_wpr); short_product.Cardinality(1); short_product.Set(0,_e,true); } //+------------------------------------------------------------------+ //| Morphisms at Product | //+------------------------------------------------------------------+ double CSignalCT::Product(ENUM_POSITION_TYPE Position) { double _product=0.0; NCT::CElement<double> _e; if(Position==POSITION_TYPE_BUY) { if(long_product.Cardinality()>=1 && long_product.Get(0,_e)) { _product=100.0*((m_longdmk*_e.Get(0))+(m_longwpr*_e.Get(1)))/(m_longdmk+m_longwpr); } return(_product); } if(short_product.Cardinality()>=1 && short_product.Get(0,_e)) { _product=100.0*((m_shortdmk*_e.Get(0))+(m_shortwpr*_e.Get(1)))/(m_shortdmk+m_shortwpr); } return(_product); }
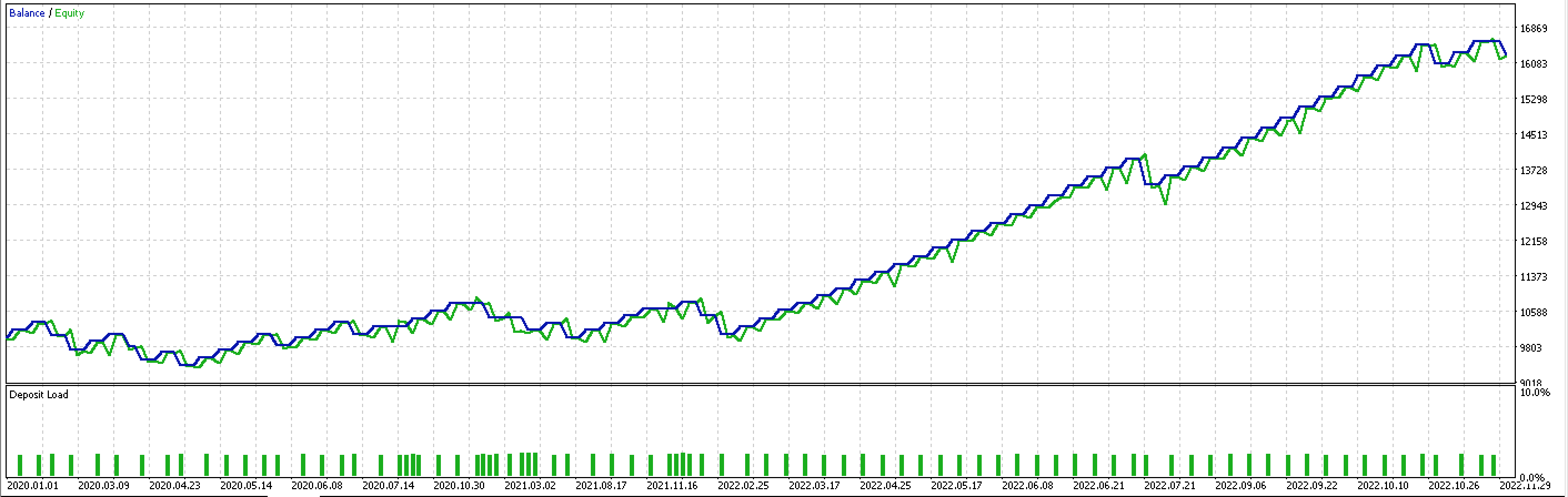
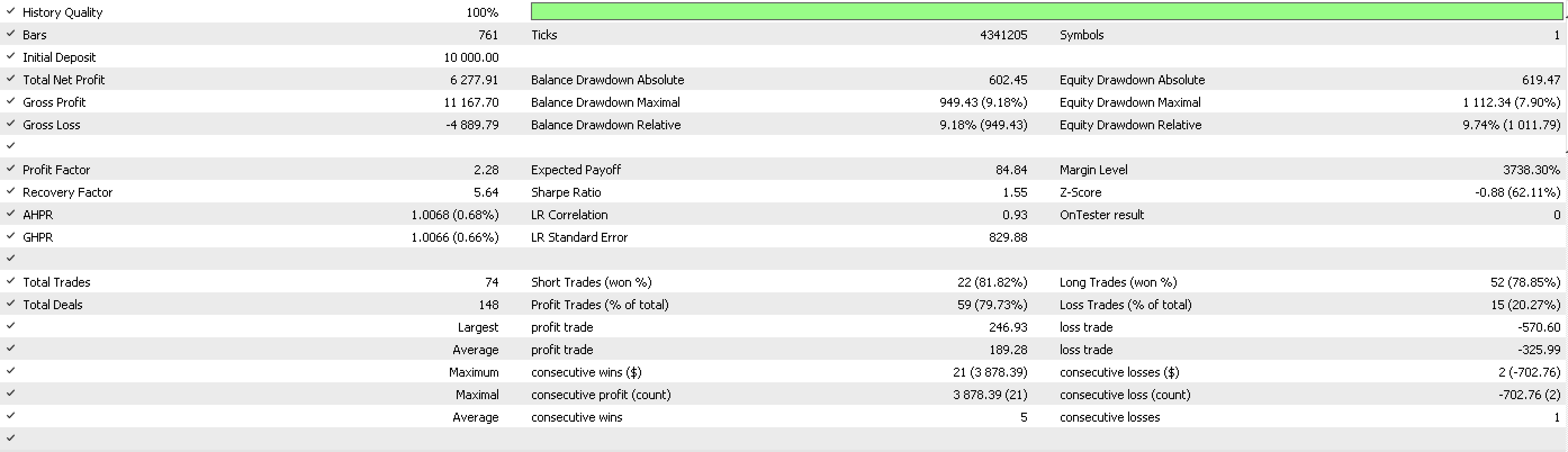
Ein Testerbericht, der auf realen Ticks über den größten Teil des Jahres 2022 für das Paar EURJPY basiert, ergibt die folgende Kurve.
Mit diesen Berichtsdetails.
Natürlich ist es kein perfektes System, aber es enthält einige Ideen, die zu einem ganzheitlicheren System weiterentwickelt werden können. Den vollständigen Quellcode finden Sie in den Anhängen.
Laut Wikipedia existieren Limites und Kolimites, wie auch die stark verwandten Begriffe der Universellen Eigenschaften, auf einer hohen Abstraktionsebene, und um sie zu verstehen, ist es hilfreich, zunächst die spezifischen Beispiele zu studieren, die diese Konzepte verallgemeinern sollen, wie z. B. Produkte und Koprodukte.
Produkte
Das Produkt zweier Bereiche A und B wird als A x B dargestellt und ist definiert als die Menge der geordneten Paare (a, b), wobei a ∈ A und b ∈ B. Symbolisch,
A x B = {(a, b) | a ∈ A, b ∈ B}
Das Produkt ist eine Verallgemeinerung des kartesischen Produkts von Domänen und beschreibt die Idee eines „Paares“ oder „Tupels“ von Domänen in einer Kategorie. Intuitiv stellt das Produkt C das „gemeinsame“ oder „zusammengesetzte“ Verhalten von A und B dar.
Zusätzlich zu der unten untersuchten Universellen Eigenschaft erfüllt das Produkt die folgenden Eigenschaften:
- Das Produkt ist assoziativ: (A × B) × C ist isomorph zu A × (B × C).
- Das Produkt ist kommutativ: A × B ist isomorph zu B × A.
- Das Produkt eines Bereichs mit dem ursprünglichen Bereich ist isomorph zum Bereich selbst: A × 1 ist isomorph zu A.
- Das Produkt einer Domäne mit der Terminaldomäne ist isomorph zur Domäne selbst: A × 0 ist isomorph zu 0.
Das Konzept der Produkte lässt sich auf verschiedene mathematische Strukturen anwenden, darunter Mengen, Gruppen, Ringe und Vektorräume, aber auch auf abstraktere Strukturen wie topologische Räume und Kategorien selbst. In jedem Fall erfasst das Produkt die Idee eines „gemeinsamen“ oder „zusammengesetzten“ Verhaltens zweier Bereiche oder Strukturen und bietet eine Möglichkeit, über das Verhalten des Systems als Ganzes nachzudenken. Ein Beispiel dafür, dass die Verwendung der Kategorientheorie im Finanzwesen eine bessere Alternative als die üblicherweise angewandte darstellt, ist das Risikomanagement.
Die Kategorientheorie ermöglicht einen abstrakteren und allgemeineren Ansatz für die Modellierung von Finanzrisiken, der auf ein breites Spektrum von Finanzinstrumenten und -märkten angewendet werden kann. Dieser Ansatz kann einen einheitlicheren und flexibleren Rahmen für das Risikoverständnis bieten als der traditionelle Ansatz, bei dem für jedes Instrument oder jeden Markt spezifische Modelle verwendet werden. Darüber hinaus kann die Anwendung der Kategorientheorie im Risikomanagement zu robusteren und skalierbaren Risikomanagementstrategien führen, die für die komplexe und vernetzte Natur der modernen Finanzmärkte besser geeignet sind.
Beim traditionellen Risikomanagement beispielsweise wird das Risiko häufig anhand spezifischer mathematischer Modelle für jedes Finanzinstrument oder jeden Markt modelliert. So wird beispielsweise das Black-Scholes-Modell üblicherweise zur Modellierung des Risikos von Optionen verwendet, während das VaR-Modell (Value at Risk) häufig zur Modellierung des Risikos eines Portfolios von Vermögenswerten eingesetzt wird. Diese Modelle können effektiv sein, aber sie sind in ihrem Anwendungsbereich begrenzt und lassen sich nur schwer auf neue Finanzinstrumente oder Märkte verallgemeinern.
Im Gegensatz dazu bietet die Kategorientheorie einen abstrakteren und allgemeineren Ansatz zur Modellierung von Risiken. Beispielsweise könnten Finanzinstrumente auf den Märkten als Domänen in einer Kategorie dargestellt werden, und das Risiko könnte als Morphismus von diesen Domänen zu einer Positionsdomäne dargestellt werden, die nur zwei Elemente hat, nämlich Long-Position und Short-Position. Dies würde einen einheitlicheren und flexibleren Rahmen für das Risikoverständnis ermöglichen, der auf ein breites Spektrum von Finanzinstrumenten und -märkten angewendet werden kann. Ein ähnlicher Ansatz wurde bei unserer Signaldatei im Prolog verwendet.
Angenommen, wir haben zwei Finanzinstrumente, A und B, und wollen das Risiko eines Wechsels von A nach B modellieren. Wir würden A und B als Domänen darstellen und das Risiko eines Wechsels von A nach B als ihre jeweiligen Morphismen. Diese Morphismen würden das Risiko erfassen, das mit dem Übergang von A nach B verbunden ist, und dabei Faktoren wie Volatilität, Liquidität und Marktbedingungen berücksichtigen. Alternativ dazu könnten wir, wie im Prolog gezeigt, ein Instrument haben und wissen wollen, welche Position wir zu einem bestimmten Zeitpunkt einnehmen müssen. Wir würden die Finanzindikatoren für dieses Instrument nehmen und ihr gewichtetes Produkt ermitteln. Dieser Wert wird für unsere Entscheidung ausschlaggebend sein. Hier ist eine halbe Liste, die nur die Kombination dieser Indikatorwerte zeigt. Zunächst benötigen wir eine Klasse, die Informationen zu den Produktbereichen verarbeitet und speichert.
//+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class CComposition { protected: int projectors; string projector[]; bool Projectors(int Value) { if(Value>=0 && Value<INT_MAX) { projectors=Value; ArrayResize(projector,projectors); return(true); } return(false); }; int Projectors(){ return(projectors); }; public: string Get(int ProjectorIndex) { string _projector=""; if(ProjectorIndex>=0 && ProjectorIndex<Projectors()) { _projector=projector[ProjectorIndex]; } return(_projector); } bool Set(int ValueIndex,string Value) { if(ValueIndex>=0 && ValueIndex<Projectors()) { projector[ValueIndex]=Value; return(true); } return(false); } CDomain<string> property; CDomain<string> cone; CComposition(void){ projectors=0;ArrayFree(projector); }; ~CComposition(void){}; }; //+------------------------------------------------------------------+ //| | //+------------------------------------------------------------------+ class CProduct :public CComposition { protected: CDomain<string> surjector[]; public: bool Surjectors(int Value) { if(Value>=0 && Value<INT_MAX) { CComposition::Projectors(Value); ArrayResize(surjector,Value); return(true); } return(false); }; int Surjectors(){ return(CComposition::projectors); }; bool Get(int SurjectorIndex,CDomain<string> &Surjector) { if(SurjectorIndex>=0 && SurjectorIndex<CComposition::Projectors()) { Surjector=surjector[SurjectorIndex]; return(true); } return(false); } bool Set(int ValueIndex,CDomain<string> &Value) { if(ValueIndex>=0 && ValueIndex<CComposition::Projectors()) { surjector[ValueIndex]=Value; return(true); } return(false); } CProduct(void){ ArrayFree(surjector); }; ~CProduct(void){}; };
Sobald wir diese definiert haben, können wir ein Produkt (oder mehrere) wie folgt bearbeiten.
////////// //PRODUCTS ////////// CDomain<double> _d_p_a,_d_p_b,_d_p_c; _d_p_a.Cardinality(__product_size);_d_p_b.Cardinality(__product_size);_d_p_c.Cardinality(__product_size); int _rsi_handle=iRSI(_Symbol,_Period,__product_size,__product_price); int _cci_handle=iCCI(_Symbol,_Period,__product_size,__product_price); int _dmk_handle=iDeMarker(_Symbol,_Period,__product_size); int _wpr_handle=iWPR(_Symbol,_Period,__product_size); int _stc_handle=iStochastic(_Symbol,_Period,8,4,4,MODE_SMA,STO_LOWHIGH); int _trx_handle=iTriX(_Symbol,_Period,__product_size,__product_price); if ( FillDomain(_d_p_a,0,__product_size,_rsi_handle) && FillDomain(_d_p_a,1,__product_size,_cci_handle) && FillDomain(_d_p_b,0,__product_size,_dmk_handle) && FillDomain(_d_p_b,1,__product_size,_wpr_handle) && FillDomain(_d_p_c,0,__product_size,_stc_handle) && FillDomain(_d_p_c,1,__product_size,_trx_handle) ) { printf(__FUNCSIG__+" domain A: "+PrintDomain(_d_p_a,2)); printf(__FUNCSIG__+" domain B: "+PrintDomain(_d_p_b,2)); printf(__FUNCSIG__+" domain C: "+PrintDomain(_d_p_c,5)); CProduct _product; GetProduct(_d_p_a,_d_p_b,_product,2); printf(__FUNCSIG__+" A & B product: "+PrintDomain(_product.cone,2)); GetProduct(_product.cone,_d_p_c,_product,5); printf(__FUNCSIG__+" A & B & C product: "+PrintDomain(_product.cone,5)); }
Diese Indikatorwerte sind zwar nicht normalisiert wie in der Signaldatei im Prolog, können aber dennoch als Risikoindikatoren für eine Handelsentscheidung angesehen oder verwendet werden. Die Ausführung des Skripts führt zu diesen Protokollen.
2023.02.17 17:31:33.199 ct_3_1 (USDCHF.ln,W1) void OnStart() domain A: {(-66.67),(66.67)} 2023.02.17 17:31:33.199 ct_3_1 (USDCHF.ln,W1) 2023.02.17 17:31:33.199 ct_3_1 (USDCHF.ln,W1) void OnStart() domain B: {(-61.99),(-68.45)} 2023.02.17 17:31:33.199 ct_3_1 (USDCHF.ln,W1) 2023.02.17 17:31:33.199 ct_3_1 (USDCHF.ln,W1) void OnStart() domain C: {(-0.00996),(-0.00628)} 2023.02.17 17:31:33.199 ct_3_1 (USDCHF.ln,W1) 2023.02.17 17:31:33.199 ct_3_1 (USDCHF.ln,W1) void OnStart() A & B product: {((66.67),(-68.45)),((66.67),(-61.99)),((-66.67),(-68.45)),((-66.67),(-61.99))} 2023.02.17 17:31:33.199 ct_3_1 (USDCHF.ln,W1) 2023.02.17 17:31:33.200 ct_3_1 (USDCHF.ln,W1) void OnStart() A & B & C product: {(((-66.67),(-61.99)),(-0.00628)),(((-66.67),(-61.99)),(-0.00996)),(((-66.67),(-68.45)),(-0.00628)),(((-66.67),(-68.45)),(-0.00996)),(((66.67),(-61.99)),(-0.00628)),(((66.67),(-61.99)),(-0.00996)),(((66.67),(-68.45)),(-0.00628)),(((66.67),(-68.45)),(-0.00996))}
Die Fähigkeit, mehrere Faktoren zu berücksichtigen, wäre für die Makroökonomie empfindlicher als beispielsweise der Value-at-Risk, der nur ein Risikokonfidenzintervall über die vergangene Performance berücksichtigt. Das Konzept der Einbettung mehrerer Faktoren in einen Morphismus könnte noch einen Schritt weiter gehen, um die mit komplexen Finanzinstrumenten wie Derivaten verbundenen Risiken zu ermitteln und zu quantifizieren, die mit herkömmlichen Ansätzen nur schwer zu modellieren sind. Dies ist wiederum dem systematischen Ansatz zu verdanken, Daten in Domänen zu trennen und durch integritätserhaltende Morphismen zu verknüpfen. Darüber hinaus könnten wir Risikomanagement-Strategien entwickeln, die der komplexen und vernetzten Natur der modernen Finanzmärkte besser gerecht werden, z. B. Strategien, die die Korrelationen zwischen verschiedenen Finanzinstrumenten und Märkten berücksichtigen.
Das Konzept der Produkte in der Kategorientheorie kann auch im Finanzwesen nützlich sein, z. B. für das Risikomanagement über mehrere Vermögenswerte hinweg. Das Produkt aus zwei Bereichen in einer Kategorie bietet die Möglichkeit, sie zu einem einzigen Bereich zusammenzufassen, der zur Modellierung des mit beiden Bereichen verbundenen gemeinsamen Risikos (Vermögenswerte) verwendet werden kann. Nehmen wir zum Beispiel an, wir haben zwei Finanzinstrumente, A und B, und wollen das gemeinsame Risiko modellieren, das mit dem Halten beider Instrumente in einem Portfolio verbunden ist. Wir können A und B als Bereiche in einer Kategorie darstellen und ihr gemeinsames Risiko als das Produkt der beiden Bereiche. Dieser Produktbereich würde das kombinierte Risiko von A und B erfassen, wobei sowohl deren Einzelrisiken als auch etwaige Wechselwirkungen zwischen ihnen berücksichtigt werden. Bei diesem Ansatz bleibt das Eingaberisiko jedes Finanzinstruments erhalten, sodass beim Training eines Modells die einzelnen Eingaben berücksichtigt werden können, um eine bessere Genauigkeit und einen besseren Einblick zu erhalten, anstatt die beiden Eingaben zu einem Durchschnitt zusammenzufassen. Im Wesentlichen verstehen wir das mit den verschiedenen Finanzinstrumenten verbundene gemeinsame Risiko besser und sind somit in der Lage, wirksamere Risikomanagementstrategien zu entwickeln. Zur Veranschaulichung könnten wir Produkte zur Modellierung des Risikos verwenden, das mit komplexen Finanzstrukturen wie Collateralized Debt Obligations (CDOs) verbunden ist, die sich aus mehreren zugrunde liegenden Vermögenswerten zusammensetzen.
Die Produkte der Kategorientheorie neigen zur Abstraktion und zu allgemeinen Rahmenbedingungen, die z. B. bei der Modellierung von Risiken zu einer breiten Palette von Anwendungen bei Finanzinstrumenten und -märkten führen können. Dies ermöglicht einen einheitlicheren und flexibleren Ansatz für das Risikomanagement, der uns helfen kann, die Wechselwirkungen und Abhängigkeiten zwischen verschiedenen Finanzinstrumenten und Märkten besser zu verstehen als die Spezifität von VaR/Black-Scholes. Angenommen, wir haben ein S&P 500-Portfolio, das aus verschiedenen Aktien besteht, und wollen das Risiko dieses Portfolios modellieren. Wir könnten dies mit Hilfe des VaR tun, der den maximalen potenziellen Verlust des Portfolios mit einem bestimmten Wahrscheinlichkeitsniveau schätzt.
Der VaR hat jedoch einige Einschränkungen, wie z. B. die Annahme einer Normalverteilung, die in der Praxis möglicherweise nicht zutrifft, die Unfähigkeit, komplexe Risikobeziehungen zwischen den Aktien im Portfolio zu erfassen, sowie die Unfähigkeit, die Höhe des Verlustes zu bewerten, wenn eine VaR-Verletzung eintritt. Die Kategorientheorie hingegen bietet eine abstraktere und flexiblere Möglichkeit zur Risikomodellierung, indem sie sich auf die Struktur und die Beziehungen zwischen den verschiedenen Elementen des Portfolios konzentriert und nicht nur auf deren individuelle Eigenschaften. Die Kategorientheorie ermöglicht es uns, das S&P 500-Portfolio als eine Kategorie darzustellen, wobei die Aktien die Domänen der Kategorie sind und die Risikobeziehungen zwischen ihnen durch die Morphismen oder Pfeile der Kategorie erfasst werden.
Beispielsweise könnte man einen Morphismus zwischen zwei Aktien so definieren, dass er die Risikobeziehung zwischen ihnen darstellt, wie z. B. das Ausmaß, in dem sich ihre Kurse in die gleiche oder die entgegengesetzte Richtung bewegen (z. B. Korrelation). Durch die Definition solcher Morphismen können wir uns ein detaillierteres und nuancierteres Bild von den Risikobeziehungen zwischen den Aktien im Portfolio machen, das möglicherweise genauer ist als die Verwendung des VaR. Indem wir die Risikobeziehungen zwischen den Aktien als Morphismen abstrahieren, können wir außerdem leistungsstarke Werkzeuge und Konzepte aus der Kategorientheorie wie Komposition, Dualität und Universelle Eigenschaften anwenden, um das Risiko im Portfolio zu analysieren und zu verwalten. Wir könnten zum Beispiel die Komposition von Morphismen verwenden, um die Risikobeziehungen zwischen mehreren Aktien zu kombinieren und das Gesamtrisiko des Portfolios abzuleiten, oder wir könnten die Duale Kategorie (wird noch behandelt) verwenden, um die inversen Risikobeziehungen zwischen den Aktien zu untersuchen.
Das folgende Zahlenbeispiel soll verdeutlichen, dass die Verwendung der Kategorientheorie, einschließlich der Produkte der Kategorientheorie, Vorteile gegenüber den zuvor genannten traditionellen Risikomessgrößen bieten kann. Angenommen, wir haben ein Portfolio, das aus zwei Finanzinstrumenten, A und B, besteht, die jeweils einen aktuellen Wert von 100 $ haben, und wir möchten das gemeinsame Risiko schätzen, das mit dem Halten beider Instrumente verbunden ist. Nehmen wir der Einfachheit halber an, dass die Renditen von A und B normal verteilt sind, mit einem Mittelwert von 10% und einer Standardabweichung von 20%. Mit traditionellen Modellen wie dem VaR könnten wir die individuellen Risiken von A und B sowie ihr gemeinsames Risiko schätzen. Wenn wir beispielsweise den VaR mit einem Konfidenzniveau von 95 % verwenden, würden wir schätzen, dass der eintägige VaR für A und B jeweils etwa 25,46 $ und der gemeinsame VaR etwa 36,03 $ beträgt.
VaR = Portfoliowert x Volatilität x Z-Score
VaR = $100 x 20% x 1,645
VaR = 36,03 $.
Alternativ könnten wir die Kategorientheorie und die Produkte der Kategorientheorie verwenden, um das gemeinsame Risiko von A und B zu modellieren. Bei diesem Ansatz würden wir A und B als Domänen in einer Kategorie darstellen und ihr gemeinsames Risiko als das Produkt der beiden Domänen. Anhand der Standardformel für das Produkt zweier normalverteilter Zufallsvariablen lässt sich berechnen, dass die gemeinsame Verteilung von A und B einen Mittelwert von 10 % und eine Standardabweichung von etwa 0,28 aufweist.
VaR = $100 x √ ((10%)2 x (28%)2 + (10%)2 x (28%)2) x 1.645
VaR = $29.15.
Mit diesem Ansatz könnten wir den Ein-Tages-VaR für das gemeinsame Risiko von A und B anhand der Standardformel für den VaR schätzen. Bei einem Konfidenzniveau von 95 % würde der Ein-Tages-VaR für das gemeinsame Risiko von A und B etwa 29,15 $ betragen. In diesem Beispiel führt die Verwendung der Kategorientheorie und des Produktmodells für das gemeinsame Risiko von A und B zu einer anderen Schätzung des gemeinsamen VaR als das obige traditionelle Modell. Die Kategorientheorie könnte jedoch einen allgemeineren und flexibleren Ansatz für das Risikomanagement bieten, der auf ein breiteres Spektrum von Finanzinstrumenten und -märkten angewandt werden kann und das mit mehreren Finanzinstrumenten verbundene gemeinsame Risiko besser erfassen kann. Die typische Ausgabe eines Gebietsprodukts wäre eine Matrix, die die Risikoergebnisse für jede Iteration auflistet. Dieses Datenkontinuum dient als Grundlage für die Bewertung des Mittelwerts und der Standardabweichung in Abhängigkeit von den Zielen und Vorgaben der Investoren.
Produkte sind eine Art von Limites, sodass es vielleicht hilfreich wäre, einige allgemeine Hinweise darauf zu geben, wie Limites als Ganzes den Händlern bei der Systementwicklung nützlich sein können. Im Finanzbereich kann die Verwendung von Grenzwerten dazu beitragen, komplexe Finanzstrukturen besser zu approximieren, was die Entwicklung präziserer Risikomanagementstrategien unterstützen kann. So können wir beispielsweise das Konzept der Limites verwenden, um den Wert eines Portfolios zu schätzen, das eine große Anzahl verschiedener Finanzinstrumente enthält. Indem wir das Portfolio als Grenzwert von einfacheren Bereichen darstellen, können wir seinen Wert genauer und effizienter schätzen.
Nehmen wir an, wir haben ein Portfolio mit 1000 Finanzinstrumenten, die jeweils einen aktuellen Wert von 100 Dollar haben. Wir wollen den Wert des gesamten Portfolios sowie das mit dem Halten aller Instrumente verbundene gemeinsame Risiko schätzen. Die Verwendung traditioneller Methoden wie VaR oder Black-Scholes könnte aufgrund der hohen Dimension des Portfolios schwierig zu berechnen sein. Mit Hilfe des Konzepts der Limites in der Kategorientheorie können wir das Portfolio jedoch als Grenzwert von einfacheren Bereichen darstellen, z. B. als Summe der ersten n Finanzinstrumente, wobei n von 1 bis 1000 reicht. Wir können dann den Wert des Portfolios schätzen, indem wir das Limes der Summe nehmen, wenn n sich 1000 nähert. Mit diesem Ansatz können wir den Wert des Portfolios genauer und effizienter schätzen.
Darüber hinaus kann die Verwendung von Limites in der Kategorientheorie Aufschluss über das Verhalten von Finanzinstrumenten und Märkten geben, wenn sie sich bestimmten Grenzwerten nähern. So können wir beispielsweise das Konzept der Limites nutzen, um das Verhalten der Finanzmärkte in Zeiten extremer Volatilität oder Stress zu analysieren und Risikomanagement-Strategien zu entwickeln, die für diese Bedingungen besser geeignet sind. Zusammenfassend lässt sich sagen, dass die Verwendung von Grenzwerten in der Kategorientheorie einen zusätzlichen Nutzen für die Anwendung der Kategorientheorie und der Produkte im Finanzwesen bringen kann, da sie es uns ermöglicht, komplexe Finanzstrukturen effektiver zu approximieren und über das Verhalten von Finanzinstrumenten und -märkten bei Annäherung an bestimmte Grenzwerte nachzudenken.
Produkt Universelle Eigenschaft
Eine Universelle Eigenschaft ist eine Möglichkeit, eine Domäne in einer Kategorie auf der Grundlage der Art und Weise zu charakterisieren, wie sie mit anderen Domänen in der Kategorie interagiert. Diese Eigenschaft kann genutzt werden, um Domänen und Operationen abstrakter zu definieren, was zu leistungsfähigeren und flexibleren Modellen führen kann. Im Finanzbereich kann die Verwendung Universeller Eigenschaften eine abstraktere Definition von Finanzinstrumenten und -märkten ermöglichen, was die Schlussfolgerungen und die Entwicklung allgemeinerer Modelle erleichtern kann. Wir können beispielsweise ein börsengehandeltes Derivat als eine Domäne in einer Kategorie definieren, die bestimmte Universelle Eigenschaften erfüllt, wie die Identifizierung der Regulierungsbehörden und die Angabe, ob es sich um eine Option oder einen Terminkontrakt handelt. Diese Identifizierung kann bei der Abschätzung der Kosten für die Einhaltung der Vorschriften und des Risikos für die Gegenpartei helfen. Hier ist ein Auszug aus dem beigefügten Skript, der dies veranschaulicht.
////////////////////////////// //PRODUCT UNIVERSAL-PROPERTY ////////////////////////////// CDomain<string> _d_security,_d_exchanges,_d_optioncycle,_d_strikewidth,_d_property; // CElement<string> _e;_e.Cardinality(1); // _d_security.Cardinality(2); _e.Set(0,"EURUSD");_d_security.Set(0,_e,true); _e.Set(0,"USDJPY");_d_security.Set(1,_e,true); // _d_exchanges.Cardinality(7); _e.Set(0,"Chicago Board Options Exchange (CBOE)");_d_exchanges.Set(0,_e,true); _e.Set(0,"Shanghai Stock Exchange (SSE)");_d_exchanges.Set(1,_e,true); _e.Set(0,"Shenzhen Stock Exchange (SZSE)");_d_exchanges.Set(2,_e,true); _e.Set(0,"Tokyo Stock Exchange (TSE)");_d_exchanges.Set(3,_e,true); _e.Set(0,"Osaka Exchange (OSE)");_d_exchanges.Set(4,_e,true); _e.Set(0,"Eurex Exchange");_d_exchanges.Set(5,_e,true); _e.Set(0,"London Stock Exchange (LSE)");_d_exchanges.Set(6,_e,true); // _d_optioncycle.Cardinality(3); _e.Set(0,"JAJO - January, April, July, and October");_d_optioncycle.Set(0,_e,true); _e.Set(0,"FMAN - February, May, August, and November");_d_optioncycle.Set(1,_e,true); _e.Set(0,"MJSD - March, June, September, and December");_d_optioncycle.Set(2,_e,true); // _d_strikewidth.Cardinality(2); _e.Set(0,"1000 points");_d_strikewidth.Set(0,_e,true); _e.Set(0,"1250 points");_d_strikewidth.Set(1,_e,true); // printf(__FUNCSIG__+" securities domain: "+PrintDomain(_d_security,0)); printf(__FUNCSIG__+" exchanges domain: "+PrintDomain(_d_exchanges,0)); printf(__FUNCSIG__+" option cycle domain: "+PrintDomain(_d_optioncycle,0)); printf(__FUNCSIG__+" strike width domain: "+PrintDomain(_d_strikewidth,0)); CProduct _product_1; GetProduct(_d_security,_d_exchanges,_product_1,0); printf(__FUNCSIG__+" securities & exchanges product: "+PrintDomain(_product_1.cone,0)); CProduct _product_2; GetProduct(_d_optioncycle,_d_strikewidth,_product_2,0); printf(__FUNCSIG__+" securities & exchanges & optioncycle product: "+PrintDomain(_product_2.cone,0)); CProduct _product_all; GetProduct(_product_1.cone,_product_2.cone,_product_all,0); printf(__FUNCSIG__+" securities & exchanges & optioncycle & strikewidth product: "+PrintDomain(_product_all.cone,0)); _d_property.Cardinality(5); _e.Set(0,"Commodity Futures Trading Commission (CFTC)");_d_property.Set(0,_e,true); _e.Set(0,"China Securities Regulatory Commission (CSRC)");_d_property.Set(1,_e,true); _e.Set(0,"Financial Services Agency (FSA)");_d_property.Set(2,_e,true); _e.Set(0,"Federal Financial Supervisory Authority (BaFin)");_d_property.Set(3,_e,true); _e.Set(0,"Financial Conduct Authority (FCA)");_d_property.Set(4,_e,true); // _product_all.property=_d_property; // _product_all.universality.domain=_product_all.property; _product_all.universality.codomain=_product_all.cone; // CMorphism<string,string> _mm; _mm.domain=_product_all.property; _mm.codomain=_product_all.cone; // for(int c=0;c<_product_all.property.Cardinality();c++) { CElement<string> _e_property;_e_property.Cardinality(1); if(_product_all.property.Get(c,_e_property) && _e_property.Get(0)!="") { for(int cc=0;cc<_product_all.cone.Cardinality();cc++) { CElement<string> _e_cone;_e_cone.Cardinality(1); if(_product_all.cone.Get(cc,_e_cone) && _e_cone.Get(0)!="") { if(_e_property.Get(0)=="Commodity Futures Trading Commission (CFTC)") { if(StringFind(_e_cone.Get(0),"Chicago Board Options Exchange (CBOE)")>=0) { if(_product_all.universality.Morphisms(_product_all.universality.Morphisms()+1)) { if(_mm.Morph(_product_all.property,_product_all.cone,_e_property,_e_cone)) { if(!_product_all.universality.Set(_product_all.universality.Morphisms()-1,_mm)) { } } } } } else if(_e_property.Get(0)=="China Securities Regulatory Commission (CSRC)") { if(StringFind(_e_cone.Get(0),"Shanghai Stock Exchange (SSE)")>=0||StringFind(_e_cone.Get(0),"Shenzhen Stock Exchange (SZSE)")>=0) { if(_product_all.universality.Morphisms(_product_all.universality.Morphisms()+1)) { if(_mm.Morph(_product_all.property,_product_all.cone,_e_property,_e_cone)) { if(!_product_all.universality.Set(_product_all.universality.Morphisms()-1,_mm)) { } } } } } else if(_e_property.Get(0)=="Financial Services Agency (FSA)") { if(StringFind(_e_cone.Get(0),"Tokyo Stock Exchange (TSE)")>=0||StringFind(_e_cone.Get(0),"Osaka Exchange (OSE)")>=0) { if(_product_all.universality.Morphisms(_product_all.universality.Morphisms()+1)) { if(_mm.Morph(_product_all.property,_product_all.cone,_e_property,_e_cone)) { if(!_product_all.universality.Set(_product_all.universality.Morphisms()-1,_mm)) { } } } } } else if(_e_property.Get(0)=="Federal Financial Supervisory Authority (BaFin)") { if(StringFind(_e_cone.Get(0),"Eurex Exchange")>=0) { if(_product_all.universality.Morphisms(_product_all.universality.Morphisms()+1)) { if(_mm.Morph(_product_all.property,_product_all.cone,_e_property,_e_cone)) { if(!_product_all.universality.Set(_product_all.universality.Morphisms()-1,_mm)) { } } } } } else if(_e_property.Get(0)=="Financial Conduct Authority (FCA)") { if(StringFind(_e_cone.Get(0),"London Stock Exchange (LSE)")>=0) { if(_product_all.universality.Morphisms(_product_all.universality.Morphisms()+1)) { if(_mm.Morph(_product_all.property,_product_all.cone,_e_property,_e_cone)) { if(!_product_all.universality.Set(_product_all.universality.Morphisms()-1,_mm)) { } } } } } } } } }
Bei der Ausführung dieses Skripts sollten die folgenden Protokolle entstehen, die den Homomorphismus zwischen dem Kegelbereich und dem Eigenschaftsbereich ausgeben. Dieser Homomorphismus kennzeichnet die Universelle Eigenschaft.
/* 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) void OnStart() universal property: 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) {(Commodity Futures Trading Commission (CFTC)),(China Securities Regulatory Commission (CSRC)),(Financial Services Agency (FSA)),(Federal Financial Supervisory Authority (BaFin)),(Financial Conduct Authority (FCA))} 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) | 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((EURUSD),(Chicago Board Options Exchange (CBOE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((EURUSD),(Chicago Board Options Exchange (CBOE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((EURUSD),(Chicago Board Options Exchange (CBOE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((EURUSD),(Chicago Board Options Exchange (CBOE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((EURUSD),(Chicago Board Options Exchange (CBOE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((EURUSD),(Chicago Board Options Exchange (CBOE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((USDJPY),(Chicago Board Options Exchange (CBOE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((USDJPY),(Chicago Board Options Exchange (CBOE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((USDJPY),(Chicago Board Options Exchange (CBOE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((USDJPY),(Chicago Board Options Exchange (CBOE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((USDJPY),(Chicago Board Options Exchange (CBOE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (Commodity Futures Trading Commission (CFTC))|----->(((USDJPY),(Chicago Board Options Exchange (CBOE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shanghai Stock Exchange (SSE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shanghai Stock Exchange (SSE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shanghai Stock Exchange (SSE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shanghai Stock Exchange (SSE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shanghai Stock Exchange (SSE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shanghai Stock Exchange (SSE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.077 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shenzhen Stock Exchange (SZSE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shenzhen Stock Exchange (SZSE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shenzhen Stock Exchange (SZSE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shenzhen Stock Exchange (SZSE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shenzhen Stock Exchange (SZSE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((EURUSD),(Shenzhen Stock Exchange (SZSE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shanghai Stock Exchange (SSE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shanghai Stock Exchange (SSE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shanghai Stock Exchange (SSE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shanghai Stock Exchange (SSE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shanghai Stock Exchange (SSE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shanghai Stock Exchange (SSE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shenzhen Stock Exchange (SZSE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shenzhen Stock Exchange (SZSE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shenzhen Stock Exchange (SZSE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shenzhen Stock Exchange (SZSE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shenzhen Stock Exchange (SZSE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (China Securities Regulatory Commission (CSRC))|----->(((USDJPY),(Shenzhen Stock Exchange (SZSE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Tokyo Stock Exchange (TSE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Tokyo Stock Exchange (TSE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Tokyo Stock Exchange (TSE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Tokyo Stock Exchange (TSE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Tokyo Stock Exchange (TSE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Tokyo Stock Exchange (TSE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Osaka Exchange (OSE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Osaka Exchange (OSE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Osaka Exchange (OSE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Osaka Exchange (OSE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Osaka Exchange (OSE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((EURUSD),(Osaka Exchange (OSE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Tokyo Stock Exchange (TSE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Tokyo Stock Exchange (TSE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Tokyo Stock Exchange (TSE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Tokyo Stock Exchange (TSE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Tokyo Stock Exchange (TSE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Tokyo Stock Exchange (TSE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Osaka Exchange (OSE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Osaka Exchange (OSE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Osaka Exchange (OSE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Osaka Exchange (OSE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Osaka Exchange (OSE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Financial Services Agency (FSA))|----->(((USDJPY),(Osaka Exchange (OSE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((EURUSD),(Eurex Exchange)),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((EURUSD),(Eurex Exchange)),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((EURUSD),(Eurex Exchange)),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((EURUSD),(Eurex Exchange)),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((EURUSD),(Eurex Exchange)),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((EURUSD),(Eurex Exchange)),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((USDJPY),(Eurex Exchange)),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((USDJPY),(Eurex Exchange)),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.078 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((USDJPY),(Eurex Exchange)),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((USDJPY),(Eurex Exchange)),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((USDJPY),(Eurex Exchange)),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Federal Financial Supervisory Authority (BaFin))|----->(((USDJPY),(Eurex Exchange)),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((EURUSD),(London Stock Exchange (LSE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((EURUSD),(London Stock Exchange (LSE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((EURUSD),(London Stock Exchange (LSE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((EURUSD),(London Stock Exchange (LSE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((EURUSD),(London Stock Exchange (LSE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((EURUSD),(London Stock Exchange (LSE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((USDJPY),(London Stock Exchange (LSE))),((JAJO - January, April, July, and October),(1000 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((USDJPY),(London Stock Exchange (LSE))),((JAJO - January, April, July, and October),(1250 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((USDJPY),(London Stock Exchange (LSE))),((FMAN - February, May, August, and November),(1000 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((USDJPY),(London Stock Exchange (LSE))),((FMAN - February, May, August, and November),(1250 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((USDJPY),(London Stock Exchange (LSE))),((MJSD - March, June, September, and December),(1000 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) (Financial Conduct Authority (FCA))|----->(((USDJPY),(London Stock Exchange (LSE))),((MJSD - March, June, September, and December),(1250 points))) 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) | 2023.02.21 09:57:41.079 ct_3_1 (USDCHF.ln,H1) {(((EURUSD),(Chicago Board Options Exchange (CBOE))),((JAJO - January, April, July, and October),(1000 points))),(((EURUSD),(Chicago Board Options Exchange (CBOE))),((JAJO - January, April, July, and October),(1250 points))),(((EURUSD),(Chicago Board Options Exchange (CBOE))),((FMAN - February, May, August, and November),(1000 points))),(((EURUSD),(Chicago Board Options Exchange (CBOE))),((FMAN - February, May, August, and November),(1250 points))),(((EURUSD),(Chicago Board Options Exchange (CBOE))),((MJSD */
Die Verwendung Universeller Eigenschaften kann es auch einfacher machen, über komplexe Finanzstrukturen wie Collateralized Debt Obligations (CDOs) nachzudenken. Diese Strukturen setzen sich in der Regel aus mehreren Basiswerten zusammen, die jeweils ein eigenes Risikoprofil aufweisen. Indem wir die zugrunde liegenden Vermögenswerte als Bereiche einer Kategorie definieren und Universelle Eigenschaften zur Definition der Struktur der CDO verwenden, können wir abstraktere und allgemeinere Modelle entwickeln, die das mit den zugrunde liegenden Vermögenswerten verbundene gemeinsame Risiko besser erfassen. Darüber hinaus kann das Konzept der Allgemeingültigkeit zur Entwicklung neuer Finanzinstrumente oder -produkte genutzt werden, indem die gewünschten Allgemeingültigkeiten ermittelt werden, anstatt zu versuchen, ein spezifisches Finanzinstrument von Grund auf zu entwickeln. Dies kann zu innovativeren und leistungsfähigeren Finanzprodukten führen, die besser auf die Bedürfnisse der Anleger und des Marktes abgestimmt sind.
//////////////////////////// //PRODUCT UNIVERSAL-PROPERTY //////////////////////////// //EX no.2 CDomain<string> _d_hedge,_d_cover,_d_postion,_d_p2_property; // CElement<string> _ep2;_ep2.Cardinality(1); // _d_hedge.Cardinality(2); _ep2.Set(0,"EURUSD");_d_hedge.Set(0,_ep2,true); _ep2.Set(0,"GBPUSD");_d_hedge.Set(1,_ep2,true); // _d_cover.Cardinality(2); _ep2.Set(0,"USDCHF");_d_cover.Set(0,_ep2,true); _ep2.Set(0,"USDJPY");_d_cover.Set(1,_ep2,true); // _d_postion.Cardinality(4); _ep2.Set(0,"EURCHF");_d_postion.Set(0,_ep2,true); _ep2.Set(0,"EURJPY");_d_postion.Set(1,_ep2,true); _ep2.Set(0,"GBPCHF");_d_postion.Set(2,_ep2,true); _ep2.Set(0,"GBPJPY");_d_postion.Set(3,_ep2,true); // printf(__FUNCSIG__+" hedge domain: "+PrintDomain(_d_hedge,0)); printf(__FUNCSIG__+" cover domain: "+PrintDomain(_d_cover,0)); printf(__FUNCSIG__+" postion domain: "+PrintDomain(_d_postion,0)); CProduct _product_hc; GetProduct(_d_hedge,_d_cover,_product_hc,0); printf(__FUNCSIG__+" hedge & cover product: "+PrintDomain(_product_hc.cone,0)); CProduct _product_hcp; GetProduct(_product_hc.cone,_d_postion,_product_hcp,0); printf(__FUNCSIG__+" hedge & cover & postion product: "+PrintDomain(_product_hcp.cone,0)); // CDomain<double> _d_p2_eu,_d_p2_gu,_d_p2_uc,_d_p2_uj,_d_p2_ec,_d_p2_ej,_d_p2_gc,_d_p2_gj; _d_p2_eu.Cardinality(1);_d_p2_gu.Cardinality(1);_d_p2_uc.Cardinality(1);_d_p2_uj.Cardinality(1); _d_p2_ec.Cardinality(1);_d_p2_ej.Cardinality(1);_d_p2_gc.Cardinality(1);_d_p2_gj.Cardinality(1); int _eu_handle=iATR("EURUSD",_Period,__product_size); int _gu_handle=iATR("GBPUSD",_Period,__product_size); int _uc_handle=iATR("USDCHF",_Period,__product_size); int _uj_handle=iATR("USDJPY",_Period,__product_size); int _ec_handle=iATR("EURCHF",_Period,__product_size); int _ej_handle=iATR("EURJPY",_Period,__product_size); int _gc_handle=iATR("GBPCHF",_Period,__product_size); int _gj_handle=iATR("GBPJPY",_Period,__product_size); if ( FillDomain(_d_p2_eu,0,1,_eu_handle) && FillDomain(_d_p2_gu,0,1,_gu_handle) && FillDomain(_d_p2_uc,0,1,_uc_handle) && FillDomain(_d_p2_uj,0,1,_uj_handle) && FillDomain(_d_p2_ec,0,1,_ec_handle) && FillDomain(_d_p2_ej,0,1,_ej_handle) && FillDomain(_d_p2_gc,0,1,_gc_handle) && FillDomain(_d_p2_gj,0,1,_gj_handle) ) { CElement<double> _e_eu,_e_gu,_e_uc,_e_uj,_e_ec,_e_ej,_e_gc,_e_gj; // if ( _d_p2_eu.Get(0,_e_eu) && _d_p2_gu.Get(0,_e_gu) && _d_p2_uc.Get(0,_e_uc) && _d_p2_uj.Get(0,_e_uj) && _d_p2_ec.Get(0,_e_ec) && _d_p2_ej.Get(0,_e_ej) && _d_p2_gc.Get(0,_e_gc) && _d_p2_gj.Get(0,_e_gj) ) { _d_p2_property.Cardinality(4); _ep2.Set(0,DoubleToString(_e_eu.Get(0),3)+","+DoubleToString(_e_uc.Get(0),3)+","+DoubleToString(_e_ec.Get(0),3));_d_p2_property.Set(0,_ep2,true); _ep2.Set(0,DoubleToString(_e_gu.Get(0),3)+","+DoubleToString(_e_uc.Get(0),3)+","+DoubleToString(_e_gc.Get(0),3));_d_p2_property.Set(1,_ep2,true); _ep2.Set(0,DoubleToString(_e_eu.Get(0),3)+","+DoubleToString(_e_uj.Get(0),3)+","+DoubleToString(_e_ej.Get(0),3));_d_p2_property.Set(2,_ep2,true); _ep2.Set(0,DoubleToString(_e_gu.Get(0),3)+","+DoubleToString(_e_uj.Get(0),3)+","+DoubleToString(_e_gj.Get(0),3));_d_p2_property.Set(3,_ep2,true); // _product_hcp.property=_d_p2_property; // _product_hcp.universality.domain=_product_hcp.property; _product_hcp.universality.codomain=_product_hcp.cone; // CMorphism<string,string> _m_p2; _m_p2.domain=_product_hcp.property; _m_p2.codomain=_product_hcp.cone; // for(int c=0;c<_product_hcp.property.Cardinality();c++) { CElement<string> _e_property;_e_property.Cardinality(1); if(_product_hcp.property.Get(c,_e_property) && _e_property.Get(0)!="") { for(int cc=0;cc<_product_hcp.cone.Cardinality();cc++) { CElement<string> _e_cone;_e_cone.Cardinality(1); if(_product_hcp.cone.Get(cc,_e_cone) && _e_cone.Get(0)!="") { if(c==0) { if(StringFind(_e_cone.Get(0),"EURUSD")>=0&&StringFind(_e_cone.Get(0),"USDCHF")>=0&&StringFind(_e_cone.Get(0),"EURCHF")>=0) { if(_product_hcp.universality.Morphisms(_product_hcp.universality.Morphisms()+1)) { if(_m_p2.Morph(_product_hcp.property,_product_hcp.cone,_e_property,_e_cone)) { if(!_product_hcp.universality.Set(_product_hcp.universality.Morphisms()-1,_m_p2)) { } } } } } else if(c==1) { if(StringFind(_e_cone.Get(0),"GBPUSD")>=0&&StringFind(_e_cone.Get(0),"USDCHF")>=0&&StringFind(_e_cone.Get(0),"GBPCHF")>=0) { if(_product_hcp.universality.Morphisms(_product_hcp.universality.Morphisms()+1)) { if(_m_p2.Morph(_product_hcp.property,_product_hcp.cone,_e_property,_e_cone)) { if(!_product_hcp.universality.Set(_product_hcp.universality.Morphisms()-1,_m_p2)) { } } } } } else if(c==2) { if(StringFind(_e_cone.Get(0),"EURUSD")>=0&&StringFind(_e_cone.Get(0),"USDJPY")>=0&&StringFind(_e_cone.Get(0),"EURJPY")>=0) { if(_product_hcp.universality.Morphisms(_product_hcp.universality.Morphisms()+1)) { if(_m_p2.Morph(_product_hcp.property,_product_hcp.cone,_e_property,_e_cone)) { if(!_product_hcp.universality.Set(_product_hcp.universality.Morphisms()-1,_m_p2)) { } } } } } else if(c==3) { if(StringFind(_e_cone.Get(0),"GBPUSD")>=0&&StringFind(_e_cone.Get(0),"USDJPY")>=0&&StringFind(_e_cone.Get(0),"GBPJPY")>=0) { if(_product_hcp.universality.Morphisms(_product_hcp.universality.Morphisms()+1)) { if(_m_p2.Morph(_product_hcp.property,_product_hcp.cone,_e_property,_e_cone)) { if(!_product_hcp.universality.Set(_product_hcp.universality.Morphisms()-1,_m_p2)) { } } } } } } } } } printf(__FUNCSIG__+" universal property hcp: "+PrintHomomorphism(_product_hcp.universality,0)); } }
Führt man dieses Skript erneut aus, erhält man den Homomorphismusausdruck der Universellen Eigenschaft, der im Wesentlichen die Risikoniveaus (in diesem Fall die ATR-Werte) auf ein Portfolio im Kegelbereich abbildet, das als Ergebnis von Produkten verschiedener Wertpapiere gebildet wurde.
2023.02.21 20:21:53.614 ct_3_1 (USDCHF.ln,H1) void OnStart() universal property hcp: 2023.02.21 20:21:53.614 ct_3_1 (USDCHF.ln,H1) 2023.02.21 20:21:53.614 ct_3_1 (USDCHF.ln,H1) {(0.002,0.001,0.001),(0.002,0.001,0.002),(0.002,0.145,0.189),(0.002,0.145,0.258)} 2023.02.21 20:21:53.614 ct_3_1 (USDCHF.ln,H1) | 2023.02.21 20:21:53.614 ct_3_1 (USDCHF.ln,H1) (0.002,0.001,0.001)|----->(((EURUSD),(USDCHF)),(EURCHF)) 2023.02.21 20:21:53.614 ct_3_1 (USDCHF.ln,H1) (0.002,0.001,0.002)|----->(((GBPUSD),(USDCHF)),(GBPCHF)) 2023.02.21 20:21:53.614 ct_3_1 (USDCHF.ln,H1) (0.002,0.145,0.189)|----->(((EURUSD),(USDJPY)),(EURJPY)) 2023.02.21 20:21:53.614 ct_3_1 (USDCHF.ln,H1) (0.002,0.145,0.258)|----->(((GBPUSD),(USDJPY)),(GBPJPY)) 2023.02.21 20:21:53.614 ct_3_1 (USDCHF.ln,H1) | 2023.02.21 20:21:53.614 ct_3_1 (USDCHF.ln,H1) {(((EURUSD),(USDCHF)),(GBPJPY)),(((EURUSD),(USDCHF)),(GBPCHF)),(((EURUSD),(USDCHF)),(EURJPY)),(((EURUSD),(USDCHF)),(EURCHF)),(((EURUSD),(USDJPY)),(GBPJPY)),(((EURUSD),(USDJPY)),(GBPCHF)),(((EURUSD),(USDJPY)),(EURJPY)),(((EURUSD),(USDJPY)),(EURCHF)),(((GBPUSD),(USDCHF)),(GBPJPY)),(((GBPUSD),(USDCHF)),(GBPCHF)),(((GBPUSD),(USDCHF)),(EURJPY)),(((GBPUSD),(USDCHF)),(EURCHF)),(((GBPUSD),(USDJPY)),(GBPJPY)),(((GBPUSD),(USDJPY)),(GBPCHF)),(((GBPUSD),(USDJPY)),(EURJPY)),(((GBPUSD),(USDJPY)),(EURCHF))}
Koprodukte
In der Algebra ist das Koprodukt von zwei Gruppen (G und H) eine Domäne, die alle Elemente sowohl von G als auch von H enthält, wobei die Domänenoperation so definiert ist, dass die resultierende Struktur die „kleinste“ Domäne ist, die sowohl G als auch H enthält. Dies unterscheidet sich vom Produkt zweier Domänen, das eine Domäne ist, die alle Paare von Elementen (g, h) enthält, wobei g in G und h in H ist, wobei die Domänenoperation komponentenweise definiert ist. Das Koprodukt ist ein Kolimes, weil es die „kleinste obere Grenze“ von G und H ist, in dem Sinne, dass jeder andere Bereich, der sowohl G als auch H enthält, auch das Koprodukt enthalten muss.
Ein Koprodukt aus zwei Gebieten A und B ist auch ein drittes Gebiet C, zusammen mit zwei Injektionsmorphismen von A bzw. B nach C, sodass für jedes andere Gebiet D mit zwei Morphismen von A bzw. B ein eindeutiger Morphismus von C nach D existiert, der bestimmte Diagramme kommutieren lässt. Das Koprodukt wird auch als „disjunkte Vereinigung“ oder „Summe“ von A und B bezeichnet, da es die Idee einer Wahl zwischen zwei verschiedenen Bereichen wiedergibt. Intuitiv stellt das Koprodukt C das „alternative“ oder „divergente“ Verhalten von A und B dar.
Koprodukte erfüllen in der Regel die folgenden Eigenschaften:
- Sie sind assoziativ: (A + B) + C ist isomorph zu A + (B + C).
- Sie sind kommutativ: A + B ist isomorph zu B + A.
- Das Koprodukt eines Gebiets mit dem ursprünglichen Gebiet ist isomorph zum Gebiet selbst: A + 0 ist isomorph zu A.
- Das Koprodukt einer Domäne mit der Enddomäne ist isomorph zur Domäne selbst: A + 1 ist isomorph zu 1.
Das Konzept der Koprodukte kann auch auf verschiedene mathematische Strukturen angewandt werden, darunter Mengen, Gruppen, Ringe und Vektorräume sowie auf abstraktere Strukturen wie topologische Räume und Kategorien selbst. In jedem Fall steht das Koprodukt für die Idee einer „Wahl“ oder „Alternative“ zwischen zwei Bereichen oder Strukturen, und es bietet eine Möglichkeit, über das Verhalten des Systems als Ganzes nachzudenken.
Aus der Sicht eines Händlers können Koprodukte der Kategorientheorie zur Modellierung und Analyse von Anlageportfolios verwendet werden und eine bessere Alternative zu den traditionellen Methoden der Portfoliobewertung darstellen. Dies liegt daran, dass sie eine Möglichkeit darstellen, Bereiche in einer Kategorie zu kombinieren, wobei der resultierende Bereich eine Auswahl zwischen den ursprünglichen Bereichen darstellt. Zum Beispiel ist das Koprodukt zweier Zahlen ihr Maximum. Diese Eigenschaft kann genutzt werden, um Anlageportfolios als eine Wahl zwischen verschiedenen Vermögenswerten zu modellieren und die Bewertung dieser Portfolios auf flexiblere und allgemeinere Weise zu analysieren.
Zur Veranschaulichung: Nehmen wir an, wir haben ein Anlageportfolio, das zwei Vermögenswerte enthält: eine Aktie und eine Anleihe. Wir wollen den Wert des Portfolios analysieren und wie er sich unter verschiedenen Marktbedingungen verändert. Traditionell wird dies mit Methoden wie der Discounted-Cashflow-Analyse oder dem Capital Asset Pricing Model (CAPM) durchgeführt. Durch die Verwendung von Koprodukten in der Kategorientheorie können wir das Portfolio jedoch als eine Wahl zwischen Aktien und Anleihen modellieren. Der sich daraus ergebende Koproduktbereich würde den Wert des Portfolios unter verschiedenen Marktbedingungen darstellen und das mit dem Halten beider Vermögenswerte verbundene gemeinsame Risiko erfassen.
Um dies zu verdeutlichen, nehmen wir der Einfachheit halber an, dass die Aktie einen aktuellen Wert von 50 $ und die Anleihe einen aktuellen Wert von 100 $ hat. Wir können das Koprodukt der Aktie und der Anleihe als ihr Maximum definieren, das 100 $ beträgt. Das bedeutet, dass der Wert des Portfolios unabhängig von den Marktbedingungen mindestens 100 $ beträgt. Mit diesem Ansatz können wir das Verhalten des Portfolios in verschiedenen Marktszenarien analysieren. Wenn beispielsweise der Aktienkurs auf 60 $ steigt und der Anleihekurs gleich bleibt, würde der Wert des Portfolios 110 $ betragen, also mehr als 60 $ oder 100 $, was den Kursanstieg erfasst, aber weniger als die Gesamtsumme von 160 $. Sinkt der Anleihekurs auf 90 $ und der Aktienkurs bleibt gleich, würde der Wert des Portfolios immer noch bei 100 $ liegen, was zwar mehr ist als 50 $ oder 90 $, aber immer noch unter der Gesamtsumme von 140 $ liegt. Im Großen und Ganzen bieten Koprodukte einen konservativen, weniger volatilen Ansatz für die Bewertung, der weniger an Marktpreisschwankungen gekoppelt ist. Wir können daher Anlageportfolios als eine Wahl zwischen verschiedenen Vermögenswerten modellieren und ihr Verhalten auf flexiblere und allgemeinere Weise analysieren. Dies könnte zu genaueren und effektiveren langfristigen Portfoliobewertungsstrategien führen und das mit dem Halten mehrerer Vermögenswerte verbundene gemeinsame Risiko besser erfassen.
Koprodukte und Universaleigenschaften
Das Konzept der Universelle Eigenschaft ist, wie oben bei den Produkten gezeigt, ein leistungsfähiges Instrument der Kategorientheorie, das auch zur weiteren Verbesserung der Analyse von Koprodukten im Finanzwesen verwendet werden kann. Es bietet eine formale Möglichkeit, die Art und Weise zu charakterisieren, in der ein Koprodukt bis zu einer bestimmten Art von Isomorphismus einzigartig ist, und dies kann zu effizienteren und präziseren Schlussfolgerungen über Investitionsportfolios führen. Nehmen wir als Beispiel ein Portfolio, das aus drei Vermögenswerten besteht: einer Aktie, einer Anleihe und einem Real Estate Investment Trust (REIT). Wir können dieses Portfolio modellieren, indem wir das Koprodukt aus Aktien, Anleihen und REITs in einer Kategorie von Anlagevermögen verwenden. Das Koprodukt dieser drei Vermögenswerte kann als die Wahl zwischen dem Besitz einer Aktie, einer Anleihe oder eines REIT betrachtet werden. Wir können die Universelle Eigenschaft von Koprodukten nutzen, um zu verstehen, warum diese Wahl bis zur Isomorphie eindeutig ist. Konkret besagt die Universelle Eigenschaft des Koprodukts, dass es für jede andere Domäne Z und Morphismen von den drei Vermögenswerten nach Z einen eindeutigen Morphismus vom Koprodukt nach Z gibt, durch den bestimmte Diagramme kommutieren.
Mit Hilfe der Universellen Eigenschaft können wir das Verhalten des Koprodukts präziser und effizienter beschreiben. Nehmen wir zum Beispiel an, wir möchten das gemeinsame Risiko berechnen, das mit dem Halten von Aktien, Anleihen und dem REIT verbunden ist. Wir können die Universelle Eigenschaft des Koprodukts nutzen, um zu zeigen, dass jede Bewertung, die die von der Universellen Eigenschaft geforderten Diagramme erfüllt, auch bestimmte Eigenschaften erfüllen muss, wie zum Beispiel die Subadditivität des Risikos. Zur Veranschaulichung: Nehmen wir an, die Aktie hat einen Wert von 50 $, die Anleihe hat einen Wert von 100 $ und der REIT hat einen Wert von 150 $. Mit Hilfe des Koprodukts können wir das Portfolio als eine Wahl zwischen diesen drei Vermögenswerten modellieren und das mit dem Halten dieser Vermögenswerte verbundene gemeinsame Risiko berechnen.
Konkret lässt sich das gemeinsame Risiko als das Maximum der mit jedem Vermögenswert verbundenen Einzelrisiken berechnen. Angenommen, das mit der Aktie verbundene Risiko beträgt 10 %, das mit der Anleihe verbundene Risiko 5 % und das mit dem REIT verbundene Risiko 8 %. Mit Hilfe des Koprodukts können wir das gemeinsame Risiko als das Maximum dieser drei Risiken berechnen, das 10 % beträgt. Dies ist das mit dem Portfolio verbundene Risiko unter der Annahme, dass die mit den einzelnen Vermögenswerten verbundenen Risiken unabhängig sind. Mit Hilfe der Universellen Eigenschaft des Koprodukts können wir das Verhalten des Portfolios unter verschiedenen Annahmen über die Korrelation zwischen den mit den einzelnen Vermögenswerten verbundenen Risiken erklären. Wir können beispielsweise die Universelle Eigenschaft nutzen, um zu zeigen, dass, wenn die mit der Aktie und dem REIT verbundenen Risiken positiv korreliert sind, das gemeinsame Risiko, das mit dem Halten der beiden verbunden ist, höher ist als das Maximum ihrer individuellen Risiken.
Zusammenfassend lässt sich sagen, dass die Verwendung der Universellen Eigenschaft in Verbindung mit Koprodukten eine präzisere und effizientere Art der Argumentation über Anlageportfolios ermöglichen kann. Sie ermöglicht es uns, die einzigartigen Eigenschaften eines Koprodukts bis zur Isomorphie zu verstehen und über das Verhalten eines Portfolios unter verschiedenen Annahmen über Korrelation und Risiko nachzudenken.
Schlussfolgerung
Zusammenfassend lässt sich sagen, dass die Kategorientheorie ein leistungsfähiges Instrumentarium für Schlussfolgerungen über komplexe Systeme bietet, und dass ihre Konzepte von Produkten, Koprodukten und der Universellen Eigenschaft wichtige Anwendungen im Finanzwesen haben, insbesondere im Bereich des algorithmischen Handels. Durch die Implementierung dieser Konzepte in MQL5 können Händler tiefere Einblicke in das Verhalten der Finanzmärkte gewinnen und effektivere Handelsstrategien entwickeln. Die Verwendung von Produkten und Koprodukten ermöglicht es den Händlern, über das gemeinsame oder abweichende Verhalten von Finanzinstrumenten nachzudenken und anspruchsvollere Portfolios zu konstruieren, die die Interdependenz zwischen den Vermögenswerten berücksichtigen.
Die Universelle Eigenschaft stellt sicher, dass diese Konstruktionen einzigartig sind und dass sie bestimmte wünschenswerte Eigenschaften erfüllen. Limites und Kolimites bieten eine abstraktere und umfassendere Möglichkeit, über das Verhalten von Sequenzen von Bereichen nachzudenken, und sie ermöglichen Händlern die Entwicklung anspruchsvollerer Risikomanagementstrategien. Insgesamt hat die Anwendung der Kategorientheorie in der Finanzwelt das Potenzial, die Art und Weise, wie wir über Finanzmärkte denken, zu revolutionieren und es Händlern zu ermöglichen, fundiertere Entscheidungen zu treffen. Durch die Einbindung dieser Konzepte in MQL5 können Händler die volle Leistungsfähigkeit der Kategorientheorie nutzen und effektivere Handelsstrategien entwickeln, die auf einem tieferen Verständnis der zugrunde liegenden Struktur der Finanzmärkte basieren.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/12085
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.