Algorithmes d'optimisation de la population : Harmony Search (HS)

Sommaire :

1. Introduction
2. Algorithme
3. Résultats des tests

1. Introduction

La composition musicale se compose de plusieurs éléments : le rythme, la mélodie et l'harmonie. Si le rythme et la mélodie forment un tout dans une œuvre musicale, l'harmonie est ce qui l'agrémente. Une pièce de théâtre ou une chanson sans harmonie est comme une image non colorée dans les livres pour enfants - elle est dessinée, mais il n'y a pas de couleur, pas de luminosité, pas d'expressivité. Une harmonie bien choisie caresse les oreilles, ennoblit le son et permet d'apprécier pleinement les merveilleuses sonorités du piano, de la guitare ou de tout autre instrument de musique. Une mélodie peut être chantée, alors qu'une harmonie ne peut être que jouée. L'harmonie musicale est un ensemble d'accords, sans lesquels aucune chanson ou aucun morceau de musique ne sera complet et sonnant.

L'harmonie apparaît exactement au moment où l'on relie deux sons - l'un après l'autre ou en flux simultané. Le terme "combinaison" serait un synonyme plus approprié. Après avoir relié un son à un autre, nous obtenons une combinaison dans laquelle la hiérarchie tente déjà de s'aligner à sa manière. Dans les écoles de musique, les collèges et les conservatoires, il existe une discipline spéciale - l'harmonie - où les étudiants étudient tous les accords existant dans la théorie musicale, apprennent à les appliquer dans la pratique et même à résoudre des problèmes d'harmonie.

Au cours d'une improvisation musicale, les musiciens tentent d'accorder la hauteur de leurs instruments afin d'obtenir une harmonie agréable (meilleure condition). Dans la nature, l'harmonie est déterminée par une relation particulière entre plusieurs ondes sonores de fréquences différentes. La qualité de l'harmonie improvisée est déterminée par l'évaluation esthétique. Afin d'améliorer l'appréciation esthétique et de trouver la meilleure harmonie, les musiciens s'exercent de plus en plus. Il existe une similitude entre l'improvisation et l'optimisation.

La méthode Harmony Search (HS) est un algorithme d'optimisation métaheuristique émergent qui a été utilisé pour résoudre de nombreux problèmes complexes au cours de la dernière décennie. L'algorithme Harmony Search (HS) a été proposé pour la première fois en 2001 par Z. W. Geem. La méthode HS s'inspire des principes fondateurs de l'improvisation musicale et de la recherche de l'harmonie musicale. Les combinaisons de l'harmonie parfaite des sons correspondent à l'extremum global dans le problème d'optimisation multidimensionnelle, tandis que le processus d'improvisation musicale correspond à une recherche de l'extremum.

Pendant l'improvisation, chaque musicien reproduit un son à n'importe quelle mesure d'un morceau de musique (dans la limite des capacités de son instrument de musique), de sorte que les sons de tous les musiciens de l'orchestre à cette mesure forment un vecteur d'harmonie. Les combinaisons de sons qui forment de "bonnes" harmonies sont mémorisées par chacun des musiciens et peuvent être utilisées pour former des harmonies encore meilleures dans les mesures suivantes du morceau de musique.

En règle générale, pendant l'improvisation, un musicien remplit l'une des trois conditions suivantes : former un son absolument aléatoire à partir de la gamme de sons disponibles ; jouer un son quelconque à partir de la mémoire des harmonies ; jouer un vecteur d'harmonie adjacent à partir de la même mémoire. Les principales caractéristiques de l'algorithme HS sont la possibilité de l'utiliser pour résoudre des problèmes d'optimisation continus et discrets.

Les caractéristiques distinctives du HS sont la simplicité de l'algorithme et l'efficacité de la recherche. Pour cette raison, l'algorithme attire une attention considérable de la part des chercheurs et se développe rapidement, tant sur le plan théorique que pratique. HS est une technique métaheuristique qui offre une grande stabilité entre les phases d'exploration et d'exploitation du processus de recherche. HS s'inspire de la créativité humaine, et la méthode pour trouver la solution parfaite à un problème donné est similaire à celle utilisée par un musicien pour trouver une harmonie agréable. La méthode utilisée pour obtenir la valeur de la fonction d'aptitude est similaire à la méthode d'obtention d'une référence à l'aide de la hauteur de chaque instrument de musique.

2. Algorithme

Le travail de la logique de la HS est similaire au travail d'un musicien qui crée une harmonie parfaite. Le musicien essaie de modifier les différentes tonalités jusqu'à ce qu'il trouve l'harmonie parfaite. Ensuite, la collection d'harmonies trouvées est stockée en mémoire. Dans un problème d'optimisation, les harmonies subissent diverses modifications ; si les résultats de la variation sont favorables, la mémoire est renouvelée en ajoutant des harmonies à la mémoire et en supprimant les éléments indésirables... Tout cela peut sembler assez confus. Qu'est-ce que l'harmonie ? Qu'est-ce qu'un ton ? Essayons de comprendre l'algorithme en utilisant nos propres termes.

Qu'est-ce qu'un morceau de musique ? Bien sûr, je ne suis pas musicien (ce qui est dommage), mais programmeur. Mais pour les besoins de la détection de l'algorithme, il suffira d'appliquer le concept de "note". Un morceau de musique est composé de notes (accords). La figure 1 montre schématiquement le "mécanisme" de construction d'un morceau de musique. La sélection des notes correspond à un morceau de musique, qui est facile à déterminer même sans oreille musicale ou sans formation musicale. Les personnes désireuses de deviner peuvent laisser un commentaire ci-dessous.

L'optimisation de l'algorithme HS consiste à déplacer les barres vertes contenant les notes sur la barre bleue du morceau lui-même. La portée de la barre verte est une octave, qui est composée de notes individuelles. Le produit (barre bleue) correspond à l'une des solutions d'optimisation. Les notes sur la barre verte sont les paramètres d'optimisation correspondants du problème. La mémoire du musicien stocke plusieurs versions du morceau (plusieurs variantes de barres bleues), c'est la population de l'algorithme.

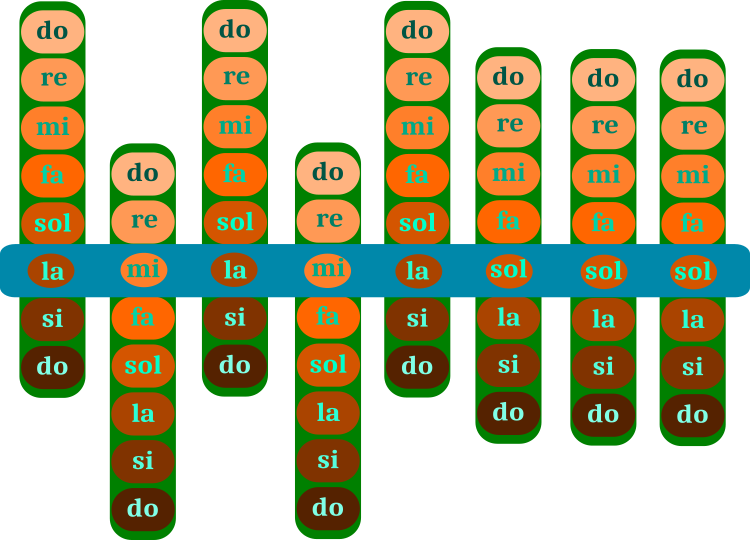
Figure 1. Sélection de notes dans un morceau de musique (recherche d'harmonie). La barre bleue est une pièce. Les barres vertes sont des ensembles de notes

L'exemple de la figure 1 correspond à la solution d'un problème discret, où il y a huit étapes dans le paramètre. L'exemple est fourni pour faciliter la compréhension du fonctionnement de l'algorithme. Cependant, dans une tâche arbitraire, il peut y avoir n'importe quel pas des paramètres optimisés et il y a aussi des notes intermédiaires - les demi-tons. Les paramètres corrects pour résoudre le problème correspondent aux notes correctes du morceau.

Ainsi, le processus de création d'un morceau de musique commence par un ensemble aléatoire de sons d'un instrument de musique qui se situent dans la gamme des fréquences reproductibles de l'instrument. Il est nécessaire de créer plusieurs variantes d'un morceau pour pouvoir combiner les différentes sections des notes de la variante. L'étape suivante consiste à changer les notes dans ces variations. Nous pouvons le faire de trois manières différentes :

1. Changer au hasard l'une des notes du morceau qui se trouve dans la tessiture de l'instrument de musique.
2. Nous pouvons prendre note du numéro de série correspondant à d'autres versions de la pièce.
3. Nous pouvons prendre une note d'une autre version du morceau et la modifier légèrement pour la rendre plus aiguë ou plus grave.

Ayant ainsi obtenu un nouvel ensemble de variantes d'une œuvre musicale, nous évaluons chacune des variantes en termes d'harmonie sonore et les stockons à leur position initiale dans la mémoire, à condition que la nouvelle version soit meilleure que la précédente. La particularité de l'algorithme est qu'il n'est pas nécessaire de trier la population, dans notre cas l'ensemble des produits. Chaque nouvelle meilleure option remplacera l'ancienne moins bonne au même endroit. Ce processus s'apparente au travail des algorithmes génétiques qui imitent l'évolution lorsque les individus les plus aptes survivent. De plus, des similitudes sont également observées avec la combinaison des gènes dans le chromosome.

Sur la base de ce qui précède, nous pouvons composer de manière préliminaire le pseudo-code de l'algorithme HS :

1. Génération d'harmonies aléatoires.
2. Mesure de la qualité des harmonies (calcul de la fonction fitness).
3. Utilisation de la sélection d'accords d'une harmonie choisie au hasard avec la probabilité de Eh.
  3.1 Changement de l'accord selon l'équation si l'accord est choisi dans une harmonie avec la probabilité de Ep.
    3.1.1 Laisser l'accord sélectionné inchangé.
  3.2 Nouvel accord selon l'équation.
4. Mesure de la qualité des harmonies (calcul de la fonction fitness).
5. répéter à partir de 3 jusqu'à ce que le critère d'arrêt soit atteint.

Passons donc à la description des paramètres d'entrée de l'algorithme, qui sont peu nombreux et intuitifs.

input int Population_P = 50; // Taille de la population
input double Eh_P = 0.9; // fréquence de sélection aléatoire
input double Ep_P = 0.1; // fréquence de l'ajustement pas à pas
input double Range_P = 0.2; // range

• Population_P - le nombre de variantes d'un morceau dans la mémoire du musicien (taille de la population) ;
• Eh_P - la fréquence à laquelle une variante d'un morceau est sélectionnée dans la mémoire influe sur la fréquence à laquelle nous nous référons à une autre variante pour emprunter une note. Une valeur plus élevée signifie que les propriétés combinatoires de l'algorithme sont plus élevées ;
• Ep_P - la fréquence à laquelle vous devez modifier légèrement la note, plus haut ou plus bas dans le ton, si la note a été sélectionnée dans une autre version du morceau ;
• Portée_P - la portée de la note dans la version éditée du morceau, si elle n'a pas été prise dans une autre version. Par exemple, 0,2 correspond à 20% de la gamme de notes d'un instrument de musique.
• 
  

L'algorithme HS fonctionne avec des harmonies (compositions musicales), qui peuvent être décrites par la structure S_Harmony. L'harmonie est constituée de notes (accords), il s'agit d'un tableau représentant les paramètres c[] à optimiser. Les meilleurs accords du morceau seront stockés dans le tableau cB[]. C'est dans ce tableau que la composition réussie sera envoyée, et c'est avec ces compositions (harmonies) que nous effectuerons des permutations combinatoires en leur empruntant des notes. La qualité de l'harmonie est stockée dans la variable h, et la meilleure harmonie est stockée dans la variable hB.

//——————————————————————————————————————————————————————————————————————————————
struct S_Harmony //musical composition
{
  double c  []; //chords
  double cB []; //best chords
  double h;     //harmony quality
  double hB;    //best harmony quality
};
//——————————————————————————————————————————————————————————————————————————————

Le tableau des structures d'harmonie est utilisé dans la classe C_AO_HS. Les déclarations de la méthode et de la classe membre sont compactes, car l'algorithme est extrêmement concis et nécessite peu de calculs. Ici, nous ne verrons pas le tri utilisé dans de nombreux autres algorithmes d'optimisation. Nous aurons besoin de tableaux pour définir le maximum, le minimum et le pas des paramètres à optimiser (ils jouent le rôle de la gamme et du pas des accords) et de variables constantes pour leur transférer les paramètres externes de l'algorithme. Passons maintenant à la description des méthodes qui contiennent la logique principale de HS.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_HS
{
  //----------------------------------------------------------------------------
  public: S_Harmony h      []; //harmonies matrix
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best chords
  public: double hB;           //best harmony quality

  public: void Init (const int    chordsNumberP,      //chords number
                     const int    harmoniesNumberP,   //harmonies number
                     const double EhP,                //random selection frequency
                     const double EpP,                //frequency of step-by-step adjustment
                     const double rangeP,             //range
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    chordsNumber;      //chords number
  private: int    harmoniesNumber;   //harmonies number
  private: double Eh;                //random selection frequency
  private: double Ep;                //frequency of step-by-step adjustment
  private: double range;             //range
  private: int    maxIterations;
  private: double frequency [];      //frequency range
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

La méthode publique Init() initialise l'algorithme. Nous définissons ici la taille des tableaux. Nous initialisons l'indicateur de qualité de la meilleure harmonie trouvée avec la valeur "double" la plus basse possible. Nous ferons de même avec les variables correspondantes du tableau des structures d'harmonie.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Init (const int    chordsNumberP,      //chords number
                    const int    harmoniesNumberP,   //harmonies number
                    const double EhP,                //random selection frequency
                    const double EpP,                //frequency of step-by-step adjustment
                    const double rangeP,             //range
                    const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  chordsNumber    = chordsNumberP;
  harmoniesNumber = harmoniesNumberP;
  Eh              = EhP;
  Ep              = EpP;
  range           = rangeP;
  maxIterations   = maxIterationsP;

  ArrayResize (rangeMax,  chordsNumber);
  ArrayResize (rangeMin,  chordsNumber);
  ArrayResize (rangeStep, chordsNumber);
  ArrayResize (frequency, chordsNumber);

  ArrayResize (h, harmoniesNumberP);

  for (int i = 0; i < harmoniesNumberP; i++)
  {
    ArrayResize (h [i].c,  chordsNumber);
    ArrayResize (h [i].cB, chordsNumber);
    h [i].h  = -DBL_MAX;
    h [i].hB = -DBL_MAX;
  }

  ArrayResize (cB, chordsNumber);
}
//——————————————————————————————————————————————————————————————————————————————

La première méthode publique Moving(), qui doit être exécutée à chaque itération, a pour entrée "iter" - l'itération en cours. Lors de la première itération, lorsque l'indicateur "revision" est "faux", il est nécessaire d'initialiser les harmonies avec des valeurs aléatoires dans la gamme des instruments de musique, ce qui équivaut à jouer des accords au hasard par un musicien. Pour réduire les opérations répétitives, stockons la gamme de fréquences sonores des accords correspondants (paramètres optimisés) dans le tableau frequency[].

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      h [har].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      h [har].c [c] = SeInDiSp  (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      h [har].h     = -DBL_MAX;
      h [har].hB    = -DBL_MAX;

      frequency [c] = rangeMax [c] - rangeMin [c];
    }
  }

  revision = true;
}

Lors de la deuxième itération et des itérations suivantes, l'improvisation intervient, c'est-à-dire le changement séquentiel des accords et de leurs combinaisons. Il existe plusieurs harmonies en mémoire, que nous allons modifier et combiner. Pour chaque nouvelle harmonie, nous trierons séquentiellement les accords. Pour chaque accord, il existe une probabilité d'être choisi au hasard dans la mémoire de l'harmonie, c'est-à-dire que l'harmonie sera choisie au hasard (de manière équiprobable pour toutes les harmonies). Si l'accord est tiré de la mémoire des harmonies, la probabilité de son changement est également vérifiée par l'équation :

h [har].c [c] = h [har].c [c] + r * B * frequency [c];

avec :

r - un nombre aléatoire entre -1 et 1
frequency - la gamme de fréquences de l'instrument
B - le coefficient calculé par la formule :

B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

avec :

maxIterations - le nombre maximum d'itérations
iter - l’itération actuelle
maxB - la limite maximale du coefficient
minB - la limite minimale du coefficient

La figure 2 montre la dépendance du coefficient B par rapport aux paramètres de réglage de l'algorithme et à l'itération en cours.

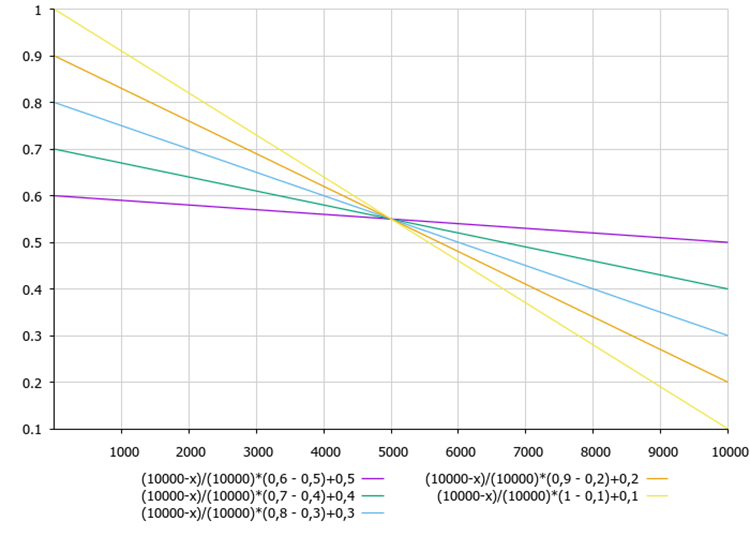
Figure 2. La dépendance du coefficient B par rapport aux paramètres de réglage de l'algorithme maxB, minB et à l'itération en cours.

L'équation de calcul du coefficient B montre que le coefficient B diminue à chaque itération. Ainsi, les extrémités trouvées sont affinées à la fin de l'optimisation.
Si un accord n'a pas été sélectionné dans la mémoire des harmonies, c'est celui qui existe déjà à ce moment-là qui sera modifié. La différence entre un changement d'accord et le changement précédent est la plage fixe des valeurs de l'onde sonore.

Une fois le processus de modification de l'accord terminé, vérifions que l'accord obtenu ne dépasse pas les valeurs autorisées par l'instrument de musique.

//----------------------------------------------------------------------------
else
{
  double r         = 0.0;
  int    harAdress = 0;
  double minB      = 0.0;
  double maxB      = 0.3;
  double B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      r = RNDfromCI (0.0, 1.0);

      if (r <= Eh)
      {
        r = RNDfromCI (0.0, harmoniesNumber - 1);
        harAdress = (int)MathRound (r);
        if (harAdress < 0) harAdress = 0;
        if (harAdress > harmoniesNumber - 1) harAdress = harmoniesNumber - 1;

        h [har].c [c] = h [harAdress].cB [c];

        r = RNDfromCI (0.0, 1.0);

        if (r < Ep)
        {
          r = RNDfromCI (-1.0, 1.0);
          h [har].c [c] = h [har].c [c] + r * B * frequency [c];
        }
      }
      else
      {
        r = RNDfromCI (-1.0, 1.0);
        h [har].c [c] = h [har].cB [c] + r * range * frequency [c];
      }

      h [har].c [c] = SeInDiSp (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Revision() est la deuxième méthode publique appelée à chaque itération après le calcul de la fonction d'aptitude. Son but est de mettre à jour la solution globale trouvée. Si l'harmonie est meilleure que sa meilleure version h > hB, alors elle met à jour la meilleure version de cette harmonie.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Revision ()
{
  for (int har = 0; har < harmoniesNumber; har++)
  {
    if (h [har].h > hB)
    {
      hB = h [har].h;
      ArrayCopy (cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
    if (h [har].h > h [har].hB)
    {
      h [har].hB = h [har].h;
      ArrayCopy (h [har].cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Après avoir étudié attentivement le code, nous constatons qu'il n'y a pas d'idées fondamentalement nouvelles dans l'algorithme de recherche d'harmonie. L'algorithme Harmony Search emprunte des idées précédemment utilisées dans les algorithmes évolutionnaires, notamment la recombinaison uniforme globale, la mutation uniforme, la mutation gaussienne et le remplacement de l'individu le plus mauvais à chaque génération. Certaines sources indiquent qu'il est nécessaire de remplacer la pire harmonie en mémoire par une nouvelle. Dans notre algorithme, l'harmonie ne peut remplacer que sa meilleure solution. Cette version est légèrement différente de la version classique, car mes études indiquent que c'est cette mise en œuvre de l'algorithme qui sera la plus productive.

La contribution de l'algorithme de recherche d'harmonie réside dans deux domaines : la combinaison de ces idées dans cet algorithme est nouvelle ; la motivation musicale de l'algorithme de recherche d'harmonie est nouvelle. Très peu de publications sur la recherche d'harmonie traitent des motifs musicaux ou des extensions de l'algorithme de recherche d'harmonie. La plupart des publications sont consacrées à l'hybridation de l'algorithme de recherche d'harmonie avec d'autres algorithmes évolutionnaires, à l'ajustement des paramètres de recherche d'harmonie ou à l'application de l'algorithme de recherche d'harmonie à des problèmes spécifiques. Si des extensions plus musicales pouvaient être appliquées à l'algorithme HS, cela permettrait de le distinguer en tant qu'algorithme évolutif distinct. Une telle recherche nécessiterait l'étude de la théorie musicale, l'étude du processus de composition et d'arrangement musicaux, l'étude des théories éducatives de la musique et l'application inventive de ces théories dans l'algorithme de recherche d'harmonie.

3. Résultats des tests

Les résultats du banc d'essai HS se présentent comme suit :

2023.02.08 17:30:05.710    Test_AO_HS (EURUSD,M1)    C_AO_HS:50;0.9;0.1;0.2
2023.02.08 17:30:05.711    Test_AO_HS (EURUSD,M1) =============================
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    5 Rastrigin's ; Func runs 10000 result : 80.62868417575105
2023.02.08 17:30:07.919 Test_AO_HS (EURUSD,M1)    Score : 0.99903
2023.02.08 17:30:11.563 Test_AO_HS (EURUSD,M1)    25 Rastrigin's ; Func runs 10000 result : 75.85009280972398
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    Score : 0.93983
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    500 Rastrigin's ; Func runs 10000 result : 50.26867628386793
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    Score : 0.62286
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1) =============================
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    5 Forest's ; Func runs 10000 result : 1.7224980742302596
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    Score : 0.97433
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    25 Forest's ; Func runs 10000 result : 1.0610723369605124
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    Score : 0.60020
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    500 Forest's ; Func runs 10000 result : 0.13820341163584177
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    Score : 0.07817
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1) =============================
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    5 Megacity's ; Func runs 10000 result : 7.959999999999999
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    Score : 0.66333
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    25 Megacity's ; Func runs 10000 result : 5.112
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    Score : 0.42600
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    500 Megacity's ; Func runs 10000 result : 0.6492
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    Score : 0.05410

Les valeurs élevées des fonctions de test sont frappantes, ce qui permet d'espérer que les résultats du score global du test seront exceptionnels. Une caractéristique de HS sur la visualisation est que nous ne voyons pas de formations structurelles sous forme de groupes de coordonnées, comme dans le cas de certains des algorithmes précédents. Visuellement, le mouvement des agents dans l'espace de recherche ne présente aucun schéma. Ce comportement est similaire à celui de l'algorithme d'optimisation RND, bien que les graphiques de convergence se comportent de manière très confiante, s'approchant progressivement de la solution du problème d'optimisation. Le fait de rester bloqué dans des extrema locaux n'est pas typique de cet algorithme.

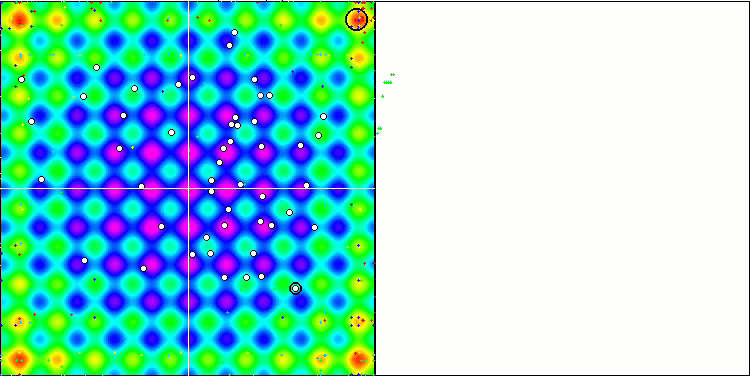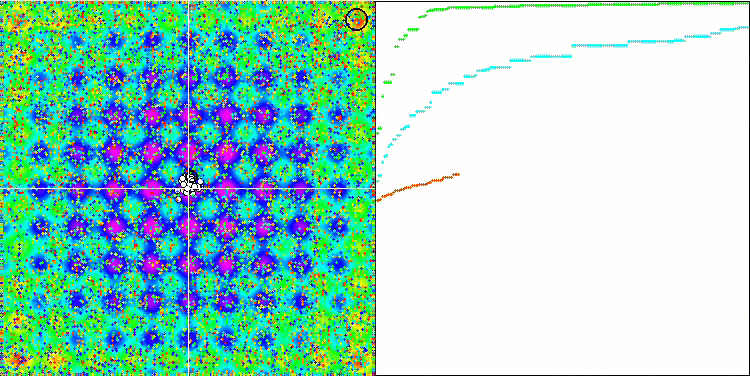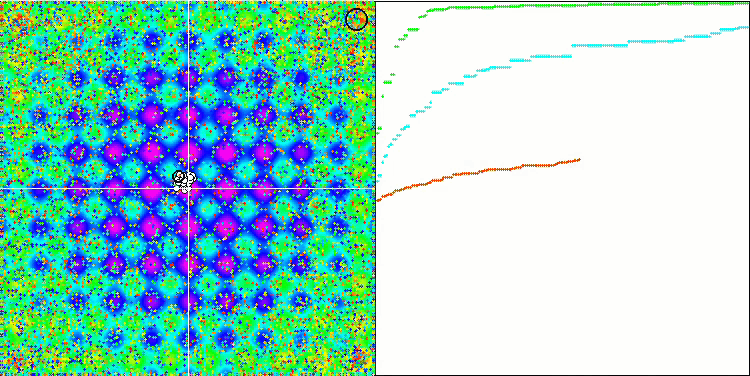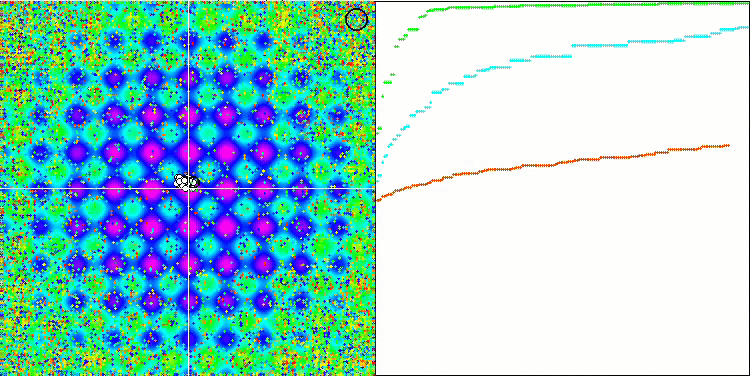
  HS sur la fonction de test de Rastrigin

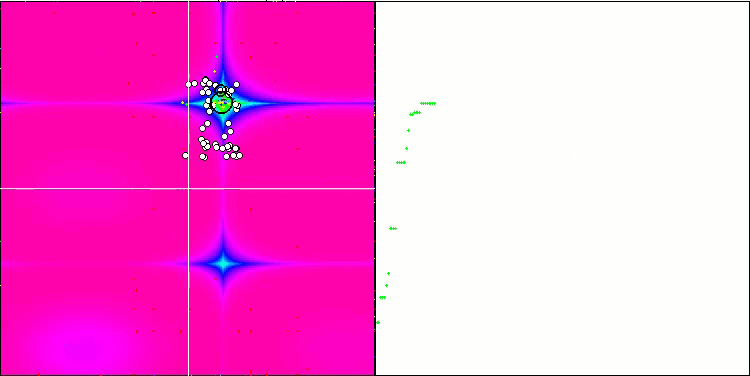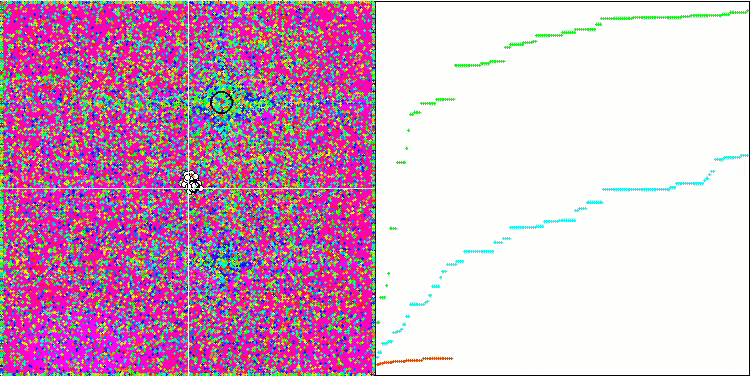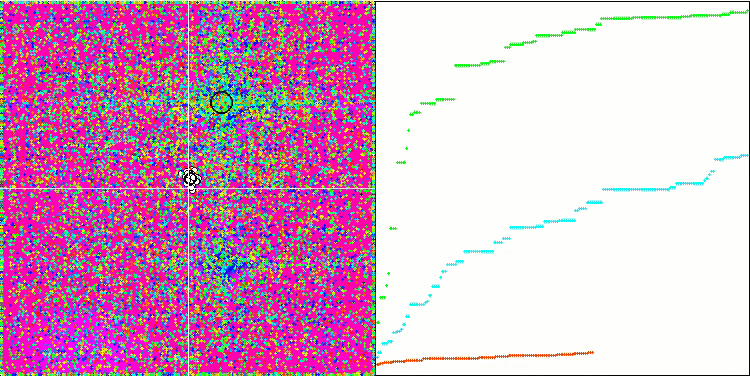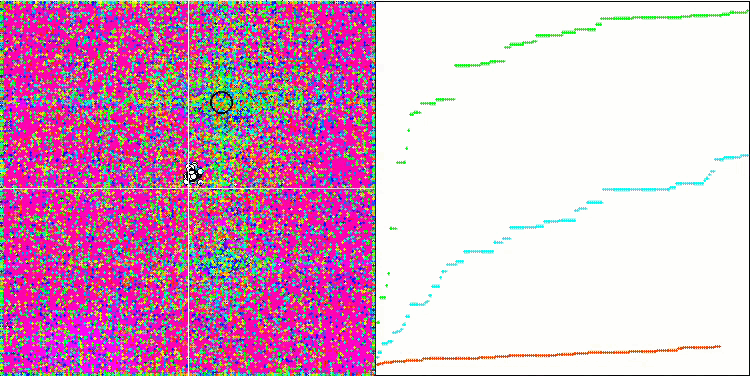
  HS sur la fonction de test forest

  HS sur la fonction de test megacity

Il est temps d'analyser les résultats du tableau et de répondre à la question posée dans le titre de l'article. Dans des articles précédents, j'ai exprimé des doutes quant à l'existence d'un algorithme permettant de contourner le leader des résultats sur une fonction discrète. L'algorithme, qui ressemble visuellement à un algorithme aléatoire, a été capable de devenir un leader non seulement sur une fonction discrète (meilleur dans trois tests), mais aussi sur d'autres fonctions de test, devenant finalement le meilleur dans 6 tests sur 9.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrète)			Megacity final	Résultat final
		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)		10 paramètres (5 F)	50 paramètres (25 F)	1.000 paramètres (500 F)
HS	recherche d'harmonie	1,00000	1,00000	0,57048	2,57048	1,00000	0,98931	0,57917	2,56848	1,00000	1,00000	1,00000	3,00000	100,00000
ACOm	optimisation par colonies de fourmis M	0,34724	0,18876	0,20182	0,73782	0,85966	1,00000	1,00000	2,85966	1,00000	0,88484	0,13497	2,01981	68,094
IWO	Optimisation des mauvaises herbes envahissantes	0,96140	0,70405	0,35295	2,01840	0,68718	0,46349	0,41071	1,56138	0,75912	0,39732	0,80145	1,95789	67,087
COAm	algorithme d'optimisation coucou M	0,92701	0,49111	0,30792	1,72604	0,55451	0,34034	0,21362	1,10847	0,67153	0,30326	0,41127	1,38606	50,422
FAm	algorithme firefly M	0.60020	0,35662	0,20290	1,15972	0,47632	0,42299	0,64360	1,54291	0,21167	0,25143	0,84884	1,31194	47,816
BA	algorithme des chauves-souris	0,40658	0,66918	1,00000	2,07576	0,15275	0,17477	0,33595	0,66347	0,15329	0,06334	0,41821	0,63484	39,711
ABC	colonie d'abeilles artificielles	0,78424	0,34335	0,24656	1,37415	0,50591	0,21455	0,17249	0,89295	0,47444	0,23609	0,33526	1,04579	38,937
BFO	optimisation du butinage bactérien	0,67422	0,32496	0,13988	1,13906	0,35462	0,26623	0,26695	0,88780	0,42336	0,30519	0,45578	1,18433	37,651
GSA	algorithme de recherche gravitationnelle	0,70396	0,47456	0,00000	1,17852	0,26854	0,36416	0,42921	1,06191	0,51095	0,32436	0,00000	0,83531	35,937
FSS	recherche d'un banc de poissons	0,46965	0,26591	0,13383	0,86939	0,06711	0,05013	0,08423	0,20147	0,00000	0,00959	0,19942	0,20901	13,215
PSO	optimisation par essaims de particules	0,20515	0,08606	0,08448	0,37569	0,13192	0,10486	0,28099	0,51777	0,08028	0,21100	0,04711	0,33839	10,208
RND	aléatoire	0,16881	0,10226	0,09495	0,36602	0,07413	0,04810	0,06094	0,18317	0,00000	0,00000	0,11850	0,11850	5,469
GWO	optimiseur du loup gris	0,00000	0,00000	0,02672	0,02672	0,00000	0,00000	0,00000	0,00000	0,18977	0,03645	0,06156	0,28778	1,000

Résumons. Au moment de la rédaction du présent document, l'algorithme HS occupe la première place dans l'histogramme des résultats des tests, avec une avance considérable par rapport aux autres algorithmes d'optimisation, ce qui témoigne de la force et de la puissance de l'algorithme et de son potentiel dans le domaine de l'optimisation des processus de résolution de problèmes plus ou moins complexes.

À mon avis, l'héritage de certaines méthodes (techniques) présentes dans d'autres algorithmes d'optimisation est un facteur très important qui permet d'obtenir des résultats impressionnants sur divers types de fonctions de test, y compris des fonctions très complexes : HS n'a pas de tri de solutions, chaque solution ne met à jour que sa décision locale - ceci est typique de l'algorithme d'optimisation de la recherche du coucou, où un nouveau chemin pour le développement d'une branche de décision ne se produit que si l'œuf est meilleur que celui qui se trouve dans le nid. Les méthodes HS sont également similaires aux méthodes utilisées dans les algorithmes génétiques - combinatoire des éléments de solution.

Le puissant algorithme d'optimisation HS, qui présente des performances exceptionnellement élevées, peut être recommandé en toute sécurité pour résoudre une grande variété de problèmes complexes comportant de nombreuses variables, à la fois pour les fonctions d'échelle lisses et pour les problèmes combinatoires discrets complexes. L'algorithme HS a déjà été appliqué avec succès dans de nombreux domaines de l'ingénierie (optimisation de la topologie des structures et de la forme optimale des pièces), de l'électronique et de la logistique.

La facilité de mise en œuvre de l'algorithme HS laisse place à la recherche, ce qui nous permet d'ajouter et de combiner diverses stratégies d'optimisation. Cela suggère que les capacités de l'algorithme sont loin d'être pleinement exploitées.

L'histogramme des résultats du test de l'algorithme est présenté ci-dessous.

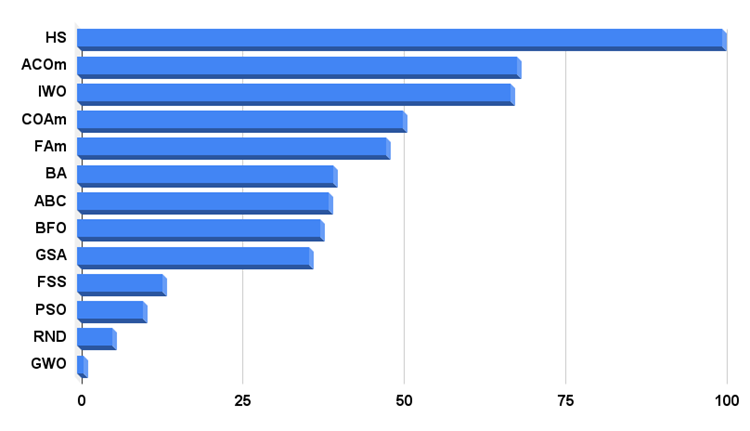
Figure 3. Histogramme des résultats des tests des algorithmes

Avantages et inconvénients de l'algorithme de recherche harmonique HS :

Avantages :
1. Mise en œuvre facile
2. Excellente convergence sur tous les types de fonctions sans exception
3. Evolutivité impressionnante
4. Très rapide
5. Nombre réduit de paramètres externes

Inconvénients :
Aucun n’a été trouvé

Chaque article présente une archive contenant les versions actuelles mises à jour des codes algorithmiques de tous les articles précédents. L'article est basé sur l'expérience accumulée par l'auteur et représente son opinion personnelle. Les conclusions et les jugements sont basés sur les expériences.