Ein neuer Ansatz für nutzerdefinierte Kriterien in den Optimierungen (Teil 1): Beispiele für Aktivierungsfunktionen

Einführung

Die Suche nach der idealen Optimierung, um die richtige Kombination von Parametern zu finden, geht weiter. Das Forum ist voll von Vorschlägen, wie man den MetaTrader Optimizer dazu bringen kann, die verschiedenen Durchläufe zurückzugeben und zu bewerten, damit ein Entwickler eine Kombination (oder mehrere Kombinationen) von Parametern wählen kann, die stabil sind. Die Einführung von Prop-Firmen mit ihren strengen Grenzen, die verständlicherweise viel strenger sind als die, die von einem privaten Händler verlangt werden könnten, hat diese Aufgabe noch schwieriger gemacht.

Die Möglichkeit, ein nutzerdefiniertes Kriterium zu definieren und sogar das komplexe Kriterium mit seiner undurchsichtigen Methodik zu verwenden, hat dazu geführt, dass das Parsen oder zumindest die Analyse der Ergebnisse in Excel, Python, R oder in proprietärer Software reduziert werden kann, um die beste Permutation der Parameter zu erhalten.

Das Problem ist, dass die Verwendung von return(0) in veröffentlichten nutzerdefinierten Kriterien immer noch nicht ungewöhnlich ist. Dies birgt tatsächliche oder potenzielle Gefahren, einschließlich der Möglichkeit, (kaum) unerwünschte Ergebnisse zu verwerfen oder, schlimmer noch, den genetischen Optimierungsprozess von potenziell produktiven Wegen abzulenken.

In einem Versuch, zu den ersten Prinzipien zurückzukehren, nachdem ich einige sehr empirische Experimente durchgeführt hatte, versuchte ich, einige Kurvengleichungen zu finden. Zu diesem Zweck habe ich mich „Activation Functions in Neural Networks“ zugewandt und einige davon für die Verwendung hier übernommen und modifiziert. Nachdem ich diese erläutert habe, habe ich einige Methoden vorgeschlagen, um sie in der Praxis anzuwenden.

Der Plan für diese Artikelserie sieht folgendermaßen aus:

1. Einführung und Standard-Aktivierungsfunktionen mit MQL5-Code
2. Modifikationen, Skalierung und Gewichtung sowie reale Beispiele
3. Ein Werkzeug zur Untersuchung verschiedener Kurven, Skalierungen und Gewichtungen
4. Alle anderen Punkte, die sich ergeben...

Aktueller Stand der Verwendung von nutzerdefinierten Kriterien

Zwei Mitwirkende, vor denen ich größten Respekt habe, haben einige ausgezeichnete Punkte zur Veranschaulichung des Problems angeführt, wobei sie Bedenken hinsichtlich der Verwendung von return(0) und der von Complex Criterion zurückgegebenen Ergebnisse äußerten. Alain Verleyen, ein Moderator des Forums, berichtet, dass ein Durchlauf, der einen Verlust von 6.000 einbringt, besser abschneidet als ein Durchlauf, der mit mehr Handelsgeschäfte einen Gewinn von 1.736 einbringt (und bei Profit Factor, RF, Sharpe Ratio UND Drawdown deutlich besser abschneidet). Alain sagt, dass das kryptische „komplexe Kriterium“ einige seltsame Ergebnisse liefert. Ich würde noch weiter gehen und sagen, dass dies sicherlich erhebliche Zweifel an der Methodik des Komplexen Kriteriums aufkommen lässt. Wenn in der Tat, wie Muhammad Fahad später im selben Thread bemerkt - und ich bin sicher, dass er Recht hat - „negative Saldi nicht besonders schlecht für die Optimierung sind, sondern eine entscheidende Rolle bei der Beurteilung der zukünftigen Generation spielen, was schlecht und was schlecht ist, während die Gene gekreuzt werden“, könnte die Rückgabe eines solchen positiven Ergebnisses den genetischen Optimierer möglicherweise in die Irre führen.

Es ist lange her, dass ich MT4 nutzt habe, aber ich erinnere mich dunkel an die Möglichkeit, Einschränkungen für bestimmte Ergebnisstatistiken einzugeben. In MQL5 scheint es auf den ersten Blick nicht möglich zu sein, dies zu tun, außer das sehr stumpfe Instrument return(0) in einem nutzerdefinierten Kriterium zu verwenden, dessen mögliche Nachteile bereits erwähnt wurden. Mir kommt der Gedanke, dass, wenn wir einen Rückgabewert erhalten können, der sehr nahe bei 1 liegt, wenn das Verhältnis oder die Kennzahl bei oder über dem gewünschten Minimum, bei oder unter dem gewünschten Maximum oder sogar bei oder nahe an einem bestimmten Ziel liegt, und wenn wir dann die Werte für jede Kennzahl/jedes Verhältnis miteinander multiplizieren und dann das Ergebnis mit 100 multiplizieren, könnten wir auf etwas stoßen...

Warum sollte man sich von Neuronalen Netzen inspirieren lassen?

i) Genetische Optimierung als Neuronales Netz... 

Unabhängig davon, ob hinter dem genetischen Algorithmus ein neuronales Netz steht oder nicht, scheint der logische Prozess derselbe zu sein: Man probiert eine Parameterkombination aus, bewertet sie (entsprechend dem gewählten Optimierungskriterium), behält potenziell profitable Auswahlen für weitere Verbesserungen und verwirft den Rest. Dieser Vorgang wird so lange wiederholt, bis die Verbesserung der ausgewählten Punktzahl zum Stillstand kommt.

ii) Täler, explodierende Gradienten, Gewichtung, Normalisierung und manuelle Auswahl 

Das Problem der nicht-konvexen Fehleroberfläche ist im Bereich des maschinellen Lernens gut bekannt. In ähnlicher Weise könnten wir bei der genetischen Optimierung in lokale Minima oder Sattelpunkte geraten, die durch return(0)-Anweisungen fehlgeleitet werden, was dazu führt, dass der genetische Algorithmus sein „Wissen“ verwirft.

Auch die Verarbeitung der verschiedenen Metriken zu einem eigenen Kriterium muss gut durchdacht sein... meine ersten Versuche waren sehr grob und verwendeten verschiedene Faktoren für Division und Multiplikation, ganz zu schweigen von Exponentialfaktoren, was zu Ergebnissen führte, die an die Grenze des Wahnsinns gingen (explodierender Gradient)... Der Algorithmus für die komplexe Kriteriumspunktezahl verwendet eindeutig eine Funktion zur Begrenzung der Punktezahl zwischen 0 und 100, was auf die Verwendung einer Funktion vom Typ Sigmoid oder Logistik hindeutet.

Die Notwendigkeit, die einzelnen Komponenten eines nutzerdefinierten Kriteriums zu gewichten, liegt auf der Hand: Wir müssen Gewichte verwenden, um die Priorität der verschiedenen Komponenten zu bestimmen, und wir müssen sowohl die Eingaben normalisieren, um die Empfindlichkeit unseres Modells einzustellen, als auch die Ausgaben, um einen Vergleich zwischen den Modellen zu ermöglichen. Auf die Gewichtung und Normalisierung werden wir in einem späteren Artikel eingehen.

Wenn wir uns die Ergebnisse eines Optimierungslaufs ansehen, entweder manuell oder in einer Tabellenkalkulation, sortieren wir vielleicht nach verschiedenen Ergebnisgrößen, filtern Ergebnisse heraus und wählen schnell, fast unbewusst, Parametersätze nach der Farbe der wichtigsten Kennzahlen aus. Wir wenden hier einfach die beschriebenen Prozesse an, die selbst ein Versuch sind, unsere eigene intellektuelle Verarbeitung des vollständigen Ergebnisses zu imitieren.

Aktivierungsfunktionen in neuronalen Netzen

Mir fällt auf, dass die Funktionen, nach denen ich gesucht habe, denen ähneln, auf die ich vor ein oder zwei Jahren gestoßen bin, als ich mir Aktivierungsfunktionen in neuronalen Netzen angesehen habe.

Aktivierungsfunktionen in neuronalen Netzen lassen sich grob in drei Typen einteilen: binär, linear und nicht-linear:

• Binäre Funktionen klassifizieren Werte in eine von zwei Klassen, indem sie 1 oder 0 zurückgeben. Diese sind in unserem Anwendungsfall nicht besonders nützlich;
• Lineare Funktionen liefern Transformationen durch einfache Addition, Multiplikation, Subtraktion oder Division oder eine Kombination davon. Sie sind auch in unserem Anwendungsfall wenig hilfreich.
• Nichtlineare Funktionen () liefern Ergebniskurven, die an den Extremen von x eingeschränkt sind, aber eine Unterscheidung der Werte von x durch einen auf 0 zentrierten Bereich erlauben. Dieser Bereich und das Zentrum können durch die Verwendung von Offsets verändert werden.

Es ist zu erwähnen, dass die Verwendung von

return(0);

sowie die uneingeschränkte Rückgabe des Produkts zahlreicher Ergebnismaße - beides Methoden, derer ich mich schuldig gemacht habe und die ich immer noch in den Foren sehe - sind Methoden, die die mit den ersten beiden Klassen verbundenen Probleme wiederholen; andererseits werden nichtlineare Funktionen in der Regel eingeschränkt, um explodierende Gradienten zu verhindern, während ein Gradient von -∞ bis ∞ beibehalten wird.

Zur Erläuterung werde ich einige der Standardbeispiele wiederholen. Wir werden uns ReLU, Softplus, Sigmoid und Tanh ansehen, sowie im nächsten Artikel meine eigenen Modifikationen, Flipped ReLU, Point ReLU, Flipped Sigmoid, Point Sigmoid, Flipped Tanh und Point Tanh.

a) ReLU-Aktivierungsfunktion

Der Sinn dieser Funktion ist es, Null zurückzugeben, wenn x <= 0, oder x, wenn x > 0, bzw. in mathematischer Notation f(x) = max(0,x). Die erhaltene Linie ist unten abgebildet, und die MQL5-Funktion kann so definiert werden:

double ReLU(double x) {
   return(MathMax(0, x));
}

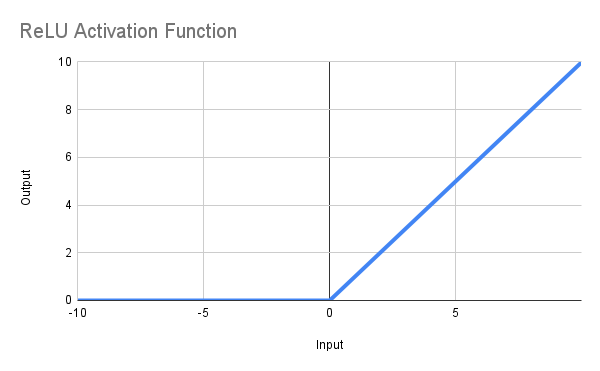
So weit, so gut, werden Sie vielleicht sagen, aber ich möchte einen Mindestwert für den Erholungsfaktor von 5 oder mehr..., nun, ändern Sie einfach den Code in*:

input double MinRF = 5.0;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double ReLU(double x) {
   return(MathMax(0, x));
}

double ScoreRF = ReLU(DeviationRF);

wodurch sich die Linie nach rechts verschiebt und bei RF = 5,0 von 0 ausgeht (siehe Abbildung):

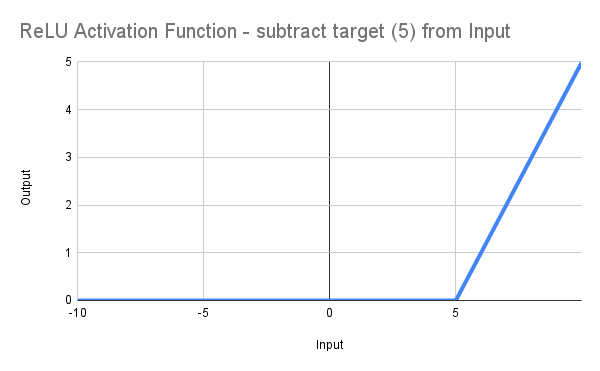
Das ist natürlich nicht viel fortschrittlicher als zu schreiben*.

input double MinRF = 5.0;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double ScoreRF = (RF - MinRF);

aber es gibt uns einen Anfang...

* Ein weiteres Problem besteht darin, dass der Zielwert, 5, tatsächlich 0 zurückgibt und nur Werte >5 einen Wert ungleich Null ergeben. Ich habe nicht die Absicht, Zeit auf dieses Problem zu verwenden, da die verschiedenen anderen Probleme mit dieser Funktion ihren weiteren Nutzen in unserem Anwendungsfall ausschließen.

Probleme

Es wird schnell klar, dass wir noch 2 Probleme haben, die beide auf die inhärente Einfachheit unseres Codes zurückzuführen sind... Ich sagte oben:

„Das ist natürlich kaum fortschrittlicher als das Schreiben

input double MinRF = 5.0;
double RF = TesterStatistics(STAT_RECOVERY_FACTOR);


double ScoreRF = (RF - MinRF);

aber es gibt uns einen Anfang...“

Die Probleme sind in Neuronalen Netzen gut bekannt:

• Sterbende ReLU: Die größte Schwäche von ReLU ist, dass Neuronen dauerhaft „sterben“ können, wenn sie nur Nullen ausgeben. Dies geschieht, wenn stark negative Eingaben Nullgradienten erzeugen, wodurch diese Neuronen inaktiv werden und nicht weiter lernen können. Dies wird auch als das Problem des verschwindenden Gradienten bezeichnet.

• Unbeschränkte Ausgabe: Die ReLU-Ausgänge können für positive Eingaben unendlich groß werden, im Gegensatz zu Sigmoid- oder Tanh-Funktionen, die eingebaute Obergrenzen haben. Das Fehlen einer oberen Beschränkung kann beim Training von tiefen neuronalen Netzen manchmal zu Problemen mit der Gradientenexplosion führen. Dies wird auch als das Problem des explodierenden Gradienten bezeichnet.

Das zweite Problem wird in der Statistik durch die Normalisierung der Werte über ein Beobachtungsfenster gelöst, aber diese Methode steht uns innerhalb der Grenzen des Optimierers nicht zur Verfügung.

Wir brauchen daher eine Lösung, die

1. eine mathematische Bedingung erstellt, die eine automatische Normalisierung ermöglicht; und
2. ein gewisses Maß an Linearität bietet, anstatt 0 zu liefern, und zwar über einen erheblichen Teil der Stichprobe hinweg...

b) die Aktivierungsfunktion Softplus

Ich möchte hier nicht näher darauf eingehen, sondern erwähne es nur am Rande als eine Stufe zwischen ReLU und den höheren Funktionen. Es ist gut beschrieben unter Geeksforgeeks und ich werde einfach das folgende Bild, die Formel und den Code posten. Es sollte klar sein, dass das Problem der uneingeschränkten Ausgabe weiter besteht, während das ReLU-Problem gelöst wird. Außerdem gibt es einen fließenden Übergang zwischen dem sehr flachen Heck und dem rechten Steigung. Dies führt dazu, dass ein Korrektur-Offset berücksichtigt werden muss - ein Konzept, auf das wir später zurückkommen werden:

Die Formel lautet Softplus(x) = ln(1 + e^x) und der MQL5-Code lautet

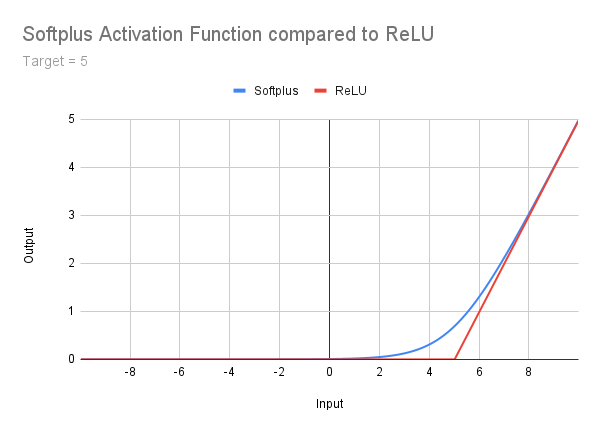
double Softplus(double x) {
   return(MathLog(1 + MathExp(x)));
}

Viel Spaß beim Lesen, wenn Sie möchten, aber jetzt kommen wir zu Funktionen, die uns eingeschränkte Ergebnisse zwischen 0 und 1 liefern...

c) Die Aktivierungsfunktion Sigmoid

Die Sigmoidfunktion wird mathematisch ausgedrückt als f(x) =𝛔(x) = 1 / (1 + e^(-x)). Sie ist identisch mit der Ableitung der Softplus-Funktion und kann so in MQL5 kodiert werden:

double Sigmoid(double x) {
   return(1 / (1 + MathExp(-x)));
}

Wenn man sich die Kurve (unten) ansieht, wird sofort deutlich, dass

1. sie zwischen 0 und 1 beschränkt ist, wodurch unser Problem der uneingeschränkten Ausgabe gelöst wird;

2. obwohl es auf dieser Skala schwer zu erkennen ist, wird ein sich ein verändernder Gradient, der niemals Null wird, von -∞ bis ∞ beibehalten; und 

3. die nicht verschobene Kurve einem Wert von 0,5 an der Stelle 0 erhält.

Um mit 3) umzugehen, dass es sich der Eins nähert, wenn x == unser Schwellenwert (Zielwert) ist, ist es notwendig, die Kurve nach links zu verschieben, nicht nur um unseren Schwellenwert, sondern auch durch eine Korrektur, die praktisch durch die Verwendung eines Korrekturwerts >= 5 erreicht wird. 

Die Implementierung in MQL5 ist daher

input double MinRF = 5.0;
sinput double SigCorrection = 5;

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double CorrectedSigmoid(double x) {
   return(1 / (1 + MathExp(-(x - SigCorrection))));
}

double ScoreRF = CorrectedSigmoid(DeviationRF);

Die Kurve der unkorrigierten Sigmoidfunktion ist unten für ein Ziel von 5 abgebildet, zusammen mit der Ableitung (multipliziert mit 4), die als Nächstes besprochen wird.

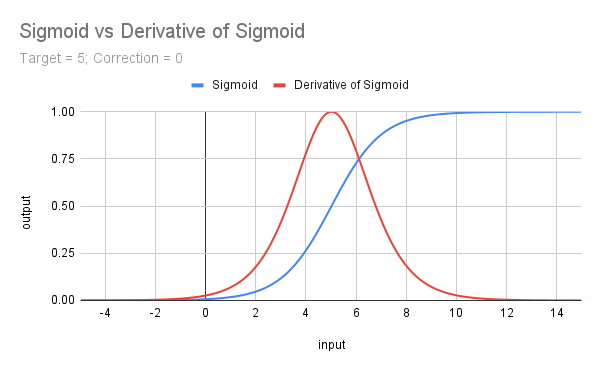
d) Ableitung des Sigmoid (𝛔')

So erhalten wir eine schöne Form, die bei x = 0 zentriert und maximiert ist... Sie stellt die Steigung der Sigmoidfunktion dar, und die Formel lautet f(x) =𝛔(x) - 𝛔^2(x) oder𝛔(x) * (1 -𝛔(x)). 

Die Funktion leidet möglicherweise (wie alle anderen Funktionen, die wir betrachten werden) unter dem Problem der verschwindenden Steigung, ein Risiko, das durch die einfache Multiplikation mit 4 (da 𝛔’(x) = 0.25) gemildert werden kann, was das Ergebnis sinnvollerweise noch einmal zwischen 0 und 1 einschränkt. Die Zentrierung auf einen Wert von x ermöglicht es uns, einen Punkt oder, besser gesagt, einen auf einen Punkt zentrierten Bereich anzuvisieren.

In MQL5 können wir Folgendes tun

input double TargetTrades = 100;

double Trades = TesterStatistics(STAT_TRADES);
double DeviationTrades = Trades - TargetTrades;

double Sigmoid(double x) {
   return(1 / (1 + MathExp(-x)));
}

double Deriv4Sigmoid(double x) {
   return(4 * (Sigmoid(x) * (1 - Sigmoid(x))));
}

double ScoreTrades = Deriv4Sigmoid(DeviationTrades);

Hinweis: Da unsere Ergebnisse für Sigmoid, seine Ableitung (multipliziert mit 4) und das folgende Tanh und seine Ableitung, die beide auf einen Wert zwischen 0 und 1 skaliert sind, alle zwischen 0 und 1 liegen, brauchen wir bei der Produktion keine weiteren Skalare anzugeben. Wir können sie natürlich mit einem beliebigen Faktor multiplizieren, um sie zu normalisieren oder ihnen gegenüber anderen Optimierungskennzahlen, die wir in unser endgültiges nutzerdefiniertes Kriterium aufnehmen, Vorrang zu geben. Wir werden uns damit im nächsten Artikel befassen.

Wir haben noch eine letzte Standardfunktion zu erforschen, und zwar Tanh...

e) Hyperbolischer Tangens oder Tanh

Tanh ist die letzte unserer Aktivierungsfunktionen, die wir auf unserer Suche nach Nützlichkeit in nutzerdefinierten Kriterien untersuchen werden. Ich werde nach einem ähnlichen Muster vorgehen, mit weniger Erklärungen als bisher, aber nach denselben Grundsätzen.

Das folgende Diagramm zeigt die Darstellung von Tanh mit seiner Ableitung.

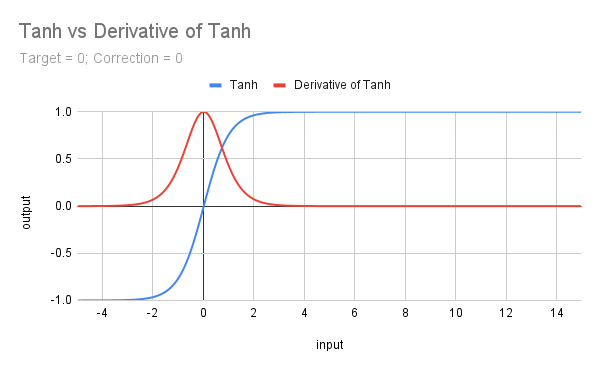
Die Formel für Tanh ist f(x) = (e^x - e^(-x))/(e^x + e^(-x)) und in MQL5 hat sie eine eigene Funktion, sodass sie einfach zu kodieren ist. Natürlich müssen wir mit Zielwerten und Korrekturfaktoren umgehen, aber es macht das Leben trotzdem einfach:

input double MinRF = 5.0;
sinput double TanhCorrection = 2.5; // Anything between 2 and 3 would be reasonable (see last figure)

double RF = TesterStatistics(STAT_RECOVERY_FACTOR);
double DeviationRF = RF - MinRF;

double CorrectedRSTanh(double x) {
   return((MathTanh(x  + TanhCorrection) + 1) / 2);  // rescaled and corrected
}

double ScoreRF = CorrectedRSTanh(DeviationRF);

Der obige Code skaliert die zugrunde liegende Funktion neu, um sie zwischen 0 und 1 einzuschränken (durch Addition von 1 und Division durch 2). Außerdem werden ein Korrekturfaktor und ein Zielwert eingeführt. Die sich daraus ergebende Kurve ist in der folgenden Grafik zur Veranschaulichung der Ableitung von Tanh dargestellt. Es sollte niemandem entgehen, dass Tanh eine ähnliche Form wie Sigmoid und die Ableitungen eine ähnliche Form wie die anderen haben; wir werden diese Ähnlichkeiten im nächsten Artikel untersuchen.

f) Ableitung von Tanh

Die mathematische Formel für die Ableitung von Tanh lautet f(x) = 1 - Tanh^2(x).

In MQL5 können wir Folgendes tun

input double TargetTrades = 100;

double Trades = TesterStatistics(STAT_TRADES);
double DeviationTrades = Trades - TargetTrades;

double DerivTanh(double x) {
   return(1 - MathPow(x, 2));

}double ScoreTrades = DerivTanh(DeviationTrades);

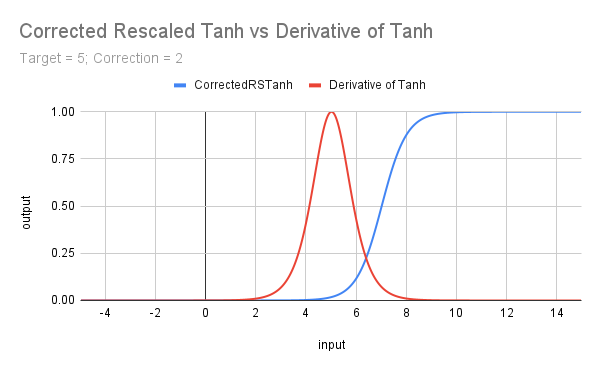
Das nächste Diagramm zeigt die Auswirkungen einer Neuskalierung von Tanh, einer Korrektur zur Annäherung an den Start von 0 mit dem Zielwert (Schwellenwert) von x und der Einführung eines Zielwerts für Tanh und die Ableitung von Tanh.

Zusammenfassung und nächste Schritte

In diesem Artikel haben wir uns kurz mit der Beziehung zwischen maschinellem Lernen einerseits und dem Optimierungsprozess mit „Post-Processing“ (ob genetisch oder vollständig) sowie Excel oder manuellem Post-Processing befasst. Wir haben damit begonnen, uns anzusehen, wie verschiedene Arten von Aktivierungsfunktionen nutzerdefinierte Kriterien verfeinern können und wie sie zu kodieren sind.

Die Probleme der verschwindenden und explodierenden Gradienten in ReLU und Softplus haben uns dazu veranlasst, unsere Aufmerksamkeit auf Funktionen mit Kurven wie die der Sigmoidfunktion und auch die ihrer Ableitung zu richten. Wir haben gesehen, wie diese es uns ermöglichen, bei unserer Bewertung einfach begrenzte Bereiche (d.h. x > t) oder doppelt begrenzte Bereiche (t1< x < t2) zu bevorzugen und dabei das Problem der explodierenden Gradienten zu beseitigen und das der verschwindenden Gradienten abzuschwächen.

Wir haben die Verwendung von Korrekturabweichungen und Zielabweichungen untersucht, um die Konzentration auf die gewünschten Attributwertbereiche zu gewährleisten.

Im nächsten Artikel werden wir uns einige Änderungen an dieser Liste von Standardfunktionen mit ähnlichen, aber nicht identischen Attributen ansehen. Wir werden auch die Idee der Skalierung und Gewichtung untersuchen, bevor wir uns Beispiele für die Verwendung verschiedener Funktionen in nutzerdefinierten Kriterien ansehen.