从Python到MQL5：量子启发式交易系统的探索之旅

概述

在这场对量子启发式交易系统的全面探索中，我们将踏上一段旅程，将量子计算的理论概念与现实世界的交易应用紧密相连。本教程从量子计算的基础知识讲起，直至最终实现一个可在实际中应用的MQL5系统，旨在引导您完成整个开发流程。我们将探讨交易如何从量子概念中获益，阐述从Python原型开发到MQL5集成的开发方法，并展示实际性能数据和代码实现。

本文探讨了量子启发式概念在交易系统中的应用，将理论量子计算与MQL5中的实际实现相结合。我们将介绍基本的量子原理，并指导您从Python原型开发过渡到MQL5集成，同时提供实际性能数据。

与传统依赖二元决策的交易不同，量子启发式交易模型利用与量子现象相似的市场行为——多重并发状态、相互关联以及状态的突然转变。通过使用Qiskit等量子模拟器，我们可以在经典计算机上应用量子启发式算法来处理市场的不确定性，并生成有预测性的见解。

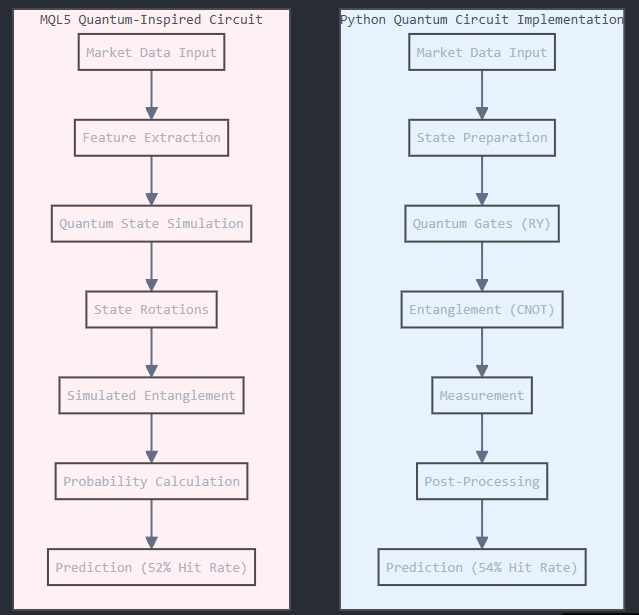
对于希望应用量子启发式系统的交易者和开发者来说，理解这些差异至关重要。

在我们的Python实现中，Qiskit用于模拟量子电路。通过RY（旋转）门将市场数据编码为量子态，以量子叠加的形式表示市场特征。CNOT门能够实现量子纠缠，捕捉复杂的市场相关性，而测量结果则可以产生预测，其准确率达到54%。

由于MQL5采用经典架构，因此其版本近似模拟量子行为。我们使用特征提取和经典数学方法来模拟量子态和量子纠缠。尽管准确率略低（52%），但MQL5实现支持实时交易和直接市场连接。

每种方法处理数据的方式不同：Python直接将数据编码为量子态，而MQL5则需要特征工程。Python的Qiskit提供真正的量子门，而MQL5则依赖于经典近似，这增加了复杂性，但也提供了灵活性。在模拟量子纠缠方面，Python的CNOT门创建了真实的量子连接，而MQL5则使用经典相关性。

这些差异揭示了每种方法的优势和局限性。Python提供了强大的原型开发能力，而MQL5则提供了一个实用、可交易的解决方案，能够在经典交易约束条件下适应量子启发式计算。

Python原型：创新的基础

我们选择Python作为起点，是因为它拥有强大的科学库——NumPy、Pandas，尤其是Qiskit，这些库使其成为开发量子启发式交易系统原型的理想选择。Python简洁的语法和丰富的资源使得实验和初始算法开发变得高效。

Python原型在各种市场条件下均保持了54%的成功率——虽然看似不高，但在合理的风险管理下，这仍是一个有意义的优势。

使用Qiskit，我们设计并测试了一个三量子比特架构，能够同时分析八种市场状态。Python的灵活性使我们能够快速调整电路、调整参数并快速获得结果，从而促进了我们的开发过程。

以下是我们在Python中实现量子电路的一个简化示例：

class HourlyQuantumForex:
    def __init__(self):
        self.n_qubits = 3
        self.simulator = BasicAer.get_backend('qasm_simulator')
        self.min_confidence = 0.15

    def create_circuit(self, input_data):
        qc = QuantumCircuit(self.n_qubits, self.n_qubits)
        # Input encoding
        for i in range(self.n_qubits):
            feature_idx = i % len(input_data)
            angle = np.clip(np.pi * input_data[feature_idx], -2*np.pi, 2*np.pi)
            qc.ry(angle, i)
        
        # Entanglement operations
        for i in range(self.n_qubits - 1):
            qc.cx(i, i + 1)
        
        return qc

向MQL5过渡：实际实现

出于实际因素的考量，我们决定将量子启发式系统迁移至MQL5。尽管Python在原型开发和测试方面表现更优，但MQL5能够直接与交易平台交互，访问实时市场数据，并具备快速执行能力。面临的难题在于，如何在保留系统预测能力的同时，将量子计算原理融入MQL5的传统计算框架中。

由于需要分析实时市场数据，且Python量子模拟器与MQL5传统计算环境的实现方式存在差异，这样导致了系统准确率略有下降（从54%降至51-52%）。

以下是我们MQL5量子启发式实现的一个简单展示：

class CQuantumForex {
private:
    int m_lookback_bars;
    double m_features[];
    
public:
    double PredictNextMove(string symbol) {
        GetFeatures(symbol, m_features);
        return SimulateQuantumCircuit(m_features);
    }
    
    double SimulateQuantumCircuit(double &features[]) {
        // Quantum-inspired calculations
        double state_probs[];
        ArrayResize(state_probs, (int)MathPow(2.0, (double)NUM_QUBITS));
        
        // Circuit simulation logic
        for(int shot = 0; shot < SHOTS; shot++) {
            // Quantum state manipulation
        }
        
        return GetWeightedVote(state_probs);
    }
};

实际应用与成果

将我们的量子启发式系统应用于实际市场预测时，出现了诸多有趣的趋势。在市场波动剧烈、传统技术分析往往失效的时期，该方法展现出了非凡的优势。这一优势源于量子启发式方法能够同时处理多种市场状态的能力。

在多种市场条件下进行测试后，我们得出了以下结论：

• 在实盘交易中，该模型在实际应用中表现可靠，因为它在各种市场条件下均能保持良好表现。

• 此外，我们还发现，在特定市场时段，模型的准确率显著提升。通过专注于这些特定时段，利用更高的可预测性，我们可以进一步提升交易策略的整体效果。

• 在市场极度波动时，模型的表现尤为突出。由于能够在波动环境中调整并表现得更好，模型的潜在盈利能力得到了提升，使我们能够从更显著的价格波动中获利。

• 最后，为了有效筛选出低概率交易，我们采用了置信度水平。这种选择性策略通过专注于高置信度信号，帮助我们降低了不必要的风险，进一步改善了交易结果。

尽管乍一看命中率可能较低，但系统在各种市场条件下保持这些结果的稳定性和一致性，验证了量子启发式方法的有效性。

性能指标与分析

有必要对我们的Python原型与MQL5的实现之间的性能差异进行全面分析。这一差异并非仅仅是MQL5平台的限制，而是反映了从受控测试环境向实时市场环境过渡的难度。Python原型处理的是历史数据，对市场条件了如指掌，而MQL5解决方案则需应对实时市场动态的复杂性和数据处理限制。

总预测次数：11544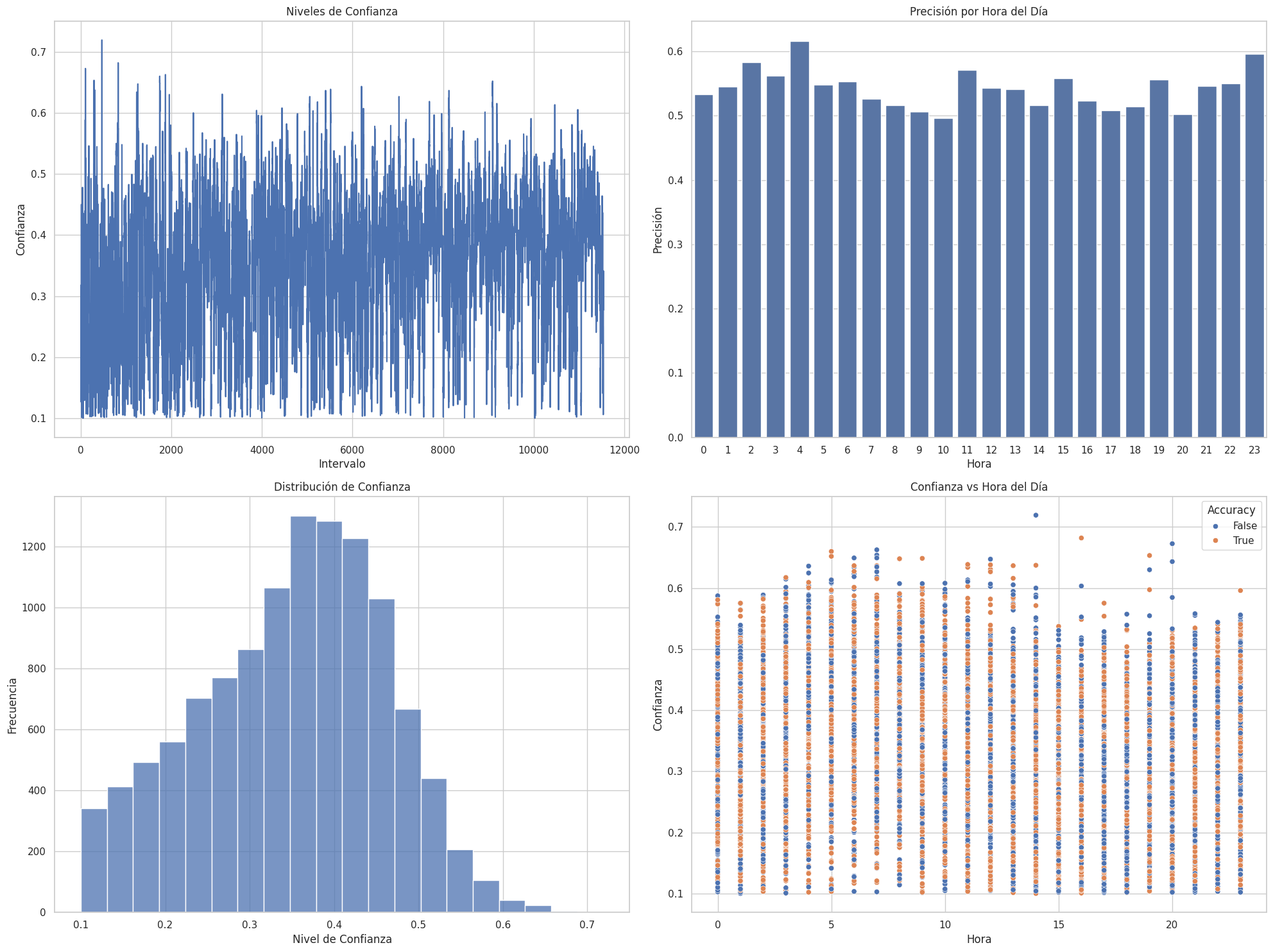

尽管准确率略有下降，但MQL5的实现具有诸多实用优势，因此，值得将其应用于实际交易。仅凭Python原型，交易者无法从系统的实时市场数据处理和即时交易信号中获得可操作的见解。

MQH集成：一种实用方法

我们的量子启发式交易逻辑已被封装在一个MQL5头文件（MQH）中，便于轻松地集成到现有的EA中。这种模块化方法使交易者无需完全重新设计其交易系统，即可将量子启发式预测融入其交易策略中。MQH文件包含了市场状态分析、置信度标准以及深入性能跟踪的全面功能。

MQH文件可以按以下方式集成到现有的EA中：

#include <Trade\Trade.mqh>
#include <Quantum\QuantumForex.mqh>

class CTradeAnalyzer {
private:
    CQuantumForex* m_quantum;
    double m_min_confidence;

public:
    CTradeAnalyzer(double min_confidence = 0.15) {
        m_quantum = new CQuantumForex();
        m_min_confidence = min_confidence;
    }

    bool AnalyzeMarket(string symbol) {
        double prediction = m_quantum.PredictNextMove(symbol);
        return MathAbs(prediction) >= m_min_confidence;
    }
};

优化与微调

量子启发式交易系统中的多个关键要素均可进行调整，以适应特定的交易环境和工具需求。这些可配置的重要选项包括：模拟中使用的量子比特数量、特征工程参数、用于筛选交易的置信度阈值，以及量子电路模拟的次数（shots）。尽管我们的初始配置已能产生稳定的结果，但通过悉心地优化参数，仍存在很大的提升空间。由于最优设置会因个人交易偏好和市场条件的不同而有所差异，因此我们将这部分工作留给读者自行尝试探索。未来发展方向与进步

这种方法只是迈向量子力学启发式交易应用的第一步。在接下来的论文中，我们将探讨更复杂的量子计算概念及其潜在的交易应用。需要进行更进一步研究的领域包括：用于更深入市场分析的高维量子电路、融入量子理论启发的优化算法、基于量子理论的高级特征工程，以及混合经典-量子交易系统的开发。实际应用指南

我们建议对这种方法感兴趣的交易者采取系统化的实施方法。首先，从Python原型入手，评估该系统在目标市场中的适用性，并熟悉基本的量子概念。之后，逐步过渡到MQL5的实现阶段，先从模拟交易开始，以验证其实际效果。在走上正轨后，根据个人的交易需求和风险承受能力调整系统设置。随着时间的推移，通过定期监控性能指标，将进一步提升系统的可靠性。

// Constants
#define NUM_QUBITS 3

如果您改变量子比特数量（NUM_QUBITS），输出状态数量可能会呈指数级变化。这是量子系统的一个基本特性，对模拟有着重大的影响。

在当前代码中，NUM_QUBITS被设置为3，因此有8（2³）种可能的状态。这就是为什么您会看到状态数组初始化为大小为8，且循环遍历8种可能状态的原因。每个量子比特都处于0和1的叠加态，当与其他量子比特组合时，可能的状态数量会成倍增加。

例如，如果您改变量子比特的数量，就会得到不同数量的可能状态：1个量子比特给您2种状态（|0⟩和|1⟩），2个量子比特给您4种状态（|00⟩、|01⟩、|10⟩、|11⟩），3个量子比特给您8种状态，4个量子比特给您16种状态，以此类推。这种模式遵循2ⁿ，其中n是量子比特的数量。

这种指数关系会影响代码的多个部分。状态数组的大小必须相应调整，量子电路模拟循环需要处理更多状态，内存需求也会显著增加。例如，当您将NUM_QUBITS从3增加到4时，就需要将数组大小和循环边界从8修改为16。

虽然增加量子比特数量提供了更大的计算能力和潜在更复杂的分析能力，但也需要权衡利弊。模拟过程的计算更加密集，需要更多的内存，处理时间也更长。这可能会影响EA的性能，尤其是在硬件性能较低或需要快速执行实时交易的情况下。

在该交易算法中，更多的量子比特可能允许进行更复杂的特征编码，并可能实现更精确的价格走势预测。然而，您需要权衡这一潜在益处与增加的计算开销，确保系统对于实际交易的应用仍然切实可行。

#define SHOTS 2000

“shots”（代码中定义为SHOTS = 2000的）代表模拟量子电路以近似量子行为的次数。每次“shot”都会运行整个量子电路并执行一次测量，从而构建出结果的统计分布。

该概念类似于多次掷骰子以了解其概率分布。在量子计算中：

// Simulation loop in the code
for(int shot = 0; shot < SHOTS; shot++)
{
    // Initialize quantum state
    double state[8];  
    ArrayInitialize(state, 0.0);
    state[0] = 1.0;  // Start in |000⟩ state
    
    // Run quantum circuit operations...
    
    // Measure and accumulate results
    const double rand = MathRand() / 32768.0;
    double cumsum = 0.0;
    for(int i = 0; i < 8; i++)
    {
        cumsum += state[i] * state[i];
        if(rand < cumsum)
        {
            state_probs[i] += 1.0 / SHOTS;
            break;
        }
    }
}

为您的量子交易系统选择最优的模拟次数（shots），需权衡多个关键因素。主要的权衡点在于准确性与执行速度之间的取舍。将模拟次数设置为较高值（通常为5000次或更多），可获得更精确的量子态概率分布，但会以执行速度变慢为代价。相反，使用较少的模拟次数（约500-1000次），则执行速度更快，但结果准确性较低。当前默认设置的2000次模拟次数，是经过审慎选择后的折中方案，旨在平衡这些相互冲突的需求。

在考虑交易的具体需求时，需考虑多个因素。您所交易的市况时间框架至关重要——更短的时间框架可能需要较少的模拟次数以保持响应速度，而更长的时间框架则需要更多模拟次数以提高准确性。可用的处理能力是另一个重要考量因素，因为更多的模拟次数需要更强大的计算资源。此外，您的交易策略所需的精确度水平也会影响您的选择——要求更高精确度的策略将需要更多模拟次数。

在实际应用中，建议在初始测试阶段从1000-2000次模拟次数开始。这样一来，就为评估系统性能提供了合理的基准。然后，您应该积极监控执行时间和准确性指标。如果您发现结果过于嘈杂或不一致，则逐渐增加模拟次数。相反，如果EA的执行速度对于您的交易需求来说过慢，则考虑减少模拟次数。这种迭代方法有助于您针对特定的交易条件和需求找到最优平衡点。

# Example of how different shot counts might affect probabilities
# With 100 shots:
State |000⟩: 0.3100 (±0.0460)
State |001⟩: 0.1800 (±0.0384)

# With 2000 shots:
State |000⟩: 0.3025 (±0.0103)
State |001⟩: 0.1750 (±0.0085)

# With 10000 shots:
State |000⟩: 0.3002 (±0.0046)
State |001⟩: 0.1752 (±0.0038)

#define FEATURES_COUNT 7

定义量子电路用于市场分析时所采用的输入特征数量。下面，让我们详细看看这7个特征：

// 1. Normalized price range
features[0] = ((rates[0].high - rates[0].low) / rates[0].close) * 2 - 1;

// 2. Normalized volatility
features[1] = (CalculateVolatility(m_returns, MathMin(12, m_lookback_bars)) / 0.01) * 2 - 1;

// 3. Momentum
features[2] = MathMax(MathMin(CalculateMomentum(m_returns, MathMin(24, m_lookback_bars)) * 100, 1), -1);

// 4-5. Time components (hour of day encoded in circular form)
features[3] = MathSin(2 * M_PI * dt.hour / 24.0);
features[4] = MathCos(2 * M_PI * dt.hour / 24.0);

// 6. Price deviation from SMA
features[5] = MathMax(MathMin((rates[0].close - sma) / sma, 1), -1);

// 7. Latest return
features[6] = MathMax(MathMin(m_returns[0] * 100, 1), -1);

所有特征均被标准化至[-1, 1]区间，以确保量子电路输入尺度的一致性。您可以通过添加或删除特征来修改这一设置。

技术考量与限制

尽管这一受量子启发的系统展现出可观的潜力，但必须承认其存在一定的局限性。值得注意的是，这是一个模拟的量子过程，而非实际的量子计算。实时处理需求可能影响性能，而不断变化的市场状况也可能影响预测的准确性。为缓解这些因素的影响，将稳健的风险管理措施融入交易框架中至关重要。

#define HOUR_LOOKBACK 24

定义历史数据分析的默认时间窗口，设置为24小时。这一参数在交易系统分析市场模式和计算各种指标时发挥着至关重要的作用。

回溯期会影响系统中的多项关键计算。在分析波动率时，代码会使用最多12个周期（回溯期的一半）来计算收益率的标准差。在计算动量时，则使用完整的24个周期来计算平均价格变动。这样能在近期市场行为与长期趋势之间取得平衡。

选择24小时回溯期很可能是为了捕捉完整的每日市场周期。这很合情合理，因为外汇市场通常会呈现出24小时的周期性模式，这是由于主要交易时段（亚洲、欧洲和美洲时段）的开盘和收盘。每个时段都可能带来不同的交易量和价格行为模式。

您可以根据自己的交易需求修改这一数值。较短的回溯期（如12小时）会使系统对近期市场变化更加敏感，但也可能更容易受到噪声干扰。较长的回溯期（如48小时）会提供更稳定的信号，但可能对市场变化的反应较慢。请记住，更改HOUR_LOOKBACK会影响内存使用量和处理时间，因为需要存储和分析更多的历史数据。

// Input parameters
input int      InpPredictBars   = 2;         // Predict Bars (1-5)
input double   InpMinMove       = 0.00001;     // Minimum Move
input double   InpMinConfidence = 0.15;       // Minimum Confidence
input int      InpLogInterval   = 1;         // Log Interval
input int      InpLookbackBars  = 200;        // Lookback Bars for Analysis

InpPredictBars = 2表示系统尝试预测未来多少根K线的走势。当该值为2时，系统会对未来两根K线的价格走势做出预测。预测范围限制在1-5根K线内，因为随着预测周期的延长，预测准确性往往会降低。较小的值（如1）能提供更即时的预测，但可能会错过较大的价格波动；而较大的值（如4-5）则试图捕捉更长期的趋势，但准确性可能较低。

InpMinMove = 0.00001设定了系统认为预测成功所需的最小价格波动幅度。对于外汇交易对而言，通常设置为1个点（对于5位小数报价的经纪商为0.00001）。这样可以防止系统将可能只是市场噪声的微小价格波动计入预测成功。根据策略，您可以增加这个值以便采取更保守的交易方式，或者减少这个值以便采取更激进的交易方式。

InpMinConfidence = 0.15（即15%）是判定预测结果值得采信的置信度阈值。量子系统产生的预测置信度在0到1之间。任何置信度低于0.15的预测都被视为“中性”并被忽略。较高的值（如0.25）会使系统更具选择性，但产生的信号较少；而较低的值则会产生更多信号，但质量可能较低。

InpLogInterval = 1决定了系统记录性能指标的频率（以时间周期为单位）。值为1表示每个周期都记录一次。这对于监控系统性能很有用，但过于频繁的记录可能会影响性能。在实盘交易中，您可以增加这个值。

InpLookbackBars = 200设置了系统用于分析的历史K线数量。使用200根K线，系统拥有足够的历史数据来计算特征和模式。更多的K线（如500根）可提供更充分的历史背景，但需要更强的处理能力；而较少的K线则对近期市场变化更敏感，但可能会错过长期模式。

这些参数可以在运行EA之前在MetaTrader平台上进行调整，找到正确的参数组合通常需要在历史数据上进行测试并监控实盘表现。

展望未来

随着量子计算技术的发展，我们预计交易领域将出现更复杂的应用。尽管当前系统使用的是受量子力学启发的算法，但这仅仅是未来可能实现的开端。请继续关注我们的下一篇文章，我们将深入探讨量子计算在交易中的应用方式，并揭示更多复杂而精妙的应用。

EA示例

这款多时段外汇EA采用受量子启发的算法，在欧洲、美国和亚洲时段进行交易，针对每个时间段使用特定的参数和分析方法。

该系统的核心优势在于其多层次风险管理，结合了动态仓位调整、反马丁格尔策略和基于账户权益的保护机制。它通过受量子启发的分析系统分析多个市场特征，包括平均真实波幅（ATR）、动量和各种技术指标，以生成稳健的交易信号。

一项关键的创新是其自适应追踪止损系统和多时间框架分析组件，确保交易与短期（H1）和长期（H4）趋势保持一致。此外，其最大有利波动（MFE）分析器根据历史价格行为持续优化出场点，帮助最大化盈利潜力。

这是一个简单的示例，展示了如何利用近乎抛硬币式的预测（结合时段和小时选择、MFE控制、风险管理）来实现盈利。

该设置从MFE中获取利润，仅使用预测来决定做多或做空。这款EA拥有大量的选项和配置，我不建议进行大规模的优化。

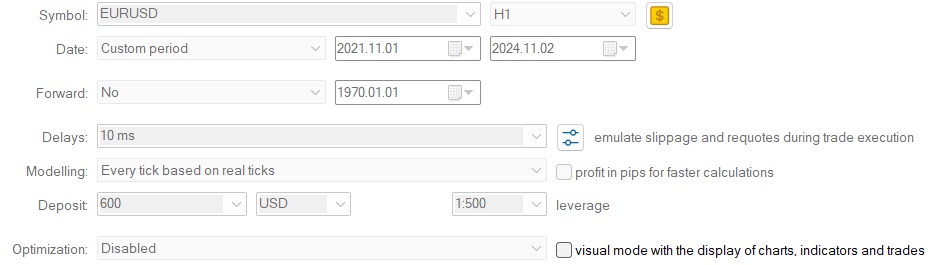
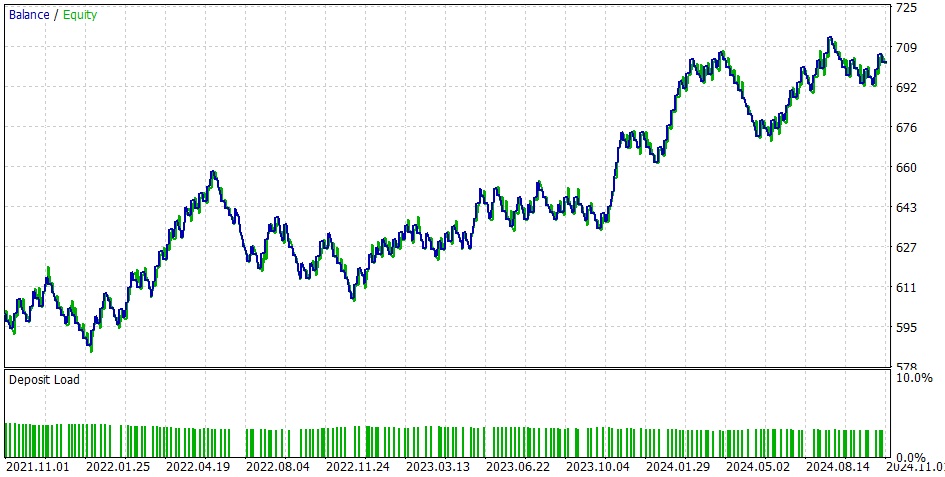
Setup #2

相同设置，不同输入。我没法进行MQL5云网络优化，因为在西班牙无法开展这项操作（受政策限制……），而且本地优化耗时太久，但这款EA有很多选项，请好好利用这些选项并完成EA的设置。如果您有时间和资源，那就进行大规模优化，看看哪些参数组合效果最优。

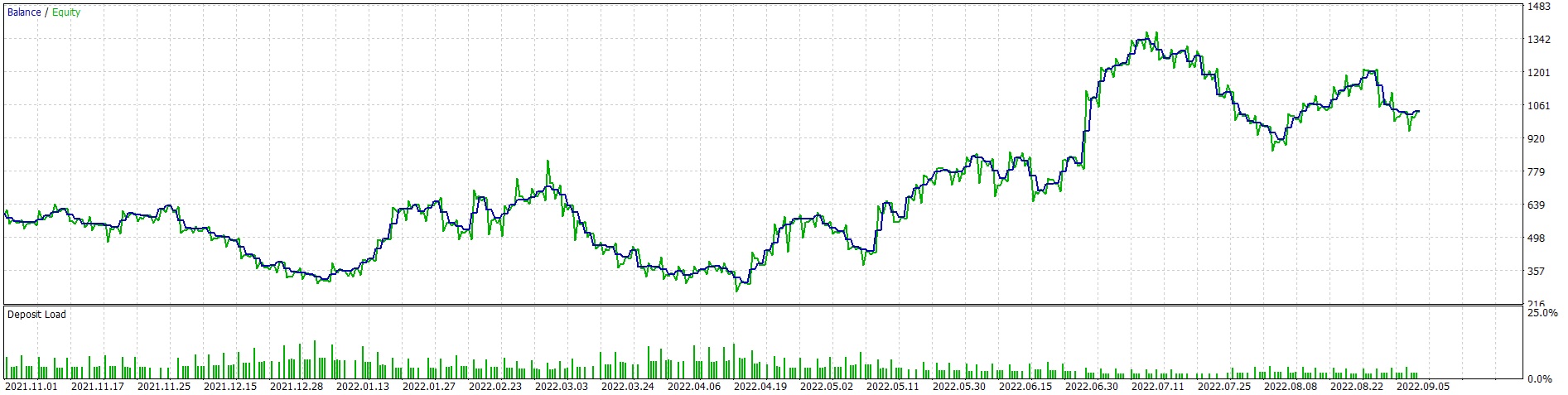
注意：特征参数已更改，策略尚未完全完善，但它可作为示例供您参考，您可以在此基础上继续完成开发。头寸规模设定与风险管理模块必须切实落地，还有大量工作有待完成。这仅是一个示例，您必须自行承担交易责任。不过，这为您开发自己的EA提供了一个良好的起点。由于输入参数过多，我将上传一组我曾用于欧元兑美元（EURUSD）1小时时间框架的输入参数（未经优化）。此外，针对本示例，我修改了相关的.mqh文件，您也可以根据自己的需求进行修改。

关于如何操作这款EA，首先，您必须理解本文的内容；之后，您需要仔细研究重要的输入参数，弄清楚它们的用途以及相关函数的作用等……关键函数是OnTick()，您只需尝试弄清楚OnTick函数中调用的其他函数来源，并从那里开始修改。如果这样上手，学习过程将会比较顺利。

结论

本研究探讨了如何将量子计算原理应用于交易行业。我们开发了一个以量子为主题的交易系统，从Python原型过渡到MQL5实现。在模拟和真实交易环境中，该系统均表现出稳定的命中率，其结果令人满意。该方法在高波动性情况下尤为成功，而传统模型在此类情况下往往表现不佳。需要牢记的是，这是一个量子模拟系统，市场状况和数据质量等变量都可能会影响其性能。

总而言之，本次对受量子启发的交易系统的探索，通过利用量子计算原理来应对金融市场的复杂性，让我们得以一窥算法交易的未来。虽然将量子概念融入MQL5标志着向实际应用迈出了重要一步，但这也凸显了在计算复杂性与实际适用性之间谨慎平衡的必要性。