种群优化算法：改变概率分布的形状和位移，并基于智能头足类生物（SC）进行测试

内容

1. 概述
2. 检查分布的测试台
3. 按所需分布规律的随机数构造
4. 优化算法模板 — “智能头足类生物”算法
5. 结束语

1. 概述

概率论是一种数学理论，它研究随机现象，并判定其发生的或然率。它允许描述和分析随机过程。概率论的基本概念是概率、随机变量、概率分布、数学期望、和散布。

概率是一种数值特征，它决定了特定事件发生的或然率。

随机变量是将随机实验的每个结果与特定数字相关联的函数。

概率分布是判定随机变量每个可能值的或然率的函数。

数学期望是一个随机变量的平均值，其可通过多次重复实验来获得。

散布是随机变量值相对于其数学期望的分布量度。

矩是描述其分布的随机变量的数值特征。矩用于判定分布的中心（期望）及其分布（散布和标准差），并分析分布的形状（偏度和峰度）。第一个矩（n=1）是数学期望，它判定随机变量分布的中心。第二点（n=2）是散布，它描述了随机变量相对于其数学期望的扩散。第三个矩（n=3）是分布偏度的峰度，第四个力矩（n=4）是分布峰度（凸度）的度量。

概率分布在随机现象建模和数据分析中扮演着重要角色，在估算参数和检验假设的统计中也是如此。它们令描述随机变量和事件的概率属性，以及判定各种结果的概率成为可能。

概率论及优化是两门重要的科学学科，广泛应用于科学技术的各个领域，如经济学、金融学、工程学、生物学、医药学、等等。这些领域的发展，及其他们的研究和优化方法的应用使得解决复杂问题和创造新技术成为可能，从而提高了各个领域的工作效率和品质，包括开发创建量子计算机的现代技术、安全超高速通信、生成式神经网络、和人工智能。 

基于概率论的概率计算在随机现象建模和分析数据中扮演者关键角色。反过来，优化旨在在各种问题中找到最优解，并允许在许多可能的选项中找到最佳解。然而，现实世界的问题具有不确定性和随机性，这就是概率分布发挥作用的地方。它们令我们能够在优化问题中参考随机性和不确定性。

概率分布也被积极用于进化和种群算法。在这些算法中，搜索空间中新状态的随机生成是使用相应的概率分布进行建模的。这令我们能够探索参数空间，并找到最优解，同时参考总体的随机性和多样性。

更复杂的优化方法会用概率分布来针对不确定性进行建模，并近似复杂函数。它们令我们能够有效地探索参数空间，并在寻找最优解时参考数据中的随机性和噪声。

在本文中，我们将研究各种类型的概率分布、它们的属性、以及在代码中相应函数的实际实现形式。在生成具有各种类型分布的随机数时，您可能会遇到大量问题，诸如无限尾部长度。或设置散布边界时的偏移概率。在设计和创建优化算法时，通常需要相对于数学期望改变概率。本文的目标是解决这些问题，并创建行之有效的函数来应对概率，以便在后续的优化算法中加以运用。

2. 检查分布的测试台

为了测试和可视化随机变量的分布，我们需要一个测试平台，令我们能够清晰地显示分布的形状。这在设计优化算法时非常重要，因为直观呈现并明白变量概率朝哪个方向移动有助于达成最佳结果。

为了建立概率分布，我们需要创建一些东西，比如落入格子当中的一序列随机数。格子本质上是计数器。例如，左边是 “min”，右边是 “max” 和 “in” 的数字线，它们之间可以想象为这样：

min|-----|-----|-----|-----|-----|-----|in|--|--|--|--|--|--|max

我们看到 “in” 值在数字线上移动，更接近 “max”。如果我们在 [min;max] 生成随机数，则在 [min;in] 范围内的随机数的数量会大于 [in;max]，因此数字落入的概率将向左侧偏移，从而产生不平衡，但我们需要左右两侧的平均下降数量相同，我们需要在不改变概率的情况下改变分布的形状。为此，左右两侧的格子数应相同（在上面的规程示例中，左右两侧各有 6 个格子）。

故此，用于构建分布的测试平台非常简单。其工作实质如下：

• 创建一个 CCanvas 对象，以便操控画布
• 按设置选择分布生成一个随机数
• 检查随机数落入相应格子的哪个区域，并在该格子上加 1
  
• 计算所有格子中的最小和最大掉落数量
• 在画布上为每个格子绘制圆圈，这对应于格子中随机数的数量
• 用从蓝色（很少）到红色（经常）的颜色为圆圈着色
  

代码的总体目标是用图形在画布上可视化概率分布，其中每个圆圈都是在格子中绘制的随机数的数量，由所有格子中的最小/最大值进行常规化。

#property script_show_inputs
#include <Canvas\Canvas.mqh>

enum E_Distribution
{
  uniform = 0,
  gauss   = 1,
  power   = 2,
  levi    = 3
};

//--- input parameters
input double         MinP       = -100.0;
input double         InpP       =  0;
input double         MaxP       =  100.0;
input int            CNT        =  1000000;
input int            Size       =  1000;
input double         SigmaP     =  3;       //Sigma for "Gauss" distribution
input double         PowerP     =  2;       //Power for "Power law" distribution
input double         LeviPowerP =  2;       //Power for "Levy flights" distribution
input E_Distribution Distr_P    = gauss;    //Distribution type

//——————————————————————————————————————————————————————————————————————————————
void OnStart ()
{
  CCanvas Canvas;

  int W = 750;
  int H = 400;
  int O = 10;

  int CountL [];
  int CountR [];

  ArrayResize     (CountL, Size);
  ArrayInitialize (CountL, 0);

  ArrayResize     (CountR, Size);
  ArrayInitialize (CountR, 0);

  string canvasName = "Test_Probability_Distribution_Canvas";
  if (!Canvas.CreateBitmapLabel (canvasName, 5, 30, W, H, COLOR_FORMAT_ARGB_RAW))
  {
    Print ("Error creating Canvas: ", GetLastError ());
    return;
  }

  ObjectSetInteger (0, canvasName, OBJPROP_HIDDEN,     false);
  ObjectSetInteger (0, canvasName, OBJPROP_SELECTABLE, true);

  Canvas.Erase (COLOR2RGB (clrWhite));
  Canvas.Rectangle (1, 1, W - 1, H - 1, COLOR2RGB (clrBlack));

  int    ind = 0;
  double X   = 0.0;

  for (int i = 0; i < CNT; i++)
  {
    switch (Distr_P)
    {
    case uniform:
      X = UniformDistribution (InpP, MinP, MaxP);
      break;
    case gauss:
      X = GaussDistribution (InpP, MinP, MaxP, SigmaP);
      break;
    case power:
      X = PowerDistribution (InpP, MinP, MaxP, PowerP);
      break;
    case levi:
      X = LeviDistribution (InpP, MinP, MaxP, LeviPowerP);
      break;
    }

    if (X < InpP)
    {
      ind = (int)Scale (X, MinP, InpP,
                        0,    Size, false);
      if (ind >= Size) ind = Size - 1;
      if (ind < 0)     ind = 0;
      CountL [ind] += 1;
    }
    else
    {
      ind = (int)Scale (X, InpP, MaxP,
                        0,    Size, false);
      if (ind >= Size) ind = Size - 1;
      if (ind < 0)     ind = 0;
      CountR [ind] += 1;
    }
  }

  int minCNT = CNT;
  int maxCNT = 0;

  for (int i = 0; i < Size; i++)
  {
    if (CountL [i] > maxCNT) maxCNT = CountL [i];
    if (CountR [i] > maxCNT) maxCNT = CountR [i];

    if (CountL [i] < minCNT) minCNT = CountL [i];
    if (CountR [i] < minCNT) minCNT = CountR [i];
  }

  int x = 0.0;
  int y = 0.0;
  color clrF;
  int centre = 0;
  int stepL  = 0;
  int stH_L  = 0;
  int stepR  = 0;
  int stH_R  = 0;

  centre = (int)Scale (InpP, MinP, MaxP, 10, W - 11, false);

  stepL = (centre - O) / Size;
  stH_L = stepL / 2;
  if (stH_L == 0) stH_L = 1;

  stepR = (W - O - centre) / Size;
  stH_R = stepR / 2;
  if (stH_R == 0) stH_R = 1;

  for (int i = 0; i < Size; i++)
  {
    x = (int)Scale (i,          0, Size - 1, O, centre - stH_L, false);
    y = (int)Scale (CountL [i], 0, maxCNT,   O, H - O,  true);

    clrF = DoubleToColor (CountL [i], minCNT, maxCNT, 0, 255);

    Canvas.Circle (x, y, 2, COLOR2RGB (clrF));
    Canvas.Circle (x, y, 3, COLOR2RGB (clrF));


    x = (int)Scale (i,          0, Size - 1, centre + stH_R, W - O, false);
    y = (int)Scale (CountR [i], 0, maxCNT,   O,      H - O, true);

    clrF = DoubleToColor (CountR [i], minCNT, maxCNT, 0, 255);

    Canvas.Circle (x, y, 2, COLOR2RGB (clrF));
    Canvas.Circle (x, y, 3, COLOR2RGB (clrF));
  }

  Canvas.Update ();
}
//——————————————————————————————————————————————————————————————————————————————

3. 按所需分布律构造的随机数

均匀分布

均匀分布是一种概率分布，其中所有随机变量值在给定区间内都具有相等的概率。均匀分布被广泛随机变量进行建模，其在给定间隔内的取值可能性均等。

图例 1. 数字均匀分布，无偏移

在所有方法中，均匀分布是最容易实现的。此处唯一要考虑的一点是，我们不能简单地生成 [min;max]，所以我们将在 In 的左侧或 In 的右侧生成一个随机数，具体取决于之前在 [0.0;1.0] 内生成的随机数。因此，In 相对于 [min;max] 在任意位置上，左右两侧所生成随机数的数量可能性均等。分布中没有超界或伪影的问题。

当需要在给定范围内生成一个数字时，且在整个范围内出现的概率相等，我们就可以在所有情况下使用均匀分布。

//——————————————————————————————————————————————————————————————————————————————
double UniformDistribution (const double In, const double outMin, const double outMax)
{
  double rnd = RNDfromCI (0.0, 1.0);

  if (rnd >= 0.5) return RNDfromCI (In, outMax);
  else            return RNDfromCI (outMin, In);
}
//——————————————————————————————————————————————————————————————————————————————

正态（高斯）分布

正态分布是一种概率分布，描述了自然、经济学和其它领域的许多随机现象。它的特点是钟形，和围绕平均值的对称性。正态分布完全由均值和方差决定。

正态分布的关键属性之一是其围绕均值的对称性。这意味着随机变量取值等于均值的概率最大，而它取值与均值不同的概率随着它远离均值而减小。该属性令正态分布对于建模和数据分析特别实用，因为它令我们能够描述和预测具有均值和偏离均值的随机现象。

正态分布还具有许多数学属性，令其适用于统计方法和模型。例如，如果随机变量是独立的，且具有正态分布，则它们的总和也会具有正态分布。该属性允许利用正态分布来建模和分析由众多随机变量组成的复杂系统。正态分布在统计学、物理学、经济学、金融学等领域有很多应用。它是许多统计方法和模型的基础，例如线性回归和时间序列分析。

对于优化算法，当我们想要将注意力集中在数字线上的特定位置时，正态分布非常实用。在这种情况下，我们可能只需要形成分布形式的曲线的一部分。例如，我们希望仅用三个标准差内的分布。至于这些边界之外的任何东西，我们不能只将数值推回边界的边缘。如果我们这样做，我们在边缘得到的掉落频率会超过平均值的频率。这个问题如图例 2 所示。我们将在下面的讲述中解决它。

为了生成具有正态分布规律的随机变量，我们可以调用 Box-Muller 方法。

• 首先，我们需要生成两个随机均匀分布的数字 u1 (0, 1] 和 u2 [0, 1]
• 然后我们需要按以下方程计算随机变量 z0：

z0 = sqrt(-2 * ln(u1)) * cos(2 * pi * u2)   

• 得到的随机变量 z0 将具有标准正态分布
  

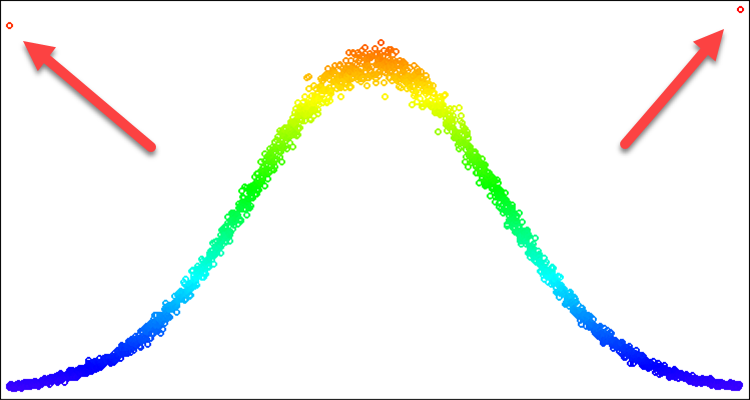
图例 2. sigma=3 的正态分布，以及尝试切断 sigma=3 以外所有内容时的伪影

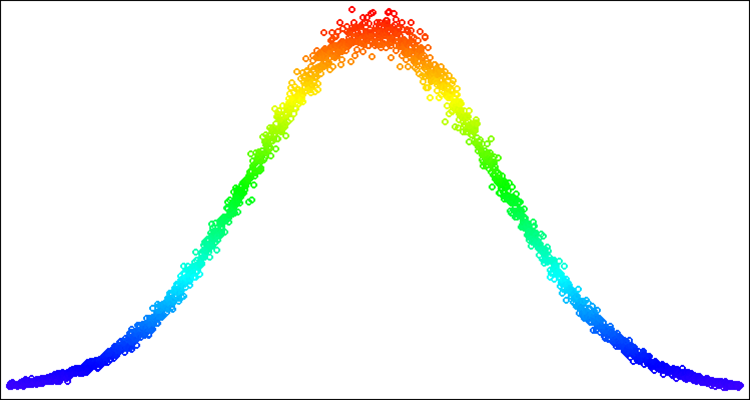
图例 3. sigma=3 的正态分布，解决了伪影问题（超出分布边界）

我们编写一个 GaussDistribution 函数的实现，该函数生成的随机值相对于 “in” 平均值具有正态分布：

• 设置以下函数参数：输入值（in）、输出范围的最小值和最大值（outMin 和 outMax）、以及标准差（sigma）。
• 计算 u1 的自然对数，该对数是在 0 到 1 的范围内随机生成的。
• 如果 u1 小于或等于 0，则为 logN 赋值 0.000000000000001。否则，logN 等于 u1。
• z0 值是利用正态分布方程计算出的。
• 检查 “sigma” 输入，看它是否超出了等于 8.583864105157389 的最大可能标准差值的范围。
  
• 如果 z0 大于或等于 sigmaN，则为 z0 分配一个介于 0 到 sigmaN 之间的随机值。否则，如果 z0 小于或等于 -sigmaN，则为 z0 分配一个随机值，范围从 -sigmaN 到 0.0。 
• 如果 z0 大于或等于 0，则返回调用 Scale 函数计算出的数值，范围从 0 到 sigmaN，输出范围从 “in” 到 “outMax”，否则，调用 “Scale” 函数计算出的数值返回 -sigmaN 到 0 的范围，且输出范围从 “outMin” 到 “in”。
  

以黄色高亮显示的点是给定标准差边缘处的掉落频率问题的解。因此，我们只是将掉落在边界之外的概率向内“扩散”到分布曲线的相应部分。在这种情况下，不会违反分布形状。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::GaussDistribution (const double In, const double outMin, const double outMax, const double sigma)
{
  double logN = 0.0;
  double u1   = RNDfromCI (0.0, 1.0);
  double u2   = RNDfromCI (0.0, 1.0);

  logN = u1 <= 0.0 ? 0.000000000000001 : u1;

  double z0 = sqrt (-2 * log (logN)) * cos (2 * M_PI * u2);

  double sigmaN = sigma > 8.583864105157389 ? 8.583864105157389 : sigma;

  if (z0 >=  sigmaN) z0 = RNDfromCI (0.0,     sigmaN);
  if (z0 <= -sigmaN) z0 = RNDfromCI (-sigmaN, 0.0);

  if (z0 >= 0.0) z0 =  Scale (z0,        0.0, sigmaN, 0.0, outMax - In, false);
  else           z0 = -Scale (fabs (z0), 0.0, sigmaN, 0.0, In - outMin, false);
  
  return In + z0;
}
//——————————————————————————————————————————————————————————————————————————————

下面是一个具有正态分布的随机数示例（图例 4）。在该示例中及以下 — 在从 “-100” 到 “100” 范围内围绕所需值 “50” 的分布 [-100;50;100]。

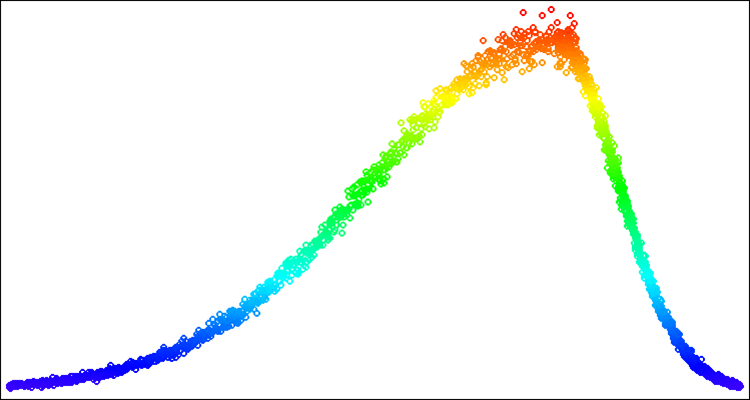
图例 4. sigma=3， [-100;50;100]

幂律分布

幂律分布是一种概率分布，它描述的是根据幂律，随机变量取到非常大数值的概率会衰减。这种分布也称为帕累托（Pareto）原理或齐普夫（Zipf）定律。幂分布已用于科学技术的各个领域。例如，它在物理学中用于针对拥有众多微粒的系统进行质量和能量分布建模，譬如星团和星系。它在经济学和社会学中也用于分析收入和财富的分配。

幂律分布有几个有趣的性质。首先，它是重尾的，这意味着随机变量取到非常大的数值的概率不为零。其次，它没有有限的数学期望，这意味着随机变量的平均值可以是无限的。

幂律分布在优化算法中有一个非常实用的形式。它允许将随机数的密度集中在搜索空间中需要特别注意和澄清的地方。然而，就其纯粹形式而言，当我们想要明确限制随机数的边界时，它不适合使用，由于它具有无限长度的尾部，不能如同正态分布情况下那样容易地“向内包裹”。

对于幂律分布的经典实现，有必要使用逆函数。然而，为了消除分布尾部的无穷大，它会干扰在已知限制内生成的数值，我们可以使用一个均匀分布数值的升幂。虽然这不是指定幂律分布的正确方式，但它将令我们能够摆脱分布尾部的无穷大，同时保持相当接近理论形状的分布形状。对于随机优化算法，这已是绰绰有余。

PowerDistribution 函数采用四个双精度值作为输入：“in”、“outMin”、“outMax” 和 “power”。它在 [-1.0;1.0]，计算 “r” 值，该值是 “power” 的幂运算结果，然后调用 Scale 函数把该值从范围 [0.0;1.0] 缩放到给定的数值范围。如果 “rnd” 为负数，则缩放在 [outMin;in] 内执行，否则 — 范围是 [in;outMax]。该函数的结果以双精度值的形式返回。

• 如果 “power” 小于 1，则结果分布中的大部分值将集中在零附近，并且分布尾部将被大幅截断。这种分布将类似于抛物线。
• 如果 “power” 为 1，则结果分布将是均匀的。
• 如果 “power” 大于 1，则结果分布中的大部分值将分布得远离零，并且分布尾部将很长。这样的分布将有一个沉重的尾部，类似于帕累托（Pareto）分布或幂律分布。
• 如果 “power” 趋于无穷大，则结果分布将类似于集中在零处的增量函数。

因此，当使用不同的 “power” 值时，我们打开了一个具有额外可能性的领域，因此，在研究最优分布的选择时，我们有更多的机会在解决特定优化问题的背景下在优化算法中获得最佳结果。

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::PowerDistribution (const double In, const double outMin, const double outMax, const double power)
{
  double rnd = RNDfromCI (-1.0, 1.0);
  double r   = pow (fabs (rnd), power);

  if (rnd >= 0.0) return In + Scale (r, 0.0, 1.0, 0.0, outMax - In, false);
  else            return In - Scale (r, 0.0, 1.0, 0.0, In - outMin, false);
}
//——————————————————————————————————————————————————————————————————————————————

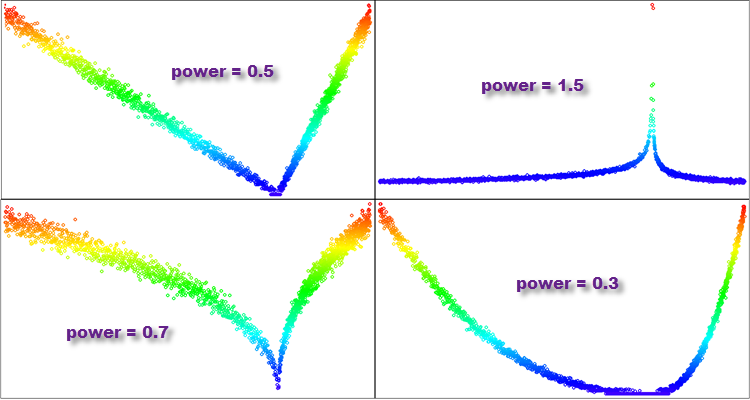
图例 5. PowerDistribution 函数按不同程度 “power” 的分布示例

Levy 分布

Levy 飞行是随机游走，其中每一步的长度由 Levy 分布判定。

Levy 分布是具有无界矩的分布的一个例子。它描述了带有重尾部的随机变量，这意味着取得非常大的数值概率很高。在 Levy 分布中，矩可能是无限的或不存在的，这令它很特殊，并且不同于有限矩的分布，譬如正态分布。

Levy 分布的重尾部及其无界矩令其可用于对可能具有极值或高变异性的现象进行建模。Levy 飞行在各个领域都有许多应用，包括物理学、金融数学、风险分析、生态学、经济学、和工程学。例如，它们可用于物理学中的随机过程建模，譬如等离子体中的扩散、湍流、和传输。它们还可用于针对动物和种群的搜索策略进行建模，并优化工程和金融中的参数。

Levy 分布由法国数学家 Paul Lévy 于 1925 年提出，并在科学技术的各个领域中发现了许多应用。

如果我们谈论的是优化中特定参数值的增量，那么在 Levy 飞行中，每个增量都是从 Levy 分布中选择的，并且方向是随机选择的。这导致了这样一个事实，即在 Levy 飞行中，某些步骤可能会很长，与具有固定步骤长度（增量）的随机游走相比，这令其对参数空间的探索更快。

Levy 飞行分布的形式与幂分布的形式相似，但在某些情况下，采用一种或另一种分布更有效。与幂律分布的情况一样，我们需要摆脱沉重的尾部。不过，在这种情况下，针对该分布我们将以不同的方式进行操作。实验发现，生成过程中采用范围 [1.0;20.0] 涉及的随机数均匀分布更优。我们需要计算随机数在分布结束时的最小值为 “power” 的幂，其将作为我们生成的数字缩放到 [0.0;1.0] 的边界。

LeviDistribution 函数采用四个双精度值作为输入：“in”、“outMin”、“outMax” 和 “power”，并执行以下步骤：

• 首先，该函数根据 “power” 参数判定最小值 “min”。这是后续缩放的最小可能函数值。
  
• 然后，从区间 [0.0;1.0] 和 [1.0;20.0] 均匀分布分别生成两个随机数 “r1” 和 “r2”。
• “y” 的值的计算方法是将 “r2” 升到 “power” 的负幂，并调用 Scale 函数将其从区间 [min,1.0] 缩放到 [0.0;1.0] 。
  
• 最后，该函数返回根据 “r1” 的值按 [outMin,outMax] 间隔缩放的生成值。如果 r1 >= 0.5，则该值按 [in,outMax] 区间缩放，否则按 [outMin,in] 区间缩放。
  

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SC::LeviDistribution (const double In, const double outMin, const double outMax, const double power)
{
  double min = pow (20.0, -power);
  double r1 = RNDfromCI (0.0, 1.0);
  double r2 = RNDfromCI (1.0, 20.0);
  
  double y = pow (r2, -power);
  y = Scale (y, min, 1.0, 0.0, 1.0, false);
 
  if (r1 >= 0.5) return In + Scale (y, 0.0, 1.0, 0.0, outMax - In, false);
  else           return In - Scale (y, 0.0, 1.0, 0.0, In - outMin, false);
}
//——————————————————————————————————————————————————————————————————————————————

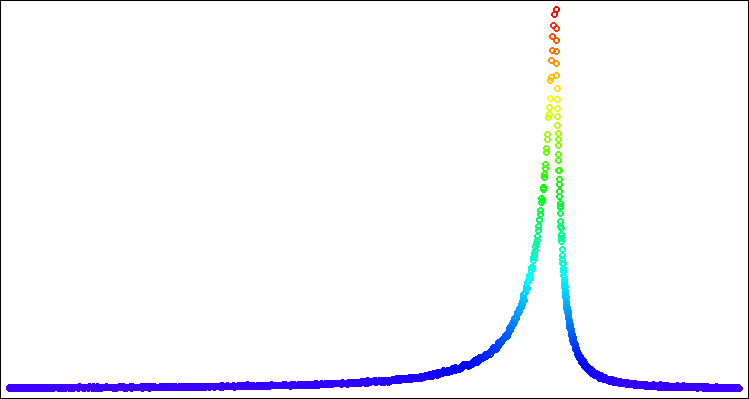
图例 6. Levy 分布 power = 1.0

4. 优化算法模板 —“智能头足类生物”算法

我们转入研究中最有趣的阶段！我们使用专门为这些目的创建的优化算法检查所有分布，称为...... 嗯，我们应该怎么称呼它？

我们来测试一下这种算法的想法：想象一个聪明的头足类生物正在寻找最美味的地方，所以我们假设它的头在食物的中心，正在吃东西。与此同时，它的触手不断向两侧伸展，寻找新的食物存货。一旦其中一条触手找到一个有美食的地方，头部就会移动。也许对于受海洋生物启发的算法来说，这是一个好主意。然后我们知道该怎么称呼它 — 它将是智能头足类生物！

我相信这将是一个激动人心的实验，它将令我们能够更好地理解不同的分布是如何起作用的，以及它们如何帮助我们解决复杂的优化问题。故此，我们开始吧，看看我们能在这个有趣的研究中发现什么！

将头足类生物的腿部特性设置为相应的分布律是合乎逻辑的。然后，凭头足类生物的足感受新地方的代码将如下所示：

//----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      double X   = 0.0;
      double in  = cB [c];
      double min = rangeMin [c];
      double max = rangeMax [c];
      
      switch (distr)
      {
      case uniformDistr: X = UniformDistribution (in, min, max);         break;
      case gaussDistr:   X = GaussDistribution   (in, min, max, powers); break;
      case powerDistr:   X = PowerDistribution   (in, min, max, powers); break;
      case leviDistr:    X = LeviDistribution    (in, min, max, powers); break;
      }

      a [i].c [c] = SeInDiSp  (X, rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }

该段代码由两个嵌套循环组成，它们遍历 popSize 大小的 “a” 数组中的每位个体，并为每个坐标元素生成一个新值。新值的生成是通过选择四种类型的分布中的一种，并将相应的分布函数（UniformDistribution、GaussDistribution、PowerDistribution 或 LeviDistribution）应用于从 “cB” 数组中获取的当前值 “in” 来完成的，该数组表示当前的最佳解（头部当前所在的位置）。然后，SeInDiSp 函数使用 rangeMin 和 rangeMax 值，以及该元素的 rangeStep 对生成的新 X 值进行常规化。结果值存储在 “a” 数组中给定的个体和坐标 。

在撰写本文，并生成具有必要分布的随机数的特定类方法时，便于在构建优化算法中使用，这令我了解到 Rastrigin 函数有几个严重的缺点，这些缺点在选择该测试函数时并不明显，因此我决定不用它。旧的 Rastrigin 将被 Peaks 函数替换（下一篇文章将提供更完整的理由）。

“智能头足类生物”在行动

5. 总结

总而言之，我们对“智能头足类生物”的实验带来了有趣的结果。该动画演示了应用特定分布的随机算法如何成功完成任务。我不会确切地透露使用了哪些分发或设置，但我留待您使用本文中的全套工具运行自己的实验。如果您在评论中分享您的成功，我将很高兴。

“智能头足类生物”不会被考虑在评级表中，因为它只是一个实验，可以帮助我们更加有意识地进行优化。

我的总体结论是，概率分布的应用和搜索策略的选择在优化问题中起着重要作用，因为它允许人们考虑随机因素，更有效地探索解空间，并发现找到最佳解的高概率区域。

然而，仅使用概率分布是不够的。考虑搜索策略的选择和特性也很重要。根据优化问题的不同，不同的搜索策略可能各有优点和缺点。

因此，为了在设计优化算法时，无论是在特定问题中、还是在一般情况下都获得更好的结果，有必要同时使用概率分布和搜索策略选择。这些元素应该协同工作，从而为所开发的优化算法提供所需的性能。总体而言，该实验的结果强调了采取深思熟虑的优化方法的重要性。例如，在机器学习领域，应用概率分布和选择相应的搜索策略可能很有用，因为在机器学习领域，需要优化和寻找最优解。

本文介绍的工具的一个重要特性是在给定数值范围内偏移分布的可能性。在专注于一般问题的专用函数库中，您不会找到分布偏移能力。这令研究人员能够根据优化算法所需的特性来操纵和调整概率分布。调整和控制概率偏差，以及搜索策略的元素确实可以创造奇迹！