Bilinmeyen Olasılık Yoğunluk Fonksiyonunun Çekirdek Yoğunluk Tahmini
270
0
Giriş
MQL5 performansının iyileştirilmesi ve PC verimliliğinin istikrarlı şekilde büyümesi, MetaTrader 5 platformu kullanıcılarının piyasa analizi için oldukça karmaşık ve gelişmiş matematiksel yöntemler uygulamasına olanak tanır. Bu yöntemler ekonominin, ekonometrinin veya istatistiğin çeşitli alanlarına ait olabilir, ancak her durumda, bunları kullanırken olasılık yoğunluk fonksiyonu kavramını ele almamız gerekecek.
Kullanılan modelde veri dağılımı normalliği veya hata normalliği varsayımına dayalı olarak birçok yaygın analiz yöntemi geliştirilmiştir. Ayrıca, analiz sonuçlarını tahmin etmek için kullanılan modelin çeşitli bileşenlerinin dağılımını bilmek çoğu zaman gereklidir. Her iki durumda da, bilinmeyen olasılık yoğunluk fonksiyonunu tahmin etmeye izin veren bir "araç" (ideal durumda evrensel bir araç) oluşturma görevimiz var.
Bu makalede, bilinmeyen olasılık yoğunluk fonksiyonunu tahmin etmek için aşağı yukarı evrensel algoritma gerçekleştiren bir sınıf oluşturma girişiminde bulunulmuştur. Orijinal fikir, tahmin sırasında herhangi bir harici aracın kullanılmayacağı, yani her şeyin yalnızca MQL5 aracılığıyla gerçekleştirileceğiydi. Ancak sonunda orijinal fikir bir dereceye kadar değiştirildi. Olasılık yoğunluk fonksiyonu görsel tahmin görevinin, iki bağımsız bölümden oluştuğu açıktır.
Yani, tahminin kendisinin hesaplanması ve görselleştirilmesi, (bir grafik veya diyagram olarak gösterilmesi.) Tabii ki hesaplamalar MQL5 aracılığıyla yapılmıştır, görselleştirme ise bir HTML sayfası oluşturularak ve bunun web tarayıcısında görüntülenmesiyle gerçekleştirilmelidir. Bu çözüm, sonunda vektör biçiminde grafikler elde etmek için kullanıldı.
Ancak hesaplama kısmı ve sonuçların gösterimi ayrı ayrı gerçekleştirildiği için, okuyucu elbette başka herhangi bir mevcut yöntemi kullanarak görselleştirebilir. Ayrıca MetaTrader 5'te grafik olanlar da dahil olmak üzere çeşitli kitaplıkların görünmesini bekliyoruz (bildiğimiz kadarıyla çalışmalar devam ediyor). MetaTrader 5'in grafikler ve diyagramlar oluşturmak için gelişmiş araçlar sağlaması durumunda, önerilen çözümde görüntü bölümünü değiştirmek zor olmayacaktır.
Öncelikle belirtilmelidir ki, dizi olasılık yoğunluk fonksiyonunun tahmini için gerçekten evrensel bir algoritmanın oluşturulmasının ulaşılamaz bir hedef olduğu kanıtlanmıştır. Önerilen çözüm çok özel bir çözüm olmasa da, tamamen evrensel olarak da adlandırılamaz. Sorun, örneğin normal ve üstel dağılımlar gibi çan şeklindeki dağılımlar için yoğunluk tahmini sırasında optimumluk kriterlerinin oldukça farklı olmasıdır.
Bu nedenle, tahmini dağılımla ilgili bazı ön bilgiler varsa, her özel durum için en uygun çözümü seçmek her zaman mümkündür. Ancak yine de tahmini yoğunluğun doğası hakkında hiçbir şey bilmediğimizi varsayacağız. Böyle bir yaklaşım kesinlikle tahminlerin kalitesini etkileyecektir, ancak umalım ki oldukça farklı yoğunlukları tahmin etme imkanı sağlayarak işe yarasın.
Piyasa verilerinin analizi sırasında genellikle durağan olmayan dizilerle uğraşmak zorunda kaldığımız için, en çok kısa ve orta dizi yoğunluğunun tahmin edilmesiyle ilgileniyoruz. Bu, kullanılan tahmin yönteminin seçimini belirleyen kritik bir andır.
Histogramlar ve P-spline eğrisi, bir milyondan fazla değer içeren gerçekten uzun diziler için başarıyla kullanılabilir. Ancak 10-20 değer içeren diziler için histogramları etkili bir şekilde oluşturmaya çalıştığımızda bazı sorunlar ortaya çıkıyor. Bu nedenle, daha sonra çoğunlukla, yaklaşık 10 ila 10 000 aralığında değerlere sahip dizilere odaklanacağız.
1. Olasılık Yoğunluk Fonksiyonu Tahmin Yöntemleri
Günümüzde oldukça çok sayıda az veya çok popüler olasılık yoğunluk fonksiyonu tahmini yöntemleri bilinmektedir. Bunlar, örneğin, "olasılık yoğunluk tahmini", "olasılık yoğunluğu", "yoğunluk tahmini" vb. gibi anahtar ifadeler kullanılarak İnternette kolaylıkla bulunabilir. Ama ne yazık ki aralarından en iyisini seçemedik. Hepsinin belirli avantajları olduğu gibi dezavantajları da vardır.
Histogramlar geleneksel olarak yoğunluk tahmini için kullanılır [1]. Histogramları kullanmak (düz olanlar dahil), yüksek kalitede olasılık yoğunluk tahminleri sağlamaya olanak tanır, ancak yalnızca uzun dizilerle uğraşmamız halinde... Daha önce bahsedildiği gibi, kısa bir diziyi çok sayıda gruba bölmek mümkün değildir, ancak 2-3 çubuktan oluşan bir histogram böyle bir dizinin olasılık yoğunluk dağılımı yasasını gösteremez. Bu nedenle, histogramları kullanmaktan vazgeçmek zorunda kaldık.
Oldukça iyi bilinen diğer bir tahmin yöntemi, çekirdek yoğunluk tahminidir [2]. Çekirdek yumuşatmayı kullanma fikri [3]'te oldukça iyi gösterilmiştir. Bu nedenle, tüm dezavantajlarına rağmen bu yöntemi seçtik. Bu yöntemin uygulanmasıyla ilgili bazı hususlar aşağıda kısaca tartışılacaktır.
"Beklenti-maksimizasyon" algoritmasını kullanan çok ilginç bir yoğunluk tahmin yönteminden de söz etmek gerekir [4]. Bu algoritma, örneğin bir normal dağılıma sahip olan bir diziyi ayrı bileşenlere ayırmaya olanak tanır. Ayrı bileşen parametreleri belirlendikten sonra elde edilen dağılım eğrilerini toplayarak bir yoğunluk tahmini elde etmek mümkündür. Bu yöntem, [5]'te belirtilmiştir. Bu yöntem, makale üzerinde ve diğerleri üzerinde çalışırken uygulanmamış ve test edilmemiştir. Çeşitli kaynaklarda anlatılan çok sayıda yoğunluk tahmin yöntemi uygulamada bunların tamamının incelenmesine engel olmaktadır.
Uygulama için seçilen çekirdek yoğunluk tahmin yöntemine geçelim.
2. Olasılık Yoğunluk Fonksiyonunun Çekirdek Yoğunluk Tahmini
Olasılık yoğunluk fonksiyonunun çekirdek yoğunluk tahmini, çekirdek yumuşatma yöntemine dayanmaktadır. Bu yöntemin prensipleri örneğin [6], [7]'de bulunabilir.
Çekirdek yumuşatmanıntemel fikri oldukça basittir. MetaTrader 5 kullanıcıları Hareketli Ortalama (MA) göstergesine aşinadır. Bu gösterge, içinde yumuşatılmış ağırlıklı değerleriyle bir dizi boyunca kayan bir pencere olarak kolayca tasvir edilebilir. Pencere dikdörtgen, üstel veya başka bir şekle sahip olabilir. Çekirdek yumuşatma sırasında aynı kayan pencereyi kolayca görebiliriz (örneğin, [3]). Ancak, bu durumda bu, simetriktir.
Çekirdek yumuşatmada en sık kullanılan pencere örnekleri [8]'de bulunabilir. Çekirdek yumuşatmada sıfır dereceli bir regresyon kullanılması durumunda, pencereye (çekirdek) gelen dizi ağırlıklı değerler MA'da olduğu gibi basitçe yumuşatılır. Filtreleme sorunlarıyla ilgilenirken aynı tür pencere işlevi uygulamasını görebiliriz. Ancak şimdi aynı prosedür biraz farklı şekilde sunuluyor. Genlik-frekans ve faz-frekans özellikleri kullanılırken, çekirdek (pencere), filtre darbe özelliği olarak adlandırılır.
Bu örnekler, bir şeyin genellikle farklı şekillerde temsil edilebileceğini göstermektedir. Bu, elbette matematiksel araca katkıda bulunur. Ancak bu tür konuları tartışırken kafa karışıklığına da yol açabilir.
Çekirdek yoğunluk tahmini, daha önce bahsedilen çekirdek yumuşatma ile aynı prensipleri kullanmasına rağmen, algoritması biraz farklıdır.
Bir noktada yoğunluk tahminini tanımlayan ifadeye gidelim.
Burada:
- x - uzunluğu n olan dizi;
- K - simetrik çekirdek;
- h - aralık, yumuşatma parametresi.
Daha sonra yoğunluk tahminleri için yalnızca Gauss çekirdeği kullanılacaktır:
Yukarıdaki ifadeden aşağıdaki gibi, X noktasındaki yoğunluk, X noktasının değerleri ile dizi arasındaki farklarla tanımlanan miktarlar için çekirdek değerlerinin toplamı olarak hesaplanır. Ayrıca, yoğunluk hesabı için kullanılan X noktaları, dizinin kendi değerleriyleörtüşmeyebilir.
Çekirdek yoğunluk tahmin algoritmasının uygulanmasının temel adımları şu şekildedir.
- Ortalama değeri ve giriş dizisi standart sapmasını değerlendirme.
- Giriş dizisini normalleştirme. Her bir değerinden önceden elde edilen ortalamayı çıkarma ve standart sapma değerine bölme. Böyle bir normalleştirmeden sonra, orijinal dizi sıfır ortalamaya ve bire eşit standart sapmaya sahip olacaktır. Bu tür bir normalleştirme, yoğunluğun hesaplanması için gerekli değildir, ancak X ölçeğindeki herhangi bir dizi için, standart sapma birimlerinde ifade edilen değerler olacağı için, ortaya çıkan grafiklerin birleştirilmesine olanak tanır.
- Normalleştirilmiş dizide yüksek ve düşük değerleri bulma.
- Boyutları, elde edilen grafikte görüntülenen istenen nokta sayısına karşılık gelen iki dizi oluşturma. Örneğin, grafik 200 nokta kullanılarak oluşturulacaksa, dizi boyutu uygun şekilde her biri 200 değer içermelidir.
- Sonucu saklamak için oluşturulan dizilerden birini ayırma. İkincisi, yoğunluk tahmini yapılan noktaların değerlerinin oluşturulması için kullanılır. Bunun için önceden hazırlanmış yüksek ve düşük değerler arasında 200 adet (bu durumda) eşit aralıklı değer oluşturmalıve bunları hazırladığımız diziye kaydetmeliyiz.
- Daha önce gösterilen ifadeyi kullanarak, adım 4'te hazırladığımız dizideki sonucu kaydederek 200 (bizim durumumuzda) test noktasında yoğunluk tahminini yapmalıyız.
Bu algoritmanın yazılım uygulaması aşağıda gösterilmiştir.
//+------------------------------------------------------------------+ //| CDens.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CDens:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth public: void CDens(void); int Density(double &x[],double hh); void NTpoints(int n); private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CDens::CDens(void) { NTpoints(200); // Default number of test points } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CDens::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Density | //+------------------------------------------------------------------+ int CDens::Density(double &x[],double hh) { int i; double a,b,min,max,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) min=X[ArrayMinimum(X)]; max=X[ArrayMaximum(X)]; b=(max-min)/(Np-1.0); for(i=0;i<Np;i++)T[i]=min+b*(double)i; // Create test points //-------------------------------- Bandwidth selection h=hh; if(h<0.001)h=0.001; H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Gaussian kernel density estimation | //+------------------------------------------------------------------+ void CDens::kdens(double h) { int i,j; double a,b,c; c=MathSqrt(M_PI+M_PI)*N*h; for(i=0;i<Np;i++) { a=0; for(j=0;j<N;j++) { b=(T[i]-X[j])/h; a+=MathExp(-b*b*0.5); } Y[i]=a/c; // pdf } } //--------------------------------------------------------------------
NTpoints() yöntemi, yoğunluk tahmininin yapılacağı gerekli sayıda eşit aralıklı test noktasının ayarlanmasına olanak tanır. Bu yöntem, Density() yöntemi çağrılmadan önce çağrılmalıdır. Giriş verilerini ve aralık değerini (yumuşatma parametresi) içeren dizinin bağlantısı, yöntem çağrıldığında parametreleri olarak Density() yöntemine iletilir.
Density() yöntemi, başarılı bir şekilde tamamlanması durumunda sıfır döndürür, test noktaları değerleri ve tahmin sonuçları ise sırasıyla o sınıfın T[] ve Y[] dizilerinde bulunur.
Dizi boyutları, varsayılan olarak 200 değere eşitken, NTpoints()'e erişirken ayarlanır.
Aşağıdaki örnek script dosyası, sunulan CDens sınıfının kullanımını gösterir.
#include "CDens.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i; int ndata=1000; // Input data length int npoint=300; // Number of test points double X[]; // Array for data double T[]; // Test points for pdf estimating double Y[]; // Array for result ArrayResize(X,ndata); ArrayResize(T,npoint); ArrayResize(Y,npoint); for(i=0;i<ndata;i++)X[i]=MathRand();// Create input data CDens *kd=new CDens; kd.NTpoints(npoint); // Setting number of test points kd.Density(X,0.22); // Density estimation with h=0.22 ArrayCopy(T,kd.T); // Copy test points ArrayCopy(Y,kd.Y); // Copy result (pdf) delete(kd); // Result: T[]-test points, Y[]-density estimation } //--------------------------------------------------------------------
Bu örnekte, test noktaları giriş dizisini ve tahmin sonuçlarını depolamak için diziler hazırlanmıştır. Ardından, X[] dizisi örnek olarak rastgele değerlerle doldurulmuştur. Tüm veriler hazırlandıktan sonra CDens sınıfının kopyası oluşturulmuştur.
Ardından, gerekli test noktası sayısı (bizim durumumuzda npoint=300) ile belirlenmiştir. NTpoints() yöntemi çağrısı. Varsayılan nokta sayısını değiştirmeye gerek olmaması durumunda, NTpoints() yöntemi çağrısı hariç tutulabilir.
Hesaplanan değerler, Density() yöntemi çağrısından sonra önceden tanımlanmış dizilere kopyalanır. Daha sonra, CDens sınıfının önceden oluşturulmuş kopyası silinir. Bu örnek, yalnızca CDens sınıfıyla etkileşimi gösterir. Elde edilen sonuçlarla (T[] ve Y[] dizileri) başka bir işlem gerçekleştirilmez.
Bu sonuçlar bir grafik oluşturmak için kullanılacaksa, bu, T[] dizisindeki değerler X grafik ölçeğine, Y[] dizisindeki uygun değerler Y ölçeğine koyularak kolaylıkla yapılabilir.
3. Optimum Aralık Seçimi
Şek. 1'de, normal dağılım yasasına ve çeşitli h aralığı değerlerine sahip dizi için yoğunluk tahmini grafikleri gösterilmiştir.
Tahminler, yukarıda açıklanan CDens sınıfı kullanılarak yapılır. Grafikler HTML sayfaları şeklinde oluşturulmuştur. Bu tür grafikleri oluşturma yöntemi makalenin sonunda sunulacaktır. Grafiklerin ve diyagramların HTML biçiminde oluşturulması [9]'da bulunabilir.
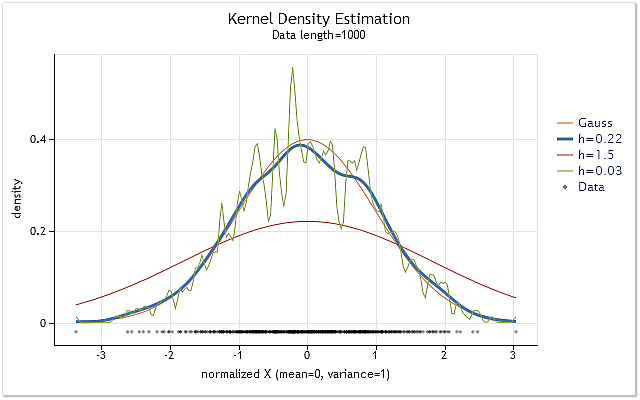
Şek. 1. Çeşitli h aralığı değerleri için yoğunluk tahmini
Şek. 1'de ayrıca üç yoğunluk tahminiyle birlikte gerçek normal dağılım yoğunluk eğrisi (Gauss dağılımı) gösterilmiştir. Bu durumda, en uygun tahmin sonucunun h=0,22 ile elde edildiği rahatlıkla görülebilir. Diğer iki durumda, kesin "fazla yumuşama" ve "az yumuşama" gözlemleyebiliriz.
Şekil 1'de, çekirdek yoğunluk tahmini kullanılırken doğru h aralığı seçiminin önemi açıkça gösterilmiştir. h değerinin yanlış seçilmesi durumunda, tahmin, gerçek yoğunluğa karşı büyük ölçüde kaydırılacak veya önemli ölçüde dağılacaktır.
Optimum h aralığı seçimine yönelik çok sayıda çeşitli çalışma vardır. Basit ve kesin olarak kanıtlanmış Silverman temel kuralı, genellikle h seçimi için kullanılır (bkz. [10]).
Bu durumda A, dizi standart sapma değerleri ve 1,34'e bölünen çeyrekler açıklığının en düşük değeridir.
Giriş dizisinin yukarıda belirtilen CDens sınıfında bire eşit standart sapmaya sahip olduğu göz önünde bulundurulduğunda, aşağıdaki kod parçasını kullanarak bu kuralı uygulamak oldukça kolaydır:
ArraySort(X); i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb
Bu tahmin, biçimine göre normale yakın olasılık yoğunluk fonksiyonuna sahip dizilere uygundur.
Çoğu durumda, çeyrekler açıklığının dikkate alınması, değerlendirilen yoğunluğun biçimi normal olandan saptığında h değerinin alt tarafa ayarlanmasına olanak tanır. Bu, bu değerlendirme yöntemini yeterince çok yönlü hale getirir. Bu nedenle, bu temel kural, başlangıç temel h değeri tahmini olarak kullanılmaya değerdir. Ayrıca, bu, uzun hesaplamalar gerektirmez.
Asimptotik ve ampirik h aralığı değeri tahminlerine ek olarak, giriş dizisinin kendisinin analizine dayanan çeşitli yöntemler de vardır. Bu durumda optimum h değeri, bilinmeyen yoğunluğun ön tahmini dikkate alınarak belirlenir. Bu yöntemlerden bazılarının etkililiğine ilişkin karşılaştırma [11], [12]'de bulunabilir.
Çeşitli kaynaklarda yayınlanan test sonuçlarına göre Sheather-Jones yerleşik yöntemi (SJPI) en etkili aralık tahmin yöntemlerinden biridir. Bu yöntemi tercih edelim. Makaleyi uzun matematiksel ifadelerle doldurmamak için ileride yöntemin yalnızca bazı özelliklerinden bahsedilecektir. Gerekirse, bu yöntemin matematiksel temeli [13]'te bulunabilir.
Sınırsız desteğe sahip bir çekirdek olan bir Gauss çekirdeği kullanıyoruz (yani, bu, parametresi eksiden artı sonsuza değiştiğinde belirtilir). Yukarıdaki ifadeden de anlaşılacağı gibi, N uzunluğuna sahip dizinin M noktalarındaki yoğunluğu doğrudan hesaplama yöntemi ve sınırsız destekli çekirdek kullanarak tahmin ederken O(M*N) işlemlerine ihtiyacımız olacak. Dizi noktalarının her birinde tahmin yapmamız gerekirse bu değer O(N*N) işlemlere kadar yükselir ve hesaplama için harcanan süre dizi uzunluğunun karesi ile orantılı olarak artar.
Hesaplama kaynakları için bu kadar yüksek bir talep, çekirdek yumuşatma yönteminin başlıca dezavantajlarından biridir. SJPI yöntemine geçersek, gerekli hesaplama miktarı açısından daha iyi olmadığını göreceğiz. Kısaca konuşmak gerekirse, SJPI yöntemini uygularken ilk olarak giriş dizisinin tüm uzunluğu boyunca iki yoğunluk türevinin toplamını iki kez hesaplamalıyız.
Ardından, elde edilen sonuçları kullanarak tahmini tekrar tekrar hesaplamalıyız. Tahmin değeri sıfıra eşit olmalıdır. Newton-Raphson yöntemi [14], bu fonksiyonun sıfıra eşit olduğu bağımsız değişkeni bulmak için kullanılabilir. Doğrudan hesaplama durumunda, optimum aralık değerini belirlemek için SJPI yönteminin uygulanması, yoğunluk tahminleri hesaplamasının yaklaşık on katı kadar zaman gerektirebilir.
Çekirdek yumuşatma ve yoğunluk çekirdek yoğunluk tahmininde hesaplamaları hızlandırmanın çeşitli yöntemleri vardır. Bizim durumumuzda, 4'ten büyük bağımsız değişken değerleri için değerlerinin ihmal edilebilecek kadar küçük olduğu varsayılabilen Gauss çekirdeği kullanılır. Bu nedenle, bağımsız değişken değeri 4'ten büyükse, çekirdek değerlerini hesaplamaya gerek yoktur. Dolayısıyla, gerekli hesaplama sayısını kısmen azaltabiliriz. Böyle bir tahmine dayalı grafik ile tam hesaplanmış sürüm arasında neredeyse hiç fark görmeyeceğiz.
Hesaplamaları hızlandırmanın bir başka basit yolu, tahminin yapıldığı nokta sayısını azaltmaktır. Yukarıda bahsedildiği gibi, M, N'den küçükse, gerekli işlem sayısı O(N*N)'den O(M*N)'ye düşürülecektir. Örneğin N=100 000 gibi uzun bir dizimiz varsa, yalnızca M=200 noktalarında tahminler yapabiliriz. Bu nedenle, hesaplama süresini önemli ölçüde azaltabiliriz.
Ayrıca, gerekli hesaplama sayısını azaltmak için daha karmaşık yöntemler kullanılabilir; örneğin hızlı bir Fourier dönüşümü algoritmasını veya dalgacık dönüşümlerini kullanan tahminler. Giriş dizisi boyutunu azaltmaya dayalı yöntemler (örneğin, "Veri gruplama" [15]) gerçekten uzun diziler için başarıyla uygulanabilir.
Hızlı Gauss dönüşümü [16], Gauss çekirdeğinin kullanılması durumunda yukarıda belirtilen yöntemlere ek olarak hesaplamaları hızlandırmak için de uygulanabilir. Aralık değeri tahmininin SJPI yöntemini uygulamak için Gauss dönüşümüne [17] dayalı algoritmayı kullanacağız. Yukarıda bahsedilen bağlantı, önerilen algoritmayı uygulayan yöntem açıklamasını ve program kodlarını içeren materyallere götürür.
4. Sheather-Jones yerleşik yöntemi (SJPI)
SJPI yönteminin özünü belirleyen matematiksel ifadelerde olduğu gibi, [17]'de bulunabilecek algoritmanın uygulanmasının matematiksel temelini bu makaleye kopyalamayacağız. Gerekirse [17]'deki yayınları inceleyebilirsiniz.
CSJPlugin sınıfı, [17]'de bulunan materyallere dayalı olarak oluşturulmuştur. Bu sınıf, optimum h aralığı değerinin hesaplanması için tasarlanmıştır ve yalnızca bir genel yöntem içerir – double CSJPlugin::SelectH(double &px[],double h,double stdev=1).
Çağrıldığında bu yönteme aşağıdaki bağımsız değişkenler iletilir:
- double &px[] – Orijinal diziyi içeren diziye bağlantı;
- double h, Newton-Raphson algoritması kullanılarak denklemler çözülürken aramanın yapıldığı başlangıç h aralığı değeridir. Bu değerin aranan değere mümkün olduğunca yakın olması arzu edilir. Bu, denklemleri çözmek için harcanan zamanı önemli ölçüde azaltabilir ve Newton-Raphson'ın güvenilirliğini kaybedebileceği durumların olasılığını azaltabilir. Silverman temel kuralı kullanılarak bulunan değer, başlangıç h değeri olarak kullanılabilir;
- double stdev=1 – orijinal dizi standart sapmasının değeri. Varsayılan değer, birdir. Bu durumda, bu yöntemin, orijinal dizinin zaten normalleştirilmiş olduğu ve standart sapmanın bire eşit olduğu, daha önce bahsedilen CDens sınıfı ile birlikte kullanılması amaçlandığı için, varsayılan değeri değiştirmemiz gerekmez.
SelectH() yöntemi, başarılı bir şekilde tamamlanması durumunda elde edilen optimum h aralığı değerini döndürür. Hata durumunda, parametre olarak başlangıç h değeri döndürülür. CSJPlugin sınıfının kaynak kodu, CSJPlugin.mqh dosyasında bulunur.
Bu uygulamanın bazı özelliklerinin açıklığa kavuşturulması gerekir.
Kaynak dizi bir kerede [0,1] aralığına dönüştürülürken, h aralığı başlangıç değeri orijinal dizi dönüşüm ölçeği ile orantılı olarak normalleştirilir. Hesaplamalar sırasında elde edilen optimum h değerine ters normalizasyon uygulanır.
eps=1e-4 – Yoğunluk ve türevlerinin tahminlerinin hesaplama doğruluğu ve P_UL=500 – algoritma iç yinelemelerinin izin verilen maksimum sayısı, CSJPlugin sınıf oluşturucusunda ayarlanır. Daha fazla bilgi için bkz. [17].
IMAX=20 – Newton-Raphson yöntemi ve PREC=1e-4 için izin verilen maksimum yineleme sayısı – bu yöntemi kullanarak denklemi çözmenin doğruluğu SelectH() yönteminde ayarlanır.
Newton-Raphson yönteminin geleneksel kullanımı, her değer yinelemesinde aynı noktada hedef fonksiyonun ve türevinin hesaplanmasını gerektirmiştir. Bu durumda, türevin hesaplaması, bağımsız değişkenin değerine küçük bir artış eklenerek hesaplanan tahmini ile değiştirilmiştir.
Şekil 2'de, optimum h aralığı değeri tahmininin iki farklı yöntemini kullanma örneği gösterilmiştir.
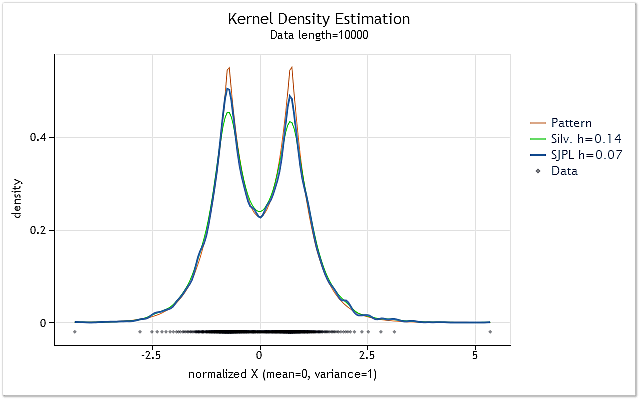
Şek. 2. Optimum h aralığı değeri tahminlerinin karşılaştırması
Şekil 2'de, gerçek yoğunluğu kırmızı grafik (Model) olarak gösterilen rastgele dizi için iki tahmin gösterilmiştir.
10 000 öğe uzunluğundaki dizi için tahminler yapılmıştır. Bu dizi için Silverman'ın temel kuralı kullanıldığında h aralığı değeri 0,14, SJPI yöntemi kullanıldığında ise 0,07 olarak elde edilmiştir.
Şekil 2'de gösterilen bu iki h değeri için çekirdek yoğunluk tahmini sonuçlarını incelediğimizde, SJPI yöntemi uygulamasının Silverman kuralına göre daha ilgi çekici bir h tahmini elde edilmesine yardımcı olduğunu rahatlıkla görebiliriz. Gördüğümüz gibi, keskin üst kısımlar çok daha iyi şekillendirilirken, h=0,07 durumunda eğimli boşluklarda neredeyse hiç yayılım artışı olmaz.
Beklendiği gibi, SJPI yönteminin kullanılması birçok durumda oldukça başarılı h aralığı tahminleri elde edilmesini sağlar. CSJPlugin sınıf oluşturması için oldukça hızlı algoritmalar [17] kullanılmış olmasına rağmen, bu yöntemi kullanarak h değeri tahmini, uzun diziler için hala çok fazla zaman alabilir.
Bu yöntemin diğer bir dezavantajı, yalnızca 10-30 değerden oluşan kısa diziler için h değerini fazla tahmin etme eğilimidir. SJPI yöntemi kullanılarak yapılan tahminler, Silverman temel kuralına göre yapılan h tahminlerini aşabilir.
Bu dezavantajları bir şekilde telafi etmek için sonraki uygulamada aşağıdaki kurallar kullanılacaktır:
- Silverman tahmini, h aralığı için varsayılan tahmin olacakken, SJPI yönteminin ayrı bir komutla etkinleştirilmesi mümkün olacaktır;
- SJPI yöntemi kullanılırken, bahsedilen iki yöntemle elde edilen değerlerden en düşük olanı her zaman h nihai değeri olarak kullanılacaktır.
5. Sınır Etkisi
Yoğunluk tahmininde mümkün olduğunca optimum aralık değeri olarak kullanma isteği, yukarıda bahsedilen ve oldukça kullanışsız CSJPlugin sınıfının oluşturulmasına yol açmıştır. Ancak, çekirdek yumuşatma yönteminin aralık boyutunun ve yüksek kaynak yoğunluğunun belirlenmesine ek olarak bir sorun daha vardır. Bu, sözde sınır etkisidir.
Sorun, basittir. Bu, [-1,1] aralığında tanımlanan çekirdek kullanılarak görüntülenecektir. Bu tür çekirdek, sonlu desteği olan çekirdek olarak adlandırılır. Bu, belirtilen aralığın dışında sıfıra eşittir (mevcut değildir).
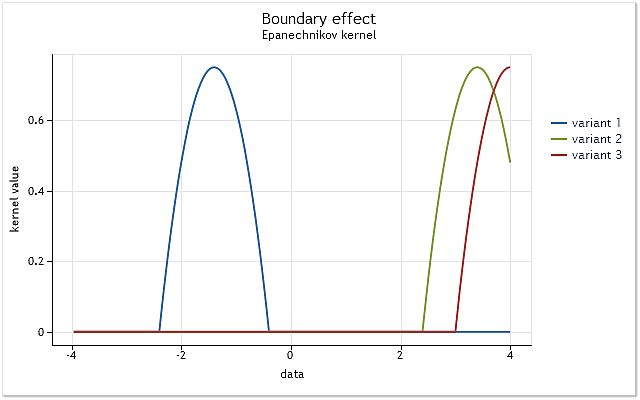
Şek. 3. Aralık sınırında çekirdek indirgemesi
Şekil 3'te gösterildiği gibi, ilk durumda çekirdek, merkezine göre [-1,1] aralığında yer alan orijinal verileri tamamen kapsar. Çekirdek yer değiştirirken (örn. sağa doğru), verilerin seçilen çekirdek işlevini tam olarak kullanmak için yeterli olmadığı durum ortaya çıkar.
Çekirdek zaten ilk duruma göre daha az veriyi kapsar. En kötü durum, çekirdek merkezinin veri dizisi sınırında bulunmasıdır. Bu durumda çekirdeğin kapsadığı veri miktarı %50'ye düşer. Yoğunluk tahmini için kullanılan veri sayısındaki böyle bir azalma, tahminlerde önemli bir kaymaya yol açar ve bunların aralık sınırlarına yakın noktalarda yayılımını arttırır.
Şekil 3'te, aralık sınırında sonlu desteği olan bir çekirdek (Epanechnikov çekirdeği) için bir indirgeme örneği gösterilmiştir. Çekirdek yoğunluk tahmin yönteminin uygulanması sırasında sonsuz aralıkta (sınırsız destek) tanımlanan Gauss çekirdeğinin kullanıldığına dikkat edilmelidir. Teorik olarak, böyle bir çekirdeğin kesilmesi her zaman gerçekleşmelidir. Ancak, bu çekirdeğin değerinin büyük bağımsız değişkenler için neredeyse sıfıra eşit olduğu gerçeği göz önünde bulundurulduğunda, sınır etkileri ona, sonlu desteği olan çekirdeklere olduğu gibi görünür.
Bu özellik, Şekil 1 ve 2'de sunulan durumlarda yoğunluk tahmini sonuçlarını etkileyemez; zira her iki durumda da olasılık yoğunluk fonksiyonu sınırlarda neredeyse sıfırın altına inen dağılımlar için tahmin yapılmıştır.
Aralık sınırlarında çekirdek kesmenin etkisini göstermek için X=1,2,3,4,5,6,…n pozitif tam sayılarından oluşan diziyi oluşturalım. Böyle bir dizi, olasılık yoğunluğu eşit dağılım yasasına sahiptir. Bu, bu dizinin yoğunluk tahmininin sıfır olmayan bir düzeyde bulunan yatay bir düz çizgi olması gerektiği anlamına gelir.
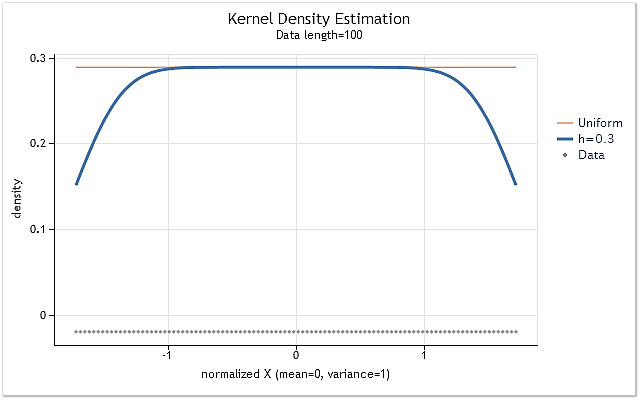
Şek. 4. Eşit dağılım yasasına sahip dizi için yoğunluk tahmini
Beklendiği gibi, Şekil 4'te, aralık sınırlarında yoğunluk tahminlerinde önemli bir kayma olduğu açıkça gösterilmiştir. Bu kaymayı daha fazla veya daha az ölçüde azaltmak için kullanılan birkaç yöntem vardır. Bunlar, kabaca aşağıdaki gruplara ayrılabilir:
- Veri yansıtma yöntemleri,
- Veri dönüştürme yöntemleri,
- Sözde veri yöntemleri,
- Sınır çekirdek yöntemleri.
Yansıtılan verileri kullanma fikri, giriş dizisinin, dizi aralığı sınırlarına göre o dizinin bir tür ayna yansıması olan verilerin eklenmesiyle özellikle arttırılmasıdır. Böyle bir artıştan sonra, orijinal dizi için olduğu gibi aynı noktalar için yoğunluk tahmini yapılır, ancak tahminde özellikle eklenen veriler de kullanılır.
Veri dönüşümünü içeren yöntemler, aralık sınırlarına yakın dizi dönüşümüne odaklanır. Örneğin, yoğunluk tahmini sırasında aralık sınırına yaklaşırken veri ölçeğinin biçimini bir şekilde bozmaya izin veren logaritmik veya başka herhangi bir dönüşüm kullanmak mümkündür.
Sözde veriler, orijinal dizinin kasıtlı olarak genişletilmesi (büyütülmesi) için kullanılabilir. Bu, orijinal dizi değerleri temelinde hesaplanan verilerdir. Bu veriler, davranışını sınırlarda değerlendirme ve onu en uygun şekilde tamamlama işlevi görür.
Sınır çekirdek yöntemlerine yönelik çok sayıda yayın vardır. Bu yöntemlerde çekirdek, sınıra yaklaşırken bir şekilde şeklini değiştirir. Çekirdeğin şekli, sınırlardaki tahminlerdeki kaymayı telafi etmek için değişir.
Aralık sınırlarında ortaya çıkan bozulmaların telafisine ayrılmış bazı yöntemler, bunların karşılaştırması ve verimlilik değerlendirmesi [18]'de bulunabilir.
Bazı kısa denemelerden sonra daha fazla kullanım için veri yansıtma yöntemi seçilmiştir. Bu seçimde, bu yöntemin yoğunluk tahmininin negatif bir değere sahip olduğu durumları kapsamaması gerçeği etkili olmuştur. Ayrıca, bu yöntem karmaşık matematiksel hesaplamalar gerektirmez. Toplam işlem sayısı, uzunluğu kasıtlı olarak artırılan dizinin her bir tahminini yapma ihtiyacı nedeniyle hala artmaktadır.
Bu yöntemi uygulamanın iki yolu vardır. İlk olarak, orijinal diziyi gerekli verilerle tamamlamak ve bu süreçte boyutunu üç kat artırmak mümkündür. Ardından, daha önce sunduğumuz CDens sınıfında gösterildiği gibi aynı şekilde tahminler yapabileceğiz. İkinci olarak, giriş veri dizisini genişletmemek mümkündür. Verileri bir kez daha belirli bir şekilde seçebiliriz. Uygulama için ikinci yol seçilmiştir.
Yukarıda bahsedilen CDens sınıfında yoğunluk tahmini void kdens(double h) işlevinde yapılmıştır. Bu işlevi sınır bozulmaları düzeltmesini ilave ederek değiştirelim.
Artırılmış işlev aşağıdaki gibi görünebilir.
//+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
İşlev, X[] dizisindeki kaynak verilerin, işlev çağrıldığında zaten sıralanmış olduğu varsayılarak uygulanır. Bu, uç aralık değerlerine karşılık gelen iki dizi öğesinin başka bir işlemeden kolayca hariç tutulmasına olanak tanır. Bu işlevi uygularken matematiksel işlemleri mümkün olduğunca döngülerin dışına koyma girişiminde bulunuldu. Sonuç olarak, işlev kullanılan algoritma fikrini daha az açık bir şekilde yansıtır.
Bağımsız değişkenlerin büyük değerleri için bir çekirdek değeri hesaplamamamız durumunda, hesaplama sayısını azaltmanın mümkün olduğundan daha önce söz etmiştik. Yukarıdaki işlevde uygulanan şey tam olarak budur. Bu durumda, değerlendirilen yoğunluk grafiği oluşturulduktan sonra herhangi bir değişikliğin fark edilmesi mümkün değildir.
kdens() işlevinin değiştirilmiş sürümü kullanıldığında, Şekil 4'te gösterilen yoğunluk tahmini düz bir çizgiye dönüştürülür ve sınır boşlukları tamamen kaybolur. Ancak böyle bir ideal düzeltme ancak sınırlara yakın dağılımın sıfır gradyana sahip olması, yani yatay bir çizgi ile temsil edilmesi durumunda elde edilebilir.
Tahmini dağılım yoğunluğu sınırın yakınında keskin bir şekilde yükselir veya düşerse, seçilen veri yansıtma yöntemi sınır etkisini tam olarak ayarlayamayacaktır. Bu, aşağıdaki şekillerde gösterilmiştir.
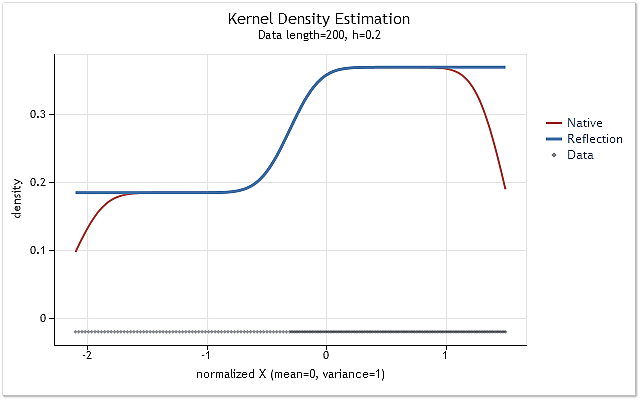
Şek. 5. Adım adım değişen olasılık yoğunluk fonksiyonu
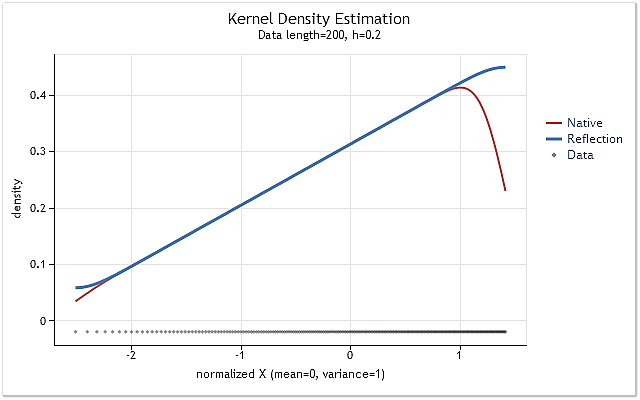
Şek. 6. Doğrusal olarak artan olasılık yoğunluk fonksiyonu
Şekil 5 ve 6'da, kdens() işlevinin orijinal sürümü kullanılarak elde edilen yoğunluk tahmini (kırmızı) ve veri yansıtma yöntemini uygulayan uygulanan değişiklikler dikkate alınarak elde edilen tahmin (mavi) gösterilmiştir. Şekil 5'te sınır etkisi tamamen düzeltilirken, Şekil 6'da sınırlara yakın kayma tamamen ortadan kaldırılmamıştır. Tahmini yoğunluk sınırın yakınında keskin bir şekilde yükselir veya düşerse, bu, o sınırın yakınında biraz daha yumuşak görünür.
Sınır etkisini ayarlamak için seçilen veri yansıtma yöntemi, bilinen yöntemlerin en iyisi veya en kötüsü değildir. Bu yöntem her durumda sınır etkisini ortadan kaldıramasa da, yeterince kararlı ve uygulanması kolaydır. Bu yöntem, mantıklı ve öngörülebilir bir sonuç elde edilmesine olanak tanır.
6. Son Uygulama. CKDensity Sınıfı
Daha önce oluşturulmuş CDens sınıfına h aralığı değerini otomatik olarak seçme ve sınır etkisi düzeltme özelliğini ekleyelim.
Aşağıda, böyle bir değiştirilmiş sınıfın kaynak kodu bulunmaktadır.
//+------------------------------------------------------------------+ //| CKDensity.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #include "CSJPlugin.mqh" //+------------------------------------------------------------------+ //| Class Kernel Density Estimation | //+------------------------------------------------------------------+ class CKDensity:public CObject { public: double X[]; // Data int N; // Input data length (N >= 8) double T[]; // Test points for pdf estimating double Y[]; // Estimated density (pdf) int Np; // Number of test points (Npoint>=10, default 200) double Mean; // Mean (average) double Var; // Variance double StDev; // Standard deviation double H; // Bandwidth int Pflag; // SJ plug-in bandwidth selection flag public: void CKDensity(void); int Density(double &x[],double hh=-1); void NTpoints(int n); void PluginMode(int m) {if(m==1)Pflag=1; else Pflag=0;} private: void kdens(double h); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CKDensity::CKDensity(void) { NTpoints(200); // Default number of test points Pflag=0; // Not SJ plug-in } //+------------------------------------------------------------------+ //| Setting number of test points | //+------------------------------------------------------------------+ void CKDensity::NTpoints(int n) { if(n<10)n=10; Np=n; // Number of test points ArrayResize(T,Np); // Array for test points ArrayResize(Y,Np); // Array for result (pdf) } //+------------------------------------------------------------------+ //| Bandwidth selection and kernel density estimation | //+------------------------------------------------------------------+ int CKDensity::Density(double &x[],double hh=-1) { int i; double a,b,h; N=ArraySize(x); // Input data length if(N<8) // If N is too small { Print(__FUNCTION__+": Error! Not enough data length!"); return(-1); } ArrayResize(X,N); // Array for input data ArrayCopy(X,x); // Copy input data ArraySort(X); // Sort input data Mean=0; for(i=0;i<N;i++)Mean=Mean+(X[i]-Mean)/(i+1.0); // Mean (average) Var=0; for(i=0;i<N;i++) { a=X[i]-Mean; X[i]=a; Var+=a*a; } Var/=N; // Variance if(Var<1.e-250) // Variance is too small { Print(__FUNCTION__+": Error! The variance is too small or zero!"); return(-1); } StDev=MathSqrt(Var); // Standard deviation for(i=0;i<N;i++)X[i]=X[i]/StDev; // Data normalization (mean=0,stdev=1) a=X[0]; b=(X[N-1]-a)/(Np-1.0); for(i=0;i<Np;i++)T[i]=a+b*(double)i; // Create test points //-------------------------------- Bandwidth selection if(hh<0) { i=(int)((N-1.0)/4.0+0.5); a=(X[N-1-i]-X[i])/1.34; // IQR/1.34 a=MathMin(a,1.0); h=0.9*a/MathPow(N,0.2); // Silverman's rule of thumb if(Pflag==1) { CSJPlugin *plug=new CSJPlugin(); a=plug.SelectH(X,h); // SJ Plug-in delete plug; h=MathMin(a,h); } } else {h=hh; if(h<0.005)h=0.005;} // Manual select H=h; //-------------------------------- Density estimation kdens(h); return(0); } //+------------------------------------------------------------------+ //| Kernel density estimation with reflection of data | //+------------------------------------------------------------------+ void CKDensity::kdens(double h) { int i,j; double a,b,c,d,e,g,s,hh; hh=h/MathSqrt(0.5); s=sqrt(M_PI+M_PI)*N*h; c=(X[0]+X[0])/hh; d=(X[N-1]+X[N-1])/hh; for(i=0;i<Np;i++) { e=T[i]/hh; a=0; g=e-X[0]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); g=e-X[N-1]/hh; if(g>-3&&g<3)a+=MathExp(-g*g); for(j=1;j<N-1;j++) { b=X[j]/hh; g=e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=d-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); g=c-e-b; if(g>-3&&g<3)a+=MathExp(-g*g); } Y[i]=a/s; // pdf } }
Density(double &x[],double hh=-1) yöntemi, bu sınıf için temel bir yöntemdir. İlk bağımsız değişken, analiz edilen giriş dizisinin içerilmesi gereken x[] dizisine olan bağlantıdır. Giriş dizisinin uzunluğu sekiz öğeden az olmamalıdır. İkinci (isteğe bağlı) bağımsız değişken, h aralığı değerinin zorunlu olarak ayarlanması için kullanılır.
Herhangi bir pozitif sayı belirtilebilir. Set h değeri alttan her zaman 0,005 ile sınırlandırılacaktır. Bu parametrenin negatif bir değeri varsa, aralık değeri otomatik olarak seçilecektir. Density() yöntemi, başarılı tamamlama durumunda sıfır, acil tamamlama durumunda eksi bir değerini döndürür.
Density() yöntemi çağrıldıktan ve başarılı bir şekilde tamamlandıktan sonra, T[] dizisi, yoğunluk tahmini yapılmış test noktaları değerlerini, Y[] dizisi ise bu tahminlerin değerlerini içerecektir. X[] dizisi, normalleştirilmiş ve sıralanmış giriş dizisini içerecektir. Bu dizinin ortalama değeri sıfıra, standart sapma değeri ise bire eşittir.
Sınıf üyesi olan değişkenlerde aşağıdaki değerler bulunur:
- N – giriş dizisi uzunluğu,
- Np – yoğunluk tahmininin gerçekleştirildiği test noktalarının sayısı,
- Mean – giriş dizisi ortalama değeri,
- Var – giriş dizisi varyansı,
- StDev – giriş dizisi standart sapması,
- H – aralığın değeri (yumuşatma parametresi),
- Pflag – h aralığı optimum değerini belirlemek için SJPI yöntemi uygulamasının bayrağı.
Yoğunluk tahmininin gerçekleştirileceği test noktalarının sayısını belirlemek için NTpoints(int n) yöntemi kullanılır. Density() temel yöntemi çağrılmadan önce test noktaları sayısının ayarlanması yapılmalıdır. NTpoints(int n) yöntemi kullanılmazsa, varsayılan nokta sayısı 200 olarak ayarlanacaktır.
PluginMode(int m) yöntemi, optimum aralık değerini değerlendirmek için SJPI yönteminin kullanılmasına izin verir veya bunu yasaklar. Bu yöntem çağrılırken bire eşit parametre kullanılırsa, h aralığını belirtmek için SJPI yöntemi uygulanacaktır. Bu parametrenin değeri bire eşit değilse SJPI yöntemi kullanılmayacaktır. Expert (int m) yöntemi çağrılmamışsa, SJPI yöntemi varsayılan olarak devre dışı bırakılacaktır.
7. Grafikler Oluşturma
Bu makale yazılırken [9]'da bulunabilecek yöntem kullanılmıştır. Bu yayın, highcharts [19] JavaScript kitaplığı ve tüm çağrılarının tam özellikleri dahil olmak üzere hazır HTML sayfasının uygulanmasıyla ilgiliydi. Ayrıca, bir MQL programı, görüntülenecek verileri içeren bir metin dosyası oluşturur ve bu dosya, yukarıda belirtilen HTML sayfasına bağlanır.
Bu durumda, görüntülenen grafiklerin yapısında herhangi bir düzeltme yapmak için, uygulanan JavaScript kodu değiştirilerek HTML sayfasının düzenlenmesi gerekir. Bunu önlemek için, doğrudan MQL programından highcharts kitaplığının JavaScript yöntemlerinin çağrılmasına olanak tanıyan basit bir arayüz geliştirilmiştir.
Arayüz oluşturulurken highcharts kitaplığının tüm olanaklarına erişimin uygulanması için herhangi bir görev olmamıştır. Bu nedenle, yalnızca makale yazılırken önceden oluşturulmuş HTML dosyasının değiştirilmemesine izin veren olanaklar sağlanmıştır.
CLinDraw sınıfının kaynak kodu aşağıda gösterilmiştir. Bu sınıf, highcharts kitaplık yöntemleri ile bağlantı sağlamak için kullanılmıştır. Bu kod, eksiksiz bir yazılım uygulaması olarak görülmemelidir. Bu yalnızca grafik JavaScript kitaplığına sahip bir arayüzün nasıl oluşturulacağını gösteren bir örnektir.
//+------------------------------------------------------------------+ //| CLinDraw.mqh | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include <Object.mqh> #import "shell32.dll" int ShellExecuteW(int hwnd,string lpOperation,string lpFile,string lpParameters, string lpDirectory,int nShowCmd); #import #import "kernel32.dll" int DeleteFileW(string lpFileName); int MoveFileW(string lpExistingFileName,string lpNewFileName); #import //+------------------------------------------------------------------+ //| type = "line","spline","scatter" | //| col = "r,g,b,y" | //| Leg = "true","false" | //| Reference: http://www.highcharts.com/ | //+------------------------------------------------------------------+ class CLinDraw:public CObject { protected: int Fhandle; // File handle int Num; // Internal number of chart line string Tit; // Title chart string SubTit; // Subtitle chart string Leg; // Legend enable/disable string Ytit; // Title Y scale string Xtit; // Title X scale string Fnam; // File name public: void CLinDraw(void); void Title(string s) { Tit=s; } void SubTitle(string s) { SubTit=s; } void Legend(string s) { Leg=s; } void YTitle(string s) { Ytit=s; } void XTitle(string s) { Xtit=s; } int AddGraph(double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double &y[],string type,string name,int w=0,string col=""); int AddGraph(double &x[],double y,string type,string name,int w=0,string col=""); int LDraw(int ashow=1); }; //+------------------------------------------------------------------+ //| Constructor | //+------------------------------------------------------------------+ void CLinDraw::CLinDraw(void) { Num=0; Tit=""; SubTit=""; Leg="true"; Ytit=""; Xtit=""; Fnam="CLinDraw.txt"; Fhandle=FileOpen(Fnam,FILE_WRITE|FILE_TXT|FILE_ANSI); if(Fhandle<0) { Print(__FUNCTION__,": Error! FileOpen() error."); return; } FileSeek(Fhandle,0,SEEK_SET); // if file exists } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(y); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("%.5g,",y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("%.5g]},\n",y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double &y[],string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y[i]); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y[n-1]); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| AddGraph | //+------------------------------------------------------------------+ int CLinDraw::AddGraph(double &x[],double y,string type,string name,int w=0,string col="") { int i,k,n; string str; if(Fhandle<0)return(-1); if(Num==0) { str="$(document).ready(function(){\n" "var lp=new Highcharts.Chart({\n" "chart:{renderTo:'lplot'},\n" "title:{text:'"+Tit+"'},\n" "subtitle:{text:'"+SubTit+"'},\n" "legend:{enabled:"+Leg+"},\n" "yAxis:{title:{text:'"+Ytit+"'}},\n" "xAxis:{title:{text:'"+Xtit+"'},showLastLabel:true},\n" "series:[\n"; FileWriteString(Fhandle,str); } n=ArraySize(x); str="{type:'"+type+"',name:'"+name+"',"; if(col!="")str+="color:'rgba("+col+")',"; if(w!=0)str+="lineWidth:"+(string)w+","; str+="data:["; k=0; for(i=0;i<n-1;i++) { str+=StringFormat("[%.5g,%.5g],",x[i],y); if(20<k++){k=0; str+="\n";} } str+=StringFormat("[%.5g,%.5g]]},\n",x[n-1],y); FileWriteString(Fhandle,str); Num++; return(0); } //+------------------------------------------------------------------+ //| LDraw | //+------------------------------------------------------------------+ int CLinDraw::LDraw(int ashow=1) { int i,k; string pfnam,to,p[]; FileWriteString(Fhandle,"]});\n});"); if(Fhandle<0)return(-1); FileClose(Fhandle); pfnam=TerminalInfoString(TERMINAL_DATA_PATH)+"\\MQL5\\Files\\"+Fnam; k=StringSplit(MQL5InfoString(MQL5_PROGRAM_PATH),StringGetCharacter("\\",0),p); to=""; for(i=0;i<k-1;i++)to+=p[i]+"\\"; to+="ChartTools\\"; // Folder name DeleteFileW(to+Fnam); MoveFileW(pfnam,to+Fnam); if(ashow==1)ShellExecuteW(NULL,"open",to+"LinDraw.htm",NULL,NULL,1); return(0); }
Bu sınıfın düzgün çalışmasını istiyorsak, JavaScript kitaplıkları uygulanmış hazır bir HTML sayfasına ihtiyacımız var. Yapı grafikleri için alanın boyutu ve konumu da belirtilmelidir. Böyle bir sayfa uygulaması örneği, bu makaleye ekli dosyalarda bulunabilir.
Bir metin dosyasında AddGraph() yöntemi çağrıldığında, uygun bir JavaScript kodu oluşturulur. Ardından, metin dosyası önceden oluşturulmuş HTML sayfasına dahil edilir. Bahsedilen kod, grafik kitaplığına başvurur ve bağımsız değişken olarak AddGraph() yöntemine gönderilen verileri kullanarak bir grafiğin oluşturulmasını sağlar. Bu yöntem tekrar çağrılırken çıkış alanına bir veya birkaç grafik daha eklenebilir.
AddGraph() aşırı yüklenmiş işlevinin üç sürümü CLinDraw sınıfına dahil edilmiştir. Sürümlerden biri, görüntülenen verilere sahip yalnızca bir dizinin bağımsız değişken olarak kendisine aktarılmasını gerektirir. Bu, dizi öğesi indeksinin X ekseninde görüntülendiği bir dizi grafiği oluşturmak için tasarlanmıştır.
İkinci sürüm, bağımsız değişken olarak iki dizi alır. Bu diziler sırasıyla X ve Y ekseninde görüntülenen değerleri içerir. Üçüncü sürüm, Y ekseni için sabit bir değer ayarlanmasına olanak tanır. Bu, yatay bir çizgi oluşturmak için kullanılabilir. Bu işlevlerin kalan bağımsız değişkenleri benzerdir:
- dize türü – görüntülenen grafik türü. "çizgi", "eğri" ve "dağılım" değerlerine sahip olabilir;
- dize adı – grafiğe atanan ad;
- int w=0 – çizgi genişliği. İsteğe bağlı bağımsız değişken. Değer 0 ise, varsayılan genişlik değeri olan 2 kullanılır;
- dize sütunu="" – çizgi rengini ve opaklık değerini ayarlar. İsteğe bağlı bağımsız değişken.
LDraw() yöntemi en son çağrılmalıdır. Bu yöntem, JavaScript kodunun çıktısını ve varsayılan olarak \MQL5\Files\ içinde oluşturulan metin dosyasındaki verileri tamamlar. Daha sonra dosya, grafik kitaplığı dosyalarını ve HTML dosyasını içeren dizine taşınır.
LDraw() yöntemi tek bir isteğe bağlı bağımsız değişkene sahip olabilir. Bağımsız değişken değeri ayarlanmazsa veya bir olarak ayarlanırsa, varsayılan bir web tarayıcısı çağrılacak ve veri dosyası uygun bir dizine taşındıktan sonra grafik görüntülenecektir. Bağımsız değişkenin başka bir değeri varsa, veri dosyası da tamamen oluşturulacak ancak bir web tarayıcısı otomatik olarak çağrılmayacaktır.
Diğer mevcut CLinDraw sınıfı yöntemleri, grafik başlıklarının ve eksen etiketlerinin ayarlanmasına olanak tanır. Highcharts kitaplığı ve CLinDraw sınıfı uygulama konularını bu makalede ayrıntılı olarak ele almayacağız. Highcharts grafik kitaplığı ile ilgili kapsamlı bilgi [19]'da, grafikler ve diyagramlar oluşturmak için uygulama örnekleri [9], [20]'de bulunabilir.
CLinDraw sınıfının normal çalışması için terminalde harici kitaplıkların kullanımına izin verilmelidir.
8. Yoğunluk Tahmini ve Dosya Düzenlemesi Örneği
Sonunda üç sınıfımız oldu - CKDensity, CSJPlugin ve CLinDraw.
Aşağıda, sınıfların nasıl kullanılabileceğini gösteren örneğin kaynak kodu bulunmaktadır.
//+------------------------------------------------------------------+ //| KDE_Example.mq5 | //| 2012, victorg | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "2012, victorg" #property link "https://www.mql5.com" #include "CKDensity.mqh" #include "ChartTools\CLinDraw.mqh" //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { int i,n; double a; int ndata=1000; // Input data length double X[]; // Array for data double Z[]; // Array for graph of a Laplace distribution double Sc[]; // Array for scatter plot //-------------------------- Preparation of the input sequence ArrayResize(X,ndata+1); i=CopyOpen(_Symbol,PERIOD_CURRENT,0,ndata+1,X); if(i!=ndata+1) { Print("Not enough historical data."); return; } for(i=0;i<ndata;i++)X[i]=MathLog(X[i+1]/X[i]); // Logarithmic returns ArrayResize(X,ndata); //-------------------------- Kernel density estimation CKDensity *kd=new CKDensity; kd.PluginMode(1); // Enable Plug-in mode kd.Density(X); // Density estimation //-------------------------- Graph of a Laplace distribution n=kd.Np; // Number of test point ArrayResize(Z,n); for(i=0;i<n;i++) { a=MathAbs(kd.T[i]*M_SQRT2); Z[i]=0.5*MathExp(-a)*M_SQRT2; } //-------------------------- Scatter plot n=kd.N; // Data length if(n<400) { ArrayResize(Sc,n); for(i=0;i<n;i++)Sc[i]=kd.X[i]; } else // Decimation of data { ArrayResize(Sc,400); for(i=0;i<400;i++) { a=i*(n-1.0)/399.0+0.5; Sc[i]=kd.X[(int)a]; } } //-------------------------- Visualization CLinDraw *ld=new CLinDraw; ld.Title("Kernel Density Estimation"); ld.SubTitle(StringFormat("Data lenght=%i, h=%.3f",kd.N,kd.H)); ld.YTitle("density"); ld.XTitle("normalized X (mean=0, variance=1)"); ld.AddGraph(kd.T,Z,"line","Laplace",1,"200,120,70,1"); ld.AddGraph(kd.T,kd.Y,"line","Estimation"); ld.AddGraph(Sc,-0.02,"scatter","Data",0,"0,4,16,0.4"); ld.LDraw(); // With WEB-browser autostart // ld.LDraw(0); // Without autostart delete(ld); delete(kd); }
Olasılık yoğunluk fonksiyonunun değerlendirmesinin yapılacağı veriler KDE_Example.mq5 script dosyasının başlangıcında hazırlanır. Bunu gerçekleştirmek için, mevcut sembol ve dönemin "open" değerleri X[] dizisine kopyalanır. Logaritmik getiriler daha sonra bunlara göre hesaplanır.
Sonraki adım, CKDensity sınıfının bir kopyasının oluşturulmasıdır. PluginMode() yöntemini çağırmak, h aralığı değerlendirmesi için SJPI yönteminin kullanılmasına olanak tanır. Daha sonra X[] dizisinde oluşturulan dizi için yoğunluk tahmini yapılır. Bu adımda değerlendirme süreci tamamlanır. Diğer tüm adımlar, elde edilen yoğunluk tahmininin görselleştirilmesi ile ilgilidir.
Elde edilen tahminler, iyi bilinen herhangi bir dağılım yasasıyla karşılaştırılmalıdır. Bunun için, Z[] dizisinde Laplace dağılım yasasına karşılık gelen değerler oluşturulur. Normalleştirilmiş ve sıralanmış giriş verileri daha sonra Sc[] dizisinde depolanır. Giriş dizisi uzunluğu 400 öğeyi aşarsa, tüm değerleri Sc[]'ye dahil edilmeyecektir. Bunların bazıları atlanacaktır. Bu nedenle, Sc[] dizi boyutu hiçbir zaman 400'den fazla öğe içermeyecektir.
Görüntülemek için gerekli tüm veriler hazırlandıktan sonra CLinDraw sınıfının bir kopyası oluşturulur. Daha sonra başlıklar belirlenir ve AddGraph() yöntemi kullanılarak gerekli grafikler eklenir.
Birincisi, bir şablon olması amaçlanan Laplace dağılım yasası grafiğidir. Bunu, giriş verileri kullanılarak elde edilen yoğunluk tahmininin grafiği takip eder. Kaynak veri grubunu gösteren alt grafik en son eklenir. Görüntüleme için gerekli tüm öğeler tanımlandıktan sonra LDraw() yöntemi çağrılır.
Sonuç olarak, Şekil 7'de gösterilen grafiği elde ederiz.
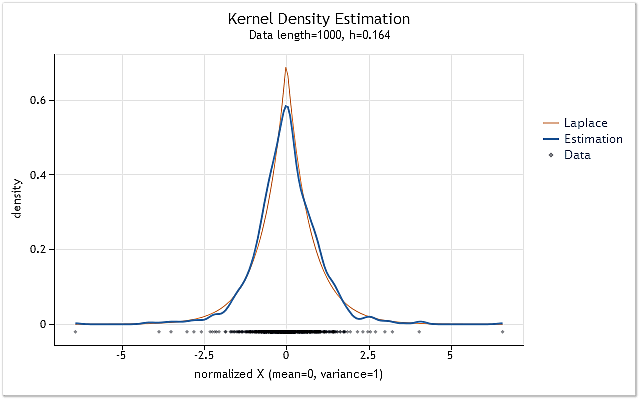
Şek. 7. Logaritmik getiriler için yoğunluk tahmini (USDJPY, Günlük)
Şekil 7'de gösterilen tahmin USDJPY, Günlük için logaritmik getirilerin 1 000 değeri için yapılmıştır. Gördüğümüz gibi, tahmin Laplace dağılımına karşılık gelen eğriye çok benzerdir.
Yoğunluk tahmini ve görselleştirme için gerekli tüm dosyalar aşağıdaki KDEFiles.zip arşivinde bulunmaktadır. Arşiv, aşağıdaki dosyaları içerir:
- DensityEstimation\ChartTools\CLinDraw.mqh – highcharts.js ile etkileşim sınıfı,
- DensityEstimation\ChartTools\highcharts.js - Highcharts JS v2.2.0 kitaplığı (2012-02-16),
- DensityEstimation\ChartTools\jquery.js – jQuery v1.7.1 kitaplığı,
- DensityEstimation\ChartTools\LinDraw.htm – Görüntülemek için HTML sayfası,
- DensityEstimation\CKDensity.mqh – yoğunluk tahminini uygulayan sınıf,
- DensityEstimation\CSJPlugin.mqh – optimum aralık değeri tahmininin SJPI yöntemini uygulayan sınıf,
- DensityEstimation\KDE_Example.mq5 – logaritmik getiriler için yoğunluk tahmini örneği.
Arşivi açtıktan sonra, tüm içeriğiyle birlikte DensityEstimation\ dizini, terminalin Script Dosyaları (veya Göstergeler) dizinine yerleştirilmelidir. Daha sonra KDE_Example.mq5'i hemen derlemek ve başlatmak mümkündür. Gerekirse, DensityEstimation dizini yeniden adlandırılabilir. Bu, programın çalışmasını etkilemeyecektir.
CLinDraw sınıfının normal çalışması için terminalde harici kitaplıkların kullanımına izin verilmesi gerektiği tekrar belirtilmelidir.
DensityEstimation\ dizini, tahmin sonuçlarını görselleştirmek için gerekli tüm bileşenleri içeren ChartTools\ alt dizinini içerir. Görselleştirme dosyaları ayrı bir alt dizinde bulunur; böylece DensityEstimation\ dizininin içeriği kolayca görülebilir. ChartTools\ alt dizin adı doğrudan kaynak kodlarında belirtilir. Bu nedenle, bunun, yeniden adlandırılmaması gerekir, aksi takdirde kaynak kodlarında değişiklik yapılması gerekecektir.
Metin dosyasının görselleştirme sırasında oluşturulduğundan daha önce bahsetmiştik. Bu dosya, grafikler oluşturmak için gerekli verileri içerir. Bu dosya, başlangıçta terminalin özel bir Dosyalar dizininde oluşturulur. Ancak daha sonra belirtilen ChartTools dizinine taşınır. Böylece, Files\ veya başka herhangi bir terminal dizininde test örneği faaliyetimizin hiçbir izi kalmayacak. Bu nedenle, bu makalenin yüklü dosyalarını tamamen kaldırmak için DensityEstimation dizinini tüm içeriğiyle birlikte silebilirsiniz.
Sonuç
Bazı belirli yöntemlerin özünü açıklayan matematiksel ifadeler makaleye dahil edilmiştir . Bu, okumayı basitleştirmek amacıyla kasıtlı olarak yapılmıştır. Gerekirse, tüm matematiksel hesaplamalar çok sayıda yayında bulunabilir. Bazılarının bağlantıları aşağıda verilmiştir.
Makalede verilen kaynak kodları ciddi testlere tabi tutulmamıştır. Bu nedenle, bunlar, tamamen işlevsel uygulamalar olarak değil, yalnızca örnek olarak değerlendirilmelidir.
Referanslar
- Histogram.
- Çekirdek yoğunluk tahmini.
- Çekirdek yumuşatıcı.
- Beklenti-maksimizasyon algoritması.
- А.V. Batov, V.Y. Korolyov, А.Y. Korchagin. Parametrik Olmayan Yoğunluk Tahminleri Oluşturma Aracı Olarak Çok Sayıda Bileşene Sahip EM-Algoritması (Rusça).
- Hardle W. Uygulanan Parametrik Olmayan Regresyon.
- Çekirdek (istatistik).
- HTML'de grafikler ve diyagramlar.
- Simon J. Sheather. (2004). Yoğunluk Tahmini.
- Max Kohler, Anja Schindler, Stefan Sperlich. (2011). Çekirdek Regresyonu için Bant Genişliği Seçim Yöntemlerinin İncelenmesi ve Karşılaştırması.
- Clive R. Loader. (1999). Bant Genişliği Seçimi: Klasik mi, Eklenti mi?.
- S. J. Sheather, M. C. Jones. (1991). Çekirdek Yoğunluğu Tahmini için Güvenilir Veri Tabanlı Bant Genişliği Seçim Yöntemi.
- Newton yöntemi.
- Veri gruplama.
- Changjiang Yang, Ramani Duraiswami and Larry Davis. (2004). İyileştirilmiş Hızlı Gauss Dönüşümünü Kullanan Verimli Çekirdek Makineleri.
- Tek değişkenli KDE için hızlı optimum bant genişliği tahmini.
- R.J. Karunamuni and T. Alberts. (2005). Çekirdek Yoğunluğu Tahmininde Sınır Düzeltmenin Yerel Olarak Uyarlanabilir Dönüşüm Yöntemi.
- Highcharts JS.
- Analysis of the Main Characteristics of Time Series.
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/396
Algoritmik ticaret makaleniz için 200 USD kazanın!
İstatistik Temelleri
Kapsamlı Olmayan İstatistiksel Dağılımların Yapısal Analizine Öz-Koordinatlar Yönteminin Uygulanması
MQL5.community'de Kim Kimdir?
- Ücretsiz ticaret uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz