İstatistiksel Tahminler
88
0
Tanıtım
Nowadys, ekonometri, fiyat serilerinin tahmini, bir modelin seçimi ve yeterliliğinin tahmin edilmesi vb. konularda yazılmış makale ve yayınlara sıklıkla rastlayabilirsiniz. Ancak çoğu durumda, akıl yürütme, bir okuyucunun matematik istatistik yöntemlerine aşina olduğu ve analiz edilen bir dizinin istatistiksel parametrelerini kolayca tahmin edebileceği varsayımına dayanır.
Matematiksel model ve yöntemlerin çoğu farklı varsayımlara dayandığı için bir dizinin istatistiksel parametrelerinin tahmini çok önemlidir. Örneğin, dağılım yasasının normalliği veya ayrılma değeri veya diğer parametreler. Bu nedenle, zaman serilerini analiz ederken ve tahmin ederken, ana istatistiksel parametreleri hızlı ve net bir şekilde tahmin etmeye izin veren basit ve kullanışlı bir araca ihtiyacımız var. Bu yazıda böyle bir araç oluşturmaya çalışacağız.
Makale, rastgele bir dizinin en basit istatistiksel parametrelerini ve görsel analizinin çeşitli yöntemlerini kısaca açıklamaktadır. Bu yöntemlerin MQL5'te uygulanmasını ve Gnuplot uygulamasını kullanarak hesaplama sonuçlarının görselleştirilmesi yöntemlerini sunar. Bu makale hiçbir şekilde bir kılavuz veya referans olarak gösterilmemiştir; bu nedenle terminoloji ve tanımlarla ilgili kabul edilen bazı aşinalıkları içerebilir.
Bir Numune Üzerindeki Parametreleri Analiz Etme
Ayrık örnekler dizisi olarak temsil edilebilecek, zaman içinde sonsuzca var olan durağan bir süreç olduğunu varsayalım. Bu örnek dizisine genel popülasyon diyelim. Genel popülasyondan seçilen örneklerin bir kısmına genel popülasyondan örnekleme veya N örnekleri örneklemesi adı verilecektir. Buna ek olarak, bildiğimiz hiçbir gerçek parametre olmadığını varsayalım, bu nedenle onları sonlu bir örnekleme temelinde tahmin edeceğiz.
Aykırı Değerlerden Kaçınmak
Parametrelerin istatistiksel tahminine başlamadan önce, örnekleme büyük hatalar (aykırı değerler) içeriyorsa, tahminin doğruluğunun yetersiz olabileceğine dikkat etmeliyiz. Örnekleme küçük bir hacme sahipse, aykırı değerlerin tahminlerin doğruluğu üzerinde büyük bir etkisi vardır. Aykırı değerler, dağılımın ortasından anormal şekilde ayrılan değerlerdir. Bu tür sapmalar, istatistiksel verilerin toplanmasında ve dizilimin oluşturulmasında ortaya çıkan, pek olası olmayan farklı olaylardan ve hatalardan kaynaklanabilir.
Çoğu durumda bir değerin aykırı değer olup olmadığını veya analiz edilen sürece ait olup olmadığını açıkça tespit etmek imkansız olduğu için aykırı değerlerin filtrelenip filtrelenmeyeceğine karar vermek zordur. Yani aykırı değerler tespit edilirse ve onları filtrelemeye karar verilirse, o zaman bir soru ortaya çıkar - bu hata değerleriyle ne yapmalıyız? En mantıklı değişken, istatistiksel özelliklerin tahmininin doğruluğunu artırabilecek olan örneklemeden hariç tutmaktır; ancak zaman dizileriyle çalışırken örneklemeden aykırı değerleri hariç tutma konusunda dikkatli olmalısınız.
Aykırı değerleri bir örneklemeden hariç tutmak veya en azından tespit etmek için, S.V. Bulashev tarafından yazılan "Satıcılar için İstatistikler" kitabında açıklanan algoritmayı uygulayalım. Bulashev.
Bu algoritmaya göre, dağıtım merkezinin beş tahmin değerini hesaplamamız gerekiyor:
- Medyan;
- %50 çeyrekler arası aralığın merkezi (orta çeyrek aralığı, MQR);
- Tüm örneklemenin aritmetik ortalaması;
- %50 çeyrekler arası aralıkta aritmetik ortalama (çeyrekler arası ortalama, IQM);
- Aralık merkezi (orta aralık) - bir örneklemedeki maksimum ve minimum değerin ortalama değeri olarak belirlenir.
Daha sonra dağılım merkezinin tahmin sonuçları artan düzende sıralanır; ve daha sonra ortalama değer veya üçüncüsü, Xcendağıtım merkezi olarak seçilir. Bu nedenle, seçilen tahminin aykırı değerlerden minimum düzeyde etkilendiği görülmektedir.
Ayrıca, Xcen dağıtım merkezinin elde edilen tahminini kullanarak, ampirik formüle göre standart sapma s, fazla K ve sansür oranını hesaplayalım:
burada N, örneklemedeki örnek sayısıdır (örnekleme hacmi).
Ardından aralığın dışında kalan değerler:
aykırı değer olarak sayılacağı için örnekleme dışında bırakılmalıdır.
Bu yöntem "Satıcılar için İstatistikler" kitabında ayrıntılı olarak açıklanmıştır, bu yüzden doğrudan algoritmanın uygulanmasına geçelim. Aykırı değerleri tespit etmeye ve dışlamaya izin veren algoritma, erremove() işlevinde uygulanır.
Aşağıda bu fonksiyonu test etmek için yazılmış betiği bulabilirsiniz.
//---------------------------------------------------------------------------- // erremove.mq5 // Copyright 2011, MetaQuotes Software Corp. // https://www.mql5.com //---------------------------------------------------------------------------- #property copyright "Copyright 2011, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #import "shell32.dll" bool ShellExecuteW(int hwnd,string lpOperation,string lpFile, string lpParameters,string lpDirectory,int nShowCmd); #import //---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[100]; double y[]; srand(1); for(i=0;i<ArraySize(dat);i++)dat[i]=rand()/16000.0; dat[25]=3; // Make Error !!! erremove(dat,y,1); } //---------------------------------------------------------------------------- int erremove(const double &x[],double &y[],int visual=1) { int i,m,n; double a[],b[5]; double dcen,kurt,sum2,sum4,gs,v,max,min; if(!ArrayIsDynamic(y)) // Error { Print("Function erremove() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function erremove() error!"); return(-1); } ArrayResize(a,n); ArrayCopy(a,x); ArraySort(a); b[0]=(a[0]+a[n-1])/2.0; // Midrange m=(n-1)/2; b[1]=a[m]; // Median if((n&0x01)==0)b[1]=(b[1]+a[m+1])/2.0; m=n/4; b[2]=(a[m]+a[n-m-1])/2.0; // Midquartile range b[3]=0; for(i=m;i<n-m;i++)b[3]+=a[i]; // Interquartile mean(IQM) b[3]=b[3]/(n-2*m); b[4]=0; for(i=0;i<n;i++)b[4]+=a[i]; // Mean b[4]=b[4]/n; ArraySort(b); dcen=b[2]; // Distribution center sum2=0; sum4=0; for(i=0;i<n;i++) { a[i]=a[i]-dcen; v=a[i]*a[i]; sum2+=v; sum4+=v*v; } if(sum2<1.e-150)kurt=1.0; kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)*(n-1.0)/(n-2.0)/(n-3.0); // Kurtosis if(kurt<1.0)kurt=1.0; gs=(1.55+0.8*MathLog10((double)n/10.0)*MathSqrt(kurt-1))*MathSqrt(sum2/(n-1)); max=dcen+gs; min=dcen-gs; m=0; for(i=0;i<n;i++)if(x[i]<=max&&x[i]>=min)a[m++]=x[i]; ArrayResize(y,m); ArrayCopy(y,a,0,0,m); if(visual==1)vis(x,dcen,min,max,n-m); return(n-m); } //---------------------------------------------------------------------------- void vis(const double &x[],double dcen,double min,double max,int numerr) { int i; double d,yma,ymi; string str; yma=x[0];ymi=x[0]; for(i=0;i<ArraySize(x);i++) { if(yma<x[i])yma=x[i]; if(ymi>x[i])ymi=x[i]; } if(yma<max)yma=max; if(ymi>min)ymi=min; d=(yma-ymi)/20.0; yma+=d;ymi-=d; str="unset key\n"; str+="set title 'Sequence and error levels (number of errors = "+ (string)numerr+")' font ',10'\n"; str+="set yrange ["+(string)ymi+":"+(string)yma+"]\n"; str+="set xrange [0:"+(string)ArraySize(x)+"]\n"; str+="plot "+(string)dcen+" lt rgb 'green',"; str+=(string)min+ " lt rgb 'red',"; str+=(string)max+ " lt rgb 'red',"; str+="'-' with line lt rgb 'dark-blue'\n"; for(i=0;i<ArraySize(x);i++)str+=(string)x[i]+"\n"; str+="e\n"; if(!saveScript(str)){Print("Create script file error");return;} if(!grPlot())Print("ShellExecuteW() error"); } //---------------------------------------------------------------------------- bool grPlot() { string pnam,param; pnam="GNUPlot\\binary\\wgnuplot.exe"; param="-p MQL5\\Files\\gplot.txt"; return(ShellExecuteW(NULL,"open",pnam,param,NULL,1)); } //---------------------------------------------------------------------------- bool saveScript(string scr1="",string scr2="") { int fhandle; fhandle=FileOpen("gplot.txt",FILE_WRITE|FILE_TXT|FILE_ANSI); if(fhandle==INVALID_HANDLE)return(false); FileWriteString(fhandle,"set terminal windows enhanced size 560,420 font 8\n"); FileWriteString(fhandle,scr1); if(scr2!="")FileWriteString(fhandle,scr2); FileClose(fhandle); return(true); } //----------------------------------------------------------------------------
Şimdi erremove() fonksiyonuna detaylı bir göz atalım. Fonksiyonun ilk parametresi olarak, analiz edilen örneklemenin değerlerinin saklandığı x[] dizisinin adresini geçiyoruz; örnekleme hacmi en az dört element olmalıdır. x[] dizisinin boyutunun örnekleme boyutuna eşit olduğu varsayılır, bu nedenle örneklemenin hacminin N değeri geçilmez. x[] dizisinde bulunan veriler, işlevin yürütülmesi sonucunda değişmez.
Sonraki parametre y[] dizisinin adresidir. İşlevin başarılı bir şekilde yürütülmesi durumunda, bu dizi, aykırı değerlerin hariç tutulduğu giriş dizisini içerecektir. y[] dizisinin boyutu, örneklemeden hariç tutulan değerlerin sayısıyla x[] dizisinin boyutundan küçüktür. y[] dizisi dinamik olarak bildirilmelidir, aksi takdirde işlevin gövdesinde boyutunu değiştirmek imkansız olacaktır.
Son (isteğe bağlı) parametre, hesaplama sonuçlarının görselleştirilmesinden sorumlu olan bayraktır. Değeri bire eşitse (varsayılan değer), fonksiyonun yürütülmesinin bitiminden önce aşağıdaki bilgileri gösteren grafik ayrı bir pencerede çizilecektir: giriş sırası, dağıtım merkezi çizgisi ve aralık sınırları, dışındaki değerler aykırı değer olarak kabul edilecektir.
Grafik çizme yöntemi daha sonra açıklanacaktır. Başarılı yürütme durumunda, işlev örneklemeden hariç tutulan değerlerin sayısını döndürür; hata durumunda -1 döndürür. Hata değeri (aykırı değerler) bulunmazsa, işlev 0 döndürür ve y[] dizisindeki dizi x[] ile aynı olur.
Fonksiyonun başlangıcında, bilgi x[]'den a[] dizisine kopyalanır, daha sonra artan düzende sıralanır ve ardından dağıtım merkezinin beş tahmini yapılır.
Aralığın ortası (orta aralık), sıralanmış a[] dizisinin uç değerlerinin toplamının ikiye bölünmesiyle belirlenir.
Medyan, N örneğinin tek hacimleri için aşağıdaki gibi hesaplanır:
ve örneklemenin eşit hacimleri için:
a[] sıralı dizisinin dizinlerinin sıfırdan başladığını düşünürsek, şunu elde ederiz:
m=(n-1)/2; median=a[m]; if((n&0x01)==0)b[1]=(median+a[m+1])/2.0;
%50 çeyrekler arası aralığın ortası (orta çeyrek aralığı, MQR):
burada M=N/4 (tamsayı bölümü).
a[] sıralı dizisi için şunu elde ederiz:
m=n/4; MQR=(a[m]+a[n-m-1])/2.0; // Midquartile range
%50 çeyrekler arası aralığın aritmetik ortalamaları (çeyrekler arası ortalama, IQM). Numunelerin %25'i numunenin her iki tarafından kesilir ve kalan %50 aritmetik ortalamanın hesaplanması için kullanılır:
burada M=N/4 (tamsayı bölümü).
m=n/4; IQM=0; for(i=m;i<n-m;i++)IQM+=a[i]; IQM=IQM/(n-2*m); // Interquartile mean(IQM)
Aritmetik ortalama (ortalama), tüm örnekleme için belirlenir.
Belirlenen değerlerin her biri b[] dizisine yazılır ve ardından dizi artan düzende sıralanır. Dağıtımın merkezi olarak b[2] dizisinin bir eleman değeri seçilir. Ayrıca, bu değeri kullanarak, aritmetik ortalamanın ve fazlalık katsayısının yansız tahminlerini hesaplayacağız; hesaplama algoritması daha sonra açıklanacaktır.
Elde edilen tahminler, sansür katsayısının hesaplanması ve aykırı değerlerin tespit edilmesi için aralığın sınırlarının hesaplanması için kullanılır (ifadeler yukarıda gösterilmiştir). Sonunda, y[] dizisinde hariç tutulan aykırı değerlere sahip dizi oluşturulur ve grafiğin çizilmesi için vis() işlevleri çağrılır. Bu yazıda kullanılan görselleştirme yöntemine kısaca bir göz atalım.
Görselleştirme
Hesaplama sonuçlarını görüntülemek için, çeşitli 2D ve 3D grafikler oluşturmaya yönelik ücretsiz bir uygulama olan gnuplot'u kullanıyorum. Gnuplot, grafikleri ekranda (ayrı bir pencerede) görüntüleme veya farklı grafik formatlarında bir dosyaya yazma olanağına sahiptir. Çizim çizelgelerinin komutları, önceden hazırlanmış bir metin dosyasından yürütülebilir. Gnuplot projesinin resmi web sayfası: gnuplot.sourceforge.net. Uygulama çoklu platformdur ve hem kaynak kod dosyaları hem de belirli bir platform için derlenmiş ikili dosyalar olarak dağıtılır.
Bu makale için yazılan örnekler, Windows XP SP3 ve gnuplot'un 4.2.2 sürümü altında test edilmiştir. gp442win32.zip dosyası http://sourceforge.net/projects/gnuplot/files/gnuplot/4.4.2/ adresinden indirilebilir. Örnekleri gnuplot'un diğer sürümleri ve yapıları ile test etmedim.
gp442win32.zip arşivini indirdikten sonra, sıkıştırılmış dosyayı açın. Sonuç olarak, \gnuplot klasörü oluşturulur, uygulamayı, yardım dosyasını, belgeleri ve örnekleri içerir. Uygulamalarla etkileşim kurmak için, \gnuplot klasörünün tamamını MetaTrader 5 istemci terminalinizin kök klasörüne koyun.
Şekil 1. \gnuplot klasörünün yerleştirilmesi
Klasör taşındığında, gnuplot uygulamasının çalışabilirliğini değiştirebilirsiniz. Bunu yapmak için, \gnuplot\binary\wgnuplot.exe dosyasını çalıştırın ve ardından "gnuplot>" komut istemi göründüğünde "plot sin(x)" komutunu yazın. Sonuç olarak, içinde sin(x) fonksiyonunun çizildiği bir pencere görünmelidir. Ayrıca uygulama tesliminde yer alan örnekleri deneyebilirsiniz; bunu yapmak için File\Demos öğesini seçin ve \gnuplot\demo\all.dem dosyasını seçin.
Şimdi erremove.mq5 betiğini başlattığınızda, şekil 2'de gösterilen grafik ayrı bir pencerede çizilecektir:
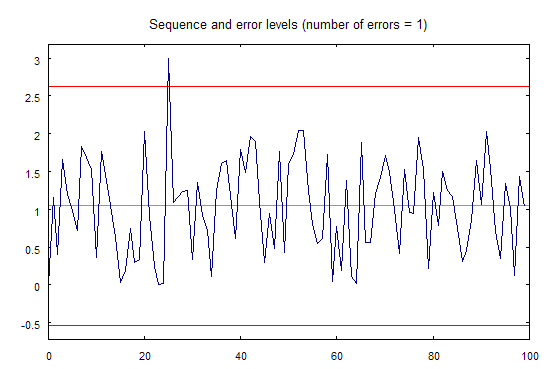
Şekil 2. erremove.mq5 komut dosyası kullanılarak çizilen grafik.
Makalenin devamında, program ve kontrolleri hakkındaki bilgiler, programla birlikte verilen belgelerde ve http://gnuplot.ikir.ru/ gibi çeşitli web sitelerinde kolayca bulunabileceğinden, gnuplot kullanmanın bazı özelliklerinden biraz bahsedeceğiz.
Bu makale için yazılmış program örnekleri, çizelgeleri çizmek için gnuplot ile en basit etkileşim yöntemini kullanır. İlk başta, gplot.txt metin dosyası oluşturulur; gnuplot komutlarını ve görüntülenecek bilgileri içerir. Ardından, komut satırında argüman olarak iletilen dosyanın adı ile wgnuplot.exe uygulaması başlatılır. wgnuplot.exe uygulaması, Shell32.dll sistem kitaplığından içe aktarılan ShellExecuteW() işlevi kullanılarak çağrılır; istemci terminalinde harici dll'lerin içe aktarılmasına izin verilmesinin nedeni budur.
Verilen gnuplot sürümü, iki tip terminal için ayrı bir pencerede çizelgeler çizmeye izin verir: wxt ve windows. wxt terminali, grafiklerin çizilmesi için kenar yumuşatma algoritmalarını kullanır; bu, windows terminaline kıyasla daha yüksek kaliteli bir resim elde edilmesini sağlar. Ancak, bu makalenin örneklerini yazmak için windows terminali kullanıldı. Bunun nedeni, Windows terminali ile çalışırken, "wgnuplot.exe -p MQL5\\Files\\gplot.txt" çağrısı ve bir grafik penceresinin açılması sonucunda oluşturulan sistem işleminin pencere kapatıldığında otomatik olarak yok edilmesidir.
Wxt terminalini seçerseniz, grafik penceresini kapattığınızda, wgnuplot.exe sistem işlemi otomatik olarak kapanmaz. Bu nedenle, wxt terminalini kullanırsanız ve wgnuplot.exe'yi yukarıda açıklandığı gibi birçok kez çağırırsanız, sistemde herhangi bir faaliyet belirtisi olmayan birden fazla işlem birikebilir. "wgnuplot.exe -p MQL5\\Files\\gplot.txt" çağrısını ve windows terminalini kullanarak, istenmeyen ek pencerelerin açılmasını ve kapatılmamış sistem işlemlerinin görünmesini önleyebilirsiniz.
Grafiğin görüntülendiği pencere etkileşimlidir ve fare tıklaması ve klavye olaylarını işler. Varsayılan kısayol tuşları hakkında bilgi almak için wgnuplot.exe'yi çalıştırın, "terminal pencerelerini ayarla" komutunu kullanarak bir terminal türü seçin ve örneğin "plot sin(x)" komutunu kullanarak herhangi bir grafiği çizin. Grafik penceresi etkinse (odakta), "h" düğmesine basar basmaz wgnuplot.exe'nin metin penceresinde görüntülenen bir ipucu görürsünüz.
Parametrelerin Tahmini
Grafik çizme yöntemiyle kısa bir tanışmadan sonra, sonlu örnekleme temelinde genel popülasyonun parametrelerinin tahminine dönelim. Genel popülasyonun istatistiksel parametrelerinin bilinmediğini varsayarsak, bu parametrelerin sadece yansız tahminlerini kullanacağız.
Matematiksel beklenti tahmini veya örnekleme ortalaması, bir dizinin dağılımını belirleyen ana parametre olarak kabul edilebilir. Örnekleme ortalaması aşağıdaki formül kullanılarak hesaplanır:
burada N, örneklemedeki örnek sayısıdır.
Ortalama değer, dağıtım merkezinin bir tahminidir ve bu parametreyi özellikle önemli kılan, merkezi momentlerle bağlantılı diğer parametrelerin hesaplanması için kullanılır. Ortalama değere ek olarak, istatistiksel parametreler olarak dağılım (dağılım, varyans), standart sapma, eğrilik katsayısı (eğrilik) ve fazlalık katsayısı (basıklık) tahminini kullanacağız.
burada m merkezi anlardır.
Merkezi momentler, genel bir popülasyonun dağılımının sayısal özellikleridir.
İkinci, üçüncü ve dördüncü seçici merkezi momentler aşağıdaki ifadelerle belirlenir:
Ancak bu değerler tarafsızdır. Burada k-Statistic ve h-Statistic.htmlh-Statistic'ten bahsetmeliyiz. Belirli koşullar altında, merkezi momentlerin yansız tahminlerinin elde edilmesini sağlarlar, böylece yansız dağılım, standart sapma, eğrilik ve basıklık tahminlerinin hesaplanmasında kullanılabilirler.
k ve h tahminlerinde dördüncü momentin hesaplanmasının farklı şekillerde yapıldığını unutmayın. k veya h kullanıldığında basıklık tahmini için farklı ifadelerin elde edilmesiyle sonuçlanır. Örneğin, Microsoft Excel'de fazlalık, k-tahminlerinin kullanımına karşılık gelen formül kullanılarak hesaplanır ve "Satıcılar için İstatistikler" kitabında, basıklığın yansız tahmini, h-tahminleri kullanılarak yapılır.
h-tahminlerini seçelim ve daha sonra daha önce verilen ifadede 'm' yerine bunları değiştirerek gerekli parametreleri hesaplayacağız.
Dağılım ve Standart Sapma:
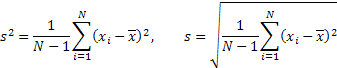
eğrilik:
Basıklık:
Normal dağılım yasasına sahip dizi için verilen ifadeye göre hesaplanan fazlalık (basıklık) katsayısı 3'e eşittir.
Hesaplanan değerden 3 çıkarılarak elde edilen değerin basıklık değeri olarak sıklıkla kullanıldığına dikkat etmelisiniz; böylece elde edilen değer normal dağılım yasasına göre normalleştirilir. İlk durumda bu katsayıya basıklık denir; ikinci durumda buna "fazla basıklık" denir.
Verilen ifadeye göre parametrelerin hesaplanması dStat() işlevinde gerçekleştirilir:
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dStat(const double &x[],statParam &sP) { int i,m,n; double a,b,sum2,sum3,sum4,y[]; ZeroMemory(sP); // Reset sP n=ArraySize(x); if(n<4) // Error { Print("Function dStat() error!"); return(-1); } sP.kurt=1.0; ArrayResize(y,n); ArrayCopy(y,x); ArraySort(y); m=(n-1)/2; sP.median=y[m]; // Median if((n&0x01)==0)sP.median=(sP.median+y[m+1])/2.0; sP.mean=0; for(i=0;i<n;i++)sP.mean+=x[i]; sP.mean/=n; // Mean sum2=0;sum3=0;sum4=0; for(i=0;i<n;i++) { a=x[i]-sP.mean; b=a*a;sum2+=b; b=b*a;sum3+=b; b=b*a;sum4+=b; } if(sum2<1.e-150)return(1); sP.var=sum2/(n-1); // Variance sP.stdev=MathSqrt(sP.var); // Standard deviation sP.skew=n*sum3/(n-2)/sum2/sP.stdev; // Skewness sP.kurt=((n*n-2*n+3)*sum4/sum2/sum2-(6.0*n-9.0)/n)* (n-1.0)/(n-2.0)/(n-3.0); // Kurtosis return(1);dStat() çağrıldığında, x[] dizisinin adresi işleve iletilir. İlk verileri ve parametrelerin hesaplanmış değerlerini içerecek olan statParam yapısının bağlantısını içerir. Dizide dörtten az eleman olduğunda bir hata oluşması durumunda fonksiyon -1 ile döner.
Histogram
dStat() işlevinde hesaplanan parametrelere ek olarak, genel popülasyonun dağılım yasası da bizim için büyük bir ilgi alanıdır. Sonlu örneklemede dağılım yasasını görsel olarak tahmin etmek için bir histogram çizebiliriz. Histogram çizilirken, örneklemenin değer aralığı benzer birkaç bölüme ayrılır. Daha sonra her bölümdeki eleman sayısı hesaplanır (grup frekansları).
Ayrıca, grup frekansları temelinde bir çubuk diyagram çizilir. Buna histogram denir. Aralık genişliğine normalleştirdikten sonra, histogram rastgele bir değerin ampirik bir dağılım yoğunluğunu temsil edecektir. Histogramı çizmek için en uygun bölüm sayısını belirlemek için "Satıcılar için İstatistikler" bölümünde açıklanan ampirik ifadeyi kullanalım:
burada L gerekli bölüm sayısıdır, N örnekleme hacmidir ve e basıklıktır.
Aşağıda, bölüm sayısını belirleyen, her birindeki eleman sayısını hesaplayan ve elde edilen grup frekanslarını normalleştiren dHist()'i bulabilirsiniz.
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dHist(const double &x[],double &histo[],const statParam &sp) { int i,k,n,nbar; double a[],max,s,xmin; if(!ArrayIsDynamic(histo)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } nbar=(sp.kurt+1.5)*MathPow(n,0.4)/6.0; if((nbar&0x01)==0)nbar--; if(nbar<5)nbar=5; // Number of bars ArrayResize(a,n); ArrayCopy(a,x); max=0.0; for(i=0;i<n;i++) { a[i]=(a[i]-sp.mean)/sp.stdev; // Normalization if(MathAbs(a[i])>max)max=MathAbs(a[i]); } xmin=-max; s=2.0*max*n/nbar; ArrayResize(histo,nbar+2); ArrayInitialize(histo,0.0); histo[0]=0.0;histo[nbar+1]=0.0; for(i=0;i<n;i++) { k=(a[i]-xmin)/max/2.0*nbar; if(k>(nbar-1))k=nbar-1; histo[k+1]++; } for(i=0;i<nbar;i++)histo[i+1]/=s; return(1); }
x[] dizisinin adresi işleve iletilir. ilk diziyi içerir. Dizinin içeriği, işlevin yürütülmesinin bir sonucu olarak değişmez. Sonraki parametreler, hesaplanan değerlerin saklanacağı histo[] dinamik dizisine bağlantıdır. Bu dizinin eleman sayısı, hesaplama için kullanılan bölüm sayısı artı iki elemana karşılık gelecektir.
histo[] dizisinin başına ve sonuna sıfır değeri içeren bir eleman eklenir. Son parametre, içinde depolanan parametrelerin önceden hesaplanmış değerlerini içermesi gereken statParam yapısının adresidir. İşleve iletilen histo[] dizisinin dinamik bir dizi olmaması veya x[] girdi dizisinin dörtten az öğe içermesi durumunda, işlev yürütmesini durdurur ve -1 döndürür.
Elde edilen değerlerin histogramını çizdikten sonra, örneklemenin normal dağılım yasasına karşılık gelip gelmediğini görsel olarak tahmin edebilirsiniz. Normal dağılım yasasına uygunluğun daha görsel bir grafik temsili için, histograma ek olarak normal olasılık ölçeği (Normal Olasılık Grafiği) ile bir grafik çizebiliriz.
Normal Olasılık Grafiği
Böyle bir grafiği çizmenin ana fikri, normal dağılıma sahip bir dizinin görüntülenen değerleri aynı doğru üzerinde olacak şekilde X ekseninin gerilmesi gerektiğidir. Bu şekilde normallik hipotezi grafiksel olarak kontrol edilebilir. Bu tür grafikler hakkında daha ayrıntılı bilgiyi burada bulabilirsiniz: "Normal olasılık grafiği" veya "e-Handbook of Statistical Methods".
Normal olasılık grafiğini çizmek için gereken değerleri hesaplamak için aşağıda gösterilen dRankit() işlevi kullanılır.
struct statParam { double mean; double median; double var; double stdev; double skew; double kurt; }; //---------------------------------------------------------------------------- int dRankit(const double &x[],double &resp[],double &xscale[],const statParam &sp) { int i,n; double np; if(!ArrayIsDynamic(resp)||!ArrayIsDynamic(xscale)) // Error { Print("Function dHist() error!"); return(-1); } n=ArraySize(x); if(n<4) // Error { Print("Function dHist() error!"); return(-1); } ArrayResize(resp,n); ArrayCopy(resp,x); ArraySort(resp); for(i=0;i<n;i++)resp[i]=(resp[i]-sp.mean)/sp.stdev; ArrayResize(xscale,n); xscale[n-1]=MathPow(0.5,1.0/n); xscale[0]=1-xscale[n-1]; np=n+0.365; for(i=1;i<(n-1);i++)xscale[i]=(i+1-0.3175)/np; for(i=0;i<n;i++)xscale[i]=ltqnorm(xscale[i]); return(1); } //---------------------------------------------------------------------------- double A1 = -3.969683028665376e+01, A2 = 2.209460984245205e+02, A3 = -2.759285104469687e+02, A4 = 1.383577518672690e+02, A5 = -3.066479806614716e+01, A6 = 2.506628277459239e+00; double B1 = -5.447609879822406e+01, B2 = 1.615858368580409e+02, B3 = -1.556989798598866e+02, B4 = 6.680131188771972e+01, B5 = -1.328068155288572e+01; double C1 = -7.784894002430293e-03, C2 = -3.223964580411365e-01, C3 = -2.400758277161838e+00, C4 = -2.549732539343734e+00, C5 = 4.374664141464968e+00, C6 = 2.938163982698783e+00; double D1 = 7.784695709041462e-03, D2 = 3.224671290700398e-01, D3 = 2.445134137142996e+00, D4 = 3.754408661907416e+00; //---------------------------------------------------------------------------- double ltqnorm(double p) { int s=1; double r,x,q=0; if(p<=0||p>=1){Print("Function ltqnorm() error!");return(0);} if((p>=0.02425)&&(p<=0.97575)) // Rational approximation for central region { q=p-0.5; r=q*q; x=(((((A1*r+A2)*r+A3)*r+A4)*r+A5)*r+A6)*q/(((((B1*r+B2)*r+B3)*r+B4)*r+B5)*r+1); return(x); } if(p<0.02425) // Rational approximation for lower region { q=sqrt(-2*log(p)); s=1; } else //if(p>0.97575) // Rational approximation for upper region { q = sqrt(-2*log(1-p)); s=-1; } x=s*(((((C1*q+C2)*q+C3)*q+C4)*q+C5)*q+C6)/((((D1*q+D2)*q+D3)*q+D4)*q+1); return(x); }
x[] dizesinin adresi fonksiyona girilir. Dize, ilk sırayı içerir. Sonraki parametreler, resp[] ve xscale[] çıkış dizelerine referanslardır. Fonksiyonun yürütülmesinden sonra sırasıyla X ve Y eksenlerinde grafiğin çizilmesi için kullanılan değerler dizilere yazılır. Daha sonra statParam yapısının adresi fonksiyona iletilir. Giriş dizisinin istatistiksel parametrelerinin önceden hesaplanmış değerlerini içermelidir. Hata durumunda ise -1 dönüşü yapar.
X ekseni için değerler oluştururken, ltqnorm() işlevi çağrılır. Normal dağılımın ters integral fonksiyonunu hesaplar. Hesaplama için kullanılan algoritma "Ters normal kümülatif dağılım fonksiyonunu hesaplamak için bir algoritma" adresinden alınmıştır.
Dört Grafik
İstatistiksel parametrelerin değerlerinin hesaplandığı dStat() fonksiyonundan daha önce bahsetmiştim. Kısaca anlamlarını tekrarlayalım.
Dağılım (varyans) – rastgele bir değerin matematiksel beklentisinden (ortalama değer) sapma karelerinin ortalama değeri. Rastgele bir değerin dağıtım merkezinden sapmasının ne kadar büyük olduğunu gösteren parametre. Bu parametrenin değeri ne kadar fazlaysa sapma o kadar fazladır.
Standart sapma – dağılım rastgele bir değerin karesi olarak ölçüldüğü için standart sapma genellikle dağılımın daha belirgin bir özelliği olarak kullanılır. Bu da dağılımın kareköküne eşittir.
Eğrilik – rastgele bir değerin dağılım eğrisini çizersek, çarpıklık, dağılım merkezine göre olasılık yoğunluğu eğrisinin ne kadar asimetrik olduğunu gösterecektir. Eğrilik değeri sıfırdan büyükse, olasılık yoğunluğu eğrisi dik bir sol eğime ve düz bir sağ eğime sahiptir. Eğrilik değeri negatif ise sol eğim düz, sağ eğim ise diktir. Olasılık yoğunluğu eğrisi dağılım merkezine simetrik olduğunda, eğrilik sıfıra eşittir.
Fazlalık katsayısı (basıklık) – olasılık yoğunluğu eğrisinin bir zirvesinin keskinliğini ve dağılım kuyruklarının eğimlerinin dikliğini tanımlar. Dağılım merkezine yakın eğri tepe noktası ne kadar keskin olursa, basıklığın değeri o kadar büyük olur.
Bahsedilen istatistiksel parametrelerin bir diziyi ayrıntılı olarak tanımlamasına rağmen, genellikle bir diziyi daha kolay bir şekilde karakterize edebilirsiniz - grafik şeklinde temsil edilen tahminlerin sonucuna dayanarak. Örneğin, bir dizinin sıradan bir grafiği, istatistiksel parametreleri analiz ederken elde edilen bir görünümü büyük ölçüde tamamlayabilir.
Yazının önceki bölümlerinde, normal olasılık ölçeğinde bir histogram veya grafik çizmek için veri hazırlamaya olanak sağlayan dHist() ve dRankit() işlevlerinden bahsetmiştim. Normal dağılım grafiği ile histogramı ve normal dağılım grafiğini aynı sayfa üzerinde görüntülemek, analiz edilen dizinin ana özelliklerini görsel olarak belirlemenizi sağlar.
Listelenen bu üç çizelge, bir diğeriyle desteklenmelidir - dizinin mevcut değerlerinin Y ekseninde ve önceki değerlerinin X ekseninde olduğu çizelge. Böyle bir çizelgeye "Lag Plot" denir. Bitişik göstergeler arasında güçlü bir korelasyon varsa, bir örneklemenin değerleri düz bir çizgide uzayacaktır. Ve örneğin rastgele bir diziyi analiz ederken, bitişik göstergeler arasında bir korelasyon yoksa, değerler tüm çizelgeye dağılacaktır.
İlk örneklemenin hızlı bir tahmini için tek bir sayfaya dört çizelge çizmeyi ve üzerinde istatistiksel parametrenin hesaplanan değerlerini görüntülemeyi öneriyorum. Bu yeni bir fikir değil; Burada bahsedilen dört grafiğin analizini kullanma hakkında bilgi edinebilirsiniz: "4-Plot".
Makalenin sonunda, s4plot.mq5 betiğini içeren ve bu dört grafiği tek bir sayfa üzerinde çizen "Dosyalar" bölümü bulunmaktadır. dat[] dizisi, betiğin OnStart() işlevi içinde oluşturulur. İlk sırayı içerir. Daha sonra dStat(), dHist() ve dRankit() fonksiyonları, grafiklerin çizilmesi için gerekli verilerin hesaplanması için çağrılır. Ardından vis4plot() işlevi çağrılır. Hesaplanan verilere dayanarak gnuplot komutları ile bir metin dosyası oluşturur ve ardından ayrı bir pencerede çizelgelerin çizilmesi için uygulamayı çağırır.
dStat(), dHist() ve dRankit() daha önce açıklandığından, bir dizi gnuplot komutu oluşturan vis4plot() işlevi, komut dosyasının tüm kodunu makalede göstermenin bir anlamı yoktur. herhangi bir önemli özellik ve gnuplot komutlarının açıklaması makale konusunun sınırlarının dışına çıkıyor. Buna ek olarak, gnuplot uygulaması yerine çizelgeleri çizmek için başka bir yöntem kullanabilirsiniz.
O halde s4plot.mq5'in sadece bir kısmını gösterelim - OnStart() işlevi.
//---------------------------------------------------------------------------- // Script program start function //---------------------------------------------------------------------------- void OnStart() { int i; double dat[128],histo[],rankit[],xrankit[]; statParam sp; MathSrand(1); for(i=0;i<ArraySize(dat);i++) dat[i]=MathRand(); if(dStat(dat,sp)==-1)return; if(dHist(dat,histo,sp)==-1)return; if(dRankit(dat,rankit,xrankit,sp)==-1)return; vis4plot(dat,histo,rankit,xrankit,sp,6); }
Bu örnekte, MathRand() işlevini kullanarak dat[] dizisini ilk verilerle doldurmak için rastgele bir dizi kullanılır. Komut dosyasının yürütülmesi aşağıdakilerle sonuçlanmalıdır:
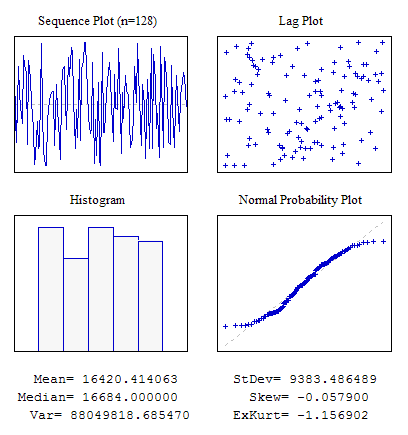
Şekil 3. Dört çizelge. Komut dosyası s4plot.mq5
vis4plot() fonksiyonunun son parametresine dikkat etmelisiniz. Çıktı alınan sayısal değerlerin biçiminden sorumludur. Bu örnekte, değerler altı ondalık basamakla çıkarılmıştır. Bu parametre, DoubleToString() işlevindeki biçimi belirleyen ile aynıdır.
Giriş sırasının değerleri çok küçük veya çok büyükse, daha belirgin bir görüntüleme için bilimsel formatı kullanabilirsiniz. Bunu yapmak için, örneğin bu parametreyi -5 olarak ayarlayın. -5 değeri, vis4plot() işlevi için varsayılan olarak ayarlanır.
Bir sıranın özelliklerini göstermek için dört çizelge yönteminin açıklığını göstermek için, bu tür dizilerin bir oluşturucusuna ihtiyacımız var.
Sahte Rastgele Sıra Oluşturucu
RNDXor128 sınıfı, sahte rastgele diziler oluşturmak için tasarlanmıştır.
Aşağıda, o sınıfı açıklayan kapsama dosyasının kaynak kodu bulunmaktadır.
//----------------------------------------------------------------------------------- // RNDXor128.mqh // 2011, victorg // https://www.mql5.com //----------------------------------------------------------------------------------- #property copyright "2011, victorg" #property link "https://www.mql5.com" #include <Object.mqh> //----------------------------------------------------------------------------------- // Generation of pseudo-random sequences. The Xorshift RNG algorithm // (George Marsaglia) with the 2**128 period of initial sequence is used. // uint rand_xor128() // { // static uint x=123456789,y=362436069,z=521288629,w=88675123; // uint t=(x^(x<<11));x=y;y=z;z=w; // return(w=(w^(w>>19))^(t^(t>>8))); // } // Methods: // Rand() - even distribution withing the range [0,UINT_MAX=4294967295]. // Rand_01() - even distribution within the range [0,1]. // Rand_Norm() - normal distribution with zero mean and dispersion one. // Rand_Exp() - exponential distribution with the parameter 1.0. // Rand_Laplace() - Laplace distribution with the parameter 1.0 // Reset() - resetting of all basic values to initial state. // SRand() - setting new basic values of the generator. //----------------------------------------------------------------------------------- #define xor32 xx=xx^(xx<<13);xx=xx^(xx>>17);xx=xx^(xx<<5) #define xor128 t=(x^(x<<11));x=y;y=z;z=w;w=(w^(w>>19))^(t^(t>>8)) #define inidat x=123456789;y=362436069;z=521288629;w=88675123;xx=2463534242 class RNDXor128:public CObject { protected: uint x,y,z,w,xx,t; uint UINT_half; public: RNDXor128() {UINT_half=UINT_MAX>>1;inidat;}; double Rand() {xor128;return((double)w);}; int Rand(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w;} return(0);}; double Rand_01() {xor128;return((double)w/UINT_MAX);}; int Rand_01(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++){xor128;a[i]=(double)w/UINT_MAX;} return(0);}; double Rand_Norm() {double v1,v2,s,sln;static double ra;static uint b=0; if(b==w){b=0;return(ra);} do{ xor128;v1=(double)w/UINT_half-1.0; xor128;v2=(double)w/UINT_half-1.0; s=v1*v1+v2*v2; } while(s>=1.0||s==0.0); sln=MathLog(s);sln=MathSqrt((-sln-sln)/s); ra=v2*sln;b=w; return(v1*sln);}; int Rand_Norm(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Norm(); return(0);}; double Rand_Exp() {xor128;if(w==0)return(DBL_MAX); return(-MathLog((double)w/UINT_MAX));}; int Rand_Exp(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Exp(); return(0);}; double Rand_Laplace() {double a;xor128; a=(double)w/UINT_half; if(w>UINT_half) {a=2.0-a; if(a==0.0)return(-DBL_MAX); return(MathLog(a));} else {if(a==0.0)return(DBL_MAX); return(-MathLog(a));}}; int Rand_Laplace(double& a[],int n) {int i;if(n<1)return(-1); if(ArraySize(a)<n)return(-2); for(i=0;i<n;i++)a[i]=Rand_Laplace(); return(0);}; void Reset() {inidat;}; void SRand(uint seed) {int i;if(seed!=0)xx=seed; for(i=0;i<16;i++){xor32;} xor32;x=xx;xor32;y=xx; xor32;z=xx;xor32;w=xx; for(i=0;i<16;i++){xor128;}}; int SRand(uint xs,uint ys,uint zs,uint ws) {int i;if(xs==0&&ys==0&&zs==0&&ws==0)return(-1); x=xs;y=ys;z=zs;w=ws; for(i=0;i<16;i++){xor128;} return(0);}; }; //-----------------------------------------------------------------------------------
Rastgele bir sıra oluşturmak için kullanılan algoritma, George Marsaglia'nın "Xorshift RNG'leri" makalesinde ayrıntılı olarak açıklanmıştır (makalenin sonundaki xorshift.zip'e bakın). RNDXor128 sınıfının yöntemleri, RNDXor128.mqh dosyasında açıklanmıştır. Bu sınıfı kullanarak, çift, normal veya üstel dağılımlı veya Laplace dağılımlı (çift üstel) diziler elde edebilirsiniz.
RNDXor128 sınıfının bir örneği oluşturulduğunda dizinin temel değerlerinin başlangıç durumuna ayarlandığı gerçeğine dikkat etmelisiniz. Böylece, RNDXor128 kullanan bir betiğin veya göstergenin her yeni başlangıcında MathRand() işlevini çağırmanın aksine, bir ve aynı sıra oluşturulacaktır. MathSrand() ve ardından MathRand() çağrılırken olduğu gibi.
Sıra Örnekleri
Aşağıda örnek olarak özellikleri ile birbirinden son derece farklı olan sıraların analizinde elde edilen sonuçları bulabilirsiniz.
Örnek 1. Eşit Dağılım Yasasına Sahip Rastgele Bir Sıra.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_01(); ... }
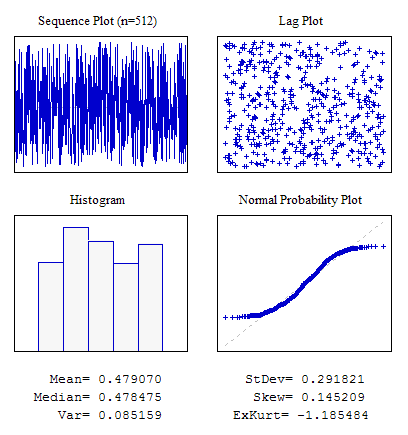
Şekil 4. Eşit dağıtım
Örnek 2. Normal Dağılım Yasasına Sahip Rastgele Bir Sıra.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Norm(); ... }
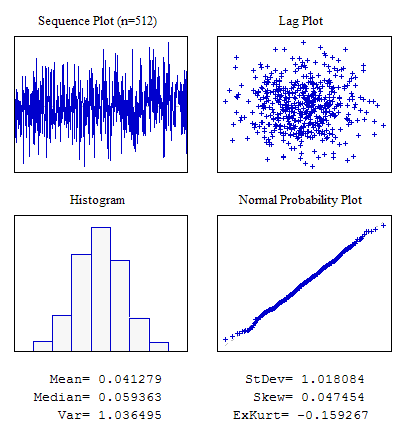
Şekil 5. Normal dağıtım
Örnek 3. Üslü Dağıtım Yasası ile Rastgele Bir Sıra.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Exp(); ... }
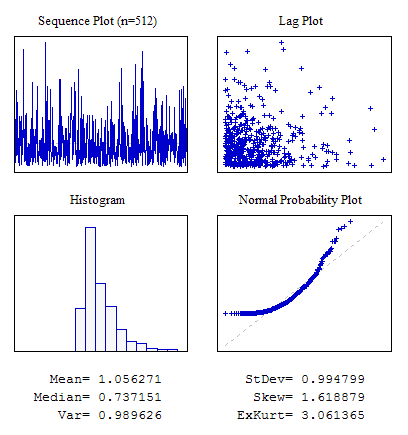
Şekil 6. Üslü dağıtım
Örnek 4. Laplace Dağılımı ile Rastgele Bir Sıra.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=Rnd.Rand_Laplace(); ... }
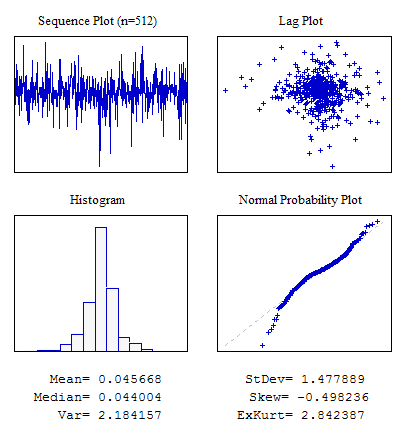
Şekil 7. Laplace Dağıtımı
Örnek 5. Sinüzoidal Sıra
//---------------------------------------------------------------------------- void OnStart() { int i; double dat[512]; for(i=0;i<ArraySize(dat);i++) dat[i]=MathSin(2*M_PI/4.37*i); ... }
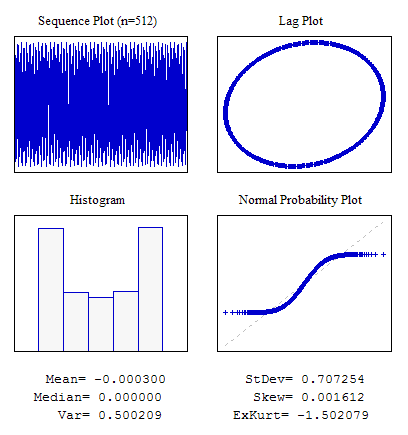
Şekil 8. sinüzoidal dizi
Örnek 6. Bitişik Göstergeler Arasında Görünür Korelasyona Sahip Bir Sıra.
#include "RNDXor128.mqh" RNDXor128 Rnd; //---------------------------------------------------------------------------- void OnStart() { int i; double dat[512],a; for(i=0;i<ArraySize(dat);i++) {a+=Rnd.Rand_Laplace();dat[i]=a;} ... }
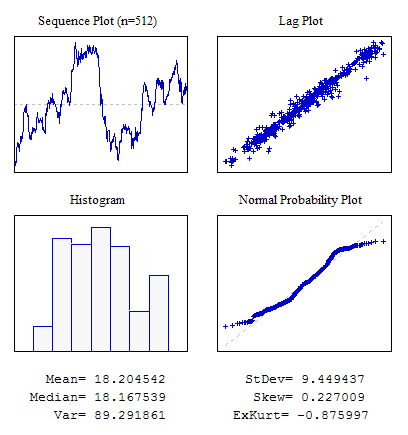
Şekil 9. Bitişik göstergeler arasındaki korelasyon
Sonuç
Her türlü hesaplamayı uygulayan program algoritmalarının geliştirilmesi her zaman zor bir iştir. Bunun nedeni, değişkenlerin yuvarlanması, kesilmesi ve taşması sırasında oluşabilecek hataları en aza indirmek için birçok gereksinimin göz önünde bulundurulması gerekliliğidir.
Makale için örnekler yazarken herhangi bir program algoritması analizi yapmadım. Fonksiyon yazılırken matematiksel algoritmalar "doğrudan" uygulandı. Bu nedenle "ciddi" uygulamalarda kullanacaksanız, kararlılıklarını ve doğruluklarını analiz etmelisiniz.
Makale, gnuplot uygulamasının özelliklerini hiç açıklamıyor. Bu sorular bu makalenin kapsamı dışındadır. Her neyse, gnuplot'un MetaTrader 5 ile ortak kullanım için uyarlanabileceğini belirtmek isterim. Bunun için kaynak kodunda bazı düzeltmeler yapıp yeniden derlemeniz gerekiyor. Gnuplot ile etkileşim bir programlama arayüzü aracılığıyla organize edilebileceği için buna ek olarak, bir dosya kullanarak komutları gnuplot'a iletme yolu muhtemelen optimal bir yol değildir.
Dosyalar
- erremove.mq5 – bir örneklemeden hataları hariç tutan bir komut dosyası örneği.
- function_dstat.mq5 – istatistiksel parametrelerin hesaplanması için işlev.
- function_dhist.mq5 - histogram değerlerinin hesaplanması için işlev.
- function_drankit.mq5 – normal dağılım ölçeğiyle bir grafik çizerken kullanılan değerlerin hesaplanması için işlev.
- s4plot.mq5 – tek bir sayfada dört grafik çizen bir komut dosyası örneği.
- RNDXor128.mqh – rastgele bir dizi oluşturucunun sınıfı.
- xorshift.zip - George Marsaglia. "Xorshift RNGs".
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/273
MetaTrader 5'te Kendi Kendini Düzenleyen Özellik Haritalarını (Kohonen Haritaları) Kullanma
Kaynak Kodun İzlenmesi, Hata Ayıklanması ve Yapısal Analizi
Uzman Danışmanlar İçin Özel Optimizasyon Kriterleri Oluşturma
MQL5'te İstatistiksel Olasılık Dağılımları
- Ücretsiz ticaret uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz